Impact of flat panel-imager veiling glare on scatter-estimation accuracy and image quality of a commercial on-board cone-beam CT imaging system

Abstract

Purpose: The purposes of this study is to measure the low frequency drop (LFD) of the modulation transfer function (MTF), associated with the long tails of the detector point spread function (PSF) of an on-board flat panel imager and study its impact on cone-beam CT (CBCT) image quality and scatter measurement accuracy.

Methods: Two different experimental methods were used to characterize LFD and its associated PSF of a Varian OBI flat-panel detector system: the edge response function (ERF) method and the disk transfer function (DTF) method. PSF was estimated by fitting parametric models to these measurements for four values of the applied voltage (kVp). The resultant PSF was used to demonstrate the effect of LFD on image contrast and CT number accuracy in CBCT images reconstructed from synthetic datasets, as well as, accuracy of scatter measurements with the beam-stop method.

Results: The MTFs derived from the measured ERF data revealed LFDs varying from 8% (at 60 kVp) to 10.5% (at 120 kVp), while the intensity of the long PSF tails was found to increase with increasing kVp. The veiling glare line spread functions derived from the ERF and DTF methods were in excellent agreement. Uncorrected veiling glare reduced contrast and the image intensity in CBCT reconstruction, near the phantom periphery (by 67 Hounsfield units in a 20 cm-in-diameter water phantom) and (to a smaller degree) near inhomogeneities. Use of the bow-tie filter mitigated these effects. Veiling glare also resulted in about 10%–15% overestimation of the scatter-to-primary ratio when measured with the beam-stop or beam-stop array method.

Conclusions: The long tails of the detector PSF were found to have a modest dependence of beam spectrum, which is reflected on the MTF curve LFD. Our findings show that uncorrected veiling glare can affect quantitative accuracy and contrast in CBCT imaging, based on flat panel imager. In addition, it results in overestimation of the scatter-to-primary ratio, measured with the beam-stop methods.

INTRODUCTION

The introduction of commercial cone-beam x-ray-computed tomography (CBCT) imaging systems into radiotherapy has the potential to dramatically reduce the impact of interfraction soft-tissue displacement on external beam and brachytherapy treatments. Linac-mounted CBCT units, employing flat panel imagers (FPI) may support daily adaptive interventions to minimize the impact of interfraction setup and tissue motion errors, while CBCT imaging during brachytherapy procedures could improve source placement accuracy. However, compared to fan-beam CT (FBCT), CBCT imaging is a relatively new modality with its own signature artifacts, including a much larger proportion of signal due to scatter, sensitivity to patient motion, and detectors with smaller dynamic range and efficiency. Streaking, signal nonuniformity, and poor soft-tissue contrast, evident on clinical CBCT images, arise from discrepancies, or mismatches, between the detector-response model assumed by analytic reconstruction algorithms and the physical process of CT signal formation.¹ Radiotherapy applications demand highly quantitative imaging performance, including excellent signal uniformity and low contrast structure visualization, so that soft-tissue structures can be accurately segmented by manual or automated techniques.

FPI performance is affected by many characteristics, including the linearity and gain of the pixel response, the effect of charge trapping, temperature, and image lag.² As a result, FPI projections require various correction and calibration procedures in order to preserve approximate proportionality between detector readings and local energy deposition. These procedures include dark field (offset) and gain correction, image lag correction, temperature correction, defect pixel detection/correction, and delta detector calibration.³ FPI nonlinear response artifacts that have been previously investigated in the context of CBCT include direct object scatter,^{4, 5, 6} temporal blurring due to ghosting, image lag, and charge trapping effects^{3, 7, 8} and fluctuations in pixel-specific gain corrections.³ A less well-investigated but potentially significant effect is FPI veiling glare, defined as the spreading of FPI signal from the site of energy impartation, giving rise to non-negligible detector signal at distances on the order of millimeters to centimeters away from the primary photon interaction sites. Veiling glare is distinguished from direct object scatter in that the causative ionizing or optical radiation scattering phenomena originate in the detector assembly. In contrast to the high frequency effects that reduce the sharpness with which the system images anatomic details, veiling glare is characterized by long tails on the detector point spread function (PSF), resulting in loss of uniformity and contrast in the reconstructed CT image. In terms of the modulation transfer function (MTF), it appears as abrupt reduction of the MTF curve at very low frequencies. Hence the term “low frequency drop” (LFD) will be used synonymously with “veiling glare” in this paper.

We hypothesize that veiling glare, along with direct object scattering and beam hardening, can introduce significant FPI system nonlinearity which is manifested by observable CT-image artifacts. Veiling glare-induced system nonlinearity arises from redistribution of FPI signal intensity from intensively irradiated detector regions into less intensively irradiated adjacent regions giving rise to field-of-view dependent detector readings, reduced object contrast which following CT image reconstruction, results in cupping, streaking, and signal nonuniformity artifacts similar to those due to object scatter.

Veiling glare has been extensively investigated in fluoroscopic imaging systems using image intensifiers, where it has been found to affect contrast and quantitative integrity.^{9, 10, 11, 12} Deconvolution of the images using a measured PSF has been shown to significantly increase contrast ratios.¹³ However, the characteristics and impact of veiling glare on clinical CBCT imaging has not been extensively studied. Several studies have reported on measurable LFD for indirectly detecting FPIs,^{14, 15, 16} the effect of veiling glare on contrast in FPI-based breast imaging,¹⁷ and deconvolution-based corrections for mammography x-ray projections.^{18, 19} Benitez et al.¹⁴ measured the MTF of two FPIs and found that deconvolving the CBCT projection data with the resultant detector PSF, prior to reconstruction, significantly improved contrast and contrast-to-noise ratio (CNR) in cases where the LFD is large. However, the extent of improvement was found to depend on the method of measuring the MTF and its associated LFD, which strongly affects the accuracy with which the PSF tails can be determined. Perhaps most directly relevant to our study is a recent paper²⁰ addressing the effect of “scatter-glare” on CBCT Hounsfield units accuracy.

The impact of veiling glare on scatter measurement have been previously noted.^{18, 19} Veiling glare will affect also the scatter measurements using any form of beam-stopper or other beam modulation devices, including beam-block array CBCT scanning to create patient specific scatter corrections.⁵

In the first part of this work, we use two experimental methods to characterize the veiling glare of the FPI of a commercial onboard CBCT imaging system in terms of MTF and LDF. In the second part, we use Monte Carlo simulated projection images to study the impact of veiling glare on CBCT image quality (namely contrast loss and image uniformity) and scatter measurement accuracy with the beam block method.

METHODS AND MATERIALS

System specifications

Experimental data were acquired on the Varian OBI CBCT imaging system (version 1.3), which is mounted on a Varian Trilogy Linac gantry for image-guided radiation therapy. The system includes an x-ray source with a 14° target operating at two focal spot sizes of 0.4 and 0.8 mm. The flat panel is a PaxScan Model 4030 CB, with 768 × 1024 pixels (in 2 × 2 binning mode) with 0.388 mm pitch. The CB 4030 FPI employs indirect detection, where x-ray photons are absorbed by the 0.6 mm thick scintillating layer of CsI:Tl, producing optical photons that are subsequently detected by an array of amorphous silicon (a-Si) photodiodes to form the image matrix. Single-gain mode gives a dynamic range of 14 bits, while dual gain readout increases the dynamic range to “pseudo 17 bits.” A 10:1 antiscatter grid (ASG) is positioned on the top of the detector system and a 0.5 mm aluminum layer covers the beam entrance area. The system is also equipped with a removable bow-tie filter (BTF), for better utilization of patient dose.²¹

Typically, 660 projection images are collected in a 1 min 360° rotation of the gantry. When large objects are scanned, the half-fan mode is used to increase the reconstructed area. In this mode the detector is laterally shifted by 14.8 cm, in a direction vertical to the rotation axis, to cover about half of the object volume. The half BTF is used in this mode to modulate the beam only to the direction that the detector is shifted.

Experimental characterization of veiling glare

Two different experimental techniques were employed to characterize the FPI veiling glare. In the first one, a theoretical model of the veiling glare PSF was fit to disk-transfer function (DTF) measurements, in which FPI readings at the center of the projection of a circular lead shield were measured as a function of disk diameter. In the second method, the edge-response function (ERF) was measured for four x-ray beam kVp settings for two purposes: to estimate the FPI MTF and to verify the PSF derived from the DTF measurements.

DTF measurements and parametric PSF model fitting

In the first approach, we estimated the detector PSF by fitting a parametric model to DTF measurements, as proposed by Seibert et al.¹¹ DTF_exp(d) is defined as following:

$${\mathrm{DTF}}_{\exp }\left(d\right)=\frac{S_{\exp }(x^{\prime },y^{\prime }|d)}{S_{\exp }(x^{\prime },y^{\prime }|0)},$$ (1)

where S_exp(x^′, y^′|d) is the experimentally measured projection image intensity (Sec. 2B3) at the center, x^′, y^′ of the FPI region shadowed by a lead disc of radius d and S_exp(x^′, y^′|0) is the corresponding intensity at the same point without the disc in place. (Seibert et al. actually uses the arithmetic inverse of DTF, which he terms the “contrast ratio”). The mathematical PSF model used to describe DTF is the following:¹¹

$$g_1\left(r\right)=(1-\rho )\frac{\delta \left(r\right)}{r}+\frac{\rho }{2kr}\exp (-r/k),$$ (2)

where r the radial distance from the origin; ρ and k are model parameters; and δ(r) is the Dirac function. In this equation, ρ is the fraction of imparted energy that is scattered, giving rise to veiling glare, while (1 − ρ) is the fraction that is locally absorbed at the interaction point. By integrating Eq. 2 over an infinite, constant-intensity radiation field, modulated in intensity by a finite opaque disc of radius d, we obtain

$${\mathrm{DTF}}_{\mathrm{fit}}\sim \rho \exp (-d/k),$$ (3)

implying that log(DTF_exp(d)) is a linear function of disc radius (as shown by Fig. 1). To better fit the slight concave shape of Fig. 1, that appears consistently at all kVps used in our measurements, we added a second exponential term¹⁰ to Eq. 2:

$$\begin{array}{ccc}\hfill g_2\left(r\right)& =& (1-{\rho }_1-{\rho }_2)\frac{\delta \left(r\right)}{r}+\frac{{\rho }_1}{2\pi k_{1}r}\exp (-r/k_1)\hfill \\ & & +\frac{{\rho }_2}{2\pi k_{2}r}\exp (-r/k_2).\hfill \end{array}$$ (4)

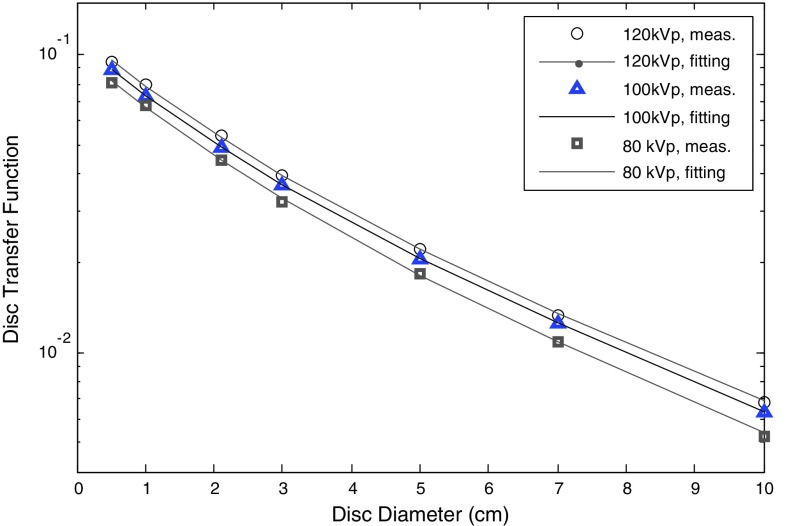
Figure 1.

DTF values as function of disc diameter for 80, 100, and 120 kVp.

The parameters ρ₁, ρ₂, k₁, and k₂ of every kVp were estimated by least squares fitting of the DTF measurements for each kVp to the area integral of Eq. 4. The zero-diameter detector signal, given by the sum ρ₁+ ρ₂, should be numerically equal to the LFD directly obtained from the corresponding MTF curve.²² Equation 3 assumes that the radiation field is infinite in size and constant in intensity. Neither of these assumptions is strictly valid in our measurements. The radiation field was collimated to 36 cm × 26 cm and was not constant in intensity due to the heel effect, inverse square law, and related effects. To include these effects and make the DTF model independent of the above assumptions, we generalized it to account for nonuniform and finite incident radiation fields. If the incident radiation field $I_{\mathrm{d}}^0(x,y)$, modulated in intensity by a lead disc of radius d, is imaged by the detector, the acquired image after dark signal and gain corrections $S_{\mathrm{d}}^{\mathrm{meas}}(x^{\prime },y^{\prime })$ will be given by the following 2D convolution:

$$S_{\mathrm{fit}}(x^{\prime },y^{\prime }|d)=\int \int I_{\mathrm{d}}^0(x,y)g_2(x^{\prime }-x,y^{\prime }-y)dxdy,$$ (5)

where g₂(x, y) is the detector PSF. To approximate $I_{\mathrm{d}}^0(x,y)$, the unattenuated, unmodulated field $I_0^0(x,y)$ was measured for each kVp and the pixels shadowed by each disc set to zero. The intensity of the convolved image at the projection of the disc center is then used to calculate the DTF according to DTF_fit(d) = S_fit(x^′, y^′|d)/S_fit(x^′, y^′|0).

The measurements were performed with seven lead discs of thickness 4.7 mm and diameters of 0.5, 1, 2, 3, 5, 7, and 10 cm placed in contact with the antiscatter grid, about 2 cm from the CsI layer and centered on the x-ray field central axis. The thin metallic front cover of the imager assembly was removed to avoid contaminant photons, created within it. The DTF for the larger disc (diameter of 10 cm) is 0.7% at 120 kVp, well inside the dynamic range of the imager. The disc thickness gives transmission of 2.7 × 10⁻¹² at 80 kVp and 9.4 × 10⁻⁶ at 125 kVp, assuming a Birch–Marshal spectral model²³ with an inherent filtration equivalent of 3.1 mm aluminum and using National Institute of Standards and Technology (NIST) attenuation coefficients.²⁴ Projection images of the discs were acquired in 2 × 2 binning mode for 60, 80, 100, and 120 kVp at 80 mA and 9 ms per projection. Twenty images for every disc size and kVp were averaged and corrected for offset and gain. The average signal in a 3 × 3 region of interest (ROI) at the center of each shadowed region was assigned to S_exp(x^′, y^′|d).

ERF acquisition and MTF calculation

The second method of characterizing the veiling glare consists of measuring an oversampled ERF and then mathematical processing it to obtain the LSF and the MTF. To acquire the ERF image, a 3 mm thick lead plate was positioned in contact with the antiscatter grid about 2 cm from the CsI layer. The thin metallic front cover of the imager assembly was removed to avoid contaminant photons, created within it. The machined edge of the plate was positioned according to the linear accelerator patient alignment lasers (1 mm accuracy at the isocenter), at the beam central axis at about a 1.5° angle with respect to the axis parallel to the long dimension of the detector pixel array. This angle corresponds to a pitch of about one pixel per 41 pixels. This tilted position of the edge is necessary to ensure oversampling, so the derived ERF will be sampled over a denser grid of sampling points, which is important for estimating high MTF frequencies. Although this study is mainly concerned with long PSF tails that can be sufficiently measured without oversampling, the tilted positioning of the edge is necessary to ensure that high frequencies are adequately sampled and do not introduce aliasing artifacts into lower frequency MTF estimates. The source-to-FPI distance and focal spot size were 150 cm and 0.4 mm, respectively. Projections were acquired at four tube potentials (60, 80, 100, and 120 kVp) at 80 mA and 9 ms per projection. For each tube potential, 30 projection images were acquired and corrected for offset and gain before averaged to reduce image noise. To reduce lag effects, the dark field image was updated between before and after acquiring images at each kVp, separated by a time delay of 3 min. A ROI of 4 cm (parallel to edge) by 14 cm (perpendicular to edge) and centered on the edge was extracted. The original edge-response data points were then plotted as a function of distance from the edge, yielding an oversampled ERF with 0.015 mm (slightly different at each kVp) spacing.

The MTF was derived from the oversampled ERF by two different approaches: numerical differentiation combined with the Fourier transform and fitting a parametric model to the acquired ERF. According to the first method,²⁵ the LSF is first calculated by numerically differentiating the ERF, yielding the LSF

$$\mathrm{LSF}\left(x\right)=\frac{d}{dx}\mathrm{ERF}\left(x\right),$$ (6)

The MTF is then obtained by computing the 1D Fourier transform of the LSF(x). After averaging the set of projections, we found that the noise at the ERF tail is small up to 3 cm distance from the edge, but rapidly increased at larger distances. At least 5 cm LSF tails were used to compute the MTF. The frequency axis is corrected for the sampling error caused by the tilted edge (the angle between the image axis and the edge was calculated by fitting a line at the points that correspond at the 50% points of the edge), while the MTF was normalized at zero frequency [MTF(0) = 1].

According to the second approach,^{26, 27} a parametric LSF model is fitted to the experimentally acquired oversampled ERF. This model describes the LSF as the weighted sum of a Gaussian (describing short range blurring) and an exponential (long range blur or veiling glare) terms:

$$\mathrm{LSF}\left(x\right)=\left(1-a_1\right)\exp \left(-\frac{x^2}{2a_2^2}\right)+a_1\exp \left(-a_3\left|x\right|\right),$$ (7)

where α₁, α₂, and α₃ are the model parameters. The LSF is normalized so that LSF(0) = 1. This method has the advantage that Fourier transform of Eq. 7, and hence the MTF, can be analytically calculated.

Projection data acquisition and preprocessing

The projection images were acquired by using the vendor's “IS3 Monitor” software. Raw projections, S_r(i, j), for the ERF, DTF, and scatter measurements below, were acquired at a rate of 30 frames/sec in 2 × 2 binning mode and a 0.4 mm focal size. The row projections were corrected for DC offset and pixel-to-pixel gain variations to obtain corrected images. The offset correction was made by subtracting the associated dark field image D_r(i, j), acquired before initiating data acquisition, while gain correction was performed by dividing by an offset-corrected flood field F_r(i, j) − D_F(i, j), where F_r(i, j) is the raw flood-field image and D_F(i, j) is its associated dark field. The gain correction mitigates the pixel-to-pixel variations in FPI gain; however, it also washes out the incident radiation field profile. As investigation of LFD effects requires an estimate of the absolute image intensity, we recovered this missing intensity information by multiplying the flood-field corrected image by an approximation to the unattenuated gain-corrected beam profile measured by detector to get the final corrected image, S_c(i, j). The estimated background and pixel-gain corrected beam profile, I_c(i, j), used by our study is given by

$$\begin{array}{c}\hfill S_c(i,j)=\frac{S_{\mathrm{r}}(i,j)-D_{\mathrm{r}}(i,j)}{F_{\mathrm{r}}(i,j)-D_{\mathrm{F}}(i,j)}·\left(F_{\mathrm{r}}(i,j)-D_{\mathrm{F}}(i,j)\right)\otimes n,\end{array}$$ (8)

where n(i, j) is a 2D Gaussian smoothing kernel, with σ = 30 pixels in both X and Y directions.

Impact of veiling glare on CBCT image quality

The redistribution of projection image intensity due to the veiling glare reduces the quantitative accuracy of the projection images, which is expected to affect the accuracy and uniformity of reconstructed CBCT image intensity. To assess these effects, we compared images reconstructed from Monte Carlo synthetic projections with and without the veiling glare effect included. The effects were quantified in terms of CT number accuracy, image uniformity, and contrast reduction. The CBCT geometry, assumed in these simulations was that of the Varian CBCT system, described in Sec. 2A, excluding the ASG.

To assess image uniformity and contrast we designed a numerical phantom consisting of a 20 cm water cylinder containing eight adipose tissue contrast inserts with diameters varying from 0.5 cm to 2 cm, positioned at the center and the periphery of the phantom [see Fig. 5a]. This tissue composition has a reference contrast of 13.8% at 60 keV.²⁴ Synthetic CBCT projection datasets of this phantom were computed for the Varian imaging geometry with and without the bow-tie filter as described below. An in-house 3D FDK²⁸ code was used to reconstruct CBCT image sets from the synthetic datasets. In order to evaluate the impact of the veiling glare on image quality near media boundaries within the phantom, another numerical phantom was designed consisting of a 20 cm diameter, 40 cm high water cylinder containing a second 2 cm diameter coaxial cylinder of cortical bone (linear attenuation coefficient of 0.604 cm⁻¹ at 60 keV).²⁴ The bone cylinder extends over only half of the water cylinder length, creating a high contrast sharp boundary in the isocenter plane. The impact of the veiling glare was assessed by evaluating transverse CBCT images, reconstructed from the corresponding synthetic dataset, as a function of distance from this boundary.

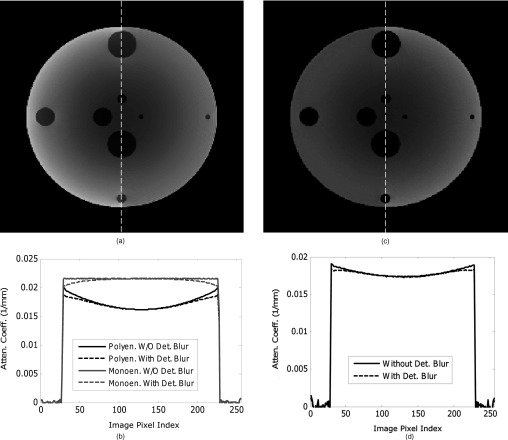
Figure 5.

(a) Split central slice image, reconstructed from synthetic projections computed without BTF with veiling glare (right half) and without (left half); (b) Profiles through images reconstructed from projections with and without veiling glare PSF convolution. No correction for scatter or beam hardening was made in the polyenergetic case while the monoenergetic simulation assumed perfect scatter compensation, (c) Split image, (veiling glare on right side, no veiling glare on left side), for polyenergetic projections with BTF; and (d) Same as (b) except for projection data assuming BTF.

The Monte Carlo code PTRAN_CT_proj^{29, 30, 31, 32, 33} was used to compute both primary and scattered photon projections, where the endpoint was ionizing radiation energy imparted to each detector element. A 0.6 mm thick compact CsI layer was assumed as the imager. The veiling glare effect was introduced into the projections by convolving the computed 120 kVp projection images with the measured PSF for the same (120) kVp accelerating potential, assuming it to be spatially invariant. The Monte Carlo projections were made by scoring the energy absorbed at the first, within the CsI layer, interaction point, of the primary photons and those scattered within the phantom or BTF, or in the air. Scatter and fluorescence photons, created within the CsI layer were not included. The reason is that we consider these photons have already contributed to the measured PSF, so they are included in the simulation by the convolution of Monte Carlo projections with it. The code used analytic ray tracing to compute primary photon projections over a 768 × 1024 array of 0.6 mm thick CsI pixels, while the corresponding scatter projections were computed on a coarser 1 cm × 1 cm grid of points and subsequently interpolated to fit the resolution of the primary component.³⁰ The simulations assumed a 120 kVp spectrum, computed by the Birch–Marshal model²³ assuming an inherent filtration equivalent to 3.1 mm of aluminum.

The FDK algorithm²⁸ was used to reconstruct 256 × 256 images with 1 mm isotropic pixels using a ramp filter. Image contrast was calculated by the following formula:

$$C=\frac{{\mu }_{\mathrm{ins}}-{\mu }_{\mathrm{wat}}}{{\mu }_{\mathrm{wat}}}\times 100,$$ (9)

where μ_ins and μ_wat are the reconstructed intensities of the contrast insert and the water outside the insert, calculated at a ROI of 5 × 5 pixels.

Assessment of veiling glare effects on scatter measurements

Beam-stop scatter measurement technique

Another effect studied here is the influence of veiling glare on accuracy of scatter projection measurements using the beam-stop technique. This technique uses circular lead discs of various diameters, placed on the top of the phantom with the beam normally incident on the block. Since the discs are thick enough to fully attenuate the primary beam, the projection image intensity in the block shadow is considered to consist of scatter signal only. The intensity at the same region in a projection acquired without the disc gives the total (scatter plus primary) intensity. Image intensity in the shadowed region depends on disc size, as well as phantom size and shape, since larger discs block larger volumes of phantom thus reducing the number of scattered photons created in the scan object. To correct for this effect, the scatter intensity or the scatter-to-primary ratio (SPR) for each disc is plotted as function of the disc diameter and the corrected intensity or SPR is obtained by extrapolating to zero disc diameter. Our hypothesis is that the blocked region detector signal will overestimate the signal due to scattered radiation originating in the scanned phantom, because of the veiling glare signal contribution from nearby unblocked regions of the FPI.

To evaluate veiling glare impact on scatter-profile and SPR measurement, beam-stop measurements and Monte Carlo simulations were performed. The measurements (120 kVp only) were performed on the AAPM CT performance phantom (a homogeneous 21.4 cm in-diameter water phantom with PMMA walls), with lead discs of 4.7 mm thickness and diameters varying between 0.5 cm and 10 cm positioned on its anterior surface. To correct for the effects of veiling glare, each measured projection, (corrected as described in Sec. 2B3), was deconvolved with the measured PSF g₂(x, y) [see Eq. 4]. The average detector reading in a 5 × 5 ROI at the center of disc shadow was taken as the scatter signal. SPR values were calculated from these projections before and after the correction for veiling glare.

To provide further verification of veiling-glare corrected beam stop measurements, Monte Carlo simulation was employed to compute projections of cylindrical water phantoms with and without lead discs. The simulation code and scoring technique, as well as, the imaging parameters are the same as outlined in Secs. 2C, 2A, respectively. The projection images were convolved with the measured detector PSF (for the same applied voltage-120 kVp) to account for the effects of the veiling glare. SPR values were calculated from these projections before and after convolution, to extract the impact of the veiling glare. Two cases were simulated: (1) a 20 cm diameter, 41 cm high cylindrical water phantom, acquired without ASG; (2) a 32 cm diameter, 41 cm high cylindrical water phantom acquired without ASG in the half-fan mode, where the detector is shifted by 14.8 cm vertical to the cylinder axis. No BTF was used/assumed in these measurement and simulations.

Beam-stop array technique

The beam-stop array technique is often used for SPR measurements, offering the advantage of obtaining scatter data at a grid of points on the detector area. According to this technique,^{4, 5, 34, 35} an array of small lead discs attached to Styrofoam or acrylic sheet is placed between the x-ray source and the object to be imaged. The discs are thick enough to effectively block the primary radiation in the shadowed regions, where the detected intensity is assumed to consist solely of the scatter signal. The distribution of total (primary and scattered) radiation is taken by a second projection acquired without the beam stop array.

Similar to the beam-stop method, the disc array blocks part of the beam, reducing the scatter created within the scan subject and subsequently the detected scatter intensity. To correct for this, the projection image intensity in the shadowed regions must be increased by the ratio of blocked to unblocked fluence to give the scatter level that would be acquired without the beam-stop array.

To quantify the effect of the veiling glare on beam-stop array measurements, we used Monte Carlo projections to simulate the case of a 20 cm diameter water phantom. The beam blocker consists of an array of 2 mm diameter and 3 mm thick lead discs arranged with 1 cm center-to-center spacing and positioned 25 cm below the x-ray source. The simulation code and scoring technique, as well as, the imaging parameters are the same as outlined in Secs. 2C, 2A, respectively. Based on geometrical considerations (comparing the area of a disc with that of a unit 1 cm × 1 cm cell), the beam-stop array blocks the 3.1% of the beam area. According to the Monte Carlo simulation, the beam-stop array reduces scatter by 3.9%. Since this study focuses on the effect of the veiling glare on the scatter measurement, the Monte Carlo calculated reduction factor of 3.9% was used to correct the beam-stop array measurements. No ASG or BTF was assumed in these simulations.

RESULTS

PSF and MTF measurements

Figure 1 presents the measured and the fitted DTF for 80, 100, and 120 kVp. For 120 kVp, the DTF varies from 0.95 × 10⁻¹ for the 0.5 mm disc to 0.7 × 10⁻² for the 10 cm disc. The parameters of the PSF model of Eq. 4, determined by fitting it to the DTF measurements, are presented in Table 1. The two-term PSF model supports excellent fits to the data, with average RMS difference between measurements and PSF model of less than 0.1%.

Table 1.

Numerical values of the parameters of Eq. 4, determined by fitting on the DTF data. (Average beam energies were calculated by using the Birch–Marshall model and filtration of 3.1 mm of Aluminum for all beams.)

kVp	Average energy (keV)	ρ1	k1 (cm)	ρ2	k2 (cm)	ρ1 + ρ2
120	56.1	0.058	2.45	0.060	0.90	0.118
100	50.8	0.053	2.45	0.056	0.90	0.109
80	44.6	0.045	2.43	0.055	0.96	0.100
60	37.2	0.044	2.40	0.051	0.97	0.095

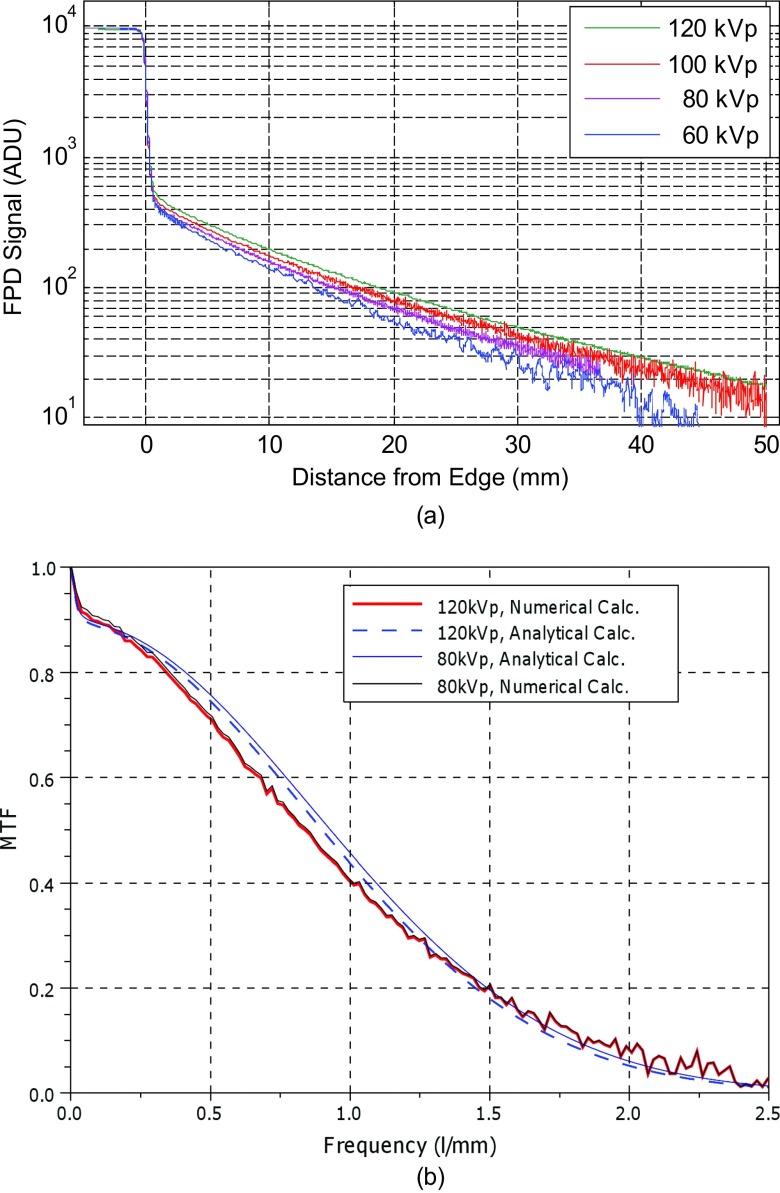
Figure 2a presents the acquired ERFs for the four tube potentials. The intensity of the ERF tails increases with kVp value by about 7%–8% for each 20 kVp increase. At 2 cm distance from the edge, the image intensity ranges between 0.5% (for 60 kVp) and 0.9% (120 kVp) of the unattenuated field intensity. Figure 2b presents the numerically [by Fourier transform on the left side of Eq. 6] calculated MTF for 80 and 120 kVp. LFDs of about 9% and 10.5% are found for 80 and 120 kVp, respectively. The LFD is larger for the 120 kVp since the ERF tail for this potential has higher intensity than that of 80 kVp. The LSF model parameters [see Eq. 7] that best fit the measured ERF are [a₁, a₂, a₃] = [3.31 × 10⁻³, 0.195 mm, 9.9 × 10⁻² mm⁻¹] for 120 kVp and [2.9 × 10⁻³, 0.189 mm, 9.7 × 10⁻² mm⁻¹] for 80 kVp. The MTFs analytically derived [by Fourier transform on the LSF model of Eq. 7] from the above best-fit parameters have slightly different shapes than the numerically derived MTFs (difference of 0.03 at 1 l/mm for 120 kVp); however, LFD estimated by the two approaches are in close agreement. The LFDs for 60 kVp and 100 kVp (MTF curves are not shown here) are 8.5% and 10%, respectively. In agreement with the DTF measurement trends, higher kVp results in larger LFD. The zero-diameter detector signals in DTF measurements, given by ρ₁ + ρ₂ are about 1% higher than the LFDs extracted by the ERF measurements. No systematic dependence of the high-frequency MTF on kVp was found.

Figure 2.

(a) Measured ERFs for four beam energies, and (b) MTF curves calculated numerically and by LSF fitting for energies 80 and 120 kVp.

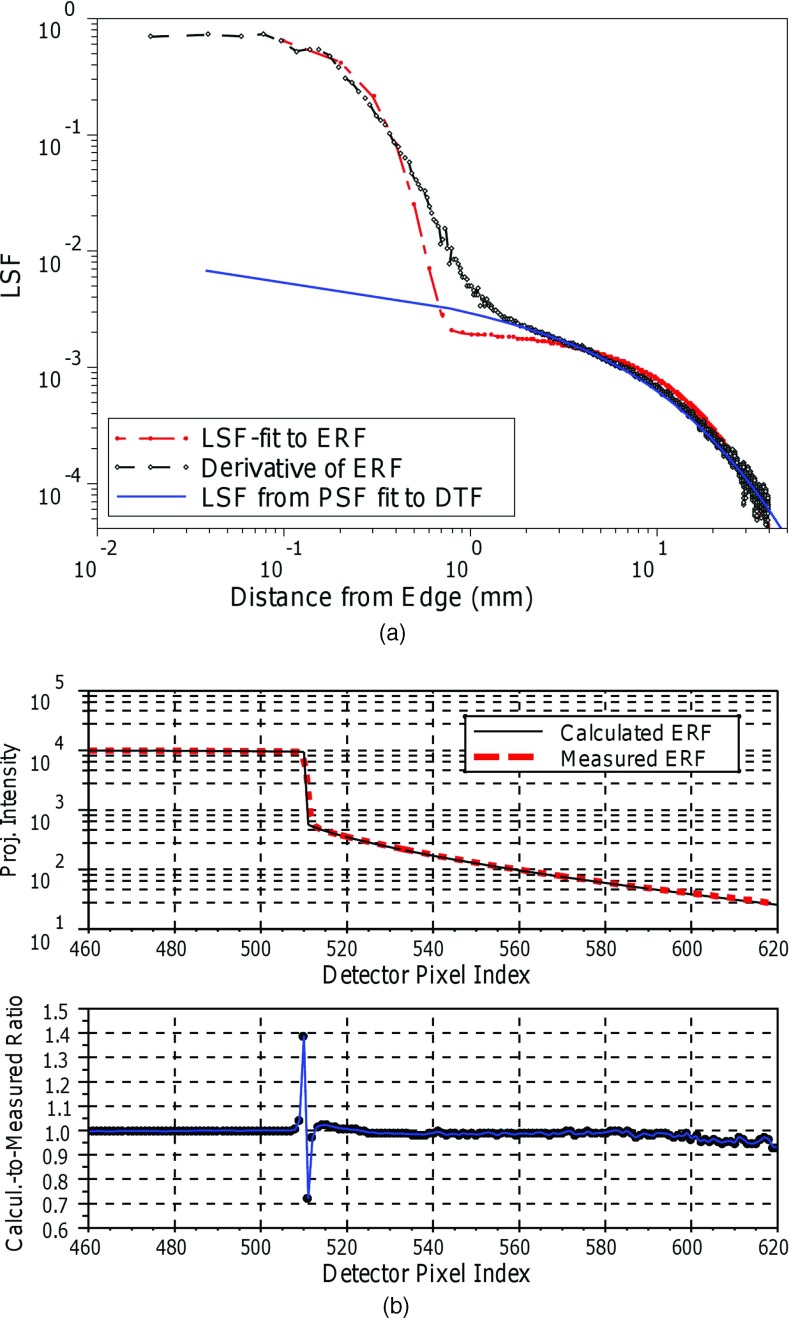
Figure 3a compares the LSFs, derived from the curve fits to the DTF and ERF measurements with the LSF obtained by direct differentiation of the ESF for 120 kVp. The LSF profile derived from fitting Eq. 7 to the measured ERF agrees with the one calculated by differentiating ERF, except at distances near 1 mm from the edge. The LSF derived from the DTF measurements [by applying a numerical Abel transform to the PSF of Eq. 4] matches the LSFs derived from ERF reasonably well at distances exceeding 1 mm, since the DTF method approximates the high spatial frequency response of the detector by a single delta function at zero distance. For distances greater than 2 mm, the DTF-derived LSF better matches (within 5%) the LSF tail obtained by differentiating the measured ERF compared with the LSF tail from the Gaussian-exponential LSF fit to the ERL, which deviates by as much as 19%. Figure 3b shows the modeled ERF predictions for 120 kVp [derived from the Eq. 4 fit to the ERF measurements] matches the ERF measurements within 7% for all pixels, except those at the edge.

Figure 3.

(a) Comparison of the LSF models derived from fitting Eq. 7 to ERF measurements (red); fitting Eq. 4 to the DTF measurements (blue); and direct differentiation of the ERF (black) for 120 kVp. Because of the logarithm scale at the x-axis, the delta peak of the LSF derived by Eq. 4 is not shown at 0 mm. (b) Ratio of ERF derived by direct and ERF derived from LSF fit.

Effect of veiling glare on reconstructed images

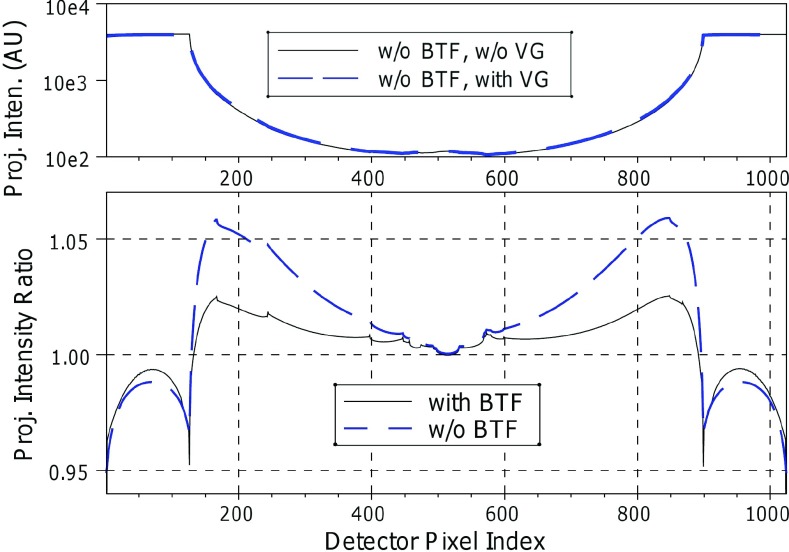
Figure 4 presents the effect of the veiling glare on synthetic projections of the water phantom derived from Monte Carlo simulation in terms of the ratio of the projection intensity with and without the veiling glare effect. Veiling glare leaves the projection image intensity at the center of the projection unchanged and increases it by 6% near the phantom edge, when BTF is not used and by 2% when BTF is used. The Monte Carlo simulation gives a SPR = 0.85 at the projection of the phantom center for the 20 cm axial field height.

Figure 4.

FPI central-plane transverse profiles before and after convolution and ratio of the profiles with veiling glare to that without veiling glare, showing the detector signal change with and without BTF.

Figures 5a, 5b show the changes in images reconstructed from synthetic projection data, computed without BTF, with and without veiling glare. When veiling glare is not included in the polyenergetic projection data, an oblique image profile through the water (not passing through inserts) shows cupping artifact (18%), caused by scatter and beam hardening [Fig. 5b]. When veiling glare is included in the data model, the image intensity near the phantom edge is reduced by up to 6.7% (from 0.205 × 10⁻¹ mm⁻¹ to 0.191 × 10⁻¹ mm⁻¹), improving the flatness of the image. This reduction corresponds to 67 Hounsfield units. Figure 5b also presents profiles from image reconstructed by monochromatic (56 keV), scatterless data (thus isolating the veiling glare effect in the absence of cupping from scatter and beam hardening), showing that veiling glare reduces image intensity by 6.5% (from 0.216 × 10⁻¹ mm⁻¹ to 0.202 × 10⁻¹ mm⁻¹) near the phantom edge. This reduction, corresponding to 65 Hounsfield units produces a small inverse cupping effect that is of opposite direction to the typical beam hardening and scatter effect. Figures 5c, 5d show reconstructed images and profiles from synthetic projections computed assuming a BTF, polyenergetic beam (120 kVp) and including scatter. The reduction in image intensity near the phantom edge is 2.9%, less than half of that found without the BTF. In both cases (projection data acquisition with and without BTF), the reduction of cupping artifact magnitude is compatible with the elevated projection signal intensity near the projection of the phantom edge [Fig. 4a].

Table 2 presents the contrast values of the 2 cm adipose tissue insert. In all cases, the contrast at periphery is better (only slightly so when BTF is used) than at the phantom center. When no BTF is used, veiling glare reduces the contrast by 13.1% near the phantom edge and by 10% at the phantom center. When the BTF is used, veiling glare-mediated contrast reduction is a more uniform 9%.

Table 2.

% contrast values in reconstructed images of the water phantom with 2 cm adipose tissue contrast inserts. Projection data were computed with and without use of the BTF, while veiling glare is introduced to the data by convolving the synthetic projections with the measured detector PSF. Simulated tube voltage: 120 kVp.

	Projection data without BTF			Projection data with BTF
	Projections without	Projections with		Projections without	Projections with
	veiling glare	veiling glare	% change	veiling glare	veiling glare	% change
Center	10.9	9.8	−10.1	12.8	11.6	−9.4
Periphery	13.0	11.3	−13.1	13.2	12.0	−9.1

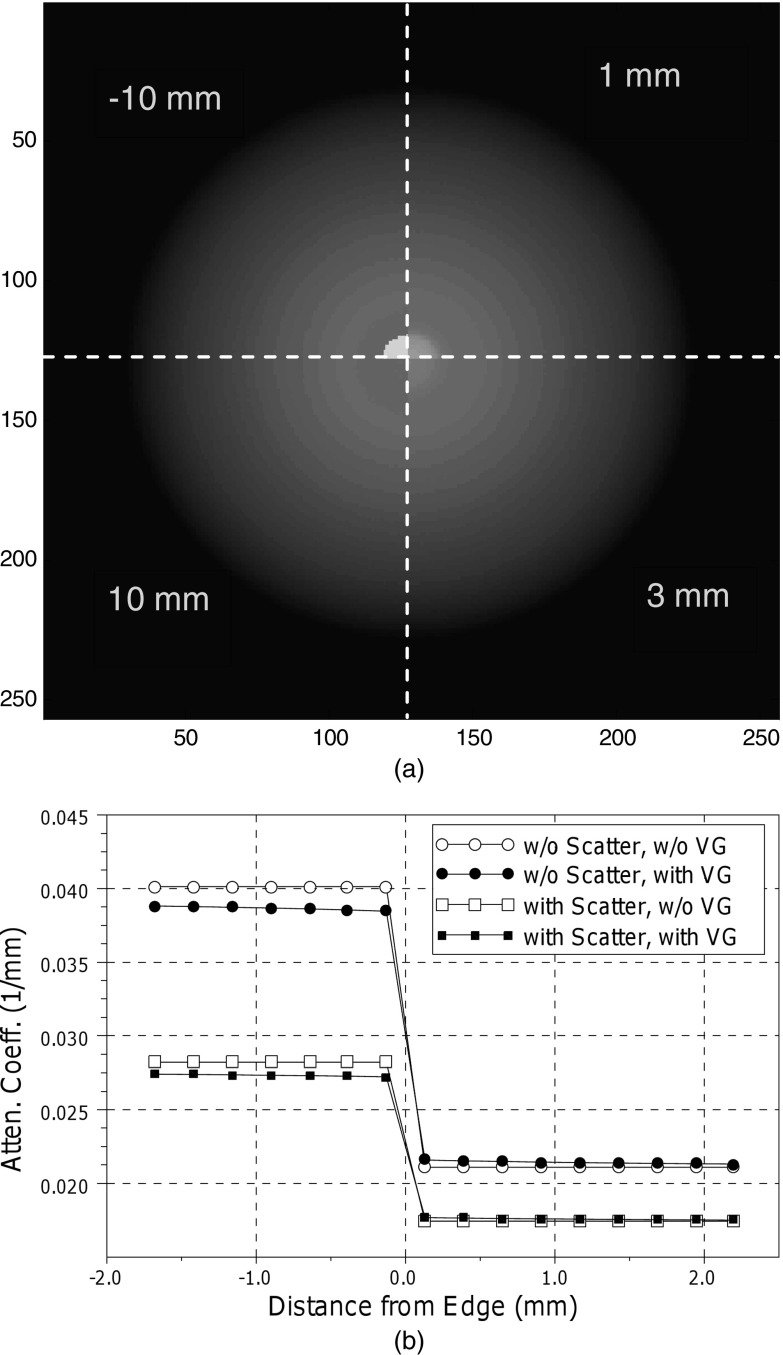
Figure 6 shows the impact of veiling glare on image quality near a high contrast boundary, assessed with the cylindrical water phantom containing a coaxial cylinder of cortical bone. In each of its quadrants, Fig. 6a presents reconstructed images in planes at different axial distances from the bone insert edge. The presence of the higher image intensities at planes passing through water only (noted in the figure by their distances from the inner cylinder edge, 1 mm, 3 mm, and 10 mm) is due to the redistribution of intensity in the projection data by the veiling glare effect. Figure 6b shows profiles of the reconstructed intensity along the central axis. The veiling glare reduces the reconstructed attenuation coefficient both in points within the bone cylinder (negative x-axis indices in the plot) and in water. This reduction is about 2.3% at 0.5 mm from the bone edge and decreases at larger distances.

Figure 6.

(a) Transverse-plane images at the noted axial distance from the bone insert edge reconstructed from synthetic projections including the effect of the veiling glare. The four quadrants of the image show reconstructed planes at the indicated axial distances from the bone insert edge. (b) Reconstructed water attenuation coefficient versus axial distance from the bone insert edge. The coefficients are sampled along the axis of the cylindrical insert.

Impact of veiling glare on scatter-measurement accuracy

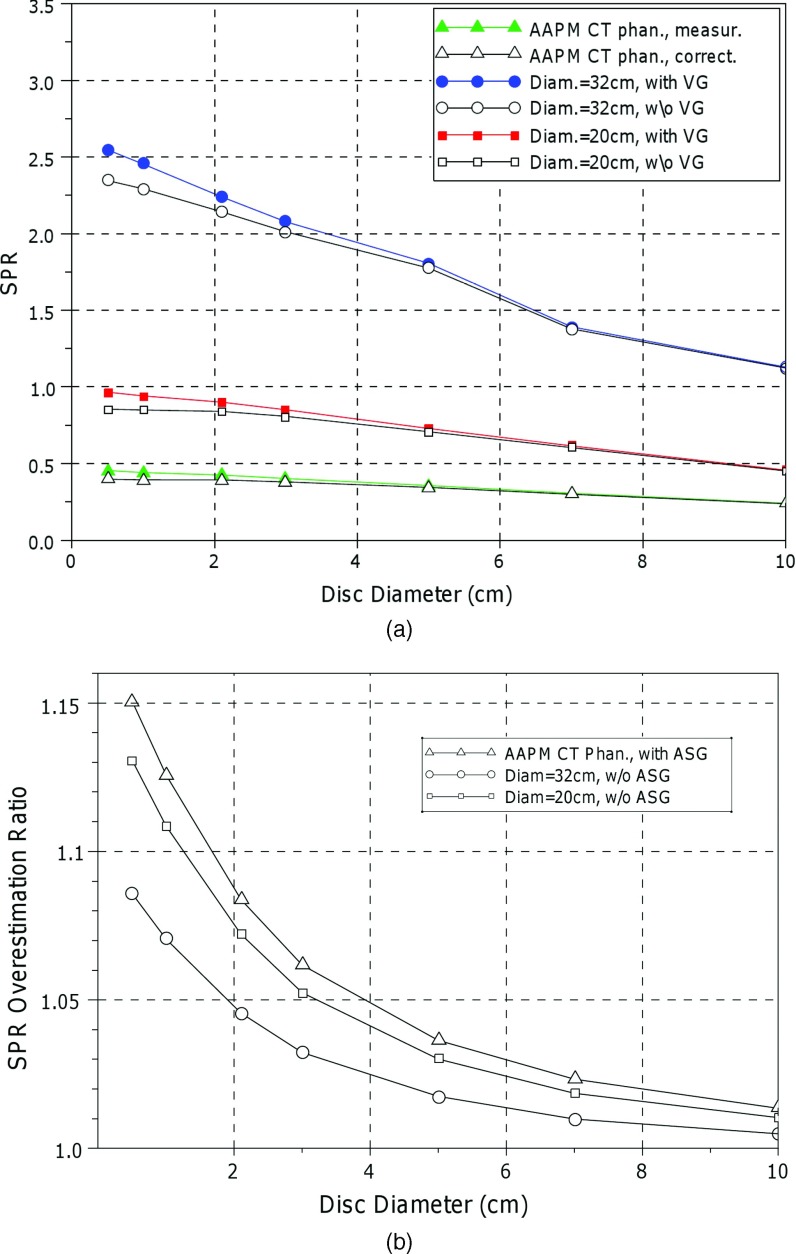
Figure 7 shows the effect of the veiling glare on the scatter measurement with beam stop technique. Figure 7a shows SPR measurements (AAPM CT performance phantom) and simulations with and without accounting for veiling glare, while Fig. 7b presents the ratio of SPR overestimation (SPR_wVG/SPR_w/oVG) due to the veiling glare. For the calculation of SPR, the primary radiation is given from the total signal by subtraction of the measured scatter. Failure to mitigate veiling glare by deconvolving the AAPM phantom projections with the PSF results in SPR overestimation by as much as 15% for the 0.5 cm diameter disc [Fig. 7b]. Monte Carlo-based synthetic projections reveal a similar veiling-glare induced overestimation of SPR. In both measurement and simulation, the SPR overestimation is larger for small disc diameters, since DTF is also larger (Fig. 1) for small diameters. Figure 7b shows also that the SPR overestimation is larger for small SPR values. By linearly extrapolating SPRs of Fig. 7a to zero diameter, it is found that the veiling glare increases the SPR from 0.87 to 1.01 (+16%), for the 20 cm water phantom without the ASG (simulation) and from 0.4 to 0.456 (+14%) for the measurements with the AAPM CT performance phantom (where the Varian OBI ASG was included in the setup). For simulated half-fan acquisition projections from the 32 cm phantom, the SPR overestimation is 9.4% (2.7 from 2.47).

Figure 7.

Demonstration of the impact of veiling glare on SPR measurements, uncorrected for scatter-volume blocking effects. (a) SPR values for a single beam stop of variable diameter extracted from synthetic projections calculated from Monte Carlo simulation with and without the veiling glare effect included. (b) Data from Fig. 7a presented as a ratio, illustrating SPR overestimation due to the veiling glare.

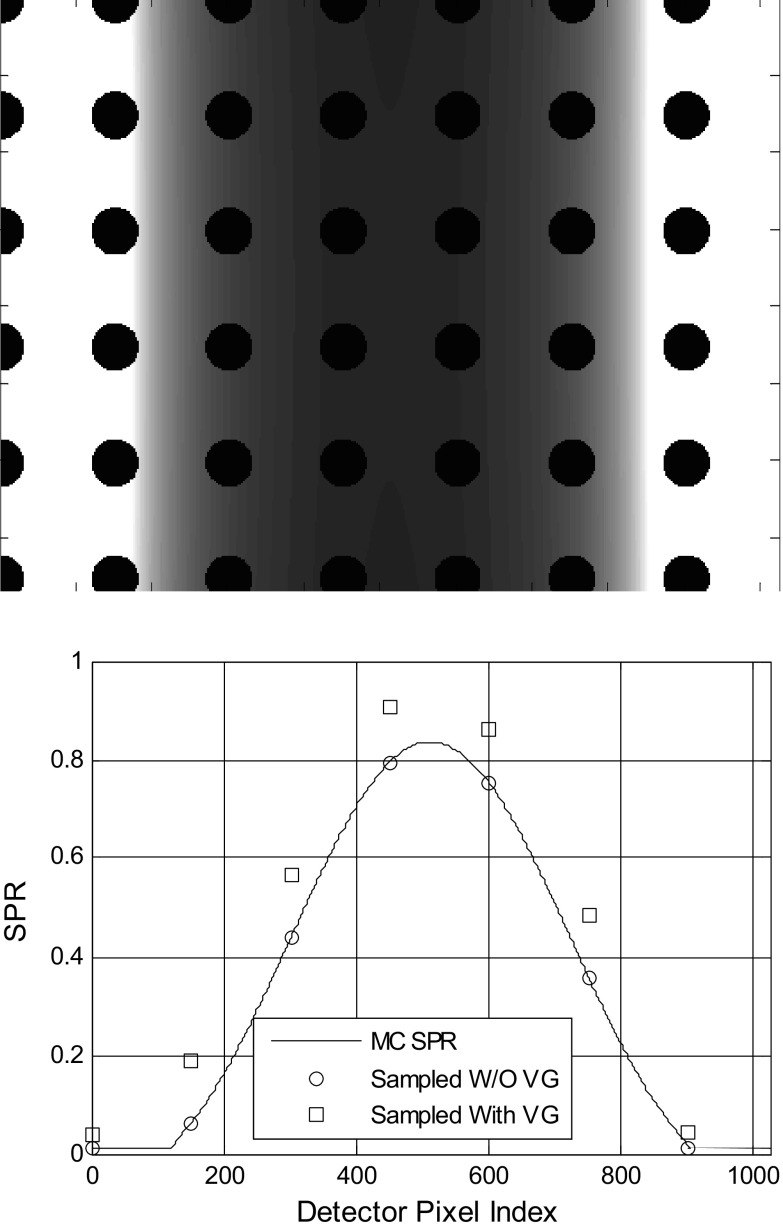
Figure 8a shows a Monte Carlo projection of the cylindrical water phantom, acquired with a beam-stop array. Figure 8b compares the central-slice SPR profile, derived from computed projections with and without the veiling glare included via PSF convolution. When veiling glare phenomenon is omitted from the synthetic projections, the resultant SPR profile (corrected for beam blocking by increasing the scatter signal by the 3.9% scatter underestimation factor, as discussed in Sec. 2D2) agrees within 1% with the SPR profile calculated by Monte Carlo simulation without the beam-stop array. Conversely, when veiling glare effects are simulated, SPR values are elevated by 0.13. Veiling glare inflated SPR measurements by both increasing the scatter signal and underestimating the primary radiation signal which is given by subtracting the scatter signal from the total signal.

Figure 8.

(a) A Monte Carlo projection of the water phantom, with a beam-stop array of 2 mm diameter discs without BTF and ASG. (b) Comparison between the calculated SPR with and without the veiling glare taken into account. The continuous curve corresponds to the SPR calculated by Monte Carlo simulation, without the beam-stop array.

DISCUSSION

The LFD for the PaxScan 4030-CB FPI, derived either by Fourier analysis of the measured ERF or fitting the measured ERF to a model, was found to range from 8% to 11% for x-ray tube potentials ranging from 60 to 120 kVp. Both data analysis approaches revealed a small but measurable dependence of MTF curve shape and LFD on applied kVp. In agreement with the findings for image intensifiers,¹¹ our data showed a trend to larger LFDs as energy is increased. This trend was also evident in the DTF measurements, where the DTF for 120 kVp are about 15% higher than those of 80 kVp. However, this is in contrast with Ref. 20, where the LSFs were not found dependent on the applied kVp.

As demonstrated by Fig. 2(d), both DTF and ERF measurements give similar estimates of the long LSF tails responsible for the veiling glare-associated artifacts phenomenon. However, because neither the DTF experimental technique nor the adopted PSF model [Eq. 4] account for FPI high spatial frequency response, the DTF-derived LSF differs from that measured by ERF by as much as ten fold at sub-mm distances. The ERF method uses only one projection and is more robust to noise (since a large number of pixels are used to fit the exponential term), while the DTF method is more sensitive to the dark-field correction variations, especially for large disk diameters, where the detector signal is very small. However, the DTF method does not require flood-field correction and correction for x-ray beam nonuniformity, since none of these corrections changes the DTF as defined in Eq. 1.

Analysis of images reconstructed from synthetic projection data demonstrates that the long PSF tails caused by the veiling glare significantly affect accuracy of the reconstructed image intensities. Veiling glare depresses image intensity (up to 67 Hounsfield units for the 20 cm water phantom) near the phantom edges when the BTF is not used. In contrast to scatter and beam hardening artifacts, which preferentially reduce contrast at the center of the reconstructed object, veiling glare tends to reduce contrast more at the object periphery. This is explained by the proximity of the projected phantom periphery to the regions of unattenuated beam intensity and the subsequent intensity contamination from these regions. Since the BTF typically reduces the difference between the high and low intensity detector regions by factors of 5–10, it reduces veiling glare-induced contrast degradation. This is in agreement with reports of improved skinline reconstruction profiles when the BTF is used.³⁶ A related study³⁷ found that the magnitude of veiling glare is approximately equivalent to (but of opposite direction) uncorrected beam-hardening artifacts. For CBCT images to achieve freedom from cupping, Hounsfield unit nonlinearity, and streaking artifacts comparable to that of standard FBCT imaging, this study suggested that both hardening spectral and veiling glare deconvolution preprocessing corrections are necessary. Our findings qualitatively agree with those of Ref. 20 in that the veiling glare reduces in general the Hounsfield numbers of the reconstructed images.

A less significant but still observable effect is blurring of reconstructed image intensities near high contrast boundaries in the direction parallel to the gantry rotation axis. In our study, the presence of the bone insert results in a small increase in the reconstructed value of water showing that the 3D PSF, which is a combination of the detector PSF, the x-ray source and the reconstruction filter,³⁸ has long tails too, though its effect regarding the object inhomogeneities is less important.

Perhaps the most immediate clinical application of our work, given the current interest in CBCT scatter mitigation, is improving the accuracy of beam-stop scatter measurements. Projections uncorrected for veiling glare were found to result in SPR overestimation by 10%–15%, for typical CBCT object dimensions and techniques using single discs or arrays of beam-stop discs. This overestimation is larger for smaller SPRs. Veiling glare also complicates analysis of beam-stop measurements. Our MC simulations show that when veiling glare is mitigated, i.e., by deconvolution of experimentally acquired projections, extrapolation of the SPR to zero beam-stop disc diameter is more robust, since the unblocked to blocked intensity varies linearly with disk blocking ratio compared to the nonlinear variation characteristic of uncorrected projections. This is in agreement with the findings in literature,^{18, 39} where it is reported that extrapolation to zero diameter with linear and logarithmic regression give different results. Deconvolution of projections with via the measured veiling-glare PSF, is expected to restore, to a certain degree, the linear convergence of the SPR to zero beam-stop disc diameter, as well as, the quantitative accuracy to scatter measurements made with the beam-stop devices.

An important issue is whether deconvolution with the veiling glare PSF can restore the quantitative accuracy of the projection data (or of the reconstructed images, when performed with the corresponding PSF). In addition to possible spatial and angular variance over the detector area, our findings show that the veiling glare PSF depends on beam energy, suggesting that the PSF tails will be longer near the phantom center where increased phantom attenuation hardens the primary spectrum. On the other hand, using a BTF would be expected to make the spectrum exiting the patient more uniform, contributing to increased spatial invariance of the deconvolution filter.

We conclude this discussion with a review of the approximations and limitations of our study. There are a number of factors, several of which merit further study, that contribute to uncertainty of ERF and DTF veiling-glare characterizations and derived image-quality or scatter corrections. Neither the DTF nor ERF measurements used collimation to diminish off-focal radiation. Thus scatter from the x-ray source mounting, filters, and air have likely affected our measurements to a small but unknown extent. In addition, the accuracy of PSF measurement may have been affected by the 2 cm distance between the CsI detector plane and the detector cover upon which both lead plate and discs were positioned for the measurements. For example, Illers et al.⁴⁰ found that a 2.8 cm gap reduced the MTF by about 10%. However, his measurements utilized a large 4 cm aluminum filtration, which is unusual in clinical practice. The ASG could also affect the measurement accuracy, since scattered and fluorescence originating in the ASG might contribute to signal intensity in blocked regions. Also, the one-dimensional ASG geometry could violate the circular symmetry assumed by the parametric PSF model. FPI signal linearity was also assumed in measurements. A significant error component is propagation of uncertainty, caused by drift and fluctuations in dark- and flood–field corrections, which could have significantly affected the accuracy with which low intensity signals, e.g., those shadowed by beam blockers, were estimated. Error in dark field, because of the time interval between the dark field acquisition and the ERF measurement, could result in ERFs that are almost constant at large distances from the edge, or even of negative value. In our measurements, the high noise characteristic of very low signals was the main reason for discarding data at large distances from the edge. The normalization method [Eq. 8] may also affect the accuracy. However the close agreement between the LSFs acquired by the two methods that implement different combinations of the above corrections indicates that the effect of the above parameters did not significantly affect our measurements.

Our work is based on measurements and simulations on a specific CBCT system, the Varian Medical Systems on-board imaging system, one specific FPI, one narrow set of image acquisition parameters, and limited generic phantoms. However, our study gives insight into the multiple effects of veiling glare on image quality and scatter-measurement accuracy that are applicable to other FPI-based systems. Our investigation of the veiling glare impact on the Hounsfield numbers accuracy is based only on simulated data without direct experimental confirmation. These findings however are in qualitative agreement with the recently published experimental study²⁰ on Hounsfield numbers accuracy for the Elekta Synergy CBCT system. We chose a simulation strategy in order to isolate the effects of the veiling glare from those of other system nonlinearities. Since the effects of the veiling glare are superimposed upon those from scatter and beam hardening, it would be difficult to experimentally distinguish between them and to quantify effects in isolation. For example, limiting the x-ray field to few centimeters in the axial direction could effectively reduce the scatter in the CBCT projections and its effect in the reconstructed images. However, this will reduce projection intensity in the regions of unattenuated beam, because of the leak of image intensity in the axial direction. Experimental results³⁷ show that when scatter and beam hardening corrections are combined with veiling glare deconvolution, the resultant reconstructed images are more uniform than when scatter and beam hardening corrections alone are applied to measured OBI projections.

Another approximation assumed by our simulations (Secs. 2C, 2D) is that the PSF, derived from central axis measurements, is applicable everywhere in the FPI plane, despite off-axis photon-spectrum variations. For example, in the absence of a BTF, the average energy of absorbed photons is expected to be higher at the projection of the phantom center than at its periphery thereby compromising spatial invariance of the PSF. However, as Fig. 3a shows, the veiling glare effects are more evident at the object periphery, where the above kVp value is a good approximation. The PSF dependence on the spectrum may need to be taken into account in optimizing CBCT outcome in terms of applied kVp and filtration.

Our study is empirical and is not designed to elucidate the underlying mechanisms that give rise to veiling glare. Off-focus radiation from the x-rays source, scatter, and characteristic radiation from the blades, the ASG, and other high atomic number materials in the imager assembly may contribute to this effect. The PSF dependence on kVp, while modest, is suggestive that part of the effect is x-ray scatter. Another hypothesis is that the effect is caused by the spread/reflection of optical photons within the CsI layer and the glass substrate (despite the needle structure of the CsI crystals, specifically adopted to mitigate lateral spread of optical photons). Because the tails of the ERFs we measured are relatively noiseless, despite the small amount of radiation detected, we speculate that the effect is caused by optical photons, rather than x-rays, with some contribution of the later, mainly through scatter and fluorescence photons from the imager assembly. A Monte Carlo study⁴¹ focusing on the high frequency detector response concluded that while scatter and fluorescence produce a sharp MTF drop at low frequencies (<0.3 lp/mm) in silicon detectors, in CsI detectors they primarily affect mid-frequency (1–5 lp/mm) response. These two hypotheses (x-ray or optical photons) are contradictory and further measurements/simulations are needed to identify their relative contributions to LFD. The authors believe this is be an important area for future study, both for better understanding the mechanisms of flat-panel detector signal formation and the potential for modestly improving image quality.

CONCLUSIONS

Our findings show that uncorrected veiling glare can affect quantitative accuracy and contrast in FPI-based CBCT imaging. Use of the BTF reduces the impact of veiling glare-induced inverse cupping and modestly reduces the 10% loss of contrast. However, the most dramatic impact of veiling glare is introduction of error into scatter measurements made using the beam-stop or beam-stop array methods. SPR measurements extracted from projections for uncorrected for veiling glare, results SPR overestimates of 10%–15%, for the SPRs in the range of 0.4 to 2.7.

In thus study, we have characterized veiling glare by describing FPI response to direct radiation interactions by means of a PSF model with long tails describing FPI response at distances greater than 1 mm from the incident irradiation. We measured these long-range PSFs using two different experimental techniques, and in the case of ERFs, by using different data analysis techniques. We achieved consistency among these results despite the simplifying assumptions of radial symmetry, detector linearity, independence from mAs, and spatial invariance. The long tails of the detector PSF were found to have a modest dependence of beam spectrum, which is reflected on the MTF curve LFD.

NOMENCLATURE

ASG

antiscatter grid

BTF

bow-tie filter

CBCT

cone-beam computed tomography

DTF

disc transfer function

ERF

edge response function

FBCT

fan-beam computed tomography

FPI

flat panel imager

LFD

low frequency drop

LSF

line spread function

MTF

modulation transfer function

OBI

on-board imager

PSF

point spread function

SPR

scatter-to-primary ratio