Extra-dimensional Demons: A method for incorporating missing tissue in deformable image registration

Abstract

Purpose: A deformable registration method capable of accounting for missing tissue (e.g., excision) is reported for application in cone-beam CT (CBCT)-guided surgical procedures. Excisions are identified by a segmentation step performed simultaneous to the registration process. Tissue excision is explicitly modeled by increasing the dimensionality of the deformation field to allow motion beyond the dimensionality of the image. The accuracy of the model is tested in phantom, simulations, and cadaver models.

Methods: A variant of the Demons deformable registration algorithm is modified to include excision segmentation and modeling. Segmentation is performed iteratively during the registration process, with initial implementation using a threshold-based approach to identify voxels corresponding to “tissue” in the moving image and “air” in the fixed image. With each iteration of the Demons process, every voxel is assigned a probability of excision. Excisions are modeled explicitly during registration by increasing the dimensionality of the deformation field so that both deformations and excisions can be accounted for by in- and out-of-volume deformations, respectively. The out-of-volume (i.e., fourth) component of the deformation field at each voxel carries a magnitude proportional to the excision probability computed in the excision segmentation step. The registration accuracy of the proposed “extra-dimensional” Demons (XDD) and conventional Demons methods was tested in the presence of missing tissue in phantom models, simulations investigating the effect of excision size on registration accuracy, and cadaver studies emulating realistic deformations and tissue excisions imparted in CBCT-guided endoscopic skull base surgery.

Results: Phantom experiments showed the normalized mutual information (NMI) in regions local to the excision to improve from 1.10 for the conventional Demons approach to 1.16 for XDD, and qualitative examination of the resulting images revealed major differences: the conventional Demons approach imparted unrealistic distortions in areas around tissue excision, whereas XDD provided accurate “ejection” of voxels within the excision site and maintained the registration accuracy throughout the rest of the image. Registration accuracy in areas far from the excision site (e.g., > ∼5 mm) was identical for the two approaches. Quantitation of the effect was consistent in analysis of NMI, normalized cross-correlation (NCC), target registration error (TRE), and accuracy of voxels ejected from the volume (true-positive and false-positive analysis). The registration accuracy for conventional Demons was found to degrade steeply as a function of excision size, whereas XDD was robust in this regard. Cadaver studies involving realistic excision of the clivus, vidian canal, and ethmoid sinuses demonstrated similar results, with unrealistic distortion of anatomy imparted by conventional Demons and accurate ejection and deformation for XDD.

Conclusions: Adaptation of the Demons deformable registration process to include segmentation (i.e., identification of excised tissue) and an extra dimension in the deformation field provided a means to accurately accommodate missing tissue between image acquisitions. The extra-dimensional approach yielded accurate “ejection” of voxels local to the excision site while preserving the registration accuracy (typically subvoxel) of the conventional Demons approach throughout the rest of the image. The ability to accommodate missing tissue volumes is important to application of CBCT for surgical guidance (e.g., skull base drillout) and may have application in other areas of CBCT guidance.

INTRODUCTION

Ongoing advances in cone-beam CT (CBCT) enable high-quality 3D imaging for image-guided interventions, including image-guided radiation therapy (IGRT) and image-guided surgery (IGS). The ability to acquire up-to-date images in the course of intervention offers the potential to overcome the limitations of conventional image guidance systems that operate in the context of preoperative data only and fail to account for anatomical change occurring during therapy. Such systems have entered broad application in IGRT,¹ cardiovascular interventions,² and high-precision IGS including orthopedic/spine surgery^{3, 4} and head and neck/skull base surgery.^{5, 6, 7, 8}

Key to many of these applications is the ability to register preoperative images (e.g., preoperative CT along with registered MR or PET images) and planning data to intraoperative CBCT. Such registration algorithms must be sufficiently fast and well integrated so as not to impede surgical workflow and provide sufficient geometric accuracy for the particular interventional task. Rigid registration is often insufficient due to variation in patient positioning between preoperative and intraoperative setups as well as anatomical deformations occurring during intervention. In head and neck/skull base surgery (the focus of investigations below), despite the largely rigid anatomical context, rigid registration alone fails to account for independent (piecewise-rigid) motion of the neck, jaw, and skull as well as soft-tissue deformations occurring during the procedure—e.g., displacement of sinus contents, herniation of the orbital wall/lamina papyracea, and deformation of the tongue and oropharynx.

These challenges motivated previous work in developing a variant of the Demons registration method^{9, 10, 11, 12, 13} well suited to CBCT-guided procedures.¹⁴ The method includes: (i) a basic morphological pyramid providing registration within ∼20 s; (ii) a “smart” convergence criterion that automatically advances each level of the pyramid to achieve subvoxel (∼0.5 mm) registration accuracy and eliminate extraneous iterations;¹⁵ and (iii) an intensity matching step concurrent with the iterative registration process to provide robustness against image intensity (voxel value) mismatch in CT-to-CBCT or CBCT-to-CBCT registration.¹⁶

In addition to the basic challenges of tissue deformation in image-guided procedures is a novel and largely unaddressed problem: what if the differences between the preoperative (“moving”) image and the intraoperative (“fixed”) image involve not only tissue deformation but also the physical removal of mass? In IGRT, an example of a missing tissue problem is weight loss over the course of multiple radiotherapy fractions. In IGS, the problem can be more explicit and includes the physical resection of tissues on surgical approach (e.g., excision of ethmoid air cells on approach to the sphenoid sinus) and removal of the surgical target itself (e.g., drillout of a bony lesion). The behavior of deformable registration algorithms in the presence of missing tissue is an important consideration, since straightforward application of conventional registration approaches may lead to spurious distortion in regions of mismatch—which are often the regions of primary interest (e.g., in proximity to a partially resected surgical target). Registration in the presence of large surgical excisions presents new technical challenges compared to registration in the presence of deformations alone. We hypothesized that a modified Demons algorithm that explicitly identifies and models tissue excision in the course of registration will provide superior registration performance compared to straightforward application of the conventional Demons approach in images featuring tissue excision. Specifically, an “extra-dimensional” Demons method (denoted XDD) is developed that adds a fourth dimension to the usual 3D registration problem into which voxels corresponding to tissues identified as missing in the fixed image may be ejected from the moving image.

As a starting point, we delineate a spectrum of scenarios involving missing tissue in surgical guidance: (i) tissue-in-air excision tasks [where tissues of interest include bone (e.g., osteotomy, ethmoidectomy, vidian canal drillout, and clival drillout) and/or soft tissues (superficial fat/muscle resection, glossectomy, lung nodule resection, mucocele resection, and suction of fluid]); and (ii) soft tissue-in-tissue resection tasks (e.g., resection of a brain tumor, liver metastasis, etc. from within the surrounding medium of normal soft-tissue). In the first, the resected volume results in an air void, whereas in the second, surrounding soft tissue in-fills the resected volume. Initial development of the XDD concept detailed below focuses on the first scenario, in which tissue excision leaves an air volume in place of the missing tissue, although deformations of the surrounding normal tissue may have occurred. The tissue-in-air scenario corresponds to a broad spectrum of surgeries, including head and neck/skull base surgery.

Previous work has identified that for accurate deformable registration in the presence of excisions, the excision area must be identified and accounted for accurate registration,¹⁷ and identification of “missing data” regions may be performed concurrently with the registration process.¹⁸ For example, Risholm et al.^{19, 20} used a Demons variant for MR-guided brain surgery and recognized that erroneous deformations were calculated within areas of resection, and these errors were found to degrade the overall registration solution. They developed a novel variant of the Demons algorithm for registration of intraoperative MRI brain images in which excisions were identified by a level-set segmentation method, and the Gaussian smoothing step of the Demons algorithm was replaced with a filter designed to accommodate errors caused by retraction of brain tissue and resection of tumor.

The work reported below is distinct in methodology (the addition of an extra dimension in the registration problem), motivation (to reduce the effect of spurious distortions induced by missing tissue, while maintaining the speed and simplicity of the Demons algorithm), and application (CBCT-guided head and neck/skull base surgery). The conventional and XDD forms of the Demons algorithm are tested in phantom and simulation to illustrate and quantify the behavior of deformable registration in the presence of missing tissue. Further experimental validation involved a series of cadavers undergoing ethmoidectomy, vidian canal drillout, and clival drillout corresponding to endoscopic skull base surgery. The performance of conventional Demons and XDD was quantified in terms of image-based metrics [e.g., normalized cross-correlation (NCC) and normalized mutual information (NMI) between deformed and fixed image volumes], target registration error (TRE), and the accuracy of voxels identified as either “missing” (and therefore ejected by XDD) or normal (and therefore preserved).

METHODS

Registration methods

Conventional Demons registration

A previously reported variant of the symmetric-force Demons algorithm was employed as a reference and basis of comparison.^{9, 12, 14} The method has been validated in phantom, cadaver, and clinical studies to provide geometric accuracy to within approximately the voxel size (∼0.5 mm) for typical deformations encountered in CBCT-guided head and neck surgery. The Demons registration framework consists of a series of iterative steps. First, an update vector field is calculated based on currently overlapping voxel intensities. Second, the update field is added to the existing solution (initialized either by a zero field or by rigid registration), and the resulting deformation vector field is regularized by smoothing with a Gaussian kernel. Finally, the smoothed deformation field is used to update the moving image, and the process is repeated with the updated version of the moving image.

The update field, $\stackrel{\rightharpoonup }{u}$, is calculated based on the image intensities of the moving and fixed images, denoted I₀ and I₁, respectively, at each overlapping position in the images:

$$\stackrel{\rightharpoonup }{u}\left(x\right)=\frac{2\left[I_0\left(x\right)-I_1\left(x\right)\right]\left[\stackrel{\rightharpoonup }{\nabla }{I}_0\left(x\right)+\stackrel{\rightharpoonup }{\nabla }{I}_1\left(x\right)\right]}{K{\left[I_0\left(x\right)-I_1\left(x\right)\right]}^2+{\Vert \stackrel{\rightharpoonup }{\nabla }{I}_0\left(x\right)+\stackrel{\rightharpoonup }{\nabla }{I}_1\left(x\right)\Vert }^2},$$ (1)

where the normalization factor K is the reciprocal of the squared voxel size (units 1/mm²).¹¹ The update field is then added to the existing solution, and the result is convolved with a Gaussian kernel such that the deformation field, $\stackrel{\rightharpoonup }{D}$, at iteration n is given by

$${\stackrel{\rightharpoonup }{D}}_n=G_{\sigma }*\left({\stackrel{\rightharpoonup }{D}}_{n-1}+{\stackrel{\rightharpoonup }{u}}_n\right),$$ (2)

where * indicates 3D convolution, and the width of the Gaussian kernel σ was fixed to 1 voxel for all experiments described below. The deformation field is then used to update the moving image, and the registration process is repeated for N_iter iterations.

Throughout this work, we consider the “moving” image, I_0, as the image obtained at an earlier time-point that is to be registered to a more up-to-date image. Similarly, the “fixed” image, I₁, is the up-to-date image to which the moving image is to be matched. For example, the moving image could be a preoperative CT, and the fixed image an intraoperative CBCT obtained at the time of surgery, allowing registration of preoperative imaging and planning data to the intraoperative scene. Alternatively, the moving image could be a CBCT acquired at the beginning of a procedure (into which CT and planning data have been registered as in the previous sentence), and the fixed image a CBCT acquired at a later point in the procedure. In this manner, registration continually moves image and planning data “forward” to the most up-to-date geometric context that matches the state of the patient at any point in the procedure.

Registration is carried out according to a multiresolution morphological pyramid to improve registration speed and robustness against local minima. The images are binned and downsampled by factors of 8, 4, 2, and 1 (denoted DS8, DS4, DS2, and DS1, respectively), and registration is performed first at the coarsest level, with the result at each level initializing registration in the subsequent level at finer detail. In the work described below, the number of registration iterations was set at (15, 25, 25, and 15) for (DS8, DS4, DS2, and DS1, respectively) based on observation of the convergence rate. Previous work¹⁵ demonstrated an optimized convergence criterion based on the difference between subsequent deformation fields (as opposed to a fixed number of iterations per level); however, the current work fixed the number of iterations for all cases to maintain consistency across experiments and study the effect of the “extra-dimensional” component specifically. Previous work¹⁶ also demonstrated a Demons variant with an iterative intensity matching process that overcomes errors associated with image intensity (CT number) mismatch between the fixed and moving images, arising, for example, due to high levels of x-ray scatter in CBCT; however, since all cases considered below involved CBCT-to-CBCT registration of images acquired on the same, calibrated CBCT imaging system, intensity mismatch was small, and no intensity correction was applied in this study.

Extra-dimensional Demons (XDD) registration

Extra dimension

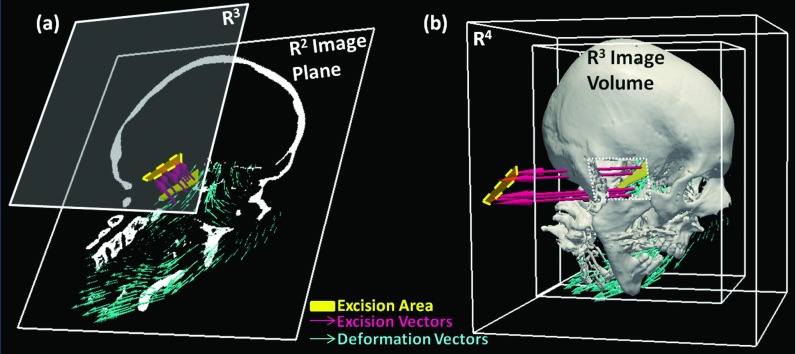
The primary conceptual change in XDD is to account for tissue excision by an increase in the dimensionality of the solution from three dimensions to include a fourth dimension into which voxels may be moved if identified as belonging to an excision (or conversely from which air may enter the image in the region of the excision). In conventional Demons registration, the update and deformation fields consist of vectors of the same dimensionality as the image space. Therefore, registration of two 3D image volumes involves a 3D deformation field made up of 3D vectors. We denote the 3D volume domain as R³ with coordinates (x,y,z) or equivalently (x₁,x₂,x₃). Conventional deformable registration therefore operates entirely within R³. The framework is extended in this work so that the solution for a 3D registration is a 3D deformation field made up of 4D vectors. As illustrated in Fig. 1, this effectively adds a fourth dimension (for 3D image registration) into which voxels may be “ejected” (or equivalently, from which voxels with image intensity corresponding to air enter the volume). As detailed below, motion along the fourth component is only considered if a voxel satisfies specific criteria identifying it as part of an excision. Within the XDD framework, therefore, the vectors comprising the fields given by Eqs. 1, 2 are four vectors, with the first three components representing deformation in (x₁,x₂,x₃), and the fourth component representing excision. Figure 1 illustrates the method in (a) a 2D image registration (more easily visualized within the constraints of 2D display) wherein excised regions are ejected from R² (x₁,x₂) to a R³ hyperplane, and (b) a 3D image registration in which excised regions are ejected from R³ (x₁,x₂,x₃) to a R⁴ hypercube.

Figure 1.

Schematic illustration of XDD for (a) 2D and (b) 3D image registration. Deformations are represented by in-plane/in-volume vectors (blue), and voxels identified within a region of excision (yellow) are subject to out-of-plane/out-of-volume “deformation” (i.e., excision).

The main challenge in such an approach is assigning the value of the fourth component of the deformation field so that only those voxels truly representative of excised tissue are removed during the registration process. Since the gradient between R³ and R⁴ is intrinsically steep, the entire 3D image would tend to move to R⁴ without constraint if the standard Demons force was applied in all dimensions. We therefore first identify the region likely to be associated with excision automatically by segmentation performed simultaneous to the iterative registration process. By performing segmentation simultaneously with the iterative registration process (as opposed to using a single initial segmentation), the process allows progressively more refined estimates of the excision volume as other tissue is deformed and improves robustness to segmentation error. This allows a fairly simple segmentation method detailed below—intensity thresholding of tissue to be ejected versus air (i.e., the material remaining in the voxel for the tissue-in-air “drill-out” scenario). It also allows the possibility of recovery from segmentation error by bringing voxels back to R³ if erroneously ejected in previous iterations.

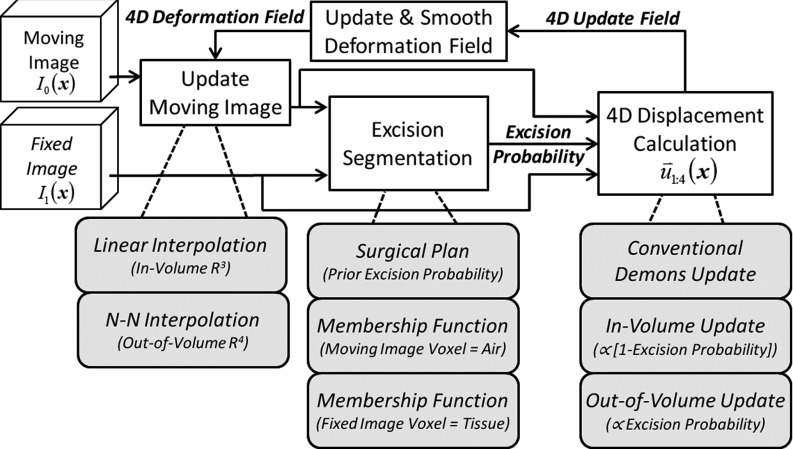
The proposed method is illustrated in Fig. 2, showing the segmentation and 4D force calculation modifications to the conventional Demons framework. At each registration iteration shown in Fig. 2, the estimate of voxels to be excised is based on the currently registered set of images. Segmentation of voxels possibly to be “ejected” employs a probability (membership function) computed from the image intensities. In subsequent registration steps, the magnitude of the “out-of-volume” component of the update force vector field is calculated proportional to the excision probability. The segmentation and extra-dimensional force calculation are detailed in Secs. 2A2b, 2A2d.

Figure 2.

Flow chart illustrating a single iteration of the XDD registration process in which segmentation of the excised volume is integrated within the Demons registration framework.

Identifying excised voxels

Initial implementation of XDD used a fairly simple segmentation method to identify candidate voxels for “ejection” based on an air-tissue intensity threshold appropriate to the tissue-in-air excision scenario (e.g., bone drill-out task). Given an intensity threshold T, two probabilistic membership functions (i.e., the probability that a voxel is associated with tissue or air) are computed at every location in the images as follows:

$$P_{\mathrm{moving}}^{\mathrm{tissue}}\left(x\right)=\mathrm{sigm}\left(I_0\left(x\right),\alpha ,T\right),$$ (3)

$$P_{\mathrm{fixed}}^{\mathrm{air}}\left(x\right)=\mathrm{sigm}\left(I_1\left(x\right),-\alpha ,T\right),$$ (4)

where the sigmoid function:

$$\mathrm{sigm}\left(I,\alpha ,T\right)=\frac{1}{1+e^{-\alpha \left(I-T\right)}}$$ (5)

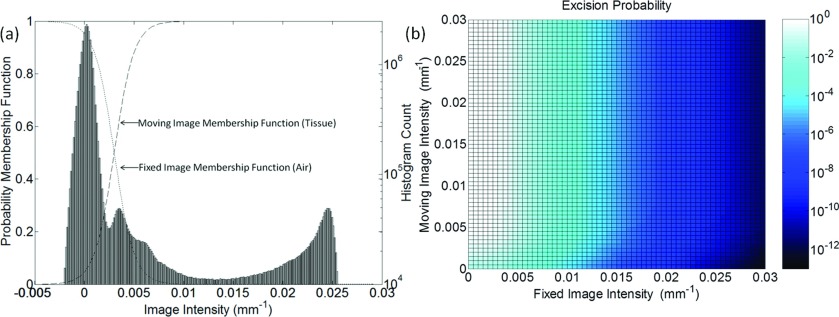
was chosen as a simple form for the probability function that allowed a more gradual transition than a binary threshold (i.e., step-function), maintained normalization between zero and one, and allowed smooth variation by adjustment of a single parameter—the “steepness” denoted as α. Adjustment of α allowed steep or gradual transition between (possibly poorly defined) intensity interfaces and accommodates issues such as partial volume effects. An example of the threshold function is shown in Fig. 3a.

Figure 3.

(a) Illustration of tissue and air membership functions used in segmenting regions of excision. The histogram corresponds to a CBCT image of the phantom in Fig. 5. (b) The resultant probability map [i.e., joint probability given by the product of membership functions in (a)] as a function of the fixed and moving image intensities.

The membership function $P_{\mathrm{moving}}^{\mathrm{tissue}}$ is the probability that a particular voxel in the moving image corresponds to tissue (not air), and $P_{\mathrm{fixed}}^{\mathrm{air}}$ is the probability that a particular voxel in the fixed image corresponds to air (not tissue). The probability P_excision of a given voxel belonging to excised tissue is given by the joint probability of Eqs. 3, 4:

$$P_{\mathrm{excision}}\left(x\right)=P_{\mathrm{moving}}^{\mathrm{tissue}}\left(x\right)·P_{\mathrm{fixed}}^{\mathrm{air}}\left(x\right).$$ (6)

Simply interpreted, Eq. 6 states that if a given voxel in the moving image is likely tissue, and that same voxel in the fixed image is likely air, then that voxel likely corresponds to “missing tissue” (i.e., tissue removed from the volume between the moving and fixed images), and thus it is assigned a higher probability of being excised. This interpretation is strictly valid only if images are perfectly registered and would not be expected to hold if images are misaligned—thus the motivation for incorporating the segmentation within the iterative registration process as shown in Fig. 2 to allow improved segmentation in each iteration. Figure 3 shows example tissue and air membership functions along with the resulting excision probability “map” (i.e., P_excision computed as a function of the fixed and moving image intensity). The example calculation corresponds to the deformable phantom used in studies detailed below, with T = 0.003 mm⁻¹ and α = 1000.

Incorporation of a Surgical Plan

The product of probabilities in Eq. 6 treats all areas of the image as equally likely to experience an excision; however, this is an oversimplification as there is almost always a volume of interest (i.e., the region of surgical approach and the volume about the surgical target) which is known a priori to be more likely to be excised. Direct implementation of Eq. 6 was found to be somewhat prone to false positives (i.e., voxels falsely identified as “excised” and ejected from the volume) arising from image noise, artifact, or gross misregistration. To mitigate such effects, and to use available prior knowledge where available, a probabilistic mask (P_plan, referred to as the surgical “plan”) was included in the joint probability. The mask acts as a weighting function that increases the probability of excision about the site of anticipated approach and excision and decreases it at locations distant from the excision:

$$P_{\mathrm{excision}}\left(x\right)=P_{\mathrm{moving}}^{\mathrm{tissue}}\left(x\right)·P_{\mathrm{fixed}}^{\mathrm{air}}\left(x\right)·P_{\mathrm{plan}}\left(x\right).$$ (7)

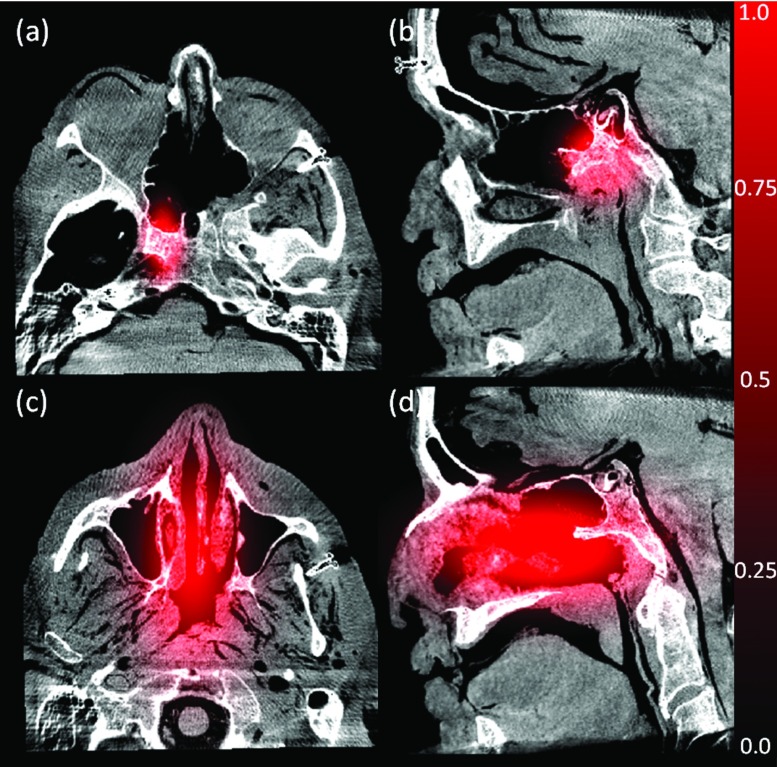
The mask function was defined simply as a long-range Gaussian cloud with peak value 1.0 centered roughly on the expected excision site and falling off with distance according to a free parameter (σ_plan) corresponding to the estimated size of the excision, thus constraining excisions to a region local to the expected surgical site. As shown in Fig. 4 for the cadaver experiments described below, the Gaussian mask can be coarsely tuned depending on the extent of anticipated excision. For example, as in Fig. 4a, the surgical plan can be placed narrowly (σ_plan = 10 mm in all directions) about the vidian canal (a structure drilled out and followed on approach to the skull base) and the clivus (the bone volume at the skull base that would be drilled out if infiltrated with tumor). Alternatively, as in Figs. 4c, 4d, the surgical plan can be placed broadly (σ_plan = 15 mm in (LR,SI) directions and 30 mm in the AP direction) to encompass the ethmoid sinuses. In practice, the P_plan multiplier in P_excision was found to reduce erroneous “salt-and-pepper” excisions far from the actual excision—particularly in areas of image noise and artifact.

Figure 4.

Illustration of two example probability maps (P_plan) associated with anticipated regions of tissue excision. (a) and (b) Example of plan (red) for drillout of the vidian canal overlaid on axial and sagittal views of a CBCT image. (c) and (d) Example large plan overlay.

Extra-dimensional deformation calculation

Tissue excision is modeled in the registration process by way of an additional (fourth) component of the deformation field vectors, denoted ${\stackrel{\rightharpoonup }{D}}_4$, whereas normal deformations (i.e., movement within R³) are described by the in-volume components ${\stackrel{\rightharpoonup }{D}}_{1:3}$. When calculating the update field, the conventional Demons algorithm force is computed for the in-volume components as in Eq. 1, with the resulting three-vector reduced in proportion to (1 − P_excision):

$$\stackrel{\rightharpoonup }{u}{\left(x\right)}_{1:3}=\left(1-P_{\mathrm{excision}}\left(x\right)\right)·\stackrel{\rightharpoonup }{u}\left(x\right).$$ (8)

In this way, regions far from the excision site (i.e., where P_excision → 0) experience deformations approximating those in the conventional Demons approach.

The extra-dimensional (“out-of-volume”) component of the update field, ${\stackrel{\rightharpoonup }{u}}_4$, is computed based on the joint probabilities $P_{\mathrm{moving}}^{\mathrm{tissue}}$, $P_{\mathrm{fixed}}^{\mathrm{air}}$, and P_plan calculated in the previous segmentation step as

$$\stackrel{\rightharpoonup }{u}{\left(x\right)}_4=P_{\mathrm{excision}}\left(x\right)·k_{\mathrm{force}}·a_{\mathrm{vox}}$$ (9)

such that the fourth component of the update field is a function of the excision probability for each voxel. A (optional) proportionality constant k_force allowed the magnitude of the out-of-volume vector component to be increased or decreased to eject voxels farther or nearer into the R⁴ hypercube at each iteration. The parameter was fixed to a value of k_force = 1.0 (dimensionless) in all experiments reported below. The term a_vox is the voxel size at the current level of the morphological pyramid. Addition of the 4D update field to the current estimate of the 4D deformation field, followed by 4D Gaussian smoothing, was performed as in conventional Demons registration and with the same smoothing parameters (but with increased dimensionality).

Image update

Through the process described above, voxels that are identified as excised see the value of the fourth component of the deformation field increase with each iteration. As shown in Fig. 2, it is during the image update step that excisions (if any) are introduced into the moving image. As in conventional Demons registration, in-volume deformations are handled by linear interpolation of surrounding intensity values. Deformations represented by the fourth component of the deformation field (i.e., out-of-volume motion) can analogously be considered as a nearest-neighbor interpolation in which the extra-dimensional space is treated as an air-filled void for the tissue-in-air excision scenario considered here. Therefore, voxels for which the fourth component of the deformation field is large enough (i.e., far enough into the R⁴ hypercube) are assigned an air intensity value upon update of the moving image. The displacement beyond which excision is considered to have occurred constitutes a “horizon” in the fourth dimension, the threshold for which is written as a_vox × k_horizon. The parameter k_horizon may be freely adjusted to modify the “gravity” of the R³ space—i.e., the ease with which voxels may escape the volume. A value of k_horizon = 1.0 was chosen for all experiments reported below. The implication: a voxel exhibiting a displacement with ${\stackrel{\rightharpoonup }{D}}_4$ > a_vox is subject to ejection on the current iteration.

Multiresolution implementation

As with conventional Demons, XDD was implemented in a multiresolution morphological pyramid with the same downsampling factors as described above (DS8, DS4, DS2, and DS1). For multiscale XDD, the magnitude of the fourth component of the deformation field, ${\stackrel{\rightharpoonup }{D}}_4$, was “reset” to zero between levels of the morphological pyramid to reduce spurious ejection in the first iteration of the new level. A variety of multiresolution XDD scenarios was examined in which the extra-dimensional aspect of the registration was turned on or off at various levels of the hierarchical pyramid—e.g., using conventional Demons at the DS8 level to provide coarse alignment and turning “on” XDD at the finer scales in DS4, DS2, and DS1.

Parameter selection

An attractive feature of the Demons registration method is the low number of algorithmic parameters—in its simplest form governed by the number of registration iterations (N_iter) and the size of the smoothing kernel (σ). New parameters associated with XDD registration are summarized in Table 1 along with nominal values where applicable. The parameters can be characterized as belonging to either the excision segmentation step or the extradimensional (XD) registration step. The key segmentation parameters are the intensity threshold (T) and the “steepness” (α) of the excision probability functions about this threshold. Depending on the application, the intensity threshold may be based on prior knowledge or chosen automatically based on the intensity profiles of the images as in the cadaver studies detailed below. The segmentation step can be fairly insensitive to threshold selection as long as T is selected (either manually or automatically) to fall in the “valley” between the air and tissue intensity peaks. Based on experience in this work, the best results were obtained when T was selected to fall close to the upper edge of the air peak. The α parameter was constant and was scaled simply based upon the units of the reconstruction (i.e., HU, mm⁻¹, or arbitrary units).

Table 1.

Glossary of symbols and parameters in the XDD registration process. Nominal values for excision segmentation given for phantom images reconstructed in units of attenuation coefficient (mm⁻¹).

Process	Symbol	Description [nominal value]
Demons registration	Niter	Number of iterations [15 (DS8), 25 (DS4), 25 (DS2), 15 (DS1)]
	σ	Size of smoothing kernel [1.0 voxel]
	$\stackrel{\rightharpoonup }{u}$	Update field
	$\stackrel{\rightharpoonup }{D}$	Deformation field
Excision segmentation	T	Air/tissue intensity threshold [0.003 mm−1]
	α	Steepness of threshold probability function [1000]
	$P_{\mathrm{moving}}^{\mathrm{tissue}}$	Probability that voxel in moving image is tissue
	$P_{\mathrm{fixed}}^{\mathrm{air}}$	Probability that voxel in fixed image is air
	Pplan	Prior information (surgical plan) probabilistic weighing of voxel for excision
	Pexcision	Probability of excision for given voxel
XDD registration	kforce	Excision force proportionality constant [1.0]
	khorizon	Excision “horizon” proportionality constant [1.0]
	${\stackrel{\rightharpoonup }{u}}_{1:3}$	Update field deformation components
	${\stackrel{\rightharpoonup }{u}}_4$	Update field excision component
	${\stackrel{\rightharpoonup }{D}}_{1:3}$	Deformation field deformation component
	${\stackrel{\rightharpoonup }{D}}_4$	Deformation field excision component

The XD registration step is parameterized by factors k_force and k_horizon that control the sensitivity with which voxels are ejected from the image during registration. Both parameters act as multipliers on voxel size with a nominal value of 1.0. A larger value of k_force increases the magnitude of the extradimensional force calculation, thereby increasing the likelihood of a voxel being ejected if identified as part of an excision. A larger value of k_horizon, on the other hand, increases the required displacement in the fourth-dimension before a voxel is ejected and therefore reduces the likelihood of a voxel being ejected. Although the k_force and k_horizon effects are closely (oppositely) related, they are not directly inverse of one other, since one is applied before deformation field smoothing, and the other after. For the excisions explored in this work, the results were relatively insensitive to values of k_horizon and k_force selected in the range 0.5–1.5.

Experimental methods

Experiments were carried out to characterize the behavior of both the conventional Demons and the proposed XDD algorithm in the presence of excised tissue in the fixed image. Three main experiments were performed. First, a custom deformable phantom was imaged in CBCT, before and after deformation and with a volume of material excised between the “preoperative” (moving) image and the “intraoperative” (fixed) image. Test cases involved deformation-only, excision-only, and deformation + excision. Second, simulation studies were conducted using images of the same phantom in which simulated excisions of varying size were imparted. Such phantom experiments allowed variation and sensitivity analysis of the parameters intrinsic to XDD. Finally, cadaver experiments were performed to quantify and validate XDD registration performance in data featuring realistic anatomy and surgical excisions in the context of CBCT-guided endoscopic skull base surgery.

Phantom and simulation studies

As illustrated in Fig. 5, a simple deformable (and excisable) phantom was constructed from a mixture of two materials—PlayFoam^TM (Educational Insights, Lake Forest, IL) sculpting beads embedded in a medium of PlayDoh^TM (Hasbro, Pawtucket, RI)—to form a roughly cylindrical shape ∼6 cm in diameter, ∼10 cm in height. This simple model provided high contrast between internal features and the background medium (∼400 HU) which could be both deformed and excised. The visibility of individual PlayFoam^TM beads (each ∼1–2 mm diameter) allowed visual assessment of deformations and spurious distortion that would not be evident in a uniform phantom. As a further aid to quantifying registration accuracy, a collection of 3.2 mm diameter acrylic spheres were mixed within the phantom to provide uniquely identifiable “target” points in analysis of TRE.

Figure 5.

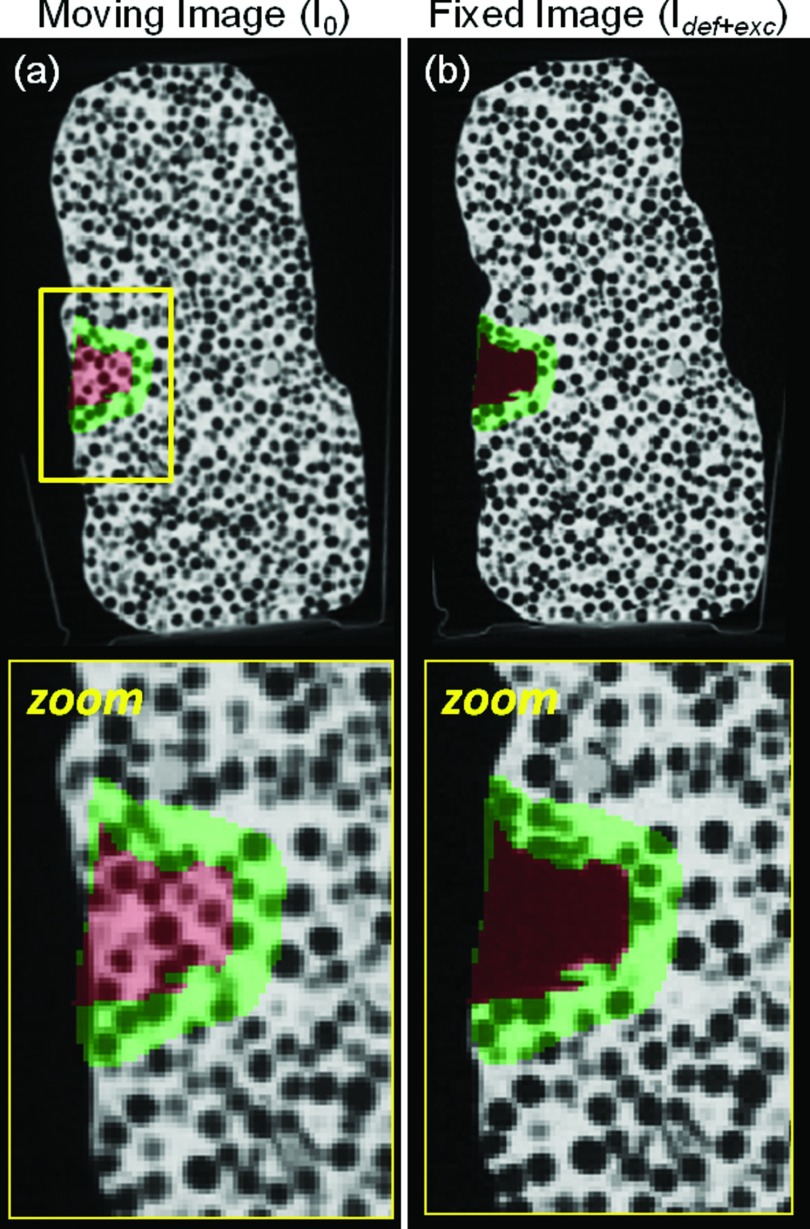
Sagittal CBCT images of a deformable phantom (Playfoam^TM beads in PlayDoh^TM medium) before and after deformation and excision. The excision area (target volume) is highlighted in red (manually segmented), and the area immediately outside the excision (adjacent normal tissue) is highlighted in green (defined by automatic dilation of the target volume).

The phantom was manually deformed (without excision) to emulate a deformation-only case, with CBCT images acquired before (I₀) and after (I_def) the deformation. Subsequently, as shown in Fig. 5b, an irregular volume (∼1 cm³) was excised from the midsection of the phantom using a curette and tweezers (without further deforming the phantom), and a third CBCT image (I_def+exc) was acquired after the excision. The resulting three CBCT image pairs (I₀ − I_def, I_def − I_def+exc, and I₀ − I_def+exc) therefore emulate cases of deformation-only, excision-only, and deformation + excision. Registration was performed with both the conventional Demons and XDD methods in each case. Registration accuracy was quantified globally (i.e., across the entire image) and locally (i.e., within the immediate area of the excision) as described below.

The CBCT images acquired in the phantom study were then extended to a simulation study to investigate the effect of excision size on registration accuracy and the robustness of XDD registration in the presence of larger excisions. The simulated data were formed from the I_def+exc image in which the excision volume was manually delineated (shown in red in Fig. 5). Simulated images were formed in which the excision volume was increased in size by dilating the excision volume with kernels of increasing size, thus expanding the excision to arbitrary size by digitally “blanking” the dilated region to the image intensity of air (0 mm⁻¹). Simulated excision volumes ranging in size from 2.5 to 17 cm³ were investigated. The largest excision encompassed approximately 10% of the phantom by volume and likely represents a much larger relative fraction of tissue removed than expected clinically, intended primarily to test the limits the registration algorithms under conditions of large amounts of missing tissue. Deformable registration was performed to match the I₀ image to each of the simulated I_def+exc images, and registration accuracy was evaluated as described below.

For both the real phantom and simulation studies, the segmentation parameters shown in Fig. 3 were held fixed, giving a threshold near the air boundary and with relatively sharp transition from air to tissue. Other parameters (e.g., k_force and k_horizon) were varied in sensitivity analysis, but none showed dramatic variation in the resulting deformation over the range investigated and the nominal values mentioned above were held fixed.

Registration accuracy was evaluated qualitatively and quantitatively. Visually, the quality of registration was assessed by examining the extent of distortion in the registered image—e.g., apparent shearing of the circular PlayFoam^TM beads. Quantitatively, the registration accuracy was assessed in terms of the TRE measured as the distance between the centroids of the implanted acrylic spheres in the fixed and moving images before and after registration. In addition, the registration accuracy was assessed in terms of image-based metrics, NCC and NMI, computed across the entire image (global assessment) and in a smaller region about the excision. As shown in Fig. 5, NMI was measured in the combined regions of excision (red) and adjacent “normal” tissue (green). The area immediately about the excision arguably requires the most accurate registration (e.g., to assess proximity of the drillout to nearby critical anatomy, such as the carotid arteries in a clival drillout), and it was hypothesized that this region would be most susceptible to spurious distortion in the conventional Demons approach.

Cadaver study

Finally, cadaver experiments were performed using three fixed human head specimens undergoing endoscopic skull base surgery guided by C-arm CBCT.^{21, 22, 23} A fellowship-trained neurosurgeon and ENT surgeon performed drill-out tasks pertinent to trans-sphenoid skull base surgery in each head, and CBCT images were acquired before and after intervention. Three drill-out tasks were evaluated (in reverse order): (i) drillout of the clivus, the bone volume posterior to the sphenoid sinus bounded laterally by the carotid canals and posteriorly by the brain; (ii) drillout of the vidian nerve canal, the bilateral corridor that provides an important landmark on approach to the clivus; and (iii) excision of the anterior and posterior ethmoid air cells, the bony architecture bilateral to the nasal septum attaching the sinus turbinates and lamina papyracea. In addition to the surgical drillout tasks, each cadaver specimen underwent differing amounts of soft-tissue deformation between image acquisitions due to specimen movement, displacement of the septum, turbinates, and other sinus anatomy during surgical approach, herniation of the orbital walls, and physical pressure placed on nearby structures during the drillout.

For each cadaver excision task, registration was performed from the pre-excision to postexcision CBCT image. For XDD registration, a surgical plan (mask function) as shown in Fig. 4 was used to mitigate erroneous excision at large distances from the anticipated site of intervention. The segmentation threshold (T) was selected automatically based on the Otsu method²⁴—specifically, T equal to half the Otsu threshold, generally giving a value near the edge of the air threshold. Setting the sigmoid parameter to α = 0.01 maintained approximately the same “steepness” of the threshold functions as in phantom experiments while accounting for the different intensity range in CBCT images reconstructed on an arbitrary 0–4000 scale (as opposed to an attenuation coefficient scale used in the phantom study).

Analysis of registration performance was carried out in a manner similar to that described above for the phantom experiments. The true excision area was manually segmented in the postoperative CBCT image. The area immediately surrounding each excision was defined as the adjacent normal tissue volume in which measures of registration quality were assessed. In addition to the image-based metrics of NCC and NMI computed across the entire image and within local subregions, the accuracy of XDD in correctly ejecting voxels within the excision volume (while preserving voxels in surrounding, unexcised normal tissue) was measured in terms of the excision “sensitivity” (i.e., fraction of excision volume correctly ejected, analogous to true-positive fraction) and “specificity” [i.e., fraction of surrounding normal tissue properly preserved, analogous to (one minus) false-positive fraction].

RESULTS

Phantom and simulation studies

Basic comparison of XDD and conventional Demons

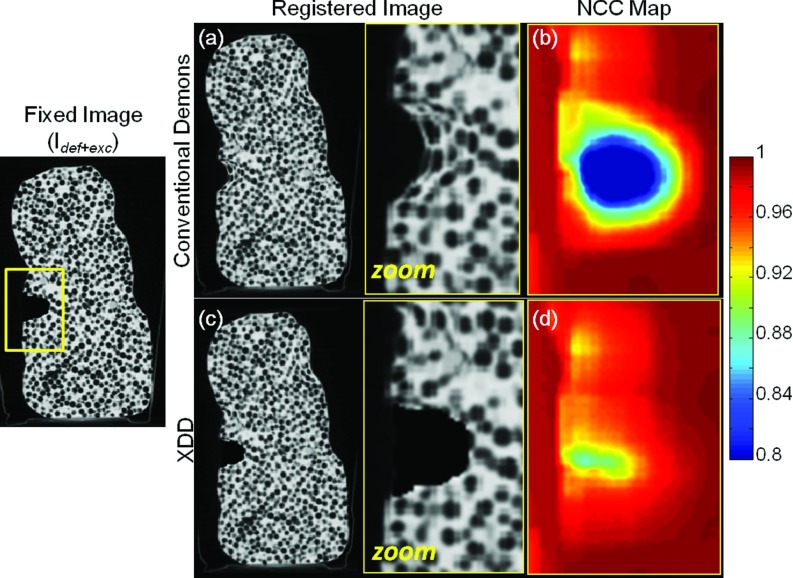
Figure 6 demonstrates image distortion imparted by the conventional Demons algorithm in the presence of missing tissue, evident in Fig. 6a as unrealistic warping of features within and adjacent to the region of excision. Registration accuracy at large distances (> ∼1 cm) from the boundary of the excision is largely unaffected and exhibits the expected (subvoxel) precision demonstrated in previous work. Figure 6b quantifies the failure in registration within and around the region of excision as a map representing the NCC between the fixed and registered moving images for every 10 × 10 × 10 voxel window in the region of the excision. The conventional Demons approach appears to force tissue “inward” toward the boundary of the excision, but does not do so in a way that provides an accurate match to the fixed image. The performance of the XDD approach is shown in Figs. 6c, 6d, showing XDD registration results to be largely free of spurious distortion. The identification of excised tissue and modeled ejection of voxels within the iterative registration process provides a close match to the fixed image right up to the excision boundary and in the adjacent “normal” tissue, while maintaining the geometric registration accuracy of the conventional Demons approach in other regions of the image. The NCC map for the XDD registered image quantifies a generally high degree of agreement between the deformed and fixed image in and around the excision; the decrease in metric values in the central void of the excision is due to the XDD algorithm introducing a completely uniform excision, whereas the real excision (air-filled void in the object) contains naturally noisy voxel values associated with quantum noise.

Figure 6.

Comparison of conventional Demons and XDD registration in a deformable phantom containing real deformations and a ∼1 cm³ excision of material emulating a tissue-in-air excision scenario. Coronal slices from the CBCT volume are shown. (a) Registered image (and zoomed-in region) resulting from the conventional Demons approach, with (b) NCC map (across the zoomed-in region) computed using a 10 × 10 × 10 voxel sliding window across the region of interest. (c) and (d) The same, for the XDD registration approach. Whereas (a) and (b) exhibit unrealistic distortion and reduction in NCC, (c) and (d) demonstrate a fairly accurate ejection of voxels within the region of excision and maintenance of NCC (with reduction within the air void likely due to quantum noise).

The locality of the excision effect involved in XDD and the maintenance of registration accuracy throughout the rest of the image is evident in the images of Fig. 6, the NMI, and the TRE computed from the entire registered image. Specifically, the NMI computed over the entire image volume was identical (NMI = 1.17) for conventional Demons and XDD registration, compared to NMI = 1.09 for rigid registration (initialization). Conversely, in the area containing and immediately surrounding the excision, the results indicate degraded registration performance for conventional Demons registration (NMI = 1.10) compared to the same region in XDD (NMI = 1.16). Similarly, the TRE calculated from six acrylic “target” spheres embedded throughout the bulk of the phantom was (0.40 ± 0.15) mm for conventional Demons and (0.40 ± 0.15) mm for XDD, compared to (1.00 ± 0.70) mm for rigid registration. These results verify that XDD maintains a high level of registration accuracy as demonstrated by the conventional Demons approach throughout the image volume (without excision), while improving performance and reducing or eliminating distortion in the region local to the excision.

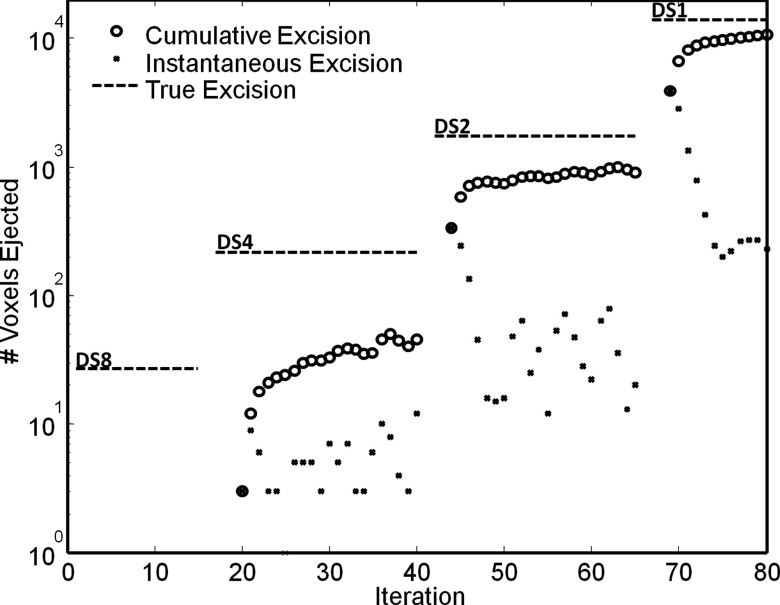
The evolution of the conventional Demons registration process across multiple levels of the morphological pyramid and iterations has been previously reported,¹⁵ typified by a fairly monotonic increase in NCC (or other metric) with each iteration (with some variability in the first few iterations of each new level of the pyramid). The evolution of XDD was anticipated to be similar in terms of image metrics, but the approach introduces an additional question regarding the behavior of the excision effect—i.e., at which level of the pyramid (and at which iterations) are voxels “ejected” from the volume. As shown in Fig. 7, simultaneous 3D deformable registration and 4D “excision” exhibits a fairly monotonic evolution at each level of the pyramid. The cumulative excision gradually approaches the “true” excision volume (as estimated by manual segmentation) at each level and converges fairly conservatively (i.e., does not overshoot) for the parameters employed. The difference between the manually defined excision volume and that estimated during XDD registration represents a combination of two factors: (1) slight underestimation of the excision volume by XDD, visible at the lateral and deep boundaries of the excision, a factor controllable through parameterization and number of registration iterations as discussed below; and (2) segmentation error in defining the boundary of the true excision (in this case, somewhat overestimating the true volume excised). More accurate observations are possible about the change in excision size from one iteration to the next. Within a given level of the pyramid, the largest number of voxels is ejected in the first few iterations, followed by a sharp decrease and nearly constant rate of ejection. The scenario illustrated is the nominal case in which XDD was “on” for all levels of the registration pyramid. Variations on this nominal scheme were tested, viz., “off” in the first (DS8) level, and “on” in the three subsequent levels (DS4, DS2, and DS1); however, it was generally found that using XDD at all levels of the morphological pyramid improved registration accuracy and reduced erroneous deformations that were difficult to correct in subsequent levels.

Figure 7.

Evolution in the number of voxels excised from the 3D volume in XDD registration. Four levels of the morphological pyramid are evident (DS8, DS4, DS2, and DS1). The horizontal dashed line in each level marks the true number of voxels within the excision volume in the fixed image. The open circles mark the cumulative number of voxels ejected from the volume, whereas the small dots mark the (instantaneous) number of voxels ejected in a given iteration. For the nominal XDD parameters described in the text, a gradual, conservative convergence on the true excision volume is observed (without overshoot).

Registration performance as a function of excision size

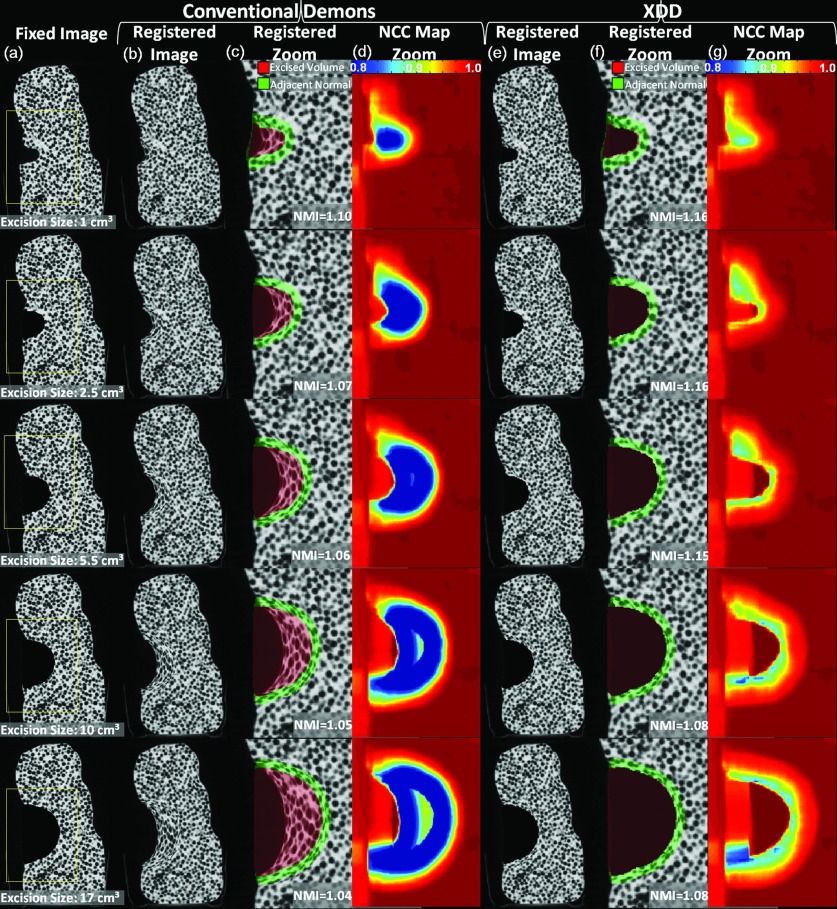
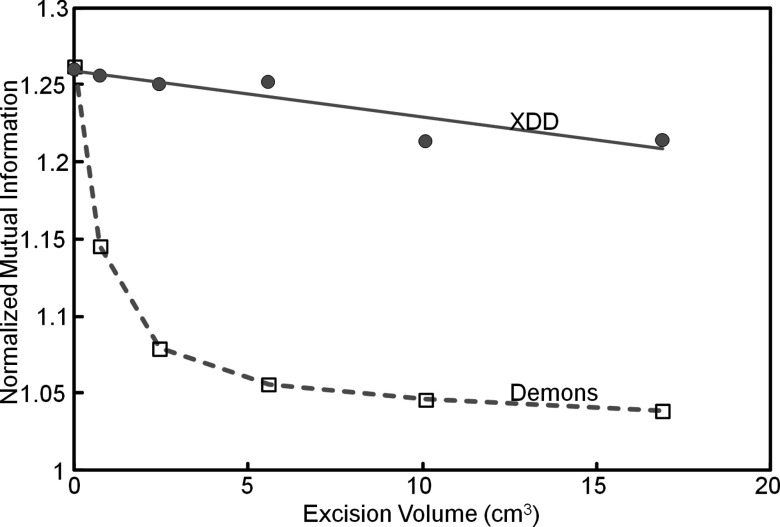
Figure 8 shows the dependence of registration accuracy on the size of the excised volume for both the conventional Demons and XDD approaches. The ∼1 cm³ excision is the same as the real data considered in Sec. 3A1, and the larger excisions were simulated by dilation as described above. Some degradation in registration quality is evident for the larger excision volumes—visible as image distortion and quantified by the reduction in NMI for each case. In the phantom model, we note lower NMI values observed at the bottom of the excision compared to the top, attributed to heterogeneity in the phantom in which a larger number of low-attenuation beads are embedded immediately below the excision than above. The beads highlight excision-induced deformation, with a larger number of features (beads) leading to more easily detectible distortion and hence lower NMI. The fairly high-contrast features are important in highlighting erroneous distortions which could be overlooked in a uniform phantom. The conventional Demons method suffers major distortion and gross misrepresentation of tissue within and around the excision, similar to that in Fig. 6 but amplified steeply for larger excisions. XDD registration on the other hand exhibited a high degree of robustness to excision across the full range of sizes investigated, with only a slight degradation of registration accuracy for the largest excisions. The results are quantified in Fig. 9, where NMI for the conventional Demons approach declines sharply with excision size, but XDD is fairly robust. The reduction in registration accuracy observed for XDD in the largest excisions could be mitigated by adjustment of parameters allowing more volatility in voxel excision. Since the force calculated at each iteration of the XDD registration is a combination of both in-volume deformation and out-of-volume excision components, larger excisions likely benefit from parameter choices that favor the excision component and reduce the (erroneous) in-volume deformation component. Such parameter changes that increase the probability of ejection in turn may increase false-positive excisions, particularly for smaller excisions. The nominal parameter values in this work (Table 1) did not exhibit a large reduction in registration accuracy for the small-to-medium size excisions, as seen in Fig. 9, and were consistent with the excision size relevant to the cadaver experiments detailed below.

Figure 8.

Dependence of deformable registration on the size of excision. A single coronal plane from the 3D volume is shown in each case. (a) Fixed images featuring an excision varying in size from ∼1 cm³ (the real excision in Figs. 567) to 2.5–17 cm³ (simulated excisions). Registered images and NCC map for the conventional Demons approach are shown in (b)–(d), and those for the XDD approach are shown in (e)–(g).

Figure 9.

Dependence of deformable registration on the size of excision. While the performance of the conventional Demons algorithm declines sharply with excision size, NMI is maintained to a fairly high degree for the XDD approach. The first point on each curve (excision volume equal to 0 cm³) corresponds to the deformation-only case.

Cadaver study

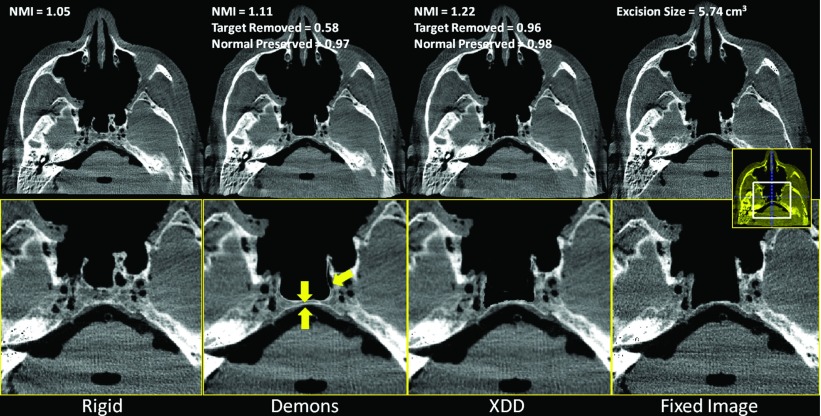
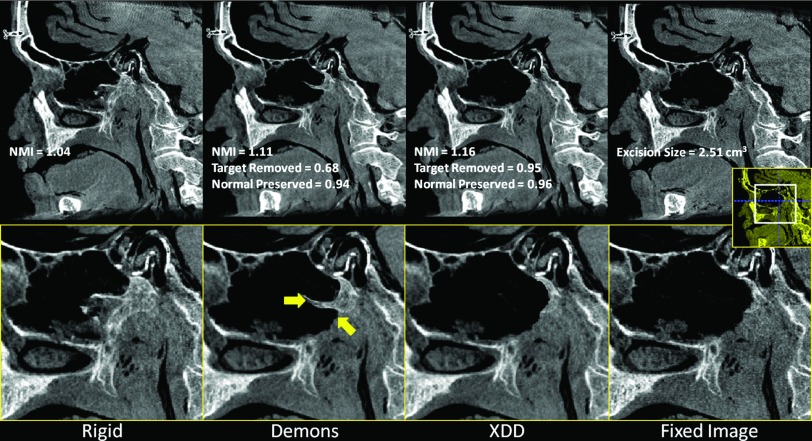
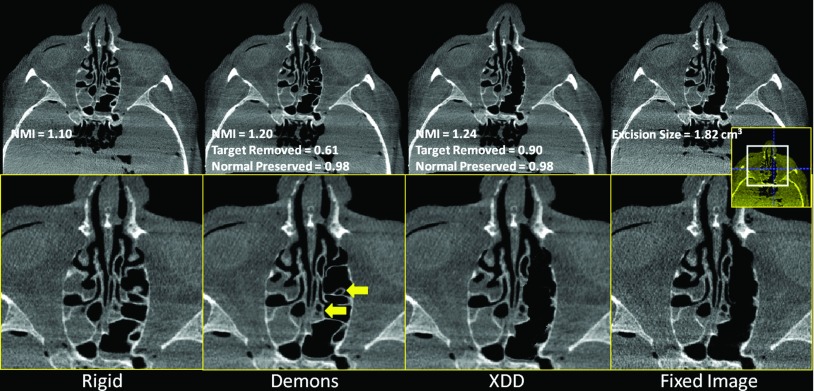
The results for realistic skull base surgery drillout tasks conducted in cadaveric specimens are summarized in Figs. 10 (clivus), 11 (vidian canal), and 12 (ethmoid sinuses). Overall, the results confirm the findings of the phantom and simulation studies: the conventional Demons approach suffers distortions in the presence of excisions and a quantifiable reduction in NMI and other metrics. The XDD approach accounts for missing tissue and maintains overall geometric accuracy in the deformable registration. A few notable features are highlighted by yellow arrows in Figs. 101112. For the clival drillout (Fig. 10), conventional Demons causes the anterior clival wall to collapse onto the posterior wall, and bony structure lateral to the excision site to collapse unrealistically. XDD yields an image closely matching the fixed image in terms of both the excision site and adjacent anatomy. For the vidian canal drillout (Fig. 11), conventional Demons collapses and distorts the bony architecture of the middle cranial fossa and pterygopalatine plate to yield a false bony protrusion within the sinus space. XDD properly reproduces the excision and exhibits little or no distortion of surrounding architecture. For the ethmoid air cell excision (Fig. 12), conventional Demons induces spurious deformations and thinning of air cell walls and even introducing an apparent (false) air cell in the excision site. Errors in the deformable registration are evident in soft tissues medial to the excision site. Again, XDD performs comparably well, even partially accounting for differences in fluid filling of the sinuses between the preoperative and intraoperative images. Small areas of failure for the XDD registration are evident in some cases at the edges of the excision area due to slight underestimation of the excision volume.

Figure 10.

Deformable registration in the presence of tissue excision about the clivus. (a) Rigid registration of the preoperative image to the fixed image shown in (d). (b) Conventional Demons registration exhibits spurious distortion and failure to account for missing tissue. Arrows highlight features of note in the text. (c) XDD registration, demonstrating a close match to the fixed image shown in (d).

Figure 11.

Deformable registration in the presence of tissue excision along the vidian nerve canal. (a) Rigid registration of the preoperative image to the fixed image shown in (d). (b) Conventional Demons registration exhibits spurious distortion and failure to account for missing tissue. Arrows highlight features of note in the text. (c) XDD registration, demonstrating a close match to the fixed image shown in (d).

Figure 12.

Deformable registration in the presence of tissue excision throughout the left ethmoid sinus. (a) Rigid registration of the preoperative image to the fixed image shown in (d). (b) Conventional Demons registration exhibits spurious distortion and failure to account for missing tissue. Arrows highlight features of note in the text. (c) XDD registration, demonstrating a close match to the fixed image shown in (d).

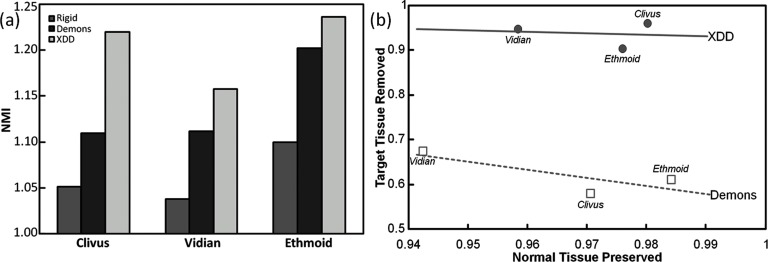
These qualitative observations are confirmed in the quantitative figures of merit shown in Fig. 13. The NMI demonstrates an increase in registration accuracy for the XDD approach in each case, and the metrics of excision sensitivity and specificity show that the excision areas are correctly modeled to a level of 90% or greater. XDD demonstrates improvement in sensitivity (i.e., fraction of target volume accurately removed) in each case (from ∼60% for conventional Demons to >90% for XDD). We had hypothesized a possible reduction in “specificity” (i.e., fraction of adjacent normal tissue correctly preserved) for XDD due to false-positive ejection of normal tissue voxels; however, XDD demonstrated improved specificity in two out of three of the surgical tasks investigated (a slight reduction in specificity observed for the ethmoidectomy case). The image metric values reported in Figs. 10111213 were calculated in the region of the image local to the excision. The (global) NMI computed over the entire image volume for the three tasks (Clivus, Vidian, and Ethmoid) was identical for conventional Demons and XDD registration (viz., NMI = 1.19, 1.23, and 1.26, respectively), compared to a global value of NMI = 1.14, 1.11, and 1.19, respectively, for rigid registration (which formed the initialization). As in the phantom and simulation studies, the cadaver results suggest the greatest improvement in registration accuracy for XDD over conventional Demons registration for the larger excision volumes.

Figure 13.

Registration performance in cadaver studies emulating CBCT-guided skull base surgery involving drillout tasks of the clivus, vidian canal, and ethmoid sinuses. (a) NMI for rigid, conventional Demons, and XDD registration. (b) Accuracy in and about the region of excision in the form of “operating curves,” i.e., fraction of target tissue correctly removed (“sensitivity”) plotted versus fraction of adjacent normal correctly preserved (“specificity”).

DISCUSSION AND CONCLUSIONS

The results presented in this work indicate that conventional Demons registration is prone to erroneous distortion of registered images in the presence of excisions, and registration accuracy degrades in the area local to the site of the excision, which is the area where increased registration accuracy may be most needed. Explicit modeling of tissue excision implemented in the XDD registration approach resolved such effects to a significant degree. XDD largely removed excision-induced distortion about the site of the excision while maintaining the same level of registration accuracy as conventional Demons registration in regions far from the excision site.

For conventional Demons registration, accuracy was found to degrade sharply with increasing excision size, whereas XDD registration performance decreased only slightly even for the largest excisions explored in this work. The results were fairly robust over the range of excision size considered, though one may envision adjustment of the XDD parameters according to the relative size of the excision compared to the surrounding volume to allow increased probability of out-of-volume ejection relative to in-volume deformation. Conversely, for small excisions, the parameters may be adjusted to favor in-volume deformation over out-of-volume excision. Applications involving either much larger or much smaller excisions than considered in this work (and the nominal parameters in Table 1) may benefit from balancing tradeoffs between the volatility in out-of-volume excision and the likelihood of false-positive ejection. For example, simulations (not shown) involving excision as small as ∼20 voxels were found to be accommodated by XDD through a doubling of k_force (2.0) and halving of k_horizion (0.5). One can even envision optimization of the XDD method to detect smaller excisions and adjust parameterization to allow a higher probability of ejection while minimizing false positive excisions at distant locations.

Initial implementation of the XDD method involved simultaneous registration and excision segmentation using a simple threshold of air-tissue intensity interfaces. Such an approach has advantages of simplicity and computational efficiency, but may be more difficult to optimize for more complex resections (e.g., tissue-in-tissue resection) as well as weighing tradeoffs between false-positive ejection (i.e., normal tissue erroneously ejected from the volume) versus true-negative deformation (i.e., normal tissue properly deformed within three-space). Incorporation of a simple surgical plan (e.g., a large Gaussian cloud marking an additional probability of excision) reduced distal, erroneous “salt-and-pepper” excision and makes reasonable use of prior information without additional computational burden.

A variety of image artifacts pose challenges to CBCT image registration in general, including the XDD method. Mismatch in image intensity (CT number) can arise due to differences in scanner calibration and the shading and streak artifacts arising from x-ray scatter, beam-hardening, metal objects, detector lag, and lateral truncation. While previous work addressed such issues in part through preprocessing²⁵ or incorporating intensity corrections within the registration process itself,¹⁶ there were no artifact correction methods applied in the current work. The PlayFoam^TM phantom presented idealized conditions of a small (untruncated) object with low x-ray scatter, and such effects were negligible. The cadaver studies presented realistic scatter and truncation effects, but the effect of image intensity differences arising from such artifacts were small, since the data were acquired on the same CBCT scanner with equivalent calibration and in a fairly short time period (hours). The specimens did not include metal objects (e.g., dental fillings, surgical implants, etc.), which could challenge the registration process. The XDD method developed in this work employed classification/segmentation based on easily defined air/tissue boundaries and incorporated a probabilistic (“fuzzy”) representation of the threshold functions—each helping to reduce the sensitivity of the approach to intensity inaccuracies. Future work, particularly in datasets with large intensity inaccuracy, poorly defined intensity interfaces, and/or metal artifacts could combine the XDD method with appropriate intensity/artifact correction schemes.

There is an analogous question to the missing-tissue problem investigated above: what if the fixed and moving images differ in the physical addition of tissue (or other material)? In IGS, for example, the fixed image (intraoperative CBCT) may contain an interventional device (e.g., needle) not present in the moving (preoperative CT) image. Although beyond the scope of the current work, a solution analogous to the XDD method for handling missing tissue is under consideration in future work—specifically, the addition of an extra dimension from which material (i.e., signal intensity) may be introduced to the moving image at voxel locations identified as regions of mismatch.

Accurate account of tissue excision is an important aspect of deformable registration in image-guided surgery. Initial implementation of a Demons variant modified to include extra dimensions in the deformation field provided an accurate means of ejecting voxels from the moving image while maintaining the overall (subvoxel) accuracy of the conventional Demons approach. Application to preclinical (cadaver) studies of CBCT-guided head and neck/skull base surgery demonstrated a major improvement in registration accuracy under conditions of realistic excision tasks.