Skip to main content
PMC home page
Springer logoLink to Springer
. 2011 Oct 12;13(Suppl 2):507–518. doi: 10.1007/s10339-011-0419-7

Action unit classification using active appearance models and conditional random fields

Laurens van der Maaten 1,✉, Emile Hendriks 1
PMCID: PMC3443486  PMID: 21989609

Abstract

In this paper, we investigate to what extent modern computer vision and machine learning techniques can assist social psychology research by automatically recognizing facial expressions. To this end, we develop a system that automatically recognizes the action units defined in the facial action coding system (FACS). The system uses a sophisticated deformable template, which is known as the active appearance model, to model the appearance of faces. The model is used to identify the location of facial feature points, as well as to extract features from the face that are indicative of the action unit states. The detection of the presence of action units is performed by a time series classification model, the linear-chain conditional random field. We evaluate the performance of our system in experiments on a large data set of videos with posed and natural facial expressions. In the experiments, we compare the action units detected by our approach with annotations made by human FACS annotators. Our results show that the agreement between the system and human FACS annotators is higher than 90% and underlines the potential of modern computer vision and machine learning techniques to social psychology research. We conclude with some suggestions on how systems like ours can play an important role in research on social signals.

Keywords: Facial expressions, Facial action coding system, Active appearance models, Conditional random fields

Introduction

One of the main aims of social signal processing is to address the social ignorance of today’s computers (Vinciarelli et al. 2009). To address this social ignorance, it is important that computers are capable of interpreting social signals. These social signals may encompass verbal communication, prompting the development of speech recognition systems, but they typically also entail behavioral cues. Ekman and Friesen (1969) distinguish five main behavioral cues, viz. (1) affective/attitudinal/cognitive states, (2) emblems, (3) manipulators, (4) illustrators, and (5) regulators. Although this taxonomy is useful to describe communicative intentions, it is not well suited as a taxonomy that describes the technologies required to allow computers to interpret these behavioral cues. Behavioral cues are primarily contained in facial expressions (cues 1, 2, 3, 4, and 5), gestures (cues 2, 3, and 4), body pose (cues 1, 2, 4, and 5), and interactions (cues 4 and 5). The interpretation of these features requires different technologies: facial expression analysis, gesture recognition, pose detection, and gaze detection, respectively. An overview on which computer technologies are required to detect which behavioral and social cues is presented by Vinciarelli et al. (2009).

In this study, we focus on one of the most important technologies required to interpret behavioral cues, viz. facial expression analysis. In particular, we develop a system that automatically annotates faces depicted in videos according to the facial action coding system [FACS; Ekman and Friesen (1978)]. FACS allows for the systematic description of facial expressions by categorizing facial expressions by describing them in terms of 46 action units (AUs) that correspond to the facial muscles. Action units can be given intensity scores: the most simple score is present or not present. Two alternative intensity scores are (1) neutral, onset, apex, and offset or (2) trace, slight, pronounced, extreme, and maximum. In our experiments, we use the simple present/non-present scoring; however, win provided with appropriate data, our system can be used with other scorings as well.

Action units can be used to recognize facial expressions and/or behavioral cues (Giudice and Colle 2007; Lucey et al. 2010). For instance, anger typically involves action unit 23 or 24, disgust involves action unit 9 or 10, and happiness involves action unit 12 (see Table 2 for an overview of action units). An action unit recognition system like one we develop in this paper can thus be used as a basis for recognizing higher-level facial expressions and/or behavioral cues.

Table 2.

Overview of the action units considered in our study

AU Name Incidence
1 Inner Brow Raiser 0.292
2 Outer Brow Raiser 0.196
4 Brow Lowerer 0.322
5 Upper Lip Raiser 0.172
6 Cheek Raiser 0.206
7 Lip Tightener 0.201
9 Nose Wrinkler 0.125
11 Nasolabial Deepener 0.056
12 Lip Corner Puller 0.187
15 Lip Corner Depressor 0.150
17 Lower Lip Depressor 0.041
20 Lip Stretcher 0.130
23 Lip Tightener 0.100
24 Lip Pressor 0.096
25 Lips Part 0.484
26 Jaw Drop 0.164
27 Mouth Stretch 0.137
Open in a new tab

The columns on the right show the incidence of the action units in the Cohn--Kanade data set

Our system for action unit recognition combines computer vision techniques that extract informative features from the depicted faces with a machine learning model for the classification of time series (as facial expressions in a video change over time). The computer vision techniques extract features from the face images that are indicative of the presence of action units in the face using a deformable template model, called the active appearance model [AAM; Cootes et al. (1998)]. The machine learning model, known as linear-chain conditional random field [CRF; Lafferty et al. (2001)], recognizes action units in each image in the sequence of face images. The key property of the linear-chain CRF is that it not only employs the face features measured in the current image to recognize action units, but that it also employs knowledge on the likelihood of an action unit changing from one intensity score to another (for instance, it can make use of the fact that an action unit does not typically change from neutral into offset). We investigate the performance of our action unit recognition system on a large data set of videos in which subjects are recorded while making posed and natural facial expressions. The videos in the data set were annotated by human FACS-certified annotators, facilitating the training and evaluation of our system.

The main aim of the paper is to illustrate what today’s most sophisticated computer vision and machine learning techniques are capable of and to provide some ideas on how these techniques may be used to facilitate social psychology research. We do not explicitly compare the performance of our system with that of other systems presented in the literature; we merely use our system to illustrate the potential of computer vision and machine learning to facial expression analysis. The results of our experiments reveal that it is likely that our system would pass certification tests for human FACS labelers.

The outline of the remainder of this paper is as follows. In "Related work", we give an overview of related work on automatic action unit recognition. "Active appearance models" provides an overview of the construction, and fitting of the active appearance model, we use as a basis for our system. In "Feature extraction", we introduce three types of features that are extracted from the face images and that are indicative of action unit presence in the depicted face. Subsequently, "Conditional random fields" describes the conditional random field model we use to assign FACS labels to each frame in a face image sequence (based on the extracted features). In "Experiments", we describe the setup and results of experiments in which we evaluate our approach on a large data set of facial expression movies that were annotated by human FACS annotators. The potential impact and applications of our system to social psychology are discussed in "Discussion". "Concluding remarks" presents our conclusions, as well as directions for future work.

Related work

In the computer vision field, there is a large body of work on face analysis. Traditionally, much of this work has focused on face detection [i.e., determining where in an image a face is located; Viola and Jones (2001)], face recognition [i.e., determining who is depicted in a face image; Phillips et al. (2005)], and emotion recognition [i.e., recognizing the six basic emotions anger, fear, disgust, joy, sadness, and surprise; Fasel and Luettin (2003)] Although the automatic recognition of action units to face images has not nearly received as much attention, there are still quite a few studies that investigate automatic action unit recognition; see Table 1. Similar to the system we present in this paper, most systems presented in earlier work consist of two main components: (1) a component that extracts features from the face images that are indicative of the presence of action units and (2) a component that learns to recognize action units based on these input features, i.e., a classifier. An overview of how other systems for action unit recognition implement these two components is given in Table 1.

Table 1.

Overview of the two main components of systems for action unit recognition

Study Features Classifier
Lien et al. (1998) Dense-flow tracking Hidden Markov model
Cohn et al. (1999) Tracked feature points Quadratic discriminant classifier
Fasel and Luettin (2000) Eigenfaces Nearest neighbor classifier
Bartlett et al. (2005, 2006) Gabor filters Boosting + support vector machine
Chang et al. (2006) Manifold learning Bayesian
Whitehill and Omlin (2006) Haar features Boosting
Littlewort et al. (2006) Gabor filters Boosting + support vector machine
Lucey et al. (2007) Active appearance model Support vector machine
Valstar et al. (2004) Motion history images Nearest neighbor classifier
Pantic and Rothkrantz (2004) Tracked feature points Rule base
Pantic and Patras (2005) Tracked feature points Rule base
Valstar and Pantic (2006, 2007) Tracked feature points Boosting + support vector machine
Tong et al. (2007, 2010) Gabor filters Boosting + dynamic bayesian network
Susskind et al. (2008) Normalized pixels Deep belief network
Koelstra et al. (2010) Free-form deformations Boosting + hidden Markov model
Open in a new tab

From the overview presented in the table, we observe that (1) features obtained from Gabor filters and (2) the locations of facial feature points are the most popular features. Gabor filters are local, high-frequency, oriented filters that resemble the filters implemented in the primate primal visual cortex V1 (Daugman 1985; Jones and Palmer 1987). Because a Gabor filter basis is highly overcomplete, a subset of filters has to be selected to obtain a feature representation with a manageable dimensionality. This subset of Gabor filters is typically selected by means of a technique called boosting (Freund and Schapire 1995). In our system, we do not use Gabor features (or boosting), but like many other studies listed in Table 1, we opt to use the location of tracked facial feature points as features for the action unit recognition. Such facial feature points contain information on the location of important parts of the face (eye corners, nostrils, mouth corners, etc.); the pixel values around the feature points contain information on the appearance of these face parts. Similar to Lucey et al. (2007), we use active appearance models to track facial feature points, but we extend their approach by extracting more sophisticated appearance features around the facial feature points identified by the tracker.

As for the classifiers that are used to perform predictions based on the extracted features, we observe that support vector machines (SVMs) are the most popular classifiers. Like the perceptron, SVMs separate the two classes (i.e., action unit present or not present) by a (hyper)plane, but they are less prone to overfitting than the perceptron (Vapnik 1995). Using the so-called “kernel trick” (Shawe-Taylor and Christianini 2004), SVMs can also be used to learn non-linear classifiers. A major shortcoming of standard SVMs, and of many of the other classifiers used in the previous work, is that they fail to incorporate the temporal structure of facial expressions. For instance, if we observe the intensity onset for a particular action unit in the current frame, we can be fairly confident that in a few frames this action unit reaches the state apex, even if the visual evidence for this state is limited (e.g., because part of the face is occluded). Previously proposed approaches fail to incorporate such knowledge. In our system, we do incorporate temporal information using linear-chain conditional random fields 1 (see "Conditional random fields")

Active appearance models

Active appearance models simultaneously describe the shape and texture variation of faces (Cootes et al. 1998; Matthews and Baker 2004). Herein, shape refers to the relative positions of feature points (such as eye corners, mouth corners, nose tip, etc.) in the face, whereas texture refers to the shape-normalized visual appearance of the face (for instance, eye color, skin color, malls, etc.). Active appearance models thus consist of two submodels: (1) a shape model that models the location of facial feature points and (2) a texture model that models the shape-normalized facial texture. We discuss the two models separately below in "Shape model" and "Texture model". "Combining the models" describes how the shape and the texture models are combined to construct the active appearance model. In "Fitting", we discuss how the active appearance model is fitted to a new face image.

Shape model

To train the shape model of an active appearance model, a data set of face images is required in which facial feature points—for instance, mouth corners, eye corners, and nose tip—are manually annotated. The feature points are required to be relatively dense, in such a way that a triangulation constructed on the feature points approximately captures the geometry of the face, i.e., in such a way that the imaginary triangles between the feature points correspond to roughly planar surfaces of the face. Three examples of annotated faces are shown in Fig. 1. The manual annotation of a collection of face images is time-consuming, but it only needs to be done once for a fixed collection of faces. If later on, we encounter a new face image, we can automatically determine the facial feature point locations by fitting the active appearance model on the new face image using the procedure described in "Fitting".

Fig. 1.

Fig. 1

Open in a new tab

Three examples of faces with manually annotated facial feature points shown as red crosses

To model the variation in facial feature point locations (due to differences in the shape of faces), we perform Principal Components Analysis (PCA) on normalized 2 facial feature point coordinates. PCA learns a model of the data that identifies (1) which facial feature points have the largest location variation and (2) how the variations in the locations of the facial feature points are correlated. In particular, PCA learns: (1) a base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}$$\end{document} that is formed by the mean of the normalized feature point coordinates averaged over the entire data set and (2) a linear basis S that contains the directions in which the facial feature points vary most. Together, the base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}$$\end{document} and the linear basis S allow us to model each plausible facial feature point configuration well (in the squared error sense) using a small number of shape parameters p. Given the vector of shape parameters p, the facial feature point configuration can be computed as \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\bf p}^{\rm T}{\bf S} + \varvec{\nu}$$\end{document}. The shape parameters p thus form a compact representation for the deviation of the face shape from the base shape.

An example of a shape model with four shape components is shown in Fig. 2. In the figure, red crosses indicate the location of the facial feature points in the base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}$$\end{document}, and blue arrows indicate the direction and magnitude of the variation in locations of each of the feature points (longer arrows represent a larger variance). For instance, the first component of the shape model represents the location of the mouth and jaw, the second component describes a forward rotation of the face, and the third describes small out-of-plane rotations, etc. (We note here that not all shape components are necessarily easily interpretable.)

Fig. 2.

Fig. 2

Open in a new tab

A shape model with four components. The red wire frame indicates the base shape. The blue arrows indicate the movement directions of the feature points (each component corresponds to one column of S)

Texture model

To model the facial texture (i.e., the shape-normalized appearance of faces), we use the feature point annotations to construct a data set of face images in which all feature points have exactly the same location. This is achieved by warping3 each face image onto the base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}$$\end{document} using the feature point annotations as control points. We can use the resulting shape-normalized face images to construct a texture model that describes features such as eye color, skin color, lip color, malls, etc.

Like the shape model, the texture model is also constructed using PCA. To construct the texture model, PCA is applied on the shape-normalized images. In other words, a low-dimensional texture representation is constructed in such a way, that as much of the pixel variance as possible is preserved. The texture model contains (1) a mean texture image \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\mu}$$\end{document} that is computed by averaging all shape-normalized face images and (2) a linear basis A that captures the main deviations from the mean texture image. The texture model allows us to model each plausible facial texture with low error (in the squared error sense) using only a small number of texture parameters \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\lambda}$$\end{document}. Given a texture parameter vector \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\lambda}$$\end{document}, a facial texture image can be constructed by evaluating \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\lambda}^{\rm T}{\bf A} + \varvec{\mu}$$\end{document}.

An example of a texture model with four components is depicted in Fig. 3. In the figure, bright areas in the images correspond to pixels in the (shape-normalized) facial texture data set with high variance. For instance, the second component models the closing of the eyes (blinking), whereas the fourth component models the opening of the mouth. The third and fourth components are also used to model the presence of glasses. (The first texture component models variations in the overall brightness of the face images.)

Fig. 3.

Fig. 3

Open in a new tab

A texture model with four components. The leftmost image represents the mean texture. The other images indicate deviations from the mean texture (each component corresponds to a single column of A)

Combining the models

To model the appearance of a face, the active appearance model combines the shape and texture models. The combination is performed by warping the texture image generated by the texture model onto the face shape generated by the shape model. Given the shape and texture parameters, the corresponding face is thus generated using a three-stage process. First, the shape model is used to generate a face shape, i.e., to lay out the facial feature points. Second, the texture model is used to generate a facial texture image. Recall that this texture image is defined in the coordinate frame of the base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}$$\end{document}. Third, the texture image is warped onto the face shape using the constructed feature points as control points to construct the final face image. This process is illustrated in Fig. 4.

Fig. 4.

Fig. 4

Open in a new tab

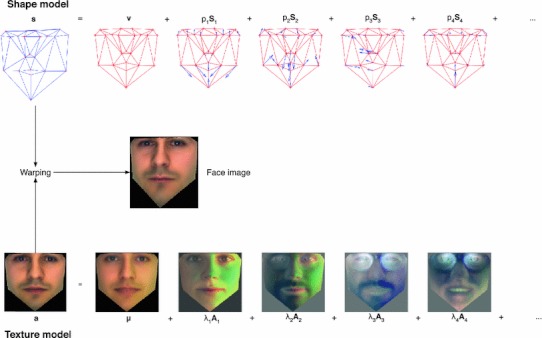
Generating a face from an active appearance model. The face shape is constructed by adding a linear combination of the shape components S to the base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}$$\end{document}. The facial texture is constructed by adding a linear combination of the texture components A to the mean texture \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\mu}$$\end{document}. The final face image is formed by warping the resulting facial texture onto the face shape

Fitting

When presented with a new face image, fitting aims to find a configuration of the shape parameters p and the texture parameters \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\lambda}$$\end{document} that minimizes the squared error between the face image and the face generated by the active appearance model. In the literature, several fitting algorithms have been proposed, e.g., by Matthews and Baker (2004); Gross et al. (2005); Papandreou and Maragos (2008). In our study, we use a fitting algorithm based on the project-out inverse compositional algorithm (Matthews and Baker 2004). This fitting algorithm performs the squared error minimization with respect to the shape parameters first; the shape parameters are set in such a way that the squared error between the shape-transformed mean texture and the observed face is minimized. Given the shape parameters, the corresponding texture parameters can be computed by solving a linear least-squares problem. The mathematical details of the project-out inverse compositional algorithm fall outside the scope of this paper but are described in detail by Matthews and Baker (2004). Our fitting procedure is initialized using a standard face detector (Viola and Jones 2001).

Feature extraction

Active appearance models identify facial feature points, and they provide a low-dimensional approximation of the facial texture, but they do not produce features that are indicative of the presence of action units in the face, i.e., they do not provide direct information about characteristics of the face that are of relevance to its facial expression. We investigate three types of features, all of which use the feature points identified by the active appearance models. The three features are discussed separately in the next three subsections.

Normalized shape variations

Changes in the location of facial feature points identified by the active appearance model are indicative of the presence of certain action units. For instance, large variations in the locations of feature points around the mouth may indicate the presence of action unit 27 (mouth stretch). Hence, we can use the differences between the locations of the feature points in the current frame and the location of the feature point in the first frame of each movie as features for action unit recognition. These differences are computed using a two-stage process. First, we normalize all frames in a movie with respect to the base shape to remove rigid transformations such as translations, rotations, and rescalings. Second, we subtract the resulting normalized shape coordinates of the first frame4 from the resulting normalized shape coordinates of the other frames to measure the changes in feature point locations. This process produces features that we refer to as normalized shape variation (NSV) features.

Shape-normalized texture variations

Normalized shape variation features do not possess information on the facial texture, such as the presence of wrinkles in the face. As a result, it may be hard to predict the presence of, e.g., action unit 24 (lip pressor), based on normalized shape variations. By contrast, the lip pressor is clearly visible in the texture of the face (as it makes most of the lip texture disappear). Using the feature point locations identified by the active appearance model allows us to extract shape-normalized texture features that capture such texture information. The features are extracted by warping the face image onto the base shape \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varvec{\nu}, $$\end{document} using the feature point locations as control points. This leads to texture images in which all feature points are in exactly the same location. Three examples of such shape-normalized textures are shown in Fig. 5. Due to the shape normalization, the differences between the texture images provide insight into the presence of wrinkles and other textural features (Ashraf et al. 2007). Similar to the normalized shape variations, we compute shape-normalized texture variation (SNTV) features by subtracting the shape-normalized textures from the the shape-normalized texture in the first frame.

Fig. 5.

Fig. 5

Open in a new tab

Three examples of shape-normalized facial textures. Note how the facial feature points (eye corners, mouth corners, nose tip, etc.) are in exactly the same location in the images

Scale-invariant feature transform

Pixel-based image representations such as shape-normalized texture variations are well known to have limitations for recognition tasks, because they are highly variable under, among others, changes in lighting (as illustrated by the first texture component in Fig. 3). To address this problem, image representations based on image gradients are often more successful (Lowe 2004; Ke and Sukthankar 2004; Dalal and Triggs 2005; Bay et al. 2008). A second problem of shape-normalized appearance features is that they may contain a lot of variables (i.e., regions in the face image) that are hardly indicative of the presence of action units, because their texture does not vary much under different expressions. Hence, local gradient-based image features may be more appropriate for action unit detection.

Scale-invariant feature transform (SIFT) features are local gradient-based image features introduced by Lowe (2004) that address both of these problems. SIFT features have been successfully used in a wide range of computer vision tasks [e.g., Sivic and Zisserman (2003); Brown and Lowe (2003); Quattoni et al. (2010)]. They construct a histogram of the magnitude and orientation of the image gradient in a small image patch around a facial feature point. The histogram consists of 16 orientation subhistograms, each of which has 8 bins, leading to a 128-dimensional feature (per feature point). The construction of the SIFT feature consists of three main steps: (1) the gradient magnitude and orientation at each pixel in the image patch are computed, (2) the gradient magnitudes are weighted using a Gaussian window that is centered onto the image patch, and (3) the weighted gradient magnitudes are accumulated into orientation histograms measured over subregions of size 4 × 4 pixels.

We compute SIFT features around all facial feature points around the eyebrows, eyes, nose, and mouth and concatenate the resulting feature vectors to construct a facial texture representation that contains information on the texture around these facial feature points.

Conditional random fields

Linear-chain conditional random fields are discriminative probabilistic models that are used for labeling sequential data (LeCun et al. 1998; Lafferty et al. 2001). Conditional random fields may be best understood by starting from the framework of linear logistic regression. A linear logistic regressor is a generalized linear model (GLM) for multinomial regression. It models the probability of a variable y having one of K states given the data x using a logistic (or soft-max) function

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ p(y=i|{\bf x})=\frac{\exp({\bf w}_i^{\rm T}{\bf x})}{\sum_{k=1}^K \exp({\bf w}_k^{\rm T}{\bf x})}. $$\end{document} 1

In the context of this paper, the event y may correspond to a certain action unit having one of K = 2 states: present or non-present. When more detailed intensity scores are available for the action units, the number of possible states increases. The data x corresponds to the features extracted from a face image. The regression weights w i are learned based on N labeled training data points \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\{(y_1, {\bf x}_1), (y_2,{\bf x}_2), \ldots (y_N,{\bf x}_N)\}$$\end{document}, i.e., based on pairs of images and their action unit labels. The learning is performed using a technique called maximum conditional likelihood, which maximizes the function \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathcal{L}=\sum_{n=1}^N \log p(y_n | {\bf x}_n)$$\end{document}. The function \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathcal{L}$$\end{document} has a single global maximum, which makes learning the regression weights relatively straightforward.

In our setting, we do not recognize action units in a collection of independent images, but in a collections of consecutive frames of a movie. Consecutive frames in a movie have strong dependencies, as the differences between two consecutive frames are typically small. Moreover, we often have prior knowledge on how action units are likely to behave; for instance, we could exploit our knowledge that is unlikely that an apex is followed by an onset (if we were recognizing these intensity scores). Hence, recognizing action units in each frame independently using a linear logistic regressor, without taking into account the temporal structure of facial expressions, would be very naive. It is exactly this naivety that conditional random fields aim to resolve.

Conditional random fields incorporate a temporal model between the label y t at time step t and the label y t+1 at time step t + 1. In particular, they learn a set of transition log probabilities \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\{{\bf v}_{1}, {\bf v}_{2}, \ldots, {\bf v}_{K}\}$$\end{document} that measure how likely it is that – in the next time step – one moves from one state to another. The log probability of moving from state y t to state y t+1 is given by v y_t, y_t+1. The conditional random field thus has two sets of parameters: transition log probabilities v and regression weights w. Together, these parameters determine the probability of a label sequence \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$y_1, y_2, \ldots, y_T$$\end{document} given a data sequence \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\bf x}_1, {\bf x}_2, \ldots, {\bf x}_T$$\end{document}. Like in logistic regression, the training is performed by maximizing the conditional log likelihood, which is now given by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathcal{L} = \sum_{n=1}^N \log p(y_{n1}, y_{n2}, \ldots, y_{nT} | {\bf x}_{n1}, {\bf x}_{n2}, \dots, {\bf x}_{nT})$$\end{document} with respect to the transition log probabilities and the regression weights. In other words, conditional random fields aim to maximize the likelihood of a label sequence. The function \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathcal{L}$$\end{document} still has a single global maximum, which makes training relatively straightforward. In our experiments, we used a stochastic gradient descent algorithm (Robbins and Monro 1951; Bottou 2004) to learn the parameters of the conditional random fields.

The prediction of frame labels on an unseen test sequence using conditional random fields is straightforward; it amounts to evaluating the posterior distribution over the label sequence \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$p(y_{1}, y_{2}, \dots, y_{T} | {\bf x}_{1}, {\bf x}_{2}, \ldots, {\bf x}_{T})$$\end{document} (which is exactly the distribution that is modeled by the conditional random field). Evaluating this distribution can be performed efficiently (Viterbi 1967), and it gives a value for each frame that indicates the probability that an action unit is present in that particular frame. Subsequently, we can apply a threshold on these probabilities to construct the final annotation; for instance, we can choose5 to label an action unit as present in a frame if its probability of being present is larger than 0.5.

Experiments

This section describes our experiments with the action unit recognition system described above. The data set we used as the basis for our experiments is described in "Data set". We discuss the setup of the experiments in "Experimental setup" and the results of our experiments in "Results".

Data set

In our automatic action unit recognition experiments, we performed experiments on version 2 of the Cohn--Kanade data set6 [also referred to as the CK+ data set; Lucey et al. (2010)]. The data set contains 593 short movies of 123 subjects producing posed expressions. Together, the movies contain 10,734 frames (i.e., images); the average length of a movie is 18.1 frames. All movies were annotated for the presence and non-presence of action units by two human FACS labelers. In our experiments, we only considered action units that are present relatively often. The action units we focused on are listed in Table 2.

The face images range in size between 640 × 490 and 720 × 480 pixels; the size of the face area in the images ranges between 250 × 250 and 300 × 300 pixels. A small number of movies is in full color, but the majority of the movies are in grayscale. For convenience, we converted all movies to grayscale in our experiments.

Experimental setup

For the shape model of the active appearance model, we determine the number of shape components by preserving 90% of the variance in the facial feature point locations. The number of texture components in the texture model is also determined by preserving 90% of the variance in the shape-normalized appearance (i.e., texture) of the faces. The conditional random fields are trained on the features that are extracted from the faces.

The evaluation of the performance of our system is performed using an approach called leave-one-subject-out cross-validation. This means that we perform a separate experiment for each of the 123 subjects: We leave out all movies containing that subject from the data and train the conditional random fields on the remaining data. Subsequently, we evaluate the performance of the conditional random fields on the movies that contain the held-out subject. This allows us to investigate how well our system works on new, unseen human subjects. The performance of the conditional random fields is averaged over all 123 runs.

We measure the performance of our automatic FACS annotation system by measuring the area under the receiver operating characteristic (ROC) curve. The ROC curve plots the rate of false positives against the true positive rate for various thresholds. The area under the ROC curve (AUC) summarizes the quality of the annotator in a single value: It measures the probability that the classifier assigns a higher score to a randomly selected positive example than to a randomly selected negative example (Bradley 1997). For a completely random annotator, this probability (i.e., the AUC) is 0.5, whereas the AUC is 1 for a perfect annotator. To give an indication of the uncertainty in the AUC values, we also present an upper bound on this uncertainty proposed by Cortes and Mohri (2005). In particular, the uncertainty measure is given by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$u = \frac{\sqrt{AUC (1-AUC)}}{\max(N_p, N_n)}$$\end{document}, where N p represents the number of positive examples and N n represents the number of negative examples.

Results

In Table 3, we present the results of training and testing conditional random fields on the three types of features presented in "Feature extraction". We also present results obtained using a feature representation that was obtained by performing PCA on the combination of three features. The results are average AUC values obtained using leave-one-subject-out cross-validation and upper bounds on the AUC uncertainties.

Table 3.

Averaged areas under the curve (AUCs) obtained by training conditional random fields on the feature sets

AU Name NSV SNTV SIFT Combined
1 Inner Brow Raiser 0.8947 ± 0.0232 0.8834 ± 0.0243 0.8170 ± 0.0292 0.8545 ± 0.0267
2 Outer Brow Raiser 0.9278 ± 0.0239 0.9270 ± 0.0240 0.8642 ± 0.0317 0.8630 ± 0.0318
4 Brow Lowerer 0.8277 ± 0.0271 0.8667 ± 0.0244 0.8078 ± 0.0283 0.8581 ± 0.0251
5 Upper Lip Raiser 0.8857 ± 0.0315 0.9070 ± 0.0288 0.8723 ± 0.0330 0.8326 ± 0.0370
6 Cheek Raiser 0.8740 ± 0.0299 0.8691 ± 0.0304 0.8756 ± 0.0298 0.8685 ± 0.0305
7 Lip Tightener 0.8484 ± 0.0326 0.8633 ± 0.0312 0.8277 ± 0.0343 0.8131 ± 0.0354
9 Nose Wrinkler 0.9415 ± 0.0271 0.9401 ± 0.0274 0.8960 ± 0.0352 0.8782 ± 0.0378
11 Nasolabial Deep. 0.8818 ± 0.0554 0.9270 ± 0.0446 0.8766 ± 0.0564 0.8799 ± 0.0558
12 Lip Corner Puller 0.9171 ± 0.0241 0.9222 ± 0.0234 0.8813 ± 0.0283 0.9066 ± 0.0254
15 Lip Corner Depr. 0.9178 ± 0.0282 0.9239 ± 0.0272 0.8939 ± 0.0316 0.8700 ± 0.0345
17 Lower Lip Depr. 0.9017 ± 0.0209 0.9125 ± 0.0198 0.8397 ± 0.0257 0.8669 ± 0.0238
20 Lip Stretcher 0.8713 ± 0.0377 0.8918 ± 0.0349 0.7810 ± 0.0465 0.8430 ± 0.0409
23 Lip Tightener 0.9399 ± 0.0307 0.9412 ± 0.0304 0.9128 ± 0.0364 0.8864 ± 0.0410
24 Lip Pressor 0.9275 ± 0.0341 0.9408 ± 0.0310 0.9179 ± 0.0361 0.8895 ± 0.0412
25 Lips Part 0.9075 ± 0.0177 0.8961 ± 0.0186 0.8816 ± 0.0197 0.9132 ± 0.0172
26 Jaw Drop 0.8847 ± 0.0452 0.8876 ± 0.0447 0.8771 ± 0.0464 0.8176 ± 0.0546
27 Mouth Stretch 0.9455 ± 0.0252 0.9459 ± 0.0251 0.9073 ± 0.0322 0.8958 ± 0.0340
ALL Averaged 0.8997 ± 0.0303 0.9086 ± 0.0288 0.8665 ± 0.0342 0.8669 ± 0.0349
Open in a new tab

All AUCs are computed using leave-one-subject-out cross-validation. An upper bound on the uncertainty of the AUCs is also presented. Best performance for each action unit is boldfaced. See text for details

From the results presented in the table, we observe that the performance of our system is strong; the best feature set has an average AUC of 0.901, with AUCs for individual action units ranging between 0.867 (on action unit 4; brow lowerer) and 0.946 (on action unit 27; mouth stretch). In order to give a reference frame for the quality of these results, a true positive rate of 0.70 is sufficient to pass FACS certification tests (Ekman and Rosenberg 2005). It thus seems likely that our system would pass such tests.

From the results, we also observe that appearance-based features typically outperform feature point locations; the normalized shape features only outperform appearance-based features on action units that lead to large feature point variations, such as the inner and outer brow raisers. Furthermore, we observe our combined features perform disappointingly; presumably, a better approach to combine the features is to train classifiers on each of the features and to linearly combine the predictions of these classifiers (Bell and Koren 2007).

Discussion

Although the results presented in "Experiments" are promising, some important issues remain. An important issue of our action unit recognition system and of most similar systems is that their performance is typically not very robust under out-of-plane rotations or partial occlusions of the face. We did not evaluate the performance of our system in such situations, because up to the best of our knowledge, there are no publicly available databases that contain FACS-coded videos with out-of-plane rotations and/or occlusions 7. As a result of the lack of such data, today’s systems are still trailing behind human observers; in particular, because the human visual system is remarkably robust to variations such as rotations and occlusions. Nonetheless, it is likely that our system would pass FACS certification tests (these tests require a true positive rate of at least 70%).

Another issue of the action unit recognition system we described (and of other recently developed systems) is that it heavily relies on the availability of facial expression videos that are labeled by human FACS annotators. In practice, the availability of such FACS-labeled data is often limited because of the high costs that are associated to manual FACS labeling. To address this issue, it may be helpful to employ approaches for semi-supervised learning (i.e., using unlabeled data to improve the action unit detectors) and/or active learning (i.e., learning which instances should be manually labeled).

The potential of systems such as the one presented in this paper extends far beyond automatically recognizing action units in data gathered by, e.g., social psychologists. In particular, automatic action unit recognition may provide a good basis for the recognition of higher-level cognitive states like interest and puzzlement (Cunningham et al. 2004) or (dis)agreement (Bousmalis et al. 2009) and for the recognition of psychological problems such as suicidal depressions (Ekman and Rosenberg 2005), pain (Williams 2003), or schizophrenia (Wang et al. 2008). Other potential applications of our system include understanding social behaviors such as accord and rapport (Ambady and Rosenthal 1992; Cunningham et al. 2004), identifying social signals such as status or trustworthiness (Ambady and Rosenthal 1992; Ekman and Friesen 1969; Ekman et al. 2002), predicting the success of marriage counseling (Gottman et al. 2001), and identifying personality traits such as extraversion and temperament (Ekman and Rosenberg 2005). An extensive overview of applications of automatic facial expression measurement is given by Bartlett and Whitehill (2010). Applications of our system may also exploit the generative capabilities of the active appearance model. For instance, the model may be used to investigate the effect of small changes in facial appearance on human perception (Boker et al. 2007) or for experiments with expression cloning (Theobald et al. 2007).

Concluding remarks

We developed a system for automatic action unit recognition. Our system uses conditional random fields to predict action unit states from features extracted using active appearance models. The performance of our system is promising, and it can be used in real time.

In future work, we aim to extend the conditional random fields to exploit correlations between action units (Sutton et al. 2007; Tong et al. 2010): For instance, if we detect the presence of action unit AU12, the probability that AU13 or AU14 is also present increases; our models should exploit this information. In addition, we intend to employ semi-supervised and active learning to obtain good performance at low labeling costs.

We also intend to use our system to detect basic emotions as well as higher-level social signals by learning mappings from action unit labels to these emotions/signals. In particular, we intend to use our system for the recognition of agreement/disagreement (Bousmalis et al. 2009; Poggi et al. 2010). We note that in a system that recognizes agreement/disagreement, more features that only AU presence should be taken into account; in particular, successfully recognizing agreement/disagreement requires the detection of nods and shakes (Kapoor and Picard 2001; Tan and Rong 2003; Kang et al. 2006).

Acknowlegments

Laurens van der Maaten is supported by the EU-FP7 Network of Excellence on Social Signal Processing (SSPNet), and by the Netherlands Organization for Scientific Research (NWO; Rubicon grant no. 680.50.0908).

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Footnotes

1

As an alternative, we could have incorporated temporal information using structured SVMs (Tsochantaridis et al. 2005).

2

The normalization removes translations, rotations, and rescalings of the face that are irrelevant for expression analysis.

3

In our implementation, we use a so-called piecewise linear warp.

4

As an alternative, one could subtract the coordinates from the previous frame instead. This would presumably work better in online settings, or on very long videos.

5

In our experimental evaluation, we try many thresholds and average the performance over all these thresholds (see 2 for details).

6

The Cohn--Kanade data set is publicly available from http://www.vasc.ri.cmu.edu/idb/html/face/facial_expressio.

7

We note here that there is an extension of the Cohn--Kanade database under development that does contain out-of-plane rotations (Lucey et al. 2010).

This article is part of the Supplement Issue on “Social Signals. From Theory to Applications,” guest-edited by Isabella Poggi, Francesca D'Errico, and Alessandro Vinciarelli.

Contributor Information

Laurens van der Maaten, Email: lvdmaaten@gmail.com.

Emile Hendriks, Email: E.A.Hendriks@tudelft.nl.

References

  1. Ambady N, Rosenthal R. Thin slices of expressive behavior as predictors of interpersonal consequences: a meta-analysis. Psychol Bull. 1992;111(2):256–274. doi: 10.1037/0033-2909.111.2.256. [DOI] [Google Scholar]
  2. Ashraf A, Lucey S, Cohn J, Chen T, Ambadar Z, Prkachin K, Solomon P, Theobald B-J (2007) The painful face: pain expression recognition using active appearance models. In: Proceedings of the 9th international conference on multimodal interfaces, pp 9–14
  3. Bartlett M, Whitehill J Automated facial expression measurement: recent applications to basic research in human behavior, learning, and education. In: Calder A, Rhodes G, Haxby JV, Johnson MH (eds) Handbook of face perception. Oxford University Press, Oxford (2010)
  4. Bartlett M, Littlewort G, Frank M, Lainscsek C, Fasel I, Movellan J (2005) Recognizing facial expression: machine learning and application to spontaneous behavior. In: Proceedings of the IEEE conference on computer vision and pattern recognition, vol 2, pp 568–573
  5. Bartlett M, Littlewort-Ford G, Frank M, Lainscsek C, Fasel I, Movellan J (2006) Fully automatic facial action recognition in spontaneous behavior. In: Proceedings of the IEEE conference on face and gesture recognition, pp 223–230
  6. Bay H, Ess A, Tuytelaars T, van Gool L. Surf: Speeded up robust features. Comput Vis Image Underst. 2008;110(3):346–359. doi: 10.1016/j.cviu.2007.09.014. [DOI] [Google Scholar]
  7. Bell RM, Koren Y. Lessons from the Netflix prize challenge. ACM SIGKDD Explor Newslett. 2007;9(2):75–79. doi: 10.1145/1345448.1345465. [DOI] [Google Scholar]
  8. Boker SM, Cohn JF, Theobald B-J, Matthews I, Brick T, Spies J. Effects of damping head movement and facial expression in dyadic conversation using real-time facial expression tracking and synthesized avatars. Philos Trans B R Soc. 2007;364(1535):3485–3495. doi: 10.1098/rstb.2009.0152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bottou L (2004) Stochastic learning. In: Bousquet O, von Luxburg U (eds) Advanced lectures on machine learning, pp 146–168
  10. Bousmalis K., Mehu M., Pantic M. (2009) Spotting agreement and disagreement: a survey of nonverbal audiovisual cues and tools. In: Proceedings of the international conferences on affective computation and intelligent interaction
  11. Bradley AP. The use of the area under the roc curve in the evaluation of machine learning algorithms. Patt Recog. 1997;30(7):1145–1159. doi: 10.1016/S0031-3203(96)00142-2. [DOI] [Google Scholar]
  12. Brown M, Lowe DG (2003) Recognising panoramas. In: Proceedings of the 9th IEEE international conference on computer vision, vol 2, pp 1218–1225
  13. Chang Y, Hu C, Feris R, Turk M. Manifold-based analysis of facial expression. J Image Vis Comput. 2006;24(6):605–614. doi: 10.1016/j.imavis.2005.08.006. [DOI] [Google Scholar]
  14. Cohn J, Zlochower A, Lien JJ, Kanade T. Automated face analysis by feature point tracking has high concurrent validity with manual FACS coding. Psychophysiology. 1999;36:35–43. doi: 10.1017/S0048577299971184. [DOI] [PubMed] [Google Scholar]
  15. Cootes TF, Edwards G, Taylor CJ (1998) Active appearance models. In: Proceedings of the European conference on computer vision, vol 2, pp 484–498
  16. Cortes C, Mohri M (2005) Confidence intervals for the area under the ROC curve. In: Advances in neural information processing systems, pp 305–312
  17. Cunningham DW, Kleiner M, Bülthoff HH, Wallraven C (2004) The components of conversational facial expressions. In: Proceedings of the symposium on applied perception in graphics and visualization, pp 143–150
  18. Dalal N, Triggs B (2005) Histograms of oriented gradients for human detection. In: Proceedings of the IEEE conference on computer vision and pattern recognition, vol 2, pp 886–893
  19. Daugman G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. J Opt Soc Am. 1985;2(7):1160–1169. doi: 10.1364/JOSAA.2.001160. [DOI] [PubMed] [Google Scholar]
  20. Ekman P, Friesen WV. The repertoire of nonverbal behavior. Semiotica. 1969;1(1):49–98. [Google Scholar]
  21. Ekman P, Friesen WV. Facial action coding system: a technique for the measurement of facial movement. Palo Alto: Consulting Psychologists Press; 1978. [Google Scholar]
  22. Ekman P, Rosenberg E. What the face reveals, 2nd edn. New York: Oxford; 2005. [Google Scholar]
  23. Ekman P, Friesen WV, Hager JC (2002) Facial action coding system (FACS): manual
  24. Fasel B, Luettin J (2000) Recognition of asymmetric facial action unit activities and intensities. In: Proceedings of the 15th international conference on pattern recognition
  25. Fasel B, Luettin J. Automatic facial expression analysis: a survey. Patt Recogn. 2003;36(1):259–275. doi: 10.1016/S0031-3203(02)00052-3. [DOI] [Google Scholar]
  26. Freund Y, Schapire RE (1995) A decision-theoretic generalization of on-line learning and an application to boosting. In: Computational learning theory: Eurocolt ’95, Springer, pp 23–37
  27. Del Giudice M, Colle L. Differences between children and adults in the recognition of enjoyment smiles. Dev Psychol. 2007;43(3):796–803. doi: 10.1037/0012-1649.43.3.796. [DOI] [PubMed] [Google Scholar]
  28. Gottman J, Levenson R, Woodin E. Facial expressions during marital conflict. J Family Commu. 2001;1:37–57. doi: 10.1207/S15327698JFC0101_06. [DOI] [Google Scholar]
  29. Gross R, Matthews I, Baker S. Generic versus person specific active appearance models. Image Vis Comput. 2005;23:1080–1093. doi: 10.1016/j.imavis.2005.07.009. [DOI] [Google Scholar]
  30. Jones JP, Palmer LA. An evaluation of the two-dimensional Gabor filter model of simple receptive fields in cat striate cortex. J Neurophysiol. 1987;58(6):1233–1258. doi: 10.1152/jn.1987.58.6.1233. [DOI] [PubMed] [Google Scholar]
  31. Kang YG, Joo HJ, Rhee PK (2006) Real time head nod and shake detection using HMMs. In: Lecture notes in computer science, vol 4253, pp 707–714
  32. Kapoor A, Picard RW (2001) A real-time head nod and shake detector. In: Proceedings of the 2001 workshop on perceptive user interfaces
  33. Ke Y, Sukthankar R (2004) Pca-sift: a more distinctive representation for local image descriptors. In: Proceedings of the IEEE computer society conference on computer vision and pattern recognition, vol 2, pp 506–513
  34. Koelstra S, Pantic M, Patras I. A dynamic texture-based approach to recognition of facial actions and their temporal models. IEEE Trans Patt Anal Mach Intell. 2010;32(11):1940–1954. doi: 10.1109/TPAMI.2010.50. [DOI] [PubMed] [Google Scholar]
  35. Lafferty J, McCallum A, Pereira F (2001) Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In: Proceedings of the international conference on machine learning, pp 282–289
  36. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–2324. doi: 10.1109/5.726791. [DOI] [Google Scholar]
  37. Lien JJ, Kanade T, Cohn JF, Ching-Chung L (1998) Automated facial expression recognition based on facs action units. In: Proceedings of the IEEE international conference on automonas face and gesture recognition, pp 390–395
  38. Littlewort G, Bartlett M, Fasel I, Susskind J, Movellan J. Dynamics of facial expression extracted automatically from video. Image Vis Comput. 2006;24(6):615–625. doi: 10.1016/j.imavis.2005.09.011. [DOI] [Google Scholar]
  39. Lowe DG. Distinctive image features from scale-invariant keypoints. Int J Comput Vis. 2004;60(2):91–110. doi: 10.1023/B:VISI.0000029664.99615.94. [DOI] [Google Scholar]
  40. Lucey P, Cohn JF, Kanade T, Saragih J, Ambadar Z, Matthews I (2010) The extended Cohn-Kanade dataset (CK+): a complete dataset for action unit and emotion-specified expression. In: IEEE computer society conference on computer vision and pattern recognition workshops (CVPRW), pp 94–101
  41. Lucey S, Ashraf A, Cohn J (2007) Investigating spontaneous facial action recognition through AAM representations of the face. In: Delac K, Grgic M (eds) Face recognition, pp 275–286
  42. Matthews I, Baker S. Active appearance models revisited. Int J Comput Vis. 2004;60(2):135–164. doi: 10.1023/B:VISI.0000029666.37597.d3. [DOI] [Google Scholar]
  43. Pantic M, Patras I (2005) Detecting facial actions and their temporal segments in nearly frontal-view face image sequences. In: Proceedings of the IEEE conference on systems, man and cybernetics, vol 4, pp 3358–3363
  44. Pantic M, Rothkrantz LJM. Facial action recognition for facial expression analysis from static face images. IEEE Trans Syst Man Cybern B Cybern. 2004;34(3):1449–1461. doi: 10.1109/TSMCB.2004.825931. [DOI] [PubMed] [Google Scholar]
  45. Papandreou G, Maragos P (2008) Adaptive and constrained algorithms for inverse compositional active appearance model fitting. In: Proceedings of the international conference on computer vision and pattern recognition, pp 1–8
  46. Phillips PJ, Flynn PJ, Scruggs T, Bowyer KW, Chang J, Hoffman K, Marques J, Min J, Worek W (2005) Overview of the face recognition grand challenge. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp 947–954
  47. Poggi I, DErrico F, Vincze L (2010) Agreement and its multimodal communication in debates. a qualitative analysis. Cogn Comput 1–14
  48. Quattoni A, Wang S, Morency LP, Collins M, Darrell T (2010) Hidden conditional random fields. IEEE Trans Patt Anal Mach Intell 29(10) [DOI] [PubMed]
  49. Robbins H, Monro S. A stochastic approximation model. Ann Math Stat. 1951;22:400–407. doi: 10.1214/aoms/1177729586. [DOI] [Google Scholar]
  50. Shawe-Taylor J, Christianini N. Kernel methods for pattern analysis. Cambridge: Cambridge Univ. Press; 2004. [Google Scholar]
  51. Sivic J, Zisserman A (2003) Video google: a text retrieval approach to object matching in videos. In: Proceedings of the IEEE international conference on computer vision, vol 2, pp 1470–1478
  52. Susskind JM, Hinton GE, Movellan JR, Anderson AK Generating facial expressions with deep belief nets. In: Or J (eds) Affective computing, focus on emotion expression, synthesis and recognition. ARS Publishers, India (2008)
  53. Sutton C, McCallum A, Rohanimanesh K. Dynamic conditional random fields: Factorized probabilistic models for labeling and segmenting sequence data. J Mach Learn Res. 2007;8(Mar):693–723. [Google Scholar]
  54. Tan W, Rong G. A real-time head nod and shake detector using HMMs. Expert Syst Appl. 2003;25:461–466. doi: 10.1016/S0957-4174(03)00088-5. [DOI] [Google Scholar]
  55. Theobald BJ, Matthews IA, Cohn JF, Baker SM (2007) Real-time expression cloning using appearance models. In: Proceedings of the international conference on multimodal interfaces, pp 134–139
  56. Tong Y, Liao W, Ji Q. Facial action unit recognition by exploiting their dynamic and semantic relationships. Trans Pattern Anal Mach Intell. 2007;29(10):1683–1699. doi: 10.1109/TPAMI.2007.1094. [DOI] [PubMed] [Google Scholar]
  57. Tong Y, Chen J, Ji Q. A unified probabilistic framework for spontaneous facial action modeling and understanding. IEEE Trans Pattern Anal Mach Intell. 2010;32(2):258–273. doi: 10.1109/TPAMI.2008.293. [DOI] [PubMed] [Google Scholar]
  58. Tsochantaridis I, Joachims T, Hofmann T, Altun Y. Large margin methods for structured and interdependent output variables. J Mach Learn Res. 2005;6:1453–1484. [Google Scholar]
  59. Valstar M, Pantic M (2006) Fully automatic facial action unit detection and temporal analysis. In: Proceedings of the IEEE conference on computer vision and pattern recognition, p 149
  60. Valstar M, Pantic M (2007) Combined support vector machines and hidden markov models for modeling facial action temporal dynamics. In: Lecture notes on computer science, vol 4796, pp 118–127
  61. Valstar M, Pantic M, Patras I (2004) Motion history for facial action detection from face video. In: Proceedings of the IEEE conference on systems, man and cybernetics, pp 635–640
  62. Vapnik V. The nature of statistical learning theory. Berlin: Springer; 1995. [Google Scholar]
  63. Vinciarelli A, Pantic M, Bourlard H. Social signal processing: survey of an emerging domain. Image Vis Comput. 2009;27:1743–1759. doi: 10.1016/j.imavis.2008.11.007. [DOI] [Google Scholar]
  64. Viola P, Jones M (2001) Rapid object detection using a boosted cascade of simple features. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 511–518
  65. Viterbi AJ. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans Inform Theory. 1967;13(2):260–269. doi: 10.1109/TIT.1967.1054010. [DOI] [Google Scholar]
  66. Wang P, Barrett F, Martin E, Milonova M, Gurd R, Gurb R, Kohler C, Verma R. Automated video-based facial expression analysis of neuropsychiatric disorders. J Neurosci Methods. 2008;168:224–238. doi: 10.1016/j.jneumeth.2007.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Whitehill J, Omlin C (2006) Haar features for FACS AU recognition. In: Proceedings of the IEEE international conference on face and gesture recognition
  68. Williams ACC. Facial expression of pain: an evolutionary account. Behav Brain Sci. 2003;25(4):439–455. doi: 10.1017/s0140525x02000080. [DOI] [PubMed] [Google Scholar]

Articles from Cognitive Processing are provided here courtesy of Springer

RESOURCES