A Simple Robust Orthogonal Background Correction Method for Two-Dimensional Liquid Chromatography

Abstract

Background correction is a very important step that must be done before peak detection or any quantification procedure. When successful, this step greatly simplifies such procedures and enhances the accuracy of quantification. In the past, much effort has been invested to correct drifting baseline in one dimensional chromatography. In fast online comprehensive two-dimensional liquid chromatography (LC×LC) coupled with diode array detector (DAD), the change in the refractive index (RI) of the mobile phase in very fast gradients causes extremely serious baseline disturbances. The method reported here can be combined with many of existing baseline correction methods for one dimensional (1D) chromatography in two dimensional (2D) liquid chromatography and recreate the background structure for further correction. When such methods are applied orthogonally to the second dimension (²D), the background correction is dramatically improved. It results in an almost zero mean background level and it provides better background correction than does a simple subtraction of a blank. Indeed, the method proposed does not require running a blank sample.

INTRODUCTION

Peak detection is one of the key steps in the overall data analysis process, especially in metabolomic studies ¹. This process is greatly affected by the background signal which can show considerable variations with time. Background correction is a very important step that should be addressed prior to any quantitative analysis to reduce the difficulty of peak detection and enhance the quality of the quantitative results ^2,3.

It has been shown that, when a first dimension (¹D) peak is sampled into the ²D, both the peak height and area of the resulting series of ²D peaks will adequately represent the ¹D peak, even with different sampling phases, provided that at least three samples are taken across the ¹D peak ⁴. When peaks are not fully resolved, finding the integration limits becomes more difficult. In this situation, peak height is recommended for quantitative purposes ⁵. Even with integration limits properly assigned, when for example an incompletely resolved small peak elutes before a larger peak, the peak height is strongly recommended over the peak area as a quantitative measurement of the smaller peak ⁶.

The peak height, along with the height of the second derivative of the signal, can be a robust method to determine the peak width when peaks are not fully resolved ⁷. For this reason, correcting the baseline is important to obtain the correct peak height and calculate the peak width. If the baseline has significant drift, the peak height can be greatly affected and correcting the baseline becomes critical. The magnitude of the effect of the baseline in peak quantification can be very different depending on the shape of the baseline, the region in the chromatogram where the peaks elute and also on the relative height of the peak.

When background signals are not corrected, chemometric analysis can be affected because most of the variance of the dataset might be due to the baseline ⁸. While the method developed in this work is illustrated with univariate data, it can be applied to all channels in a multivariate dataset.

In this work, an orthogonal background correction (OBGC) method is developed and shown to be very useful for correcting the complex DAD background signals in fast online LC×LC.

EXPERIMENTAL

Two types of data were employed in this work to show and discuss the principle of the OBGC method. The first data type consists of real LC×LC chromatographic data acquired in this lab. The second data type is hybrid data created by adding simulated 2D Gaussian peaks to a series of real replicates of the background acquired by doing experimental dummy (blank) LC×LC runs.

Real Dataset

The chromatograms corresponding to online LC×LC runs, where gradient elution was used in both ¹D and ²D, are explained in detail in our previous work ⁹. A general description of the conditions is provided here:

The ¹D column was a Zorbax Bonus-RP 100 mm long by 2.1 mm internal diameter packed with 3.5 μm particles (Agilent Technologies, Inc., Wilmington, DE). The ¹D eluent was 10 mM phosphate buffer (pH: 5.7) on channel A and acetonitrile on channel B. A linear gradient program was used from 0 to 24 min, 0 to 50 % of channel B. At 24.01 min the program changed to initial conditions. The flow rate in the column was 0.1 mL/min and temperature was controlled at 40 °C.

The ²D column was an in-house 33 mm long by 2.1 mm internal diameter packed with 3.0 Em ZirChrom-CARB particles (ZirChrom Separations, Anoka, MN). The mobile phase was 10 mM phosphoric acid on channel A and acetonitrile on channel B. A linear gradient was used from 0 to 0.30 min, 0 to 100 % of channel B. At 0.31 min the gradient returned to the initial conditions allowing 3 s for system re-equilibration, corresponding to a cycle time of 21 s. The flow rate in the column was 3.0 mL/min and the temperature was controlled at 110 °C.

A standard mixture of various indole derivatives was injected, using the same conditions as previously described. The experimental procedure for sample preparation and system configuration is described in detail in the given reference ⁹.

Hybrid Dataset

A simple in-house program was developed using Matlab R14 (R2011b, The Mathworks Inc, MA) to simulate 20 2D Gaussian peaks using the following equation:

$$\mathit{Signal}=\mathit{Area}\times exp-\frac{1}{2}\left({\left(\frac{X-{{}^{1}t}_R}{{}^1\sigma }\right)}^2+{\left(\frac{Y-{{}^{2}t}_R}{{}^2\sigma }\right)}^2\right)$$

where X and Y correspond to the independent variable on each dimension; ¹t_R and ²t_R are the retention time of the ¹D and ²D; ¹σ and ²σ are the standard deviation of the Gaussian peak on the ¹D and ²D respectively.

The retention times in both dimensions for each peak were pseudo-randomly generated (uniformly distributed) using the rand() function provided in Matlab. The peak height was also pseudo-randomly generated (exponentially distributed) using an average peak height of 20. The generated 2D peaks were then added to the corresponding data matrix of real LC×LC chromatograms acquired from five replicate dummy runs. In this way, the characteristics of the peaks were perfectly known and the background was representative of real experiments.

Experimental Conditions for the Dummy Runs

Chemicals

Chromatographic grade water and acetonitrile were obtained from Fisher Scientific (Pittsburg, PA). Reagent grade perchloric acid was purchased from Mallinkdrodt-Baker (Paris, KY). All materials were used as received. All mobile phases were prepared gravimetrically (± 0.01 g) and used without any further filtration. Chromatographic conditions: The mobile phases used for both the ¹D and ²D were 10 mM perchloric acid in water in channel A and acetonitrile in channel B. In the ¹D, the column used was a Zorbax SB-C3 100 mm long by 4.6 mm internal diameter, packed with 3.5 Em particles (Agilent Technologies, Inc., Wilmington, DE). The gradient was 0–56 % B in 0–24.5 min, 0 % B at 24.51 min. The flow rate in the ¹D column was 0.5 mL/min and the flow rate in the splitting pump was 0.1 mL/min ¹⁰. The column was maintained at a temperature of 40 °C. In the ²D, the column was the same as previously described for the ²D of the Real Dataset. The gradient was 0–100 % B in 0–0.15 min, 0 % B at 0.16 min. The cycle time was 0.2 min (12 s). The flow rate was 3 mL/min with the column maintained at a temperature of 110 °C. The instrument configuration was the same as in a previous publication from this group, using the split mode ¹⁰.

Data Processing

All data were acquired by Agilent Chemstation software version B.04.03 (Agilent Technologies GmbH, Waldbronn, Germany) as a single chromatogram for each LC×LC run and then exported as a comma separated values (csv) file and processed using Matlab with in-house written programs.

Convention and Nomenclature

The terminology adopted for this work is as much as possible in agreement with the recent update by Marriot et al. ¹¹.

RESULTS AND DISCUSSION

Background Structure in Fast Online LC×LC-DAD

Many authors have shown that using a gradient in both dimensions in LC×LC is the best way to maximize the peak capacity ^12–13. When gradient elution is used, the change in mobile phase composition causes drifts in the baseline due to two different effects: (1) the difference in absorbance between the blended solvents and (2) changes in the refractive index (RI) of the mobile phase. Since the ²D gradients have to be very fast (e.g.: 100 % in 9 s gradient for 12 s cycle time) to minimize the undersampling effect ¹⁴, the baseline is greatly affected, as shown in Figure 1 for an 18 s gradient with 3 s of re-equilibration time (21 s cycle time).

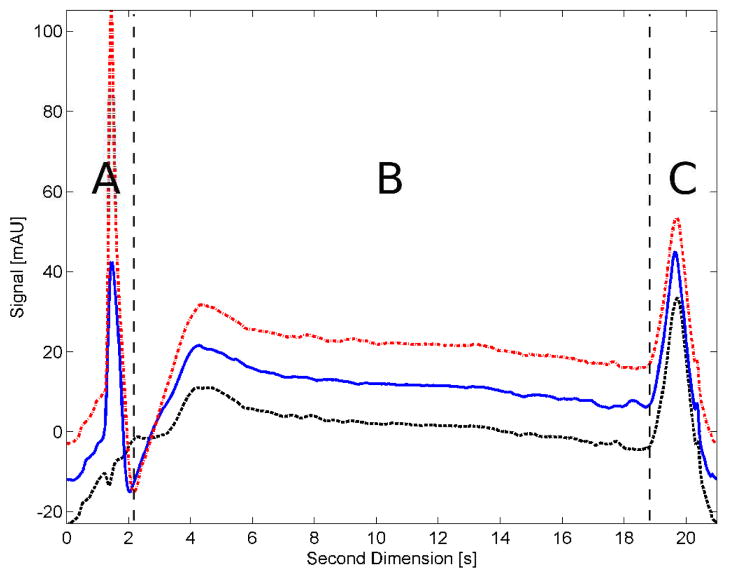
Figure 1.

Structure of the LC×LC background represented by three single ²D chromatograms of a dummy run sampled at different times of the gradient in the ¹D. The amount of acetonitrile in the sample solvent transferred from the ¹D to the ²D (region A) corresponds to 10 % for the black dotted curve, 30 % for the blue curve and 50 % for the red dashed curve. Region B is where most peaks elute and region C shows the system flush-out peak.

Structure of the LCxLC Background

Figure 1 shows three single ²D chromatograms of an entire LC×LC run (typically about 90 single ²D runs for a 30 min experiment). For convenience, we will divide the ²D chromatograms into three different regions (A, B, and C), corresponding to three different features:

1. In the first region (0 to 2 s) we observe a very sharp peak caused principally by the RI mismatch of the ¹D eluent which delivers the sample in the initial gradient conditions of the ²D (100 % aqueous). The ¹D gradient also starts with a 100 % aqueous mobile phase with a linearly increasing volume fraction of organic solvent. As the ²D always starts at 100 % water, the sharp initial peak in region A will increase in magnitude as the chromatographic run in the ¹D progresses (see Figure 1). In a 3D plot of the LC×LC chromatogram, this effect manifests itself as a ridge (see Figure 4). As the organic fraction of the sample solvent increases, so does the ridge due to the RI mismatch. Usually only a few sample peaks elute in this region.

2. Next is the region from 2 s to 19 s in Figure 1, where the broad “bump” and slightly negatively going baseline is due to RI and absorbance mismatch between both channels in the ²D gradient, but some very small baseline disturbances are probably due to incomplete mixing of the two solvents during these very fast gradients. Also, the first few seconds of the baseline can be affected, but the magnitude of the impact depends on the switching speed of the sampling valve, the relative volume of sample transferred to the ²D and the solvent’s composition. We find that the faster the valve switches, the less the baseline is perturbed. This is the region in which most sample peaks elute.

3. The last region, from 19 to 21 s, shows a broader peak of essentially fixed height which is caused by the system “flush-out” (²D pump’s mixer, tubing and column) when the gradient rapidly returns to 100% aqueous mobile phase after completing each ²D gradient. This again is principally due to RI mismatch, but because the mobile phase passes through the ²D pump’s gradient mixer, the resulting peak is much wider than the first sharp peak in region A. Some sample peaks that occasionally do not completely elute during the gradient, may elute in this region though this is not desirable.

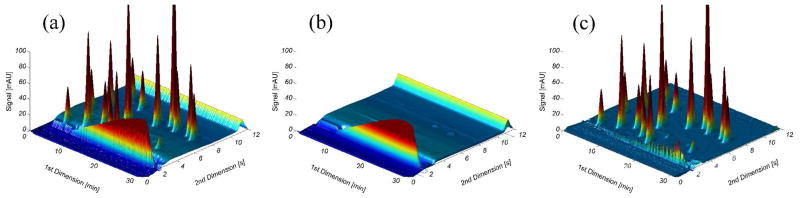
Figure 4.

3D plots of the OBGC method represented as (a) the original hybrid chromatogram of 20 simulated 2D peaks over a dummy LC×LC chromatogram, (b) the recreated background structure obtained applying the OBGC method in combination with the moving-median filter; (c) the result of subtracting the recreated background shown in (b) to the original hybrid chromatogram shown in (a).

Clearly, the baselines observed in LC×LC with dual gradients and very fast ²D coupled with a DAD, show large and very irregular drifts (frequently tens of mAUs) and these baseline disturbances must be removed (subtracted) from the individual ²D chromatograms when a real sample is analyzed.

As noted above, the signal taken in the direction of the ¹D is expected to be very reproducible across the large number of ²D chromatograms that comprise a single LC×LC chromatogram; the ¹D signal varies only slowly, if at all, except in region A where the ¹D injection solvent peak exists (see Figure 1, region A). This slow change across the ¹D is the key characteristic underlying the OBGC method.

Many different methods for baseline correction in chromatography and spectroscopy have been developed for use with univariate and multivariate data. It is beyond the scope of this work to review and test all of them. The interested reader is referred to the following references ^8,15–18.

Two popular baseline correction methods are used here to show the principle of the OBGC approach. One is the moving-median filter applied to separation science for the first time by Moore and Jorgenson in 1993 ¹⁹. In this method a median filter is applied as a moving window, where the window has to be, at least, twice the width of the signal peaks to properly “filter” the data; in a second step, the filtered signal is subtracted from the original chromatogram to correct the baseline. As they point out in their article, “it works best when the peaks of interest are on a very different time scale from the undesirable background”. The criterion of using a filter window size that is at least twice the width of the largest peak was used in this work. The median filter was implemented by means of the medfilt2() function in Matlab. The other baseline correction method used here was proposed by Mazet et al. ²⁰. They applied an explicit asymmetric cost function where the baseline is fitted by a polynomial, which is subtracted from the original signal in a second step (asymmetric polynomial fitting). The Matlab code of their method was graciously shared by the authors under the BSD license and it is available online at Matlab Central ²¹. In the authors’ experience, polynomial orders no higher than five provided the best fitting to the data, although the specific parameters of the method must be tailored to the data to provide the best results.

When we consider the baseline of a single ²D chromatogram with the structure shown in Figure 1, we found that no single method could effectively fit the background structure as shown in Figure 2(a).

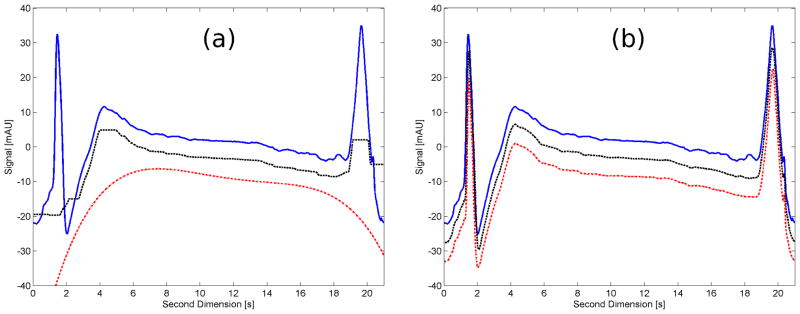
Figure 2.

Comparison of the effect of two different baseline correction methods on a typical single ²D chromatogram. The chromatograms are intentionally offset by 7 mAU to help visualization. (a) Conventional baseline correction methods: the blue solid line chromatogram is the original single ²D chromatogram; the black dashed line is the corrected baseline using a moving-median filter and the red dot-dashed line is the corrected baseline by the asymmetric polynomial fitting method. (b) The two methods are applied in combination with the OBGC method; line format same as in (a).

While the filter parameters used could probably be improved, clearly neither method is able to precisely reproduce the baseline and thus subtracting it from a sample bearing chromatogram will leave a lot of extraneous background. In the case of the moving-median filter, if a narrower window would have been used, real peaks would also have been removed from the chromatogram. With the asymmetric polynomial fitting method, we were not able to mimic the background by using a higher order polynomial.

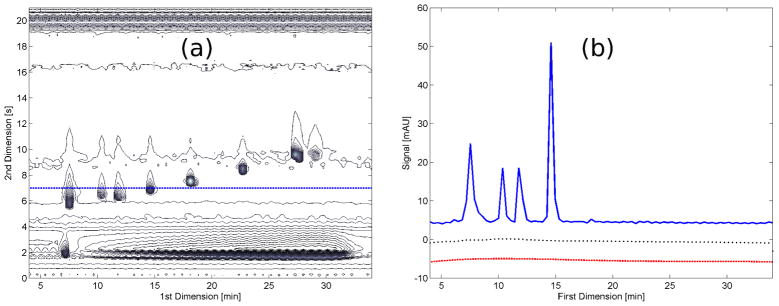
To understand how the OBGC is applied, let us consider the contour plot shown in Figure 3(a) . If we take the cut shown as the blue dashed line and plot the intensities vs. ¹D time, this will represent a ¹D chromatogram, sampled at a time of 7.0 s of the ²D, as shown in Figure 3(b) . This process has to be repeated for every ²D time point, which for a 21 s cycle time using an acquisition rate of 80 Hz in the detector, will result in 1680 ¹D chromatograms that will recreate the complete LC×LC background. Figure 2(b) shows the corrected baseline with the OBGC method for the same baseline as in Figure 2(a) . This way, the OBGC method is also applied in two steps as the two conventional methods:

Figure 3.

(a) Contour plot of a LC×LC chromatogram of an indole standard sample, the blue dotted line shows a cut taken at 7.0 s in the ²D. (b) Blue curve: chromatogram taken as the ¹D cut represented by the blue dotted line in panel (a); black dotted curve: baseline generated by the moving-median filter; red dashed curve: baseline resulting from the asymmetric polynomial fitting.

1. Apply a specific conventional method across the ¹D direction to each ²D data point to recreate the LC×LC background.

2. Subtract the LC×LC background generated in the previous step from the original LC×LC chromatogram.

The chief advantage of this procedure is that any background effect from the sample of the ¹D, basically “elutes” at about the dead volume of the ²D, leaving a very reproducible baseline from thereafter.

Comparison with the Dummy Subtraction Method

One common way for doing background correction is to run a sample, run a blank, and subtract the blank from the sample. However, there are two problems associated with this approach. First, one must do an extra blank run to do the correction. The second and the more important problem, is that the quality of the correction depends on the reproducibility of the background. The dummy run background subtraction approach is likely to be acceptable if the dummy run is acquired within a short time of the sample run, but it becomes less acceptable the longer is the time interval between the sample and the dummy runs. In considering the results here, one should understand that the dummy runs used were acquired over ten hours. The reproducibility of this approach was measured as the standard deviation of the difference between all 10 possible pairwise combinations of the five dummy runs. This standard deviation (0.26 mAU) was compared to the standard deviation of the same five dummy runs after applying the OBGC method (0.035 mAU). It should be noted that the standard deviation was calculated for data taken over all regions (A, B and C in Figure 1). Clearly, the reproducibility of the background obtained by the OBGC method is much better than what one gets with a simple dummy subtraction.

In real applications, we need to correct LC×LC chromatograms that contain many peaks of interest. In Figure 4(a) a typical hybrid LC×LC chromatogram is shown, in which 20 simulated 2D Gaussian peaks were added to a real dummy LC×LC chromatogram. The OBGC method was applied in combination with the moving-median filter and the recreated background is shown in Figure 4(b) . It is evident that the ridge in region A (see Figure 1) is not exactly reproduced, but the use of a smaller window for the moving-median filter results in the removal of some non-resolved peaks across the ¹D axes. In Figure 4, subtracting the recreated background in (b) from (a), gives the corrected LC×LC chromatogram in (c). It is evident in Figure 4(c) that a very large percentage of the background is removed; however, despite the evident power of the OBGC method to remove background, some of the sample solvent ridge remains. The highly reproducible end of the gradient in region C (see Figure 1) is virtually obliterated.

To measure how the background affects the measured peak heights and their reproducibility when the OBGC method is applied, the same set of 20 simulated 2D peaks was added to five replicate real dummy LC×LC runs. Peaks were detected and peak height measured for both OBGC corrected and non-background-corrected chromatograms. When no background correction is applied, the heights of the smaller peaks are greatly affected by the baseline as shown in Table 1. The average error without background correction is 3.07 ± 1.9 mAU, and while this seems to be a reasonably small number, it decreased to −0.07 ± 0.054 mAU (a factor of 40) upon applying the OBGC method. When the background is not corrected, the percent relative standard deviation (% RSD) of the peak heights is a measure of the reproducibility of the LC×LC instrument, since the peaks are simulated and exactly the same in each replicate dummy LC×LC chromatogram. The average reproducibility of the corrected chromatogram is improved by a factor of 3.5, as can be inferred from the corresponding % RSD in Table 1.

Table 1.

Peak Height Detection Error and Reproducibility with and without the OBGC Method

Simulated Valuesa			Detected without OBGCb			Detected with OBGCc
Real Height [mAU]	1tR [min]	2tR [s]	Apparent Height [mAU]d	% REe	% RSDf	Apparent Height [mAU]d	% REe	% RSDf
1.76	6.0	5.11	6.36	261	7.77	1.73	−1.87	3.34
2.16	16.0	7.44	5.38	148	6.29	2.14	−1.09	1.71
3.91	22.2	9.99	6.91	76.6	4.07	3.79	−3.23	5.07
4.85	9.8	4.26	9.54	97.0	3.54	4.78	−1.25	0.58
5.10	27.6	8.81	7.88	54.5	3.17	4.99	−2.04	0.40
5.83	9.4	8.05	8.77	50.4	4.67	5.80	−0.57	0.86
7.16	24.2	6.01	11.4	58.9	2.82	7.12	−0.55	0.39
7.85	27.2	9.84	10.8	37.3	2.43	7.80	−0.58	0.20
10.8	21.6	2.64	7.05	−34.7	6.63	10.7	−0.50	0.74
11.2	18.0	4.74	15.8	40.9	2.20	11.2	−0.32	0.22
12.4	10.0	10.4	15.6	26.2	2.38	12.2	−1.54	0.68
12.8	3.2	9.18	15.8	23.5	3.75	12.7	−0.52	0.50
14.2	20.4	9.69	17.1	20.4	1.67	14.1	−0.54	0.41
16.1	15.2	4.69	20.7	28.5	1.97	16.1	−0.22	0.44
20.2	10.8	3.39	24.8	22.9	2.43	20.0	−0.51	0.12
22.7	25.2	9.14	25.6	12.6	0.93	22.7	−0.24	0.13
24.4	6.4	9.35	27.3	12.1	1.76	24.3	−0.16	0.27
38.5	18.4	3.00	38.8	0.76	0.17	38.5	−0.02	0.98
40.5	5.8	3.96	45.3	11.8	0.79	40.4	−0.22	0.12
66.2	11.4	10.4	69.5	4.86	0.51	66.0	−0.32	0.07
			Average	47.7	3.00	16.7	−0.81	0.86
			Median	27.3	2.43	11.7	−0.53	0.42

^aReal features of the simulated 2D peaks that were added to the five real dummy LC×LC chromatogram replicates.

^bPeak detection applied without any background correction to the 2D chromatograms obtained by adding the simulated 2D peaks to each of the five real dummy LC×LC chromatogram replicates (hybrid replicates).

^cPeak detection applied after OBGC using the moving-median filter to the chromatograms used in (b).

^dAverage detected peak height in the five hybrid replicates.

^ePercent relative error in the measured vs. the real peak height.

^fPercent relative standard deviation of the measured peak height in the five hybrid replicates.

Also, when considering long term reproducibility (even for the same instrument), the ability to remove the background plays an important role in facilitating comparison of results. The result is a simple, more accurate and reproducible quantification procedure.

The method described here has been put into practice with real (non-synthetic) chromatograms. We have seen no problems other than the need to adjust the parameters of the specific function (polynomial fit, median-moving filter, etc) used to separate the peaks from the background.

While the fast gradients will have less impact in baselines obtained with other types of detectors such as mass sensitive detectors, the high reproducibility, insensitivity to co-eluent, ability to handle very high flow rates and low initial cost and maintenance, makes the DAD a very useful detector for fast online LC×LC.

CONCLUSIONS

The OBGC method is a very effective background correction method for LC×LC when used conjointly with currently existing baseline correction methods. The requirement of the current methods is that changes in the background be slow relative to the width of the real peaks is readily achieved in LC×LC by use of OBGC. The OBGC method should be useful with any 2D technique wherein the ¹D has lower frequency fluctuations than the ²D. Reproducibility of the peak height of measured peaks was significantly enhanced after applying the OBGC method since the system variability reflected in the background was greatly reduced, leaving an almost zero-mean background. After use of the OBGC method the standard deviation corresponding to the average background noise was reduced to about 0.05 mAU.