Docking Phospholipase A₂ on Membranes Using Electrostatic Potential–Modulated Spin Relaxation Magnetic Resonance

Abstract

A method involving electron paramagnetic resonance spectroscopy of a site-selectively spin-labeled peripheral membrane protein in the presence and absence of membranes and of a water-soluble spin relaxant (chromium oxalate) has been developed to determine how bee venom phospholipase A₂ sits on the membrane. Theory based on the Poisson-Boltzmann equation shows that the rate of spin relaxation of a protein-bound nitroxide by a membrane-impermeant spin relaxant depends on the distance (up to tens of angstroms) from the spin probe to the membrane. The measurements define the interfacial binding surface of this secreted phospholipase A₂.

Many interfacial enzymes such as phospholipases are water-soluble and must bind to the membrane-water interface in order to hydrolyze components of the membrane. Although the high-resolution structures of aqueous forms of several phospholipases and lipases are known (1), there are no reports that reveal the positioning of an interfacial enzyme at the membrane-water interface. The same can be said for most membrane-bound proteins. In the case of 14-kD secreted phospholipases A₂ (sPLA₂s), such as bee venom phospholipase A₂ (bvPLA₂), the interfacial recognition surface is thought to surround the active site slot; the latter is a deep cavity into which a single phospholipid molecule enters to reach the catalytic residues (2) (Fig. 1). Here we describe a high-resolution structure determination tool based on electron paramagnetic resonance (EPR) spectroscopy that allows peripheral membrane proteins such as sPLA₂s to be oriented with respect to the membrane-aqueous interface.

Fig. 1.

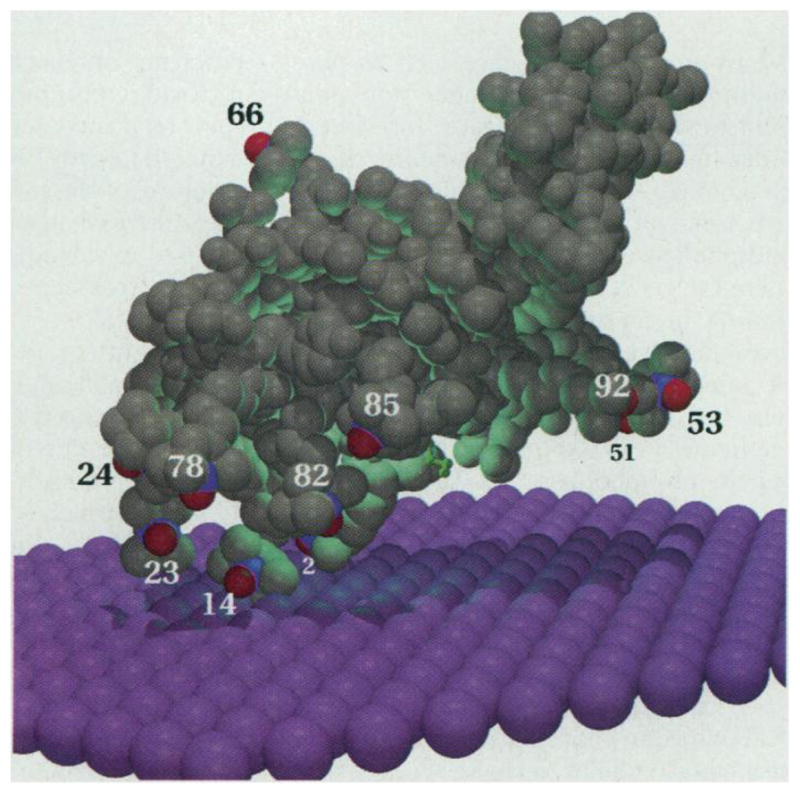
bvPLA₂ (gray) positioned on the membrane surface (purple) with the use of the EPR data in Table 1 and the theory developed in this study. The nitrogen and oxygen of each spin label (N-O•) are colored blue and red, respectively. The distance from each spin label to the membrane is as shown in Fig. 3. Spin labels 13 and 15 are hidden from view. A short-chain phospholipid analog inhibitor in the active site slot, as seen in the x-ray structure (14), is shown in green (1). This inhibitor is replaced by a DTPM molecule in these studies. Each membrane sphere has a radius of 2.2 Å, and thus there are about three spheres per phospholipid. The image was created with MOL-SCRIPT and Raster3D (25).

EPR methods have been developed that make use of protein site-specific spin labeling and spin relaxants for probing the membrane penetration depth of segments of integral membrane proteins that pass through the membrane (3). In theory developed below, it will be shown that the efficiency of relaxation of a protein-bound nitroxide spin probe by a water-soluble spin relaxant such as tris(oxalato)chromate(III) (Crox) is dependent on the positioning of the membrane with respect to the spin probe, even when the probe is exposed to the aqueous phase. By measuring the Crox-dependent relaxation of several nitroxides placed at defined locations on the surface of bvPLA₂, both in the presence and absence of membranes to which the enzyme binds, it is possible to position the enzyme on the membrane.

In order to apply this method to bvPLA₂, 13 site-selectively spin-labeled enzymes were prepared (4), 12 with the spin label located on or near the putative interfacial recognition surface (1,2) and 1 with the probe on the opposite side. The ability of Crox to relax the spin label of each bvPLA₂ mutant can be quantified by obtaining the continuous-wave EPR spectra as a function of microwave irradiation power. This series of experiments was carried out in the presence and absence of 10 mM Crox for the enzyme in the aqueous phase or bound to small unilamellar vesicles of the nonhydrolyzable, anionic phospholipid 1,2-dimyristoyl-snglycero-3-phosphomethanol (DTPM) (5). bvPLA₂ binds tightly to such vesicles (6). For each data set, the power dependence of the peak to peak height of the central line of the first derivative EPR spectrum, ΔY, was fit by least squares to the power saturation rollover equation (3,7)

$$\mathrm{\Delta }Y=c\frac{h_1}{{\left(1+\frac{{(h_1)}^2}{P_2}\right)}^{\epsilon }}$$ (1)

where $h_1=\alpha P_0^{0.5}$ is the microwave amplitude in gauss, P₀ is the power incident on the sample, and α is the conversion efficiency factor for the resonator (5) (4.5 G/W^1/2). The quantities c, ε, and P₂ were allowed to vary during curve fitting. The parameter c is a scaling factor, and P₂ is a power parameter that depends only on the properties of the nitroxide (7):

$$P_2=R_2·R_1,R_1=\frac{1}{{\gamma }_e{T}_1},R_2=\frac{1}{{\gamma }_e{T}_2}$$ (2)

Here, R₁ and R₂ are the spin lattice and spin-spin relaxation rates (in gauss) and are related by the electron gyromagnetic ratio γ_e to the relaxation times T₁ and T₂ as shown (7). The parameter ε is a measure of the curvature of the power dependence and is 3/2 for a homogenous line and 1/2 for a completely inhomogeneous line shape (7). This parameter enables us to obtain very high-quality fits to the data, as it absorbs the effects of inhomogeneous broadening and partially slowed rotational tumbling of the nitroxide.

The change in the fitted value of P₂ on addition of Crox is taken as a measure of the effect of this metal on relaxation. The presence of Crox increases both R₁ and R₂ as follows (8):

$$\begin{array}{l}{R}_1=R_1^0+\chi ·[\text{Crox}]\\ R_2=R_2^0+\chi ·[\text{Crox}]\end{array}$$ (3)

where χ is the relaxivity of Crox (9) and the superscript zero refers to the absence of Crox. The quantity ΔP₂ is defined as the difference in P₂ values in the presence and absence ( $P_2^0$) of Crox:

$$\mathrm{\Delta }{P}_2=P_2-P_2^0\approx \chi (R_1^0+R_2^0)·[\text{Crox}]$$ (4)

Thus, ΔP₂ is directly proportional to the concentration of Crox in the vicinity of the spin probe; because $R_2^0\gg R_1^0$, the term that is quadratic in [Crox] is small and neglected (8). ΔP₂ is measured in the presence and absence of DTPM vesicles, and these two quantities are used to obtain the exposure factor (Φ) as follows:

$$\mathrm{\Phi }=\frac{{(\mathrm{\Delta }{P}_2)}_{+\text{membrane}}}{{(\mathrm{\Delta }{P}_2)}_{-\text{membrane}}}=\frac{{[\text{Crox}]}_{+\text{membrane}}^{\text{local}}}{{[\text{Crox}]}_{-\text{membrane}}^{\text{local}}}$$ (5)

The superscript “local” refers to the effective concentration of Crox near the spin label and the presence of the membrane reduces this concentration. The equality on the right side of Eq. 5 follows directly from Eq. 4. The quantity 1 – Φ is a measure of the ability of the membrane to shield the protein-bound nitroxide from Crox in the aqueous phase (there is negligible Crox in membranes).

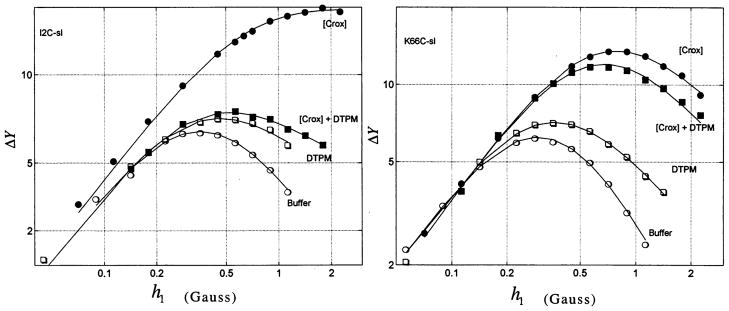
Power saturation rollover curves for the mutant in which isoleucine 2 is replaced with spin-labeled cysteine (I2C-sl) and K66C-sl are shown in Fig. 2 along with the fit to Eq. 1. Values of ε and P₂ for all mutants are listed in (10), and values of Φ are listed in Table 1. Ideally, one would expect $P_2^0$ to be independent of the presence of the membrane, but it is not (10, 11). K66C-sl has its spin label on the face of bvPLA₂ that is opposite the putative interfacial recognition surface, and, as expected, Φ for this mutant is close to unity (maximum exposure; Fig. 2 and Table 1). At the other extreme are I2C-sl, K14C-sl, and I78C-sl, which display values of Φ close to zero (Fig. 2 and Table 1), and thus the membrane confers nearly complete protection from Crox relaxation on these nitroxides. The other nine mutants display Φ values of intermediate magnitude (Table 1).

Fig. 2.

Power saturation rollover curves for I2C-Sl and K66C-sl. Curves are shown for bvPLA₂ mutant in buffer with and without Crox ([Crox] and buffer) and bound to membranes with and without Crox ([Crox] + DTPM and DTPM). The fit to Eq. 1 is shown by the solid lines. The units of ΔY are arbitrary.

Table 1.

Exposure factor Φ for spin-labeled bvPLA₂s.

Mutant	Φ*
I2C-SI	0.01 ± 0.04
N13C-Sl	0.38 ± 0.03 (0.78 ± 0.04)†
K14C-Sl	0.03 ± 0.02
S15C-Sl	0.17 ±0.02 (0.32 ±0.03)†
R23C-Sl	0.33 ± 0.02
F24C-Sl	0.25 ±0.13
T51C-Sl	0.30 ± 0.03
T53C-Sl	0.30 ± 0.01
K66C-Sl	0.85 ± 0.08
I78C-Sl	0.01 ± 0.01
F82C-Sl	0.27 ±0.12
K85C-Sl	0.58 ±0.13
D92C-Sl	0.44 ± 0.03

^*Calculated according to Eq. 5 with the use of the experimental EPR data (10).

^†Numbers in parenthesis were obtained with the use of 10 mM nickel(ethylenedia-minediacetic acid) instead of Crox.

The key to understanding the data in Table 1 is that the highly negative surface electrostatic potential of DTPM vesicles reduces the concentration of anions in solution near the membrane relative to their bulk concentrations. This results from the Boltzmann equation, which says that the concentration of Crox is a function of the electrostatic potential due to the membrane

$${\text{C}}_{\text{Crox}}(r)={\text{C}}_{\text{Crox}}(r=\infty )exp\left(\frac{-z_{\text{Crox}}F\psi (r)}{RT}\right)$$ (6)

Here C_Crox (r) is the molar concentration of Crox at a normal distance r from the membrane; ψ(r) is the electrostatic potential; z_Crox is the charge on Crox; and F, R, and T have their usual meanings Poisson’s equation describes the electrostatic potential around any set of charges, and for a planar membrane surface of uniform charge density, the potential depends only on r. The final result is the Poisson-Boltzmann equation appropriate for a planar charged membrane (12), which can be written as a first-order differential equation as follows:

$$\frac{\partial \psi (r)}{\partial r}={\left[\left[\frac{8\pi RT}{\epsilon }9·{10}^{12}\right]\sum _i{\text{C}}_i\{{exp}^{(-{\text{Z}}_{\text{i}}\psi (\text{r})\text{F}/\text{RT})}-1\}\right]}^{1/2}$$ (7)

Here C_i is the bulk molar concentration of each electrolyte of charge z_i in solution, and ε is the dielectric of bulk water (a value of 78). Given the experimental value of ψ(0) = − 77 ± 3 mV for our system (13), Eq. 7 can be solved numerically to obtain ψ(r), and C_Crox (r) is obtained using Eq. 6.

Theoretical exposure factors Φ (r) can be calculated as

$${\text{C}}_{\text{Crox}}(r)/{\text{C}}_{\text{Crox}}(\infty )$$

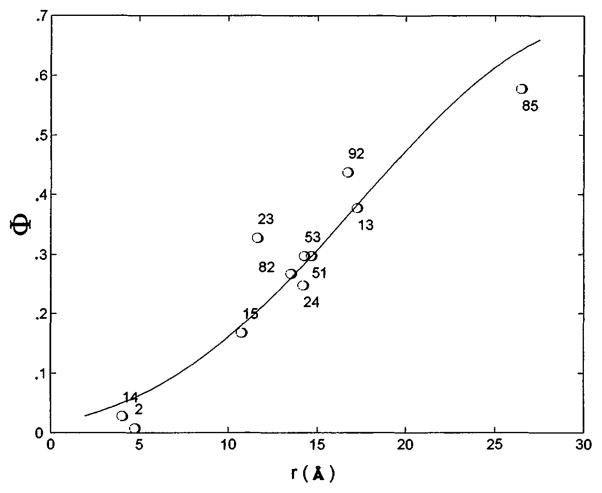
(by analogy to Eq. 5) and compared with experimental Φ values (Table 1) to obtain the normal distance of each spin label to the membrane. To do this, it was assumed that the x-ray structure determined for bvPLA₂ in solution (14) is maintained for the enzyme at the interface and that the membrane that contacts the enzyme is a plane. Marquardt-Levenberg regression analysis (15) was carried out by varying the protein-to-membrane distance and the Euler angles for the rotation of bvPLA₂ about its center. Several trials were executed with systematic variation of the initial conditions. In all cases, the analysis converged to a single bvPLA₂-membrane orientation. Figure 3 shows the remarkably good fit of experimental Φ to calculated Φ (16–18) and Fig. 1 shows the derived structure. The data in Table 1 and (10) also show that values of Φ are significantly larger when the neutral spin relaxant nickel(ethylenediaminediacetic acid) is used instead of Crox, proving that there is a significant electrostatic component to Φ.

Fig. 3.

Regression analysis of the bvPLA₂-membrane orientation. The solid line shows calculated values of Φ as a function of the distance from the spin label to the membrane (r), and the circles are the experimental Φ as a function of the modeled distance from the spin label to the membrane for each residue.

Because the effect of Crox on the EPR parameters was measured for bvPLA₂ in solution and bound to membranes, to a first approximation the effect of the electrostatic potential at each nitroxide due to the protein alone is removed from the problem because Φ is the ratio (ΔP₂)_+membrane/ (ΔP₂)_−membrane Strictly speaking, this is true if the electrostatic potential at each spin label of the protein-membrane complex is equal to the sum of the potentials from the membrane and protein alone. To examine this in more detail, we numerically solved the nonlinear Poisson-Boltzmann equation for bvPLA₂ bound to DTPM vesicles as given by Fig. 1 in 50 mM monovalent salt solution and for enzyme and vesicles alone (19). The electrostatic potential of the complex was generally similar to the sum of the potentials due to enzyme and vesicles alone. Very close to the membrane [near spin labels at positions 2 and 14, for which values of Φ near zero were measured (Table 1)], however, the low-dielectric enzyme enhances the negative electrostatic potential of DTPM vesicles by causing the Faraday electric field lines to bend around it and increase in density (20). However, this does not affect the conclusion that these residues are closest to the membrane. Overall, the results suggest that the first-order approach of simply ignoring the nonlinear electrostatic effects is valid.

A clear result of the present study is that bvPLA₂ sits on the membrane surface rather than digging into the membrane. This is consistent with monolayer pressure studies showing poor penetration of sPLA₂ into an anionic phospholipid monolayer at the air-water interface (21). The opening to the active site slot of bvPLA₂ faces the membrane (Fig. 1); however, this opening is not firmly against the membrane. This result is unequivocal as several diagnostic spin labels (at positions 51, 53, 82, 85, and 92) are clearly not as close to the membrane as those at positions 2 and 14 (Table 1). This implies that the alkyl chains of a long-chain phospholipid bound in the active site slot of the enzyme at the interface are partly in contact with the interior of the bilayer, with the hydrophobic walls of the active site slot, and with solvent water [because these experiments were done in the presence of CaCl₂, a molecule of DTPM occupies the active site of bvPLA₂ at the interface (22)].

The surface of bvPLA₂ that contains the opening to the active site slot contains eight cationic residues and only one anionic residue. bvPLA₂ and other sPLA₂s bind more tightly by orders of magnitude to anionic vesicles than to zwitterionic ones, and it has been hypothesized that these surface cations drive interfacial binding by means of electrostatics. However, our recent study shows that these cationic residues, individually and collectively, are not very important for interfacial binding, because mutating them to glutamates has virtually no effect on the binding of bvPLA₂ to anionic vesicles (23). The present study shows that the membrane contact surface of bvPLA₂ corresponds to a prominent patch of hydrophobic residues found on all sPLA₂s and that all basic residues except K14 are not in close contact with the membrane [see figure 1 of (23)]. The hydrophobic residues are not deeply inserted into the hydrophobic interior of the bilayer but somehow provide a microinterfacial environment that drives interfacial binding to the “polar” phospholipid headgroups (23). The nature of these interactions remains to be understood It is interesting to note that interfacial binding of cellulases to the “hydrophilic” surface of microcrystalline cellulose is driven by hydrophobic residues, including tryptophans on a cellulose-binding domain (24) Finally, the structure shown in Fig 1 provides a physical basis for the kinetic data that indicate that the interfacial recognition and catalytic sites are distinct (22).

The docking technique described in this study should be useful for determining the relative position of any macromolecule of virtually any size and of known three-dimensional structure with respect to any surface with known electrostatic properties, as long as there are no gross conformational changes in the structures of the components when they bind to each other However, useful membrane proximity data should also be obtainable for flexible membrane-bound peptides.

Scheme 1.