Velocity-Dependent Actomyosin ATPase Cycle Revealed by In Vitro Motility Assay with Kinetic Analysis

Abstract

The actomyosin interaction plays a key role in a number of cellular functions. Single-molecule measurement techniques have been developed to study the mechanism of the actomyosin contractile system. However, the behavior of isolated single molecules does not always reflect that of molecules in a complex system such as a muscle fiber. Here, we developed a simple method for studying the kinetic parameters of the actomyosin interaction using small numbers of molecules. This approach does not require the specialized equipment needed for single-molecule measurements, and permits us to observe behavior that is more similar to that of a complex system. Using an in vitro motility assay, we examined the duration of continuous sliding of actin filaments on a sparsely distributed heavy meromyosin-coated surface. To estimate the association rate constant of the actomyosin motile system, we compared the distribution of experimentally obtained duration times with a computationally simulated distribution. We found that the association rate constant depends on the sliding velocity of the actin filaments. This technique may be used to reveal new aspects of the kinetics of various motor proteins in complex systems.

Introduction

The interaction of myosin with actin drives micro- and macroscopic biological motions, including cell division, heartbeat, muscle contraction, and others. To elucidate the dynamic properties of the actomyosin contractile system, various spectroscopic and microscopic techniques have been used. For example, the kinetic parameters of the actomyosin ATPase cycle have been analyzed spectroscopically in bulk solution for many years (1). An in vitro motility assay permits study of the motility of actomyosin, and the characteristics of various species of myosin related to their sliding velocity have been studied using such assays (2–4). Moreover, techniques for measuring the behavior of molecular motors at nano-pico scale that use a glass microneedle or optical tweezers have been developed and used to understand the elementary process at the single- molecule level (5,6). In addition, a recently developed high-speed atomic force microscope has successfully imaged the motion of functioning single-molecule machines (7).

Using these techniques, the elementary processes and kinetic mechanisms of motor proteins, such as kinesin, myosin V, and Chara myosin, have been revealed (8–11). However, only a handful of specialized laboratories have the equipment to perform most such nanoscale measurements, therefore only a limited number of investigators can verify the results by replicating the experiments. Another difficulty in studying these molecules is that their behavior as an isolated single molecule does not always reflect their behavior when functioning in a complex system. For example, in a muscle fiber, the interaction between actin and myosin molecules is restricted by their steric positions. For axonemal dynein in eukaryotic flagella, a single dynein molecule attached to the axoneme can produce coordinated oscillation (12); in contrast, similar oscillation is not reported for the isolated dynein molecules.

To bridge the information from studying a single myosin molecule with its behavior in a complex system, we developed a simple method for studying the kinetic parameters of the actomyosin interaction in an in vitro motility assay using small numbers of molecules, which does not require a nanoscale measurement system. We made the assumption that the actomyosin ATPase cycle could be described by dividing the actomyosin kinetics into two states, an attached state (from A-M-ADP-Pi to A-M-ATP) and a detached state (from M-ATP to M-ADP-Pi), as shown in Fig. 1. To describe the kinetic scheme between the attached state and the detached state, we defined q and p as the rate constants for the dissociation and association of the actin filament. To determine these parameters during sliding, we used an in vitro motility assay with sparsely distributed heavy meromyosin (HMM) on a glass surface. Here, we focused not on the actin filaments' sliding velocity, but on the time spent in continuous sliding. The sliding of a single actin filament was supported by one or more myosin molecules on the glass surface. The sliding duration time depended on the number of cross-bridges, N, the association rate constant p, and the dissociation rate constant q. We performed the in vitro motility assay with various densities of skeletal muscle HMM and ATP concentrations. The distribution of sliding duration times obtained from the assay was then verified by fitting the curve against the distribution, which was obtained from a kinetic model. From the fittings, we estimated the parameters for the actomyosin interaction and investigated their properties, especially those of the association rate constant p.

Figure 1.

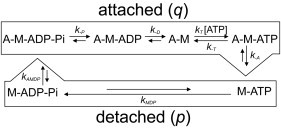
Actomyosin ATPase cycle, with the association rate constant p and dissociation rate constant q. p is the association rate constant for the detached state (M-ATP to M-ADP-Pi) and q is the dissociation rate constant for the attached state (A-M-ADP-Pi to A-M-ATP) in the actomyosin ATPase cycle.

Materials and Methods

Proteins

Skeletal muscle myosin was extracted from rabbit skeletal muscle by Guba-Straub solution (0.3 M KCl, 0.1 M KH₂PO₄ (pH 6.5)) and purified by the method of Hynes et al. (13). Skeletal HMM was prepared by α-chymotryptic digestion of purified myosin (14). Skeletal HMM was frozen rapidly with liquid N₂ and stored at −80°C until usage. G-actin was extracted from rabbit skeletal muscle acetone powder by the method of Spudich and Watt (15). The G-actin was polymerized to F-actin, which was labeled with tetramethylrhodamine-phalloidin (Life Technologies, Carlsbad, CA), following the method of Yanagida et al. (16). All the experimental procedures and rabbit care followed the regulations for animal experiments and related activities at Tohoku University.

Actomyosin interaction kinetics

A scheme of the kinetic interactions of actin and myosin, with rate constants, is shown in Fig. 1. Here, we defined the combined rate constant for the reactions from A-M-ADP-Pi to M-ATP as q, and those from M-ATP to A-M-ADP-Pi as p; using the combined rate constants p and q, Fig. 1 is simplified to

$$Attach\underset{p}{\overset{q}{\rightleftarrows }}Detach$$ Scheme 1

The rate constant q for the actomyosin dissociation during sliding in Scheme 1 is then expressed using the parameters in Fig. 1 as follows. (For details, see Fig. S1 in the Supporting Material.):

$$q=\frac{k_{-PD}·k_T\left[\mathrm{ATP}\right]·k_{-A}}{k_T\left[\mathrm{ATP}\right]·k_{-A}+k_{-PD}\left(k_T\left[\mathrm{ATP}\right]+k_{-A}+k_{-T}\right)}$$ (1)

where k_-PD represents $k_{-P}·k_{-D}/(k_{-P}+k_{-D})$. The reported rate constants for the individual substeps of the actomyosin working cycle (k_-P, k_-D, k_T, k_-T, and k_-A) were used to calculate the dissociation rate constant q.

In vitro motility assay

The in vitro motility assay was performed as described in Harada et al. (3) with some modifications. Coverslips (24 × 32 mm and 18 × 18 mm; Matsunami, Osaka, Japan) were coated with silicone by immersing them in 5% (v/v) Sigmacote (Sigma-Aldrich, St. Louis, MO) in heptane. A 9 × 18 × 0.2-mm flow cell was constructed, and then 0.1–0.3 mg/mL HMM solution was applied to the flow cell and adsorbed onto the silicone-coated coverslip by incubating for 1 min at room temperature. Unbound HMM was washed away with a washing buffer (WB: 25 mM KCl, 5 mM MgCl₂, 20 mM HEPES (pH 7.8)), which was then replaced with WB containing 0.5 mg/mL bovine serum albumin to block the remaining surface on the silicone-coated coverslip. After 1 min of incubation, the flow cell was set onto an inverted microscope (IX70; Olympus, Tokyo, Japan) equipped with a charge-coupled device camera (Neptune 100; Watec, Yamagata, Japan) and an objective lens (UplanApo 100×/1.35; Olympus). The motility solution (WB containing 10 nM tetramethylrhodamine-phalloidin-labeled F-actin, 4.5 mg/mL glucose, 0.22 mg/mL glucose oxidase, 0.036 mg/mL catalase, 0.5% 2-mercaptoethanol, 3 mM phosphoenolpyruvate (Sigma-Aldrich), 20 units/mL pyruvate kinase (Sigma-Aldrich), and 10–500 μM ATP) was vortexed vigorously for 30 s just before the assay to shorten the labeled F-actin. After adding the motility solution to the flow cell, the labeled F-actin was observed, and the movement of the actin filaments was video-recorded. The observation was performed at 30 ± 1.0°C.

The lengths of the actin filaments moving on the HMM were determined from their fluorescence intensity. First, a standard curve showing the relationship between the length of the filaments (>1 μm, measured from the fluorescence image) and their fluorescence intensity was obtained using Image J (http://rsb.info.nih.gov/ij/). Using the standard curve, the lengths of the filaments (0.24–0.52 μm) were then determined from their fluorescence intensity. The lengths are listed in Table S1 in the Supporting Material. The sliding movement of long actin filaments over 1 μm was also observed, but we did not include these observations in our analysis, because the filaments took a long time to dissociate, therefore they underwent bleaching or left the observed portion of the screen before dissociating. We also did not include actin filaments for which the fluorescence intensity corresponded to a length <0.24 μm, to exclude inaccurate length estimates and the effects of photobleaching.

Determination of the number of HMM molecules adsorbed on the coverslip

The density of HMM molecules on the coverslip was estimated from sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE) followed by densitometry using Image J. The HMM adsorbed on the coverslip was eluted with 30 μL of SDS sample buffer (1% SDS, 6.25 mM Tris-HCl (pH 6.8), 10% glycerol, 10% 2-mercaptoethanol). This elution was performed twice so that no HMM remained. The eluate was collected and boiled for 5 min, and SDS-PAGE was performed using the buffer system of Laemmli (17). The separated HMM was stained by Coomassie Brilliant Blue G-250 solution (Bio-Safe Coomassie G-250 stain, Bio-Rad Laboratories, Hercules, CA). The signal intensities of the HMM were analyzed by Image J. The intensities were compared with those of known quantities of HMM, and a standard curve between the concentration of applied HMM and the density of HMM molecules on the coverslip was made (see Fig. S2). The random distribution of HMM molecules on the coverslip was confirmed by analyzing the number, autocorrelation, and nearest-neighbor distance of the positions of the labeled F-actin under rigor conditions (see Fig. S3).

Measurement of the duration time of the actomyosin interaction

In the in vitro motility assay, labeled short actin filaments are floated in a flow cell, and the microscope is focused on the coverslip to which HMM molecules are adsorbed. The actin filaments in solution touch the glass surface by their Brownian motion, where they interact with the HMM. By using fully shortened actin filaments and sparsely distributed HMM molecules, we could examine the actin filaments, which attached to the coverslip, showed sliding movement, and then detached after a while (Fig. 2 A). We analyzed the actin filaments that moved >0.2 μm during an interaction time of 0.066–10 s at a motor speed of <7 μm/s. These measurement criteria excluded the nonspecific binding of actin filaments on the glass surface, and the shot noise of the measurement system. In addition, actin filaments that showed an instantaneous speed of >7 μm/s in random directions or large fluctuations in the direction perpendicular to the surface (i.e., a change in fluorescence intensity of ∼65%, whereas the change for normal sliding movement is ∼15%) were also excluded, to distinguish the normal sliding movement from Brownian movement. We measured the time interval between the moment the actin filament appeared on the surface (t₀) and the moment it disappeared (t₀ + τ), and defined the time interval as the duration time for the actomyosin interaction (τ). Histograms for τ were then made showing the ratio of the number of actin filaments that maintained the actomyosin interaction for 0 to τ to the total number of observed actin filaments (all histograms are shown in Fig. S4).

Figure 2.

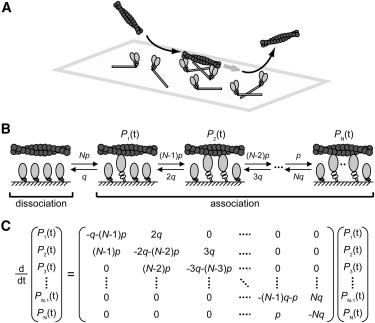
Concept of the duration time of the interaction between one actin filament and several HMM molecules. (A) Schematic diagram of the experiment. (B) Scheme of the interaction between one actin filament and N HMM molecules, with an association rate constant p and dissociation rate constant q. (C) Simultaneous differential equation of the Nth order for the duration time of the actomyosin interaction. P_i(t) is the probability at time t that i HMM molecules interact with the actin filament at the same time.

Estimation of kinetic parameters of the actomyosin ATPase cycle

The sliding of an actin filament is supported by one or more HMM molecules on the glass surface. When the actin filaments slide, the number of interacting HMM molecules, i, changes with time. The probability that i HMM molecules interact with actin at the same time (P_i) can be represented as a function of the number of available cross-bridges N, the association rate constant p, and the dissociation rate constant q (Fig. 2 B). Overall, each state can be described by a simultaneous differential equation of the Nth order (Fig. 2 C). The probability of attached states, P_attach, is the sum of the probability of each state (except P₀):

$$P_{\mathrm{attach}}=\sum _{i=1}^N{P}_i\left(t\right).$$

By calculating the summation with a program constructed by Mathematica (Wolfram Research, Champaign, IL), the duration time of the actomyosin interaction was simulated (Fig. S5). Comparing the simulation with the experimentally obtained histograms, the values of N, p, and q with the highest coefficient of determination were determined.

Results

Duration time depends on the ATP concentration and the density of HMM

The binding of single actin filaments to the HMM-coated surface, sliding movement, and subsequent dissociation were observed (Fig. 3, A–D, see also Movies S1–S4). Even in the situation of short actin filaments (0.24–0.52 μm) on sparse HMM molecules (633–1900 molecules/μm²), the smooth sliding movement of the filaments was clearly observed. The filaments' sliding velocity depended on the ATP concentration (Fig. 3 E), although the velocities were slower than those reported previously using an in vitro motility assay at the same ATP concentration (see Discussion). The duration time decreased as the ATP concentration increased (Fig. 3 F), and it increased as the HMM density increased (Fig. 3 G).

Figure 3.

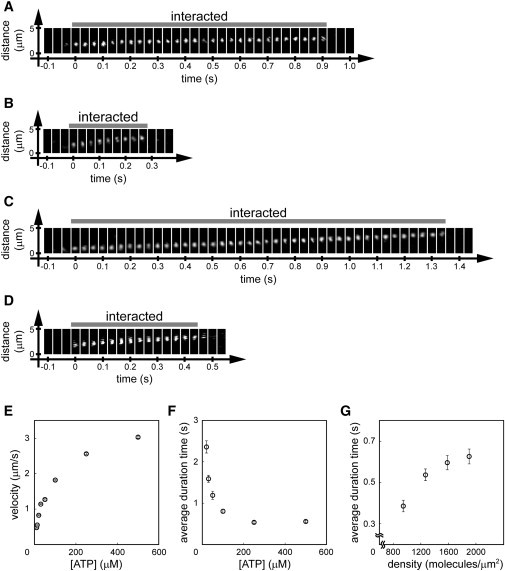
Measurement of the duration time of the actomyosin interaction. (A–D) Examples of actin sliding under the following conditions: (A) 945 HMM molecules/μm² and 30 μM ATP, (B) 945 HMM molecules/μm² and 500 μM ATP, (C) 1267 HMM molecules/μm² and 30 μM ATP, and (D) 1267 HMM molecules/μm² and 500 μM ATP. (E) Relationship between ATP concentration and the sliding velocity of actin filaments under all the experimental conditions: 10 and 13 μM ATP, 633–945 HMM/μm²; 20 and 30 μM ATP, 633–1900 HMM/μm²; and 50–500 μM ATP, 945–1900 HMM/μm². Error bars indicate SE for 351–925 observations. (F) An example of the relationship between ATP concentration and average duration time, at 1267 HMM molecules/μm². Error bars indicate SE for 107–160 observations. (G) An example of the relationship between HMM density and the average duration time, at 250 μM ATP. Error bars indicate SE for 104–148 observations.

Estimation of the association rate constant p

Histograms of the proportion of interactions that were maintained for a certain duration time τ are shown in Fig. 4, A–I. The histograms revealed a similar tendency as the average duration time (Fig. 3, F and G). That is, the average duration time decreased as the ATP concentration increased (Fig. 4, A–I, rightward), whereas the distribution shifted to the longer side as the density of HMM molecules increased (Fig. 4, A–I, downward).

Figure 4.

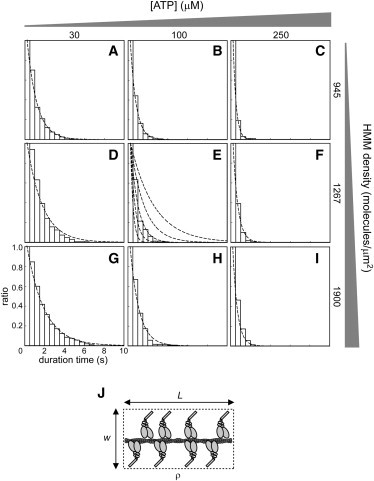
Experimentally obtained histograms of the duration time of actomyosin interactions with the calculated duration time. (A–C) 945 HMM molecules/μm²; (A) 30 μM, (B) 100 μM, and (C) 250 μM ATP. (D–F) 1267 HMM molecules/μm²; (D) 30 μM, (E) 100 μM, and (F) 250 μM ATP. (G–I) 1900 HMM molecules/μm²; (G) 30 μM, (H) 100 μM, and (I) 250 μM ATP. Dotted line in each histogram represents the duration time obtained computationally. Each bin represents the ratio of the number of actin filaments that maintained the actomyosin interaction from t₀ to t to the total number of observed actin filaments (n = 104–160 for each panel). In E, dotted lines were drawn with N = 16, q = 75, and p = 23, 28, 32.7, 38, 43 (from left to right). (J) Schematic diagram of the band model. L, length of actin filaments; ρ, the density of HMM molecules; w, the band width.

Next, the histograms were fitted with the calculated duration time obtained from the kinetic model (Fig. 2, B and C), to estimate the association rate constant of the actomyosin interaction. The fitting was performed as follows. For the prediction of N, the band model (Fig. 4 J and (2)) and the nearest neighbor distance model (3) were examined (see also Fig. S6). Considering that the actin filaments examined in this study were much shorter than the persistence length of actin filaments (15 μm (16), ), the filaments could be assumed to be rigid rods, therefore we used the band model with a 30-nm band width (Fig. S6). According to this model, N was determined as $N=0.03\times \rho \times L$ (Fig. 4 J). In this study, the HMM density ρ (633–1900 molecules/μm²) and the length of actin filaments L (0.24–0.52 μm) resulted in an N of 6.0–20.3. For the prediction of q, the reversal reactions in Fig. 1 were neglected, because they are slow enough to ignore (18,19). Therefore, from Eq. 1, q was determined to be 11.3–150 s⁻¹ with 200 s⁻¹ for k_-PD, 1.2 μM^-1s⁻¹ for k_T, 2000 s⁻¹ for k_-A, and 10–500 μM ATP (1,20–22). The calculated duration time was then obtained from the kinetic model with N, q, and p. We then determined the p that yielded the highest coefficient of determination between the histogram and the calculation (e.g., Fig. 4 E, see also Fig. S7). All the data analyzed and the parameters obtained are shown in Table S1.

Association rate constant p depends on the sliding velocity of the actin filaments

The values of p thus estimated were plotted against the ATP concentration (Fig. 5 A). The association rate constant for M-ADP-Pi binding to actin is reported to be 30 s⁻¹ (20); however, the value of p estimated in this study depended on the ATP concentration. When p was plotted against the sliding velocity v, which was also ATP-dependent (Fig. 3 E), they showed a linear relationship (Fig. 5 B, open circles); that is, $p=\alpha ·v,$ where α = 23.5 (1/s)/(μm/s), and the range of p was 7.30–76.6 s⁻¹, corresponding to a v range of 0.480–3.03 μm/s. The linear relationship was maintained even if the ATP dissociation from the A-M-ATP ternary complex (k_-T, 500 s⁻¹) was taken into consideration (Fig. 5 B, closed circles).

Figure 5.

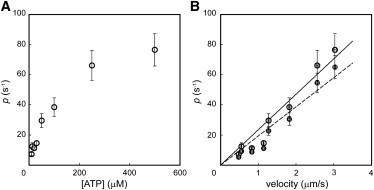
Dependence of the association rate constant of the actomyosin interaction on its sliding velocity. (A) Relationship between ATP concentration and the estimated association rate constant. At these ATP concentrations, the actin filament moved at 0.480–3.03 μm/s (see Fig. 3E). Bars indicate SE (n = 3–8). (B) Relationship between the sliding velocity (obtained from Fig. 3E) and the estimated association rate constant. Open circles, without reversible ATP binding (slope, solid line: 23.5 ± 1.39 (1/s)/(μm/s) (mean ± SE), coefficient of determination R², 0.936). Closed circles, with reversible ATP binding (slope, dotted line: 19.4 ± 1.32 (1/s)/(μm/s) (mean ± SE), coefficient of determination R², 0.922). Bars indicate SE (for p, n = 3–8; for velocity, n = 351–925).

Discussion

We showed that the duration time, i.e., the time during which short actin filaments slide continuously on a sparsely coated HMM surface, depended on the ATP concentration and on the density of HMM on the coverslip (Fig. 3, F and G). These experimental results contained the information about the kinetics of the actomyosin ATPase cycle during sliding. By analyzing these results with a simple kinetic model (Fig. 2), we were able to estimate the association rate constant p during sliding under various experimental conditions. From this estimation, we found that the association rate constant increased linearly with the sliding velocity of the actin filaments (Fig. 5 B). This linear relationship was still maintained when the number of cross-bridges was overestimated compared with the band model-estimated number (Fig. S8).

When the in vitro motility assay is performed with a low density of HMM and short actin filaments (0.24–0.52 μm), the sliding velocities of the actin filaments may become slow. In previous studies on the relationship between the cross-bridge number and the sliding velocity at 30°C (2,4,23), the sliding velocity at a low HMM density was predicted to be 3.5–5.0 μm/s. In this study, the maximum sliding velocity extrapolated to a saturated ATP concentration was 3.36 ± 0.137 μm/s (mean ± SE) at 30 ± 1.0°C (Fig. 3 E), which roughly matches the predicted value. We conclude that the sliding velocities in this study were slower than those previously reported (4–7 μm/s at 30°C in (2,4,23); 8 μm/s at 22°C in (3)), because of the low HMM density and short actin filaments, and not because of inactivity of the HMM.

The association rate constant for the binding of M-ADP-Pi to actin has been investigated from the kinetics of the ATP hydrolysis of myofibrils (20) and by experiments in solution (21,22). From measurements using myofibrils, the association rate constant was determined to be 30 s⁻¹, calculated using the values of the phosphate burst, and the transient and steady-state hydrolysis of ATP. However, the relationship between shortening velocity and ATP hydrolysis was not studied, so the possibility remained that the association rate constant is depending on sliding velocity. In the experiments performed in solution, the second-order association rate constant, which depends on the concentration of actin, was studied. In this situation, the association rate constant in solution does not always reflect the characteristics of the actomyosin motile system, because there is no geometric restriction. In any case, the dependence of the association rate constants on the sliding velocity was not reported.

The distance between the binding sites on an actin filament that participate in cross-bridge formation (path distance) is 36 nm, as determined from electron micrographs (24), x-ray diffraction (25), and studies using optical tweezers (26–28), and it is assumed that actomyosin interacts in the same manner in an in vitro motility assay. Taking into account the reports (24–28) described previously and the actomyosin ATPase cycle (Fig. 1), the association rate constant, M-ADP-Pi to A-M-ADP-Pi, in the motile system should be considered from the rate at which myosin moves from one binding site to the next, which depends on the shortening velocity.

Our finding that the association rate constant p depended on the sliding velocity of the actin filaments is reasonable, because irrelevant interactions with actomyosin would occur if the association rate constant was a fixed value. That is, given that an actin filament slides on HMM molecules at v μm/s, each HMM molecule will interact with the actin filament every v (μm/s)/p (s⁻¹). If we assume that p is a fixed value, 30 s⁻¹, and the myosin-binding sites are located every 36 nm on an actin filament, a myosin molecule can bind a proper binding site while other myosin molecules propel an actin filament at > 1.08 μm/s (= 36 nm × 30 s⁻¹). On the other hand, when the sliding velocity is < 1.08 μm/s, each myosin molecule will bind an arbitrary position on an actin filament (e.g., every 18 nm at 0.5 μm/s). This latter result does not agree with previous findings about the myosin-binding sites on an actin filament (26–28).

Next, let the number of cross-bridges N or the dissociation rate constant q be simulated using our technique when p is assumed to be 30 s⁻¹. When N is estimated with p = 30 s⁻¹, k_-PD = 200 s⁻¹, k_T = 1.2 μM^-1s⁻¹, k_-A = 2000 s⁻¹, N increases as the ATP concentration increases (Fig. S9 A). This is, however, unlikely. When q is estimated with p = 30 s⁻¹ and the band model-derived N (band width = 30 nm), k_T and k_-PD are estimated to be 5.0 ± 1.0 μM⁻¹s⁻¹ and 69 ± 10 s⁻¹, respectively (Fig. S9 B). Although q can be estimated when the association rate constant p is a fixed value, the irrelevant interactions mentioned previously would occur. From these considerations, it is unlikely that the association rate constant p is a fixed value in an in vitro motile system. However, because the kinetics of ADP release is expected to be affected by the load (29), it is still possible that the k_-PD changes as the sliding velocity increases. To clarify the dependence of q on sliding velocity, it may be necessary to use conditions in which Pi or the ADP release step become rate-limiting (e.g., high ATP concentration, high density of HMM molecules).

Therefore, we propose that the association rate constant p, which depends on the sliding velocity, can be defined as the reciprocal of the time required for actin filament to move 36 nm. In considering the actomyosin interaction during sliding, the axial Brownian rotation of the short actin filaments would not matter, because the attached myosin molecules will suppress it, even during the sliding movement. Although it was reported that actin filaments slide with rotational motion in an in vitro motility assay (30), such motion would not influence cross-bridge formation, because the degree of the rotation is small (one revolution per sliding distance of 1 μm).

The rate-limiting step of the actomyosin ATPase cycle (Fig. 1) could depend on the sliding velocity. It is thought that at low ATP concentrations the rate-limiting step is the ATP-binding step, whereas at high ATP concentrations, it is the ADP- or Pi- release step. In addition to these rate-limiting steps, cross-bridge formation in an in vitro motile system could also be rate-limiting when the sliding velocity is slow, at low ATP concentrations. Under our experimental conditions (a low density of HMM and 10–500 μM ATP), the association rate constant p would become the rate-limiting step, because of the slow sliding velocity (Fig. 6, A and B). When actomyosin slides faster than examined in this study (e.g., Harada et al. (3) and in muscle fibers (31), which contain many myosin molecules and mM levels of ATP), cross-bridge formation is not rate-limiting (Fig. 6 C. From Fig. 5 B, >8.44 μm/s sliding velocity gives >198 s⁻¹ for the p). In this case, the dissociation rate constant q, especially for ADP release, will become a rate-limiting step for the actomyosin ATPase cycle (32).

Figure 6.

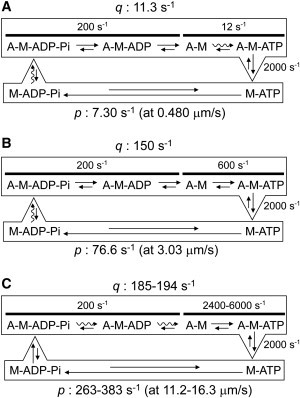
Summary of the actomyosin ATPase cycle and kinetic parameters. The wavy arrows in the ATPase cycle represent the probable rate-limiting step. (A and B) Kinetic parameters at the low HMM density described in this study. The dissociation rate constants q at (A) 10 μM and (B) 500 μM ATP were calculated from Eq. 1. The values of the association rate constants p were obtained in this study. (C) Kinetic parameters at high HMM density estimated using the values for ATP concentration and sliding velocity reported in Harada et al. ((3); 2 mM ATP, 11.2 μm/s at 30°C, in vitro motility) and Pate et al. (31); 5 mM ATP, 16.3 μm/s at 30°C, muscle fiber). The association rate constant p was calculated using the slope of Fig. 5B and the sliding velocity reported in (3,31).

The technique reported here is unique because the parameters for actomyosin interaction during the sliding movement can be estimated, which is in contrast to solution experiments. Moreover, we can estimate the parameters without using any sophisticated nanoscale measurement techniques, such as optical tweezers or glass microneedles. Therefore, analyses and verifications can be performed in many laboratories for various motor proteins in different systems. Using this technique, we revealed the velocity-dependent association of actomyosin. Our findings suggest that the velocity affects the chance of association. In other words, the actual concentration of an actin filament increases as it slides; in addition, the likelihood that a myosin molecule will associate with actin increases when other myosin molecules propel an actin filament. This means that myosin molecules could cooperatively bind to sliding actin filaments in an actomyosin motile system. In addition, actomyosin is thought to interact cooperatively by changes in the actin-filament structure upon myosin attachment (33,34). The cooperative structural change of actin filaments and our findings together indicate that the actomyosin interaction in vivo is accelerated when it is sliding. Thus, functions such as muscle contraction and cell division take place in a highly cooperative manner. It is reasonable that the actomyosin contractile system is constructed to perform its function very efficiently. The velocity-dependent association found in this study may be a key feature for coordinating the performance of multiple myosin molecules through a single actin filament in the hierarchical structure of muscle and other actomyosin systems.