Identification of Minimally Interacting Modules in an Intrinsically Disordered Protein

Abstract

The conformational characterization of intrinsically disordered proteins (IDPs) is complicated by their conformational heterogeneity and flexibility. If an IDP could somehow be divided into smaller fragments and reconstructed later, theoretical and spectroscopic studies could probe its conformational variability in detail. Here, we used replica molecular-dynamics simulations and network theory to explore whether such a divide-and-conquer strategy is feasible for α-synuclein, a prototypical IDP. We characterized the conformational variability of α-synuclein by conducting >100 unbiased all-atom molecular-dynamics simulations, for a total of >10 μs of trajectories. In these simulations, α-synuclein formed a heterogeneous ensemble of collapsed coil states in an aqueous environment. These states were stabilized by heterogeneous contacts between sequentially distant regions. We find that α-synuclein contains residual secondary structures in the collapsed states, and the heterogeneity in the collapsed state makes it feasible to split α-synuclein into sequentially contiguous minimally interacting fragments. This study reveals previously unknown characteristics of α-synuclein and provides a new (to our knowledge) approach for studying other IDPs.

Introduction

Intrinsically disordered proteins (IDPs) are a class of proteins that lack ordered structure under physiological conditions and exist in a heterogeneous ensemble of conformations (1–3). IDPs are more abundant in higher organisms and are estimated to comprise large regions (>50 residues) in ∼30% of all eukaryotic proteins (4,5). IDPs are functional even in the absence of a well-defined three-dimensional structure, which challenges the long-held belief that the function of a protein depends on its unique folded structure (6). IDPs are associated with a large number of cellular functions, including, but not limited to, transcription, translation, signal transduction, and the regulation of protein assembly (7). However, the disordered nature of the conformational ensemble of IDPs makes them particularly susceptible to oligomerization and amyloidogenesis (8).

The heterogeneous nature of the conformational landscape of IDPs has been proposed to play an important role in their binding to multiple targets and self-aggregation (9). Unlike the energy landscape of a globular protein that has a few stable energetic minima, the energy landscape of an IDP is either weakly funneled or composed of a fuzzy landscape (6,10). In the weakly funneled model, a weakly stabilized conformation becomes more stable upon binding to a target protein or surface (11). In contrast, the fuzzy landscape model predicts that an IDP does not need to fold, even in its functional form. Signaling proteins that employ multivalent binding provide examples of intrinsically disordered regions that use both a fuzzy landscape and a weakly funneled landscape within the same protein. The motifs on signaling proteins gain structure only after binding to their partner, whereas the linker regions connecting these motifs function as entropic chains increasing the intramolecular concentration of multivalent binding (12,13). It is imperative, therefore, to develop experimental and theoretical methods to characterize IDPs at high temporal and spatial resolutions (14,15).

In this study, we consider human α-synuclein, a 140-residue prototypical IDP, using all-atom molecular-dynamics (MD) simulations in explicit water. Despite a large amount of previous work, the nature of its conformational variability in an aqueous environment and its function remain unknown. Parkinson’s disease is associated with β-stranded aggregates of α-synuclein (16,17) and is diagnosed postmortem by the presence of Lewy bodies in neurons. α-Synuclein consists of three regions: the N-terminal region (residues 1–60), the hydrophobic nonamyloid β component (NAC) region (residues 61–95), and the highly acidic proline-rich C-terminal region (residues 96–140). NMR and electron paramagnetic resonance (EPR) studies show that α-synuclein has very low residual secondary structure (18), even though it is more compact than an ideal polymer in water (19,20). Single-molecule atomic force microscopy combined with Forster resonance energy transfer (FRET) shows that α-synuclein exists in an ensemble of different conformations (21). α-Synuclein forms either an ordered helix-turn-helix structure or an elongated α-helix with a disordered C-terminal tail upon binding to phospholipids (22–24).

It has been well established that MD simulations are suited to study the conformational landscape of proteins on the submicrosecond timescale (25,26). However, IDPs present a challenge to MD simulations. First, efficient sampling of the phase space of an IDP requires a huge amount of computational resources. Second, the empirical force fields used in MD simulations have been tested on the dynamics of globular proteins and may contain secondary structure bias (27,28). As a result, MD simulations must be rigorously compared against experimental data (26). Generalized ensemble methods, such as replica-exchange MD simulations, were developed to sample relevant phase space efficiently without getting trapped in local minima (29–31). However, all-atom representations based on these methods can only be used to study relatively small proteins in an aqueous environment.

In this work, we developed a strategy by combining MD simulations and network theory to fragment moderately sized IDPs into more tractable peptide fragments. We were motivated to fragment IDPs such as α-synuclein for several reasons: smaller fragmented IDPs are easier to characterize both experimentally (e.g., vibrational spectroscopy) and computationally because most IDPs are moderately large in size. Furthermore, by reconstituting the conformational variability of these fragments back to extract the conformational distribution of the full protein, we should be able to gain new insights into the disorder-to-order transition exhibited by IDPs upon binding to their target proteins. In addition, it is more challenging to express and purify larger IDPs due to the formation of insoluble inclusion bodies. Therefore, if a divide-and-conquer approach can be devised, then smaller fragments of IDPs can be generated from chemical synthesis. Recently, Ullman et al. (32) reported a similar method that enumerates the conformational ensemble of an IDP from conformation of the fragments using the divide-and-conquer approach. We propose a complementary approach that can fragment an IDP based on minimally interacting modules.

Methods

The initial conformations for the partially helical simulation were chosen based on a 350-ns all-atom MD simulation starting with the NMR structure (PDB 1XQ8 (22); Fig. S1 in the Supporting Material). In addition, we also started simulations from the extended helix conformation, which is stable in a lipid environment. The initial conformations for the random simulations were generated using the random coil generator (33) (Fig. S2). The protein was placed in explicit solvent and 150 mM NaCl concentration in all of the simulations. All simulations were performed using the NPT ensemble with the OPLS-AA force field (34,35) in GROMACS (36). The OPLS-AA force field was used for all our simulation because the percentage helicity was consistent with circular dichroism (CD) measurements of α-synuclein (Fig. S3). The radius of gyration (R_g) and secondary structure was calculated using the GROMACS analysis suite. In the network, a node represents a residue, and edges represent contacts between the residues. Two residues are said to be in contact if any heavy atoms (nonhydrogen) from the two monomers are within 4.5 Å of each other in any of the compact states. We identified the community structure in the network using the Girvan-Newman algorithm (37). Additional details on the method and parameters are provided in the Supporting Material.

Results

It remains challenging to characterize the heterogeneous conformations of IDPs at atomistic resolution (19,26). We performed >100 MD simulations of monomeric α-synuclein starting with different initial conditions for 100 ns each. These simulations differed in the initial configurations and/or initial velocities, and can be divided into two sets as shown in Table 1. Additionally, we considered a few very long simulations (350 ns) that were started from the known NMR structure.

Table 1.

Types of simulations performed in this study

Initial conformation	Number of simulations	Time
Helix turn helix	One	350 ns
Partially helical	10 conformations × 5 = 50	100 ns each
Random	50	100 ns each

We performed a 350-ns simulation starting from the NMR structure of α-synuclein (22) to study conformations of α-synuclein that are likely to be present in a lipophilic environment. We chose eight diverse conformations from this simulation and started five simulations from each of these conformations (Fig. S1). In addition, we also started another five simulations each from the helix-turn-helix NMR structure and the extended helix conformation of α-synuclein, which is stable in a lipid environment (23,24). This set of 50 simulations is labeled “partially helical” to emphasize that the protein has varying degrees of helical content in these simulations. In addition, we also started a second set of 50 simulations from diverse random coil conformations (labeled “random”; Fig. S2). These 100 MD simulations were run for 100 ns each to produce a total of 10 μs of simulation trajectories.

Compact states of α-synuclein in water

All simulations led to the collapse of α-synuclein into a stable compact state. The collapse of α-synuclein corresponds to the fast timescale decay (Fig. S4, A and B) in the R_g, whereas the conformational rearrangements within the collapsed state led to fluctuations in R_g of the collapsed states (Fig. 1). These compact states were stable up to hundreds of nanoseconds, as is evident from the longest simulation (350 ns; Fig. S4 C). The R_g-values of these partially collapsed states are in the range of 16–30 Å, with a mean of 21.1 Å. This corresponds to a hydrodynamic radius of 27.4 Å, assuming that α-synuclein is partially collapsed and the ratio of the R_g to the hydrodynamic radius is close to that of globular proteins (0.77) (38). α-Synuclein is more compact compared with the R_g expected for a self-avoiding polypeptide chain of the same size (41.9 Å) (19). This nonrandom chain-like behavior of α-synuclein is consistent with experimental observations (19,20,39). The measured hydrodynamic radius of α-synuclein in water is 26.6 ± 0.5 Å and is comparable to the size of α-synuclein observed in our simulations (20).

Figure 1.

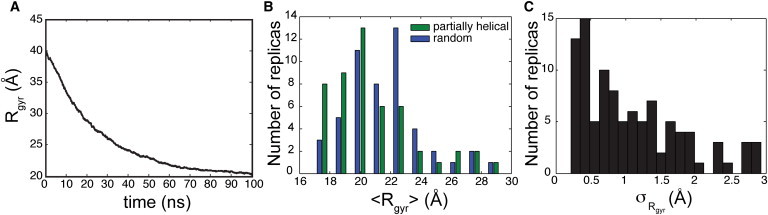
Early collapse of α-synuclein. (A) The mean R_g in the 100 simulations is shown as a function of time. (B and C) Histogram of the (B) average and (C) standard deviation of the R_g of the protein from 50 to 100 ns in the 100 replicas.

The distributions of the mean and standard deviation of R_g of the various collapsed states are shown in Fig. 1, B and C. The partially helical simulations tend to form slightly smaller collapsed states compared with those from random simulations. In most random simulations, the initial collapse of α-synuclein fits to a single exponential decay in the R_g. In addition, Fig. S4 shows that there is no significant change in the R_g after the initial collapse. Some of these partially collapsed states contain pores in the protein. In addition, some of these partially collapsed states contain locally extended regions in the protein.

Residual secondary structure content in collapsed coil states

The average helicity of all 100 replica simulations is ≈9.7% during the 50-ns interval from 50 to 100 ns. This is consistent with CD measurements showing that the helical content of α-synuclein is 5–10% at room temperature (40). However, no significant secondary structure is observed in the 50 replicas started with random initial conformations (Fig. 2 A and Fig. S5). In a previous study (41), it was shown that the secondary structure properties of a 13 amino acid peptide converged only after 225 ns. Therefore, the secondary structure properties of α-synuclein could not have converged in these relatively short timescale MD simulations. Regardless, the overall trend and propensities of secondary structure obtained from the simulations are in agreement with CD and NMR measurements, as shown below.

Figure 2.

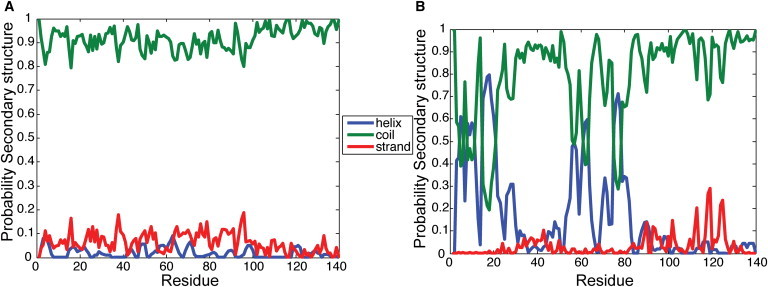
(A and B) Probability of the residue displaying a particular secondary structure in 50 replicas starting from (A) random conformations and (B) partially helical simulations.

Further characterization of residue-level helical propensity was carried out in the 50 simulations in which the initial configurations had varying levels of helical content. The trends observed in these 50 simulations are similar to the trends observed in all 100 simulations. Even though predominantly random coils are seen after the first 10 ns, consistent with experiments (18), the N-terminal region displays a higher propensity to form transient α-helices (Fig. 2 B and Fig. S5). In particular, residues 1–25 are implicated in seeding the interaction of α-synuclein to sodium dodecyl sulfate (SDS) and phospholipids during the formation of the helix-turn-helix and extended helix conformations (42,43), and residues 31–55 have been proposed to have high affinity for lipid vesicles (43). In similarity to previous simulations of α-synuclein interacting with SDS micelles (44), residues 1–25 and 31–55 display some of the strongest propensities to form helical regions in water, and the helices do not shift during the timescales of our simulations (Fig. S6 and Fig. S7).

Consistent with NMR results (18), the NAC and C-terminal tail exhibit a slight tendency to form β-bridges and are mostly found in a coiled state. Some of the strongest strands and bridges are formed between residues 80 and 130. At least part of the region that forms β-sheets in oligomeric fibrils of α-synuclein (residues 35–100) (45) also shows a tendency to form β-strands when monomeric α-synuclein is present in an aqueous environment. The propensity toward transient β-strands in the C-terminal tail was slightly higher in the simulations that considered initial configurations with varying levels of helical content (Fig. 2). This weak correlation between the formation of β-strands and the presence of helical content between residues 40 and 90 supports recent observations of a helical intermediate in 2,2,2-trifluoroethanol (TFE)-induced α-synuclein aggregation into β-stranded fibrils (46), and helix-helix interactions leading to β-sheet formation and propagation (47). The trends observed in the long-timescale simulations (350 ns) were similar to those seen in the 100 replica simulations (Fig. S8 and Fig. S9).

Heterogeneous ensemble of collapsed coil states

Even though α-synuclein forms compact states of similar size during different simulations, it still exhibits a heterogeneous distribution of conformations. In a typical IDP, one would expect internal contacts to be formed and broken at random, resulting in a large standard deviation in distance between residues. We found that α-synuclein was trapped in local energy minima for >50 ns in all 100 replica simulations. To determine whether the minima observed in all 100 simulations were the same, we calculated the average distance and standard deviation of distance between the heavy atoms of different residues in each compact state.

The resulting distance matrix over a combined trajectory is shown in Fig. 3, A and B. We prepared the combined trajectory by concatenating the final 50 ns of all 100 100-ns MD simulations. During this time period, the protein is compact in each of these simulations. If the same contacts had formed in all of the simulations, the distance between the residues in these contacts would be small in all of the simulations. Hence, the mean distance and standard deviation of distance between these residues in the combined trajectory would also be small. However, there are no contacts between sequentially distant regions of the protein that are common to all the compact states formed in these simulations (Fig. 3 A). Consistent with this, most of the sequentially nonlocal regions that were structurally close in any of the simulations display large deviations in distance (Fig. 3 B). A cluster analysis of the combined trajectory also displays a similar trend, because only a few clusters are common to distinct replicates (Fig. S10). Thus, the compact states formed in the different simulations consist of a heterogeneous ensemble of conformations. The long-timescale simulation of α-synuclein confirms that the tertiary contacts are long-lived (Fig. S11). This justifies our decision to consider many short simulations rather than one long simulation to explore the phase space of α-synuclein efficiently.

Figure 3.

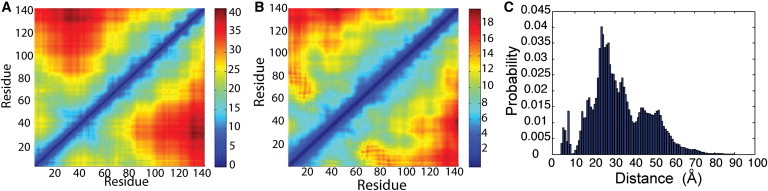
Tertiary contacts in α-synuclein. (A) Average distance and (B) standard deviation of distance between residues in α-synuclein in the collapsed state of all 100 simulations. (C) Probability distribution of the distance between the C_α atoms of Gly-7 and Gly-84 in the random MD simulations.

Ferreon and co-workers (24) introduced FRET labels on residues 7 and 84 of α-synuclein and observed a wide range of FRET efficiencies between these two residues in an aqueous environment. In other words, the distance between these two residues displays a broad distribution. In wild-type human α-synuclein, glycines are present in these two positions. We plot the probability distribution of the distance between these two residues in the replicas in Fig. 3 C. Consistent with the FRET data, the simulation data show a broad range of distances between the two residues in the compact states, with an average distance of 33.2 Å. Although the protein is compact in our simulations, the distance between residues far off in sequence can display a broad range of distances.

Fragmentation based on network theory

Here, we implement a network-based approach that can be used to optimally identify minimally interacting fragments of α-synuclein. The physical basis for the module boundaries in our approach relies on the observation that residues that are not in contact exert the least influence on each other’s conformation. In globular proteins, residues in the same domain have a larger density of contacts compared with residues belonging to different domains. Also, some of the individual domains of a multidomain protein are capable of folding and functioning independently of each other. Therefore, we assume that the conformation of any residue within a module is highly dependent on other residues within the same module.

We build this network based on trajectories from MD simulations. In the network, a node represents a residue in the protein, and an edge represents a contact between two residues. The edges are weighted by the frequency of contacts in our simulations (see Materials and Methods). Then, a community analysis of this network generated from MD simulations is used to identify the fragments that influence each other the least in the full-length α-synuclein. Nodes within a community are densely connected, and relatively fewer edges connect nodes in different communities. In other words, residues occurring in different communities are expected to have the least effect on each other’s motions and conformations. The communities can contain residues that are spatially close in a majority of the simulations (see Fig. S12) but not close in sequence.

Analysis from the previous section (Heterogeneous ensemble of collapsed coil states) showed that α-synuclein is composed of a heterogeneous ensemble of compact states that are stabilized by tertiary contacts. Therefore, we performed a community analysis on the network formed by the combined trajectory of all 100 compact states. This ensures that the contact network is an approximate representation of the IDP’s ensemble of conformations. The community analysis produced nine communities (Fig. 4). These fragments should minimally affect each other’s conformations in the full-length protein on average. These communities are all contiguous in sequence, as only sequentially local contacts are formed in a majority of the compact states.

Figure 4.

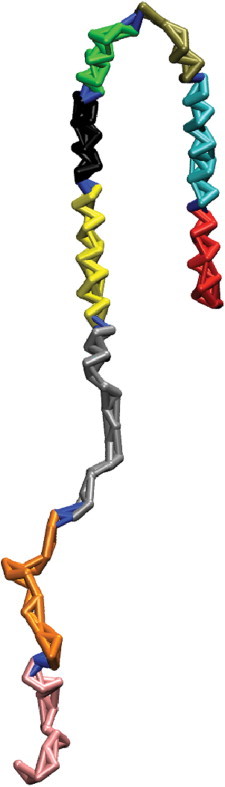
Network analysis. The nodes and edges in α-synuclein are colored according to the community to which they belong. The nine communities of α-synuclein in the combined trajectory are shown in red (residues 1–14), cyan (residues 15–31), tan (residues 32–42), green (residues 43–55), black (residues 56–68), yellow (residues 69–86), silver (residues 87–105), orange (residues 106–123), and pink (residues 124–140). Intercommunity edges are shown in blue.

The beginning of the NAC region (residues 61–68) is in the same community as the end of the N-terminal region (residues 56–60). Similarly, the beginning of the C-terminal region (residues 96–105) and the end of the NAC region (residues 87–95) are in the same community. In other words, the conformations displayed by the NAC region in full-length α-synuclein are dependent on the conformation of certain regions in the N- and C-terminal regions. This implies that fragmenting α-synuclein into the N-terminal, NAC, and C-terminal regions may not be fruitful. Thus, the heterogeneous nature of α-synuclein collapsed states allows us to split the protein into fragments regardless of whether it is collapsed or not.

We evaluated the convergence of the communities by considering the network analysis on trajectories derived by the combination of six different sets of 50 simulations. To prepare these trajectories, we split the 50 random and 50 partially helical simulations into two sets of 25 simulations each. We prepared six trajectories by combining any two sets of simulations from the original four sets of simulations. The community analyses based on five of these trajectories are very similar to the communities presented in Fig. 4. In the network analysis of the 50 partially helical simulations, one of the communities is formed by a combination of residues in the N-terminal helix and the C-terminal helix due to persistent contacts between these regions in these simulations (Fig. 5 and Fig. S11). The community analysis was also performed on the network derived from the four sets of 25 simulations. The community analyses in three of the four combined trajectories are similar to the communities derived from the 100 simulations. This indicates that the network analysis of α-synuclein converges in 25 or 50 simulations unless certain contacts are persistent in these sets of simulations.

Figure 5.

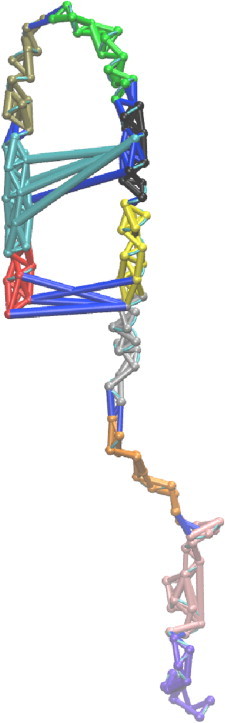
Robustness of modules. This community distribution in two of the 10 test cases contains modules with sequentially distant regions.

We also performed a network analysis with contacts that persisted for 1–75% of the frames in the combined trajectory (Fig. S13). Regardless of the chosen cutoff for contacts, the results are similar, with sequentially contiguous residues forming communities. This is because in the absence of persistent nonlocal contacts, the local contacts dominate over the nonlocal contacts, and the modules are formed by contiguous segments of the protein. Transient nonlocal contacts can be formed when the conformation of the full-length IDP is built from parts of the protein, and such contacts may be important for the function of IDP or to inhibit aggregation (32).

Verification of the proposed modularity of α-synuclein

We carried out three independent tests to verify the modularity of α-synuclein with a frequency cutoff of 50% to define an edge in the network (Fig. 6). The first test verified that residues within a module have a higher probability of contact with other residues from the same module. The mean contact probability of residues (all pairs) within a community is 0.28, whereas the mean contact probability of residues belonging to different communities is 0.01. In other words, any two residues within a module have a much higher probability of being in contact during our simulations than residues belonging to two different communities.

Figure 6.

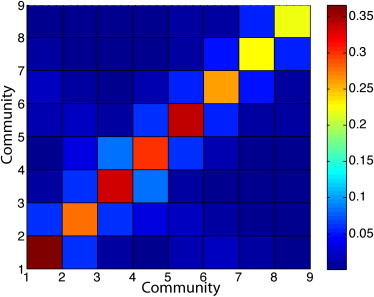
Modularity of protein. The average probability of contact between any two residues belonging to the same or different modules is plotted.

Second, we measured the mutual information between all pairs of torsion angles in α-synuclein to verify that there were no correlated motions between residues from two different modules. We also carried out a control study on a folded protein for comparison. For a globular protein, we show that regions with high density of contacts are correlated to one another (Fig. S14 A). Thus, we confirm that residues in a community of a globular protein are highly correlated to one another (48). Here, we show that the motions of residues in different communities of α-synuclein are not correlated to one another (Fig. S14 B).

Interestingly, the mutual information analysis shows that α-synuclein behaves similarly to a self-avoiding polymer chain model. We find that the size of α-synuclein is smaller than the mean R_g of a self-avoiding polymer in good solvent (R_g = 41 Å), indicating that α-synuclein behaves like a self-avoiding polymer in a poor solvent (R_g = 20 Å) (49). For ideal polymers, such as a random flight chain, the contact probability of two residues depends on the sequence separation between the two residues (50). When such a polymer collapses, the conformational space available to each residue in the protein decreases, leading to an increase in the probability of contacts between residues. In such a polymer, we should be able to split the protein into sequentially contiguous modules that are nearly independent of one another. However, it is difficult to predict the junctions of these modules without such a network analysis formulation.

Finally, we solidified our assertion by measuring the modularity of the network. This analysis assesses whether the network is highly modular in nature. Modularity is the fraction of edges for each node that fall within the community to which it belongs minus the fraction that would be expected if the edges were distributed randomly (37). It is positive if the number of edges within communities exceeds the number expected on the basis of chance. The modularity of networks constructed for real-world problems, such as communities in social networks and authorship networks, lies in the range of 0.4–0.7 (37). The modularity for the contact network of α-synuclein is 0.83, indicating that this network is highly modular in nature. This indicates that there are very few strong contacts between residues belonging to different communities.

Discussion

Despite the use of both experimental and simulation approaches, the atomistic details of the conformational variability of an IDP remain elusive. The unstructured flexible regions of an IDP, which play an important role in its function, present a challenge because they are influenced by properties such as temperature, pH, ionic strength, and solvent. It is challenging to achieve convergence in simulations of a large IDP such as α-synuclein from a single or a few long-timescale simulations (51). However, the probability of converging to the experimental ensemble is more likely with many short simulations (19). Therefore, it is critical to compare both the local and global properties of many shorter-timescale simulations with the corresponding properties measured experimentally. Such a comparison may indicate whether the ensembles generated computationally are similar to the true ensemble. It is still possible that we may not have a proper ensemble when we group many short-timescale simulations with equal weight. Given experimental data, one could use Bayesian statistics to calculate the relative population (or weights) of different states that are most consistent with experimental data, as shown in a recent study (32).

We find that α-synuclein adopts a heterogeneous ensemble of collapsed coil states, as suggested by many experimental studies (16–19,52–54). These collapsed states are stable up to hundreds of nanoseconds in our simulations. The R_g-values of the different collapsed coil states converge in different simulations and are very similar (≈16–30 Å) at room temperature. The sizes of these collapsed states are comparable to the experimentally measured hydrodynamic radius of α-synuclein (26.6 ± 0.5Å) (20).

An interesting question is whether α-synuclein is able to preserve any stable secondary structural features when it attains a collapsed coil state in such a rapid manner. Although the secondary structure content does not converge in different 100-ns simulations, the average of all 100 simulations matches the corresponding measured quantities. We find that the protein forms ≈10% helical content, as observed in CD (40), Raman (55), and infrared measurements (56). Consistent with NMR experiments (18), the N-terminal half of the protein displays a propensity to form a α-helical structure in the simulations. In addition, the C-terminal tail of monomeric α-synuclein forms transient β-strands in the presence of α-helices in the N-terminal half of the protein in these simulations. These β-strands are formed in regions that overlap with the regions that form β-strands in fibrils of α-synuclein (45).

The all-atom MD simulations also capture the formation of heterogeneous collapsed states that are stabilized by tertiary contacts between distant regions of the protein. Consistent with paramagnetic and residual dipolar coupling studies using NMR (19,54,57) and FRET measurements (39,53), some of these collapsed states are stabilized by heterogeneous contacts between the N- and C-terminal regions. However, most of the contacts are heterogeneous (58). Even though the nature of the stable compact state from different simulations depends on the initial configuration, we do not observe any interchange between different compact states during the timescales of these simulations.

Importantly, our network analysis shows that even in cases where an IDP forms heterogeneous collapsed states, there are modules that collapse independently of one another. We show that the modules identified using just 25 or 50 simulations are similar to those identified using all 100 simulations. One of the predictions of our method is that residues in α-synuclein that affect each other are sequentially contiguous. This is consistent with previous nuclear Overhauser effect measurements by NMR showed that only residues up to i ± 6 occur close in space to residue i of α-synuclein in both lipid-free and lipid-associated states (59). Also, the length of these effects (up to 12 neighbors affecting the conformation of a central residue) is coincidentally similar to the length of our modules (13–20 residues). Another prediction for three different modules spanning the NAC region conforms to independent secondary structure motifs identified by NMR (60). According to Bisaglia et al. (60), a long peptide fragment from α-synuclein (residues 57–102) forms three helices with no tertiary interactions between the helices in the presence of SDS. The helices are formed at residues 58–63 (community 3), 70–80 (community 4), and 88–92 (community 5), and there are no tertiary contacts between the helices. Each helix in this fragment falls within a different community, consistent with our analysis.

Conclusion

Our computational study provides insight into the random coil state of α-synuclein. This random coil state has often been misinterpreted as an exclusive ensemble of extended conformations with no distinct secondary structural features. However, our simulations show that the random coil state of α-synuclein could also represent an ensemble of compact collapsed conformations. These compact collapsed states contain residual secondary structures that are inherent to its sequence. Specifically, we observe that the C-terminal tail transiently forms β-strands in the presence of α-helices in the NAC region. The β-strands formed in monomeric α-synuclein could seed the formation of fibrils in oligomers. On the basis of our simulations, it is reasonable to consider the random coil state of α-synuclein to be an ensemble of conformations that includes both collapsed and extended states. Importantly, we show that it is possible to fragment such a heterogeneous collapsed state of α-synuclein into sequentially contiguous peptide fragments for further detailed characterizations. We carried out three independent tests to verify the proposed modularity of α-synuclein; however, we believe that heteronuclear single quantum coherence NMR experiments on fused and unfused modules can unequivocally confirm our predictions.