Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2012 Aug 22;103(4):640–648. doi: 10.1016/j.bpj.2012.07.023

Decoupling Substrate Stiffness, Spread Area, and Micropost Density: A Close Spatial Relationship between Traction Forces and Focal Adhesions

Sangyoon J Han †, Kevin S Bielawski †, Lucas H Ting †, Marita L Rodriguez †, Nathan J Sniadecki †,‡,∗
PMCID: PMC3443781  PMID: 22947925

Abstract

Mechanical cues can influence the manner in which cells generate traction forces and form focal adhesions. The stiffness of a cell’s substrate and the available area on which it can spread can influence its generation of traction forces, but to what extent these factors are intertwined is unclear. In this study, we used microcontact printing and micropost arrays to control cell spreading, substrate stiffness, and post density to assess their effect on traction forces and focal adhesions. We find that both the spread area and the substrate stiffness influence traction forces in an independent manner, but these factors have opposite effects: cells on stiffer substrates produce higher average forces, whereas cells with larger spread areas generate lower average forces. We show that post density influences the generation of traction forces in a manner that is more dominant than the effect of spread area. Additionally, we observe that focal adhesions respond to spread area, substrate stiffness, and post density in a manner that closely matches the trends seen for traction forces. This work supports the notion that traction forces and focal adhesions have a close relationship in their response to mechanical cues.

Introduction

Mechanotransduction pathways associated with a cell’s focal adhesions can affect its survival, fate, and behavior (1–5). Focal adhesions form a physical connection between a cell and its substrate, enabling cytoskeletal tension to be transmitted to the extracellular matrix as a traction force. A cell needs to transfer its cytoskeletal tension through its focal adhesion to migrate or contract (6), but it also uses cytoskeletal tension to probe its environment by means of integrin-related pathways that are activated by traction forces (7–9). For example, cells need to produce cytoskeletal tension to sense the stiffness of their substrate so that they can regulate the progression of their cell cycle or commitment toward specific lineages (10–12). Cytoskeletal tension also plays an essential role in the mechanotransduction of cell spreading, and can influence proliferation and differentiation (13–15). The notion that cytoskeletal tension is indispensable for mechanotransduction further supports the idea that traction forces and focal adhesions play a key role in interpreting these mechanical cues.

In previous studies using deformable gels or micropost arrays, investigators observed that substrate stiffness can strongly influence the generation of a cell’s traction forces (11,16–21). Although these studies provided insights into cell mechanics, they did not control cell spreading. This omission is critical because cells are able to spread to a greater extent when cultured on stiffer substrates (19,22). Moreover, a cell’s spread area has a strong influence on the generation of its traction forces (21,23–28). The coupled relationship between spread area and substrate stiffness makes it difficult to conclude whether cells have higher traction forces due to the stiffness of their substrate or to the effect of stiffness on cell spreading, which in turn stimulates higher traction forces.

Understanding how stiffness and spreading affect traction forces can also shed light on the formation of focal adhesions, which are both regulators and products of traction forces. The initial assembly of a nascent adhesion leads to the generation of traction forces, and their maturation into a stable, focal adhesion is strongly dependent on the strength of the local force (7–9). Focal adhesions have been observed to be larger for cells on stiff substrates compared with those on soft substrates, but these findings have been mostly descriptive and without direct quantification on the correlation between size and force (18,19,29). Similarly, spread area can promote focal adhesion growth (27,28). Given the underlying relationship between area and stiffness, we sought to decouple the role of stiffness and area on traction force generation and focal adhesion growth.

We used micropost arrays and microcontact printing to control substrate stiffness, cell spreading, and post density, and then studied the effects of these factors on the generation of traction forces and focal adhesions. We assessed traction forces of a cell by analyzing the sum of their magnitudes (total force) and average of their magnitudes (average force). We found that increasing substrate stiffness leads to an increase in the total force and average force for a cell. Moreover, we determined that substrate stiffness can affect the generation of traction forces without requiring cell spreading. We also found that cell spreading causes an increase in total force but a decrease in average force. The opposing effects of cell spreading on total force and average force can be attributed to changes in the spatial distribution of traction forces. Furthermore, we conjectured that cell spreading causes an increase in the number of focal adhesions underneath a cell, so we used arrays with a high or low density of posts to compare cell spreading with the number of posts underneath a cell. We found that the post density, rather than cell spreading, strongly determines the total force and average force. Finally, we show that the size of focal adhesions also increases with substrate stiffness and spread area, and exhibits trends that closely match those observed for traction forces.

Materials and Methods

Cell culture

Human pulmonary artery endothelial cells (HPAECs; Lonza, Walkersville, MD) were cultured in F-12K Kaighn’s modified media (Hyclone, Logan, UT) containing 50 μg/ml ECGS (Biomedical Technologies), 100 μg/ml heparin (Sigma Aldrich, St. Louis, MO), 10% fetal bovine serum (Gibco/Invitrogen, Grand Island, NY) on tissue culture dishes that were precoated with 1% gelatin (Sigma Aldrich). NIH 3T3 fibroblasts (a gift from C. Chen, University of Pennsylvania) were grown in Dulbecco’s modified Eagle’s medium (DMEM; Hyclone) plus 10% bovine serum (Gibco), 100 U/ml penicillin, 0.1 mg/ml streptomycin, and 2 mM L-glutamine. Human aortic smooth muscle cells (HA-SMCs; Lonza) were cultured in DMEM with 10% fetal bovine serum, 100 U/ml penicillin, 0.1 mg /ml streptomycin, and 2 mM L-glutamine. All cell types were grown in a humidified incubator at 37°C and 5% CO2.

Traction force micropost arrays

Arrays of microposts were manufactured as previously described (23) (see Supporting Material for details).

Microcontact printing

Micropost arrays were stamped with 50 μg/ml fibronectin (BD Biosciences, Franklin Lakes, NJ). Polydimethylsiloxane stamps that did not have topographical features were used for the studies on unconfined cells (23). A stamp-off method was used as previously described (30), but here was used to produce patterns of square islands of fibronectin that could be transferred onto the tips of the microposts to confine the spread area of the cells (see Supporting Material for post-stamping processes).

Immunofluorescent staining

After culturing cells on the arrays for 14 hr, we permeabilized the samples using a Triton-extraction protocol and stained them with Hoechst 33342 (Invitrogen, Carlsbad, CA), phalloidin (Invitrogen), IgG anti-vinculin (hVin1; Sigma Aldrich), and anti-IgG antibodies (Invitrogen; see Supporting Material for details).

Image analysis of traction forces, spread area, and focal adhesions

Images obtained from fluorescence microscopy were analyzed with custom-built codes in MATLAB (The MathWorks, Natick, MA) to measure the spread area of a cell, the area of its focal adhesions, and deflections in the microposts underneath it (see Supporting Material for details).

Statistical analysis

All data were obtained from at least three replicate experiments, and error bars in all figures represent the standard error of the mean. Regression analyses for the data were performed using Igor (Wavemetrics, Lake Oswego, OR), Minitab (Minitab, State College, PA), and R code (www.r-project.org). R-squared (R2) values were reported for both linear and nonlinear curve-fittings of the data. We labeled the data as having a strong correlation if R2 > 0.9, a good correlation if R2 > 0.75, a moderate correlation if R2 > 0.4, and a weak correlation if R2 < 0.4. SPSS (IBM, Armonk, NY) was used for the multivariable nonlinear fitting surfaces shown in Figs. 3 D and 5 D, Fig. S2 D, and Fig. S3 D.

Figure 3.

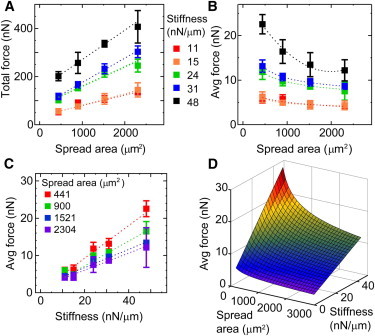
Figure 3

Open in a new tab

Spread area and post stiffness influence traction forces independently. (Color online) (A) Total force increases with spread area for HPAECs on each array type. (B) Average force decreases with spread area for each array stiffness. (C) Average force increases with substrate stiffness for each patterned area. Table S5 shows the number of HPAECs that were measured per condition and the R2 values of the best-fit lines. (D) A multiparameter fit of the data for average force shows they are a function of both spread area and stiffness. Table 1 shows the fit coefficient for nonlinear regression analysis.

Figure 5.

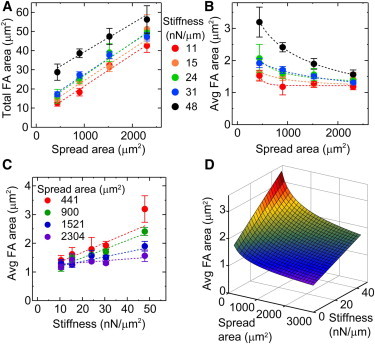
Figure 5

Open in a new tab

Spread area and post stiffness influence focal adhesion area independently. (Color online) (A) Total focal adhesion area increases with spread area. (B) Average focal adhesion area decreases with spread area. (C) Average focal adhesion area increases with substrate stiffness. Table S10 and Table S11 show R2 values of the best-fit lines. (D) A multiparameter fit of the data for average focal adhesion areas shows that they are a function of both spread area and stiffness. Table S12 shows the fit coefficient for the nonlinear regression analysis.

Results

Substrate stiffness affects traction forces and cell spreading

To examine the influence of substrate stiffness on traction forces, we seeded HPAECs onto five different types of arrays of posts, with each array having a unique stiffness (Table S1). HPAECs cultured on the arrays had different shapes and sizes, and produced traction forces that deflected the posts centripetally (Fig. 1, A and B). Total force and average force were analyzed for cells on each array and compared with their spread area (Fig. 1, C and D). A positive relationship between total force and spread area was found for cells on each of the arrays, and the statistical correlation for each array was moderate to good (0.40 < R2 < 0.85; Table S2). On the other hand, a negative relationship between average force and spread area was found for cells on each of the arrays, but the statistical correlations were weak (0.01 < R2 < 0.26; Table S3). Thus, there is suggestive but not strong evidence from the linear regression analysis that the spread area affects traction forces.

Figure 1.

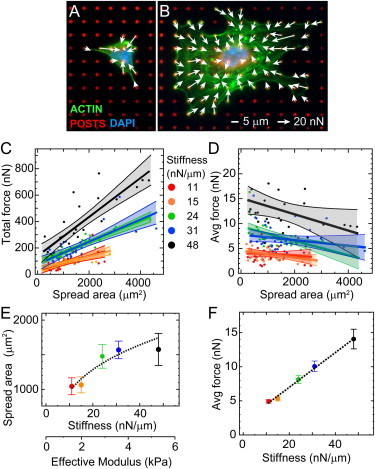
Figure 1

Open in a new tab

Traction forces of HPAECs versus spread area and substrate stiffness. (Color online) (A and B) Representative fluorescent micrographs and traction forces are shown for HPAECs on arrays of microposts with a spring constant of (A) k = 24 nN/μm and (B) k = 48 nN/μm (blue: DNA; green: actin; red: microposts). Traction forces were measured by analyzing the deflections of the posts, and reported as a force vector (arrows). (C) Total force increases with spread area for HPAECs on arrays with different post stiffness. (D) Average forces decrease with spread area. Each data point represents measurement from an individual HPAEC. Straight colored lines denote the linear least-squares fits to the data, and shaded regions report the 90% confidence interval for each fit. (E) Spread area versus substrate stiffness follows a power-law relationship (dashed line). (F) Average force versus substrate stiffness has a positive linear relationship (dashed line).

We noted that the effect of spread area and stiffness may be interrelated, because we observed that HPAECs tended to have increased cell spreading on the stiffer arrays (Fig. 1 E). If one considers the effective shear modulus of the arrays, the relationship between area and stiffness can be fitted to a power-law function, as reported previously (22). We found that the power-law function has a good fit to our data as well (R2 = 0.83; Table S4). When cells were analyzed together regardless of spread area, their average forces were found to increase with stiffness (Fig. 1 F) and with a good statistical correlation (R2 = 0.81; Table S5). Thus, these results indicate that the stiffness of the microposts can promote cells to increase their average force, but stiffness can also influence cell spreading, which in turn contributes to lower average forces. As a consequence, we used a stamp-off printing approach that enabled us to control cell spreading directly so that we could independently assess the effects of spreading and substrate stiffness on traction forces.

Spread area and substrate stiffness affect traction forces independently

To decouple the influence of substrate stiffness on a cell’s spread area, we confined cell spreading by printing fibronectin on the arrays of posts with stamps that had patterns of square islands with 441, 900, 1521, or 2304 μm2 area. HPAECs cultured on these arrays were confined to spread inside the square islands (Fig. 2, A–D). We observed that the average force for confined HPAECs did not change significantly at 10–14 hr of culture time, even though individual traction forces fluctuated over time (Fig. S1). Analysis of traction forces revealed that the total force produced by the confined HPAECs had a positive, linear relationship with spread area and was statistically identical to the fit for unconfined HPAECs on the same substrate stiffness (Fig. 3 A). Statistical correlations in the data were good to strong (0.76 < R2 < 0.98; Table S6). Confined cells had average forces that decreased with spread area (Fig. 3 B). A negative power law matched closely to the trends in the data, with strong statistical correlations (0.94 < R2 < 0.99; Table S6). For the data obtained on unconfined cells (Fig. 1 D), a negative power law could be applied, but the statistical correlation was weak (0.01 < R2 < 0.48; Table S7). Thus, controlling cell spreading by microcontact printing allowed us to demonstrate that a cell’s total force increases with its spread area, but its average force decreases with spread area in a manner that is independent of substrate stiffness.

Figure 2.

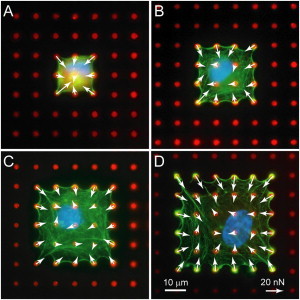
Figure 2

Open in a new tab

Microcontact printing was used to confine the spread area of HPAECs. (Color online) Representative micrographs and traction forces of HPAECs on printed areas of (A) 441 μm2, (B) 900 μm2, (C) 1521 μm2, and (D) 2304 μm2 (blue: DNA; green: actin; red: microposts).

In addition, HPAECs confined to the square patterns had average forces that increased with substrate stiffness (Fig. 3 C). Statistical correlations in the data were moderate to good (0.41 < R2 < 0.88; Table S6). This finding indicates that substrate stiffness can directly influence traction forces and does not require cell spreading. Taking the results for average force versus stiffness and average force versus spread area together, we were able to apply a multiparameter fit to the data (Fig. 3 D and Table 1). The surface fit incorporated a linear relationship for substrate stiffness and a negative power-law relationship for cell spreading, resulting in a strong fit to the data (R2 = 0.97). Similar trends were also observed in the traction forces of 3T3s and HA-SMCs that were consistent with the findings for HPAECs (Fig. S2 and Fig. S3). The same multiparameter fit was applied to the data (Table 1). In comparing the fit parameters, we find that all three cell types have a similar power-law relationship between force and spread area (parameter b). However, HPAECs are the most sensitive of the three to changes in substrate stiffness (parameter d), and HA-SMCs are the most sensitive to changes in spread area (parameter a). Together, these results indicate that spread area and substrate stiffness can affect traction forces independently of each other.

Table 1.

Nonlinear regression coefficients of the average force of HPAECs, 3T3s, and HA-SMCs with respect to substrate stiffness and spread area shown in Fig. 3 D, Fig. S2 D, and Fig. S3 D

a b c d R2
HPAECs 0.69 −0.32 16.65 4.25 0.97
3T3s 1.10 −0.32 −1.36 1.50 0.93
HA-SMCs 3.49 −0.32 5.29 0.39 0.93
Open in a new tab

Model’s fit function is Average force = (a × Areab) × (c + d × Stiffness).

Spread area reduces average force due to the spatial distribution of traction forces

We theorized that the increase in total force and decrease in average force with cell spreading is due to a change in the spatial distribution of traction forces. We compared data for HPAECs with areas of 441, 900, 1521, or 2304 μm2, and analyzed the average traction force per post (Fig. 4 A). All of the HPAECs analyzed were on arrays that had the same stiffness of 31 nN/μm. Color maps showed that the traction forces were highest on posts at the corners and edges of the cells, and lowest on posts in the interior regions. For cells confined to the smallest area (441 μm2), traction forces along the perimeter were consistently high in magnitude. However, for cells that were able to spread to a large area, traction forces were strongest at the corners and were only moderate along the edges. We found that the average force at a post did not correlate with the distance from the geometric center of the cell. Instead, for cells with either small or large spread areas, the average forces at posts at the corners of the cells were similar in magnitude, even though the distances from the cells’ centers were different.

Figure 4.

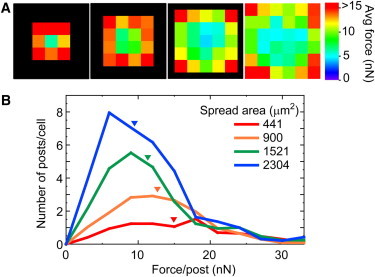
Figure 4

Open in a new tab

Spatial distribution of traction forces determines the total force and average force for an HPAEC. (Color online) (A) Color map of average traction force at each post underneath HPAECs on 441, 900, 1521, and 2304 μm2 printed areas. High traction forces are found at the edges and corners of HPAECs. (B) Histogram of traction forces for HPAECs on each patterned area. The area under the histogram curve is equivalent to the total force of an average cell. Inverted triangles indicate average force for the data.

We plotted histogram curves of the average force per post to clarify how the spread area leads to an increase in total force but also causes a decrease in the average force for an HPAEC (Fig. 4 B). We noted that the area under each curve is equivalent to the total force for an average cell because it is the sum of the traction forces. Consequently, analysis of the area under the histogram curves confirmed that cells with the largest spread area produced the most total force. In contrast, HPAECs with a smaller area had a similar range of traction forces, but the area under their histogram curves was significantly smaller, and hence these cells produced less total force.

Additionally, the relationship between average force and spread area is evident from the skew in the distributions toward lower traction forces per post. HPAECs with the largest spread areas had a significant number of traction forces that were low in magnitude, which contributed to their overall low average force (Fig. 4 B). Based on the color maps, we presume that these lower traction forces are located predominantly within the interior region of a cell. Likewise, HPAECs with the smallest spread areas had only one post within their interior and had significantly more adhesions at the perimeter. This spatial distribution led to the highest average force among the different groups. Therefore, our data show that the total force for an HPAEC increases with spreading due to the addition of more adhesions (i.e., microposts), but cell spreading decreases the average force by shifting the proportion of strong traction forces at the perimeter with weaker traction forces within the interior of a cell.

Focal adhesion area versus spread area and substrate stiffness

To examine the response in focal adhesions to substrate stiffness and spread area, we stained HPAECs for vinculin to quantify their focal adhesion area. Our data show a weak, linear correlation between the area of an individual focal adhesion and its local traction force (0.2 < R2 < 0.4; Fig. S4). However, we observed that the total area and average area of focal adhesions follow closely with the trends observed for traction forces: total focal adhesion area increased with spread area with moderate-to-good linear correlations (0.59 < R2 < 0.98; Fig. 5 A and Table S10), average focal adhesion area decreased with spread area according to a negative power-law relationship with moderate-to-strong correlations (0.40 < R2 < 0.99; Fig. 5 B and Table S10), and average focal adhesion area increased with substrate stiffness with moderate-to-strong linear correlations (0.48 < R2 < 0.92; Fig. 5 C and Table S11). As before, a multiparameter fit was applied to the data and had a good statistical correlation (R2 = 0.84; Fig. 5 D and Table S12). Thus, as seen in the traction force study, the results for focal adhesions suggest that substrate stiffness and spread area may have different effects, that is, stiffness may affect individual adhesion size, whereas spread area affects the number of adhesions.

As seen previously with traction forces, spread area caused the total area of focal adhesions to increase and their average area to decrease. To better understand the response to spreading, we combined the focal adhesion data for HPAECs with 441, 900, 1521, or 2304 μm2 area (Fig. 6 A), and represented the average focal adhesion area at each post using a color-coding scheme (Fig. 6 B). The spatial distributions of focal adhesion area were seen to correlate with traction forces. The color maps showed that focal adhesions were large at the corners of cells and small within the interior regions. Histogram curves of the average focal adhesion per post were plotted and showed that the total area increased with spreading, whereas the average area decreased with spreading (Fig. 6 C). These findings demonstrate that there is a close spatial relationship between traction force and focal adhesion area in response to stiffness and area.

Figure 6.

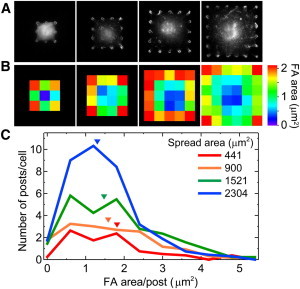
Figure 6

Open in a new tab

Focal adhesions are large at the corners and edges of an HPAEC, but small in its interior. (Color online) (A) Vinculin images of HPAECs on each pattern area. (B) Color map of average focal adhesion area. (C) Histogram of focal adhesion area per post for HPAECs on patterned areas. The area under the histogram curve is equivalent to the total focal adhesion area of an average cell. Inverted triangles indicate average focal adhesion area for the data.

Post density affects traction forces and focal adhesion area

The spatial distributions of the traction forces and focal adhesion areas raise the question as to whether the spread area affects contractility or acts by increasing the number of focal adhesions underneath a cell. To address this question, we used a pair of arrays that had similar spring constants but different post densities (arrays 4 and 6; Table S1). HPAECs with the same area (1521 μm2) but with a different number of post underneath them were compared (Fig. 7, A and B). Conversely, HPAECs on the same number of posts but with different areas were examined (Fig. 7, C and D). Our results indicate that for HPAECs with similar spread areas, those that were attached to more posts produced larger total forces (p < 0.08; Fig. 8 A) and lower average forces (p < 0.005; Fig. 8 B). Similar results were seen for HPAECs with 441 μm2 area (p < 0.09 and 0.03; Fig. 8, E and F, respectively). On the other hand, HPAECs that occupied the same number of posts but had different spread areas produced total forces and average forces that were statistically identical to each other (Fig. 8, C and D). A similar trend was seen for HPAECs on 16 posts, but with different areas (Fig. 8 E). For all HPAECs examined, their total forces were seen to increase with the number of posts underneath a cell, whereas their average forces were seen to decrease with the number of posts (Fig. 8 E and F).

Figure 7.

Figure 7

Open in a new tab

Representative immunofluorescence images and force vectors of HPAECs with spread areas of 1521 μm2 and occupying (A) 25 posts or (B) 49 posts, and HPAECs occupying 36 posts and with (C) 1089 μm2 or (D) 2304 μm2 area. (blue: DNA; green: actin; red: microposts; color online).

Figure 8.

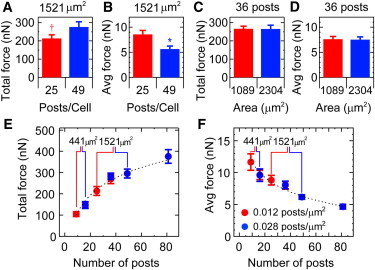
Figure 8

Open in a new tab

Traction forces depend on post density rather than spread area. (Color online) For HPAECs with similar spread area, (A) total forces increase with post density and (B) average forces decrease with post density (†p < 0.08, ∗p < 0.005). (C) Total force and (D) average force are similar for HPAECs occupying the same number of posts but with different areas. (E) Total force increases logarithmically with the number of posts that an HPAEC occupies (R2 = 0.99). (F) Average force per post decreases according to a power-law fit with the number of posts underneath a cell (R2 = 0.92).

To confirm that post density affects the spatial relationship between focal adhesions and traction forces, we analyzed the total area and average area of focal adhesions as before. Post density was found to have an effect on focal adhesion area that mirrored its effect on traction forces. HPAECs with the same spread area had a total focal adhesion area that changed with post density (Fig. 9 A), whereas their average focal adhesion area decreased with post density (Fig. 9 B). HPAECs on the same number of posts but with different spread areas had total and average focal adhesion areas that were statistically identical (Fig. 9, C and D). The trends for total focal adhesion area and average focal adhesion area versus the number of posts they occupied was observed for all HPAECs examined (Fig. 9, E and F). Thus, these results indicate that cell spreading does not directly influence traction forces. Instead, it appears that cell spreading increases the number of individual focal adhesions underneath a cell, which in turn affects the total and average force, as well as the total and average focal adhesion area, of an HPAEC.

Figure 9.

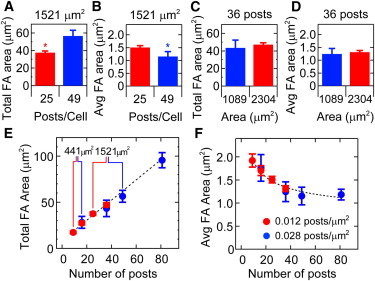
Figure 9

Open in a new tab

Focal adhesion area depends on the post density rather than the spread area. (Color online) For HPAECs with similar spread areas, (A) the total focal adhesion area increases with post density and (B) the average focal adhesion area decreases with post density (∗p < 0.05). (C) The total focal adhesion area and (D) average focal adhesion area are similar for HPAECs occupying the same number of posts but with different area. (E) The total focal adhesion area increases linearly with the number of posts occupied by a cell (R2 = 0.91). (F) The average focal adhesion area decreases according to a power-law fit with the number of posts underneath a cell (R2 = 0.92).

Discussion

Mechanosensing of substrate stiffness

We observed that substrate stiffness can influence traction forces and focal adhesions of cells with confined spread areas. This finding is novel (to our knowledge) because it reveals that the effect of substrate stiffness on traction forces and focal adhesions is independent of cell spreading. The effect of substrate stiffness and cell spreading on traction forces was previously investigated by Califano and Reinhart-King (21) through a statistical analysis of unconfined cells using substrates of different stiffness. They inferred that the effects of stiffness and cell spreading on traction forces were independent; however, they did not control cell spreading. Here, by using microcontact printing, we were able to demonstrate that both traction forces and focal adhesion areas are affected by stiffness in a manner that is independent of cell spreading.

It has been proposed that for cells to sense the stiffness of a substrate, they need to use their traction force to pull at their focal adhesions until they reach a displacement of 100–150 nm (1,8,18). It is thought that displacements such as these cause conformational changes in focal adhesion proteins, which in turn activate signaling pathways that play a role in sensing substrate stiffness (31,32). With our data, we can determine the average displacements at focal adhesions from the slopes of the best-fit lines in Fig. 3 C. We find that average displacements in our data are significantly higher (230–440 nm; Table S6) than those reported previously by Saez et al. (18) (130 nm). This difference suggests that the displacement required for mechanosensing is significantly greater than previously expected. Moreover, we also find an inverse relationship between spread area and average displacement: the average displacement for cells with 441 μm2 area is 440 nm, whereas for HPAECs with 2304 μm2 areas it is 230 nm.

Cytoskeletal differences at the periphery versus the interior

Our results demonstrate that the total force, average force, total focal adhesion area, and average focal adhesion area change with cell spreading. These aggregate measurements receive a strong contribution from traction forces and focal adhesions at the periphery of a cell, and a weak contribution from forces and adhesions at the interior regions. Previously, Rape et al. (28) patterned cells with various aspect ratios and found that a cell’s traction forces and focal adhesions increase with distance from the geometric center of the cell. Moreover, Lemmon and Romer (33) predicted distributions of traction forces using an elegant model that postulates that forces increase linearly with distance from the cell’s center. Our data are partially consistent with these observations, in that we see large forces and focal adhesions at the corners of confined cells. However, our data also show that forces and adhesions do not correlate with the absolute distance from a cell’s center. This discrepancy is apparent if one compares the heat maps for cells with 441 versus 1521 μm2 areas or the heat maps for cell with 900 versus 2304 μm2 (Figs. 4 and 6). Here, cells confined to the smaller area are seen to have forces and adhesions at their periphery that are much larger than those found at the same geometric distance, but instead are located within the interior region of a cell.

These comparisons indicate that traction forces and focal adhesion sizes are not a linear function of distance from the center of a cell. Instead, it is more likely that forces and focal adhesion area are affected by the degree of cytoskeletal organization at the periphery versus the interior. Larger traction forces and focal adhesions at the periphery have been attributed to the presence of circumferential actin bundles, which likely generate a majority of the force produced during spreading (34,35). The periphery and in particular the corners of cells confined to square islands have a higher degree of cell stiffness than the interior, which is indicative of increased cytoskeletal organization (36). The notion that cytoskeletal organization leads to greater traction forces is supported by observations that cell stiffness correlates with traction forces (37). Moreover, computational models of active cell contraction have predicted that large traction forces occur at the periphery of cells in correspondence with the degree of actin-myosin assembly (38,39). Thus, our results lend support to the notion that there are regional differences in the cytoskeleton that affect traction force generation and focal adhesion growth.

Cell area versus focal adhesion density

Our finding that traction forces increase with cell area is consistent with previous studies (17,23,25,26,28). However, we show that cell area does not affect traction forces directly, but instead acts by increasing the number of posts underneath a cell. This finding is specific to micropost arrays, which allow us to limit the number of adhesions for a cell by controlling post density and cell spreading. Previously, McGarry et al. (39) used a bio-chemo-mechanical model to predict that average force should decrease with the number of posts underneath a cell. Our data confirm that prediction (Fig. 8 F).

It has been argued that local ligand density has a stronger effect than global ligand density on the formation of focal adhesions (40). However, by changing the post density, we were able to increase the global ligand density without affecting the local ligand density on the tips of the posts. We found that a change in the post density led to an increase in the total focal adhesion area and a decrease in the average focal adhesion area. Thus, these results suggest that when the local ligand density is high enough for focal adhesion formation, the global ligand density can still have an effect on the focal adhesion area.

Role of global stiffness

We have postulated that increasing post density increases the effective shear modulus of the array, which in turn creates a stiffer environment for the cells (41). Consequently, it could be argued that the effect of post density on traction forces and focal adhesions is due to a change in the global stiffness of the arrays. This argument has some merit, because we observed that cells had larger total forces and total focal adhesion areas on the globally stiffer arrays (Figs. 8 A and 9 A). On the other hand, this argument fails when one considers the effect of global stiffness on the average force and average focal adhesion area. Based on our findings regarding local substrate stiffness (Figs. 3 C and 5 C), one would expect global stiffness to increase the average force and average focal adhesion area in cells. However, we find that global stiffness causes lower average forces and adhesions (Figs. 8 B and 9 B). It may be that global stiffness and local stiffness provide different mechanical cues that affect a cell’s traction forces and focal adhesions.

Close spatial relationship for traction forces and focal adhesions

Several studies have shown a correlation between individual focal adhesion size and local traction force (23,42,43). However, other studies have shown inconsistent results regarding the relationship between traction forces and focal adhesion areas (23,44,45). Our data indicate that traction forces and focal adhesion areas show similar trends in response to mechanical cues. We find that traction forces and focal adhesions have a close relationship for cells with different substrate stiffnesses, spread areas, or post densities (Fig. 3 versus Fig. 5, and Fig. 8 versus Fig. 9). This correlation indicates that traction forces and focal adhesions are tightly coordinated to maintain the proper balance of cytoskeletal tension.

In summary, our results demonstrate an independent role of substrate stiffness and spread area in traction force generation. Our data indicate that for multiple cell types, substrate stiffness affects the average traction force, whereas spread area reduces average forces through the addition of more focal adhesions. This finding demonstrates that a cell’s contractility can be controlled through combinations of substrate stiffness, spread area, and post density. Because cell forces play an important role in regulating cell differentiation, proliferation, and migration, one could tailor these biophysical parameters in a biomaterial or scaffold so that it has the desired mechanical and adhesive properties to influence cell function.

Acknowledgments

We thank A. Rodriguez, S. Feghhi, X. Liang, M. Walner, and S. Ahn for helpful discussions and ideas.

This work was supported in part by a National Science Foundation CAREER Award and grants from the National Institutes of Health (HL097284 and EB001650) and the University of Washington’s Royalty Research Fund.

Supporting Material

Document S1. Four figures, 12 tables, materials and methods, and two references
mmc1.pdf (810.1KB, pdf)

References

  • 1.Discher D.E., Janmey P., Wang Y.L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
  • 2.Vogel V., Sheetz M. Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Cell Biol. 2006;7:265–275. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
  • 3.Chen C.S. Mechanotransduction—a field pulling together? J. Cell Sci. 2008;121:3285–3292. doi: 10.1242/jcs.023507. [DOI] [PubMed] [Google Scholar]
  • 4.Geiger B., Spatz J.P., Bershadsky A.D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 2009;10:21–33. doi: 10.1038/nrm2593. [DOI] [PubMed] [Google Scholar]
  • 5.Schwartz M.A. Integrins and extracellular matrix in mechanotransduction. Cold Spring Harb. Perspect. Biol. 2010;2:a005066. doi: 10.1101/cshperspect.a005066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Ridley A.J., Schwartz M.A., Horwitz A.R. Cell migration: integrating signals from front to back. Science. 2003;302:1704–1709. doi: 10.1126/science.1092053. [DOI] [PubMed] [Google Scholar]
  • 7.Geiger B., Bershadsky A., Yamada K.M. Transmembrane crosstalk between the extracellular matrix—cytoskeleton crosstalk. Nat. Rev. Mol. Cell Biol. 2001;2:793–805. doi: 10.1038/35099066. [DOI] [PubMed] [Google Scholar]
  • 8.Moore S.W., Roca-Cusachs P., Sheetz M.P. Stretchy proteins on stretchy substrates: the important elements of integrin-mediated rigidity sensing. Dev. Cell. 2010;19:194–206. doi: 10.1016/j.devcel.2010.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Puklin-Faucher E., Sheetz M.P. The mechanical integrin cycle. J. Cell Sci. 2009;122:179–186. doi: 10.1242/jcs.042127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Klein E.A., Yin L., Assoian R.K. Cell-cycle control by physiological matrix elasticity and in vivo tissue stiffening. Curr. Biol. 2009;19:1511–1518. doi: 10.1016/j.cub.2009.07.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Paszek M.J., Zahir N., Weaver V.M. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
  • 12.Engler A.J., Sen S., Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
  • 13.Chen C.S., Mrksich M., Ingber D.E. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
  • 14.Huang S., Chen C.S., Ingber D.E. Control of cyclin D1, p27(Kip1), and cell cycle progression in human capillary endothelial cells by cell shape and cytoskeletal tension. Mol. Biol. Cell. 1998;9:3179–3193. doi: 10.1091/mbc.9.11.3179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.McBeath R., Pirone D.M., Chen C.S. Cell shape, cytoskeletal tension, and RhoA regulate stem cell lineage commitment. Dev. Cell. 2004;6:483–495. doi: 10.1016/s1534-5807(04)00075-9. [DOI] [PubMed] [Google Scholar]
  • 16.Lo C.M., Wang H.B., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Wang N., Ostuni E., Ingber D.E. Micropatterning tractional forces in living cells. Cell Motil. Cytoskeleton. 2002;52:97–106. doi: 10.1002/cm.10037. [DOI] [PubMed] [Google Scholar]
  • 18.Saez A., Buguin A., Ladoux B. Is the mechanical activity of epithelial cells controlled by deformations or forces? Biophys. J. 2005;89:L52–L54. doi: 10.1529/biophysj.105.071217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Ghibaudo M., Saez A., Ladoux B. Traction forces and rigidity sensing regulate cell functions. Soft Matter. 2008;4:1836–1843. [Google Scholar]
  • 20.Mitrossilis D., Fouchard J., Asnacios A. Single-cell response to stiffness exhibits muscle-like behavior. Proc. Natl. Acad. Sci. USA. 2009;106:18243–18248. doi: 10.1073/pnas.0903994106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Califano J.P., Reinhart-King C.A. Substrate stiffness and cell area predict cellular traction stresses in single cells and cells in contact. Cell. Mol. Bioeng. 2010;3:68–75. doi: 10.1007/s12195-010-0102-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Engler A., Bacakova L., Discher D. Substrate compliance versus ligand density in cell on gel responses. Biophys. J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Tan J.L., Tien J., Chen C.S. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc. Natl. Acad. Sci. USA. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Reinhart-King C.A., Dembo M., Hammer D.A. Endothelial cell traction forces on RGD-derivatized polyacrylamide substrata. Langmuir. 2003;19:1573–1579. [Google Scholar]
  • 25.Reinhart-King C.A., Dembo M., Hammer D.A. The dynamics and mechanics of endothelial cell spreading. Biophys. J. 2005;89:676–689. doi: 10.1529/biophysj.104.054320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Tolić-Nųrrelykke I.M., Wang N. Traction in smooth muscle cells varies with cell spreading. J. Biomech. 2005;38:1405–1412. doi: 10.1016/j.jbiomech.2004.06.027. [DOI] [PubMed] [Google Scholar]
  • 27.Fu J., Wang Y.K., Chen C.S. Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat. Methods. 2010;7:733–736. doi: 10.1038/nmeth.1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Rape A.D., Guo W.H., Wang Y.L. The regulation of traction force in relation to cell shape and focal adhesions. Biomaterials. 2011;32:2043–2051. doi: 10.1016/j.biomaterials.2010.11.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Yeung T., Georges P.C., Janmey P.A. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskeleton. 2005;60:24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
  • 30.Desai R.A., Khan M.K., Chen C.S. Subcellular spatial segregation of integrin subtypes by patterned multicomponent surfaces. Integr. Biol. (Camb.) 2011;3:560–567. doi: 10.1039/c0ib00129e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.del Rio A., Perez-Jimenez R., Sheetz M.P. Stretching single talin rod molecules activates vinculin binding. Science. 2009;323:638–641. doi: 10.1126/science.1162912. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Giannone G., Sheetz M.P. Substrate rigidity and force define form through tyrosine phosphatase and kinase pathways. Trends Cell Biol. 2006;16:213–223. doi: 10.1016/j.tcb.2006.02.005. [DOI] [PubMed] [Google Scholar]
  • 33.Lemmon C.A., Romer L.H. A predictive model of cell traction forces based on cell geometry. Biophys. J. 2010;99:L78–L80. doi: 10.1016/j.bpj.2010.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Cai Y., Biais N., Sheetz M.P. Nonmuscle myosin IIA-dependent force inhibits cell spreading and drives F-actin flow. Biophys. J. 2006;91:3907–3920. doi: 10.1529/biophysj.106.084806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Hotulainen P., Lappalainen P. Stress fibers are generated by two distinct actin assembly mechanisms in motile cells. J. Cell Biol. 2006;173:383–394. doi: 10.1083/jcb.200511093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Park C.Y., Tambe D., Fredberg J.J. Mapping the cytoskeletal prestress. Am. J. Physiol. Cell Physiol. 2010;298:C1245–C1252. doi: 10.1152/ajpcell.00417.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Tee S.Y., Fu J., Janmey P.A. Cell shape and substrate rigidity both regulate cell stiffness. Biophys. J. 2011;100:L25–L27. doi: 10.1016/j.bpj.2010.12.3744. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Deshpande V.S., McMeeking R.M., Evans A.G. A bio-chemo-mechanical model for cell contractility. Proc. Natl. Acad. Sci. USA. 2006;103:14015–14020. doi: 10.1073/pnas.0605837103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.McGarry J.P., Fu J., Deshpande V.S. Simulation of the contractile response of cells on an array of micro-posts. Philos. Transact. A Math. Phys. Eng. Sci. 2009;367:3477–3497. doi: 10.1098/rsta.2009.0097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Deeg J.A., Louban I., Spatz J.P. Impact of local versus global ligand density on cellular adhesion. Nano Lett. 2011;11:1469–1476. doi: 10.1021/nl104079r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Rodriguez A.G., Han S.J., Sniadecki N.J. Substrate stiffness increases twitch power of neonatal cardiomyocytes in correlation with changes in myofibril structure and intracellular calcium. Biophys. J. 2011;101:2455–2464. doi: 10.1016/j.bpj.2011.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Balaban N.Q., Schwarz U.S., Geiger B. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
  • 43.Goffin J.M., Pittet P., Hinz B. Focal adhesion size controls tension-dependent recruitment of alpha-smooth muscle actin to stress fibers. J. Cell Biol. 2006;172:259–268. doi: 10.1083/jcb.200506179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Beningo K.A., Dembo M., Wang Y.L. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 2001;153:881–888. doi: 10.1083/jcb.153.4.881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Stricker J., Aratyn-Schaus Y., Gardel M.L. Spatiotemporal constraints on the force-dependent growth of focal adhesions. Biophys. J. 2011;100:2883–2893. doi: 10.1016/j.bpj.2011.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Four figures, 12 tables, materials and methods, and two references
mmc1.pdf (810.1KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES