Abstract
RNAs are negatively charged molecules that reside in cellular environments with macromolecular crowding. Macromolecular confinement can influence the ion effects in RNA folding. In this work, using the recently developed tightly bound ion model for ion fluctuation and correlation, we investigate the effect of confinement on ion-mediated RNA structural collapse for a simple model system. We find that for both Na+ and Mg2+, the ion efficiencies in mediating structural collapse/folding are significantly enhanced by the structural confinement. This enhancement of ion efficiency is attributed to the decreased electrostatic free-energy difference between the compact conformation ensemble and the (restricted) extended conformation ensemble due to the spatial restriction.
Introduction
The cellular functions of nucleic acids are intrinsically related to their folding in cellular environments (1–3). Because DNAs/RNAs are highly negatively charged molecules, folding into compact native structures requires metal ions to overcome the strong Coulombic repulsions (1–13). Furthermore, RNAs in vivo are surrounded by many other molecules (14–16), and the volume percentage of macromolecules in cells can reach 40% (14–16). The presence of other macromolecules around an RNA can cause spatial confinement for DNA/RNA folding. Macromolecular crowding can greatly influence RNA folding (17–21); however, the problem of how the spatial constraint affects ion-induced RNA folding is not fully solved. In this work, we constructed a simplified structural model to investigate the effect of macromolecular crowding on ion-mediated RNA collapse/folding.
For folding of RNA secondary structure (1–3), the thermodynamic parameters under standard salt conditions (i.e., 1 M Na+) have been experimentally determined. Parameters for other ionic conditions have also been fitted from experimental data and theoretical calculations (22–33). These parameters have led to many accurate predictions for RNA/DNA secondary structures and folding kinetics (22–33). For tertiary structure folding, however, our understanding of the role of ions, especially the effects of multivalent ions such as Mg2+, remains incomplete (1–13). Experimental and computational studies showed that metal ions with higher charge density are more efficient in promoting RNA collapse, and stronger ion correlations could potentially contribute to the efficient role of Mg2+ ions (34–40). A series of experiments involving short DNA helices suggested the existence of a helix-helix attractive force at high multivalent ion concentration and a repulsive force at low ion concentration (41,42). Furthermore, experiments on a paradigm system consisting of two helices tethered by a loop suggested that Mg2+ is >10-fold more efficient than predicted by the Poisson-Boltzmann (PB) theory for promoting structural collapse (43–45).
In cells, the presence of other molecules can cause a crowded environment that can cause spatial confinement for the conformations of RNAs and consequently influence the free-energy landscape of the RNAs. For proteins, macromolecular crowding has been shown to play an important role in folding stability, structure, and kinetics (14,15,46–51). For RNAs, however, the effect of macromolecular crowding on folding (52), especially its impact on the role of ions in folding (19), is a relatively new subject of investigation.
RNA tertiary structural collapse involves a high charge density, and it is challenging to obtain a quantitative description of the role of metal ions, especially multivalent ions. Molecular-dynamics studies of ion-RNA interactions have provided insights into ion- and structure/sequence-specific forces in RNA folding, especially the force arising from site-specific binding of ions (53–58). The two classic polyelectrolyte theories—the counterion condensation theory (59) and the PB theory (60–65)—have been used successfully to predict the electrostatic properties of biomolecules (59–65). However, for complex RNA tertiary structures, the line-charge structural model used in the counterion condensation theory may be oversimplified (59). Furthermore, RNAs with a high charge density generally induce a high ion concentration and consequently may cause ion-ion correlations for multivalent ions in the vicinity of the RNA surface. The PB theory ignores such potentially important effects for multivalent ion solutions (66–68). To take into account the effects of ion correlations and the ion-binding ensemble, investigators developed the tightly bound ion (TBI) model (66,67) (see the Supporting Materialfor a description of the TBI model). Experimental comparisons suggest that the TBI model may offer improved predictions regarding the ion effect of the thermodynamic stability of DNA/RNA helices/hairpins (31–33), the DNA helix assembly (69–71), and the ion-binding properties and tertiary folding stability of RNAs in the presence of Mg2+ (72–74).
In this work, we employ the newly refined TBI model (72,73) to investigate a paradigm system with two nucleic acid helices tethered by a loop. We focus on the effect of conformational constraint on the role of ions in RNA folding. The conformational constraint can arise from the macromolecular crowding effect. Moreover, our study goes far beyond previous studies that involved only planar configurations (70). Specifically, we consider the conformational fluctuation of helices at the all-atom level with three-dimensional (3D) rotations, and compare our predictions with recent experimental data as well as predictions from the PB theory (44).
Methods
Structural model
The model system consists of two helices tethered by a flexible loop (see Fig. 1). In the model, we allow for 3D rotation of the helical axes. We note that in a previous study (70), only symmetric coplanar model rotations were allowed. As shown in Fig. 1, a configuration of the system can be constructed through the following operations: First, the two parallel helices are separated by an axis-axis distance x. Second, the two helices are symmetrically rotated around the respective ends (O and O′) of the helical axis in the axis-axis plane with an angle θ. Third, the two helices are rotated so that the projections of two helical axes in the plane perpendicular to the line of O-O′ are separated by an angle γ. The configuration of the system can be described by three parameters: distance x, angle θ, and angle γ. Here, the parameter γ is used to produce nonplanar configurations. The (DNA) helices here are assumed to adopt the B-form structure (75). We use the intervals of (3 Å, 20°, 20°) to sample the conformational space of (, , ). To reduce the computational time, we randomly select ∼600 configurations from the full 3D conformation ensemble for calculations. Tests with the different samplings showed that our results are quite robust. In the structural model, the three parameters (x, θ, γ) are used to produce the major portion of the full conformational ensemble, including the nonplanar/planar and compact/extended conformational ensembles. Although this approximation may be valid while we focus on the low-resolution energy landscape of the system, it would be useful in further studies to examine the effects of other degrees of freedom, such as the spin of helices and the asymmetrical rotations of helical axes.
Figure 1.
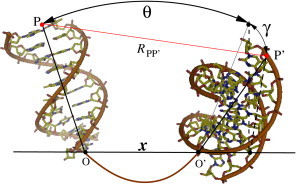
Conformation of two (DNA) helices tethered by a loop can be characterized by three structural parameters: the end-to-end distance x (O-O′), angle θ, and angle γ. The freedom of γ (rotation of the axis into the page) is used to produce nonplanar configurations. The P-P′ distance represents the spatial restriction for the two helices due to, e.g., the macromolecular crowding effect. The between the centers of the helices is used to quantify the compactness of the model. Tertiary contact energy can be added for conformations with a small value. The DNA helices were constructed with the software X3DNA (75) and displayed with the software PyMol (http://pymol.sourceforge.net/).
Free energy
For a given configuration of the system described by (x,θ,γ), the total free energy can be calculated as
| (1) |
where is the electrostatic free energy for the two helices in an ionic solution, is the free energy of the loop, is the coaxial stacking free energy between the two helices, and is the tertiary contact energy when the two helices are in close contact.
In the study, we calculate using the all-atom TBI model (72,73) (see the Supporting Material for a detailed description of the model). We calculate from
| (2) |
where is the probability of a loop of length L with end-to-end distance x. can be estimated from an approximate analytical expression (76): , where A is the normalization constant (76–78) and is the persistence length of the loop. In our calculations, to make a direct comparison with the experiment, we assume that the loop is a polyethylene glycol (PEG) chain (44) and the persistence length is 3.8 Å (44,70).
The coaxial stacking free-energy term is an important energetic factor for nucleic acid helix alignment (28,79). We model this term based on the thermodynamic parameters (23,79) and an RNA structure analysis (28):
| (3) |
| (4) |
where . Here, is the coaxial stacked basepairs, kcal/mol for (at 25°C) in the experimental system (44), and is an offset between the coaxial stacking energy and the corresponding canonical basepairs (79).
is added to account for the possible tertiary contacts (45):
| (5) |
| (6) |
where is a constant negative energy. In the calculation, we use −10 T, −12 T, and −14 T to investigate the effect of the tertiary contact. We use the condition , a typical interaxial distance for ion-induced DNA aggregates (80–83), to simulate a close contact where tertiary contact can occur. Our control tests showed that small changes in the criteria around 28 Å would not cause significant changes in our quantitative predictions or qualitative conclusions.
For the purpose of visualizing the free-energy landscape, we also use the interaxis angle Θ to represent the two angles θ and γ (shown in Fig. 1)
| (7) |
to show the electrostatic free-energy landscape in a 2D () plane instead of in a 3D () space.
Spatial confinement
As shown in Fig. 1, we use , the distance between the centers of the two axes of the helices, to describe the compactness of the system. Furthermore, we use the distance between the outer axial ends , to quantify the spatial constraint of the system. A smaller corresponds to a stronger spatial confinement due to, for example, macromolecular crowders.
To quantify the compactness of the system for an ensemble of conformations, we use a Boltzmann-weighted averaged value for the distance between the centers of the helix pair (70):
| (8) |
Results and Discussion
To investigate how the different ionic conditions affect the folding properties of the model system, we apply the TBI model to calculate the electrostatic free-energy landscape for a wide range of Na+ and Mg2+ conditions: [Mg2+] ∈ [0.01 mM, 0.1 M] and [Na+] ∈ [0 M, 2 M]. To simulate the experiments directly (44), we assume that the system is always immersed in a 16 mM Na+ background (from the Na-MOPS buffer). For convenience, we define two specific states for the model system: 1), the random relaxation state, in which the two helices can fluctuate randomly, corresponding to the state with fully neutralized helices (43,44); and 2), the (electrostatically) folded (collapsed) state, where (3,69,80–83).
In the following, we first present our results regarding the electrostatic free-energy landscape. We then discuss the role played by ions in the structural collapse (without the possible tertiary contact). Finally, we discuss the effects of spatial confinement and tertiary contacts on the role of ions in structural folding.
Electrostatic free-energy landscape
In Na+solutions
Fig. 2, A–D, show the electrostatic free-energy landscape for the different concentrations of [Na+]. At low added [Na+], the helices tend to avoid each other, with the largest x and Θ (see Fig. 2 A) due to weak charge neutralization. An increased [Na+] would enhance the ion binding and charge neutralization due to a lower entropic penalty for ion binding, thus causing a weakened interhelix repulsion. As shown in Fig. 2 B, the helices fluctuate around less extended conformations with smaller x and Θ values. When [Na+] becomes very high ( M), the helices become nearly fully neutralized and thus can fluctuate randomly in the full conformational space (Fig. 2, C and D), except for very compact configurations (very small x and Θ), where helix-helix and ion-helix exclusions play a dominant role.
Figure 2.
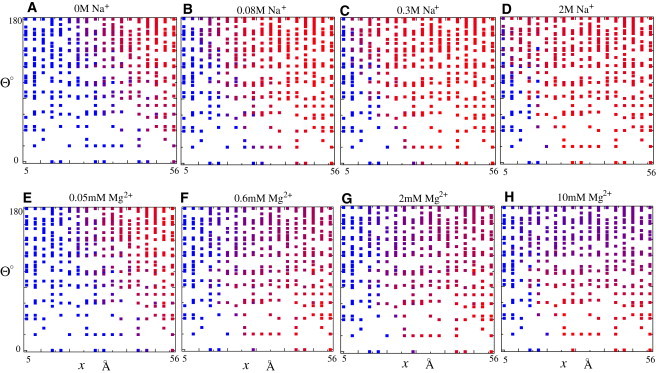
(A–F) Electrostatic free-energy landscapes as a function of [Na+] (A–D) and [Mg2+] (E and F). Here x is the end-to-end distance and Θ is the angle between the two helical axes; Θ is determined by the (θ,γ) angles (see Eq. 7). The color scale represents the energy difference between the configuration (x, Θ) and the state with the minimum free energy. From 0 to 5 , the color changes gradually from red to blue. Note that the system is in a 16 mM Na+ background due to the Na-MOPS buffer (44).
In Mg2+solutions
Fig. 2, E–H, show the electrostatic free-energy landscapes for the helices with different concentrations of [Mg2+]. At low [Mg2+], the helices form extended conformations with large x and Θ. With the increase of [Mg2+], the two helices switch to the conformations with smaller Θ and x (Fig. 2, F and G). For high [Mg2+] ( mM), the helices tend to adopt the conformations with very small Θ and intermediate x (Fig. 2 H). The above transition with increasing [Mg2+] can be attributed to divalent ion-mediated helix-helix interactions (43,69,70). When [Mg2+] is very low, background Na+ of low concentration in buffer gives only a weak neutralization to the helices. Therefore, the helices would repel each other and the conformations with largest x and Θ would be favorable. With an increase of [Mg2+], Mg2+ would compete with background Na+, and the self-organization of Mg2+ could induce a (slight) attractive force between helices (69,70). This attraction would become stronger for the helix-helix near-parallel configurations at intermediate separation and at higher [Mg2+] (70). As a result, the helices would transform to the conformations with small Θ and intermediate x (69).
Compared with previous results for 2D (coplanar) configurations (see Fig. 2 in Tan and Chen (70)), our 3D free-energy landscapes show more-extended conformations (large Θ), which cause an increase in the conformational entropy of the two helices and weaken the effect of the possible Mg2+-mediated helix-helix attractive force in the structural collapse.
Ion-mediated structural collapse: without spatial confinement
First, we discuss the role of ions in structural collapse without spatial confinement and tertiary contact by setting in Eq. 1. In the following, we present the general features of the system and discuss comparisons with experimental data (44).
General features
As shown in Fig. 3 A, with the increase of [Na+] to 2 M, decreases from a large value to that of the random relaxation (fully neutralized) state. Such a trend of is a result of the electrostatic free-energy landscapes shown in Fig. 2, A–D, and can be attributed to the aforementioned enhanced Na+ binding at higher [Na+]. Also shown in Fig. 3 A is the loop-length dependence of the structural compaction at low and high [Na+]. A PEG chain is quite flexible . The loop (length ) tends to minimize the loop entropic loss upon structure formation. Therefore, the loop drives the system to fluctuate around a relatively smaller end-to-end distance x, because a larger x corresponds to a smaller loop entropy. For example, for PEG loops with and , and , respectively, are the most favorable according to Eq. 2. The loop effect is slightly stronger for low [Na+] conditions, where the favorable configurations are extended and the effect of the (short) tether can become more important.
Figure 3.
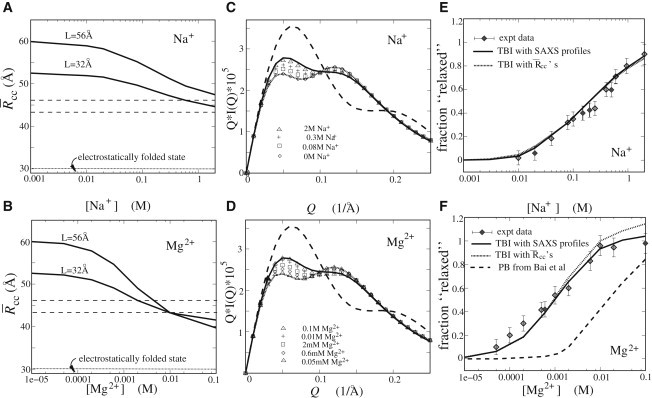
Ion-mediated structural collapse in the absence of the tertiary contact and spatial confinement. (A and B) Ion concentration dependence of the compactness (the mean distance between the helix centers) as a function of Na+ (A) and Mg2+ (B). Dashed lines denote the random relaxation (fully neutralized) state, and dotted lines denote the upper limit of the electrostatically folded state (69,70,80–82). (C and D) SAXS profiles calculated for the different added Na+ (C) and Mg2+ (D). Lines are the reference SAXS profiles. Dashed lines: Upper limit of the electrostatically folded state . Solid lines: Random relaxation (fully neutralized) state. Dotted lines: Extended state (with no added salts). The SAXS profiles were calculated with the software CRYSOL (84), and the statistical weight was determined from the free energy . (E and F) The relaxed fraction χ as a function of [Na+] (E) and [Mg2+] (F), respectively (see Eq. 9). Symbols: Experimental data from Bai et al. (44). Solid lines: Calculated results with the SAXS profiles determined from the TBI model. Dotted lines: Calculated with the compactness determined from the TBI model. Dashed lines: Calculated with the SAXS profiles determined according to the PB theory by Bai et al. (44). The relaxed state is taken as the fully neutralized state. Note that the system is in a 16 mM Na+ background due to the Na-MOPS buffer (44).
In a solution with added [Mg2+], at low [Mg2+], the favorable conformations are those with large x and Θ, and thus a loop length can contribute to the compaction of the system. In contrast, at a high [Mg2+], Mg2+ induces a (slightly) attractive force between helices at small interaxis angles Θ (see Fig. 2 H). When the helices are driven by the loop to a smaller x (to gain loop conformation entropy), the low free-energy conformations (in the small x regime in Fig. 2, G and H) correspond to a range of Θ. As a result, a small x does not necessarily lead to compaction of the system (characterized by a small ). We note that a high [Mg2+] can induce a state that is slightly more compact than the random relaxation (fully neutralized) state but is much looser than the upper limit of the electrostatically folded state (3,80–83), as shown in Fig. 3 B.
Comparisons with experiments
To make a direct comparison with the experimental system (44), we assume the loop length to be . We calculate the Boltzmann-weighted averaged small-angle x-ray scattering (SAXS) profiles over the conformation ensemble for each ionic condition. Here Q is the scattering vector, which is equal to , where ϑ is the Bragg angle and λ is the wave length of the radiation.
Fig. 3, C and D, show the SAXS profiles for the different added [Na+] and [Mg2+], respectively. As the added [Na+] is increased from 0 to 2 M, and Mg2+ is increased from 0 to 0.1 M, the SAXS profile changes from that of the extended state to that of the nearly fully neutralized state. In addition, the profiles indicate that the system at high [Mg2+] (∼0.1 M) is slightly more compact than that at high [Na+] (∼2 M). Because the experimental SAXS profiles are in arbitrary units and with vertical shifts (44), we cannot make direct comparisons for the SAXS profiles between the experiments and our predictions.
Based on the calculated SAXS profiles and compactness , we can estimate the fraction relaxed χ for the system by (44)
| (9) |
where Ω stands for a structural parameter, such as or . is that in a 16 mM Na+ background from the Na-MOPS buffer without added salt, and is taken as that of the fully neutralized state in our estimation. Based on the equation, we estimate χ from the calculated and , and compare our predictions with experiments for the cases with added Na+ and Mg2+.
Fig. 3, E and F, show the fraction relaxed χ as a function of added [Na+] and [Mg2+], respectively. When [Na+] is added, χ increases from 0 to ∼0.9 at 2 M [Na+], suggesting that the system is close to the random relaxation (fully neutralized) state. The lines estimated from and are almost identical, and the predictions agree well with the experimental data, as shown in Fig. 3 E.
As shown in Fig. 3 F, when Mg2+ is added, χ increases from 0 to ∼0.9 at ∼8 mM [Mg2+], and may slightly exceed 1 when 10 mM, suggesting a slightly more compact state induced by high [Mg2+]. In addition, the χ predicted from is slightly larger than that predicted from at high [Mg2+] (shown in Fig. 3 F), which is in accordance with the above-described relations of and with [Na+] and [Mg2+]. Fig. 3 F also shows that the predicted χ-values from the TBI model are in good accordance with the experimental data, whereas PB theory predicts a >10-fold higher midpoint of [Mg2+] for the Mg2+-mediated collapse. This result may be attributed to the ignored ion-ion correlations in the PB theory. The inclusion of ion correlations would allow ions to self-organize to form a low-energy state, and thus the TBI model predicts a more efficient role of Mg2+ than does the PB theory (67,72,73).
It is important to note that although the system has a similar global compactness at high [Na+] and [Mg2+], the free-energy landscapes are very different, as shown in Fig. 2.
The PEG loop used in the above calculation is electrically neutral, whereas a realistic RNA loop is a polyanionic chain. Recent experiments suggest that the hinge stiffness can become an energetic barrier for RNA folding (39). As shown previously (70), a nucleotide loop may enhance the sharpness of ion-mediated structural collapse due to the ion dependence of the persistence length of the loop (70).
Ion-mediated folding: with spatial confinement
In this section, we investigate the influence of spatial restriction and a tertiary contact on the ion-mediated collapse of the two-helix system described above.
Electrostatic free-energy landscape with spatial confinement
With the conformational confinement defined by the limit for the distance between the outer ends of the two helices (see Fig. 1), the conformational space of the system is confined. The electrostatic free-energy landscape of the confined system is given by
| (10) |
where is the distance between the two centers of the two helices (see Fig. 1).
As shown in Fig. 4, the spatial restriction influences the free-energy landscape significantly for both Na+ and Mg2+ solutions. For large , the free-energy landscape is close to that obtained without spatial restriction. At low [Na+], the favorable conformations are clustered in the region of large . At high [Na+] (e.g., 2 M), the helices can fluctuate nearly in the whole region with all of the different values. With the decrease of , the conformations of the two helices are confined by the restriction and the extended conformations are severely limited. This causes the free energy at high [Na+] to become close to that at low [Na+]. In the limit of strong spatial confinement, such as , the free energy at the different Na+ concentrations can become nearly identical (see Fig. 4, A–D, in the small regime).
Figure 4.
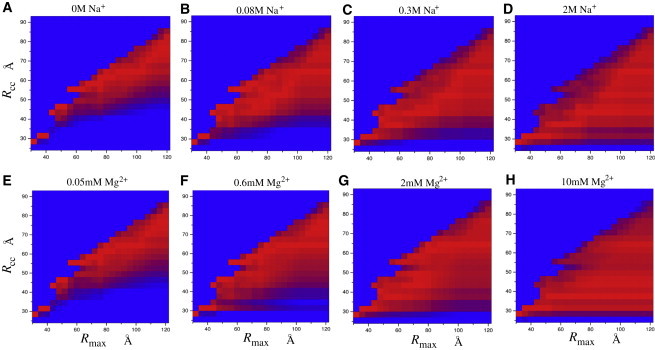
Electrostatic free-energy landscapes , where represents the spatial restriction for the helices (e.g., due to the macromolecular crowding; see Eq. 10). The color scale denotes the energy difference between and the minimum value for each : . From 0 to , the color changes uniformly from red to blue.
For Mg2+ solutions, the spatial confinement effect on is similar to that for Na+ solutions, except for the much more efficient role of the Mg2+ ions in promoting the collapse of the system. The electrostatic free-energy landscapes show that with the spatial confinement, the extended conformations are much more significantly restricted than the compact conformations, causing the destabilization of the extended state. In an ion-promoted collapse, the spatial confinement would effectively enhance the ion effect on folding.
Ion-mediated folding: effects of spatial confinement and tertiary contacts
To investigate the role of tertiary contacts in ion-induced structural collapse, we add a negative constant energy to model the effect of the tertiary contacts. Specifically, we choose three values for : −10 T, −12 T, and −14 T (see Eq. 6).
A helix-helix attraction arising from the tertiary contacts would cause a shift in the conformational distribution toward the compact state and lower the ion concentration required to induce the collapse of the structure. Furthermore, the tertiary contact results in a much sharper ion-induced structural collapse (than the tertiary contact-free case). The effect is more pronounced for stronger tertiary contacts. As shown in Fig. 5, A, C, and E for Na+, the midpoint for the folding transition occurs at [Na+] M for and [Na+] M for , respectively, and the stronger tertiary contacts cause a slightly more compact state. As shown in Fig. 5, B, D, and F, the midpoints of Mg2+-dependent folding are ∼0.8 mM and ∼0.2 mM for and , respectively. Again, we note that much lower [Mg2+] (∼ mM) is required to cause folding compared with [Na+] (∼ M), which is in accordance with the experimental data (13,34,72,73).
Figure 5.
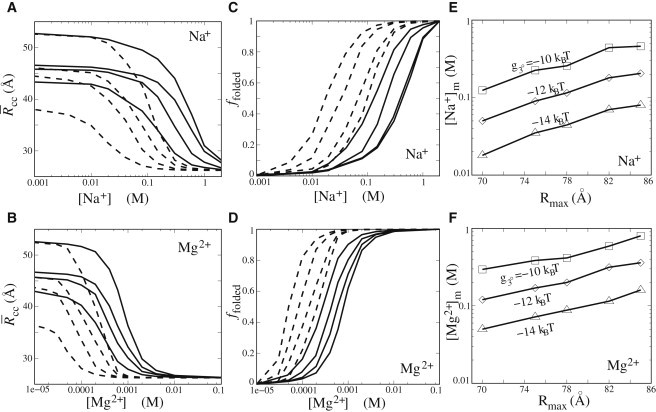
Ion-mediated structural folding in the presence of tertiary contact and spatial restriction. (A and B) The compactness of the loop-tethered helices as functions of [Na+] (A) and [Mg2+] (B) for the different values (from right to left: 120 Å, 82 Å, 78 Å, and 70 Å) and tertiary contact energies (solid lines: −10 ; dashed lines: −14 ). (C and D) The folded fraction as a function of [Na+] (C) and [Mg2+] (D) for the different values (from right to left: 120 Å, 82 Å, 78 Å, and 70 Å) and tertiary contact energies (solid lines: −10 , and dashed lines: −14 ). (E and F) Ion concentration midpoints for the folding transition as a function of and the different tertiary contact energies (from top to bottom: = −10 , −12 , and −14 ).
To further examine the effect of spatial confinement in the presence of tertiary contacts, we calculated with a given constraint (the maximum distance of P-P′ shown in Fig. 1). As shown in Fig. 5, A–F, the spatial confinement significantly enhances the ion efficiency in mediating the structural collapse/folding in both Na+ and Mg2+ solutions. For example, for , with the decrease of from 120 Å to 70 Å, the [Na+] and [Mg2+] at the midpoint of the folding transition decreases from ∼0.5 M to M, and from ∼1 mM to ∼0.3 mM, respectively. For a stronger tertiary contact (e.g., ), the spatial confinement would further enhance the ion efficiency for both Na+ and Mg2+, as shown in Fig. 5, A–F. The higher efficiency of Mg2+ compared with Na+ is attributed to the higher valence of Mg2+, which corresponds to less entropy for ion binding and a stronger ion-ion correlation, leading to a higher Mg2+ binding affinity (72) and consequently a higher efficiency for stabilizing RNA (73).
The above-described spatial confinement-promoted ion (Na+ and Mg2+) efficiency in mediating structural folding is in accordance with the recent finding that a lower Mg2+ concentration is required to fold the Azoarcus ribozyme in PEG environments (19). The spatial confinement can be caused by molecular crowding or other in vivo effects. The spatial confinement can destabilize the low-salt (extended) state by reducing the conformational space, and consequently decrease the electrostatic free-energy difference between the compact conformations and the (restricted) extended conformations (52). In addition, the tertiary contacts can further stabilize the compact state. Together, these two effects lead to a reduced ion concentration, which is required to induce the folding transition. Therefore, Na+ and Mg2+ are more efficient for RNA folding in a crowded environment.
Conclusions
In this work, we employed the newly refined TBI model (72,73) to investigate how ions cause compaction in a system of loop-tethered helices. The main advantage of the TBI model is its ability to account for possible ion correlation and fluctuation effects. Our study is distinguished from previous studies (70) on similar systems in several ways, as described below:
First, we based our study on 3D (instead of planar) rotational degrees of freedom in the conformational sampling of the system. In comparison with coplanar (2D) helix orientations, the 3D random orientation of the helices reduces the (ensemble-averaged) ion correlation effect and the associated force between the helices.
Second, in this work we focused mainly on investigating the influence of spatial confinement and tertiary contacts on the ion effect, and making comparisons with PB-based predictions and recent experimental results. On the basis of our results, we drew the following conclusions:
-
1.
Na+ can induce a transition from an ensemble of extended conformations to an ensemble of random relaxed conformations with a flat energy landscape. In contrast, Mg2+ can induce a transition from an extended state to a conformation ensemble that is slightly more ordered and slightly more compact than the random relaxation conformational ensemble. However, the Mg2+-induced state is far looser than the (electrostatically) folded state. The predictions from the TBI model are in accordance with the experimental data for both Na+ and Mg2+ solutions, whereas the PB theory significantly underestimates the efficiency of Mg2+.
-
2.
A tertiary contact would make the ion (Na+ and Mg2+)-dependent folding transition much sharper than the tertiary contact-free case. Furthermore, stronger tertiary contacts can fold RNAs at lower ion concentrations for both Na+ and Mg2+.
-
3.
Spatial confinement (e.g., due to macromolecular crowding) significantly promotes the ion efficiency in mediating RNA folding for both Na+ and Mg2+. The effect of the spatial confinement can be attributed to the decreased electrostatic free-energy difference between the compact ensemble and the (restricted) extended ensemble.
Overall, the current theory shows good agreement with the experiment results, suggesting an overall reliable analysis and predictions regarding ion-induced compaction and the effects of spatial confinement. Further investigation of the problem requires several improvements of the model. First, in the structural modeling, although we took nonplanar conformations into account, we ignored conformations generated from the spin of the helices and the nonsymmetric rotations of the helical axes. Including these conformations may cause changes in the free-energy landscape; however, a detailed study of such changes would entail an exceedingly high computational cost. Second, the current form of the TBI model cannot treat the sequence preference in ion binding (71,85). The specific binding could make important contributions to the ion effect, although for the PEG-tethered helix system used here, the contribution of the specific binding may be weak. Finally, we neglected the interference from the helix on the loop conformations, except for the constraint of the end-end distance x. The effect of the loop-helix interference may not be significant for a PEG loop. However, such an effect can be important for a polynucleotide loop, which is highly charged.
Acknowledgments
This research was supported by the National Science Foundation (grants MCB0920067 and MCB0920411), National Institutes of Health (grant GM063732 (to S.-J.C.)), National Science Foundation of China (grants 11074191, 11175132, and 10844007), Program for New Century Excellent Talents (NCET 08-0408), Fundamental Research Funds for the Central Universities, National Key Scientific Program (973)-Nanoscience and Nanotechnology (No. 2011CB933600), and Scientific Research Foundation for Returned Overseas Chinese Scholars, State Education Ministry (to Z.-J.T.).
Contributor Information
Zhi-Jie Tan, Email: zjtan@whu.edu.cn.
Shi-Jie Chen, Email: chenshi@missouri.edu.
Supporting Material
References
- 1.Bloomfield V.A., Crothers D.M., Tinoco I., Jr. University Science Books; Sausalito, CA: 2000. Nucleic Acids: Structure, Properties and Functions. [Google Scholar]
- 2.Tinoco I., Jr., Bustamante C. How RNA folds. J. Mol. Biol. 1999;293:271–281. doi: 10.1006/jmbi.1999.3001. [DOI] [PubMed] [Google Scholar]
- 3.Bloomfield V.A. DNA condensation by multivalent cations. Biopolymers. 1997;44:269–282. doi: 10.1002/(SICI)1097-0282(1997)44:3<269::AID-BIP6>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 4.Brion P., Westhof E. Hierarchy and dynamics of RNA folding. Annu. Rev. Biophys. Biomol. Struct. 1997;26:113–137. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
- 5.Sosnick T.R., Pan T. RNA folding: models and perspectives. Curr. Opin. Struct. Biol. 2003;13:309–316. doi: 10.1016/s0959-440x(03)00066-6. [DOI] [PubMed] [Google Scholar]
- 6.Draper D.E. RNA folding: thermodynamic and molecular descriptions of the roles of ions. Biophys. J. 2008;95:5489–5495. doi: 10.1529/biophysj.108.131813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chu V.B., Herschlag D. Unwinding RNA’s secrets: advances in the biology, physics, and modeling of complex RNAs. Curr. Opin. Struct. Biol. 2008;18:305–314. doi: 10.1016/j.sbi.2008.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen S.J. RNA folding: conformational statistics, folding kinetics, and ion electrostatics. Annu. Rev. Biophys. 2008;37:197–214. doi: 10.1146/annurev.biophys.37.032807.125957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Woodson S.A. Compact intermediates in RNA folding. Annu. Rev. Biophys. 2010;39:61–77. doi: 10.1146/annurev.biophys.093008.131334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wong G.C., Pollack L. Electrostatics of strongly charged biological polymers: ion-mediated interactions and self-organization in nucleic acids and proteins. Annu. Rev. Phys. Chem. 2010;61:171–189. doi: 10.1146/annurev.physchem.58.032806.104436. [DOI] [PubMed] [Google Scholar]
- 11.Vander Meulen K.A., Butcher S.E. Characterization of the kinetic and thermodynamic landscape of RNA folding using a novel application of isothermal titration calorimetry. Nucleic Acids Res. 2012;40:2140–2151. doi: 10.1093/nar/gkr894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stellwagen E., Muse J.M., Stellwagen N.C. Monovalent cation size and DNA conformational stability. Biochemistry. 2011;50:3084–3094. doi: 10.1021/bi1015524. [DOI] [PubMed] [Google Scholar]
- 13.Tan Z.J., Chen S.J. Importance of diffuse metal ion binding to RNA. Met. Ions Life Sci. 2011;9:101–124. [PMC free article] [PubMed] [Google Scholar]
- 14.Minton A.P. Implications of macromolecular crowding for protein assembly. Curr. Opin. Struct. Biol. 2000;10:34–39. doi: 10.1016/s0959-440x(99)00045-7. [DOI] [PubMed] [Google Scholar]
- 15.Zhou H.X., Rivas G., Minton A.P. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Burz D.S., Shekhtman A. Structural biology: inside the living cell. Nature. 2009;458:37–38. doi: 10.1038/458037a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lambert D., Leipply D., Draper D.E. The osmolyte TMAO stabilizes native RNA tertiary structures in the absence of Mg2+: evidence for a large barrier to folding from phosphate dehydration. J. Mol. Biol. 2010;404:138–157. doi: 10.1016/j.jmb.2010.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pincus D.L., Hyeon C., Thirumalai D. Effects of trimethylamine N-oxide (TMAO) and crowding agents on the stability of RNA hairpins. J. Am. Chem. Soc. 2008;130:7364–7372. doi: 10.1021/ja078326w. [DOI] [PubMed] [Google Scholar]
- 19.Kilburn D., Roh J.H., Woodson S.A. Molecular crowding stabilizes folded RNA structure by the excluded volume effect. J. Am. Chem. Soc. 2010;132:8690–8696. doi: 10.1021/ja101500g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zheng K.W., Chen Z., Tan Z. Molecular crowding creates an essential environment for the formation of stable G-quadruplexes in long double-stranded DNA. Nucleic Acids Res. 2010;38:327–338. doi: 10.1093/nar/gkp898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rajendran A., Nakano S., Sugimoto N. Molecular crowding of the cosolutes induces an intramolecular i-motif structure of triplet repeat DNA oligomers at neutral pH. Chem. Commun. (Camb.) 2010;46:1299–1301. doi: 10.1039/b922050j. [DOI] [PubMed] [Google Scholar]
- 22.Serra M.J., Turner D.H. Predicting thermodynamic properties of RNA. Methods Enzymol. 1995;259:242–261. doi: 10.1016/0076-6879(95)59047-1. [DOI] [PubMed] [Google Scholar]
- 23.SantaLucia J., Jr. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Xia T., SantaLucia J., Jr., Turner D.H. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base pairs. Biochemistry. 1998;37:14719–14735. doi: 10.1021/bi9809425. [DOI] [PubMed] [Google Scholar]
- 25.Chen S.J., Dill K.A. RNA folding energy landscapes. Proc. Natl. Acad. Sci. USA. 2000;97:646–651. doi: 10.1073/pnas.97.2.646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang W.B., Chen S.J. RNA hairpin-folding kinetics. Proc. Natl. Acad. Sci. USA. 2002;99:1931–1936. doi: 10.1073/pnas.032443099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tyagi R., Mathews D.H. Predicting helical coaxial stacking in RNA multibranch loops. RNA. 2007;13:939–951. doi: 10.1261/rna.305307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Blake R.D., Delcourt S.G. Thermal stability of DNA. Nucleic Acids Res. 1998;26:3323–3332. doi: 10.1093/nar/26.14.3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Owczarzy R., You Y., Walder J.A. Effects of sodium ions on DNA duplex oligomers: improved predictions of melting temperatures. Biochemistry. 2004;43:3537–3554. doi: 10.1021/bi034621r. [DOI] [PubMed] [Google Scholar]
- 31.Tan Z.J., Chen S.J. Salt dependence of nucleic acid hairpin stability. Biophys. J. 2008;95:738–752. doi: 10.1529/biophysj.108.131524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tan Z.J., Chen S.J. RNA helix stability in mixed Na+/Mg2+ solution. Biophys. J. 2007;92:3615–3632. doi: 10.1529/biophysj.106.100388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tan Z.J., Chen S.J. Nucleic acid helix stability: effects of salt concentration, cation valence and size, and chain length. Biophys. J. 2006;90:1175–1190. doi: 10.1529/biophysj.105.070904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Heilman-Miller S.L., Thirumalai D., Woodson S.A. Role of counterion condensation in folding of the Tetrahymena ribozyme. I. Equilibrium stabilization by cations. J. Mol. Biol. 2001;306:1157–1166. doi: 10.1006/jmbi.2001.4437. [DOI] [PubMed] [Google Scholar]
- 35.Koculi E., Hyeon C., Woodson S.A. Charge density of divalent metal cations determines RNA stability. J. Am. Chem. Soc. 2007;129:2676–2682. doi: 10.1021/ja068027r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Takamoto K., He Q., Brenowitz M. Monovalent cations mediate formation of native tertiary structure of the Tetrahymena thermophila ribozyme. Nat. Struct. Biol. 2002;9:928–933. doi: 10.1038/nsb871. [DOI] [PubMed] [Google Scholar]
- 37.Soto A.M., Misra V., Draper D.E. Tertiary structure of an RNA pseudoknot is stabilized by “diffuse” Mg2+ ions. Biochemistry. 2007;46:2973–2983. doi: 10.1021/bi0616753. [DOI] [PubMed] [Google Scholar]
- 38.Kim H.D., Nienhaus G.U., Chu S. Mg2+-dependent conformational change of RNA studied by fluorescence correlation and FRET on immobilized single molecules. Proc. Natl. Acad. Sci. USA. 2002;99:4284–4289. doi: 10.1073/pnas.032077799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schlatterer J.C., Kwok L.W., Pollack L. Hinge stiffness is a barrier to RNA folding. J. Mol. Biol. 2008;379:859–870. doi: 10.1016/j.jmb.2008.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lipfert J., Sim A.Y., Doniach S. Dissecting electrostatic screening, specific ion binding, and ligand binding in an energetic model for glycine riboswitch folding. RNA. 2010;16:708–719. doi: 10.1261/rna.1985110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Qiu X., Andresen K., Pollack L. Inter-DNA attraction mediated by divalent counterions. Phys. Rev. Lett. 2007;99:038104. doi: 10.1103/PhysRevLett.99.038104. [DOI] [PubMed] [Google Scholar]
- 42.Qiu X., Andresen K., Pollack L. Abrupt transition from a free, repulsive to a condensed, attractive DNA phase, induced by multivalent polyamine cations. Phys. Rev. Lett. 2008;101:228101. doi: 10.1103/PhysRevLett.101.228101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bai Y., Das R., Doniach S. Probing counterion modulated repulsion and attraction between nucleic acid duplexes in solution. Proc. Natl. Acad. Sci. USA. 2005;102 doi: 10.1073/pnas.0404448102. 1035C1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bai Y., Chu V.B., Doniach S. Critical assessment of nucleic acid electrostatics via experimental and computational investigation of an unfolded state ensemble. J. Am. Chem. Soc. 2008;130:12334–12341. doi: 10.1021/ja800854u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chu V.B., Lipfert J., Herschlag D. Do conformational biases of simple helical junctions influence RNA folding stability and specificity? RNA. 2009;15:2195–2205. doi: 10.1261/rna.1747509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cheung M.S., Klimov D., Thirumalai D. Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc. Natl. Acad. Sci. USA. 2005;102:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kudlay A., Cheung M.S., Thirumalai D. Crowding effects on the structural transitions in a flexible helical homopolymer. Phys. Rev. Lett. 2009;102:118101. doi: 10.1103/PhysRevLett.102.118101. [DOI] [PubMed] [Google Scholar]
- 48.Wang W., Xu W.X., Wolynes P.G. Confinement effects on the kinetics and thermodynamics of protein dimerization. Proc. Natl. Acad. Sci. USA. 2009;106:5517–5522. doi: 10.1073/pnas.0809649106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Qin S., Zhou H.X. Atomistic modeling of macromolecular crowding predicts modest increases in protein folding and binding stability. Biophys. J. 2009;97:12–19. doi: 10.1016/j.bpj.2009.03.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jiao M., Li H.T., Liang Y. Attractive protein-polymer interactions markedly alter the effect of macromolecular crowding on protein association equilibria. Biophys. J. 2010;99:914–923. doi: 10.1016/j.bpj.2010.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wang Q., Liang K.-C., Cheung M.S. The effect of macromolecular crowding, ionic strength and calcium binding on calmodulin dynamics. PLoS Comput. Biol. 2011;7:e1002114. doi: 10.1371/journal.pcbi.1002114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Denesyuk N.A., Thirumalai D. Crowding promotes the switch from hairpin to pseudoknot conformation in human telomerase RNA. J. Am. Chem. Soc. 2011;133:11858–11861. doi: 10.1021/ja2035128. [DOI] [PubMed] [Google Scholar]
- 53.Chen A.A., Marucho M., Pappu R.V. Simulations of RNA interactions with monovalent ions. Methods Enzymol. 2009;469:411–432. doi: 10.1016/S0076-6879(09)69020-0. [DOI] [PubMed] [Google Scholar]
- 54.Chen A.A., Draper D.E., Pappu R.V. Molecular simulation studies of monovalent counterion-mediated interactions in a model RNA kissing loop. J. Mol. Biol. 2009;390:805–819. doi: 10.1016/j.jmb.2009.05.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Auffinger P., Bielecki L., Westhof E. The Mg2+ binding sites of the 5S rRNA loop E motif as investigated by molecular dynamics simulations. Chem. Biol. 2003;10:551–561. doi: 10.1016/s1074-5521(03)00121-2. [DOI] [PubMed] [Google Scholar]
- 56.Dong F., Olsen B., Baker N.A. Computational methods for biomolecular electrostatics. Methods Cell Biol. 2008;84:843–870. doi: 10.1016/S0091-679X(07)84026-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Joung I.S., Cheatham T.E., 3rd Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. J. Phys. Chem. B. 2009;113:13279–13290. doi: 10.1021/jp902584c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kirmizialtin S., Pabit S.A., Elber R. RNA and its ionic cloud: solution scattering experiments and atomically detailed simulations. Biophys. J. 2012;102:819–828. doi: 10.1016/j.bpj.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 60.Gilson M.K., Sharp K.A., Honig B. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comput. Chem. 1987;9:327–335. [Google Scholar]
- 61.You T.J., Harvey S.C. Finite element approach to the electrostatics of macromolecules with arbitrary geometries. J. Comput. Chem. 1993;14:484–501. [Google Scholar]
- 62.Baker N.A., Sept D., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Boschitsch A.H., Fenley M.O. A new outer boundary formulation and energy corrections for the nonlinear Poisson-Boltzmann equation. J. Comput. Chem. 2007;28:909–921. doi: 10.1002/jcc.20565. [DOI] [PubMed] [Google Scholar]
- 64.Chen D., Chen Z., Wei G.W. MIBPB: a software package for electrostatic analysis. J. Comput. Chem. 2011;32:756–770. doi: 10.1002/jcc.21646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lu B., Cheng X., McCammon J.A. AFMPB: an adaptive fast multipole Poisson-Boltzmann solver for calculating electrostatics in biomolecular systems. Comput. Phys. Commun. 2010;181:1150–1160. doi: 10.1016/j.cpc.2010.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tan Z.J., Chen S.J. Predicting electrostatic forces in RNA folding. Methods Enzymol. 2009;469:465–487. doi: 10.1016/S0076-6879(09)69022-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tan Z.J., Chen S.J. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. J. Chem. Phys. 2005;122:44903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Grochowski P., Trylska J. Continuum molecular electrostatics, salt effects, and counterion binding—a review of the Poisson-Boltzmann theory and its modifications. Biopolymers. 2008;89:93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 69.Tan Z.J., Chen S.J. Ion-mediated nucleic acid helix-helix interactions. Biophys. J. 2006;91:518–536. doi: 10.1529/biophysj.106.084285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Tan Z.J., Chen S.J. Electrostatic free energy landscapes for nucleic acid helix assembly. Nucleic Acids Res. 2006;34:6629–6639. doi: 10.1093/nar/gkl810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tan Z.J., Chen S.J. Electrostatic free energy landscapes for DNA helix bending. Biophys. J. 2008;94:3137–3149. doi: 10.1529/biophysj.107.122366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tan Z.J., Chen S.J. Predicting ion binding properties for RNA tertiary structures. Biophys. J. 2010;99:1565–1576. doi: 10.1016/j.bpj.2010.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Tan Z.J., Chen S.J. Salt contribution to RNA tertiary structure folding stability. Biophys. J. 2011;101:176–187. doi: 10.1016/j.bpj.2011.05.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Chen G., Tan Z.J., Chen S.J. Salt-dependent folding energy landscape of RNA three-way junction. Biophys. J. 2010;98:111–120. doi: 10.1016/j.bpj.2009.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lu X.J., Olson W.K. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Thirumalai D., Ha B.Y. Statistical mechanics of semiflexible chains. In: Grosberg A., editor. Vol. 1. CA Academic Press; San Diego: 1998. p. 135. (Theoretical and Mathematical Models in Polymer Research). [Google Scholar]
- 77.Hyeon C., Dima R.I., Thirumalai D. Size, shape, and flexibility of RNA structures. J. Chem. Phys. 2006;125:194905. doi: 10.1063/1.2364190. [DOI] [PubMed] [Google Scholar]
- 78.Murphy M.C., Rasnik I., Ha T. Probing single-stranded DNA conformational flexibility using fluorescence spectroscopy. Biophys. J. 2004;86:2530–2537. doi: 10.1016/S0006-3495(04)74308-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Walter A.E., Turner D.H. Sequence dependence of stability for coaxial stacking of RNA helixes with Watson-Crick base paired interfaces. Biochemistry. 1994;33:12715–12719. doi: 10.1021/bi00208a024. [DOI] [PubMed] [Google Scholar]
- 80.Rau D.C., Parsegian V.A. Direct measurement of the intermolecular forces between counterion-condensed DNA double helices. Evidence for long range attractive hydration forces. Biophys. J. 1992;61:246–259. doi: 10.1016/S0006-3495(92)81831-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Raspaud E., Durand D., Livolant F. Interhelical spacing in liquid crystalline spermine and spermidine-DNA precipitates. Biophys. J. 2005;88:392–403. doi: 10.1529/biophysj.104.040113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Todd B.A., Parsegian V.A., Rau D.C. Attractive forces between cation condensed DNA double helices. Biophys. J. 2008;94:4775–4782. doi: 10.1529/biophysj.107.127332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Várnai P., Timsit Y. Differential stability of DNA crossovers in solution mediated by divalent cations. Nucleic Acids Res. 2010;38:4163–4172. doi: 10.1093/nar/gkq150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Svergun D., Barberato C., Koch M.H.J. CRYSOL-a program to evaluate X-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Cryst. 1995;28:768–773. [Google Scholar]
- 85.Stellwagen E., Dong Q., Stellwagen N.C. Quantitative analysis of monovalent counterion binding to random-sequence, double-stranded DNA using the replacement ion method. Biochemistry. 2007;46:2050–2058. doi: 10.1021/bi062132w. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


