Hybrid Dynamics Simulation Engine for Metalloproteins

Abstract

Quality computational description of metalloproteins is a great challenge due to the vast span of time- and lengthscales characteristic of their existence. We present an efficient new method that allows for robust characterization of metalloproteins. It combines quantum mechanical (QM) description of the metal-containing active site, and extensive dynamics of the protein captured by discrete molecular dynamics (DMD) (QM/DMD). DMD samples the entire protein, including the backbone, and most of the active site, except for the immediate coordination region of the metal. QM operates on the part of the protein of electronic and chemical significance, which may include tens to hundreds of atoms. The breathing quantum-classical boundary provides a continuous mutual feedback between the two machineries. We test QM/DMD using the Fe-containing electron transporter protein, rubredoxin, and its three mutants as a model. QM/DMD can provide a reliable balanced description of metalloproteins’ structure, dynamics, and electronic structure in a reasonable amount of time. As an illustration of QM/DMD capabilities, we then predict the structure of the Ca²⁺ form of the enzyme catechol O-methyl transferase, which, unlike the native Mg²⁺ form, is catalytically inactive. The Mg²⁺ site is ochtahedral, but the Ca²⁺ is 7-coordinate and features the misalignment of the reacting parts of the system. The change is facilitated by the backbone adjustment. QM/DMD is ideal and fast for providing this level of structural insight.

Introduction

Metalloproteins can be exceptionally hard to characterize computationally (1,2). The presence of the metal cation (or several of them) results in strong Coulombic forces acting on charged amino acids and the backbone. Indeed, proteins are known to respond dramatically to the installation or removal of metal cations, including large conformational changes, and to aggregation (3–9). More subtly, metals with incomplete populations of d-shells of atomic orbitals have strongly preferred coordination geometries, whether tetrahedral, octahedral, or square planar. This preference imposes directionality on the positions of amino acids surrounding the metal and thus impacts protein structure.

From the point of view of the metal, the structure and dynamics of the surroundings mean favorable or unfavorable accommodation of one of its preferred coordination modes. Deviations from the preferred geometry reduce the protein-metal affinity. Also, the electronic structure of a metal is highly sensitive to its coordination environment, both within and beyond the first coordination sphere. Different electronic configurations may be possible for a metal, depending on the chemical nature of its ligands; for example, Fe can be low-spin or high-spin, depending on how hard or soft, respectively, its ligands are. A very specific electronic configuration of the metal is essential for the proper biological function of a metalloprotein. Thus, the electronic structure of the metal and the macromolecular structure of the protein are intimately coupled and faithfully respond to changes in each other.

Metalloproteins operate on a variety of scales, and their functionalities are difficult to capture, predict, and design computationally. The focus of our work is the development of a balanced method for quality modeling of metalloproteins at all scales. Classical molecular dynamics (MD) or Monte Carlo (MC) modeling of metalloproteins is very challenging even in the case of structureless cations, such as Mg²⁺ or Zn²⁺, due to the difficulties of parameterization of corresponding classical force fields (FFs). FFs can be parameterized for a metal found in specific coordination geometry and ligated by specific ligands. However, if the coordination environment changes unpredictably in the course of the simulation, for example, through ligand exchange, attachment, or dissociation, a classical description would fail. Although full quantum mechanical (QM) computational description of large biomolecules is prohibitively expensive, multiresolution methods utilize a focused approach, representing the total Hamiltonian as a sum of QM and classical (MM) components (10), with additional electrostatic (11), and boundary interaction terms. QM/MM methods aim to accurately model the active site (10–100 atoms (12,13)) using first-principles QM techniques, and yet to achieve structural and dynamic sampling of the entire system with MM, using one of the parameterized atomistic FFs, such as CHARMM (12,14,15) or AMBER (16,17). The treatment of the boundary between QM and MM regions is the most challenging part of QM/MM, especially with molecules spanning across this boundary. Typically, the QM region is capped with hydrogen atoms or electron pairs, during QM calculations. In addition, different schemes have been proposed to treat bonded and nonbonded interactions at the boundary (10,17–22).

The QM/MM approach was first used by Levitt and Warshel (10) to calculate energies of intermediate states of enzymatic reaction. In years since the early works, QM/MM methods have undergone a remarkable advancement, making it possible to study reaction pathways in large systems, such as solvated enzymes (23,24). QM methods employed in QM/MM now range from semiempirical (25–31), to Hartree-Fock and post-Hartree-Fock methods (13,18,32,33), to density functional theory (DFT) (14,16,34–36), as well as ab initio molecular dynamics (AIMD) (17,37–40) and Car-Parrinello MD (37,41). Car-Parrinello-MD-based algorithms are especially reliable, and the spectacular advances made in their development over recent years have improved both performance and parallelization efficiency (42,43). However, they are still quite expensive, and simulations beyond nanosecond-range and large-scale structure optimizations of large protein systems are out of reach. The problem of affordability is so far best solved by running dynamic QM/MM simulations on a graphics processing unit (44–46), but QM codes for graphics processing units are not fully developed yet. Various advanced methods have been proposed for calculations of electrostatic interactions between the QM and MM regions (11,17,18,32,38,40). At the same time, the MM component has been more conservative, commonly being variants of classical MD (14,35,47) or MC (25–31,34).

Modern QM/MM applications can be loosely categorized (47) into analysis of specific system states and reaction intermediates (12,16,18,32,48–51), problems requiring local geometry optimization of known structures (13–15,33,38,52,53), or full energy landscape sampling for global minimization (13,34–36). Current QM/MM methods are most instrumental when a high-resolution starting structure of the protein is available. However, to date, no QM/MM method can robustly predict the dynamic response of a nonmetal protein to the installation of a metal. Similarly, no method can dock substrates or inhibitors to metalloproteins, if significant protein adjustment is required to mold around the substrate. In general, there is no method of performing affordable extensive sampling of metalloproteins for structural or mechanistic studies.

Capitalizing on the previously demonstrated ability of discrete MD (DMD) (54–57) to extensively sample protein conformations, we have designed the hybrid QM/DMD approach to study protein systems, undergoing large conformational rearrangements. In QM/DMD, classical MD is replaced by the recently developed method of atomistic event-driven DMD (54–57). In DMD, equations of motion are integrated along space coordinates, and not time, as in classical MD. This feature allows easier conjugation of QM and DMD regions, since DMD permits discontinuous potentials and does not need to compute or input interaction forces. In QM/DMD, the management areas of QM and DMD in the protein structure overlap. Via this shared-domain approach, structural information can be exchanged between the QM and MM (DMD) regions. This approach makes it possible to model complex active sites, which are not directly supported by classical FFs. For an additional acceleration, QM/DMD takes advantage of partial geometry relaxations on the Born-Oppenheimer potential energy surface of the metal-containing active site, instead of quantum dynamics. Finally, DMD algorithm and FFs have been optimized for efficient sampling of protein chains, making the combined QM/DMD method best suitable for studies of metalloproteins and enzymes.

We test our method on the electron-transporting iron-sulfur protein, rubredoxin. Present in numerous forms of life, it exhibits backbone structural similarity and 50–60% sequence similarity among homologs. However, intriguingly, it covers a wide range of sequence-dependent reduction potentials, between −80 and +40 mV (58), which found some rationalization in recent theoretical work by Knapp et al. (59,60). Thus, rubredoxin and its mutants represent a simple and yet intricate model for revealing the strengths and limitations of our, to our knowledge, new method at a range of scales. Specifically, we predict the macro- and microscopic structures of rubredoxin and its mutants, restore distorted rubredoxin to the equilibrium geometry, and predict the changes in reduction potential in response to mutations in the second coordination sphere of Fe.

We further highlight the capabilities of QM/DMD by predicting the structural effects of the metal substitution by modeling ion exchange in the catechol-O-methyl transferase (COMT) enzyme. COMT is an enzyme involved in the biology of pain; it degrades catecholamines (such as dopamine) by methylating them in the presence of a divalent metal cation (Mg²⁺) and S-adenosyl-L-methione (SAM). The role of the Mg²⁺ ion is merely coordination and positioning of the substrate (61). Yet surprisingly, the Ca²⁺ form of COMT is catalytically inactive. In many cases, Mg²⁺ and Ca²⁺ act as physiological antagonists of each other, but in the case of COMT, the mechanism of its inhibition by Ca²⁺ remains unclear.

QM/DMD Method

Partitioning the protein

One of the key features of QM/DMD is its approach to partitioning the protein into the areas of management of QM and DMD (Fig. 1 A). Our strategy is to sample with DMD all of the protein but the region immediately surrounding the metal center (Fig. 1 A, dark gray). On the other hand, the chemically meaningful description of the active site, needed to assess the electronic structure of the metal, or simulating mechanisms of catalyzed reactions, requires a QM treatment of a fairly large area in the protein, including the metal, its immediate ligands, substrates, and occasionally amino acids of the second coordination sphere. The region treated at the QM level in QM/DMD contains hundreds of atoms (Fig. 1 A, light gray). This shared QM-DMD region is modified quantum mechanically through gradient after relaxation, instead of ab initio dynamics. Thus, there are a total of three regions in the protein: QM only (dark gray), QM-DMD (light gray), and DMD only (Fig. 1 A). The QM-DMD boundary is breathing, and goes around the dark gray region or the light gray region, depending on the stage in the simulation. A breathing boundary ensures extensive communication between the regions, as will be demonstrated. Hence, besides capping with H atoms, no further treatment of the boundaries, such as electrostatic embedding, is introduced. Indeed, even traditional QM/MM with stationary boundaries, performed with and without embedding schemes, has been shown to produce comparable errors, questioning the quality of and need for any embedding (62).

Figure 1.

(A) Areas of management of QM and DMD in QM/DMD simulations. The metal is denoted M. Only QM can move the dark gray area. The light gray area is managed by both QM and DMD, depending on the phase of the simulation. It contains M, its ligands, such as amino acids up to Cα (thin green lines) and substrates (blue line), and potentially other amino acids and cofactors. The rest of the system is sampled by DMD only. (B) The full rubredoxin protein. (C) The QM-DMD region used in QM/DMD simulations of rubredoxin. (D) Schematic representation of the QM-DMD region: black lines indicate covalent bonding; red dashed lines indicate H-bonds between the S_Cys and the backbone; side chains of Val-8 and Val-44 are light gray.

QM and DMD constituents

In the simulations reported here, DFT was used in the description of the QM region, as it has become the workhorse for simulation of biologically relevant metals (63). The BP86 (64–68) functional was used in conjunction with the resolution of identity and multipole accelerated resolution of identity (69,70), empirical dispersion correction (71), and the double zeta quality basis set (def2-SV(P)) (72). In evaluations of reduction potentials, single-point energy calculations were done with TPPS (73,74)/def2-TZVPP (75). To account for the effect of the solvent, the conductorlike screening model (COSMO) continuum solvation model was used (76). The dielectric constant of the implicit solvent was set to 78.4, since the QM-DMD region is mostly surrounded by water rather than the protein. TURBOMOLE v.6.3 (77) was used for all QM calculations.

DMD was described in detail elsewhere (54–57). Briefly, it is the type of MD that is based on solving the equations of conservation of momentum and energy, rather than Newtonian equations of motion. DMD uses the implicit solvent atomistic model of proteins, based on the discretized CHARMM/EEF1 FF (78). It operates on a set of square-well potentials, such that interactions between atoms are nonzero only when atoms are within the given square well. DMD was proven to be exceptionally fast and efficient in sampling of biomolecules for a variety of applications. Here, DMD underwent several modifications to become more context-dependent in consistency with QM (Supporting Material).

Simulation strategy

Simulations are iterative. First, DMD is run on all but the QM/only region, which remains fixed. A frozen QM/only region during the DMD phase means that the DMD engine is virtually unaware of the exact nature of the metal but responds to the metal + surrounding atoms moiety. This in turn means that any metal or active site can be simulated, even if its DMD FF parameterization is not available. In addition, atoms in the shared QM-DMD region have constraints imposed on them to maintain bond lengths and angles relative to the frozen QM region in accord with those observed during the QM phase (see Section Ib in the Supporting Material). All other interactions between the DMD, QM, and QM-DMD regions (such as Van der Waals, solvation, and H-bond formation) are calculated in the same way as interactions within the DMD region. The simulation proceeds in an annealing regime for the first 3,500 DMD time units (t.u.) and then at a low temperature for 10,000 t.u. (0.5 ns), at which point data are collected. The cold ensemble of 10,000 structures is clustered according to geometric similarity. Geometric centroids and lowest-energy structures are selected from each cluster, and single-point QM energies of their QM-DMD regions are calculated. Structures are then evaluated, based on the combined scoring index (SI), which depends on both the QM and DMD energies and their differences from the minimum energies found for the given set of structures:

$$S{I}^{\mathrm{i}}=n\left(E_{\mathrm{DMD}}^{\mathrm{i}}-E_{\mathrm{DMD}}^{\min }\right)+\left(1-\mathit{n}\right)\left(E_{\mathrm{QM}}^{\mathrm{i}}-E_{\mathrm{QM}}^{\min }\right)$$

In this work, n is set to 0.5. The structure having the smallest SI is chosen, and its QM-DMD region is partially optimized quantum mechanically, with fixed positions for the atoms bridging the QM region to the rest of the protein. The QM optimization is bottleneck for the procedure, and to accelerate the method, we found it adequate to interrupt the optimizations after a preset number of steps (100–200), when optimization is typically close to convergence. However, tightly optimized structures are still obtained to calculate the properties of the metal. The partially optimized QM region is then reinstalled in the protein, and the QM-DMD boundary shrinks back from the dark gray region. In the course of the following iteration, in the DMD stage, the structural information from the optimized QM-DMD region can propagate to the rest of the protein. The alternating QM and DMD jobs with the breathing QM-DMD boundary are performed for 20 to hundreds of iterations, depending on the task (this roughly corresponds to 10–50 ns of dynamics). More specific details of QM/DMD can be found in the Supporting Material.

Capabilities and Limitations of QM/DMD

We test the performance of QM/DMD on the electron-transporting iron-sulfur protein rubredoxin (PDB ID 1FHM (79)) and its mutants. The protein consists of 52 residues (Fig. 1 B), 13 of which are included in the QM-DMD region (Fig. 1 C). This QM-DMD region is well structured and possesses numerous H-bonds in which the Fe-bound deprotonated S_Cys atoms serve as H-bond acceptors (80,81). The major H-bond donors are the six backbone amide groups (Fig. 1 D). In addition, there are several unusual H-bonds where the donors are the aliphatic C-H groups of Val, which normally do not engage in H-bonding (81). We test QM/DMD at three scales: large (structure recapitulation and recovery), intermediate (subtle structural details, such as lengths of H-bonds), and small (electronic properties of the metal center with the accuracy of 1–2 kcal/mol from the experimental data).

Large-scale test 1: structure recapitulation

Our first task is to test stability of the QM/DMD simulated wild-type (WT) rubredoxin. The simulations starting from the x-ray structure lead the protein away from it, stabilizing in the found QM/DMD basin (Fig. 2 A). The RMSD of the entire protein backbone between the QM/DMD and the x-ray structures stabilizes at 1.4 Å, and the all-atom RMSD of the QM-DMD region stabilizes at 1.1 Å (Fig. 2 A). The QM energy of the QM-DMD region is conserved to −6320.387 ± 0.005 a.u. for the reduced form of the protein (6.3 ± 3.0 kcal/mol above the QM energy of the QM-DMD region obtained in the first iteration). The DMD energy also converges, though fluctuations are larger than those of the QM energies due to a larger number of atoms in the DMD region.

Figure 2.

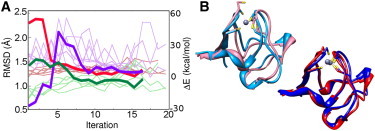
Large-scale testing of QM/DMD: structure recapitulation and recovery for reduced rubredoxin. (A) The QM-DMD region RMSD from the x-ray structure (light green lines), the QM energies (pink lines), and the DMD energies (light purple lines) stabilize by the fifth iteration. Thick lines illustrate the return of the distorted WT structure to equilibrium in terms of the QM-DMD region RMSD (green), QM energy (red), and DMD energy (purple). (B) The overlay of the x-ray structure (light blue) and the distorted structure (pink), and of representative QM-DMD equilibrated structures, starting from x-ray (dark blue) and from the distorted structure (red).

Similar robust performance of QM/DMD was found for the three mutants of rubredoxin, V44I, V44A, and V44G (Fig. 3). The structure of the V44A variant agrees well with the available x-ray structure (PDB ID 1C09 (82); see Fig. S10 in the Supporting Material). For the V44G mutant, we observe a fairly large void space in the area of the missing side chain of residue 44 (Fig. 3 C). This area is likely to be solvent-accessible. An interesting structural feature was detected for the V44I mutant (Fig. 3, A and B). The bulkier side chain of Ile does not fit well within the space in the protein originally occupied by Val, so adjustments and repacking of the protein were required to accommodate Ile-44. QM/DMD predicts the existence of two isoenergetic structures for V44I. In one, Ile-44 points up toward the Fe center, and in the other it points down and away from the metal. All structures are available upon request.

Figure 3.

Overlay of the x-ray structure of the WT rubredoxin (white) and representative QM/DMD snapshots of equilibrated structures of the three mutants: two isoenergetic variants of V44I, with I44 pointing down (A) and up (B), V44A (C), and V44G (D). The side chains are shown for the four Cys residues and residue 44. The overlays of the QM-DMD regions are presented beneath each structure. Nonpolar H atoms are omitted for clarity.

Large-scale test 2: structure recovery from deformation

Next, we demonstrate that QM/DMD can restore a distorted structure of rubredoxin, which also is a test for the general ability of QM/DMD to predict the structural response of a protein to the installation of a metal. We also show that metalloprotein structure stabilization is a result of cooperation between QM and DMD and is not due to the specific traits of either component.

First, rubredoxin was distorted from the equilibrium by removing Fe, protonating the four Cys residues coordinating Fe, and allowing DMD to relax the protein for 10,000 t.u. Not surprisingly, even in this short relaxation, the demetallated structure visibly changed, and the DMD energy of the protein decreased. Fe was then reinstalled into the distorted protein, and the four Cys residues were once again deprotonated. In the distorted structure, the tetrahedral coordination of the Fe center was disrupted, and one Cys was completely detached (Fig. 2 B). This structure was then passed to QM/DMD for reequilibration.

The starting QM energy of the distorted QM-DMD region is higher than that of the WT by ∼50 kcal/mol. The starting DMD energy is lower than that of the WT by ∼40 kcal/mol. The QM/DMD simulation returns the protein at the original WT basin, approximately by the eighth iteration (Fig. 2 A). During the relaxation process, the conformation of the entire protein changes to accommodate the metal center. The Cys residues return to coordinating Fe. The actual event of Cys-Fe binding is controlled purely at the QM level. Since in this case it was known that the four Cys residues must eventually bind Fe, the S-Fe moiety constituted the QM-only region even at large S-Fe separations. The RMSD values converge to those characteristic of the WT. The QM energy decreases, the DMD energy increases accordingly, and both also converge to the values from the simulation started from the x-ray structure. This result shows that QM/DMD energy function has at least a local minimum at the native structure. It also illustrates the quality of the communication between QM and DMD in QM/DMD and the chosen SI function.

A more challenging problem arises in the case of ion substitution. We substituted Fe(II) in rubredoxin with Pd(II) in a low-spin state, which is known to prefer a square planar coordination. QM/DMD simulation yields a structure of the protein representing a clear compromise between the structural preferences of Pd (square planar) and the rest of the protein (accommodating a tetrahedrally coordinated metal). The protein is distorted, and the metal coordination sphere approached, though it did not fully reach, square planar geometry. Details of this test are presented in the Supporting Material. Overall, we conclude that QM/DMD is capable of reproducing the protein structure and recovering it after a moderate distortion from the equilibrium.

Intermediate-scale test: finer structural details sensitive to the oxidation state of Fe and mutations

Next, we test that QM/DMD reproduces structural trends in the QM-DMD region with chemical accuracy. Upon oxidation from Fe²⁺ to Fe³⁺, the Fe coordination is expected to become tighter due to the stronger coulombic attraction of the ligands to the cation. This is observed experimentally: the average Fe-S_Cys distance in the Fe²⁺ form (PDB ID 1FHM) is 2.36 ± 0.03 Å, and that in the Fe³⁺ form (PDB ID 1FHH) is 2.27 ± 0.02 Å. This trend is reproduced in our simulations. The calculated Fe-S_Cys distances are 2.32 ± 0.03 Å and 2.21 ±0.04 Å, for the Fe²⁺ and Fe³⁺ forms, respectively. At the same time, the six H-bonds formed by S_Cys atoms ligating Fe and the backbone N-H groups become weaker and longer on average by 5–18%, as expected (Table S1).

Next, we focus on the specific H-bond between S_Cys42 and the backbone N-H group of Val-44 in the WT. According to Lin et al. (80), the reduction potential of Fe can be modulated by mutations of Val at this position, which is quite remarkable, considering that residue 44 belongs to the second coordination sphere of Fe. It was hypothesized that this impact was due to the changing strength and length of the H-bond of Cys-42 to the backbone of residue 44. However, at present, not all of the structures of the mutants are available to fully confirm this hypothesis, and the H atoms are invisible for the x-ray diffraction. According to QM/DMD, of all H-bonds in the QM-DMD region, the H-bond to the backbone of the residue 44 undergoes the strongest change upon mutation (10–18%). In full accord with experimentally derived H-bond distances, it gets progressively shorter in the sequence WT, V44I, V44A, and V44G. In the Fe³⁺ form, its length is 3.07, 3.03/2.77 (depending on the conformation of Ile-44), 2.55, and 2.50 Å, and in the Fe²⁺ form it is 2.63, 2.75/2.49, 2.33, and 2.29 Å, respectively (Fig. 4). This confirms that QM/DMD reliably reproduces these rather delicate structural details.

Figure 4.

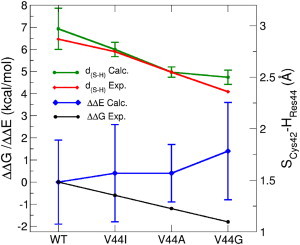
Experimental ΔΔG and predicted ΔΔE values for the four variants of rubredoxin, and the corresponding theoretical and experimentally derived H-bond lengths between S_Cys42 and the backbone of residue 44 for the oxidized form of the protein.

Small-scale test: reduction potential as a function of off-site mutations

We used the QM/DMD ensembles of structures to estimate the changes in reduction potential in the mutants and compare those to the experiment. The reduction potential, E₀, changes from −77 mV in the WT to −53 mV in V44I, −24 mV in V44A, and 0 mV in V44G (80). Through the definition of E₀, these values translate to ΔG of Fe reduction, and its changes (ΔΔG) upon mutation, which read as 0.0 kcal/mol (reference, WT), −0.6 kcal/mol (V44I), −1.2 kcal/mol (V44A), and −1.8 kcal/mol (V44G). Reproducing the ΔG and ΔΔG trends is a challenging test for QM/DMD, calling for true chemical accuracy from the method. In fact, this accuracy would be on the verge of what modern high levels of ab initio theory can do, and so a qualitative agreement with the experiment would be adequate for QM/DMD.

We make two assumptions in our estimations of ΔΔG. First, the experimentally measured E₀ is an adiabatic quantity, i.e., the protein has a chance to fully relax in the time frame of the measurement, and the E₀ corresponds to ΔG between the minima of the Fe²⁺ and Fe³⁺ forms of the protein. The second assumption (based on Marcus theory (83) and our QM/DMD simulations for the WT) is that the overall structure and dynamics of the protein do not change substantially upon oxidation/reduction, except for the slight tightening of the Fe coordination sphere. Thus, the associated change of entropy, ΔS, is small and is similar for all the mutants, and ΔΔS, characterizing the difference in the change of entropy for different mutants, can be ignored in predicting ΔΔG. Hence, ΔΔG can be approximated by QM ΔΔE.

ΔE and ΔΔE values averaged over QM/DMD ensembles were calculated with inclusion of implicit solvation. Without solvation, experimental data could not be qualitatively reproduced, especially for the V44G mutant. From the QM/DMD structure of V44G, we know that there is a surface-accessible void space beneath S_Cys42. Hence, it is likely that solvation of this area is partially responsible for the change in the reduction potential of V44G. Calculated QM ΔE and ΔΔE are qualitatively correct, and for all four proteins the ΔE values fall into a narrow range, in agreement with the experimental spread of ΔG values (Table S2). In Fig. 4, ΔΔE values are compared to the experimental ΔΔG values. The predicted values of the ΔΔE for each protein fall within an ∼4-kcal/mol window due to the structural fluctuations in each ensemble. Qualitatively, the experimentally observed trend for ΔΔG and the theoretical trend for ΔΔE agree, which is quite remarkable considering the resolution of the theoretical method. Indeed, here, we aim to resolve differences in ΔG < 2 kcal/mol. Even for high-level ab initio calculations on much smaller systems than the QM-DMD region chosen for rubredoxin, this level of resolution would be nearly prohibitive. For example, in predictions of photoelectron spectra of clusters smaller than 10 atoms, using methods including a large amount of electron correlation, an accuracy of 0.1–0.2 eV (2–5 kcal/mol) is considered normal and sufficient (84,85). Thus, the accuracy of the QM/DMD method is virtually the same as that of regular stationary DFT for systems of the same size as our QM-DMD region or smaller. Others have reported more sophisticated calculations of the reduction potentials of rubredoxin that produce a better agreement with experiment (59,60). Such quantitative techniques can be applied to the obtained QM/DMD ensemble, but such elaboration is not the goal of this study. Overall, we conclude that QM/DMD is capable of semiquantitative description of the delicate electronic effects at the metal center.

The active Mg²⁺ and inactive Ca²⁺ forms of COMT

Replacement of the metal ion can have dramatic effects on protein structure, especially when the two ions have different coordination. An example of such ion-driven structural rearrangement is the enzyme-inactivating replacement of the native Mg²⁺ with Ca²⁺ in the active site of COMT.

Mg²⁺ in COMT is coordinated octahedrally by the side chains of Asp-141, Asp-169, and Asn-170, one water molecule, and the substrate (61). In QM/DMD simulations, the shared QM-DMD region included all these moieties as well as the side chains of Lys-144 and Glu-199 that form H-bonds to the substrate and the side chain of Met-40 that shields the active site from solvent. Using QM/DMD, we recapitulated the native Mg²⁺ structure of COMT. As compared to the available x-ray structure (61), the average heavy-atom RMSD of the QM-DMD region is 0.7 Å and that of the backbone of the protein is 1.2 Å. A representative structure of the active site is shown in Fig. 5 A. SAM and the O atom of catechol, which act as the methyl group donor and acceptor, are aligned for transfer. Substitution of Mg²⁺ by Ca²⁺ induces a significant change in the coordination environment of the metal: contrary to Mg²⁺, Ca²⁺ is coordinated by both oxygen atoms of Asp-141 and is thus 7-coordinate. In this configuration, Asp-141 is unable to engage in an H-bond with the water molecule, which instead interacts with Glu-199 (Fig. 5 B). Finally, the catechol O atom and the methyl group of SAM are not properly aligned for methyl transfer. Changes are accompanied by the adjustment of the backbone (backbone RMSD from the crystal structure is 1.3 Å). It is important to stress that the observed repacking of the active site could not be obtained by a simple substitution of the metal in the crystal structure and subsequent geometry optimization of the active site at the fixed position of the backbone (Fig. S15). Analysis of Ca²⁺ COMT may shed light on the mechanism of COMT inhibition.

Figure 5.

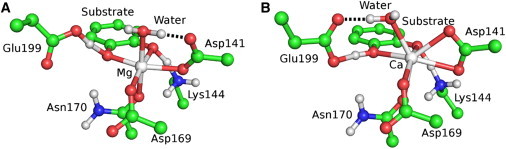
Coordination of the ion in the active site of COMT depends on the nature of the metal. (A) Mg²⁺. (B) Ca²⁺. Nonpolar hydrogens are removed for clarity.

Conclusions

Modeling metalloproteins is a challenge for computational biology due to the strong interactions and coupling between the ion and protein conformations. We reported on a new, to our knowledge, method for modeling metalloproteins, QM/DMD. It combines the capabilities of QM—producing ab initio-quality energies, genuine wave-function-driven structures, and electronic properties of the metal-containing active sites—with those of DMD—aggressively sampling the protein, including large-scale domain motions. Innovative algorithms, such as a breathing QM-DMD boundary, are implemented in QM/DMD to make simulations on experimentally relevant scales computationally affordable. QM/DMD also takes advantage of more traditional techniques, such as annealing, clustering, and scoring based on both QM and DMD. QM/DMD is successful in modeling metalloproteins at a range of scales, from large (>10 Å), to intermediate (1–10 Å), to small (<1 Å).

We tested QM/DMD on the Fe-S electron-transporting protein rubredoxin and several of its mutants. QM/DMD faithfully reproduces the structures of the metalloproteins, in agreement with x-ray data, and even down to the finest structural details, such as lengths of weak H-bonds and their variations upon mutations in the protein. The method also can restore the structure of the protein to equilibrium after a mild distortion due to the property of the combined potential energy function reaching its minimum at the native structure. With the structural information provided by QM/DMD, delicate electronic properties of the active site, such as changes in the reduction potential of the metal upon off-active-site mutations, can be qualitatively reproduced. In view of the subtlety of these changes (on the order of tens of mV, i.e., ∼k_BT), and the large size of QM-treated active sites, even a qualitative agreement is quite remarkable.

We illustrated the capabilities of the method on the Mg²⁺ and Ca²⁺ forms of COMT. Metal replacement in this protein is found to lead to the active-site repacking and adjustment of the protein backbone, which could not be captured without a combination of QM treatment of the active site and sampling of the protein structure. QM/DMD is a general method that can be used for sampling structures of metalloproteins, predicting conformational changes in proteins upon metal installation or replacement, and changes in the electronic structure of the metal in response to the changes in the protein, and flexible docking of substrates and inhibitors to metal-containing active sites. In particular, it can be instrumental for structural and mechanistic studies on metalloenzymes. Developed software is available upon request; its use is subject to the license agreements of the parallel version of DMD (available for distribution through Molecules in Action, LLC, http://moleculesinaction.com), and TURBOMOLE (77).