Femtosecond-Pulsed Plasmonic Nanotweezers

Abstract

We demonstrate for the first time plasmonic nanotweezers based on Au bowtie nanoantenna arrays (BNAs) that utilize a femtosecond-pulsed input source to enhance trapping of both Rayleigh and Mie particles. Using ultra-low input power densities, we demonstrate that the high-peak powers associated with a femtosecond source augment the trap stiffness to 2x that of nanotweezers employing a continuous-wave source, and 5x that of conventional tweezers using a femtosecond source. We show that for trapped fluorescent microparticles the two-photon response is enhanced by 2x in comparison to the response without nanoantennas. We also demonstrate tweezing of 80-nm diameter Ag nanoparticles, and observe an enhancement of the second-harmonic signal of ~3.5x for the combined nanoparticle-BNA system compared to the bare BNAs. Finally, under select illumination conditions, fusing of Ag nanoparticles to the BNAs is observed which holds potential for in situ fabrication of three-dimensional, bimetallic nanoantennas.

Plasmonic optical trapping has seen rapid development since its introduction due in part to an increasing demand for control of matter on the micro and nanoscale. The technique relies on plasmonic nanotweezers that are characterized by localized surface plasmon resonances which produce sub-diffraction confinement and large enhancement of the incident optical intensity¹. Together, this results in large near-field intensity gradients which yield greatly amplified optical forces. The near-field forces have been shown to significantly relax the constraints of conventional optical trapping, providing efficient microparticle manipulation with low input power density (~1 mW/µm²), low-numerical aperture (NA) focusing, and sub-optimal spatial mode quality². These features are met with an assortment of applications including trapping of quantum dots, lab-on-achip devices, and manipulation of biological species (e.g., e-coli bacteria)³,⁴,⁵.

Plasmonic nanotweezers come in a variety of geometries including dipole antennas⁵, nanodots⁶, bowtie nanoantennas², and diabolo antennas⁷, and while the optimum nanotweezer geometry continues to be an active area of research, a common feature is the use of continuous-wave (CW) illumination for plasmonic trapping. Using CW illumination it has previously been shown that plasmonic nanostructures can act as efficient heat sources that generate significant fluid flow near the illumination point, especially when illuminated near their peak plasmon resonance⁸,⁹. The localized Rayleigh-Bénard convection currents can be mitigated by using heat sinks or “thin” sample chambers in applications where they might be deleterious to trapping¹⁰. However, for off-resonance illumination these currents have been shown to produce distinct trapping phases that can be useful in size-selective particle trapping and sorting applications². Notwithstanding these advancements, there is still much effort devoted to optimizing plasmonic optical trapping.

One potential avenue for increasing nanotweezer performance that has been largely overlooked is the use of a femtosecond (fs) input source. In conventional optical trapping, the theoretical model of optical forces derived from a pulsed source is still under investigation, yet experimental results have shown that it can have relative advantages over a CW source¹¹,¹²,¹³. For instance, De et. al. showed that latex nanoparticles can be stably trapped using a fs-pulsed input at power densities (75 mW/µm²) lower than a comparable CW system (285 mW/µm²)¹¹. Additionally, Jiang et. al. demonstrated novel “trap splitting” behavior which results from the nonlinear polarization of trapped metallic nanoparticles induced by fs pulses at power densities above 75 mW/µm^{2 12}. In yet another study, Shane et. al. demonstrated two-photon fluorescence (TPF) from trapped fluorescent microspheres near their low-power trapping threshold (~ 8 mW/µm²) with stable trapping lifetimes on the order of minutes¹³. Based on these results, combining a fs source with plasmonic nanoantennas appears to be a promising method to enhance the optical forces and diagnostic capabilities over standard CW nanotweezers.

In this paper, we demonstrate for the first time a plasmonic nanotweezer that utilizes a fs-input source to achieve trapping of particles in both the Rayleigh and Mie regimes, where particles are either much smaller or larger than the incident wavelength, respectively¹⁴. Based on Au bowtie nanoantenna arrays (BNAs), the fs nanotweezer provides trap stiffnesses up to 2x and 5x that of comparable CW nanotweezers and conventional (pulsed) optical tweezers, respectively. Using ultra-low power densities (20 µW/µm²), we show that the two-photon response from a 1.2-µm diameter fluorescent microbead trapped by the BNAs can be enhanced by 2x in comparison to the particle response without the nanoantennas. Furthermore, the fs nanotweezer can successfully trap 80-nm diameter Ag nanoparticles and simultaneously probe the nonlinear response of the coupled nanotweezer-nanoparticle system. The emission spectrum of the BNAs is modified in the presence of the Ag nanoparticle, resulting in a 3.5x increase in the emitted second-harmonic generation (SHG) signal during the trapping event. At input average powers above 65 µW (70 µW) metallic nanoparticles (dielectric micro and nanoparticles) fuse to the BNA surface and we suggest that this behavior is promising for nano-scale particle placement and possible in situ fabrication of 3D, bimetallic nanoantennas.

Results

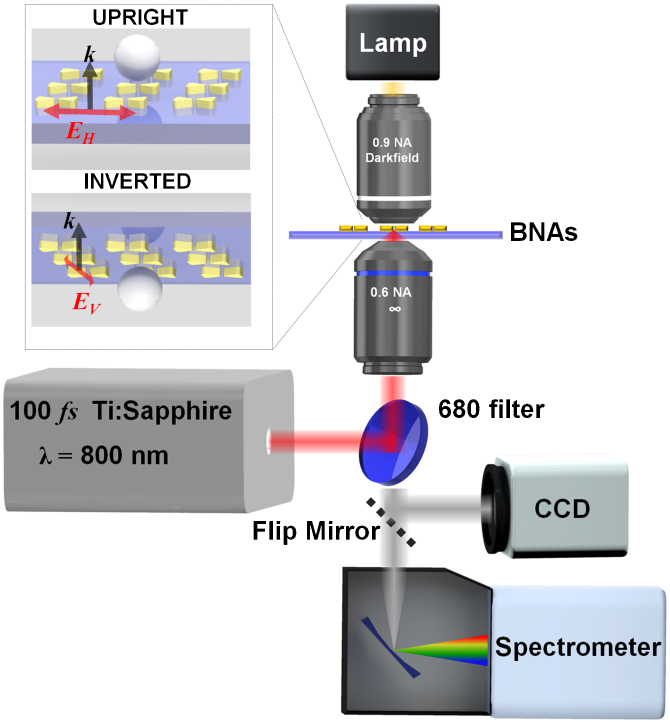
The experimental setup is detailed in Fig. 1. The plasmonic nanotweezers are built around a customized inverted microscope (Olympus IX81) with a 0.6 NA, collar-adjustable microscope objective (Olympus LUCPlanFLN 40x) and switchable brightfield-darkfield illumination (Olympus MPlanFL N 100x). The BNAs are fabricated in 80 x 80 µm² arrays with 4 different lattice constants: 425, 475, 525, and 575 nm center-to-center spacing, as described elsewhere². The excitation source is a 100-fs pulsed, 80-MHz repetition rate, Ti:Sapphire laser (Spectra Physics Mai Tai) spectrally centered at a wavelength λ = 800 nm and coupled into the microscope via a 680-nm rejection filter (Semrock). A flip mirror allows switching between a CCD for viewing trapped particles and a custom built spectrometer (Jobin Yvon CP140-103 grating, Andor DU420A camera) for analyzing the nonlinear emission spectra from the trapped particles and BNAs. An integration time of 1 second is used to collect the signals, and the spectra are the average of 5 runs.

Figure 1. Schematic of the experimental setup.

The inset depicts the two sample orientations with respect to the incident illumination. The black arrows indicate the main incident wave vector whereas the red arrows indicate the incident polarization: E_H and E_V for horizontal and vertical polarization, respectively.

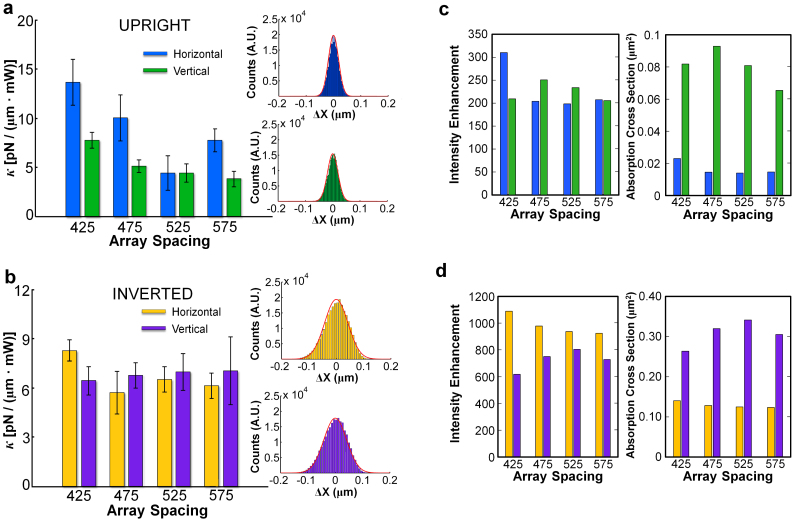
The strength of the fs nanotweezer is assessed by measuring the lateral trap stiffness with 1.2-µm diameter fluorescent spheres (Duke Scientific, G0100) as a function of array spacing, input polarization (horizontal - parallel to the bowtie long axis, vertical - orthogonal to it), and BNA orientation with respect to the incident optical field. We note that while there is an asymmetry in trap stiffness between the lateral and axial directions, the former is sufficient to demonstrate the difference between CW and fs nanotweezers since the axial stiffness is much more sensitive to heating effects, e.g. convection. Figure 2a shows the stiffness results for the upright orientation, where the field is incident from the substrate side and impinges on the BNAs before the trapped particle; Fig. 2b shows the stiffness in the opposite, inverted orientation, where the field first encounters the trapped particle before the BNAs. The insets show particle displacement histograms in the upright (Fig. 2a) and inverted (Fig. 2b) orientation with calculated Gaussian fits overlaid; the close fit indicates that the particles experience an approximate harmonic potential. In all cases, the collar on the 0.6 NA trapping objective is adjusted to produce a sharp focus, thereby mitigating the effects of spherical aberration¹⁵.

Figure 2.

Experimentally measured trap stiffness for the (a) upright BNA orientation and (b) the inverted BNA orientation. Error bars represent the standard deviation in the stiffness measurement. The insets are representative particle displacement histograms measured on the 425 array and fitted to a Gaussian distribution. Blue bars correspond to stiffness measurements using horizontal-input polarization whereas green bars correspond to vertical-input polarization. FDTD calculations of the intensity enhancement and absorption cross-section for the (c) upright BNA orientation and the (d) inverted orientation. Yellow (purple) bars are results for horizontal (vertical) polarization.

Overall, the largest stiffness measured is 14 pN /(µm · mW) which occurs with horizontal-input polarization on the 425 array in the upright orientation. Note that all trap stiffness measurements are performed with 50 µW of input power corresponding to a very low input power density of 20 µW/µm². The maximum stiffness is ~ 2x that of a comparable CW system⁹, which directly indicates that a fs source can improve the performance of a plasmonic nanotweezer. In order to avoid issues associated with sample variation, the experiments performed herein use the same sample as those in Ref. [9]. Interestingly, Shane et. al. found that a fs source yields the same trap strength as a CW source in a conventional optical tweezer, and thus average power in this case determines trapping behavior rather than peak power¹³. However, the notable increase in trap strength of fs nanotweezers over CW suggests that the high-peak power (6.25 W) of the 100-fs pulses augments the near-field optical forces generated by the BNAs. Furthermore, the minimum average power required to trap these particles is ~ 10 µW, whereas previous studies have shown comparable particles could not be trapped for input-powers < 25 µW using a CW source².

The behavior of the trap strength over the parameter space can be partially understood as a trade-off between the local intensity enhancement and the absorption cross-section of the bowties, which is proportional to the heat power generation⁸,¹⁶. We note that while the near-field coupling of the triangles comprising each bowtie is important for determining the field enhancement, the far-field coupling between individual bowties in an array has been shown to increase the field enhancement by several orders of magnitude compared to an individual bowtie¹⁷. This modification of intensity enhancement plays a direct role in the change of trap stiffness due to array spacing. Figures 2c and 2d give the theoretical intensity enhancements and absorption cross-sections calculated for the upright and inverted orientations, respectively. For the upright, horizontally-polarized case the relative stiffness follows the same rank order as the intensity enhancement across all arrays which is expected given that larger enhancements imply larger intensity gradients and thus increase gradient forces. Vertical polarization likely produces lower stiffness due to the fact that the absorption is ~4x larger compared to the horizontal case, which promotes BNA heating and leads to increased thermal perturbation of the trapped bead. To this end, while the inverted case produces 3.5–4.5x and 3–3.5x larger intensity enhancements for horizontal and vertical polarization, absorption is increased by 6–8x and 3–4x, respectively. Thus, heating offsets the increased intensity enhancements in the inverted orientation and leads to lower overall stiffness values. In addition, we have previously shown that in the upright orientation, the nanotweezers functions as a quasi-3D trap, in which the gradient force supplied by the nanostructures balances axial scattering and fluid forces⁹. In contrast, the inverted orientation functions as a 2D trap, where the scattering force from the illumination source pins particles to the substrate, providing axial stability. These differences may also contribute to the stiffness difference between the two orientations.

Experimentally, we observe both metallic nanoparticles and dielectric micro/nanoparticles adhering to the 425 and 475 arrays with horizontal polarization at input powers above ~ 65 µW and 70 µW, respectively. To the best of our knowledge, this “particle fusing” behavior has not been observed CW nanotweezers. To exclude the possibility of particles melting to the BNAs, consider the heat power generation resulting from optical absorption by the nanostructures:

where σ_abs (λ) is the spectral absorption cross-section of the BNAs and 〈I (λ)〉 is the incident average intensity¹⁹. This leads to a uniform temperature increase in the bowties, due to a large thermal conductivity ratio (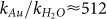), which for pulsed illumination is given by

where V is the bowtie volume (0.0011 µm³), ρ_Au = 19320 kg/m³ is the density of gold, c_Au = 129 J/kg/K, and f is the pulse repetition rate¹⁹. The calculated absorption cross-sections for the 425 and 475 arrays in the upright orientation are 0.065 µm² and 0.055 µm², respectively. These values give a maximum temperature increase of 3.8°C and 2.4°C, which results in absolute bowtie temperatures of 23.8°C and 22.4°C, respectively. Given the size-dependent particle melting point of Ag (~ 900°C at 80 nm)²⁰ or polystyrene (~240°C), the bowties are not expected to reach a temperature at which any particle investigated herein will melt to the surface. Furthermore, no visible signs of particle melting are observed in scanning electron microscopy (SEM) images of the fused particles. Moreover, the observation of fusing of polystyrene particles (in addition to Ag) suggests a mechanism other than plasmonic welding, which relies on the highly localized temperature increase between metallic contacts, is responsible for particle fusing¹⁸. We therefore expect that fusing results from large peak gradient forces that bring particles into close contact with the BNAs; above the experimentally determined threshold of 70 µW for polystyrene particles (both 1.2-µm and 300-nm in diameter) and 65 µW for 80-nm diameter Ag nanoparticles, the particle-BNA separation becomes small enough for Van der Waals interactions to bind particles to the BNA surface²¹. In a similar experiment, Deng et. al. showed that large peak gradient forces can overcome the Van der Waals force between a “stuck” particle and the substrate, thereby separating the particle provided that the gradient force is directed away from the substrate²². Thus it is clear how, in this case, the peak gradient forces supplied by the highly confined and enhanced near fields of the BNAs are sufficient to initiate Van der Waals forces between the BNAs and trapped species.

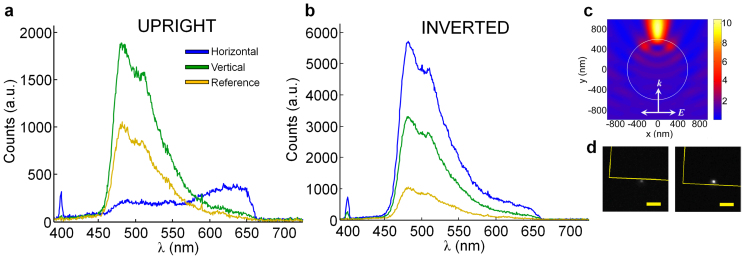
A key feature of optical tweezers is their usefulness in the biological sciences. For instance, the field of single-molecule biophysics has seen much progress due to the advent of optical trapping. However, implementation of combined optical trapping and single molecule fluorescence often involves complex setups requiring several co-aligned laser sources²³. A major benefit of fs nanotweezers is the ability to access the nonlinear optical response of trapped species, such as two-photon fluorescence. This not only improves the sample diagnostic capabilities of plasmonic nanotweezers, but may lead to simplified single-molecule fluorescence and trapping setups. To demonstrate this, we analyze the two-photon response acquired from a trapped microsphere on the 425 array in the upright and inverted orientations with both horizontal and vertical polarization, as shown in Fig. 3. The reference signal is the TPF due to the 0.6-NA focused input beam alone. In the upright case, the reference is taken from a bead adhered to the glass substrate 5 µm from the BNAs, whereas in the inverted orientation it is taken from a bead forced against the glass substrate. The reference TPF is nearly identical in both cases.

Figure 3.

Two-photon fluorescence measurements from a trapped fluorescent microsphere on the 425 array with 50 µW input power in (a) the upright orientation and (b) the inverted orientation. Blue and green curves represent the horizontally and vertically-polarized results, respectively. The reference signal (given in yellow) is from a particle attached to the glass substrate in 3(a) and a free particle forced up against the substrate in 3(b). (c) FDTD simulation of the scattered intensity of a plane-wave illuminated 1.2-µm diameter polystyrene sphere in water which leads to the particle “lensing” effect. The outline of the particle is shown as the white circle. (d) CCD frames showing the single particle fluorescence in the inverted orientation for the reference (left) and on the 425 array (right). The array outline is sketched in yellow and the scale bar is 5 µm.

We have previously shown¹⁷ that fs-pulsed illumination of BNAs in the inverted configuration yields a strong and broad nonlinear optical response from the BNAs. The emitted spectrum is strongest for horizontal illumination, spans several hundred nm, and is characterized by a secondharmonic response at 400 nm (for 800-nm illumination) and a broad two-photon photoluminescent (TPPL) response. In our current study, in the inverted orientation shown in Fig. 3b, the trapped fluorescent microbead initially both focuses the input fs pulse onto the BNAs, via particle lensing, and generates a TPF signal. The TPF is then added to the overall BNA response, which is increased due to particle lensing and again is strongest for horizontal (resonant) polarization. We observe the characteristic SHG signal, present for both horizontal and vertical illumination, and a subtle difference in lineshape (e.g., slopes around 500 and 650 nm) for the horizontal and vertical response compared to the reference response and the previously reported BNA spectral response. The particle lensing effect is evident in Fig. 3c which shows the calculated the forward-scattered light from a 1.2 µm polystyrene sphere in water. Beyond the particle (shown as the white circle), the local intensity is 8–10x that of the incident, indicating that the particle acts as an auxiliary lens that further focuses the incident illumination onto the BNAs in the inverted orientation. This effect also explains the larger intensity enhancements in Fig. 2d compared to 2c.

In the upright orientation (Fig. 3a), we observe that the fs-pulsed illumination gives rise to the signature BNA spectral response for horizontal (resonant) polarization, again with the characteristic SHG signal at 400 nm. Conversely, for vertical polarization, the theoretical intensity enhancement without particle lensing and strong spatial field confinement are insufficient to generate the nonlinear BNA response. Rather, the incident field couples out to the trapped bead, located 10–15 nm above the surface, subsequently leading to enhanced TPF. We note that in this case, we do not observe SHG and the lineshape follows very closely that of the reference spectrum, consistent with the notion that the fluorescence is truly enhanced and is in the absence of the nonlinear response from the BNAs. At its peak, the enhancement is ~ 2x in comparison to the reference. The dramatic increase in TPF is evident in Fig. 3d, which shows CCD-collected images of a trapped bead in the inverted orientation (see Supplementary video S1). The left frame is a darkfield image of the reference fluorescence collected off the array, whereas the right frame shows the BNA-enhanced fluorescence signal; a prominent TPF enhancement by the BNAs is clearly visible.

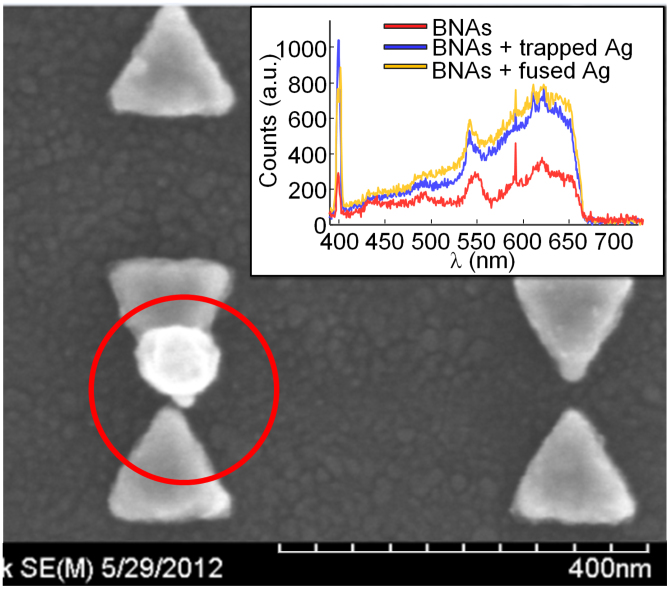
Femtosecond nanotweezers can also enhance particle trapping in the Mie size regime, where the particle size is much smaller than the illumination wavelength. Using 50-µW input power, 300-nm diameter fluorescent polystyrene spheres can be trapped and manipulated across the 425 and 475 arrays using horizontal polarization (see Supplementary video S2). We have previously shown that comparable CW nanotweezers require at least 700 µW input power to achieve such manipulation⁹. Additionally, clusters consisting of > 6 particles can be trapped and manipulated across the array (see Supplementary video S3). At this same power level, we also successfully trap 80-nm diameter Ag nanoparticles with trapping lifetimes > 10 s (see Supplementary video S4). Using 50 µW-input power in our comparable CW system leaves the trajectory of nanoparticles completely unperturbed by the illuminated BNAs, i.e., the fs pulses increase the near field forces generated on the nanoparticle by the plasmonic nanotweezers compared to a CW source. Furthermore, we find that during the trapping event the nonlinear optical response of the coupled BNA-nanoparticle system exhibits a 3.5x increase in the SHG signal as well as a slight modification to the TPPL, as shown in the Fig. 4 inset. After the signal is collected, we increase the input power to 75 µW to adhere the particle to the BNAs (via fusing behavior), which allows for post-processing measurement of the nanoparticle dimensions. Figure 4 shows an SEM image of the Ag nanoparticle adhered to an individual bowtie and it can be seen that the particle has a diameter of approximately 80 nm.

Figure 4. Scanning-electron micrograph of the 80-nm Ag nanoparticle adhered to an individual bowtie marked by the red circle.

The inset shows the spectrum measured for the BNAs alone and the coupled BNA-nanoparticle system.

The SHG enhancement by the coupled BNA-nanoparticle system is an interesting phenomenon that may be due to plasmon coupling between the bowties and the nanoparticle. In order to be effectively trapped, the Ag nanoparticle must be within 10–15 nm of the BNAs to experience a sufficient intensity gradient. Given that this distance is on the same order as the bowtie gap size, the coupled system can be regarded as a hybrid, 3D bimetallic nanoantenna, whereby the addition of the nanoparticle increases the local field enhancement by increasing field confinement in the axial direction. To this end, we find (via FDTD) that the temporary structure consisting of 425- nm spaced bowties and an 80-nm Ag sphere placed 10 nm above produces a 100x increase in the intensity enhancement at λ = 800 nm and 50x increase at λ = 400 nm, compared to the plain BNAs. This additional enhancement may play a part in the increased far-field SHG measurement.

Discussion

Given that a theoretical model for fs-pulsed trapping in a conventional optical tweezer is still not fully developed¹³,²⁴, the exact nature of the optical forces generated in the fs plasmonic nanotweezer remains elusive. However, the observed increase in trapping performance over CW nanotweezers in both Mie and Rayleigh size regimes offers strong evidence that fs pulses could augment the near-field gradient force produced by the BNAs. This result warrants furthur investigations on optical forces in a pulsed, plasmonic nanotweezer.

While the trend in trap stiffness can be explained somewhat via intensity enhancement and absorption, discrepancies arise in part due to the complex potential energy landscape generated by plasmonic “hot spots”. At least 9 bowties are simultaneously illuminated by the ~ 1.6-µm diameter focal spot which produces a potential landscape similar to a holographic optical pinscape²⁵. Thus, the trapped particle samples many potential wells simultaneously, rather than a single well as in the case of conventional optical trapping, and the measured stiffness cannot be completely understood from the intensity enhancement alone. Consequently, the stiffnesses measured using 1.2- µm particles are “effective” single-potential stiffness values, verified by the close-fit of the position histograms to a Gaussian distribution shown in Fig. 2. In the Rayleigh particle case, both the 300-nm polystyrene and 80-nm Ag spheres are comparable to the size of a single bowtie (~ 260 nm x 80 nm) and are thus small enough to interact with only one of the illuminated bowtie hot spots at a time. As such, the Rayleigh particles experience discrete jumps between illuminated bowties but overall they are confined to the illuminated focal spot. A direct result off the more discrete nature of the trapped Rayleigh particles is that we do not observe a Lorentzian lineshape in the position fluctuation analysis, and a Gaussian particle displacement histogram cannot be obtained. Thus, we rely on dark field video microscopy of the particles to verify that they are indeed trapped⁹,²⁶. Despite these apparent complications, fs nanotweezers can greatly benefit biological applications not only because they function at power levels approximately 3 orders of magnitude lower than the optical damage threshold⁵, but they also offer increased sample diagnostic capabilities by probing the nonlinear optical response of the specimen. This makes fs nanotweezers particularly well-suited for studying live fluorescent-tagged cells or viruses, for example.

The spectral response of the BNAs can be further modified by fusing the nanoparticle to the bowties, with the fused Ag-BNA system again displaying a significant SHG increase along with an increase in TPPL as in Fig. 4. Moreover, particle fusing can be utilized for placing single metallic nanoparticles of varying shape and material onto individual bowties. This capability opens the door to fabricating 3-dimensional, bimetallic nanostructures in situ by trapping/fusing a variety of nanoparticle geometries and materials onto an existing structure using a fs source (to date, few demonstrations of fabricated bimetallic nanoantennas exist³⁰). Thus, fs plasmonic nanotweezers potentially offer an additional degree of control in creating novel nanostructures, which may be useful for tailoring the second-harmonic response of nanoantennas²⁷ or in the burgeoning field of magnetic plasmonics, in which complex structures including “shorted” bimetallic gap antennas can be fabricated to enhance local magnetic fields²⁸,²⁹.

Methods

The BNAs are fabricated by spin-coating a 100-nm polymethyl methacrylate layer onto a 25-nm thick ITO-coated quartz substrate and using e-beam lithography to create the features. Electronbeam evaporation is used to deposit a 3-nm thick Ti adhesion layer followed by a 50-nm Au layer; lift-off is performed by soaking the sample in acetone for 30 mins. Trap stiffness measurements are performed by imaging the forward scattered light from the trapped particle onto a quadrant photodetector (Thorlabs PDQ80A) using the 0.9 NA condenser. Stiffness data are collected at a 4096-Hz sampling rate using custom LabView code; custom-written MATLAB routines are used to calculate the power spectrum of the position fluctuation signal and fit the result to a Lorentzian line shape using a Levenberg-Marquardt algorithm¹⁴. The trap stiffness is found from the obtained corner frequency f_c: κ = 2πγf_c, where 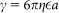is the Stokes' drag coefficient, η is the local fluid viscosity, a is the particle radius, and is the correction factor accounting for particle proximity to the substrate³¹. Reported stiffness values are the average of 10 independent runs performed on the same particle.

The FDTD simulations closely model the physical system by including a semi-infinite SiO₂ substrate with refractive index n = 1.48, 25-nm ITO (n = 1.95), and the bowties consisting of 3-nm Ti and 50-nm Au using material data from Palik³². The BNAs are built in 3 × 3 arrays with a 2x2x2-nm refined mesh over each bowtie.

Author Contributions

B.J.R. fabricated the samples and performed the simulations and all analyses in this work. B.J.R. and K.C.T. devised all experiments and co-wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Info

Supplementary Information

Supplementary Video S1

Supplementary Information

Supplementary Video S2

Supplementary Information

Supplementary Video S3

Supplementary Information

Supplementary Video S4