Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Sep 17;2:658. doi: 10.1038/srep00658

How to suppress undesired synchronization

V H P Louzada 1, N A M Araújo 1,a, J S Andrade Jr 1,2, H J Herrmann 1,2
PMCID: PMC3443817  PMID: 22993685

Abstract

Examples of synchronization can be found in a wide range of phenomena such as neurons firing, lasers cascades, chemical reactions, and opinion formation. However, in many situations the formation of a coherent state is not pleasant and should be mitigated. For example, the onset of synchronization can be the root of epileptic seizures, traffic congestion in networks, and the collapse of constructions. Here we propose the use of contrarians to suppress undesired synchronization. We perform a comparative study of different strategies, either requiring local or total knowledge, and show that the most efficient one solely requires local information. Our results also reveal that, even when the distribution of neighboring interactions is narrow, significant improvement is observed when contrarians sit at the highly connected elements. The same qualitative results are obtained for artificially generated networks and two real ones, namely, the Routers of the Internet and a neuronal network.

In the year 2000, Londoners were presented with the Millennium Bridge, a futuristic footbridge that became the center of attention on the inauguration day. The elbowing of the crowd, eager to be the first to cross it, forced the synchronization of walkers causing a lateral swing of the structure1. Once on this wobbly structure, how could one avoid such uncomfortable situation? Abnormal synchronization is also the origin of neurological diseases such as epilepsy and Parkinson2. Brain pacemakers have been developed and implanted in the patient to discharge an electrical signal into the brain tissue and restore the normal activity3,4,5. But imagine a, still to develop, device able to interact with individual neurons. What would be the best strategy to break the synchronization? A third source of inspiration can be found in the Internet, where several interconnected Routers receive and redistribute the information packages in the network. When multiple Routers synchronize their delivering events, the network collapses, a dysfunction known as TCP global synchronization. To avoid it, several algorithms have been developed and implemented in some Routers6. What is the fraction of such proactive Routers required to avoid global synchronization? In social context, avoiding synchronization might represent a political tool to fight a charismatic leader. Consider a speech that inflames a crowd. Initially every individual claps at his/her own rhythm but rapidly a coherent clap emerges7. If a set of political adversaries (contrarians) try to destroy the harmony, what would be the best strategy, the proper amount of contrarians, and their spatial distribution in the hall?

The Kuramoto model has extensively been used as the paradigm to study synchronization8,9,10,11. In a first attempt to address the questions raised above, we generalize this well-established model to include contrarians which try to suppress the emergence of global synchronization. We present a systematic study of how the synchronizability depends on the fraction of contrarian oscillators for two different strategies and analyze the influence of the topology in the mitigation process. To illustrate our results, contrarian oscillators have been studied in silico for two real networks, namely, the Routers that compose the Internet12 and the network of neurons of the organism C. elegans13,14. Our results suggest that local contrarians can be used as a powerful way to control synchronization, avoiding the necessity of monitoring the global state. Moreover, spreading contrarians as hubs is also much more effective.

The described examples are characterized by a set of N oscillators (walkers, neurons, Routers, or spectators), mutually interacting. Hereafter we take the example of the walkers but the model can be straightforwardly extended to all other cases. The stepping of each walker i is characterized by the phase θi(t) and its natural frequency ωi, corresponding to the stepping frequency when isolated. When the crowd moves, all walkers initially step at their natural frequency but herding (under strong coupling) rapidly leads to coherent walking1. In the Kuramoto model, the motion of each oscillator is described by a phasor 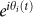Inline graphic, where θi(t) is the phase, and the coupling between walkers is such that the dynamics of each is governed by,

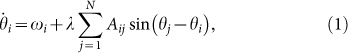graphic file with name srep00658-m1.jpg

where the sum is over all other walkers (i ≠ j), λ is the coupling strength, ωi is the walker's natural frequency, and A is the connectivity matrix such that Aij = 1 if walker i is influenced by walker j or zero otherwise. The collective walking can be characterized by the complex order parameter defined as,

graphic file with name srep00658-m2.jpg

where the sum is over all walkers, the amplitude 0 ≤ |r(t)| ≤ 1 measures the global coherence, and Ψ(t) is the average phase.

To account for contrarians we introduce a second population of Nc walkers also coupled with the others but following a different dynamics. A contrarian k is also characterized by the phase θk(t) and its natural frequency ωk. We consider two types of coupling: a mean-field (Model A) and a pairwise (Model B). In the mean-field coupling the dynamics of contrarians is governed by,

graphic file with name srep00658-m3.jpg

where Ψ(t) is the average phase and δ is a phase shift. In the pairwise coupling the dynamics of contrarians is governed by,

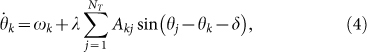graphic file with name srep00658-m4.jpg

where the sum is over all the NT walkers (NT = N + Nc). Hereafter, we take δ = π in both cases. Such phase shift between two walkers (k and j) would correspond to a walking such that when k steps with the left foot j steps with the right. It is noteworthy that these two models yield different types of frustration. While in Model A frustration between regular and contrarian walkers is mediated by the average phase, in Model B the frustration results from a pairwise interaction between regular and contrarian walkers where the former attempts to mutually synchronize while the latter tries to dephase.

Two models accounting for frustration in the mean-field Kuramoto model have recently been discussed in the context of a mixture of positive and negative couplings. Zannette15 considered a pairwise coupling where the strength and sign of the interaction between two oscillators is symmetric. This model, in the limit ωk = 0, is equivalent to a magnetic XY model with a distribution of couplings. Hong and Strogatz proposed a different scheme, where regular walkers are also solely coupled with the average phase Ψ(t) and the spatial distribution of regular walkers is not considered16,17. This model is similar to the mean-field limit of Model A discussed here. In contrast to the model discussed here, synchronization cannot be suppressed in any of these previous models.

Results

In the absence of contrarians, the classical Kuramoto model is characterized by the emergence of synchronization at a critical coupling λc which depends on the distribution of natural frequencies (ω) and on the degree. While under weak coupling (λ < λc) the motion is incoherent (r = 0), above the critical coupling a coherent motion emerges (r > 0). In the limit of very strong coupling (λ ≫ λc) all oscillators participate in the coherent motion.

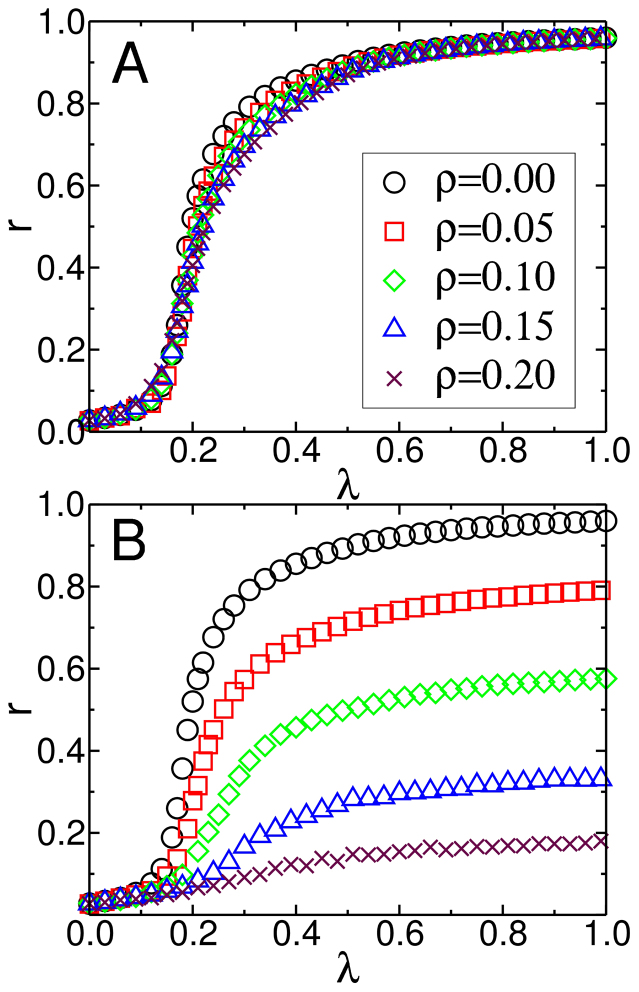
The presence of contrarians can affect the coherent motion. In Figure 1, different fractions ρ = Nc/N of contrarian oscillators are considered in the mean-field (A) and pairwise (B) models. While mean-field contrarians are not able to reduce the value of r, a fraction as small as 5% of pairwise contrarians is enough to significantly reduce the synchronizability. Further investigation shows that, although contrarians enable the system to desynchronize, meanfield contrarians drive the system to a polarized state, where oscillators are concentrated around two phases: −π and π. It is possible to understand this splitting through the analysis of the stable point (given by 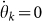Inline graphic) for contrarians in the mean-field model, yielding

graphic file with name srep00658-m5.jpg

Assuming that ωk is symmetrically distributed around zero, this equation shows that the difference between the phase of contrarians and the average phase must be equal to π. Thus, contrarians have a tendency towards the extremes of the possible phases, dragging their conformist neighbors in the process. Hence, mean-field contrarians introduce differences in the dynamic behavior of oscillators by polarizing them in two distinct phases (see Supplementary Fig. S1).

Figure 1. Comparison between mean-field and pairwise coupling.

Figure 1

Open in a new tab

Dependence of the order parameter r on the coupling strength λ, for the mean-field (A) and the pairwise (B) couplings. Different curves stand for different fractions of contrarians ρ randomly distributed in a random graph with average degree equal to four.

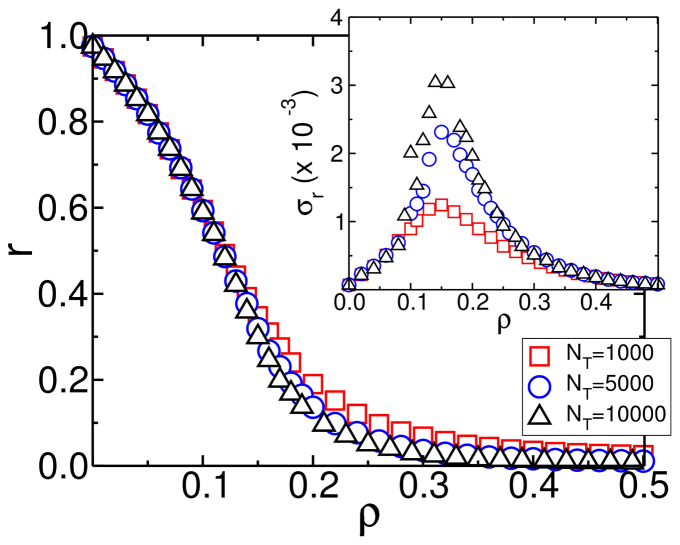
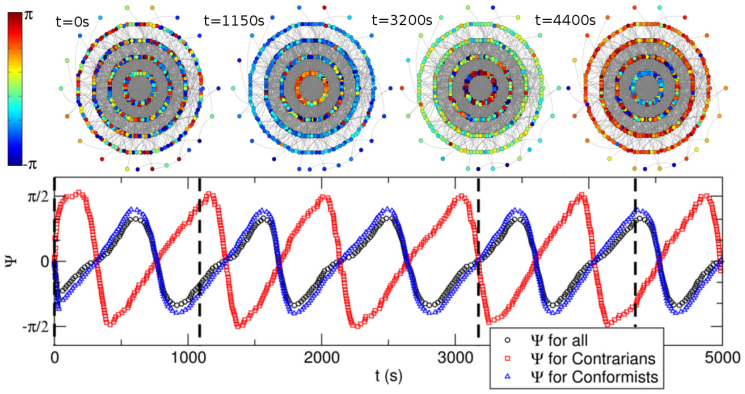
For the pairwise (B) contrarians, the emergence of a coherent state is suppressed above a certain fraction of contrarians (Figure 2). We notice that synchronization is suppressed for values of ρ > 0.15, as shown by the peak in the standard-deviation of r in the inset of Figure 2. The peak increases with the network size. For small values of ρ synchronization is maintained, r > 0, as conformists synchronize their phases with each other and the small fraction of contrarians dephase from their neighbors without destroying global synchronization. In this situation, the average phase of contrarians and conformists create a periodic alternating wave over time, an interesting mechanism that resembles, for instance, the oscillation of populations of predators and preys which characterizes the classical Lotka-Volterra model18. Figure 3 shows an example where contrarians (the central layer of the networks in the upper part) are in opposition to their first neighbors conformists, which in turn try to synchronize with them. The sequence of networks in the figure are snapshots of the oscillators and their phase over time. Before all conformists could match their phases with contrarians, the latter already have an opposite phase. The periodic wave that conformists and contrarians create is clear in the lower part of Figure 3 which shows the average phase of different types of oscillators.

Figure 2. Impact of pairwise contrarians on the synchronization.

Figure 2

Open in a new tab

Order parameter r dependence on the fraction of contrarians ρ showing suppression of synchronization. Different curves stand for different network sizes. The inset contains a plot of the standard deviation of r among samples showing a transition around ρ = 0.15. A coupling strength of λ = 2.0 has been used.

Figure 3. Time dependence of the phase.

Figure 3

Open in a new tab

Upper part: Snapshot of a network of 200 oscillators at 4 different time steps (vertical dashed lines in the lower part). A total of 20 pairwise contrarians are displayed in the central layer. Each concentric layer i, from inside to outside, contains the ith neighbors of the contrarians. The color of each node represents its phase. Lower part: Time dependence of the average phase of contrarians (red squares), conformists (blue triangles), and the whole set of oscillators (black circles) showing a periodic oscillation over time.

As the fraction of contrarians overcomes a certain threshold, the effect of contrarians spreads over the entire network completely suppressing global synchronization. This suppression is a consequence of an increasing fraction of contrarian/contrarian interactions, which naturally tend to be dephased, reinforcing their impact. For ρ > 0.15, neither synchronization (r = 0) nor a periodic wave is observed (see Supplementary Fig. S2).

The phenomenon of synchronization is known to result from the interplay between the network topology and the dynamics of oscillators19,20. We discuss now the improvement in the desynchronization efficiency by distributing the contrarians among the oscillators (nodes) with higher degree and compare this strategy with the random distribution case discussed above.

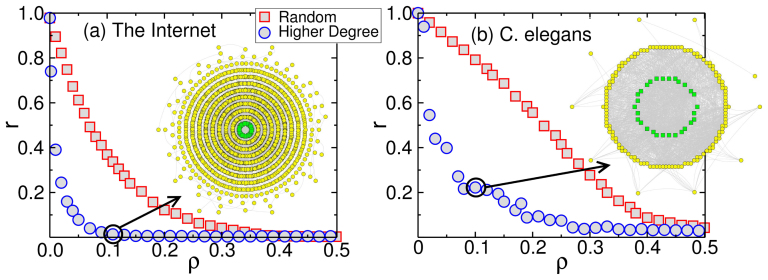
We start considering the case of a random graph (Erdös-Rényi (ER) network), characterized by a Poisson distribution of degree. As shown in the Supplementary Fig. S3, in spite of the narrow degree distribution, the fraction of contrarians necessary to reduce synchronization is reduced to one third (ρ = 0.05) when contrarians sit at the nodes with higher degree. In this case, the disturbing effect of contrarians occurs even for smaller fractions ρ and synchronization is efficiently suppressed. In scale-free networks, where degree distribution is scale free, and highly connected nodes are more frequent, the assignment of hubs as contrarians favors desynchronization (see Supplementary Fig. S4).

In real networks, the presence of communities and other features, such as assortativity and clustering, also play a role in synchronization21,22. Here we consider two real networks and show that the same behavior holds (see Figure 4). The first one is the network of Routers in the Internet. This network is believed to have grown through the mechanism of preferential attachment, being characterized by a scale-free degree distribution of exponent γ = 3.0023. Moreover, it has been shown to have a hub dominant structure, where many hubs share low degree neighbors24. In this case, similarly to scale-free networks, hubs play a major role in the synchronization, and only 10% of them are necessary to suppress synchronization. Highly connected contrarians have a disordering effect on a great number of conformists and a few hubs control the phase of the entire set of oscillators. The second one is the neuronal network of the organism C. elegans, a Small-World network and the largest network of neurons that has been totally mapped25. There, random or degree-based distribution of contrarians suppress synchronization, although the network seems to be more resilient to such control than ER networks. The presence of functional communities of neurons that are highly connected within themselves might be the cause of this resistance26. It is interesting to note that this biological system, evolved under evolutionary pressure, has converged to a resilient structure regarding synchronization.

Figure 4. Pairwise contrarians on real networks.

Figure 4

Open in a new tab

Fraction of contrarian oscillators randomly assigned and based on the degree for different networks: (a) the Routers of the Internet, (b) neurons on C. elegans. The insets are snapshots of the referred networks where each concentric layer i, from inside to outside, contains the ith neighbors of the contrarians. The color of each node represents its type: contrarians (green) and conformists (yellow). A coupling strength of λ = 4.0 has been used.

Discussion

The use of agents to control the dynamics of a network has recently been a subject of research interest27,28. In this work, we have shown that global synchronization can be suppressed with local agents (contrarians) which systematically dephase from their nearest neighbors. We show that solely local information is required to efficiently avoid a coherent oscillatory state. If instead, global information is considered, the set of oscillators splits into two oscillatory states with different phases and a global coherent state is still possible. Analyzing the impact of the network topology in desynchronization we concluded that, when contrarians sit at the nodes of higher degree, the process is more efficient than in the random case. Even with random graphs, characterized by a narrow degree distribution, the degree strategy reduces to one third the amount of required contrarians to suppress synchronization. We also show that the synchronization of real networks that present underlying features such as communities and dominant hubs is also suppressed with the use of contrarians.

The present work is the first attempt to understand the interplay between the desynchronization dynamics and the topology when considered to mimic real systems. The Kuramoto model provides a standard framework to study synchronization, however it entails several approximations when discussing real networks. For example, social systems are composed of adaptive agents that might change their strategy over time and avoid being trapped in a locked state. Developments build up on top of this work should account for further details on the coupling scheme and on the contrarian dynamics. For instance, here we have focused on the distribution of contrarians, but recent works have shown that rewiring interventions, such as swapping, adding, or removing edges, have a crucial role in the collective dynamics29,30. Nevertheless, general conclusions can be drawn shedding light on the problems discussed in the introduction. For instance, as referred, some Routers on the Internet have a special algorithm implemented to avoid synchronization. We have shown that placing contrarian Routers as hubs on the network could optimize the fraction of proactive Routers necessary to prevent global synchronization. Also, modifying the coupling mechanism between two Routers and the contrarian strategy implemented, it becomes possible to extend our work to define the best location of contrarians on the Internet.

Regarding the development of brain pacemakers, our study suggests that a set of small size devices spread throughout the brain, and solely tracking the phase of neighboring neurons, would be more effective to prevent a seizure than monitoring the global state. After the mapping of a neural network31, and the characterization of the coupling dynamics between neurons, our work also gives helpful hints about the minimum amount and the optimal spatial distribution of these active devices.

Interesting applications could also be found in social dynamics. Whenever a “social synchronization” is achieved, such as clapping after a speech, a small amount of influential agents can be trained to prevent this synchronization. Political opponents could be spread in the crowd to avoid a proper salutation simply by “dephasing” their claps with their close neighbors. The same method might be used to prevent a synchronized walk on a bridge where instructed actors could walk dephased from others. Evidently crowd behavior control is a very hard task32, but here we show that it could theoretically be achieved.

Methods

Equations 1, 3, and 4 have been numerically solved using a fourth order Runge-Kutta method with discrete time steps δt = 0.001. The complex order parameter was computed in the interval t ∈ [90, 100] using the average value of Equation 2. For all considered cases, natural frequencies of oscillators have been uniformly distributed between −0.5 and 0.5 and initial phases have also been uniformly distributed between −π and π. A coupling strength of λ = 2.0 has been used. For the Internet and the C. 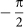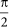elegans, natural frequencies and initial phases have been distributed uniformly between −0.1 and 0.1, and between Inline graphic and Inline graphic, respectively, and a coupling strength of λ = 4.0 has been used.

Networks of oscillators have been constructed as undirected ER networks of average degree four, unless otherwise stated. The network of Internet Routers has been analyzed through data retrieved from the Opte Project that represents all the communication among 40028 Routers on January 15th of 200512. Each node of this network is a Router with an associated IP address and the links (edges) are established between two IP address which have communicated at least once. The network of neurons was constructed through data obtained on the WormWeb website14 and is mostly based on the work by Chen et al13. In this network, links have been established whenever an interaction between neurons has been registered, regardless of their type or direction. Other measures regarding these networks are available in Supplementary Table S1.

All results have been averaged over several samples. The error bars were omitted in all figures, being smaller than the symbols. For the Internet and the C. elegans only the natural frequencies and initial phases change among samples. Plots in Figure 1 are constructed using the average value over 100 networks of size N = 1000. Figure 2 shows averages of 5000 networks of size N = 1000, 1000 networks of size N = 5000, and 600 networks of size N = 10000. In Figure 3, we represent a single network of N = 200 with ρ = 0.1 and λ = 1.0. For Figure 4, plot (a) is an average over 200 initial distributions of phases and frequencies, and plot (b) is an average over 10.

Author Contributions

All authors contributed equally to the paper.

Supplementary Material

Supplementary Information

Supplementary information

srep00658-s1.pdf (1.8MB, pdf)

Acknowledgments

Authors would like to thank the Swiss National Science Foundation under contract 200021 126853, the CNPq, Conselho Nacional de Desenvolvimento Cientfico e Tecnolgico - Brasil, the CNPq/FUNCAP Pronex grant, and the INCT-SC for financial support, and the Cuttlefish Project, responsible for the network visualization tool.

References

  1. Strogatz S., Abrams D., McRobie A., Eckhardt B. & Ott E. Theoretical mechanics: Crowd synchrony on the millennium bridge. Nature 438, 43–44 (2005). [DOI] [PubMed] [Google Scholar]
  2. Glass L. Synchronization and rhythmic processes in physiology. Nature 410, 277–284 (2001). [DOI] [PubMed] [Google Scholar]
  3. Kringelbach M. L., Jenkinson N., Owen S. L. F. & Aziz T. Z. Translational principles of deep brain stimulation. Nature Reviews Neuroscience 8, 623–635 (2007). [DOI] [PubMed] [Google Scholar]
  4. McIntyre C., Savasta M., Goff L. K.-L. & Vitek J. Uncovering the mechanism(s) of action of deep brain stimulation: activation, inhibition, or both. Clin Neurophysiol. 115(6), 1239–1248 (2004). [DOI] [PubMed] [Google Scholar]
  5. Volkmann J., Herzog J., Kopper F. & Deuschl G. Introduction to the programming of deep brain stimulators. Mov Disord. 17(S3), S181–S187 (2002). [DOI] [PubMed] [Google Scholar]
  6. Floyd S. & Jacobson V. Random early detection gateways for congestion avoidance. IEEE/ACM Transactions on Networking 1(4), 397–413 (1993). [Google Scholar]
  7. Néda Z., Ravasz E., Vicsek T., Brechet Y. & Barabási A. Physics of the rhythmic applause. Phys. Rev. E 61, 6987–6992 (2000). [DOI] [PubMed] [Google Scholar]
  8. Pikovsky A., Rosenblum M. & Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge Nonlinear Science Series). Cambridge University Press, Cambridge, (2003). [Google Scholar]
  9. Acebrón J. A., Bonilla L. L., Pérez-Vicente C. J., Ritort F. & Spigler R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185 (2005). [Google Scholar]
  10. Osipov G., Kurths J. & Zhou C. Synchronization in oscillatory networks. Springer, Berlin, (2007). [Google Scholar]
  11. Arenas A., Díaz-Guilera A., Kurths J., Moreno Y. & Zhou C. Synchronization in complex networks. Physics Reports 469(3), 93–153 (2008). [Google Scholar]
  12. Lyon B. et al. The opte project, http://opte.org (2003).
  13. Chen B., Hall D. & Chklovskii D. Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. USA 103(12), 4723–4728 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bhatla N. et al. Wormweb, http://wormweb.org (2009).
  15. Zanette D. Synchronization and frustration in oscillator networks with attractive and repulsive interactions. Europhys. Lett. 72, 190–196 (2005). [Google Scholar]
  16. Hong H. & Strogatz S. Kuramoto model of coupled oscillators with positive and negative coupling parameters: An example of conformist and contrarian oscillators. Phys. Rev. Lett. 106(5), 054102 (2011). [DOI] [PubMed] [Google Scholar]
  17. Hong H. & Strogatz S. Conformists and contrarians in a kuramoto model with identical natural frequencies. Phys. Rev. E 84(4), 046202 (2011). [DOI] [PubMed] [Google Scholar]
  18. Castillo-Chavez C. & Brauer F. Mathematical Models in Population Biology and Epidemiology, volume 40. Springer, New York, (2001). [Google Scholar]
  19. Gomez-Gardenes J., Gomez S., Arenas A. & Moreno Y. Explosive synchronization transitions in scale-free networks. Phys. Rev. Lett. 106(12), 128701 (2011). [DOI] [PubMed] [Google Scholar]
  20. Assenza S., Gutiérrez R., Gómez-Gardeñes J., Latora V. & Boccaletti S. Emergence of structural patterns out of synchronization in networks with competitive interactions. Scientific Reports 1(99) (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Oh E., Rho K., Hong H. & Kahng B. Modular synchronization in complex networks. Phys. Rev. E 72, 047101 (2005). [DOI] [PubMed] [Google Scholar]
  22. Arenas A., Diaz-Guilera A. & Pérez-Vicente C. Synchronization processes in complex networks. Physica D 224(1), 27–34 (2006). [DOI] [PubMed] [Google Scholar]
  23. Faloutsos M., Faloutsos P. & Faloutsos C. On power-law relationships of the internet topology. SIGCOMM, 251–262 (1999). [Google Scholar]
  24. Lancichinetti A., Kivela M., Saramaki J. & Fortunato S. Characterizing the community structure of complex networks. PLoS ONE 5(8), e11976 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Watts D. Small worlds: the dynamics of networks between order and randomness. Princeton University Press, Princeton, (2003). [Google Scholar]
  26. Hu Y., Nie Y., Yang H., Cheng J., Fan Y. & Di Z. Measuring Significance of Community Structure in Complex Networks. Phys. Rev. E 82(6), 066106 (2010). [DOI] [PubMed] [Google Scholar]
  27. Liu Y., Slotine J. & Barabási A. Controllability of complex networks. Nature 473, 167–173 (2011). [DOI] [PubMed] [Google Scholar]
  28. Yan G., Ren J., Lai Y.-C., Lai C.-H. & Li B. Controlling complex networks: How much energy is needed? Phys. Rev. Lett. 108, 218703 (2012). [DOI] [PubMed] [Google Scholar]
  29. Volman V. & Perc M. Fast random rewiring and strong connectivity impair subthreshold signal detection in excitable networks. New J. Phys. 12, 043013 (2010). [Google Scholar]
  30. Volman V., Perc M. & Bazhenov M. Gap Junctions and Epileptic Seizures - Two Sides of the Same Coin? PLoS ONE 6(5), e20572 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Eguiluz V., Chialvo D., Cecchi G., Baliki M. & Apkarian A. Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102 (2005). [DOI] [PubMed] [Google Scholar]
  32. Lorenz J., Rauhut H., Schweitzer F. & Helbing D. How social influence can undermine the wisdom of crowd effect. Proc. Natl. Acad. Sci. USA 108(22), 9020–9025 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep00658-s1.pdf (1.8MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES