Visual Orientation and Directional Selectivity through Thalamic Synchrony

Abstract

Thalamic neurons respond to visual scenes by generating synchronous spike trains on the timescale of 10–20 ms that are very effective at driving cortical targets. Here we demonstrate that this synchronous activity contains unexpectedly rich information about fundamental properties of visual stimuli. We report that the occurrence of synchronous firing of cat thalamic cells with highly overlapping receptive fields is strongly sensitive to the orientation and the direction of motion of the visual stimulus. We show that this stimulus selectivity is robust, remaining relatively unchanged under different contrasts and temporal frequencies (stimulus velocities). A computational analysis based on an integrate-and-fire model of the direct thalamic input to a layer 4 cortical cell reveals a strong correlation between the degree of thalamic synchrony and the nonlinear relationship between cortical membrane potential and the resultant firing rate. Together, these findings suggest a novel population code in the synchronous firing of neurons in the early visual pathway that could serve as the substrate for establishing cortical representations of the visual scene.

Introduction

Natural visual stimuli have highly structured spatial and temporal properties (Field, 1987; Stanley et al., 1999; Simoncelli and Olshausen, 2001), which strongly shape the activity of neurons in the early visual pathway (Mante et al., 2005; Lesica et al., 2007). In response to natural scenes, neurons in the lateral geniculate nucleus (LGN) are temporally precise on a time scale of 10–20 ms both within single cells and across cells within a population (Butts et al., 2007; Desbordes et al., 2008). Given that thalamic neurons with overlapping receptive fields are likely to converge at common cortical targets (Reid and Alonso, 1995; Alonso et al., 1996), that the thalamocortical synapse is highly sensitive to the timing of thalamic inputs on a time scale of ∼10 ms (Alonso et al., 1996; Usrey et al., 2000; Roy and Alloway, 2001; Azouz and Gray, 2003; Wehr and Zador, 2003; Wilent and Contreras, 2005; Bruno and Sakmann, 2006; Kumbhani et al., 2007; Cardin et al., 2010; Q. Wang et al., 2010), and that cortical neurons can be reliably driven with a small number of thalamic inputs (H. P. Wang et al., 2010), a potential role for the synchronous activity of thalamic input in the establishment of cortical response properties emerges in ethologically relevant contexts. Input from thalamic neurons with large spatial separation (i.e., >2 receptive field centers) would naturally provide a highly selective signal for orientation (Andolina et al., 2007), but given their receptive field separation, they are unlikely to project to a common recipient cortical neuron or even a common orientation column (Jin et al., 2011), creating a paradox in the emergence of important kinds of selectivity in visual cortex.

Here, we show in the anesthetized cat that the synchronous firing of geniculate cell pairs with highly overlapped receptive fields was strongly selective for orientation, a property arising from the precise timing of the thalamic response that was invariant to changes in visual contrast and temporal frequency. A significant fraction of the cell pairs exhibited directional selectivity, an asymmetry in the synchrony of firing along the axis of preferred orientation. A thalamocortical model suggests that thalamic synchrony could play a role in the nonlinear relationship between cortical membrane potential and cortical firing rate that has been linked to sharpening of orientation tuning in the suprathreshold cortical response. Combining increasing numbers of thalamic neurons revealed that an estimated 18–46 thalamic inputs would be necessary to achieve physiologically reported levels of cortical firing rate, a number of thalamic projections consistent with previous estimates. Together, the results here suggest an extremely simple conceptual model of the constituent elements of the cortical representation of the visual scene that relies only on the intrinsic spatial and temporal diversity of a highly localized thalamic population, and provide support for a feedforward model of thalamocortical processing (Priebe and Ferster, 2005, 2008) that incorporates the physiological role of thalamic timing/synchrony in shaping cortical response properties (Alonso et al., 1996; Usrey et al., 2000; Roy and Alloway, 2001; Bruno and Sakmann, 2006; Q. Wang et al., 2010).

Materials and Methods

Surgical preparation.

Single-cell activity was recorded extracellularly in the LGN of anesthetized and paralyzed male cats using a seven-electrode system (Weng et al., 2005). Three animals were used for a total of five electrode penetrations. Surgical and experimental procedures were performed in accordance with United States Department of Agriculture guidelines and were approved by the Institutional Animal Care and Use Committee at the State University of New York, State College of Optometry. As described by Weng et al. (2005), cats were initially anesthetized with ketamine (10 mg kg⁻¹ intramuscular) and acepromazine (0.2 mg/kg), followed by propofol (3 mg kg⁻¹ before recording and 6 mg kg⁻¹ h⁻¹ during recording; supplemented as needed). A craniotomy and durotomy were performed to introduce recording electrodes into the LGN (anterior, 5.5; lateral, 10.5). Animals were paralyzed with vecuronium bromide (0.3 mg kg⁻¹ h⁻¹ intravenous) to minimize eye movements, and were artificially ventilated.

Electrophysiological recordings.

Geniculate cells were recorded extracellularly from layer A of LGN with a multielectrode matrix of seven electrodes. The multielectrode array was introduced in the brain with an angle that was precisely adjusted (25–30° anteroposterior, 2–5° lateral-central) to record from iso-retinotopic lines across the depth of the LGN. A glass guide tube with an inner diameter of ∼300 μm at the tip was attached to the shaft probe of a multielectrode with a circular tip array (interelectrode separation: 254 μm). Because the elevation axis is better represented in LGN than the azimuth axis, some of the populations of LGN receptive fields showed greater lateral than vertical scatter in the visual field (Sanderson, 1971). Layer A of LGN was physiologically identified by performing several electrode penetrations to map the retinotopic organization of the LGN and center the multielectrode array at the retinotopic location selected for this study (5–10° eccentricity). Recorded voltage signals were conventionally amplified, filtered and passed to a computer running the RASPUTIN software package (Plexon). Each electrode was independently moved until a well isolated unit was identified. Each single unit was sorted online and then the spike sorting was carefully verified following the experiment using a commercially available offline sorter algorithm (Plexon). Cells were eliminated from this study if they did not have at least 1 Hz mean firing rates in response to all stimulus conditions, or if the maximum amplitude of their spike-triggered average in response to spatiotemporal white noise stimuli was not at least five times greater than the amplitude outside of the receptive field area. Cells were classified as ON or OFF according to the polarity of the receptive field estimate. The full dataset included 24 ON-centered cells and 14 OFF-centered cells across five penetrations, resulting in 133 cell pairs (pairs were formed from simultaneously recorded neurons within the same electrode penetration only). For the majority of recordings, cells were also classified as X or Y according to their responses to counterphase sinusoidal gratings, but no significant differences were observed along this classification scheme.

Visual stimulation.

For each cell, visual stimulation consisted of multiple repetitions of a drifting sinusoidal grating at 0.5 cycle/degree, at 100% contrast unless otherwise noted. The direction of the drifting grating was varied. The orientation of a particular drifting grating was one of eight possible values: 0, 45, 90, 135, 180, 225, 270, 315°. The convention was that a vertically oriented grating drifting rightward was referred to as 0°, a horizontally oriented grating drifting downward was referred to as 90°, and so on. For one dataset (7 neurons), the drifting gratings were presented at three temporal frequencies: 5, 10, and 15 Hz, corresponding to speeds of 10, 20, and 30°/s at the fixed spatial frequency of 0.5 cycle/degree. The temporal frequency for all other datasets was 4 Hz, corresponding to 8°/s. For one dataset (6 neurons), the drifting gratings were presented at a range of contrasts: 100%, 64%, 32%, and 16%. The spatial resolution for the drifting gratings was 0.0222 degree per pixel. As a control for each cell we also used visual stimulation consisting of spatiotemporal binary white noise shown at high contrast (0.55 root-mean-square contrast). The refresh rate of the white noise stimulus was the same as those of the drifting gratings; the spatial resolution was 0.90 degree per pixel. All stimuli were presented at a 120 Hz monitor refresh rate. A small amount of data (n = 6 cells) was collected for drifting gratings of a fixed orientation, but at a range of spatial frequencies (0.07, 0.1, 0.14, 0.28, 0.56, 0.79, 1.11, 2.22, 2.96, 6.67 cycles/degree). In this small group of cells (n = 6 cells, 15 cell pairs) we also compared the spatial frequency tuning of thalamic synchrony and thalamic sum. The spatial frequency tuning resulting from thalamic synchrony was slightly sharper than that obtained from a sum, however, there were no significant differences in the spatial frequency peak (n = 16, p = 0.46, Wilcoxon test).

Receptive fields.

For each cell, the spatiotemporal receptive field (RF) was estimated by standard spike-triggered-averaging techniques based on spatiotemporal white noise stimuli. The center of each RF was identified in the following manner. The spatiotemporal RFs were spatially interpolated to match the resolution of the sinusoidal gratings using splines. The lag (frame) of the spatiotemporal receptive field at which the peak absolute value occurs was first identified. The spatial center of the RF was defined as the spatial location at which this peak occurred. The contours that are shown throughout the figures are the contours at 20% of the peak value of the spatial RF map at the peak temporal lag.

As a means of quantifying the spatial separation and overlap of the receptive fields of two neurons, we fit ellipses to the 20% contours using the direct method of fitting (Fitzgibbon et al., 1999). Percentage overlap of the spatial RFs was calculated as the area of intersection of the regions defined by the two contours, divided by the area of the smaller of the two RFs, times 100% (Alonso et al., 1996). Note that the 20% contour provides the most accurate estimation of receptive field size and it is the best predictor of monosynaptic connectivity, as demonstrated in retinogeniculate and geniculocortical connections (Reid and Alonso, 1995; Alonso et al., 1996; Usrey and Reid, 1999; Alonso et al., 2001; Yeh et al., 2009). Below 20%, the receptive field includes surround, which would result in even larger values of receptive field overlap than those conservatively reported here. The distance between RF centers was reported as both the absolute spatial separation of the two centers in degrees, and as a fraction of the size of the RF center. In the second case, the average was taken of the major and minor diameters of the ellipsoidal fit of the RF for each cell, and then these two numbers were averaged across the pair. Here, when describing neurons as having highly overlapped receptive fields, we are referring to neurons with percentage overlap of ∼50% or more. Note that for a subset of neurons, the receptive fields were mapped with a high spatial resolution stimulus (Ringach et al., 1997), but were found to be consistent in the mapping of the RF with the spatiotemporal white noise stimulus used here.

For the purpose of highlighting the role of precise spike timing in the tuning properties, recorded neurons were fit using a Generalized Linear Model (GLM) approach recently applied to in vitro recordings of retinal ganglion cells (Pillow et al., 2008). This class of model is a generalization of the well known linear-nonlinear-Poisson cascade model (Paninski et al., 2004; Truccolo et al., 2005; Pillow et al., 2008). The present GLM is an encoding spiking model whose input is a spatiotemporal visual stimulus and whose output consists of the times of spikes emitted by each cell in response to the visual input.

The model for each cell i included a spatiotemporal filter k_i, a constant μ_i specifying the logarithm of the baseline firing rate, a static exponential nonlinearity, and a Poisson spike generator. Note that the spike-history dependence term used in full GLM framework was excluded here to maintain the quasi-linearity of the model. The terms representing coupling between neurons used in the in vitro data (Pillow et al., 2008) also were excluded from this analysis, as they were shown to be negligible across the LGN population (Desbordes et al., 2010), and likely unimportant for the timescale of the stimulus correlations that we are analyzing here.

The spatiotemporal filter k_i consisted of a spatial filter (25 parameters) and a temporal filter (10 parameters) for the center and surround each, for a total of 70 parameters. The spatial receptive field encompassed 25 pixels (arranged in a square), where the length of one pixel spanned 0.2 degree of visual angle. The temporal filter was 300 ms long and was parameterized by a linear combination of 10 basis functions, using a basis of raised cosine “bumps” of the form

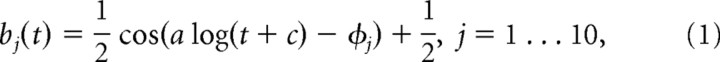for t such that a log(t + c ∈ [φ_j − π, φ_j + π] and 0 elsewhere, with π/2 spacing between the φ_j. The constants a and c were free parameters which could be adjusted to improve model fits. This basis allowed for the representation of fine temporal structure near the time of a spike and coarser (smoother) dependency at later times (Pillow et al., 2008).

The model was fitted to the responses to spatiotemporal binary white noise at 0.1 ms temporal resolution using maximum likelihood estimation (Paninski et al., 2004). The conditional intensity for each individual cell i was given by

where s(t) is the spatiotemporal stimulus, and μ_i is the logarithm of the cell's baseline firing rate. The log-likelihood for each cell was

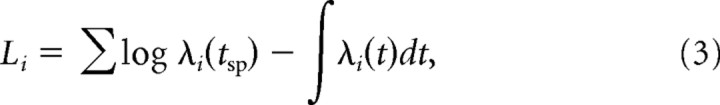where t_sp denotes the set of (actual) spike times. The population log-likelihood was the sum over single-cell log-likelihoods. The optimization procedure used to maximize this function was implemented in Matlab (MathWorks) using the native function “fminunc” from the Optimization toolbox. The model was then cross-validated on a segment of the spatiotemporal white noise data not used for the fitting. Both the model fitting and the simulations were implemented for parallel processing on a computer grid (n = 50 processors) using Matlab Parallel Computing Toolbox.

Properties of neural response.

For a particular trial, the firing rate of the ith neuron, r_i, was calculated as the number of spikes over the trial, normalized by the trial duration T, resulting in units of spikes per second or Hz. The mean firing rate across trials for the ith neuron was denoted r̄_i. The peristimulus time histogram (PSTH) was computed as the cumulative response of the cell over all cycles of the drifting grating in a temporal bin Δt, which captures the instantaneous mean firing rate of the ith neuron across trials as a function of time, r̄_i(t). All PSTHs were computed with a 8.3 ms bin.

Correlation analysis.

The cross-correlogram for cell i to cell j was calculated as:

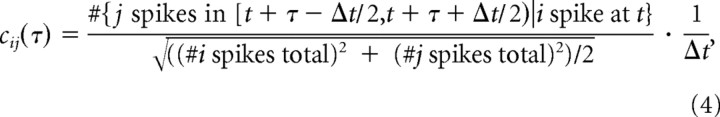resulting in units of spikes per second, with a bin size Δt = 5 ms unless otherwise specified. The number of spikes used for the cross-correlogram estimates varied across cell pairs. The mean number of spikes used was 1800 per orientation of the drifting gratings, with a minimum of 100 and maximum of 6258. Synchrony was defined as the central area under the cross-correlogram within a synchrony window (Temereanca et al., 2008; Q. Wang et al., 2010), and was relatively robust to the number of spikes used in the correlogram estimate.

Synchronous spiking.

For the ith and jth neurons of an ensemble, we identified the synchronous spiking of the two neurons and generated activity of a hypothetical third neuron that represented the synchronous activity across the two cells. Specifically, for each spike of the ith neuron, if the jth neuron spiked in a temporal window ±Δt centered at the spike of the ith neuron, then a spike was created for the synchronous neuron half-way between the synchronous spikes of the ith and jth neurons. Note that this defines a window of width 2Δt, but the interspike interval between the two neurons will be no larger than Δt. The trial-by-trial firing rate of this neuron was denoted r_ij, representing the total number of spikes (spike count) in the trial divided by the time interval of the trial T. The mean firing rate across all trials r̄_ij was equivalent to the area under the cross-correlation function in a window centered at lag τ = 0. The size of the synchrony window was ±5 ms for the majority of analyses, but was also systematically varied to determine the role of this parameter in the tuning properties. Note that for the experimentally recorded LGN neurons, the frequency of short interspike interval (ISI) spiking (<10 ms ISI) of individual neurons was comparable to the frequency of the synchronous spiking across neurons (34 Hz vs 25 Hz instantaneous firing rate, at the peak), and both were modulated by the sinusoidal input. Note that on average, the synchronous firing rate during visual stimulation was 37 times larger than that during spontaneous firing (7.7 Hz during visual stimulation, 0.2 Hz spontaneous, n = 133 pairs). Of course, cortical neurons require the concerted spiking of many geniculate inputs, and thus the presence of short ISI events synchronized across nearby neurons would even further reinforce the tuning properties we present (i.e., nonpreferred orientations would produce events across neurons that are out-of-phase, and thus ineffective in driving the cortical target).

Orientation tuning properties.

The orientation tuning was always calculated as the trial averaged mean firing rate r as a function of the direction of the drifting gratings θ. In all cases, the trial length was 400 ms. To quantify the sharpness of the tuning, we calculated a measure that was half of the width of the tuning curve at firing rates that were 50% of the maximum, often described as half-width at half-height (HWHH) (Ringach et al., 2002). Note that this measure was computed after subtracting the background firing rate. Given that we measured the firing rate in response to a drifting grating at a finite number of directions, we linearly interpolated between measurements. As a separate measure, we also calculated the circular variance, as used in a number of studies to express the strength of tuning (Ringach et al., 2002). Finally, in many cases, the cell pair responded synchronously to a drifting grating in a particular direction, but exhibited a significantly attenuated response to the drifting grating in the opposite direction (±180°). To capture this property of directional selectivity, we defined the directionality index as one minus the ratio of the firing rate at the direction opposite the maximum to the maximum firing rate. The result is an index that ranges from 0, when equally responsive in the two directions, to 1, when there is no response at all in the direction opposite the maximum.

Tuning curves were also generated for each individual LGN neuron, typically exhibiting a uniform firing rate across different directions. For tuning properties across cell pairs, we calculated the tuning as a function of the trial-averaged synchronous activity r̄_ij, and the tuning measures described above were calculated for a number of different stimulus conditions.

Simulation.

A simple, leaky integrate-and-fire model (Gerstner and Kistler, 2002; Gabernet et al., 2005; Q. Wang et al., 2010) was used for the analysis of the relationship between thalamic synchrony and the cortical power law. Note that this model by construction only captures the direct excitatory feedforward input to cortical layer 4, and does not explicitly incorporate feedforward inhibition or other cortical inputs (see below). The model neuron had a resting potential of V_rest = −70 mV and membrane time constant of 10 ms. When the membrane potential reached −55 mV, the model neuron fired an action potential and was reset to −65 mV. Upon arrival of a presynaptic spike, an EPSC (0.05 nA, exponentially decaying with a time constant of 0.85 ms) was injected into the model neuron, whose membrane had a conductance of 14.2 nS (70 MΩ) (Cardin et al., 2008). To first systematically control the input to the model with a high degree of accuracy, spikes were generated from a homogeneous Poisson process, for varying rate parameters. The spike train was replicated to produce 50 neurons in the ensemble, and the timing of each spike was randomly jittered according to the given jitter. Jitter was defined as the SD of a zero mean Gaussian random variable added to the timing of the spikes. Note that the timescale of the neural response that we have previously quantified is equal to twice the value of the jitter (Butts et al., 2007). For computing the power-law relationship between the cortical membrane potential and cortical spike count, the spikes of all 50 spike trains were combined and fed into the integrate-and-fire model. For computing the LGN power-law relationship between synchrony and firing rate, two of the 50 spike trains were randomly selected, and used to compute the synchrony, where the synchronous rate was compared with the firing rate when the two spike trains were simply combined. All simulations were repeated >30 times to estimate the mean value of the power law exponents reported here between simulated cortical membrane potential and the corresponding firing rate. We further used experimentally recorded LGN spiking activity to drive the simple integrate-and-fire model (see Fig. 10H). Specifically, single recorded trials of LGN neuron in response to the sinusoidal grating were used as templates, replicated to produce 50 neurons in the ensemble, and the timing of each spike was randomly jittered according to the given jitter (defined above). Although some degree of the precise control of the input is lost when using recorded data, the experimental data nevertheless replicated the result of the homogeneous Poisson process input in terms of the relationship between thalamic synchrony and the cortical power law exponent. To incorporate the influence of inputs not directly projecting from the LGN, we further included an injected “noise” current into the model (see Fig. 10D). Specifically, zero mean Gaussian white noise was injected, where the SD was modulated by an envelope created from the LGN PSTH. This provided a gross modulation of the noise that captures some of the indirect, but stimulus-driven input to the target cortical neuron. The peak amplitude of the injected noise was systematically varied in this set of simulations. Note that while a membrane time constant of 10 ms was used for all simulations in Figure 10, the qualitative results held for time constants below ∼15 ms.

Figure 10.

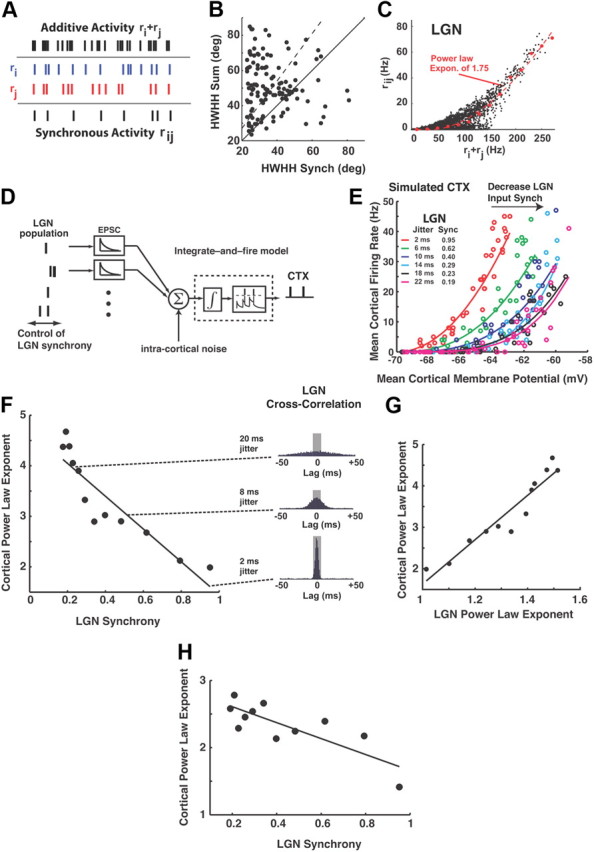
Thalamic synchrony and the nonlinearity of cortical spike generation. A, Geniculate responses to drifting sinusoidal gratings combined in an additive and synchronous manner (see Results). B, The HWHH for the synchronous activity of each pair versus the HWHH of the sum (35% broader tuning, p < 0.001, n = 133). Solid line is unity slope line; dashed line is linear regression. C, Plotted is the instantaneous firing rate of the linearly summed activity of the two neurons r_i and r_j, versus the corresponding value of the instantaneous firing rate of the hypothetical neuron representing the synchronous activity of the pair, r_ij. Each point in the scatter represents one point in time. The larger (red) symbols represent the average synchronous firing rate in a 20 Hz bin, and the curve is a power-law fit of the form A[r_i + r_j + φ]^p, where A = 0.006, φ = 42, p = 1.75. D, The spiking activity from a simulated population of LGN neurons was used as the input to an integrate-and-fire model of the cortical response. Firing of an LGN input generates an EPSC, the sum of which is integrated in the model to affect the cortical membrane potential. Upon crossing a threshold, the model cortical cell fires a spike, then resets. The synchrony of the LGN input to the model was systematically controlled (see Materials and Methods). E, The mean cortical firing rate exhibits a power law relationship with the underlying mean cortical membrane potential of the form A[V_m]^p, where A is a proportionality constant and p is the exponent. The nonlinearity of the relationship becomes more dramatic with increasing LGN timing jitter (or decreasing LGN synchrony). F, The power law exponent of the relationship in E is strongly negatively correlated with LGN synchrony (slope = −3.2, r² = 0.83, p < 0.001). Shown to the right are LGN spike cross-correlation functions at different degrees of jitter (and synchrony). G, The exponent of the power-law relating additive and synchronous thalamic activity in C is strongly predictive of the exponent of the power law relating cortical membrane potential to cortical firing rate (slope = 5.3, r² = 0.91, p < 0.001). H, For experimentally measured LGN spiking as input to the model, the LGN synchrony was again strongly predictive of the cortical power law exponent (slope = −1.2, r² = 0.64, p < 0.001).

Results

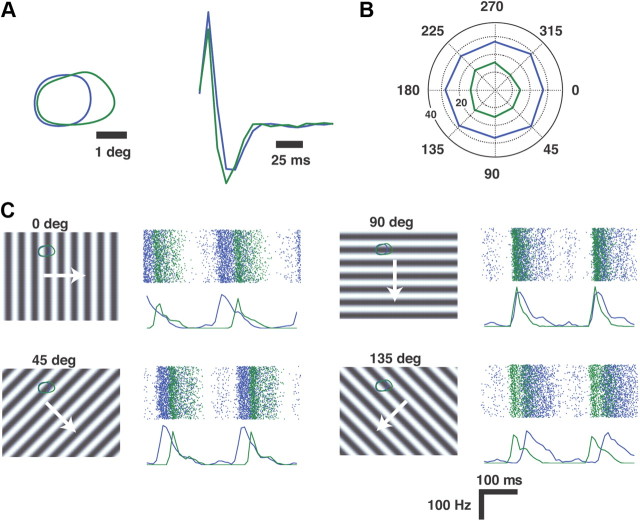
Drifting sinusoidal gratings were presented to anesthetized cats while recording extracellular activity of multiple single units in the LGN in vivo. Figure 1A shows the contours of the receptive fields of two typical geniculate neurons (both ON, X cells), and the temporal kernels at the center of the RF, mapped from spatiotemporal white-noise stimuli (see Materials and Methods). When presented with drifting sinusoidal gratings (0.5 cycle/degree, 5 Hz, 100% contrast), the neurons do not exhibit any sensitivity to the direction of the drift, as shown in Figure 1B (see quantification below). From Figure 1C it is apparent that the relative timing of firing of the two neurons is being systematically modulated by the direction of the drift.

Figure 1.

Geniculate response to drifting sinusoidal gratings. A, Spatial and temporal RF properties of two geniculate neurons recorded simultaneously. Maps were created from spatiotemporal white noise (see Materials and Methods). On the left are the 20% contours of the spatial RF at the peak latencies. On the right are the temporal kernels at the center of the RF. B, The mean firing rate as a function of the direction of drift of a sinusoidal grating across the RFs (spatial frequency of 0.5 cycle/degree, temporal frequency of 5 Hz). Radial axis represents firing rate, in Hz. C, Rasters and PSTHs for each of the neurons in response to the drifting grating in 4 of the 8 directions presented. The direction of drift for each case is illustrated to the left of each raster/PSTH. The bin size for the PSTH was 8 ms.

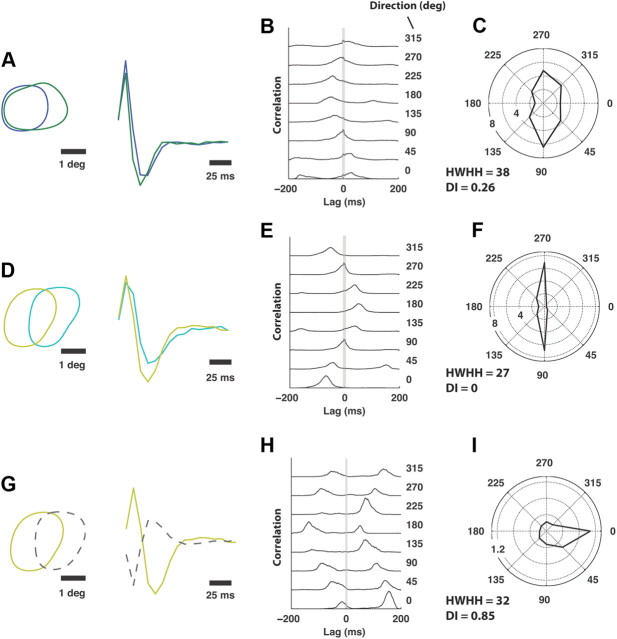
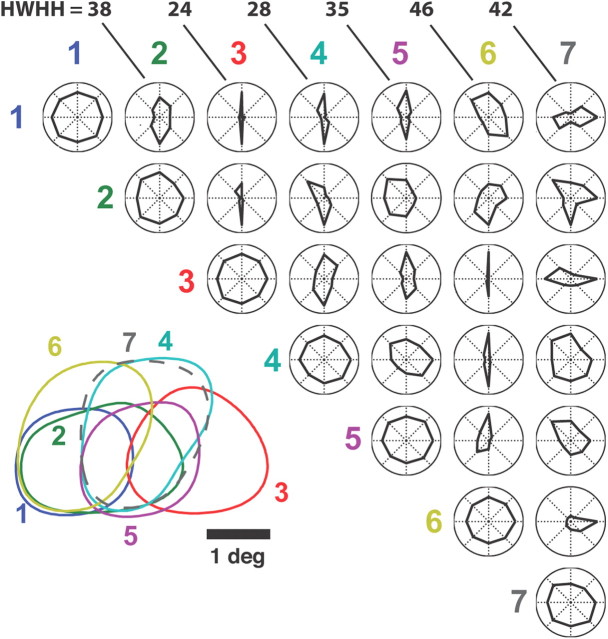
The modulation in relative timing shown in Figure 1C, caused by slight spatiotemporal differences in the receptive fields (shown again in Fig. 2A for reference), is well captured by the cross-correlation in spiking activity across the pair, as shown in Figure 2B. The wide peak in the cross-correlation is due to receptive field overlap of the two neurons (89% overlap in the spatial RFs). Superimposed on this broad correlation, some thalamic cell pairs showed a precise ±1 ms peak, indicating a shared input from the same retinal ganglion cell (Alonso et al., 1996; Yeh et al., 2009). The time-lag associated with the peak of the cross-correlation function is determined by the orientation and direction of motion. We define synchronous activity across two neurons as spiking activity of the second neuron within a ±5 ms time window of a spike of the first, also captured by the area under the cross-correlation within the gray band at the center. In this way, for a neuron pair we define a joint tuning property based on the synchronous activity, as a means of describing the activity most likely to elicit activity in a common downstream cortical target. As shown in Figure 2C, the pair exhibits strong tuning for gratings that drift in either downward (90°) or upward (270°) directions. The same is shown for another ON-ON neuron pair in Figure 2D–F, exhibiting even sharper tuning along the same axis, while still exhibiting significant overlap (45%) in the RF. A third example is shown in Figure 2G–I, for an ON-OFF pair (47% overlap), exhibiting a fairly sharp tuning for rightward (0°) motion and very little response in the opposite direction (180°). Figure 3 shows the tuning properties of all pairwise combinations (21) from 7 simultaneously recorded LGN neurons. Each polar plot represents the pairwise combination of one of the neurons whose spatial RF is shown in the array in the lower left (numbered 1–7) with another neuron of the array. Note that although it is expected that the joint activity of LGN neurons with well separated receptive fields (>2 receptive field centers) would reflect orientation tuning (Andolina et al., 2007), what is surprising here is the sharpness of the tuning even when the RFs are highly overlapped, and thus much more likely to project to a common cortical target. Further, there exists an asymmetry in the orientation tuning suggesting a directional bias in many of the pairs.

Figure 2.

Example tuning properties derived from synchronous firing of pairs of neurons. A, Spatial and temporal RF properties for a particular ON-ON pair of LGN neurons. B, Spike cross-correlation for the pair as a function of the direction of the drifting grating. All correlograms were plotted with the same vertical scale across all orientations. Synchronous activity was defined as coincident activity of the two neurons within a time-window of ±5 ms, which is captured by the area under the cross-correlogram within the gray band in the figure. To the right of each panel is the associated angle of the drifting grating, in degrees. The blue and green cells of A had an average of 3392 and 1763 spikes per orientation, respectively. C, Synchronous firing rate as a function of direction. HWHH and directionality index (DI) corresponding to the polar plot are given. D–F, Same as A–C for a different ON-ON pair of geniculate cells. The aqua and yellow cells of D had an average of 2867 and 1915 spikes per orientation, respectively. G–I, Same as A–C for a different ON-OFF pair of geniculate cells. The yellow and gray cells of G had an average of 1915 and 1978 spikes per orientation, respectively.

Figure 3.

Geniculate neuron pairs exhibit a diverse range of tuning properties. Shown in the lower left are the contours of the spatial RFs of 7 geniculate neurons recorded simultaneously, each represented by a different color and number. ON cells are represented by solid lines, OFF cells by dashed. The upper triangle shows the array of tuning properties for all pairwise combinations of cells. HWHH values in degrees are given for the polar plots in the top row.

To more precisely quantify the tuning properties of the pairs, several conventional measures were computed across a larger sample of neurons (n = 133 pairs). The results were separated into pairs that consist of two ON-center cells (ON-ON, n = 61), two OFF-center (OFF-OFF, n = 16), and a mixture (ON-OFF, n = 56). Note that only neurons recorded from simultaneously were paired together. Figure 4A shows the distribution of preferred angles across the sample. The bias toward vertical orientations is likely due to the anisotropy of the LGN retinotopic map. That is, the receptive fields of neighboring LGN cells are more scattered in the azimuth than the elevation axis (Sanderson, 1971).

Figure 4.

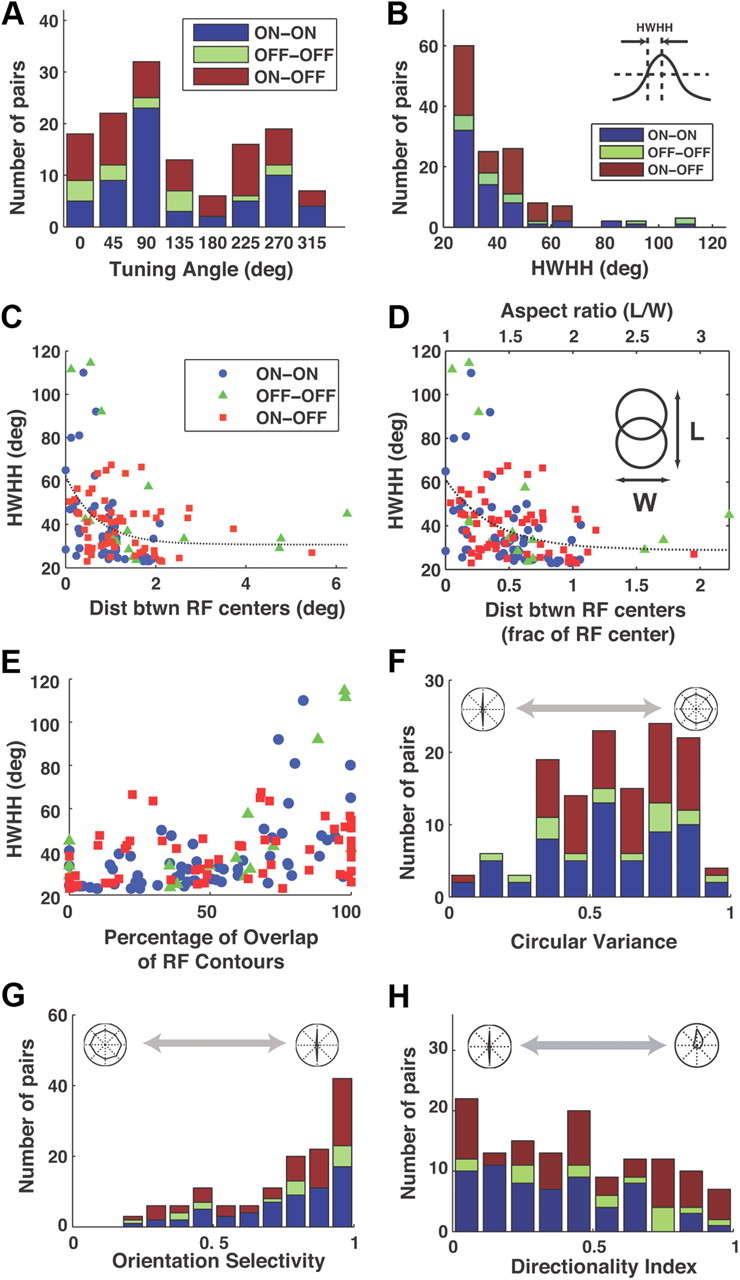
Geniculate neuron pairs exhibit a diverse range of tuning properties. Sample consists of 24 ON cells and 14 OFF cells, resulting in 61 ON-ON pairs, 16 OFF-OFF pairs, and 56 ON-OFF pairs. Note that only cells recorded simultaneously were used to form pairs. A, Distribution of the angle associated with the peak pairwise firing rate. Pair types (ON-ON, OFF-OFF, and ON-OFF) are designated by the color scheme in the inset. B, The pairwise tuning widths in degrees, measured as the HWHH (defined in inset) of the peak in the tuning curve (ON-ON: 37 ± 18°, mean ± SD; OFF-OFF: 49 ± 30; ON-OFF: 39 ± 12). C, HWHH as a function of the absolute distance between RF centers. Dotted line is exponential fit to all data of form y = α + βexp(−x/γ), where α = 30°, β = 33°, γ = 0.7°. D, HWHH as a function of the fractional distance between RF centers, where distance is measured relative to the size of the RF center (see Materials and Methods). Dotted line is exponential fit to all data of form y = α + βexp(−x/γ), where α = 29°, β = 33°, γ = 0.4°. Shown along the top axis is the corresponding aspect ratio, defined as the length of the RF tiling to the width, as illustrated in the inset. This measure assumes that each of the two RFs has a diameter equal to the average of the two actual RFs. E, HWHH as a function of the percentage of overlap between the RFs, defined as the ratio of the area of the intersection of the contours to the area of the smaller of the two contours, multiplied by 100%. F, Circular variance, as a measure of orientation tuning of the pair of neurons. Measure indicates strong orientation tuning as it tends to 0, and no orientation preference as it tends to 1 (ON-ON: 0.56 ± 0.24, mean ± SD; OFF-OFF: 0.57 ± 0.24; ON-OFF: 0.61 ± 0.19). G, Orientation selectivity of the pairs of neurons. Measure indicates strong orientation tuning as it tends to 1, and no orientation tuning as it tends to 0 (ON-ON: 0.77 ± 0.2, mean ± SD; OFF-OFF: 0.73 ± 0.28; ON-OFF: 0.72 ± 0.26). H, Directionality index as a measure of how strongly directionally tuned the pair is. Measure indicates strong directional tuning as it tends to 1, and no directional tuning as it tends to 0 (ON-ON: 0.36 ± 0.25, mean ± SD; OFF-OFF: 0.53 ± 0.28; ON-OFF: 0.50 ± 0.31).

As a measure of the sharpness of the orientation tuning, Figure 4B shows the HWHH of the orientation tuning curve (see inset for definition), which is similar to that observed experimentally at the level of V1 (Ringach et al., 2002; Moore and Freeman, 2012). Examples of individual HWHH values are provided in Figures 2 and 3. Figure 4C plots the HWHH as a function of the absolute distance between the RF centers, showing an increase in sharpness of tuning with RF separation. Note that even at very small separations (<0.5°), there are still pairs that exhibit very sharp tuning properties. Figure 4D plots the HWHH as a function of the fractional separation between RF centers, defined here as a fraction of the average of the size of the two RF centers. Along the top axis is the corresponding aspect ratio, which is defined as the ratio of the length of the RF tiling to the width, as illustrated in the inset, assuming two neurons with identical spatial RFs. Although some amount of orientation sensitivity would be predicted based on the retinotopic relationship between the two receptive fields, the tuning is extremely sharp for many of the neuron pairs that have nearly completely overlapped receptive fields (with correspondingly low aspect ratios, points in the lower left corner). Figure 4E shows the same measure of orientation tuning width as a function of the percentage of overlap of the spatial RFs of the pairs. Percentage overlap here was defined as the percentage of the area of the smaller receptive field contour that overlaps with that of the larger (Reid and Alonso, 1995; Alonso et al., 1996, 2001). As another measure of the sharpness of orientation tuning, circular variance was computed for each pair (Ringach et al., 2002), as shown in Figure 4F. A value of 1 indicates no dependence of firing rate on orientation, whereas a value of 0 indicates responsiveness along one axis only. As another measure of the sharpness of orientation tuning, orientation selectivity was computed for each pair, as shown in Figure 4G. This was defined as 1 minus the ratio of the average firing rate in the two directions orthogonal to the preferred direction, to the firing rate in the preferred direction. This yields a quantity that is 0 when the pair is not selective for orientation, and 1 when it is perfectly selective. Importantly, this quantity gives a sense of the relative firing rate in preferred and nonpreferred directions without removal of the background/mean firing rate, thus reflecting the relative impact in postsynaptic neurons. It is important to note that, as for the examples along the diagonal in Figure 3, individual LGN neurons had weak orientation tuning [circular variance: 0.85 ± 0.014, HWHH: 61 ± 5°, orientation selectivity: 0.35 ± 0.04 (mean ± SE, n = 39)]. Direction selectivity is another primary emergent feature in visual cortex whose underlying neuronal mechanism has also been source of great debate (Priebe and Ferster, 2005). Figure 4H shows the directionality index for the LGN synchrony (see Materials and Methods), where a value of 0 indicates no directional selectivity, and a value of 1 indicates responsiveness in one direction only along the axis of tuning. Examples of individual direction selectivity values are provided in Figure 2. As is the case in V1, the pairwise tuning properties here exhibited a range of properties, from strong directional tuning to no directional preference (Ringach et al., 2002; Peterson and Freeman, 2004; Priebe and Ferster, 2005). Note that directional selectivity was observed in pairs of the same polarity (ON-ON, OFF-OFF) and pairs of different polarity (ON-OFF). As exemplified by the tuning curves along the diagonal in Figure 3, individual LGN neurons had weak direction selectivity [directionality index 0.4 ± 0.05 (mean ± SE, n = 39)].

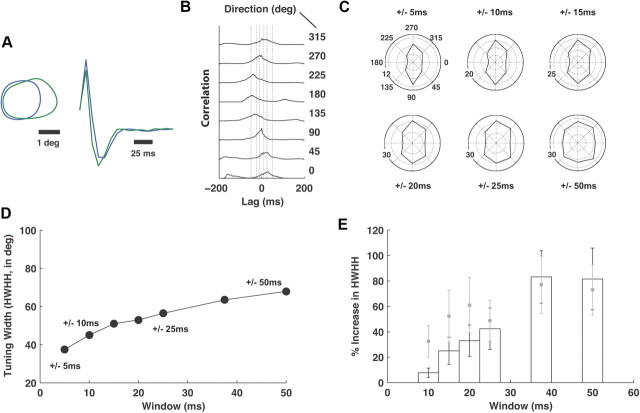
Effect of varying synchrony window

Synchronous firing thus far was defined as a spike of a second neuron within a ±5 ms window of the time of the spike of the first neuron. Figure 5A–E shows that the effect of varying the size of this window on the properties we measured. Figure 5A shows the contours of the spatial component of the RF for two typical neurons, along with the temporal kernel at the center of the RFs, calculated from responses to spatiotemporal white noise. Figure 5B shows the cross-correlations as a function of the direction of the drifting gratings. The firing rate of the synchronous activity of the two neurons is equivalent to the area under the cross-correlation function within a defined window around 0 lag. The vertical lines denote several window sizes for which the calculations were repeated. Note that the location of the peak of the cross-correlation function is smoothly modulated by the direction of the drifting gratings. Figure 5C shows the orientation tuning curves for the different window sizes for the example pair in Figure 5, A and B, exhibiting a decrease in sharpness of orientation tuning with increasing window size, summarized by the HWHH measure in Figure 5D. Figure 5E shows the percentage increase in the HWHH (compared with that of ±5 ms used for the main analyses), for 21 pairs of neurons, exhibiting a general loss of orientation selectivity with increasing window size. Note that, by construction, “opening up” the window from ±5 ms to ±10 ms does not exclude spikes that were synchronous at the ±5 ms window size. The analysis of the tuning properties at the ±10 ms window size, therefore, is influenced both by synchronous spikes falling within the ±5 ms window, and those falling outside that window but within the ±10 ms window. To specifically disentangle this issue, we conducted a separate analysis in which, for example, tuning properties at the ±10 ms window size were evaluated from synchronous activity between two neurons within the ±10 ms window, while excluding those within the smaller ±5 ms window, as shown for the analysis across the 21 pairs by the solid gray symbols in Figure 5E. This degraded the sharpness of the orientation tuning relative to the measure when including all synchronous spikes within the window, especially at the window sizes of ±10, 15, and 20 ms, suggesting that the very synchronous spiking at the ±5 ms timescale really dominated this analysis.

Figure 5.

Effect of varying synchrony window. A, Spatial and temporal RF properties for an example pair, as in previous figures. B, Cross-correlation function for different directions of the drifting gratings. Vertical lines define windows of ±10, 25, and 50 ms. The blue and green cells of A had an average of 3392 and 1763 spikes per orientation, respectively. C, Joint tuning as a function of the window width (indicated above each polar plot). The radial scale shown in Hz. D, HWHH, in degrees, as a function of window width in milliseconds for the example pair in A–C. E, Percentage increase in the tuning width (HWHH) as a function of window width, relative to the HWHH corresponding to a ±5 ms window. Bars are the mean and the SEM, for 21 neuron pairs. In gray are the mean (symbols) and SEM (bars) of the tuning widths for the analysis at each window size, while excluding synchronous spiking within smaller windows (see Results).

Invariance of tuning properties

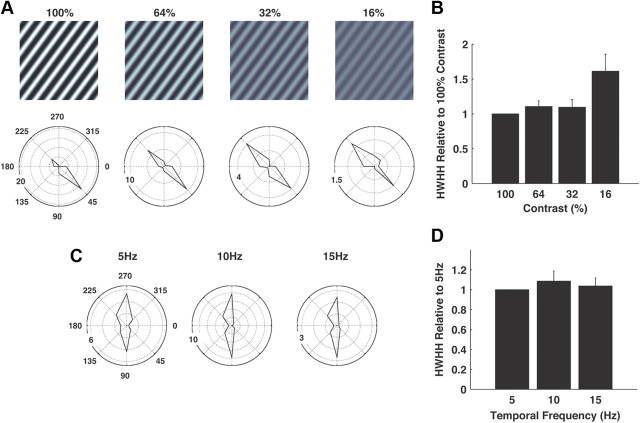
The thalamic synchrony was invariant to several aspects of the analysis and the visual stimulus. There has been significant debate on the relative roles of feedforward thalamic projections and intracortical connectivity in establishment of the tuning properties at the level of cortex, with particular emphasis on the sharpness and contrast-invariance of orientation tuning (Sclar and Freeman, 1982; Skottun et al., 1987). For a subset of the neurons, the same set of gratings was presented at different contrasts (16, 32, 64, and 100%), as shown in the top row of Figure 6A. Although there is a marked decrease in firing rate with contrast (see radial scales), as would be expected, the sharpness of the tuning along the axis of preferred orientation exhibits little change, as shown for one example pair of neurons in Figure 6A, and across 15 neuron pairs in Figure 6B (showing the percentage increase in HWHH with decreasing contrast, relative to 100% contrast). For another subset of neurons, the analysis was repeated at different temporal frequencies (and thus “speeds”), showing little if any changes in the sharpness of the tuning with speed, for a particular cell pair in Figure 6C and across 21 pairs in Figure 6D.

Figure 6.

Invariant properties of thalamic synchrony. A, Shown are the polar plots of the joint tuning properties for a typical ON-OFF pair at different contrasts (100%, 64%, 32%, and 16%). Shown above are the corresponding grating stimuli. The window width defining synchrony was ±5 ms. Radial scale indicates firing rate in Hz. B, Summary statistics across 15 neuron pairs. Plotted is the HWHH at different contrasts normalized by the HWHH at 100% contrast (mean ± SEM). C, Shown are the polar plots of the joint tuning properties for a typical ON-ON pair at different temporal frequencies (5, 10, and 15 Hz, corresponding to 10, 20, and 30°/s). The window width defining synchrony was ±5 ms. Radial scale indicates firing rate in Hz. D, Summary statistics across 21 neuron pairs. Plotted is the HWHH at different temporal frequencies normalized by the HWHH at 5 Hz (mean ± SEM).

The role of precise timing of thalamic spiking

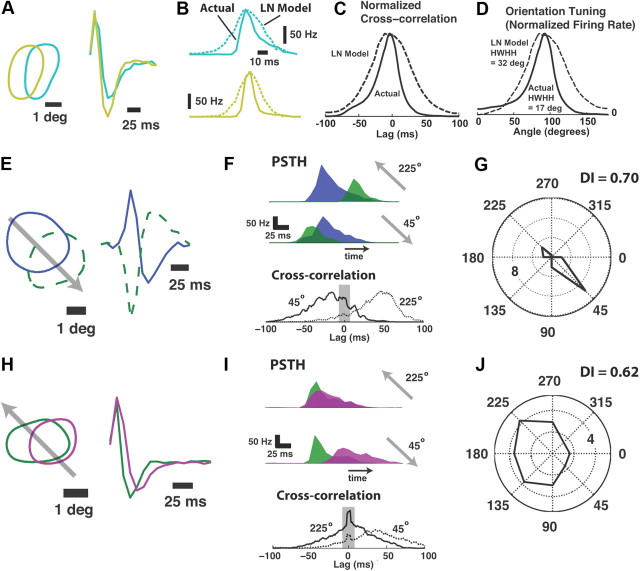
The rich tuning properties we observe in the synchronous activity across neurons in the LGN arise from the precise timing of spiking that we and others have previously reported (Reinagel and Reid, 2000; Liu et al., 2001; Butts et al., 2007). We have previously shown that LGN neurons are temporally precise in their firing, as reflected in the narrow width of the PSTH events, which is a nonlinear property of the pathway not captured by a simple linear function of the sensory input (Butts et al., 2007). It is this temporal precision that provides the degree of sharpness in the orientation tuning of the synchronous firing across two neurons that goes beyond what would be predicted with a simple linear model, as we illustrate with the following example. Figure 7A shows the receptive fields of two ON cells in the LGN (contours of the spatial component and temporal kernels at the center), with the corresponding PSTHs in Figure 7B (solid curves). Shown are the PSTH firing events at the peak of modulation in response to a drifting grating at 90°. The narrow width of the PSTH events results in a relatively narrow cross-correlation function (solid, Fig. 7C). Figure 7C shows the spike cross-correlation functions in response to a drifting grating (0.5 cycle/degree, 5 Hz) in the preferred direction (90°). The narrow cross-correlation function in turn determines the sharpness of the orientation tuning (solid, Fig. 7D). For comparison, an LN model was used to illustrate the loss in orientation tuning sharpness in the presence of purely linear encoding. Each neuron was separately fit with a linear nonlinear (LN) Poisson model using maximum likelihood estimation from the responses of these cells to spatiotemporal white noise stimuli (Pillow et al., 2008; see Materials and Methods). The LN model predictions are significantly less temporally precise compared with the actual observations (Fig. 7B, dashed curve), as we have previously reported (Butts et al., 2007), resulting in a wider cross-correlation function (Fig. 7C, dashed curve), and a significantly less sharp orientation tuning (Fig. 7D, dashed curve). For this example, the actual tuning derived from synchronous activity of recorded neurons is nearly twice as sharp as the LN model prediction. For the 133 pairs of the full dataset, tuning properties of the LN predictions were assessed relative to the recorded synchronous activity across pairs. A total of 123 of 133 pairs exhibited a larger circular variance than the experimental observation from the synchronous activity, and thus did not capture the sharpness of the tuning. Overall, the mean circular variance across the model pairs was significantly larger than for the synchronous activity over all recorded pairs (0.8 compared with 0.57, t test, p < 0.05). The sharp orientation tuning in the synchronous thalamic activity is thus due to the precise timing of the thalamic spiking that is not captured by the LN model.

Figure 7.

Tuning properties result from precise timing properties of LGN firing. A, Spatial and temporal receptive field properties for an example ON-ON pair. B, PSTHs of the actual firing activity of each neuron (solid) and PSTH predicted from the LN model (dashed), in response to a drifting sinusoidal grating (0.5 cycle/degree, 5 Hz, at preferred orientation for synchronous firing of 90°). C, Spike cross-correlation function for the actual (solid) and LN model predicted (dashed) activity in response to a drifting sinusoidal grating (0.5 cycle/degree, 5 Hz) in the direction (90°) eliciting the strongest synchronous activity, normalized to the peak correlation for comparison of the temporal structure of the correlation. D, Actual (solid) and LN model predicted (dashed) tuning curves, normalized to the peak firing rate for comparison of the sharpness of the tuning for the two cases. HWHH for the LN model prediction was nearly double that of the experimental data. E, Spatial and temporal RF properties for an example ON-OFF pair. F, Superimposed PSTHs of each neuron at 45 and 225° (top), and corresponding spike cross-correlograms for each direction (bottom, solid 45°, dashed 225°). Gray region highlights relative proportion of synchronous firing falling within a ±5 ms window. G, Joint tuning of the synchronous activity of the pair in a ±5 ms window. The radial axis is firing rate, in Hz. H, Spatial and temporal RF properties for an example ON-ON pair. I, J, Same as in F and G.

Perhaps even more surprising, however, was the presence of strong directional tuning, as shown in a cell pair in Figure 2G–I and quantified in the entire sample in Figure 4H. As illustrated in Figure 7E–G, this property arises from distinct timing asymmetries across the two neurons when stimulated with drifting gratings in opposite directions. Figure 7E shows the spatial and temporal RF properties for a particular pair of neurons (ON-OFF pair). Figure 7F shows the PSTHs for gratings drifting at 45° and 225°, with both exhibiting a fairly rapid onset of activity, followed by a more gradual decline (top). More importantly, the absolute latency between the peaks of the PSTH is distinctly different in the two directions. This results in cross-correlation functions that are not just simply time-reversed. As described previously, the synchronous activity is that which falls within a temporal window centered at 0 in the cross-correlation function, clearly a larger value for 45° compared with 225°, as highlighted in the figure. The joint tuning of this pair is shown in Figure 7G, exhibiting a strong directional preference (strong response to 45°, weak response to 225°). Note that although this example is of an ON-OFF pair, directional selectivity does not require pairs of opposite polarity cells, as shown in Figure 4H, and illustrated here for an ON-ON pair in Figure 7H–J. Across the 21 pairs of neurons in Figure 3, the directionality index was strongly correlated with the disparity in the absolute latency between the responses of the two neurons in the preferred and anti-preferred direction (correlation coefficient = 0.7, p < 0.01, see Materials and Methods).

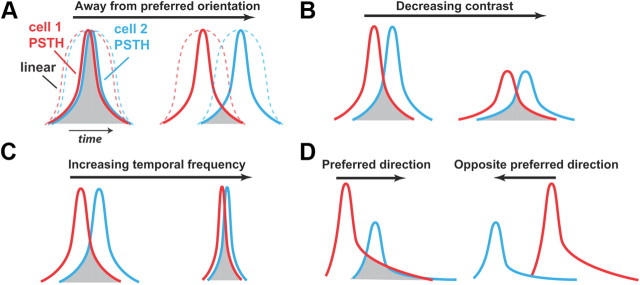
Figure 8A–D summarizes the heuristic role of precise timing in establishing the properties described here. Shown are the PSTHs, or the temporal response profiles, with time along the horizontal axis. The overlap between the neurons' temporal response profiles dictates the degree of synchrony, as indicated by the shaded region in each of the cases. As illustrated in Figure 8A, the functional explanation for the surprising sharpness in the orientation tuning exhibited by pairs of cells is revealed in the shape of the PSTH: the temporal focus of activity, as first illustrated in the PSTHs of Figure 1, results in a fairly dramatic fall-off in temporal overlap (and therefore synchronous activity) as the responses vary in their phase relationship with the direction of the motion. To the extent that the simple LN model does not predict the precision of the neural response, it also does not predict the sharpness in tuning. The temporal precision of the neurons, as expressed in the narrow PSTH (solid, cell 1 in red, cell 2 in blue), results in a dramatic fall-off in temporal overlap, and thus synchrony, when the orientation varies from the preferred, as in Figure 8A. By comparison, the linear response (dashed) is much less sensitive. With decreasing contrast, at a fixed orientation, the overall magnitude of the neural response is attenuated, but the response also becomes less precise temporally (Desbordes et al., 2008), resulting in a degree of synchrony that is relatively insensitive to contrast (Fig. 8B; see also Fig. 6A,B). With increasing temporal frequency, for a fixed orientation, the relative time difference between peaks in activity decreases, but the activity also becomes more precise (Butts et al., 2007), resulting in synchronous activity that is relatively invariant to temporal frequency (Fig. 8C; see also Fig. 6C,D). Finally, the direction selectivity of a given pair of neurons was the result of differences in absolute latencies between the responses of the two neurons in response to drifting gratings in two opposing directions (Fig. 8D, as in Figs. 7E–G,H–J). We also generally observed that the PSTH events themselves were not temporally symmetric, generally exhibiting a long right tail, which exacerbated the effect of the latency difference on the overlap and therefore the level of synchrony in the two directions. Together, the above results illustrate the potential importance in the timing of the activity in establishing the selectivity in the population code beyond what we would superficially predict.

Figure 8.

Heuristics of relationship between spike timing and tuning properties. Shown are diagrams of PSTHs of two hypothetical neurons in response to various stimulus manipulations. A, The overlap between the PSTHs of two neurons (cell 1 in red, cell 2 in blue) decreases as the angle of stimulus orientation varies from the preferred angle (left to right), where the degree of overlap (shaded gray) illustrates the resultant synchronous activity. The corresponding synchronous activity from linear response (dashed) falls off much more gradually. B, With decreasing contrast, the degree to which the responses overlap, and thus the synchronous activity, remains relatively unchanged, resulting in the observed contrast invariance. C, For a given orientation, the relative time difference between the peak of activity of the two neurons decreases with increasing temporal frequency or speed of the stimulus. However, with increasing temporal frequency, the timing of the firing of each becomes more precise, offsetting this effect, resulting in a synchronous activity that is relatively invariant to temporal frequency. Note that for display purposes a moderate degree of synchrony is shown to exaggerate this effect, but this argument holds more generally for strong synchronous activity at the preferred orientation. D, Disparities in the absolute latencies in the responses and temporal asymmetries of the PSTHs of the two neurons leads to asymmetries in the overlap and thus the synchronous activity for motion in opposite directions.

Construction of the cortical receptive field

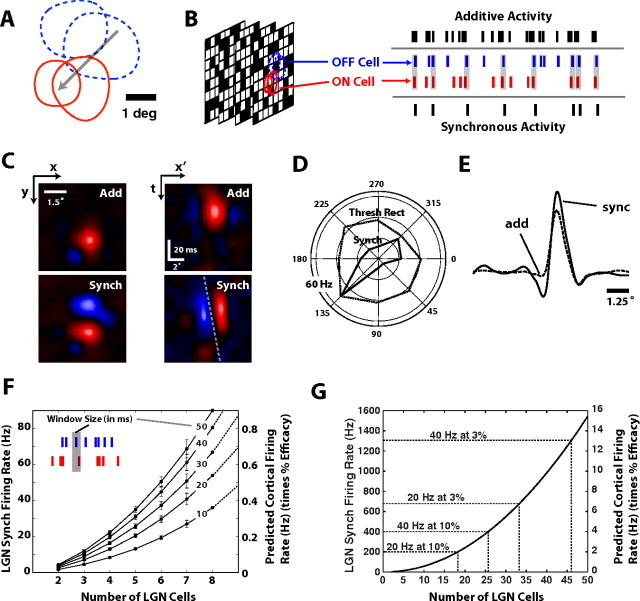
The results thus far have focused on thalamic pairs. The question remains how these geniculate projections might give rise to the properties observed in cortex, given the reported anatomical convergence from thalamus to cortex. Figure 9A shows the contours of the RFs of 4 geniculate neurons (2 ON, 2 OFF) whose geometric arrangement resembles the receptive field of a cortical simple cell. The activity of these 4 neurons was recorded in response to spatiotemporal white noise, as illustrated in Figure 9B. Although for these simulations we chose thalamic receptive fields arranged as in a classical Hubel and Wiesel model, the conclusions could be generalized to other cortical cells showing more pronounced receptive field overlap between ON and OFF thalamic inputs. The activity from the 4 neurons was then combined in two ways. First, the activity was simply added together, combining the firing of all of the units, which we refer to as “Additive.” The hypothetical neuron thus fires if any of the projecting thalamic neurons fires, and is thus insensitive to input synchrony. Second, the activity was formed by combining the pairwise synchronous activity, which we refer to as “Synchronous” activity. The hypothetical neuron thus fires if any of the projecting thalamic pairs fire synchronously. From these two perspectives, standard spike-triggered average techniques were used to map the spatiotemporal RF from the resultant spike train in each case. The spatial RF for each case is shown on the left of Figure 9C. Note that the central ON region is similar for both cases, but the additive case is lacking the strong flanking OFF subregion above the ON region. Further, in this example, the synchronous case shows a tilt in the x-t plane (Fig. 9C, right images), indicative of direction selectivity. That is, an oriented bar or sinusoidal grating sweeping in the positive x' direction as time moves forward will generate a stronger response compared with the same moving in the opposite, negative x' direction. The dashed line in the synchronous RF illustrates this bias, while no such bias appears in the additive case. Figure 9D shows the corresponding tuning curves of the activity obtained from responses to sinusoidal gratings drifting in different directions. The population synchrony exhibits a very sharp orientation tuning, and a strong directional bias along the dimension denoted by the arrow in Figure 9A. The additive activity exhibits no orientation tuning (data not shown), but more importantly, when the additive activity is threshold rectified such that the peak firing rates of the two representations match, the activity is still only very weakly orientation tuned, with no apparent directional bias. Although the differences between the RFs derived from additive and synchronous activity varied on a case-by-case basis, there was a consistent trend of an enhanced flanking subregion in the spatial RF. To further quantify this observation, the spatial RF map was reduced to one dimension by “slicing” along the axis defined by the arrow in Figure 9A. The additive case does show some structure, but the RF is spread out along the spatial dimension, compared with the synchronous case (Fig. 9E). Note that the flanking region is significantly weaker in the additive case, a phenomenon that we observed consistently across the majority of sets of geniculate neurons analyzed (ratio of weakest to strongest subregion significantly 130% greater for synchronous case, Wilcoxon test, p < 0.02, n = 5 sets). Thus the synchronous activity captures the sharpness of the push-pull nature of the RF subregions, which has been shown to be predictive of many of the observed tuning properties in cortex (Jones and Palmer, 1987; Reid et al., 1987; McLean and Palmer, 1989; DeAngelis et al., 1993; Gardner et al., 1999).

Figure 9.

Construction of the cortical receptive field. A, Shown are the RFs of 4 geniculate cells, collectively aligned in a cortical cell-like RF. B, Geniculate responses to spatiotemporal white noise stimulus combined in an additive and synchronous manner (see Results). C, RFs from the spike-triggered average stimulus, for spatial (left) and space-time (right) representations. For each, top image shows the representation for an additive combination of LGN spiking, whereas the bottom image shows that for the synchronous activity (see Results). Dashed line in space-time plot indicates tilt in the x-t plane, indicative of direction selectivity. D, Tuning curves from analogous combinations of responses to drifting sinusoidal gratings (0.5 cycle/degree, 5 Hz) in different directions. The additive activity was threshold-rectified, matching the peak firing rate of the synchronous activity. E, One-dimensional “slice” of spatial RF for additive (solid) and synchronous (dashed) cases, illustrating the enhanced flanking subregion for synchronous activity. F, Firing rate of the synchronous activity averaged across 8 combinations of geniculate cells similar to that in A, while systematically varying the number of cells included. Right axis shows the predicted cortical firing rate in Hz (when multiplied by assumed efficacy, in %). G, Projected relationship between number of LGN cells and LGN synchronous firing rate (left axis) and predicted cortical firing rate (right axis). Dashed lines indicate numbers of LGN cells required for cortical firing rates of 20 and 40 Hz, at efficacies of 3 and 10%.

Given that the synchronous firing rate of thalamic pairs is relatively low, and cortical layer 4 neurons are driven by a larger pool of projecting geniculate inputs, how does the above proposal for the generation of selectivity scale? It has been previously estimated that cortical layer 4 neurons receive between 15 and 100 primary thalamic inputs (Freund et al., 1985; Peters and Payne, 1993; Alonso et al., 2001). On the other hand, each thalamic input has higher firing rate than its cortical target. Therefore, it is clear that the spikes generated by a cortical neuron are only a small proportion of the total spikes from its multiple inputs. To consider synchrony to be a candidate mechanism for generating the tuning properties observed in cortex, we must investigate the relation between the mean rates of thalamic synchronous spikes and cortical spikes. For 8 collections of thalamic neurons (ranging from 4 to 8 geniculate cells), the number of cells was systematically varied, along with the time window used to define the synchronous activity, as shown in Figure 9F. The right axis shows the predicted cortical firing rate, when multiplied by the synaptic efficacy of a thalamic spike resulting in a cortical spike (Usrey et al., 2000; Alonso et al., 2001; Swadlow and Gusev, 2001; Swadlow, 2002). The synchrony of an individual thalamic pair (2 cells on horizontal axis) would result in cortical firing rates that are far below those observed experimentally, when taking reported ranges of synaptic efficacy into account (Usrey et al., 2000; Alonso et al., 2001; Swadlow and Gusev, 2001; Swadlow, 2002). Figure 9G shows an extrapolation of the relationship in Figure 9F for larger numbers of LGN cells, for the 10 ms window case. The dashed lines in Figure 9G highlight predicted numbers of LGN cells needed to achieve 20–40 Hz in cortical firing, under different assumed ranges of synaptic efficacy. Overall, for a temporal window of 10 ms defining thalamic synchrony and a synaptic efficacy of between 3 and 10%, this relationship predicts that 18–46 thalamic neurons projecting to a single cortical target would lead to cortical firing rates of 20–40 Hz in response to the sinusoidal gratings. This number of thalamic inputs is consistent with previous estimates of thalamocortical convergence based on cortical receptive field size, the probability of geniculocortical connection (Freund et al., 1985; Peters and Payne, 1993; Alonso et al., 2001) and direct measurements from multiple geniculocortical neurons making monosynaptic connection at the same orientation column (Jin et al., 2011). It should be noted that the efficacy of the combined thalamic inputs to a cortical neuron is currently unknown. The average efficacy of randomly selected thalamic inputs to different cortical neurons is ∼3% in both visual and somatosensory cortex (Usrey et al., 2000; Alonso et al., 2001; Bruno and Simons, 2002). However, the combined thalamic efficacy for a single cortical neuron depends on a large number of factors including the receptive field similarity among thalamic inputs and cortical target (Alonso et al., 2001; Miller et al., 2001; Bruno and Simons, 2002), the type of cortical neuron (e.g., inhibitory or excitatory; Bruno and Simons, 2002) and the level of cortical depolarization, which is greater in awake than anesthetized animals (Constantinople and Bruno, 2011). Also, the thalamocortical efficacy depends on the interspike interval (Usrey et al., 2000; Swadlow and Gusev, 2001) and can reach values as high as 50% when a thalamic spike is preceded by a long interspike interval in awake animals (Swadlow and Gusev, 2001).

Thalamic synchrony and the nonlinearity of cortical spike generation

We might envision two extreme ways in which the activity of thalamic neurons combines to generate a cortical spike (Fig. 10A). The first is a spike addition: 1 spike from the ith LGN neuron and 1 spike from jth LGN neuron causes 2 cortical spikes (additive activity). The second is a spike product: 1 spike from the ith LGN neuron synchronized with 1 spike from the jth LGN neuron causes 1 cortical spike (synchronous activity). Both scenarios have been used in models of cortical function and, physiologically, they represent cortical neurons with different thresholds and temporal windows of synaptic integration. Our results demonstrate that orientation tuning is significantly sharper for ±5 ms synchronous LGN activity than additive activity (35% smaller HWHH, paired t test, p < 0.001, n = 133, pairs), as shown in Figure 10B.

This result could be in part explained by a nonlinear relation between additive and synchronous activity. Figure 10C shows a scatter plot of the additive LGN activity for pairs of neurons r_i and r_j, versus the synchronous firing of the pair, r_ij. Each point represents one moment in time. The larger (red) symbols are the binned averages of the synchronous firing rate (see figure caption), and the dashed curve is a power-law fit of the binned rates. This relationship is strikingly similar to that of the power-law relationship between membrane potential and firing rate in visual cortex, as measured through cortical intracellular recordings (Priebe and Ferster, 2005) and this may not be just a coincidence. Each LGN spike causes a postsynaptic excitatory potential (EPSP) in a cortical neuron and the fluctuations in the cortical membrane potential reflect the additive activity of multiple EPSPs caused by multiple LGN spikes. If cortical spikes are driven predominantly by LGN synchrony, the nonlinear relationship between the additive and synchronous LGN activity could be closely related (and in part responsible) for the nonlinear relationship that has been demonstrated between the cortical membrane potential and spike output (Anderson et al., 2000; Carandini, 2007). This is important because it has been argued that this nonlinear relationship is responsible for sharpening cortical tuning.

To explore systematically a possible role of neuronal synchrony in the nonlinear relationship between cortical membrane potential and spike output, we used a very simple integrate-and-fire model of the thalamocortical circuit, as illustrated in Figure 10D (Q. Wang et al., 2010). To finely control the level of synchrony in the input, we first used artificially generated homogeneous Poisson process spike trains as inputs to the model. We then systematically varied the degree of synchrony of the input to the model. Specifically, spike times were “jittered” by adding a value to the spike time that was drawn from a Gaussian distribution with zero mean, and SD σ (which we refer to as the “jitter”; see Materials and Methods). A different but related measure is that of synchrony, which we define as the area under the spike cross-correlogram within a window centered at zero lag (see Materials and Methods). Figure 10E shows the corresponding relationship between the simulated cortical membrane potential and the corresponding cortical firing rate, for different amounts of input synchrony (or timing jitter). With decreasing amounts of input synchrony (or increasing timing jitter), the relationship between cortical membrane potential and cortical firing rate becomes increasingly nonlinear. For each case, a power law function was fit, as illustrated by the solid curves in the plot (see figure caption). As Figure 10F demonstrates, there was a strong negative correlation between the degree of input synchrony and the exponent of the power law (slope = −3.2, r² = 0.83, p < 0.001). To the right are spike cross-correlation functions for 3 levels of input synchrony, with the central ±5 ms window defining the synchrony highlighted. Figure 10G shows that the exponent of the power law describing the relationship between cortical membrane potential and cortical firing rate is directly related to the power law describing the relationship between additive and synchronous input activity (slope = 5.3, r² = 0.91, p < 0.001). To confirm that the above findings extend to experimentally observed LGN inputs, we conducted a separate set of simulations that used experimentally recorded LGN input to drive the integrate-and-fire model. Specifically, single trials of recorded LGN spiking in response to the drifting sinusoidal grating were again artificially jittered to explore the relationship between the level of input jitter and the cortical response. As shown in Figure 10H, the relationship between the LGN input synchrony and the cortical power law exponent again exhibited a trend similar to that in Figure 10F (slope = −1.2, r² = 0.64, p < 0.001). Finally, it is important to emphasize that this is a very simplistic model that does not incorporate intracortical inputs and, therefore, the values of LGN synchrony are higher than those observed experimentally. To incorporate modulatory inputs that were not direct excitatory input from LGN, we included an injected “noise” current (Fig. 10D, see Materials and Methods). For relatively small amplitudes of injected noise, the relationship between the LGN synchrony and the cortical power law exponent was unchanged. However, for increasing amplitudes of injected noise, the power law exponent became increasingly insensitive to the thalamic synchrony, leveling off at exponents between 1.5 and 2 (data not shown).

Discussion

As demonstrated here, the synchrony of thalamic inputs with highly overlapped receptive fields contains much richer information about visual stimuli than was originally thought and is currently assumed by models of thalamocortical function. This information could potentially give rise to orientation and direction selectivity at the neuronal targets where the synchronous thalamic inputs converge. Synchronous thalamic inputs (within <10 ms) have been shown to be more effective at driving cortical targets than nonsynchronous inputs (Alonso et al., 1996; Usrey et al., 2000; Roy and Alloway, 2001; Bruno and Sakmann, 2006; Kumbhani et al., 2007; Cardin et al., 2010). Interestingly, the temporal value of ∼10 ms matches the duration of the episodic visual response from thalamic neurons to movies of natural scenes (Butts et al., 2007; Desbordes et al., 2008). Neuronal synchrony is thought to play a major role in visual function (Gray and Singer, 1989; Usrey and Reid, 1999) and cognition (Womelsdorf et al., 2006), and has been shown to be a reliable means by which to convey information from thalamus to cortex (H. P. Wang et al., 2010). The results reported in this paper illustrate the potential importance of neuronal synchrony and spike timing precision, as well as the diversity and asymmetries of spatiotemporal receptive field properties, in encoding visual information (Mainen and Sejnowski, 1995; Butts et al., 2007). It is important to note that the mechanism of selectivity we describe for the thalamocortical circuit is only feasible for neurons that receive convergent inputs from several afferents. Cells in the LGN of cats and primates are strongly dominated by one retinal input (Cleland and Lee, 1985; Hamos et al., 1987; Mastronarde, 1992; Weyand, 2007) and, consequently, they cannot build orientation and direction selectivity with the mechanism that we propose. Interestingly, in neuronal structures where convergence may be more abundant (e.g., superior colliculus), cells do exhibit direction selectivity (Mendola and Payne, 1993).

Since the seminal work of Hubel and Wiesel (1959, 1962), there has been significant debate on the relative roles of feedforward thalamic projections and intracortical connectivity in establishment of the tuning properties at the level of cortex, with particular emphasis on the sharpness and contrast-invariance of orientation tuning (Skottun et al., 1987). In this spirit, models of varying complexity have been proposed to capture the subtleties of cortical tuning properties (Somers et al., 1995; Sompolinsky and Shapley, 1997; Ferster and Miller, 2000; Troyer et al., 2002). Recently, it has been shown that many of the observed properties might arise from nonlinearities of integration at the thalamocortical synapse and the subsequent spike generation in the recipient cortical cells, without relying on significant intracortical processing. Specifically, when linear combinations of geniculate inputs are nonlinearly transformed through an expansive nonlinearity (power law), the resultant signal exhibits many of the properties observed in cortical neurons experimentally. It has been proposed that interactions between noise fluctuations in the membrane potential and the threshold for spike generation (Anderson et al., 2000; Miller and Troyer, 2002) are important for cortical tuning properties (for a discussion see Carandini, 2007). As we show, the thalamic synchrony predicts the power-law characteristics observed in cortex, and thus may also play a role in regulating the nonlinear mechanism that gives rise to response selectivity (orientation and direction) and response invariance (contrast and temporal frequency). Our findings thus provide support for a feedforward model of thalamocortical processing (Priebe and Ferster, 2005, 2008), and unite this with physiological findings related to the role of thalamic timing/synchrony in shaping cortical response properties (Alonso et al., 1996; Usrey et al., 2000; Roy and Alloway, 2001; Bruno and Sakmann, 2006; Q. Wang et al., 2010). It should be noted that the findings here suggest a potential role for thalamic synchrony in the observed cortical tuning properties at the level of the thalamocortical interface, but this does not preclude a role for cortico-cortico interactions, which are almost certainly involved in shaping the cortical response properties and would likely carry much of the stimulus-driven characteristics of the direct thalamic input itself (Shapley et al., 2003; Monier et al., 2003; Priebe et al., 2004; Cardin et al., 2007; Constantinople and Bruno, 2011). Importantly, the findings here suggest that cortical selectivity for visual orientation and direction does not require extreme spatial separation of geniculate input to cortex, upon which current models of cortical properties are based. When coupled with recent findings that geniculate input to V1 is much more spatially restricted than previously thought (Jin et al., 2011), the results here paint a compelling picture of the potential origins of cortical selectivity.

The tuning properties we observe in the synchronous activity of thalamic neurons are due to the precise details of the timing of thalamic spiking. In response to natural scenes, neurons in the LGN are temporally precise—on a time scale of 10–20 ms—both within single cells and across cells within a population (Butts et al., 2007; Desbordes et al., 2008), and thus the mechanism we describe is potentially an important element of vision in the natural environment. The classical LN model was used here to illustrate that the failure to capture these details of the neuronal response (which we and others have previously documented for the LN model), results in a loss of the tuning properties we observe in the synchronous activity across geniculate cells. That is not to say that more sophisticated modeling approaches might not capture the fine temporal details of the LGN response, and thus the tuning properties we observe. In fact, our recent work has demonstrated that the inclusion of simple spike-history dependence in the GLM framework can to some degree temporally sharpen the temporal profile of the geniculate response through interactions with the correlation structure of the visual input (Desbordes et al., 2010), and the inclusion of explicitly nonlinear models of inhibitory surrounds can further capture the fine timing precision of LGN neurons (Butts et al., 2007, 2011). Further, recent modeling of geniculate neurons using techniques that capture multiple stimulus projections suggest that such strategies enhance the ability to capture the information conveyed by early visual neurons (Sincich et al., 2009; X. Wang et al., 2010), and thus may be another means by which to capture the features that go beyond the simple LN model.

Although there has been a significant advance in our understanding of how simple cells become orientation selective in visual cortex (Ferster and Miller, 2000; Shapley et al., 2007), much less is known about the origin of orientation selectivity in complex cells. Some complex cells acquire their orientation selectivity from intracortical inputs, either from simple cells or other cortical circuits. However, the origin of orientation and direction selectivity in complex cells driven by strong thalamic inputs (Martin and Whitteridge, 1984; Alonso and Martinez, 1998) remains unclear, seemingly requiring input from other cortical neurons that are orientation/direction selective. Our results here suggest a new possible mechanism that would allow complex cells to become orientation and direction selective from the input of a few synchronous thalamic neurons with overlapping receptive fields. The synchrony of the thalamic inputs could also explain why orientation and direction selectivity can remain unaffected when the ON-channel is blocked in the retina (Schiller, 1982; Sherk and Horton, 1984). In particular, a recent study in mice with the ON channel blocked early in development has found that most cortical cells develop circularly symmetric receptive fields but yet are still orientation and direction selective (Sarnaik and Cang, 2009). Finally, the synchrony of thalamic inputs could provide a mechanism to generate direction selectivity in the cortex with pairs of geniculate cells that do not have large differences in response latency (Saul and Humphrey, 1990), and without relying on large separation of receptive fields, for which there is little or no evidence in the anatomy of thalamocortical projections. Therefore, a novel insight of our results is that it is possible to compute direction of movement from the synchronous activity of thalamic inputs with similar response latencies and highly overlapped receptive fields. Due to the asymmetry in the fine temporal precision of geniculate responses, neurons with highly overlapped receptive fields and similar response latencies can generate direction selectivity in a cortical target that reads out the synchronous inputs. It has been estimated that as many as 30 geniculate cells may project to a common cortical target (Alonso et al., 2001), which is completely consistent with the predictions here based on the collective synchronous firing and thalamocortical efficacy.

There is a large body of literature related to the representation of motion in higher visual areas of mammals (for review, see Clifford and Ibbotson, 2002). It is of course the case that any higher order representations must be built on the distributed activity of populations of neurons in the retina and LGN. Existing motion models are primarily based on coincidence detection that involves significant temporal delays to establish the appropriate sensitivity (Reichardt, 1957). Here, the “motion” we describe is strongly coupled to changes in luminance, which is often the case in the natural visual environment (Roth and Black, 2007). Within the context of a natural visual scene, as objects move in and out of the visual field at different speeds, it is likely that the correlation/synchrony of small subpopulations of neurons is being continually modulated (Desbordes et al., 2010), which in turn modulates the reliability of the cortical response (H. P. Wang et al., 2010), all of which may be amplified through cortical feedback mechanisms (Andolina et al., 2007). Regulation of thalamic synchrony thus potentially provides a powerful mechanism for the control of visual selectivity, and therefore discriminability, at the level of cortical layer 4, as we have recently demonstrated in the somatosensory pathway (Q. Wang et al., 2010).