Methods for the Study of Development – Developing Methods: Introduction to a Special Issue of Research in Human Development

Abstract

This collection of articles explores how contemporary methods interface with and can be used effectively to test developmental perspectives and hypotheses. The authors review some of the latest advancements in measurement and scale equating, multilevel models of change, growth mixture models, longitudinal models of mediation, and survival models and illustrate how these methods can be applied to developmental data. In this introduction, we present the data-box as a useful heuristic for both assessing the conceptual assumptions and implications of a given research approach and selecting the appropriately aligned statistical models for measurement, change, and interindividual differences. Together, the articles provide accessible introductions, illustrations, and discussions of how some of the recent methodological innovations might be applied in the study of development.

Developmental research is a difficult endeavor. Articulating and testing theoretical notions about developmental phenomena often requires dealing with a variety of entities, multiple levels of inquiry, and multidirectional change simultaneously occurring on multiple time scales. As such, developmental researchers have demanded and continue to demand innovative analytical methods, research designs, and measurement tools. In turn, methodological innovations and the empirical results derived from them have challenged existing theoretical perspectives and pushed for further precision and refinement in how we think about behavioral change. Wohlwill (1991) described this dialectic interchange as a dance where theory and method stand toe-to-toe – each sometimes leading and sometimes following the steps and movements of the other. With this special issue we hope to drive the beat forward and quicken the pace of this dance by explicitly highlighting the influence that methodology has on the progression of developmental inquiry.

Drawing expertise from some of the young methodologists emerging from quantitative methodology programs around the country, this collection of articles explores how contemporary methods can interface and be used effectively in the study development. Our goals are at least twofold – to demonstrate how some of the recent methodological innovations might be applied in the study of development, and to foster the future development of methods for articulating developmental questions. While not quite a true “rave” – we hope that this compilation promotes the “techno”(−logy) of today so that the dancing continues all-night and into tomorrow.

M. Edwards and R.J. Wirth (2009) start us off by highlighting the importance of measurement in the study of developmental change. They provide an introduction to and review of classical and contemporary measurement models, and illustrate how innovations in scale equating and measurement invariance provide for additional opportunities to chart change in constructs that are expressed and must be measured differently at different times (e.g., delinquency). Acknowledging and dealing with the realities and necessities of age-appropriate measurement head on, they outline a measurement framework that opens up new possibilities for effective use of longitudinal data that might have been, in previous times, viewed as problematic.

L. Hoffman and R. Stawski (2009) illustrate how multilevel models can be used to unpack various sources of behavioral change and stability. They explain and illustrate with didactic precision how multilevel models can be used to separate and investigate within-person and between-person sources of variance. Underscoring the link between theoretical considerations and model specifics, they provide a guidebook for implementing and making effective use of the latest innovations in analysis of repeated measures (e.g., daily diary) data and investigation of context effects.

K. Grimm and N. Ram (2009) target another issue that is at the heart of lifespan research, interindividual differences in development. They introduce and illustrate the utility of a second-order growth mixture model for describing unobserved heterogeneity in change. Combining factor analytic, measurement invariance, latent growth, and mixture models, they illustrate how the benefits of multivariate assessment might be combined with the utility of categorical latent variables for identifying typologies – groups of individuals who follow qualitatively different change trajectories.

J. Selig and K. Preacher (2009) explore the interface between contemporary mediation models for longitudinal data and the study of development. They discuss the goals of mediation analyses, highlight the importance of longitudinal data for testing meditation hypotheses, and discuss how a variety of longitudinal models may be used to investigate the mechanisms by which contextual factors or developmental processes affect developmental change. Their review and illustrations point to the ways in which longitudinal models of change might be used to study possible causes and outcomes, while also underscoring the cautions that must be taken in doing so.

K. Masyn (2009) reviews a family of frailty and survival models and places them within a general latent variable modeling framework. She illustrates how the incorporation of categorical latent variables opens up the possibility for modeling and examining unobserved heterogeneity in the experience and timing of recurrent life events. For the study of development, such an approach promises to help us better understand a multitude of both single and repeated events or transitions ranging across the lifespan (e.g., delinquency, pregnancy, or disability).

Each article provides an introduction/overview of a method or class of methods and illustrates through example how the method can be applied to developmental data. These are meant to be the type of articles we would give to our students (or advisors) to learn more about these analytical approaches and methods with which they might up to now be peripherally familiar or would like to review. In the process of putting them together, we have certainly learned from each other and had the types of interdisciplinary dialogues that lay the groundwork for future work. In this regard, RHD hopes, somewhat selfishly, to have fostered these young methodologists’ thinking about developmental questions. There is no doubt that with their involvement the study of development will continue to be the best dance-party on the block.

Choosing the Dance: Theory, Method, & Data

Ideally, the study of development is characterized by the seamless integration of well-articulated theory, statistical methods that operationalize those theories, and data to which those methods can be applied (cf. Collins, 2006). Developmental research questions focus on describing, explaining, predicting, and modifying how and when the many characteristics of an individual change over time (Baltes, Reese, & Nesselroade, 1977). The wide array of available analytical methods, and the increasing ease with which longitudinal data can be obtained, provide many possibilities for aligning theory, method, and data. Of course, with this flexibility comes a burden – the burden of aligning them in a manner that allows for proper inferences regarding how well our theories approximate reality. As a prelude to the articles, we would like to elaborate a heuristic framework we have found particularly useful when faced with decisions about which methods to use and which analyses to conduct.

The Data-Box Heuristic

Cattell (1952) introduced the data-box as a practical schema to systematically identify and present different ways data could be organized and subsequently analyzed via covariation analysis. Given a particular research question, the data box can be used to identify the appropriate subset of data and associated analysis. Here, we attempt to adapt Cattell’s schema as a general heuristic that may be useful in identifying the analytical methods that can be used to connect a given set of developmental hypotheses with a given set of longitudinal data.

Components of the data-box

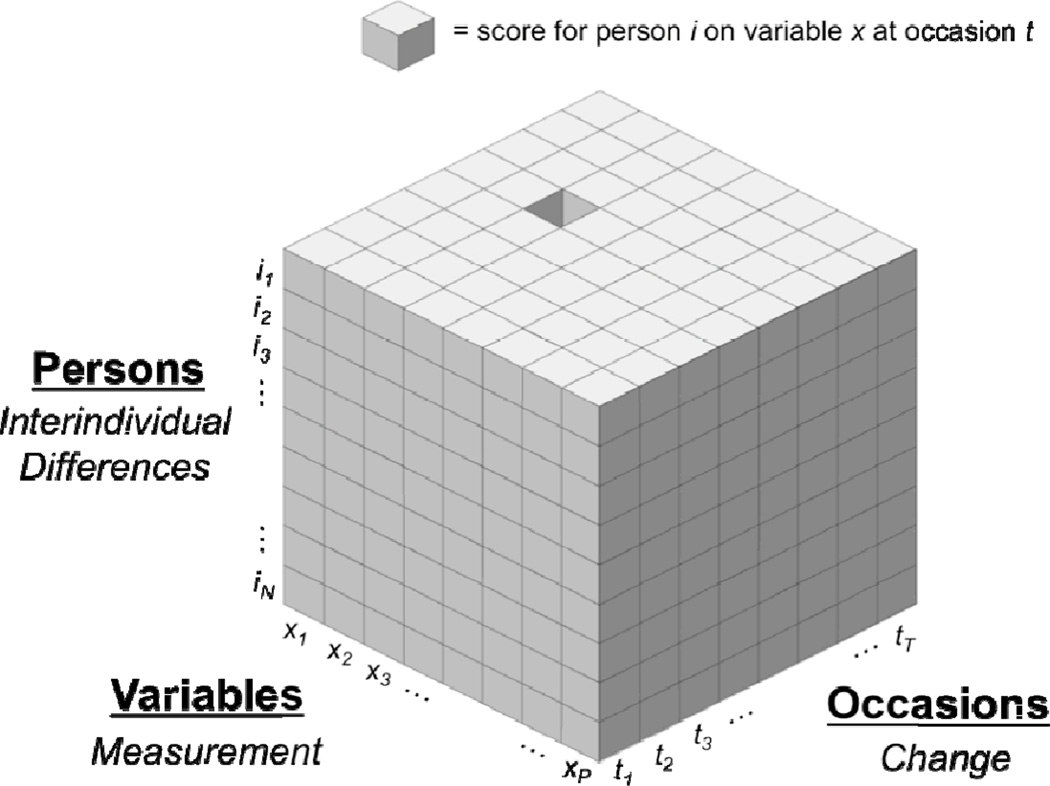
Longitudinal data can be located within a three-dimensional space (persons × variables × occasions) as shown in Figure 1. Each little cube represents a single individual’s score on a particular variable that was obtained at a specific occasion (e.g., time or age) and roughly correspond with cells or entries in a data spread-sheet or file. The individual to whom the score/cube belongs is indexed by placement along the persons axis, with all the data associated with that person filling a distinct horizontal slice in the space. The particular variable or item to which a score pertains is indexed by column along the variables axis, and the time (e.g., age, grade, or other index of time) at which that observation was obtained is indexed along the occasions dimension.

Figure 1.

Adaptation of Cattell’s (1952) three-dimensional data-box of persons × variables × occasions to represent multivariate longitudinal data. Each small cube represents the score for a single person on a particular variable obtained at a specific occasion. The person to whom the score/cube belongs is indexed by placement along the persons axis (i₁, i₂, …, i_N), with all data associated with that person filling a distinct horizontal slice in the space. The variable to which a score pertains is indexed by a column along the variables axis (x₁, x₂, …, x_P), and the time at which that observation was obtained is indexed along the occasions dimension (t₁, t₂, …, t_T). The data-box is a useful heuristic for both assessing the conceptual assumptions and implications of a given research approach and selecting the appropriately aligned statistical models for measurement (variables dimension), change (occasions dimension), and interindividual differences (persons dimension).

Heuristically, the three dimensions of the data-box map onto three theoretical and methodological issues that must be considered when choosing analytical methods that are appropriately attuned to one’s hypothesis: (1) the variables dimension refers to measurement and the organization of multiple variables, (2) the occasions dimension refers to how, when, and for how long, individuals are expected to change or remain stable, and (3) the persons dimension refers to when and in what manner individuals are expected to differ from (or be similar to) one another, interindividual differences. Precision in how research questions address these issues and the associated dimensions of the data-box can make the process of selecting appropriate statistical models more straightforward.

Organization across variables (x₁ to x_P)

Theoretical considerations that apply across the variables dimension of the data-box include the measurement of constructs and the organization of variables. As addressed in detail by Edwards and Wirth (this issue), developmentalists are often interested in how particular constructs change over time. To measure these constructs, researchers often make use of multiple items, reporters, or indicators – multiple columns in the data-box – and a theory of measurement that organizes and/or combines these items (columns) together. Important considerations include dimensionality, relevant indicators, relative weighting of those indicators, and the relative distances between response categories (cf. Nunnally & Bernstein, 1994). At another level of abstraction, developmentalists are also often interested in how, at a given age, variables are organized. For instance, based on theories of differentiation and de-differentiation over the life span (e.g., Baltes, Cornelius, Spiro, Nesselroade, & Willis, 1980; Garrett, 1946), one might ask, what is the structure of intellectual ability in old age? Is it characterized by many distinct abilities, by two higher-order abilities (e.g., fluid and crystallized), or a single, general ability (i.e., g)? The key point is that, in any given study, it is important to make explicit the underlying theoretical views and assumptions about how items or constructs are organized and operationalized (Meredith & Horn, 2001).

Organization across occasions(t₁ to t_T)

The occasions dimension brings a special, and often overlooked, organizing feature to the data-box. It provides a dimension along which data can (and must) be organized with respect to time. Because time proceeds in a forward manner, we can precisely place each datum within the space. For example, data obtained at younger ages can be placed to the “left” side of the box and data obtained at older ages placed to the “right” side of the box. Other possibilities include arranging boxes in relation to time of first-use, time of disease diagnosis, onset of puberty, etc. Once organized, the scores housed within a single horizontal slice of data can be examined for systematic patterns of intraindividual change over time (cf. Baltes & Nesselroade, 1979). Theoretical considerations of within-person change include predictions about when or at what age the changes begin, what the direction, shape (e.g., linear or nonlinear), and rate of change is, and when or at what ages the changes end or asymptote (Adolph et al., 2008; Baltes, Lindenberger, & Staudinger, 2006; Ford & Lerner, 1992; Hertzog & Nesselroade, 2003; Lerner, 1986; McArdle & Nesselroade, 2003; Wohlwill, 1973).

Organization across persons (i₁ to i_N)

In turn, we also carry expectations/hypotheses about the ways in which individuals (or entities) differ from one another – differential manifestation and organization of variables (e.g., factorial invariance) and/or differential trajectories of change (e.g., interindividual differences in rates or patterns of change). For example, individuals may differ in not only their level of function or ability at one occasion (e.g., intercept), but also in the rates at which they grow or decline across time (e.g., slopes), the “shape” of development, lead/lag associations and so on. Theoretical considerations include precisely which aspects of organization or change differ, how those differences are distributed, and whether the differences manifest as typologies (groups) or along a continuum, (e.g., Birren, 1959; Hertzog & Nesselroade, 2003; Bergman, Magnusson, & El-Khouri, 2003, Muthén & Muthén, 2000; Schroots & Yates, 1999).

Translating Theories to Models

When converted into a mathematical language, our theories of measurement/organization of variables, change (or development), and interindividual differences become models – the mathematical expressions that allow for statistical testing of theory against quantitative data. For example, along the occasions dimension, a theory of linear change might take the form of a regression model where age – or another time variable that is used to organize the occasions dimension (e.g., grade, time since puberty, or distance-to-death) – is used as a predictor of the repeated measurements of the construct of interest, η_ti,

$${\eta }_{\mathit{\text{ti}}}={\beta }_{\mathit{0}}+{\beta }_{\mathit{1}}{\mathit{\text{Age}}}_{\mathit{\text{it}}}+e_{\mathit{\text{ti}}}.$$ (1)

Applied to longitudinal data obtained from individual i across t = 1 to T occasions, the model allows for assessment of if and how his or her development is driven by the participant’s age at each assessment. Similarly, along the variables dimension, a theory about how the construct of interest was measured via p multiple indicators might be articulated via a common factor measurement model,

$$X_{\mathit{\text{ti}}}=\lambda {\eta }_{\mathit{\text{ti}}}+{\epsilon }_{\mathit{\text{ti}}},$$ (2)

where X, λ, and ε are vectors of length p. The model, in essence, articulates that individuals’ observed behaviors are driven by an unobservable construct of interest. A corresponding theory of interindividual differences might suggest between-person differences in the change trajectories, but not in how the construct was measured (i.e., measurement invariance). Here, three equations might be used to articulate the theory of organization along the persons dimension, two for capturing differences in change across occasions (i.e., in intercept and rate of change),

$${\beta }_{\mathit{0}i}={\gamma }_{\mathit{00}}+U_{\mathit{0}i}\mathit{,}\text{and}$$ (3)

$${\beta }_{\mathit{1}i}={\gamma }_{\mathit{10}}+U_{\mathit{1}i},$$ (4)

and one for capturing the across-person similarity in the organization of variables,

$${\mathit{\lambda }}_i=\mathit{\lambda }.$$ (5)

In combination, these three sets of models provide the opportunity to check if and how a set (or subset) of data are organized with respect to particular theories of measurement, change, and interindividual differences. The comprehensive statistical model tested against the data is thus built from the multiple parts. For example, combining the models above by placing one equation into another we get,

$$X_{\mathit{\text{ti}}}=\mathit{\lambda }[({\gamma }_{\mathit{00}}+U_{\mathit{0}i})+({\gamma }_{\mathit{10}}+U_{\mathit{1}i}){\mathit{\text{Age}}}_{\mathit{\text{ti}}}+e_{\mathit{\text{ti}}}]+{\mathit{\epsilon }}_{\mathit{\text{ti}}},$$ (6)

in principle, a complete, testable description of how the theory is expected to manifest in the data.

A Modular Approach for Model Construction

Mathematical functions can be used to describe many types of linear relationships, nonlinear relationships, directional (i.e., non-stationary) changes, reversible changes (e.g., stationary cycles), continuity and discontinuity of differences along continuous or categorical variables, and so on. Accordingly, a multitude of models are available for organizing each of the three dimensions: Measurement models include classical composite score models, factor analytic models, item response models, and models for censoring thresholds (i.e., ceilings and floors); change models include linear, quadratic, logistic, sinusoidal, auto-regressive, and latent difference trajectories of continuous change and event-history models of categorical change; and interindividual differences models might include categorization among known or unknown group differences, normally distributed differences, or differences aligned along a mixture of multiple distributions. Beyond these short lists, many many models are available – each of which invokes a particular theory about how data are organized along the three dimensions of the data-box.

In pursuing a particular research question, measurement, change, and individual differences are addressed simultaneously by (implicitly or explicitly) combining multiple models. For instance, in the example given above, a common factor measurement model was combined with a linear change model that articulated interindividual differences in two aspects of change (intercept and slope) along normally distributed continuums. Alternatively, item response measurement models might be combined with exponential models of change, and a model of interindividual differences that characterizes group-level differences, but within-group homogeneity. Of course, given the plethora of available models, many such combinations are possible – each of which articulates or implies a particular set of theories.

Example 1a

Consider the variety of models that could be used to examine if and how emotions rise and fall with the days of the week. In a series of studies, data obtained from 180 undergraduates who provided daily reports about how often they felt particular emotions were organized along the three dimensions of the data-box in different ways – each organization articulated a slightly different set of theories. In one study (Ram, Chow et al., 2005), participants’ responses to 16 items were organized theoretically into two latent variables, pleasant affect (PA: love, affection, caring, fondness, joy, happiness, contentment, and satisfaction) and unpleasant affect (depression, unhappiness, shame, nervousness, loneliness sadness, anxiety, and irritation), using an item response measurement model that accommodated unequal spacing between response categories (1 “never” to 7 “always” on a Likert-type scale). A theory of nonlinear change was invoked through a sinusoidal function (e.g., PA_t = R[cos(ωt) + ϕ]; cf. Warner, 1998) that described change over time in terms of the amplitude (extent of systematic fluctuation), frequency (speed of fluctuation), and phase shift (location of peaks and troughs, e.g., Monday Blues). The authors were particularly interested in individuals’ entrainment to a weekly cycle. Thus, the interindividual differences model was focused on a 7-day frequency. Specifically, frequency was taken as fixed across individuals, while other aspects of change (amplitude and phase shift) were theorized/assumed to differ across individuals along a normally distributed, continuous scale.

Example 1b

In another analysis of the same data set (Chow, Ram et al., 2004) the interest was in describing how regulatory processes might cause emotional fluctuations to diminish over time (cf. Boker, 2001). Participants’ responses to 24 items were organized theoretically into six latent variables (love, joy, sadness, fear, anger, and shame) using a common factor measurement model that accommodated unequal weighting of items. Interest in regulatory behavior wherein emotions oscillate as they return to equilibrium suggested change of the type exhibited by a swinging pendulum. A latent differential equation model was used to invoke a damped linear oscillator. Specifically, in line with physical models of a pendulum whose swinging slows and eventually stops, accelerations in the rate of change of the emotion were modeled as a function of current state and rate of change. Unlike Example 1a where interindividual differences in key aspects of the change function were theorized/assumed to be normally distributed (i.e., standard assumptions within a multilevel model of change), each individual’s change function was estimated independently, one individual at a time. The resulting model of interindividual differences allowed for the distribution of frequency and damping across persons to take any shape (skewed, kurtotic, bimodal, etc.).

Example 2a

In a separate investigation, data obtained from 400 older adults who provided yearly reports about their current level of life satisfaction were used to examine changes in life satisfaction occurring near the end of life (Gerstorf, Ram et al., 2008). The measurement theory and model used to organize the variables dimension was simplistic. Participants had responded to a single question on a 0 “very unsatisfied” to 10 “very satisfied” scale. These raw integer responses were taken as reliable “true” scores (i.e., X_ti = η_ti). Along the occasions dimension, theoretical models of terminal decline (see Bäckman & MacDonald, 2006) were invoked using a multi-phase model of change that empirically distinguished a ‘pre-terminal’ phase of decline from a ‘terminal’ phase of decline via spline regression (Cudeck & Harring, 2007). Interindividual differences in four features of change – rate of pre-terminal change (slope1), level of life satisfaction at the transition point (intercept), rate of terminal change (slope2), and timing of the transition (location) – were obtained simultaneously and assumed, via a standard multilevel model (i.e., Level 2 random effects), to follow a multivariate normal distribution.

Example 2b

Other models could be used to investigate the late-life changes in life-satisfaction manifest in this data – each combination of which would organize the dimensions of the data box in a different manner and operationalize a different set of theories and hypotheses. For example, an item response measurement model could be used to accommodate a theory about differential spacing between response categories (e.g., that the difference between a 2 and a 3 may be greater than the difference between a 5 and a 6). Alternatively, a threshold measurement model could be used to transform the 11-point response scale into a binary (yes/no) indicator of life satisfaction (cf. Nunnally & Bernstein, 1994). Alternative theories of change might suggest use of a single-phase quadratic model that allows for systematic acceleration in the rate of decline over time, or, in line with a cascade theory, use of a catastrophe model, wherein approaching a specific level of life satisfaction (as opposed to a location in time as above) precipitate a catastrophic decline (Birren, 1959; van der Maas & Molenaar, 1996). Interindividual differences might be distributed non-linearly, with individuals falling into two categories or classes – those who exhibit late-life declines (‘normal aging’), and those who maintain life satisfaction all the way until death (‘successful aging’). Such a typology of individual differences could be modeled using categorical latent variables within a mixture model (McLachlan & Peel, 2000). Another theory might be that the process of dying is homogenous – the only differences between-persons being when, in time, the process begins (e.g., asynchrony in onset; cf. puberty). The associated model of interindividual differences would allow for heterogeneity in onset, but impose between-person similarities among all other aspects of change.

In presenting these examples we have tried to make explicit the “modules” the authors selected and combined together, thereby highlighting three theoretical and methodological issues that might be considered when choosing analytical methods that are appropriately attuned to one’s hypotheses about (1) how multiple variables (items) are organized, (2) how and when individuals are expected to change, and (3) when and in what manner individuals are expected to differ from (or be similar to) one another. Considering in turn, how constructs are measured and operationalized (for further discussion see e.g., Edwards & Wirth), the expected timing and progression of within-person changes (Masyn; Selig & Preacher), and where and in what form the interindividual differences may be (see Grimm & Ram; Hoffman & Stawski), the data-box heuristic can be a useful tool for both assessing the assumptions and implications of a given research approach and selecting the appropriately aligned statistical models.

Methods for the Study of Development: Developing Methods

The articles in this special issue introduce and explore how contemporary longitudinal methods interface with the study of development. Each addresses multiple dimensions of the data box. Edwards and Wirth highlight the importance of sound measurement as a foundation for sound examinations of change. Hoffman and Stawski demonstrate the importance of separating within-person and between-person sources of variance for understanding processes of intraindividual change and the interindivdual differences therein. Grimm and Ram introduce a combined measurement, change, and categorical interindividual difference model for examining heterogeneity in development. Selig and Preacher illustrate the ways in which mediation models for longitudinal data accommodate both interindividual differences and change. Masyn shows how event history models for recurrent changes from state to state can be coupled with latent class models to examine unobserved heterogeneity of interindividual differences in developmental sequences. Together, the articles provide accessible explanations and demonstrations of a number of contemporary methodological tools. At the same time, the authors push the envelope to see what the future might hold – presenting views that might be considered ‘on the edge’ of what is currently possible, statistically or methodologically. In working through the papers, we encourage you to dance with them – to consider both how the methods might be used to test your own developmental theories, and if and how the ideas might prompt some new ideas for further inquiry. In doing so, we hope that you have as much fun as we are!