Abstract
Background
The majority of manual wheelchair users will experience upper extremity injuries or pain, in part due to the high force requirements, repetitive motion and extreme joint postures associated with wheelchair propulsion. Recent studies have identified cadence, contact angle and peak force as important factors for reducing upper extremity demand during propulsion. However, studies often make comparisons between populations (e.g., able-bodied vs. paraplegic) or do not investigate specific measures of upper extremity demand. The purpose of this study was to use a musculoskeletal model and forward dynamics simulations of wheelchair propulsion to investigate how altering cadence, peak force and contact angle influence individual muscle demand.
Methods
Forward dynamics simulations of wheelchair propulsion were generated to emulate group-averaged experimental data during four conditions: 1) self-selected propulsion technique, and while 2) minimizing cadence, 3) maximizing contact angle and 4) minimizing peak force using biofeedback. Simulations were used to determine individual muscle mechanical power and stress as measures of muscle demand.
Results
Minimizing peak force and cadence had the lowest muscle power requirements. However, minimizing peak force increased cadence and recovery power, while minimizing cadence increased average muscle stress. Maximizing contact angle increased muscle stress and had the highest muscle power requirements.
Interpretation
Minimizing cadence appears to have the most potential for reducing muscle demand and fatigue, which could decrease upper extremity injuries and pain. However, altering any of these variables to extreme values appears to be less effective; instead small to moderate changes may better reduce overall muscle demand.
Keywords: biofeedback, forward dynamics simulation, musculoskeletal model, biomechanics
INTRODUCTION
More than half of manual wheelchair users will develop upper extremity overuse injuries or pain during their lifetime, in part due to the high physical demand and repetitive nature of wheelchair propulsion (Finley and Rodgers, 2004; Sie et al., 1992). Studies have shown wheelchair users are exposed to at least three biomechanical factors associated with upper arm pathology: high force requirements, repetitive motion and extreme joint postures (Fay et al., 1999; Mercer et al., 2006; NIOSH, 1997; NRC, 2001). High forces are generated by muscles and applied to the handrim to propel the wheelchair, creating high intersegmental forces and joint moments that often exceed 50% of maximum achievable values (e.g., Dubowsky et al., 2008; Lin et al., 2009; Robertson et al., 1996; Sabick et al., 2004; van Drongelen et al., 2005b). The shoulder, elbow and wrist all undergo large ranges of motion during propulsion and, in some instances, are required to generate substantial forces at joint angles near the physiological limit (Rao et al., 1996; Shimada et al., 1998; Veeger et al., 1998). Wheelchair propulsion is also repetitive, with cadences (i.e. stroke rate) usually between 1.1 and 1.6 Hz (Boninger et al., 2002). Since wheelchair propulsion is still the most common method for providing mobility to this population, research is needed to understand the relationships between propulsion mechanics and upper extremity demand.
Recent studies have focused on reducing upper extremity demand during wheelchair propulsion by modifying wheelchair configuration and/or propulsion technique (e.g., Boninger et al., 2005; Bregman et al., 2009; Guo et al., 2006; Mulroy et al., 2005; van der Woude et al., 2003; Wei et al., 2003). Three variables related to propulsion technique (cadence, contact angle and peak force) have been shown to influence several quantities related to upper extremity demand, including mechanical efficiency (Lenton et al., 2009), joint moments (Richter, 2001; Robertson et al., 1996), EMG activity (Dubowsky et al., 2009) and nerve conduction (Boninger et al., 2005). The Paralyzed Veterans of America have also established propulsion technique guidelines in an effort to reduce upper extremity demand and injuries, which recommends wheelchair users incorporate long, smooth push strokes (i.e., large contact angles), reduce cadence and minimize peak handrim force (i.e., maximum applied handrim force) during propulsion (PVA, 2005).
However, few studies have directly investigated the influence of cadence, contact angle and peak force on specific measures of upper extremity demand using within-subject study designs, with most focusing on cadence. These studies found lower cadences increased mechanical efficiency and reduced self-reported perceived exertion measures, suggesting that lower demand is placed on the upper extremity (Goosey-Tolfrey and Kirk, 2003; Lenton et al., 2009). To our knowledge, only one study has investigated how altering contact angle influences wheelchair mechanics (using a single subject), but did not analyse specific measures of upper extremity demand (Rice et al., 2009). Potential reasons for the lack of studies may be due to the extreme difficulty in obtaining specific measures of upper extremity demand (e.g., muscle stress) or that longitudinal intervention studies can be confounded by other influences (e.g., physiological adaptation). Musculoskeletal modelling and simulation techniques provide an alternative method to quantify muscle demand without these potentially confounding effects, making the technique well-suited to systematically investigate different wheelchair propulsion strategies. Therefore, the purpose of this study was to use a detailed upper extremity musculoskeletal model and forward dynamics simulations of wheelchair propulsion to investigate how altering cadence, peak force and contact angle influence upper extremity muscle demand (i.e., muscle power and stress).
METHODS
Experimental Data
Data collection procedures have been previously described (Rankin et al., 2010; Richter et al., 2011) and will be summarized here. After obtaining informed consent, experimental data were collected from 13 wheelchair users (Table 1) as part of a larger study (Richter et al., 2011). Four conditions were performed on a wheelchair treadmill (Kwarciak et al., 2011) set to each subject’s self-selected speed determined prior to data collection. During three conditions, a custom built video biofeedback system provided real-time visual representation of a single propulsion technique variable (cadence, contact angle or peak force) and subjects were instructed to propel their own wheelchair with the assistance of the biofeedback to 1) minimize cadence, 2) maximize contact angle and 3) minimize peak force (Fig. 1). In the fourth condition, subjects were instructed to push with a self-selected technique without biofeedback (control condition). During each trial, right side shoulder, elbow and wrist kinematics were collected using an active marker set and a 3-camera motion capture system (Phoenix Technologies, Burnaby, BC, CA). Six degree-of-freedom handrim kinetics and wheel angle were collected using an OptiPush force sensing wheel (Guo et al., 2011; MAX Mobility, LLC, Antioch, TN, USA). EMG data were collected from the anterior, middle, and posterior deltoid, sternal pectoralis major, biceps brachii and long head triceps brachii using surface electrodes.
Table 1.
Individual subject attributes and experimentally obtained stroke characteristics, including subject pool average (standard deviation, SD). Because data were not available for all conditions for each subject, average data were calculated from 12, 9, 10 and 11 subjects for the Self-selected, Maximize Contact Angle, Minimized Peak Force and Minimize Cadence conditions, respectively.
| Subject Characteristics | Self-Selected | Experimental Stroke Characteristics | Min Cadence | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max Contact Angle | Min Peak Force | |||||||||||||||||||||
|
| ||||||||||||||||||||||
| Subject Number | Gender | Injury Level | Age (yrs) | Height (cm) | Mass (kg) | Time Since Injury (yrs) | Stroke Time (s) | Push Time (s) | Stroke Power (W) | Speed (m/s) | Stroke Time (s) | Push Time (s) | Stroke Power (W) | Speed (m/s) | Stroke Time (s) | Push Time (s) | Stroke Power (W) | Speed (m/s) | Stroke Time (s) | Push Time (s) | Stroke Power (W) | Speed (m/s) |
| 1 | M | T-8 | 37.1 | 172.7 | 75.6 | 14.1 | 1.18 | 0.47 | 11.00 | 1.13 | 1.88 | 0.53 | 11.05 | 1.13 | 1.05 | 0.42 | 11.36 | 1.11 | 2.74 | 0.52 | 13.87 | 1.13 |
| 2 | M | T11-T12 | 25.6 | 177.8 | 62.3 | 3.6 | 1.05 | 0.36 | 5.39 | 1.08 | - | - | - | - | - | - | - | - | - | - | - | - |
| 3 | M | T8 | 26.4 | 182.9 | 86.9 | 2.2 | 1.05 | 0.40 | 6.36 | 1.07 | 2.22 | 0.51 | 6.24 | 1.06 | 0.92 | 0.35 | 6.20 | 1.06 | 3.16 | 0.48 | 7.87 | 1.07 |
| 4 | F | L4-L5 | 24.4 | 162.6 | 48.4 | 24.4 | 1.88 | 0.45 | 5.18 | 0.99 | 2.30 | 0.55 | 5.54 | 0.97 | 0.89 | 0.31 | 5.89 | 0.98 | 4.02 | 0.52 | 6.60 | 0.99 |
| 5 | M | Spinal lipoma | 23.1 | 167.6 | 44.8 | 3.4 | 1.19 | 0.29 | 6.00 | 1.61 | - | - | - | - | - | - | - | - | 4.46 | 0.33 | 7.71 | 1.48 |
| 6 | M | T12 | 35.9 | 152.4 | 80.3 | 35.9 | - | - | - | - | 1.08 | 0.40 | 4.47 | 0.83 | 1.06 | 0.30 | 4.65 | 0.84 | 1.37 | 0.39 | 5.80 | 0.87 |
| 7 | M | T4 | 27.7 | 180.3 | 76.5 | 3.6 | 1.09 | 0.28 | 9.61 | 1.39 | 3.16 | 0.42 | 10.45 | 1.38 | - | - | - | - | - | - | - | - |
| 8 | M | L1 | 46.5 | 182.9 | 80.0 | 17.1 | 1.28 | 0.48 | 7.90 | 1.14 | 1.47 | 0.62 | 10.89 | 1.13 | 0.84 | 0.29 | 4.68 | 1.14 | 5.24 | 0.63 | 9.64 | 1.14 |
| 9 | M | T11-T12 | 38.5 | 185.4 | 69.6 | 21.9 | 1.19 | 0.33 | 6.76 | 1.25 | 3.01 | 0.49 | 7.77 | 1.26 | 1.32 | 0.38 | 6.10 | 1.25 | 6.99 | 0.49 | 7.21 | 1.35 |
| 10 | M | C6-C7 | 41.1 | 177.8 | 71.4 | 22.9 | 1.16 | 0.52 | 9.01 | 0.96 | 1.37 | 0.57 | 10.12 | 0.96 | 0.68 | 0.26 | 7.14 | 0.96 | 3.68 | 0.63 | 6.78 | 0.96 |
| 11 | M | L-1 | 38.0 | 180.3 | 75.2 | 7.3 | 1.11 | 0.47 | 5.11 | 0.83 | - | - | - | - | 1.10 | 0.42 | 4.75 | 0.81 | 5.54 | 0.62 | 4.19 | 0.82 |
| 12 | M | T-10 | 42.1 | 157.5 | 74.7 | 42.1 | 1.37 | 0.52 | 9.52 | 1.16 | 1.35 | 0.52 | 10.67 | 1.17 | 1.02 | 0.43 | 9.61 | 1.15 | 1.87 | 0.38 | 12.09 | 1.17 |
| 13 | F | Cerebral Palsy | 24.1 | 149.9 | 51.4 | 24.1 | 0.84 | 0.30 | 5.63 | 0.71 | 3.05 | 0.54 | 5.30 | 0.70 | 0.73 | 0.26 | 3.83 | 0.70 | 1.34 | 0.31 | 4.84 | 0.70 |
|
| ||||||||||||||||||||||
| Average (SD) | 33.12 (8.1) | 171.5 (12.3) | 69.0 (13.3) | 17.2 (13.1) | 1.20 (0.25) | 0.41 (0.09) | 7.29 (2.04) | 1.11 (0.24) | 2.09 (0.78) | 0.51 (0.06) | 7.67 (3.60) | 1 .06 (0.20) | 0.96 (0.19) | 0.34 (0.07) | 6.42 (2.38) | 1.00 (0.18) | 3.67 (1.81) | 0.48 (0.12) | 7.87 (2.95) | 1.06 (0.23) | ||
Fig. 1.
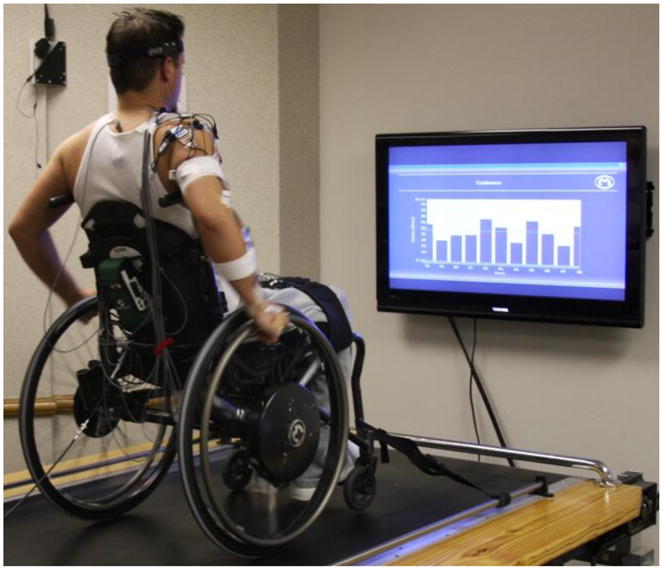
Custom built biofeedback system used to collect the experimental data. Subjects propelled their own wheelchair on a custom-made wheelchair treadmill and visual biofeedback was provided during each trial. Average, target (green line) and individual stroke (bars) values were provided to the subject.
Conditions were randomized and data were collected for at least 10 propulsion strokes per trial following an adaptation period that allowed subjects to acclimatize to each condition and reach steady-state. Each stroke began when the wheel axle torque exceeded 1Nm and ended at the start of the following stroke. The stroke was divided into push and recovery phases, with the push phase defined to be from the start of the stroke to the time when axle torque fell below the 1Nm threshold (Kwarciak et al., 2009). Individual subject stroke data were normalized to 101 points, with each point representing one percent of the stroke, using cubic-spline interpolation and averaged over all strokes. Subject mean data were then averaged across subjects to create representative biomechanical and electromyographic (EMG) profiles and standard deviations were calculated to assess inter-subject variability. Group-average data were used as an input to generate the forward dynamics simulations (described below).
Musculoskeletal Model
A detailed upper extremity musculoskeletal model and optimization framework for generating forward dynamics simulations of wheelchair propulsion described in detail elsewhere (Rankin and Neptune, 2010; Rankin et al., 2011) were used in this study. The model was developed using SIMM (Musculographics, Inc., Santa Rosa, CA, USA) based on the work of Holzbaur et al. (2005) and consisted of rigid segments that represent the trunk and right side upper arm, forearm and hand. Articulations between segments were defined by six rotational degrees of freedom representing trunk lean, shoulder plane of elevation, shoulder elevation angle (thoracohumeral angle), shoulder internal-external rotation, elbow flexion-extension and forearm pronation-supination. Trunk lean over the entire stroke and hand translations during the push phase were prescribed based on collected kinematic data. The model’s equations of motion were generated using SD/FAST (Parametric Technology Corp., Needham, MA, USA).
The model was driven by twenty-six Hill-type musculotendon actuators that represented the major upper extremity muscles of the shoulder and elbow (Rankin and Neptune, 2010). A total of twenty-two distinct excitation patterns controlled the musculotendon actuators, which were generated from a linear sum of four parameterized Henning patterns defined by twelve parameters. Musculotendon actuators corresponding with measured EMG data had excitation onset and offset timing constrained to match experimental values. Actuators with no available data were left unconstrained. Muscle excitation-activation dynamics were modeled using a first order differential equation (Raasch et al., 1997) with muscle-specific activation and deactivation time constants (Happee and Van der Helm, 1995; Winters and Stark, 1988).
Forward Dynamics Simulations
A global optimization algorithm (simulated annealing, Goffe et al., 1994) was used to generate four simulations, one representing their self-selected technique and three representing each of the biofeedback conditions (i.e., minimize cadence, maximize contact angle, minimize peak force). For each simulation, the algorithm identified the excitation pattern parameters that minimized differences between simulated and measured group-average stroke mechanics (i.e., joint kinematics and 3D handrim forces) using an optimal tracking cost function (Neptune et al., 2001). A second term was also included in the cost function that minimized the square of muscle stress to reduce co-contraction.
Analysis
To assure the simulations reached steady-state, consecutive propulsion strokes were simulated for each condition and data were analyzed during the second stroke. First, average differences between simulated and experimental data were determined for each condition in order to assess how well the simulation tracked the experimental data. The simulated stroke was then broken into two phases based on hand-handrim contact (i.e., push and recovery phases) and individual muscle data were obtained from the simulation for analysis. The ratio between instantaneous force and maximum isometric muscle force was calculated at each simulation time step to quantify muscle stress. Peak and average values were then determined for each muscle during the push phase, recovery phase and over the entire stroke. Instantaneous mechanical power was obtained for each muscle at each time step and mean positive (negative) power generation was calculated by averaging the instantaneous positive (negative) power within the two phases and over the entire stroke. Total (absolute value sum) and net (linear sum) mean power were calculated from the individual muscle data for each condition. Muscle data from each of the twenty-six muscles were combined into fifteen groups based on anatomical location: ADELT (anterior deltoid), MDELT (middle deltoid), PDELT (posterior deltoid), PECM (sternal and clavicular pectoralis major), CORB (corachobrachialis), LAT (three part latissimus dorsii), TMIN (teres minor), SUBSC (subscalularis), SUPSP (supraspinatus), INFSP (infraspinatus), BIC (long and short heads of biceps brachii), TRI (long, medial and lateral heads of the triceps brachii), BRD (brachioradialis), PQ (pronator quadrates, pronator teres) and SUP (supinator).
RESULTS
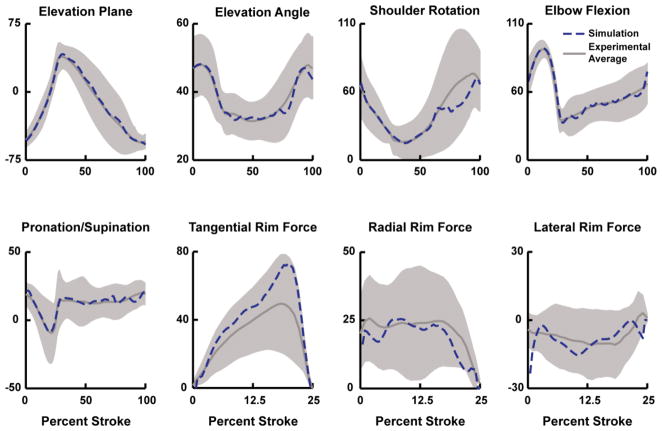
Simulations of all four conditions accurately reproduced the group-average experimental joint kinematics and handrim forces with average differences within one standard deviation of the experimental average, with the exception of the minimize cadence condition radial force (Fig. 2, Table 2).
Fig. 2.
Example comparison between the experimental and simulation kinematics and handrim kinetic data. Data are presented for the maximize contact angle condition, but all conditions had similar comparisons. Average experimental and simulation values are represented by solid and dashed lines, respectively. Shaded regions represent ± 1SD of the experimental data.
Table 2.
Root mean square (RMS) differences between the simulated joint kinematics and handrim forces and corresponding mean experimental value for each biofeedback condition. For comparison, one standard deviation (SD) of the experimental data is provided (in parentheses) to indicate inter-subject variability.
| Tracking Differences (Simulation vs. Experimental) | Biofeedback Condition
|
||||
|---|---|---|---|---|---|
| Self-Selected | Max Contact Angle | Min Peak Force | Min Cadence | ||
|
| |||||
| Joint Kinematics (degrees) | Elevation Plane | 1.7 (14.7) | 4.8 (20.5) | 2.5 (17.0) | 4.3 (18.7) |
| Elevation Angle | 0.3 (5.8) | 3.3 (7.7) | 0.4 (6.3) | 2.7 (7.7) | |
| Shoulder Rotation | 5.5 (15.5) | 9.1 (24.3) | 2.4 (14.3) | 4.5 (18.9) | |
| Elbow Flexion-Extension | 1.0 (13.0) | 5.4 (13.4) | 0.9 (10.8) | 4.3 (13.9) | |
| Pronation-Supination | 1.4 (12.4) | 2.5 (13.7) | 1.0 (12.4) | 2.8 (10.6) | |
|
| |||||
| All Joints | 2.0 (12.3) | 5.0 (15.9) | 1.5 (12.2) | 3.7 (14.0) | |
|
| |||||
| Handrim Forces (N) | Tangential | 2.57 (7.67) | 11.97 (17.15) | 6.49 (6.11) | 18.98 (20.78) |
| Radial | 3.80 (9.40) | 4.42 (15.51) | 3.44 (7.70) | 30.00 (27.71) | |
| Lateral | 1.16 (7.77) | 4.76 (12.47) | 1.36 (5.66) | 9.35 (17.93) | |
|
| |||||
| All Forces | 2.51 (8.28) | 7.05 (15.04) | 3.78 (6.50) | 19.45 (22.14) | |
Stroke Mechanics
The average simulation stroke power was similar across conditions and within one standard deviation of the experimental values, ranging from 6.4W–7.1W (Table 1 – Average Power; Table 3 – Handrim Power). Relative to the self-selected condition, the simulations of the maximize contact angle and minimize cadence conditions increased stroke time, push time and contact angle while the minimize peak force condition decreased push and stroke times and contact angle (Table 3). Minimizing peak force produced the lowest peak force generated to the handrim (37.7 N), while the minimize cadence condition generated the largest (115.7 N). There was a wide range of cadences across the four simulations, ranging from 0.36 Hz to 0.95 Hz (Table 3).
Table 3.
Simulated wheelchair stroke characteristics for each condition.
| Simulated Biofeedback Condition | Stroke Time (s) | Push Time (s) | Handrim Power (W) | Contact Angle (degrees) | Peak Force (N) | Cadence (Hz) |
|---|---|---|---|---|---|---|
| Self-Selected | 1.20 | 0.41 | 7.1 | 76.1 | 46.43 | 0.83 |
| Max Contact Angle | 2.09 | 0.53 | 6.8 | 83.9 | 74.44 | 0.48 |
| Min Peak Force | 0.96 | 0.35 | 6.4 | 63.5 | 37.65 | 1.04 |
| Min Cadence | 3.66 | 0.51 | 6.9 | 82.9 | 115.65 | 0.27 |
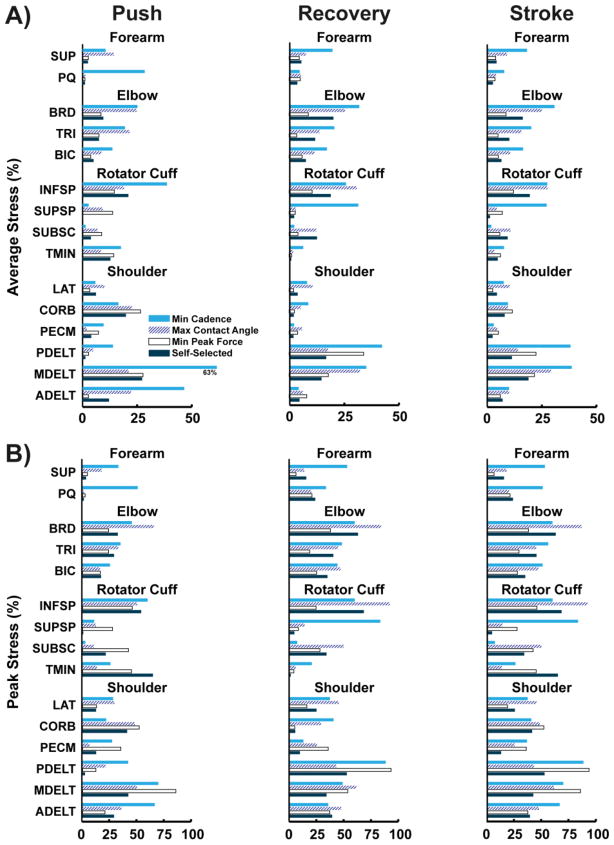
Muscle Stress
Total average muscle stress calculated from each simulation was similar between the push and recovery phases for all four conditions (Table 4). However, values varied across conditions, with the highest and lowest average stresses occurring in the minimize cadence and minimize peak force conditions, respectively (17.7% vs. 8.4%, Table 4). In general, individual muscle stress showed similar trends between the four conditions in that muscle groups with higher peak stress also had higher average stress (Fig. 3). For all conditions, the muscles crossing the elbow (BRD, TRI, BIC), MDELT, PDELT and INFSP had the largest average stress values over the entire stroke, with values exceeding 25% in many instances (Fig. 3). CORB, PECM and ADELT had higher average stresses during the push phase, while PDELT had higher average stress during the recovery phase (Fig. 3A). Both INFSP and MDELT had similar stress values between the two phases (Fig. 3). Peak stresses were more variable between simulated conditions, but at least one muscle had peak stress values greater than 50% in every condition (Fig. 3B). Relative to the other conditions, the minimize cadence condition had much higher peak stresses in the forearm muscles during both push and recovery phases and in supraspinatus during the recovery phase (SUP, PQ, SUPSP, Fig. 3).
Table 4.
Model-derived average muscle stress and power generation for each of the four simulated conditions. Values represent mean data from all muscles during the push phase (Push), recovery phase (Recovery) and entire propulsion stroke (Stroke). Net and Total Muscle Power represent the sum and absolute value sum, respectively, of the positive and negative powers.
| Simulated Biofeedback Condition
|
|||||
|---|---|---|---|---|---|
| Self-Selected | Max Contact Angle | Min Peak Force | Min Cadence | ||
|
| |||||
| Muscle Stress (%) | Push | 8.9 | 13.1 | 9.7 | 20.8 |
| Recovery | 8.2 | 12.3 | 7.7 | 17.1 | |
| Stroke | 8.5 | 12.5 | 8.4 | 17.7 | |
|
| |||||
| Positive Muscle Power (W) | Push | 40.9 | 65.8 | 32.1 | 98.9 |
| Recovery | 19.0 | 18.8 | 19.4 | 8.1 | |
| Stroke | 26.5 | 30.7 | 24.0 | 20.8 | |
|
| |||||
| Negative Muscle Power (W) | Push | 19.7 | 38.2 | 16.4 | 50.4 |
| Recovery | 16.5 | 17.5 | 14.5 | 7.4 | |
| Stroke | 17.6 | 22.7 | 15.2 | 13.4 | |
|
| |||||
| Total Muscle Power (W) | Push | 60.7 | 104.0 | 48.5 | 149.3 |
| Recovery | 35.5 | 36.3 | 33.9 | 15.5 | |
| Stroke | 44.1 | 53.4 | 39.3 | 34.1 | |
|
| |||||
| Net Muscle Power (W) | Push | 21.2 | 27.6 | 15.7 | 48.5 |
| Recovery | 2.5 | 1.3 | 4.9 | 0.8 | |
| Stroke | 8.9 | 8.0 | 8.8 | 7.4 | |
Fig. 3.
Individual muscle stress during the push phase, recovery phase and entire stroke obtained from the model during each of the simulated conditions. A) Average stress, and B) Peak stress. Note the average scale is half that of the peak stress.
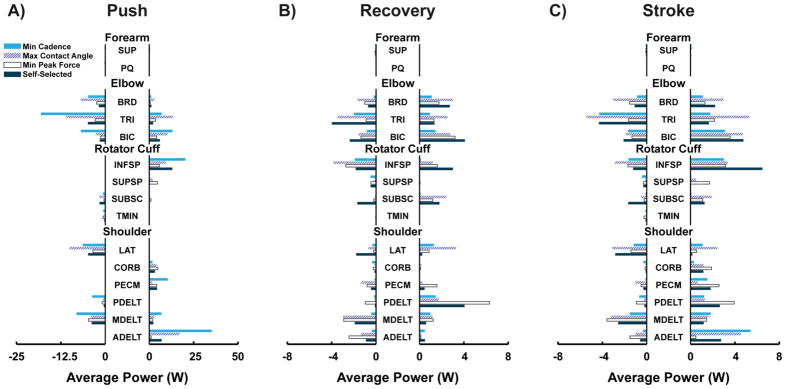
Net Muscle Power
Over the entire stroke, net (i.e., linear sum) muscle power varied between the four conditions, with the lowest power generated by the minimize cadence condition and the highest by the self-selected condition (7.4W vs. 8.9W, Table 4). Relative to the other conditions, the minimize cadence condition required the least amount of total (i.e., absolute value sum) muscle power to propel the wheelchair, while the maximize contact angle required the most (34.1W vs. 53.4W, Table 4). The push phase had large amounts of positive (active shortening) and negative (active lengthening) muscle power generation. However, the net power during the push phase was always positive and much greater than during the recovery phase (Fig. 4), with the smallest difference between phases occurring in the minimize peak force condition (15.7W vs. 4.9W, Table 4). For all conditions, the recovery phase had similar amounts of positive and negative muscle power, resulting in a large total and low net muscle power during this phase (Table 4).
Fig. 4.
Average positive and negative power generated by each muscle group in the model during the push phase (Push), recovery phase (Recovery) and entire stroke (Stroke) for each of the simulated conditions. Note the change in scale between A) and B).
Individual Muscle Power
The elbow flexors (BIC, BRD) and extensors (TRI) consistently generated a large amount of both positive and negative muscle power during the push and recovery phases in all four conditions, resulting in similar amounts of positive and negative power generation over the entire stroke (Fig. 4). INFSP, LAT and MDELT also generated large amounts of positive and negative muscle power over all conditions (Fig. 4C). However, their pattern of power generation was different than that of the elbow muscles. Similar to the elbow muscles, these muscles generated both positive and negative power during recovery (Fig. 4B). However, these muscles mainly generated either positive or negative power during the push phase, but not both (Fig. 4A). The forearm muscles did not consistently generate power (positive or negative) during the stroke (Fig. 4). Comparisons between conditions showed that the minimize cadence and maximize contact angle conditions increased ADELT, TRI and BIC power generation during the push phase relative to the other conditions (Fig 4A). SUPSP and PDELT power generation was higher in the minimize peak force condition, due to increased positive power generation during the push and recovery phase, respectively (Figs. 4A, C).
DISCUSSION
The optimization framework successfully identified muscle excitation patterns to generate simulations that emulated well the major biomechanical features of the group-average experimental data from all four conditions (Fig. 2, Tables 1–3). Muscle stress values for the self-selected condition were also generally consistent with previous EMG and static optimization studies. ADELT, MDELT and INFSP had high average stresses during the push phase (Fig. 3), which agreed with the high EMG activity and stress values reported by others (Lin et al., 2004; Mulroy et al., 2004; van Drongelen et al., 2005a; Veeger et al., 2002). In addition, average elbow flexor muscle stress was near 12% during the push, similar to the 8% value reported for the biceps by Veeger et al (2002) during similar power and speed conditions. During recovery MDELT and PDELT had high average stresses, also consistent with EMG observations (Mulroy et al., 2004).
Despite generating similar stroke power (Table 3), the simulations of the contact angle, cadence and peak force biofeedback conditions altered individual muscle stress and power generation (Figs. 3, 4), which are likely a result of wheelchair users employing different propulsion strategies when performing the diverse biofeedback tasks (Richter et al., 2011). Recent studies have shown biofeedback can help users change these three variables (de Groot et al., 2008; de Groot et al., 2002; Lenton et al., 2009; Rice et al., 2010). However, little is known about how changing these variables influence upper extremity demand, with the most relevant results correlating cadence with mechanical efficiency in able-bodied subjects (de Groot et al., 2008; Lenton et al., 2009). The present work builds on these previous studies by using modelling and simulation techniques to show how altering these variables influences specific measures of muscle demand (i.e., muscle stress and power), and thus their potential to influence the onset of overuse injuries and pain.
Muscle Power
Relative to the self-selected condition, simulations of the minimize cadence and peak force conditions showed a reduction in total muscle power during the stroke (Table 4), suggesting that these conditions have the greatest potential to reduce overall muscle mechanical demand. Others have found that lower cadences also increase mechanical efficiency (de Groot et al., 2008; Lenton et al., 2009), which could reduce muscle power demand and explain the lower power generated during this condition. In contrast, minimizing peak force increased cadence. However, individual muscle power requirements differed greatly between the two conditions.
When minimizing cadence, a large increase in positive power was generated by ADELT, PECM and INFSP during the push (Fig. 4). To balance this increase in push power, the simulation greatly reduced recovery muscle power (Table 4), with large decreases in MDELT, PDELT, BRD, TRI and BIC (Fig. 4). Because a division of labor exists between push and recovery phase muscles (Mulroy et al., 2004; Rankin et al., 2011), this pattern of muscle power generation (i.e., low cadence and recovery power) allows additional time for the major power producing muscles of the push phase to relax during recovery, likely reducing muscle fatigue. These findings are consistent with the current view that longer strokes reduce upper extremity demand (PVA, 2005). On the other hand, minimizing peak force decreased power generation by most muscles during the push phase, with the exception of SUPSP (Fig. 4). During recovery, negative ADELT and INFSP muscle power and positive and negative PDELT muscle power increased (Fig. 4). The increase in ADELT and INFSP negative muscle power is likely due to an insufficient deactivation time during the transition between the push and recovery phases as a result of the increased cadence. PDELT functions to retract the hand during recovery (Rankin et al., 2011) and increased power generation by this muscle is necessary due to the higher demands associated with increased segment velocities and accelerations during recovery (Lenton et al., 2009).
Similar to the minimize cadence condition, maximizing contact angle also reduced push cadence relative to the self-selected condition. However, this condition had the highest total muscle power (Table 4) due to increased negative LAT, positive ADELT, and positive and negative elbow muscle power during the push phase and increased power generation in the elbow muscles and LAT during recovery (Fig. 4). The high muscle power requirements may be because maximizing contact angle resulted in the most extreme joint postures that require users to generate power in non-optimal joint configurations. This increases the need for co-contraction during the push phase and requires relocation of the hand to a difficult location during the recovery phase. Thus, encouraging users to maximize push angle does not appear to be an effective technique to reduce muscle demand. However, smaller changes in push angle would reduce the extreme joint postures observed and may prove effective in reducing demand.
Muscle Stress
Despite the promising reduction in muscle power requirements when minimizing cadence, net muscle stress was higher relative to the self-selected condition (Table 4). Minimizing cadence produced the highest peak handrim force (115.65N, Table 3), which greatly exceeds the 39N value suggested to be an upper limit to minimize injury during a repetitive task (Silverstein et al., 1987). Higher handrim forces also result in increased intersegmental moments (Finley et al., 2004) that require higher muscle forces. This effect was evident in PQ, which had high average and peak muscle stresses (>25% and >50%, respectively, Fig. 2). PQ acts isometrically to transfer power between the arm and the handrim during the push phase (Rankin et al., 2011). As a result, higher handrim power requirements will require higher PQ muscle force and increase muscle stress. Wrist muscle function is likely similar (i.e., to transfer power) resulting in similar increases in stress consistent with the findings of Boninger et al (2005) that high handrim forces are associated with wrist injury in wheelchair users. During recovery, both SUPSP and PDELT had large average stresses (>25%, Fig. 3B). Again, these muscles are likely acting isometrically at some point during recovery, as the long recovery time will likely allow the users to slow down or pause when retracting their arm to delay the start of the next push phase. High activity in SUPSP is a particular concern as this muscle has been identified by others to be particularly susceptible to injury (e.g., Mulroy et al., 2004).
Average muscle stress in the peak force condition was the lowest of all the conditions (Table 4). Although net muscle power was reduced when minimizing peak force, this condition increased the stress in three rotator cuff muscles (SUPSP, SUBSC, TMIN), with average and peak stresses greater than 15% and 25%, respectively (Fig. 3). PECM stress also increased, which has high excitation intensities during the push phase (e.g., Mulroy et al., 2004). Therefore, minimizing peak force likely increases the potential for injury to muscles that already have high incidences of pain and injury (e.g., Finley and Rodgers, 2004). Small differences in muscle stress occurred during the recovery phase relative to the self-selected condition except for PDELT average stress, which increased greatly to exceed 25% (Fig. 3). This condition also had a cadence three times faster than the minimize cadence condition (Table 3), which would reduce relaxation time for muscles under high stress and likely increase fatigue. The high cadence and elevated muscle stress during the push phase likely outweigh any positive effects from the reduced peak handrim force and muscle power generation.
Previous studies have observed that contact angle, cadence and peak force are not independent because they are coupled through stroke power requirements (Rice et al., 2010; Richter et al., 2011). For a given speed, the same amount of power must be applied to the handrim to overcome external loads during each stroke. A decrease in cadence reduces hand-handrim contact time relative to total stroke time, which increases push phase power requirements to maintain a constant average stroke power. To compensate, one must either increase handrim forces or increase contact angle (increasing hand-handrim contact time) to generate more power. In extreme cases, such as the minimize cadence condition, increasing both peak force and contact angle are necessary to produce sufficient power to satisfy external power requirements. Therefore, investigating how each of these variables independently influence muscle demand to determine the optimal propulsion technique is difficult. Purely theoretical studies that alter each variable while holding other quantities constant or optimize all three variables simultaneously to minimize different measures of muscle demand may better isolate each variable’s influence on demand and provide novel insight into how to optimize propulsion technique to minimize muscle demand.
Although this study provided insight in how specific feedback variables influence upper extremity muscle demand, there are some potential limitations. First, the musculoskeletal model in this study incorporated a fixed wrist, which prevented the generation of free moments on the handrim. However, this moment is generally small relative to the elbow and shoulder moments and should not change the study conclusions (e.g., Robertson et al., 1996; Sabick et al., 2004). Also, the musculoskeletal model used in this study was a generic model that represented a healthy 50th percentile male while the experimental data were averaged across a group of wheelchair users. Previous studies have shown that self-selected muscle activity and push techniques can vary between users (e.g., Finley et al., 2004; Mulroy et al., 2004). However, regardless of self-selected technique, the different biofeedback conditions elicited similar responses in all users (Richter et al., 2011) and the present study used a consistent model to investigate relative changes in muscle demand between the conditions. Therefore, the influence of using a generic model on the relative changes in muscle demand is expected to be minimal. Last, only maximal changes in the three variables were investigated to infer their influence on muscle demand. However, maximal changes may not be optimal. In addition, future longitudinal studies should assess whether improvements can be made in these variables and sustained over time and whether combinations of sub-maximal values of these variables may be more effective in reducing muscle demand.
CONCLUSION
Using cadence, peak force and contact angle as biofeedback variables influences upper extremity muscle demand. However, determining the specific influence each variable has on muscle demand is challenging because the three variables are not independent. The minimize peak force condition had low muscle power generation and net muscle stress. However, some individual muscles still had high peak and average stresses which, combined with the increased cadence of this condition, may negate the positive effects of lower muscle power generation on muscle demand. The maximize contact angle condition had the highest muscle power requirements over the entire stroke and a higher average muscle stress relative to the self-selected and peak force conditions, and therefore increased muscle demand. Although average muscle stress was higher in the minimize cadence condition, peak muscle stresses were similar to the other conditions and total muscle power required was reduced. Muscle power requirements during the long recovery phase were especially low, indicating that muscles were able to relax and reduce the need for continuous, elevated muscle force. Therefore, instructing users to reduce cadence appears to have the most potential for reducing muscle demand and fatigue, which may decrease the likelihood of developing upper extremity injuries and pain. However, in all cases, altering these variables to extreme values appears to be less effective; instead small to moderate changes may produce better reductions in overall muscle demand. Investigating this premise remains an important area for future work.
Acknowledgments
This work was supported by NIH grant R01HD053732. The contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH, National Institute of Child Health and Human Development (NICHD).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Boninger ML, Koontz AM, Sisto SA, Dyson-Hudson TA, Chang M, Price R, Cooper RA. Pushrim biomechanics and injury prevention in spinal cord injury: recommendations based on CULP-SCI investigations. Journal of Rehabilitation Research and Development. 2005;42(3 Suppl 1):9–19. doi: 10.1682/jrrd.2004.08.0103. [DOI] [PubMed] [Google Scholar]
- Boninger ML, Souza AL, Cooper RA, Fitzgerald SG, Koontz AM, Fay BT. Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 2002;83(5):718–723. doi: 10.1053/apmr.2002.32455. [DOI] [PubMed] [Google Scholar]
- Bregman DJ, Drongelen SV, Veeger HE. Is effective force application in handrim wheelchair propulsion also efficient? Clinical Biomechanics. 2009;24(1):13–19. doi: 10.1016/j.clinbiomech.2008.09.003. [DOI] [PubMed] [Google Scholar]
- de Groot S, de Bruin M, Noomen SP, van der Woude LH. Mechanical efficiency and propulsion technique after 7 weeks of low-intensity wheelchair training. Clinical Biomechanics. 2008 doi: 10.1016/j.clinbiomech.2007.11.001. [DOI] [PubMed] [Google Scholar]
- de Groot S, Veeger DH, Hollander AP, Van der Woude LH. Wheelchair propulsion technique and mechanical efficiency after 3 weeks of practice. Medicine and Science in Sports and Exercise. 2002;34(5):756–766. doi: 10.1097/00005768-200205000-00005. [DOI] [PubMed] [Google Scholar]
- Dubowsky SR, Rasmussen J, Sisto SA, Langrana NA. Validation of a musculoskeletal model of wheelchair propulsion and its application to minimizing shoulder joint forces. Journal of Biomechanics. 2008;41(14):2981–2988. doi: 10.1016/j.jbiomech.2008.07.032. [DOI] [PubMed] [Google Scholar]
- Dubowsky SR, Sisto SA, Langrana NA. Comparison of kinematics, kinetics, and EMG throughout wheelchair propulsion in able-bodied and persons with paraplegia: an integrative approach. Journal of Biomechanical Engineering. 2009;131(2):021015. doi: 10.1115/1.2900726. [DOI] [PubMed] [Google Scholar]
- Fay BT, Boninger ML, Cooper RA, Baldwin MA, Koontz AM. Wrist Kinematics and Indicators of Carpal Tunnel Syndrome During Manual Wheelchair Propulsion. Proceedings of The First Joint BMES/EMBS Conference Serving Humanity, Advancing Technology; Atlanta, GA. 1999. [Google Scholar]
- Finley MA, Rasch EK, Keyser RE, Rodgers MM. The biomechanics of wheelchair propulsion in individuals with and without upper-limb impairment. Journal of Rehabilitation Research and Development. 2004;41:385–394. doi: 10.1682/jrrd.2004.03.0385. [DOI] [PubMed] [Google Scholar]
- Finley MA, Rodgers MM. Prevalence and identification of shoulder pathology in athletic and nonathletic wheelchair users with shoulder pain: A pilot study. Journal of Rehabilitation Research and Development. 2004;41(3B):395–402. doi: 10.1682/jrrd.2003.02.0022. [DOI] [PubMed] [Google Scholar]
- Goffe WL, Ferrier GD, Rogers J. Global Optimization of Statistical Functions With Simulated Annealing. Journal of Econometrics. 1994;60:65–99. [Google Scholar]
- Goosey-Tolfrey VL, Kirk JH. Effect of push frequency and strategy variations on economy and perceived exertion during wheelchair propulsion. European Journal of Applied Physiology. 2003;90(1–2):154–158. doi: 10.1007/s00421-003-0875-6. [DOI] [PubMed] [Google Scholar]
- Guo L, Kwarciak AM, Rodriguez R, Sarkar N, Richter WM. Validation of a Biofeedback System for Wheelchair Propulsion Training. Rehabilitation Research and Practice. 2011;2011:Article ID 590780. doi: 10.1155/2011/590780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo LY, Su FC, An KN. Effect of handrim diameter on manual wheelchair propulsion: mechanical energy and power flow analysis. Clinical Biomechanics. 2006;21(2):107–115. doi: 10.1016/j.clinbiomech.2005.08.015. [DOI] [PubMed] [Google Scholar]
- Happee R, Van der Helm FC. The control of shoulder muscles during goal directed movements, an inverse dynamic analysis. Journal of Biomechanics. 1995;28(10):1179–1191. doi: 10.1016/0021-9290(94)00181-3. [DOI] [PubMed] [Google Scholar]
- Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Annals of Biomedical Engineering. 2005;33(6):829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- Kwarciak AM, Sisto SA, Yarossi M, Price R, Komaroff E, Boninger ML. Redefining the Manual Wheelchair Stroke Cycle: Identification and Impact of Nonpropulsive Pushrim Contact. Archives of Physical Medicine and Rehabilitation. 2009;90(1):20–26. doi: 10.1016/j.apmr.2008.07.013. [DOI] [PubMed] [Google Scholar]
- Kwarciak AM, Turner JT, Guo L, Richter WM. Comparing handrim biomechanics for treadmill and overground wheelchair propulsion. Spinal Cord. 2011;49(3):457–462. doi: 10.1038/sc.2010.149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenton JP, van der Woude L, Fowler N, Goosey-Tolfrey V. Effects of arm frequency during synchronous and asynchronous wheelchair propulsion on efficiency. International Journal of Sports Medicine. 2009;30(4):233–239. doi: 10.1055/s-0028-1105949. [DOI] [PubMed] [Google Scholar]
- Lin CJ, Lin PC, Su FC, An KN. Biomechanics of Wheelchair Propulsion. Journal of Mechanics in Medicine and Biology. 2009;9(2):229–242. [Google Scholar]
- Lin HT, Su FC, Wu HW, An KN. Muscle forces analysis in the shoulder mechanism during wheelchair propulsion. Proceedings of the Institution of Mechanical Engineers Part H-Journal of Engineering in Medicine. 2004;218(H4):213–221. doi: 10.1243/0954411041561027. [DOI] [PubMed] [Google Scholar]
- Mercer JL, Boninger M, Koontz A, Ren D, Dyson-Hudson T, Cooper R. Shoulder joint kinetics and pathology in manual wheelchair users. Clinical Biomechanics. 2006;21(8):781–789. doi: 10.1016/j.clinbiomech.2006.04.010. [DOI] [PubMed] [Google Scholar]
- Mulroy SJ, Farrokhi S, Newsam CJ, Perry J. Effects of spinal cord injury level on the activity of shoulder muscles during wheelchair propulsion: an electromyographic study. Archives of Physical Medicine and Rehabilitation. 2004;85(6):925–934. doi: 10.1016/j.apmr.2003.08.090. [DOI] [PubMed] [Google Scholar]
- Mulroy SJ, Newsam CJ, Gutierrez DD, Requejo P, Gronley JK, Haubert LL, Perry J. Effect of fore-aft seat position on shoulder demands during wheelchair propulsion: part 1. A kinetic analysis. The Journal of Spinal Cord Medicine. 2005;28(3):214–221. doi: 10.1080/10790268.2005.11753815. [DOI] [PubMed] [Google Scholar]
- National Institue for Occupational Safety and Health. Musculoskeletal Disorders and Workplace Factors: A Critical Review of Epidemiology for Work Related Musculoskeletal Disorders of the Neck, Upper Extremity, and Low Back. Cincinnati, OH: 1997. [Google Scholar]
- National Research Council . Musculoskeletal Disorders and the Workplace: Low Back and Upper Extremities. National Academies Press; Washington, DC: 2001. [PubMed] [Google Scholar]
- Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. Journal of Biomechanics. 2001;34(11):1387–1398. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
- Paralyzed Veterans of America. Preservation of upper limb function following spinal cord injury: a clinical practice guideline for health-care professionals. Washington (DC): 2005. Consortium for Spinal Cord Medicine. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raasch CC, Zajac FE, Ma B, Levine WS. Muscle coordination of maximum-speed pedaling. Journal of Biomechanics. 1997;30(6):595–602. doi: 10.1016/s0021-9290(96)00188-1. [DOI] [PubMed] [Google Scholar]
- Rankin JW, Kwarciak AM, Richter WM, Neptune RR. The Influence of Altering Push Force Effectiveness on Upper Extremity Demand during Wheelchair Propulsion. Journal of Biomechanics. 2010;43(14):2771–2779. doi: 10.1016/j.jbiomech.2010.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rankin JW, Neptune RR. The Influence of Seat Configuration on Maximal Average Crank Power during Pedaling: A Simulation Study. Journal of Applied Biomechanics. 2010 doi: 10.1123/jab.26.4.493. [DOI] [PubMed] [Google Scholar]
- Rankin JW, Richter WM, Neptune RR. Individual muscle contributions to push and recovery subtasks during wheelchair propulsion. J Biomech. 2011;44(7):1246–1252. doi: 10.1016/j.jbiomech.2011.02.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SS, Bontrager EL, Gronley JK, Newsam CJ, Perry J. Three-dimensional kinematics of wheelchair propulsion. IEEE Transactions on Rehabilitation Engineering. 1996;4(3):152–160. doi: 10.1109/86.536770. [DOI] [PubMed] [Google Scholar]
- Rice I, Gagnon D, Gallagher J, Boninger M. Hand rim wheelchair propulsion training using biomechanical real-time visual feedback based on motor learning theory principles. J Spinal Cord Med. 2010;33(1):33–42. doi: 10.1080/10790268.2010.11689672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice I, Impink B, Niyonkuru C, Boninger M. Manual wheelchair stroke characteristics during an extended period of propulsion. Spinal Cord. 2009;47(5):413–417. doi: 10.1038/sc.2008.139. [DOI] [PubMed] [Google Scholar]
- Richter WM. The effect of seat position on manual wheelchair propulsion biomechanics: a quasi-static model-based approach. Medical Engineering and Physics. 2001;23(10):707–712. doi: 10.1016/s1350-4533(01)00074-1. [DOI] [PubMed] [Google Scholar]
- Richter WM, Kwarciak AM, Guo L, Turner JT. Effects of single-variable biofeedback on wheelchair handrim biomechanics. Arch Phys Med Rehabil. 2011;92(4):572–577. doi: 10.1016/j.apmr.2010.11.001. [DOI] [PubMed] [Google Scholar]
- Robertson RN, Boninger ML, Cooper RA, Shimada SD. Pushrim forces and joint kinetics during wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 1996;77(9):856–864. doi: 10.1016/s0003-9993(96)90270-1. [DOI] [PubMed] [Google Scholar]
- Sabick MB, Kotajarvi BR, An KN. A new method to quantify demand on the upper extremity during manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 2004;85(7):1151–1159. doi: 10.1016/j.apmr.2003.10.024. [DOI] [PubMed] [Google Scholar]
- Shimada SD, Robertson RN, Bonninger ML, Cooper RA. Kinematic characterization of wheelchair propulsion. Journal of Rehabilitation Research and Development. 1998;35(2):210–218. [PubMed] [Google Scholar]
- Sie IH, Waters RL, Adkins RH, Gellman H. Upper extremity pain in the postrehabilitation spinal cord injured patient. Archives of Physical Medicine and Rehabilitation. 1992;73:44–48. [PubMed] [Google Scholar]
- Silverstein B, Fine L, Stetson D. Hand-wrist disorders among investment casting plant workers. J Hand Surg Am. 1987;12(5 Pt 2):838–844. doi: 10.1016/s0363-5023(87)80245-9. [DOI] [PubMed] [Google Scholar]
- van der Woude LH, Formanoy M, de Groot S. Hand rim configuration: effects on physical strain and technique in unimpaired subjects? Medical Engineering & Physics. 2003;25(9):765–774. doi: 10.1016/s1350-4533(03)00102-4. [DOI] [PubMed] [Google Scholar]
- van Drongelen S, van der Woude LH, Janssen TW, Angenot EL, Chadwick EK, Veeger DH. Glenohumeral contact forces and muscle forces evaluated in wheelchair-related activities of daily living in able-bodied subjects versus subjects with paraplegia and tetraplegia. Archives of Physical Medicine and Rehabilitation. 2005a;86(7):1434–1440. doi: 10.1016/j.apmr.2005.03.014. [DOI] [PubMed] [Google Scholar]
- van Drongelen S, van der Woude LH, Janssen TW, Angenot EL, Chadwick EK, Veeger DH. Mechanical load on the upper extremity during wheelchair activities. Archives of Physical Medicine and Rehabilitation. 2005b;86(6):1214–1220. doi: 10.1016/j.apmr.2004.09.023. [DOI] [PubMed] [Google Scholar]
- Veeger HE, Meershoek LS, van der Woude LH, Langenhoff JM. Wrist motion in handrim wheelchair propulsion. Journal of Rehabilitation Research and Development. 1998;35(3):305–313. [PubMed] [Google Scholar]
- Veeger HE, Rozendaal LA, van der Helm FC. Load on the shoulder in low intensity wheelchair propulsion. Clinical Biomechanics. 2002;17(3):211–218. doi: 10.1016/s0268-0033(02)00008-6. [DOI] [PubMed] [Google Scholar]
- Wei SH, Huang S, Jiang CJ, Chiu JC. Wrist kinematic characterization of wheelchair propulsion in various seating positions: implication to wrist pain. Clinical Biomechanics. 2003;18(6):S46–52. doi: 10.1016/s0268-0033(03)00084-6. [DOI] [PubMed] [Google Scholar]
- Winters JM, Stark L. Estimated mechanical properties of synergistic muscles involved in movements of a variety of human joints. Journal of Biomechanics. 1988;21(12):1027–1041. doi: 10.1016/0021-9290(88)90249-7. [DOI] [PubMed] [Google Scholar]