Competence with Fractions Predicts Gains in Mathematics Achievement

Abstract

Competence with fractions predicts later mathematics achievement, but the co-developmental pattern between fractions knowledge and mathematics achievement is not well understood. We assessed this co-development through examination of the cross-lagged relation between a measure of conceptual knowledge of fractions and mathematics achievement in sixth and seventh grade (n = 212). The cross-lagged effects indicated that performance on the sixth grade fractions concepts measure predicted one year gains in mathematics achievement (β = .14, p<.01), controlling for the central executive component of working memory and intelligence, but sixth grade mathematics achievement did not predict gains on the fractions concepts measure (β = .03, p>.50). In a follow-up assessment, we demonstrated that measures of fluency with computational fractions significantly predicted seventh grade mathematics achievement above and beyond the influence of fluency in computational whole number arithmetic, performance on number fluency and number line tasks, and central executive span and intelligence. Results provide empirical support for the hypothesis that competence with fractions underlies, in part, subsequent gains in mathematics achievement.

The National Mathematics Advisory Panel (NMAP, 2008) concluded conceptual understanding of fractions and fluency in using procedures to solve fractions problems are central goals of children’s mathematical development (see Siegler, Thompson, & Schneider, 2011). The NMAP also determined that these competencies provide the critical foundation for algebra learning. Although this determination follows logically from the mathematical structure of algebra, there is not a strong empirical link between fractions competence and ease of learning algebra or other complex forms of mathematics. The best available evidence is provided by Siegler et al.’s (in press) analyses of nationally representative data sets from the United States and United Kingdom that demonstrated competence with fractions in fifth or sixth grade predicted performance on algebra and mathematics achievement tests five or six years later, controlling for whole number arithmetic, intelligence, working memory, family background, and other factors. The results support the NMAP’s focus on the importance of children gaining competence with fractions before taking high school algebra.

However, it cannot be definitively concluded that fractions competence at the end of elementary school contributed to subsequent gains in mathematics achievement without simultaneously controlling for general mathematics achievement at the end of elementary school and fractions competence in high school; these assessments were not available in the data bases analyzed by Siegler et al. (in press). It is possible that this is the case, but an alternative (not mutually exclusive) hypothesis for the longitudinal association between fractions knowledge and mathematical achievement is that children with a firm grasp of basic mathematical concepts, as indicated by high initial mathematical achievement, will more easily understand and learn to solve fractions problems. Our first goal was to provide such a cross-lagged assessment of the relations between fractions knowledge and mathematics achievement across sixth and seventh grade. If fractions competence contributes to gains in mathematics achievement, then sixth grade fractions knowledge will predict seventh grade mathematics achievement, controlling for seventh grade fractions knowledge, sixth grade mathematics achievement, and working memory and intelligence (Geary, 2011).

The second goal was to determine if measures of conceptual knowledge of fractions and computational fractions skills concurrently predict mathematics achievement, controlling for other factors. As noted, Siegler et al. (in press) demonstrated that fractions competence at the end of elementary school predicted later mathematics achievement, controlling for whole number arithmetic, working memory, and intelligence. In another study, Siegler and colleagues (Siegler, et al., 2011) reported significant correlations among a measure of fractions magnitude comparison, the ability to accurately place fractions on a number line, and mathematics achievement in sixth and eighth graders. After controlling for the conceptual fractions measures, the effect of fluency with fractions computations was not significant for either sixth or eighth graders, although both samples were small (n = 24) and they did not control for working memory or intelligence (see Hecht, 1998; Hecht, Close, & Santisi, 2003).

The current study provided a more comprehensive assessment of the importance of fractions competencies and concurrent mathematics achievement by first controlling for computational skills in whole number arithmetic, more basic number skills, and working memory and intelligence. Second, we examined the extent to which fractions competence also predicted word reading skills. Although Siegler et al. (in press) demonstrated that fractions competence predicts mathematical achievement significantly better than it predicts literacy measures, we attempt to replicate this finding and extend it by including a measure of knowledge of fractions concepts. A finding that fractions measures predict word reading would suggest these measures are proxies for more general cognitive abilities (e.g., working memory) and thus weaken the argument that it is competence with fractions in particular that is critical to mathematics achievement.

Method

Participants

The participants are from a longitudinal study of mathematical development (see Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007). For the original sample, 288 children completed the first year and during the fifth year 22 children were added to the study; they scored below the 30^th percentile on the State of Missouri mathematics assessment and were thus considered at risk for poor long-term mathematics outcomes. These current analyses are based on the 212 children (192 from the original and 20 from the second sample) who completed at least two of the tasks described below. For the cross lagged analysis, all available data were used, with missing data estimated in Mplus version 6.0 (Muthén & Muthén, 1998–2010), using full information maximum likelihood.

At the end of first grade, the mean intelligence of the 192 children from the original sample was average (M = 102, SD = 15) based on the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999), and that of the fifth grade sample was comparable (M = 97, SD = 10; t[207] = 1.5, p = .14). The mean age was 86 (SD = 4) months at the time of the first assessment (spring, first grade) and 158 (SD = 4) months at the time of the last assessment (spring, seventh grade). Girls composed 56% of the total sample, and 74% were White; the remaining children were Black (7%), Asian (5%), or more than one race (9%), with the parents of 5% of the children identifying them as Native American, Pacific Islander, or unknown. Across racial categories, 4% of the sample identified as ethnically Hispanic. The schools from which the samples were drawn were socioeconomically diverse.

Standardized Measures

Intelligence

The Vocabulary and Matrix Reasoning subtests of the WASI were administered and used to estimate full scale IQ (Wechsler, 1999).

Achievement

Mathematics and reading achievement were assessed using the Numerical Operations and Word Reading subtests from the Wechsler Individual Achievement Test-II-Abbreviated (Wechsler, 2001), respectively. For the grades assessed here, the Numerical Operations items include multi-digit addition and subtraction, multiplication and division, rational number, and simple algebra problems solved with pencil-and-paper. The Word Reading items assess accuracy of reading increasingly difficult words.

Working Memory

The Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) consists of nine subtests that assess the central executive, phonological loop, and visuospatial sketchpad. All of the subtests have six items at each span level. Across subtests, the span levels range from one to six to one to nine. Passing four items at one level moves the child to the next. At each span level, the number of items to be remembered is increased by one. Failing three items at one span level terminates the subtest. The battery was administered in first and fifth grade, but the focus here is on fifth grade central executive span scores (age of testing, M = 128 months, SD = 5). These scores were used because they are from the most recent assessment relative to the outcome of interest, and because central executive measures are more consistently related to arithmetic development than are measures of the phonological loop or visuospatial sketch pad (Geary, Hoard, & Nugent, in press; Geary et al., 2007).

The central executive is assessed using three dual-task subtests. Listening Recall requires the child to determine if a sentence is true or false, and then recall the last word in a series of sentences. Counting Recall requires the child to count a set of 4, 5, 6, or 7 dots on a card, and then at the end of the series, to recall the number of counted dots on each card. Backward Digit Recall is a standard format backward digit span. The score was the sum across these three subtests (α = .62).

Mathematical Tasks

Number sets

The test assessed fluency of reprenting and adding magnitudes associated with sets of objects and Arabic numerals. Two types of stimuli are used: objects (e.g., squares) in a 1/2″ square and an Arabic numeral (18 pt font) in a 1/2″ square. Stimuli are joined in domino-like rectangles with different combinations of objects and numerals (some rectangles include only objects, some include only numerals, and some include both), with 36 items on each of two pages for the target sums of 5 and 9 (Geary, Bailey, & Hoard, 2009). The tester begins by explaining two items matching a target sum of 4; then, uses the target sum of 3 for practice. The measure is then administered. The child is told to move across each line of the page from left to right without skipping any; to “circle any groups that can be put together to make the top number, 5 (9)”; and to “work as fast as you can without making many mistakes.” The child has 60 sec per page for the target 5; 90 sec per page for the target 9. Performance is consistent across target number and item content (e.g., whether the rectangle included Arabic numerals or shapes) and thus the scores were combined to create an overall frequency of hits (alpha, α = .88) and false alarms (α = .90; Geary et al., 2007).

The variable used here was based on the d-prime measure, with an adjustment for processing speed; specifically, (hits − false alarms)/total RT. Thus, the scores of children who completed the test before the 120 (for two pages) or 180 sec time limit were adjusted upward. The adjustment was made because, very few children completed the test in the allotted time when they were younger, but some of them completed the test in less time in later grades. The adjustment enabled us to maintain the sensitivity of the test, despite faster processing times across successive grades.

Number line estimation

In sixth and seventh grades, a series of twenty-four 25 cm number lines containing a blank line with two endpoints (0 and 1000) was presented, one at a time on a laptop monitor, to the child with a target number (e.g., 450) in a large font printed above the line. The child’s task was to mark the line using the computer mouse (Siegler & Booth, 2004). Because learning the linear structure of the number line is correlated with mathematics achievement (Geary, 2011; Siegler, Thompson, & Schneider, 2011), we used absolute accuracy in these analyses. Accuracy is defined as the absolute difference between the child’s placement and the correct position of the number. The overall score is the sum of these differences across trials. However, because this variable was approximately exponentially distributed, the natural log of the mean absolute error was used.

Psychometric Measures

Computational arithmetic

The first form of three tests from the Educational Testing Service (ETS) kit of factor-referenced tests (Ekstrom, French, & Harman, 1976) were used; Addition, (e.g., 19+8+27), Subtraction and Multiplication (e.g., 93–67; 85×4), and Division (e.g., 634÷8). For each test, the score was the number of problems solved correctly in 2 min. Scores were summed to create a Arithmetic Computations measure (α = .88).

Computational fractions

Based on Hecht (1998), three tests were used; Addition (e.g., 1/3 + 2 ¼), Multiplication (e.g., 2/4 × 4/6), and Division (e.g., 1/3÷1/6). For each test, the score was the number of problems solved correctly in 1 min. Multiplication and Division scores were highly correlated with each other (r = .65, p<.0001) but less so with Addition scores (rs = .25, .35, respectively). Thus, two scores were used, Fraction Addition and a sum of Multiplication and Division scores (α = .79).

Fractions comparison test

The 16 item test was developed based on common errors or strategies children use when solving fractions problems (Hecht, 1998; Hecht et al., 2003), and requires children to circle the larger of two fractions in 120 sec. The pairs vary in terms of the relations among the numerators and denominators (four items for each type). In the first type the numerator is constant but the denominator differs (e.g., 1/5 1/9), which assesses children’s understanding of the inverse relation between the value of the numerator and the quantity represented by the fraction. The larger fraction will have the smaller denominator. In the second type numerators have a ratio of 1.5 and denominators a ratio between 1.1 and 1.25 (e.g., 6/20 4/24), making identification of the larger magnitude easier using numerators (larger value is correct), whereas focus on the denominators will results in errors (larger value is incorrect). The ratios were determined based on the Weber fraction for ease of magnitude discrimination for adolescents (Halberda & Feigenson, 2008). In the third type numerators and denominators are reversed (e.g., 4/5 5/4), which requires children to choose the fraction with the larger numerator and smaller denominator. The final type involves skill at using ½ as an anchor for estimating fraction values (e.g., 20/40 7/9). The foils are always close to one but contain smaller numerals than the ½ fraction. A child who understands fractions should be able to quickly determine that one equals ½ and the other is close to one and thus choose the latter. For these problems, a child must choose the larger fraction based on both the numerator and the denominator. Therefore, a child who guesses based only on the magnitude of the numerator will answer half of the questions incorrectly (types 1 and 4), as will a child who guesses based only on the magnitude of the denominator.

Answers were scored at hits (coded 1) or misses (coded −1). Hits were significantly correlated across the four problem types (rs = .39 to .74, ps<.0001) and thus summed to create a total hits variable (α = .81). Misses were also significantly correlated (rs = .36 to .74, p<.0001) and summed (α = .79). The fractions comparison score was hits minus misses.

Procedure

Assessments

The achievement, number line, and fractions comparisons tests were administered in the spring of sixth and seventh grades, and the number sets test in the fall of these grades. The majority of children were tested in a quiet location at their school site, and occasionally on the university campus or in a mobile testing van. Testing in the van occurred for children who had moved out of the school district or to a non-participating school and for administration of the WMTB-C (e.g., after school). The psychometric tests were generally administered to groups of 5 to 20 participants between the fall and spring seventh grade assessments.

Results

The first set of results focuses on whether mathematics achievement, controlling for central executive span and intelligence, is associated with next-grade gains in fractions knowledge, or whether fractions knowledge is associated with gains in mathematics achievement. The second set provides an assessment of the concurrent relation between fractions knowledge and skill at solving fractions problems and mathematics achievement, controlling for basic number skills, whole number computational arithmetic, intelligence, and central executive span.

Cross-Lagged Relations

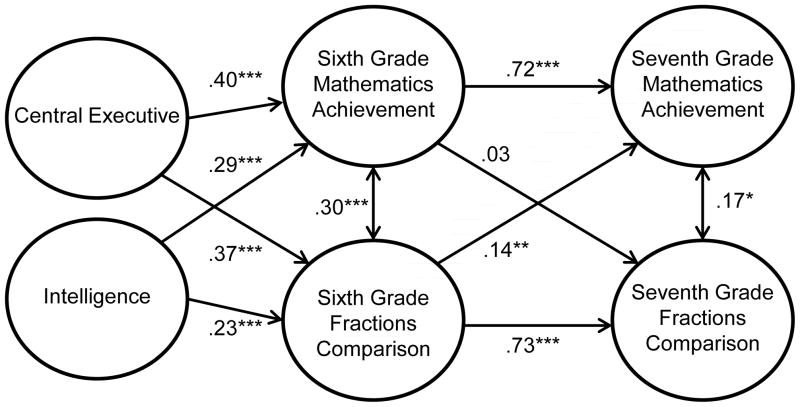
The simultaneous and cross-lagged relations between mathematics achievement and fractions comparison scores in sixth and seventh grades are shown in Figure 1; the model showed a good fit to the data (χ²[14] = 533.01, p = 0.015, RMSEA = .042, CFI = .997). The cross-lagged path from the sixth grade fractions comparison score to seventh grade mathematics achievement (β =.14, p = .005) was larger than the path from sixth grade mathematics achievement to the seventh grade fractions comparison score (β =.03, p = .64), which was not significant. Both variables showed similarly high cross-grade consistency (β =.73, β =.72 for fractions comparison and mathematical achievement, respectively, ps < .001).

Figure 1.

Sixth and seventh grade cross-lagged relations (βs) between mathematics achievement and scores on the fractions comparison test. *p<.05, **p<.01, ***p<.001.

Fractions Predictors of Seventh Grade Achievement

Mathematics

The first model (Math 1) in Table 1 shows that each of the three fractions competence variables contributed uniquely to seventh grade mathematics achievement, R² = .52; all variables were standardized (M = 0, SD = 1). Inclusion of the computational arithmetic, number sets, and number line variables as predictors (Math 2) significantly increased the explained variance, ΔR² = .19, F(3, 188)= 39.6, p < .0001, and revealed that each of these variables explained unique variance in mathematics achievement. The computational fractions tests remained significant, but the fractions comparison test was no longer significant. The same pattern was observed when central executive span scores and intelligence were added to the first model (Math 3), ΔR² = .08, F(2, 184)= 23.7, p < .0001. For the full model (Math 4), all predictors remained statistically significant except for the fractions comparison score and the central executive.

Table 1.

Regression Models Predicting 7^th Grade Mathematics Achievement

	Math 1 Estimate (S.E.)	Math 2 Estimate (S.E.)	Math 3 Estimate (S.E.)	Math 4 Estimate (S.E.)	Read 1 Estimate (S.E.)	Read 2 Estimate (S.E.)	Read 3 Estimate (S.E.)	Read 4 Estimate (S.E.)
(Intercept)	0.001 (0.05)	0.005 (0.04)	−0.025 (0.047)	−0.028 (0.039)	−0.006 (0.063)	−0.006 (0.06)	−0.037 (0.057)	−0.035 (0.056)
FC	0.241* (0.057)	0.073 (0.048)	0.108 (0.056)	0.028 (0.048)	0.331* (0.072)	0.211* (0.073)	0.151* (0.068)	0.127 (0.069)
FMD	0.402* (0.051)	0.208* (0.044)	0.377* (0.047)	0.227* (0.043)	0.106 (0.063)	−0.006 (0.067)	0.075 (0.056)	0.016 (0.062)
FADD	0.367* (0.057)	0.139* (0.05)	0.298* (0.054)	0.116* (0.049)	0.209* (0.072)	0.073 (0.076)	0.087 (0.065)	0.032 (0.071)
WNA	-	0.437* (0.059)	-	0.404* (0.06)	-	0.181* (0.089)	-	0.164 (0.087)
NL	-	−0.148* (0.051)	-	−0.106* (0.051)	-	−0.175* (0.077)	-	−0.053 (0.073)
NS	-	0.114* (0.052)	-	0.119* (0.057)	-	0.106 (0.079)	-	−0.034 (0.082)
CE	-	-	0.219* (0.054)	0.053 (0.048)	-	-	0.212* (0.065)	0.164* (0.069)
IQ	-	-	0.191* (0.055)	0.187* (0.047)	-	-	0.323* (0.066)	0.319* (0.067)
N	195	195	190	190	195	195	190	190
RMSE	0.699	0.552	0.637	0.529	0.875	0.836	0.765	0.761
R2	0.519	0.705	0.596	0.725	0.248	0.324	0.383	0.4
AIC	419.92	330.38	375.54	308.12	507.29	492.37	445.14	445.98

^*p ≤ 0.05

The dependent variable for first four models is seventh grade Numerical Operations scores, and Word Reading scores for the last four models; FC = seventh grade fractions comparison score, FMD = seventh grade fractions multiplication and division score, FADD = seventh grade fractions addition score, WNA = seventh grade whole number arithmetic score, NL = seventh grade log of the absolute error on the number line task, NS = seventh grade number sets score, CE = fifth grade central executive span score, IQ = first or fifth grade intelligence score (see Method)

Reading

To test for discriminant validity of the mathematical predictors, the same procedure was used to predict Word Reading scores (Table 1, last four models). The critical result is found in the full model (Read 4), whereby none of the mathematics variables are significant predictors of word reading, once central executive span scores (β = .16, p<.05) and intelligence (β = .32, p<.05) are controlled, R² = .40.

Discussion

The results add empirical support for the conclusions of the NMAP (2008) and Siegler et al. (in press) regarding the critical importance of competence with fractions for mathematics learning and achievement. The cross-lagged results help to address the question of whether the relation between fractions measures and later mathematics achievement is due to competence with fractions driving gains in mathematics learning or whether mathematics competence, generally, is driving the gains in fractions competence. The analysis of concurrent predictors of mathematics achievement helps to rule out alternative explanations for the relation between performance on fractions tests and mathematics achievement and thus bolsters the basic findings from the cross-lagged analyses.

Fractions Knowledge and Gains in Mathematics Achievement

Scores on the fractions comparison test in sixth grade significantly predicted seventh grade mathematics achievement, controlling for central executive span, intelligence, seventh grade fractions comparison performance, and sixth grade mathematics achievement. The corresponding cross-lagged path from sixth grade mathematics achievement to seventh grade scores on the fractions comparison test was not statistically significant. The pattern is consistent with the hypothesis that competence with fractions underlies, at least in part, subsequent gains in mathematical skills more generally and inconsistent with the hypothesis that the correlation between fractions knowledge and mathematics achievement is simply due to a more general competence with mathematics or to intelligence or working memory (Siegler et al., in press). We did not estimate the co-developmental pattern between skill with use of computation procedures for solving fractions problems and mathematics achievement, because the fractions computation tests were not administered in sixth grade.

It is possible, given the findings from the regression analyses for seventh grade mathematics achievement, that gains in fractions procedural competence may be responsible for the observed cross-lagged relation between sixth grade fractions comparison scores and seventh grade mathematics achievement. However, this is not likely to be the full story, as Hecht and colleagues have found while both computational and conceptual competence with fractions predict outcomes on other mathematic measures, conceptual measures are generally the better predictor (Hecht, 1998; Hecht & Vagi, 2010). If anything, our results may underestimate the importance of conceptual knowledge of fractions, because–due to time constraints for testing sessions–the fractions comparison test is a brief measure of children’s understanding of a few key aspects of fractions (e.g., the inverse relation between size of denominator and magnitude) and more intensive and elaborate measures of this conceptual knowledge may yield a more robust pattern (Mazzocco & Devin, 2008; Siegler et al., 2011). This hypothesis remains to be tested, however.

Also, we note that had we assessed fractions knowledge and mathematics achievement at different grades or for shorter or longer intervals, we may have obtained different results (Rogosa, 1980). Future research that replicates these findings or clarifies the developmental process across different grades and for longer time intervals will be important. Finally, the causal structure assumed in the current model may be fit equally well by a model that does not assume that fractions knowledge and mathematical achievement are causally related (Tomarken & Waller, 2003).

Fraction Predictors of Concurrent Mathematics Achievement

With no other predictors, measures of conceptual and procedural competence with fractions predicted mathematics achievement, as found by others (Hecht, 1998; Siegler et al., 2011; Siegler et al., in press), and this relation remained significant for the computational fractions measures but not the fractions comparison test, once whole number computational skills, two measures of basic number skills (the number sets and number line tasks; see Geary et al., 2007; Siegler & Booth, 2004), and central executive span and intelligence were included as additional predictors. Again, we note that the finding for the fractions comparison test may be due to its abbreviated assessment of children’s conceptual knowledge of fractions and that more thorough assessments are likely to produce more robust findings for conceptual knowledge (Mazzocco & Devin, 2008; Siegler et al., 2011). We will test this hypothesis with follow up assessments of these children.

In any case, an important finding was that, consistent with Siegler and colleagues (in press), neither the computational fractions measures nor any of the other mathematical cognition measures predicted word reading fluency, once central executive span and intelligence were controlled. The pattern provides evidence for the discriminant validity of the computational fractions measures; that is, they are important for mathematics but not reading.

Conclusion

The NMAP’s (2008) determination that competence with fractions was critical for learning algebra was based on the mathematical structure of algebra (i.e., fractions are heavily embedded in much of algebra). The current study adds to an emerging body of empirical work on the importance of fractions competence for mathematics achievement beyond the elementary school years (Siegler et al., 2011; Siegler et al., in press) and supports the hypothesis that improving children’s competence with fractions is likely to facilitate gains in mathematics achievement.