1 Introduction
Molecular recognition forms the basis for virtually all biological processes. Understanding the interactions between proteins and their ligands is key to rationalize molecular aspect of enzymatic processes and the mechanisms by which cellular systems integrate and respond to regulatory signals. From a medicinal perspective there is great interest in the development of computer models capable of predicting accurately the strength of protein-ligand association.[1] Structure-based drug discovery models seek to predict receptor-ligand binding free energies from the known or presumed structure of the corresponding complex.[2, 3] Within this class of methods docking and empirical scoring approaches,[4, 5] which are useful in virtual screening applications,[6, 7] are now routinely employed in drug discovery programs. This review focuses on a class of computational methodologies based on the fundamental physical and chemical principles that govern molecular association equilibria.[8, 9, 10, 11, 12] Given a sufficiently accurate model of molecular interactions these methods have the potential to incorporate greater detail and achieve sufficient accuracy to address aspects of drug development such as ligand optimization, and to address questions such as drug specificity and resistance.
Despite their potential, physics-based models of protein-ligand binding are not widely employed in academic and industrial research, and their effectiveness as predictive tools remains uncertain.[10, 3, 12] There are clearly many reasons that this is the case. Models of this kind are more computationally demanding than alternative empirical techniques, and require expert training for setting them up properly. Early applications of physics-based models of binding, when molecular models, computer algorithms, and computer hardware technologies had not reached a sufficient level of maturity, eventually yielded discouraging results, likely dissuading adoption by the current generation of researchers.[13]
In the past decade however a revival of the field has taken place with the development of better atomistic models and simulation algorithms, and more powerful computers. A new awareness of the limits of applicability of the technologies and the interplay between the various elements of the models have recently led to more trustworthy and realistic outcomes. As the models become more widely employed and these technical developments progress to produce more precise and reproducible results, it is also important to remain aware and deepen our understanding of the statistical mechanics theory of binding on which these models are based.
Thermodynamically, the strength of the association between a ligand molecule and its target receptor is measured by the standard free energy of binding. A statistical mechanics theory of molecular association equilibria exists which is nowadays well understood and widely accepted.[14] Various computational implementations of this theory have been proposed. Computational models can not capture all of the complexities of molecular interactions and all of them, implicitly or explicitly, apply approximations or simplifications. Knowledge of the relationships between the theory and its implementation helps to appreciate the meaning and limits of approximations. This knowledge can also serve as a guide in the design of more realistic computational models and can suggest approaches for the analysis of the results in ways that further our understanding of the binding process. It is only relatively recently that subtle but potentially critical aspects of the theory have been fully appreciated and are being incorporated into computational models.
Theoretical accounts of the theory of binding are somewhat scattered in the current literature and the various descriptions are often tailored to specific numerical implementations and applications, making it often difficult to resolve commonalities. The purpose of this review is to partially fill this gap. The first part describes a statistical mechanics theory of non-covalent association, with particular focus on deriving the fundamental formulas on which computational methods are based. This section also introduces the thermodynamic quantities that often appear in the recent literature as well as their nomenclature. The second part reviews the main computational models and algorithms in current use or development, pointing out the relations with each other and with the theory developed in the first part.
2 Theory of non-covalent binding
2.1 Statistical mechanics formulation of molecular association equilibria
Consider an ideal solution of receptor molecules R and ligand molecules L in equilibrium with their complexes RL. The affinity between the two species can be expressed by the standard binding free energy associated with the bimolecular reaction
| (1) |
given by
| (2) |
where Kb is the dimensionless binding constant expressed as
| (3) |
where […] are concentrations, C○ is the standard state concentration (often set as 1M or 1 molecule/1668 Å3), and the eq subscript states that all concentrations are evaluated at equilibrium. It should be noted that this quasi-chemical description of binding is based on the idea that the bound complex RL can be treated as a distinct chemical species. As further discussed below, this is a reasonable approach if the interaction between the ligand and the receptor is strong, yielding a thermodynamically stable complex. We make this implicit assumption in what follows, noting however that if the receptor-ligand interactions are weak and non-localized, it would be more appropriate to treat the receptor/ligand mixture as a non-ideal solution of the components.
A statistical mechanics expression for the binding constant is available under these assumptions, which, when a generally small pressure-volume term is neglected, can be expressed as[14]
| (4) |
where ZN is the configurational partition function of the solvent bath composed of N molecules, and ZN,RL, ZN,R, and ZN,L are the configurational partition functions of the complex, receptor, and ligand, respectively, in solution. A critical aspect of this formulation is that each partition function includes only the internal degrees of freedom of each species.1 For example (to simplify notation here and elsewhere we omit Jacobian factors for curvilinear coordinates)
| (5) |
is the configurational partition function of the ligand placed in an arbitrary position and orientation in solution integrated over the 3nL – 6 internal degrees of freedom of the ligand xL where nL is the number of atoms of the ligand, rs denotes the degrees of freedom of the solvent and U(xL, rs) is the potential energy of solvent+ligand system. The six external degrees of freedom of the ligand ζL (three translations and three rotations) correspond to as many additional internal degrees of freedom of the complex specifying the position and orientation of the ligand relative to the receptor.[15] The configurational partition function of the complex is then written as
| (6) |
where the integral runs over all conformations of the complex that are deemed bound, for example those in which the ligand is within a specified binding site. A convenient choice is to use the the external coordinates of the ligand relative to the receptor to define this state.[14, 15] An indicator function I(ζL) is introduced set to 1 for values of ζL corresponding to positions and orientations of the ligand which are considered bound to the receptor and zero otherwise. Note that in this formalism the value of the binding constant depends on this arbitrary definition of the complex, raising the question of how to choose it appropriately. This is a more general issue which is further discussed below.
The integral of I(ζL) measures the extent of the defined bound state
| (7) |
where Vsite is the integral over translational coordinates and Ωsite the integral over the orientational coordinates. Vsite represents the physical volume of the binding site, while Vsite measures the allowed range of orientations of the ligand in the complex. If I(ζL) is independent of the orientational coordinates (such that is the definition of the complex is based only on the position of the ligand relative to the receptor), then Ωsite = 8π2.
2.2 Alchemical formulation
In order to make Eq. (4) amenable to computation it is convenient to express it in terms of combinations of ensemble averages. To do so we need to express ratios of partition functions in Eq. (4) such that numerators and denominators have the same number and types of degrees of freedom. This is achieved by multiplying and dividing Eq. (4) by Eq. (7) times the configurational partition function of the ligand in vacuum
| (8) |
yielding the following equivalent expression for Kb
| (9) |
where V○ = 1/C○. In Eq. (9) ΔG2, defined by
| (10) |
is the free energy for establishing receptor-ligand and solvent-ligand interactions, while the ligand is in the receptor binding site (where I(ζL) is non zero). The quantity
| (11) |
is the binding energy between the ligand and the receptor plus solvent environment; U(xR rs), is the potential energy of the receptor-solvent system in absence of the ligand and U(xL) the internal potential energy of the ligand. Similarly ΔG1, defined by
| (12) |
is the free energy for establishing ligand-solvent interactions (the same as the solvation free energy of the ligand).
As specified in Eqs. (10) and (12), the free energy changes ΔG2 and ΔG1 are expressed as averages over the ensembles corresponding to, respectively, the free solvated receptor with the ligand in the gas phase (Rslv + Lgas), and the pure solvent with the ligand in the gas phase (slv + Lgas). In either case the ligand is located in the binding site, as specified by the indicator function I(ζL), but not interacting with the receptor and the solvent. We will therefore refer to these states as decoupled.2
By inserting Eq. (9) in Eq. (2) we finally obtain an expression for the standard binding free energy
| (13) |
where
| (14) |
is a free energy penalty (Ωsite is smaller than 8π2) for restricting the isotropic distribution of ligand orientations in solution to the those allowed in the complex, and
| (15) |
is the free energy for transferring the ligand from a solution at concentration C○ to a volume of size Vsite. For later use we define here the quantity ΔGI, as the concentration-independent component of the standard free energy of binding,
| (16) |
which will be referred to as the interaction free energy of binding. As the other terms in Eq. (13) can be evaluated analytically, it is the computation of the interaction free energy which is the main goal of computer simulations of binding.
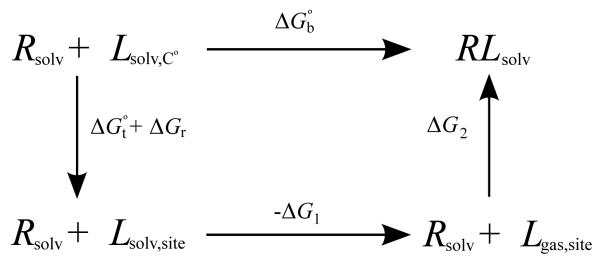
The alchemical thermodynamic path underlying Eq. (13) is illustrated in Fig. 1. The overall binding process (upper horizontal equilibrium) is decomposed into a thermodynamic cycle with three distinct processes. The ligand is first transferred from the bulk solution at concentration C○ to a volume in the bulk solution identical to the binding site volume (left downward process) including any imposed orientational restraints. The free energy associated with this first step is given by Eqs. (15) and (14). In the second step (bottom horizontal process) the ligand is transferred from this volume in solution to an equivalent volume in the gas phase; as noted above the free energy change for this step is the negative of the solvation free energy of the ligand. Finally (right upward process), the interactions of the ligand with the receptor and the solvent are turned on while the ligand is confined within the receptor binding site. This decomposition of the binding free energy forms the basis of the double decoupling class[11, 10] of computational methods that will be discussed later in this review.
Figure 1.
Thermodynamic cycle illustrating the decomposition of the standard binding free energy [Eq. (13)]. Rsolv is the solvated receptor, Lsolv,C○ (upper left) is the ligand in solution at concentration C○, Lsolv,site (lower left) is the ligand solvated sequestered in the binding site, Lgas,site (lower right) is the ligand in the gas phase in a volume equal to the binding site volume, and RLsolv is the solvated complex.
2.3 Potential of mean force formulation
An equivalent statistical mechanics formulation for the binding constant follows from the direct binding process corresponding to the upper horizontal process in Fig. 1. The binding constant effectively measures the probability of occurrence of configurations of the system in which the ligand is found within the binding site, that is conformations in which I(ζL) is non-zero, relative to the unbound conformations where I(ζL) = 0. It should be therefore possible to compute the binding constant by means of a suitable direct thermodynamic path connecting these two conformational states without resorting to intermediate gas phase thermodynamic states. To derive such a formalism note that the product of partition functions in the numerator of Eq. (4) can be written as ZN,RLZN = Z2N,RL, where Z2N,RL is the configurational partition function of the complex in a solution with twice as many solvent molecules. Similarly, the denominator can be written as Z2N,R+L, the partition function of the unbound state when the receptor and the ligand are at infinite separation in a solution with 2N solvent molecules. For sufficiently large N so that finite size effects are negligible, the ratio between Z2N,RL and Z2N,R+L is independent of N and can be written as ZN,RL/ZN,R+L. The expression for the binding constant then becomes
| (17) |
where specifies an arbitrary position of the ligand in the solvent bulk sufficiently removed from the receptor so that it does not interact with it. Eq. (17) can be rewritten as[16, 17]
| (18) |
where ΔF(ζL) is the potential of mean force (PMF) along the ζL coordinates, that is the free energy of the system when the position and orientation of the ligand is fixed at ζL relative to the receptor. From Eq. (17) we see that ΔF(ζL) is defined as
| (19) |
which explicitly sets to zero the potential of mean force at . In practice, the binding PMF is computed along only one of the dimensions of ζL (a receptor-ligand distance d, typically) while the other five coordinates are averaged or kept fixed.[18, 19]
2.4 Implicit representation of the solvent
More concise expressions for the binding constant are obtained by removing explicit integration over the solvent degrees of freedom by introducing the solvent potential of mean force. Starting, for example, from Eq. (4) we multiply and divide by and divide each partition function by ZN. The solvent partition function yields a factor of 1. The ZN,R/ZN ratio can be expressed as
| (20) |
where U(xR) is the intramolecular potential energy of the receptor, u(xR, rs) denotes the receptor-solvent interaction energy, U(rs) is the solvent-solvent potential energy and W(xR) is the solvent potential of mean force for the xR conformation of the receptor defined by[20]
| (21) |
Based on Eq. (21) the solvent potential of mean force is interpreted as the solvation free energy of the of the receptor when this is fixed in conformation xR. The other ratios of partition functions can be treated similarly to define the solvent potentials of mean force, W(xL) and W(xR, xL, ζL), for the ligand and the complex. Finally by a similar derivation that yielded Eq. (9) we can write[14]
| (22) |
where ZRL and ZR+L are the configurational partition functions of the complex in the bound and uncoupled states, respectively, and the interaction free energy ΔGI is defined by their ratio as
| (23) |
which is formally equivalent to Eq. (10) with potential energies U replaced by effective potential energies Ueff = U + W. The effective binding energy u in Eq. (23) has the same form as in Eq. (11) expressed in terms of differences of effective potential energies
| (24) |
It is straightforward to show, from the definition of the solvent potential of mean force [Eq. (21)], that the effective binding energy is the interaction free energy with explicit solvation [Eq. (16)] for a fixed conformation (xL, ζL, xR) of the complex. Eq. (23) then expresses a combination rule to obtain the total interaction free energy for binding by averaging over the ensemble of the conformations of the uncoupled state of the complex.
Note that the meaning of the average in Eq. (23) is different than in Eq. (10). In both averages the ligand is sequestered in the binding site region, however in Eq. (10) the ligand is considered as not interacting with either the receptor or the solvent, whereas in Eq (23) the average is over the conformations of the receptor and the ligand while both of these interact with the solvent continuum in absence of the binding partner [note the absence of the binding energy term in the denominator of Eq. (23)]. The standard binding free energy can then be written as
| (25) |
where and have the same meaning as in Eq. (13) and ΔGI is defined by Eq. (23). The potential of mean force ΔF(ζL) in Eq. (19) can be similarly expressed in terms of the solvent potential of mean force and the effective potential energy.
From a computational point of view the most noticeable difference between the expression for the binding free energy in explicit solvent [Eq. (13)] and that in implicit solvent [Eq. (25)] is that the latter involves only one free energy calculation (ΔGI) whereas the former is based on the difference between two free energy calculations (one for the transfer of the ligand in solution, yielding ΔG1, and another for its transfer to the complex, ΔG2).
2.4.1 Connection with Potential Distribution Theory
A useful representation for the standard binding free energy in the implicit solvent representation is obtained by writing the average in Eq. (23) in terms of a probability distribution density of the effective binding energy:[21]
| (26) |
where p0(u), formally defined as
| (27) |
is the probability distribution for the effective binding energy over the ensemble of conformations in the uncoupled state (see above), that is the state in which the ligand is in the binding site of the receptor but both interact only with the solvent continuum. Note that, as discussed above, Eq. (26), although derived in the implicit solvent representation, is valid in general. In the explicit solvent representation p0(u) is interpreted as the distribution of binding free energies for fixed conformations of the complex drawn from the ensemble of conformations obtained when the ligand and the receptor are not interacting.
The larger the value of the integral in Eq. (26), the more favorable is the binding free energy. An example of a p0(u) distribution is illustrated in Fig. 2. As further discussed in Section 3.3, the magnitude of the p0(u) distribution at positive, unfavorable, values of the binding energy u measures the entropic thermodynamic driving force which opposes binding, whereas the tail at negative, favorable, binding energies measures the energetic gain for binding due to the formation of ligand-receptor interactions. The interplay between these two opposing forces ultimately determines the strength of binding.
Figure 2.
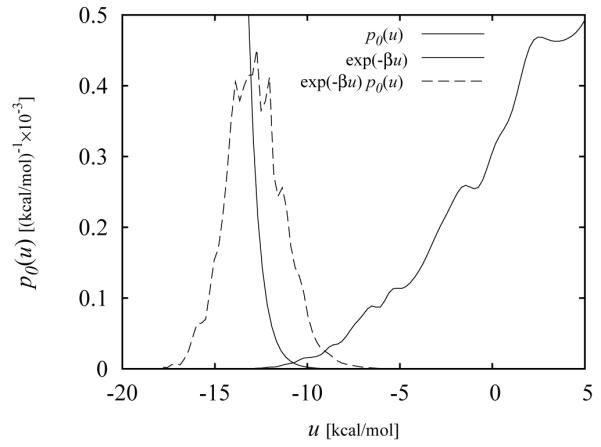
Example of a calculated binding energy distribution p0(u) from reference [21]. The curves to the left correspond to the exp(−βu) and k(u) ∝ exp(−βu)p0(u) functions (rescaled to fit within the plotting area). The integral of the latter is proportional to the binding constant [Eq. (26)].
Eq. (26) has the same form as the fundamental equation of the potential distribution theorem (PDT)[22, 23], of which the particle insertion method of solvation thermodynamics[24] is a particular realization.[25] In particle insertion the standard chemical potential of the solute, μ, is written in terms of the probability distribution p0(v) of solute-solvent interaction energies, v, corresponding to the ensemble in which the solute is not interacting with the solvent:
| (28) |
This expression, is equivalent to Eq. (26) with the solute-solvent interaction energy v replaced by the protein-ligand binding energy u. It follows that the formalism described above for the binding free energy can be regarded as a ligand insertion theory for protein-ligand binding, where the protein atoms and the solvent continuum play the same role as the solvent molecules in particle insertion.
A known result of PDT is a relationship between p0(v), the probability distribution of solute-solvent interaction energies in the absence of solute-solvent interactions, and p1(v), the corresponding probability distribution in the presence of solute-solvent interactions.[26] In the present notation we have
| (29) |
where μ is the chemical potential. The corresponding expression linking p0(u), the probability distribution of ligand-protein binding energies for the uncoupled (R+L) reference state, and p1(u), the probability distribution for the bound state RL is
| (30) |
where ΔGI is defined by Eq. (26). It follows that p1(u) is proportional to the integrand in Eq. (26) for the interaction free energy. Note however that this does not imply that the interaction free energy can be computed by integration of p1(u), as obtained for example from a conventional simulation of the complex in the presence of ligand-receptor interactions. The integral of the normalized probability distribution p1(u), which is by definition unitary, does not contain any information about the interaction free energy. As expressed by Eq. (30), the proportionality constant between p1(u) and the integrand of Eq. (26) is related to the interaction free energy, which is exactly the quantity we are seeking to compute.
The p1(u) distribution is nevertheless a useful quantity for the analysis of the relative contributions to the binding free energy. Using Eq. (26) we can write Eq. (22) as
| (31) |
where, based on Eq. (30),
| (32) |
can be interpreted as a measure of the contribution of the conformations of the complex with binding energy u to the binding constant. We thus call the function k(u) the binding affinity density.[21] See Fig. 2. The binding affinity density k(u) is proportional to p1(u), the binding energy probability distribution in the bound state. (The critical distinction between the two is that the integral of the latter is equal to 1 whereas the integral of the binding affinity density is equal to the binding constant.) It thus follows that the relative contributions to the binding constant of two macrostates, one with binding energy u1 and another with binding energy u2, is simply given by their relative populations in the ligand-bound state when the interactions between the ligand and the receptor are fully turned on.
2.5 Definition of the bound state
The expressions for the standard binding free energy presented above depend on the definition of the bound state through the indicator function I(ζL). This function can be chosen for example so as to as much as possible include only conformations that lack receptor-ligand clashes or it can be defined at a coarser level by specifying for example an enveloping sphere containing the binding site of interest. Since the choice of I(ζL) is to some level arbitrary, there is a question as to which definition is appropriate. This issue has been reviewed in a number of studies.[14, 17, 27] The main conclusion is that if the binding is strong and specific (as formally defined below) the specific choice for the definition of the bound state is for the most part irrelevant as long as it covers all important conformations of the complex. The conditions of strong and localized binding are the same conditions at the basis of the quasi-chemical description of the non-covalent binding equilibrium embodied in Eq. (3).
Consider for example Eq. (18). The largest contributions to the integral come from regions where the binding potential of mean force ΔF(ζL) is large and favorable and exp[−βΔF(ζL)] is large compared to 1, the value obtained in regions where the receptor and the ligand are not significantly interacting. If the minima of ΔF(ζL) are deep and localized, that is binding is strong and specific, the choice of the domain of integration has a small effect on the value of the integral as long as it covers all the regions where ΔF(ζL) is deep.
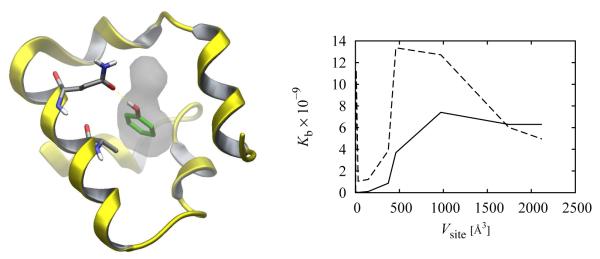
This analysis has been confirmed in at least one recent molecular simulation study,[21] in which the binding constant of a T4-Lysozyme complex was computed using Eq. (22) by varying the extent of the definition of the binding site region (Fig. 3). The results showed that, provided that it contains the main binding site, the binding site volume has a small effect on the computed binding constant. The variations at small binding site volumes in Fig. 3 are due to the fact that in this regime the binding site definition misses some important conformations of the complex. The nearly constant behavior at larger binding site volumes are found to be due to a cancellation between the increasing Vsite term in Eq. (22) and the linear decrease of the exp[−βΔGI] term with increasing binding site volume definition. Enlarging the binding site definition beyond the space that can be physically occupied by the ligand does not appreciably change the value of the integral in the numerator of Eq. (23) because the additional volume contains only points ζL that cause ligand-receptor overlaps, where u(xL, ζL, xR) is large and exp[−βu(xL, ζL, xR)] is small. On the other hand the integral at the denominator, which does not contain the u(xL, ζL, xR) energy term, increases linearly with increasing binding site volume definition thereby canceling the Vsite term at the numerator of Eq. (22). The result is a nearly invariant value of the binding constant. This example also shows that the values of , ΔGr, and ΔGI in Eqs. (13), (16) and (25) are not unique. An increase in the chosen binding site volume, for instance, lowers the values of and ΔGr at the expense of ΔGI that becomes less favorable, so that their sum remains nearly constant. Therefore it is important in binding free energy calculations of this kind to include the appropriate standard state terms to obtain answers that are not as affected by arbitrary model parameters.
Figure 3.
The complex between phenol and the L99A/M102Q T4 lysozyme (PDB id 1LI2, left). The ligand is highlighted in green. The surface surrounding the ligand represents the binding site which is buried and completely surrounded by protein atoms. The computed binding constant for this complex as a function of the size of the binding site volume (left), using Eq. (22) with (full line) and without (dashed line) the inclusion of the Vsite/V○ term (in this calculation Ωsite/8π2 = 1). The binding constant (full line) is fairly constant around Kb = 6 × 109 for Vsite > 500 Å3, whereas exp[−βΔGI] (dashed line) decreases linearly in this region. The two curves meet fortuitously at Vsite = 1668 Å3 where Vsite/V○ = 1. These calculations were conducted with a distance-dependent model,[21] which underestimates desolvation effects and overestimates affinity. The dependence on Vsite is however representative of systems of this kind.
The example above involved a buried binding site. For calculations involving surface sites (as well as buried sites for binding site volumes large enough to extend into the solvent) however, the binding constant is expected to vary linearly with the volume of the binding site for large enough binding sites. Which value of the binding site volume is then appropriate? One simple answer is that in practical terms, as discussed above, if the binding is strong and localized most reasonable choices for the binding site will yield reasonably accurate results. For example, doubling Vsite would decrease the binding constant by a factor of two and increase the binding free energy by only ~ 0.4 kcal/mol at room temperature; a relatively small change compared to typical strong protein-ligand binding affinities of the order of −10 kcal/mol. This occurs because the slow logarithmic dependence of the binding free energy on Vsite is not as significant compared to the larger effect due to strong ligand-receptor interactions.
For weak and less localized binding, however, the dependence on Vsite would be more noticeable. In addition, from a theoretical perspective we would like to understand the paradox that, even though Eq. (4) depends on an arbitrary definition of the complex, the binding constant is a measurable quantity. This has led to the conclusion that, apparently, “Nature knows how to define the complex, even if we do not.”[28] Mihailescu & Gilson have reviewed this issue,[27] and concluded that, first of all, the theoretical expression for the binding constant depends on the experimental technique used. Only methods based on spectroscopic reporting (such as fluorescence quenching)[29] can be shown to be modeled by the quasi-chemical theory considered here. (Equilibrium dialysis techniques, for example, follow a different but related law,[27] which does not require a definition of the binding site volume.) Moreover Mihailescu & Gilson conclude that the definition of the binding site volume most appropriate to reproduce measurements based on spectroscopic reporting is the exclusion zone of the complex, generally defined as the region that includes the binding minimum and the source of the spectroscopic signal, and extends up to a point where there would be enough space to allow a second ligand to interact more strongly with the receptor.[27]
2.6 Thermodynamic decompositions
The free energy of binding is the result of a delicate balance between opposing thermodynamic forces. The main driving force towards binding is the formation of receptor-ligand interactions. However these occur at the expense of solvent interactions producing desolvation effects that often oppose binding. Intuitively binding is necessarily accompanied by the loss of translational freedom and therefore entropic forces tend to disrupt complex formation. In addition, both the ligand and the receptor lose free energy to adapt their conformations to match those compatible for binding. Given the complexity of the process it is very difficult to predict variations of the binding equilibrium. To rationalize binding affinities it is therefore often beneficial to consider contributions to the binding free energy each easier to rationalize than the total. We summarize below three relevant decompositions.
2.6.1 Enthalpy/entropy decomposition
A decomposition of the binding free energy into entropic and enthalpic contributions seeks to separate energetic factors from factors related to the loss of conformational freedom.[30] Obvious candidates in this role are the entropy and enthalpy of binding, which reflect changes in standard thermodynamic potentials. The standard binding entropy is by definition given by the temperature derivative of the standard binding free energy. From Eq. (13):
| (33) |
where
| (34) |
is the change in average potential energy for establishing receptor-ligand and solvent-ligand interactions, and
| (35) |
the change in average potential energy for establishing solvent-ligand interactions. The standard binding enthalpy is given by:
| (36) |
From these expressions we immediately see that only the entropy of binding depends on the standard concentration C○ = 1/V○ through the first term on the r.h.s. of Eq. (33) which corresponds to the work for imposing translational and orientational constraints. We will refer to this term as the translational entropy of binding
| (37) |
whereas we will use the term interaction entropy to refer to the concentration-independent remainder ΔSI defined from Eq. (16) by
| (38) |
The standard entropies and enthalpies of binding are measurable quantities. They are often obtained directly by isothermal calorimetry or by measuring variations of binding constant with temperature.[31] Although they yield quantities directly comparable to experimental measurements, Eqs. (33) and (36) are rarely used in computational studies with explicit solvation because of the difficulties of converging the changes in total average potential energies ΔU2 and ΔU1, which are given by the difference of two large values [each average in Eqs. (34) and (35) scales as O(N), where N is the size of the system, whereas their difference, which is local to the binding site, is O(1)]. Estimating by evaluating over a range of temperatures and evaluating the derivative by finite differences[32] is also problematic because using a small temperature range causes amplification of statistical errors whereas using a large temperature range may introduce systematic bias.
Eq. (33) is not valid with implicit solvation because in this case, unlike the potential energy U(x), the effective potential energy Ueff(x) is temperature dependent. From Eq. (23) we have:[33]
| (39) |
where
| (40) |
is the change in total effective potential energy upon turning on receptor-ligand interactions and
| (41) |
is the corresponding change in the average temperature derivative of the solvent potential of mean force. The binding enthalpy is again given by or
| (42) |
The sum of the first two terms in the r.h.s. of Eq. (39) is usually referred to as the configurational entropy of binding,[30]
| (43) |
whereas the last term, which would be zero for a temperature-independent potential, corresponds to the change in solvent entropy. Similarly, the last term in the r.h.s. of Eq. (42) is the solvent contribution to the binding enthalpy.
It can be shown that[30] Eq. (43) is equivalent to taking the difference of the entropies of the bound and uncoupled states each evaluated using the fundamental equation
| (44) |
where ρ(x) = exp[−βU(x)]/Z is the configurational distribution function.3
One interesting result from Eqs. (39) and (42) is that the ∂W/∂T terms cancel out when evaluating the interaction free energy as ΔGI = ΔHb – TΔSI, yielding
| (45) |
Consequently, the configurational entropy and the effective enthalpy of binding form a valid decomposition in that their sum, together with the appropriate concentration-dependent terms in Eq. (25), and without approximation, gives the standard binding free energy. On the other hand ΔUeff and ΔSconf, lacking proper solvent contributions, do not directly reflect the measurable entropies and enthalpies of binding. Conversely, ΔUeff and ΔSconf are not directly measurable thermodynamic quantities. Nevertheless the effective enthalpy/configurational entropy decomposition can yield valuable insights on the driving forces in favor and against association. Moreover, because they are evaluated with implicit solvation, these quantities are also more amenable to computation relative to the full binding entropies and enthalpies. Indeed, as discussed below, some computational methods with implicit solvation, such as MM/PBSA, are based on Eq. (45) and independent estimates of ΔUeff and ΔSconf.
2.6.2 The reorganization free energy
Working within the implicit solvent representation, we can think of the binding process as occurring in two separate steps. First the ligand and the receptor reorganize their conformational ensembles to match those of the bound complex, and then receptor-ligand interactions are established. Since there is no change in the configurational distributions of the binding partners, from Eq. (44) we see that the entropy change for the second step is zero. Moreover the enthalpy change for the second step is limited to the establishment of the receptor-ligand interaction energy , where u is the binding energy defined by Eq. (24) and the RL subscript denotes averaging over the bound conformations of the complex. The remainder. ΔGreorg, defined by the identity
| (46) |
is then the free energy for the reorganization step.
By adding and subtracting from Eq. (46) and using Eqs. (24), (40), and (43), we can rewrite the reorganization free energy as
| (47) |
where δSconf is the configurational entropy defined above, and
| (48) |
is the reorganization energy defined as the change in the average internal potential energies of the receptor and the ligand in going from to the unbound state to the bound state while they are not interacting. Eq. (47) confirms that the configurational entropy corresponds to the entropic cost of reorganizing the conformational ensembles of the binding partners to form the complex.
The reorganization free energy is necessarily positive because without mutual interactions the ligand and the receptor would spontaneously relax to their conformational ensembles at a lower free energy. Therefore based on Eq. (46) we conclude that the average binding energy is the only term that can be favorable to binding, while reorganization always opposes it.
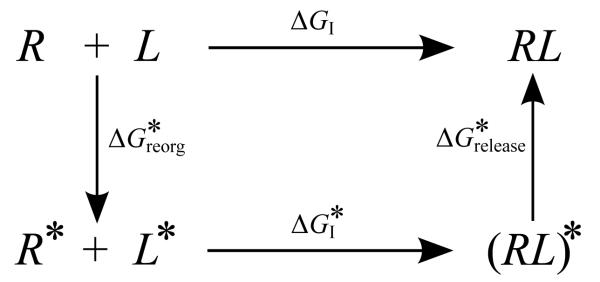
In some applications other definitions of the reorganization free energy appear in which the intermediate state is one in which the receptor and the ligand conformational ensembles by construction do not match exactly those of the complex.[34] Consider for example Fig. (4) in which the binding free energy (here the ligand is assumed to be already placed in the binding site) is decomposed into the free energy of restraining the ensembles of conformations of the receptor and the ligand in solution to chosen macrostates R* and L* (for instance an application is described below in which the R* macrostate is defined with respect to a sidechain conformation). The free energy for this process is related to the population , defined as the probability of finding a conformation belonging to the macrostate, in the absence of restraints:
| (49) |
Following this step, we consider the binding free energy, , between the R* and L* species, that is the binding free energy when the receptor and the ligand are limited to the chosen macrostates. is defined, for example, as in Eq. (23) where in addition to the binding site indicator function I(ζL), indicator functions I(xR) and I(xL) are present which limit the range of the receptor and ligand internal degrees of freedom. In general the resulting state of the complex, denoted by (RL)* in Fig. 4, does not match the full complexed state RL because in the former the receptor and the ligand are limited to their respective macrostates. If the chosen macrostate encompasses most of the conformational ensemble of the complex, the (RL)* and RL species are virtually equivalent. Otherwise we need to consider the free energy difference, , of releasing the macrostate restraints in the complexed state, given by
| (50) |
where is the population of the macrostate when the ligand and the receptor are interacting. Putting all together we finally obtain
| (51) |
which expresses ΔGI as the sum of a term, corresponding to the binding free energy of a macrostate of the complex plus a free energy term corresponding to the preparation and release of this macrostate.
Figure 4.
Thermodynamic cycle illustrating the restrain-and-release decomposition of the interaction free energy [Eq. (51)]. Although not indicated, the ligand here is assumed to be always sequestered in the binding site. R and L represent the free receptor and ligand, R* and L* represent the receptor and ligand restrained within a conformational macrostate, (RL)* represents the complex in which receptor and ligand are restrained within their macrostates, and RL represents the free complex.
The result in Eq. (51) also very clearly shows that to accurately estimate the binding free energy it is sufficient to sample only those macrostates whose population is affected by the binding reaction. From Eq. (51) we see that as long as , that is the binding free energy computed within a chosen macrostate is an accurate estimate of the binding free energy if the population of the macrostate is approximately the same in the unbound and bound states. So for example, it is not strictly necessary to thoroughly sample regions of a protein receptor far away from the binding site as these are often not substantially affected by the binding of the ligand. Arguably, it is precisely for this reason that computer simulations, which necessarily sample a very small fraction of conformational space, can be applied to the computation of binding free energies. Eq. (51) is also the basis for the “restrain-and-release” double decoupling method discussed below which is useful in cases when it is convenient to conduct the binding free energy calculation within a limited portion of conformational space.
2.6.3 Conformational decomposition
We showed in Section 2.4.1 that the binding affinity density measures the contribution of the conformations with a particular binding energy to the overall binding constant. In this section we generalize this result in the conformational dimension. Often the affinity between a receptor and a ligand is the result of not one but multiple binding modes differing for example in the orientation of the ligand in the binding site. We would then like to estimate the contribution of each mode to the total binding free energy. As discussed later, this question has computational relevance in that if we have a way to combine the binding free energies of multiple modes into a single overall binding free energy, then it would be possible to simplify the calculation by treating each mode separately. As we show in this section, a conformational decomposition of this kind is possible.
Let us work in the implicit solvent representation using the binding energy distribution formalism presented in Section 2.4.1. Given a set of macrostates i = 1, …, n of the complex we consider the joint probability distribution p0(u, i), expressing the probability of observing the binding energy u while the complex is in macrostate i. Assuming that the set of macrostates collectively covers all possible conformations of the complex (which is always possible by including a “catch-all” macrostate), we can express p0(u) as a marginal of p0(u, i):
| (52) |
where we have introduced the conditional distribution p0(u|i) and the population P0(i) of macrostate i in the uncoupled reference state, and used the relationship p0(u, i) = P0(i)p0(u|i) between the joint and conditional distributions. By inserting Eq. (52) into Eq. (32), we have
| (53) |
where
| (54) |
represents the binding affinity density for macrostate i. In analogy with Eq. (31) we define a macrostate-specific binding constant
| (55) |
where represents an ensemble average in the unbound state of the complex limited to macrostate i. The macrostate-specific binding constant Kb(i) represents therefore the binding constant that would be measured if the conformations of the complex were limited to macrostate i. From Eqs (55) and (53), the sum of the macrostate-specific binding constants weighted by the macrostate populations P0(i) is the total binding constant:
| (56) |
Eq. (56) expresses the fact that each conformational macrostate contributes to the total binding constant proportionally to its macrostate-specific binding constant Kb(i) weighted by the population, P0(i), of the macrostate in the unbound state.[35] Using Eq. (2), the composition formula for the binding free energy corresponding to Eq. (56) is
| (57) |
where is the standard binding free energy for macrostate i.
Although Eqs. (56) and (57) have been derived in the implicit solvation representation, it can be shown that they are valid in general. In the explicit solvent representation, the macrostate i refers to the solvated state for the receptor and for the gas phase for the ligand, and it is assumed that the same definition of macrostate i is used for both legs of the double-decoupling process [Eqs. (10) and (12)]. Eq. (57) also forms the basis of integration over parts approaches[35, 36, 37] to the calculation of binding free energies. The idea is that the binding free energy can be obtained by the appropriate combination of the binding free energies of a series of binding modes. These methods are attractive because it is easier to localize the calculation to a macrostate than achieving equilibration between distinct binding modes. The challenge is to to identify the collection of modes that contribute the most to the total binding free energy. Misidentification of the highest contributing mode can introduce major errors, while neglecting secondary modes generally has a smaller effect on accuracy.[36, 21]
The ratio P0(i)Kb(i)/Kb measures the relative contribution of macrostate i to the overall binding constant. We can see that a large macrostate-specific binding constant Kb(i) is not a sufficient condition for a large contribution to the overall affinity. It must be also the case that the macrostate has a significant population P0(i) in the unbound state. This result can be interpreted as a generalization of the reorganization free energy concepts developed in Section 2.6.2. ΔGreorg = −kT ln P0(i) measures the reorganization free energy penalty for restraining the system into macrostate i in the unbound state, whereas measures the association free energy in that macrostate. For a macrostate to contribute significantly to the binding affinity, the reorganization penalty and the association gain must combine so as to be favorable overall to binding.
It is straightforward to show from Eqs. (55) and (30) that[21]
| (58) |
where
| (59) |
is the population of macrostate i in the bound state. In other words, this analysis shows that the relative contribution of macrostate i to the binding constant is equal to the physical population of that macrostate of the complex. If a particular binding mode of the complex can be observed, by for example X-ray crystallography, it can be concluded therefore that its population is high and that it likely contributes significantly to the binding affinity.
It is also of interest to estimate the effect of having missed a particular binding mode in a binding free energy calculation. An expression for the binding constant, Kb(−j), when macrostate j, say, has been missed can be derived by removing the corresponding term in the sum in Eq. (56) and, in addition, by renormalizing the macrostate populations so that they add to one. The result is:
| (60) |
From this result we can see that, as expected, missing macrostate j has a large effect in the computed binding constant if this macrostate provides a large contribution to the overall binding constant [the P0(j)Kb(j) term in Eq. (60)]. It also shows, however, that the binding constant can also be severely overestimated if the j macrostate is highly populated in solution [the 1 – P0(j) term at the denominator is small]. In other words, large errors in binding free energy calculations are expected either if important macrostates of the bound complex are missed or if important macrostates of the unbound states are missed. The latter occurs because the calculation would underestimate the free energy required to reorganize the binding partners into their bound ensembles.
3 Computational methods
The development of a statistical mechanics theory of non-covalent association is only the first step in the development of computational models and methods for the calculation of binding affinities. To begin with, the expressions for the free energy of binding presented above depend on the definition of a potential energy function U(x). We also require some prescription to generate ensembles, or set of conformations x of the system, compatible with the thermodynamic state of the system and the potential energy model. In this review we focus on all-atom classical force fields[38, 39, 40, 41] energy models, and on Molecular Dynamics (MD) or Monte Carlo (MC)-based conformational sampling methods, which are most commonly applied models for protein-ligand binding free energy estimation. Atomistic force field models are not reviewed further here except to say that they are parametrized functions of the Cartesian coordinates of the atoms of the system, describing electrostatic, dispersion, and steric non-covalent interactions as well as covalent interactions between atoms. Force fields are used with explicit representations of solvent molecules (water in the applications described below), as well as in conjunction with implicit models of hydration.[42, 43, 44, 45, 46]
A very active and rich area of research is focused on the development of computer algorithms for the evaluation of free energies[13] given an energy model. One class of free energy methods applicable to binding free energy simulations is based on connecting the unbound and bound states by a suitable thermodynamic path. At a fundamental level thermodynamic path methods are capable of computing ratios of partition functions as in Eq. (4). Another class of free energy methods, often referred to as end point methods compute binding free energies by explicitly estimating the free energies of the bound and unbound states.[47]
3.1 Free energy estimators
Eqs. (10) and (12), for explicit solvation, and Eq. (23), for implicit solvation, suggest a simple algorithm to the computational evaluation of binding free energies by means of exponential averaging of the binding energy in an appropriate reference ensemble. In practice these expressions suffer from several limitations, and are rarely implemented as such. Instead, suitable free energy estimators have been developed which are discussed in this section.
Eqs. (10), (12), and (23) are particular realizations of the free energy perturbation (FEP) identity,[48] which states that the free energy difference ΔG between two states 1 and 0 is
| (61) |
where Z1 and Z0 are the corresponding configurational partition functions and ΔU(x) = U1(x) – U0(x) is the difference of potential energies between state 1 and 0 (the perturbation), and the average is over conformations x sampled from the reference state 0. In our case state 1 is the bound state and state 0 is the uncoupled state of the complex. Because they are very difficult to converge, however, in binding free energy applications the FEP formulas are rarely evaluated directly. To understand why consider for example Eq. (26) and Fig. 2. The distribution of binding energies in the unbound state, p0(u), is largest for large positive values of u. This is expected since in this state the ligand is restrained in the binding site where, in the absence of receptor-ligand interactions, the ligand is more likely to sample conformations with unfavorable clashes with receptor atoms rather than conformations with favorable interactions. The values of u in the extreme negative binding energy range correspond to the low energy conformations of the complex, which are very rarely visited in absence of ligand-receptor interactions. On the other hand the exponential factor, exp(−βu), amplifies the contribution of these conformations to the integral in Eq. (26), causing the average to be dominated by rare events. This results in unreliable results, requiring the accumulation of an inordinate, and practically unachievable, number of independent samples to reach convergence.[49]
An equivalent way to assess this problem is to consider the distribution, p1(u) of binding energies in the bound ensemble (illustrated in Fig. 2 as a dashed curve). We concluded above [Eq. (31)] that most of the contribution to binding comes from conformations where p1(u) is large. The amount of overlaps between p1(u) and p0(u) is a measure of the probability that one of these conformations is generated by chance in the uncoupled ensemble. As we can see from Fig. 2, the amount of overlap is small and the binding affinity is expected to be difficult to assess by sampling only the uncoupled ensemble. This is a general result, which states that the FEP formula is applicable for the computation of free energy difference between closely related states whose distributions of the perturbation energy overlap significantly.[50, 13, 49]
The technique known as stratification[13] is a general way to circumvent the problem of poor distribution overlap in FEP binding free energy calculations. The first ingredient is a λ-dependent hybrid potential, which at λ = 0 typically corresponds to the unbound state and at λ = 1 corresponds to the bound state. A straightforward, although not necessarily optimal, choice for the hybrid potential in binding free energy calculations is
| (62) |
where U(xR)+U(xL) represents the energy in the unbound state and u is the binding energy. Here we have used the notation for implicit solvation denoting for simplicity the effective potential as U. The expression for hybrid potential, Eq. (62), can easily adapted to the solvation and binding steps [Eqs. (12) and (10)] with explicit solvation. The hybrid potential defines a thermodynamic path connecting the unbound and bound states through an arbitrary number of unphysical intermediate states at 0 < λ < 1 in which the receptor and the ligand are only partially coupled. In addition, states with similar λ have similar characteristics and, in particular, binding energy distributions with significant overlap, allowing the application of the FEP formula for the computation of their free energy difference:
| (63) |
where Δλ = λ2 − λ1. Given a set of n intermediate states at λ = λi the free energy difference can then be evaluated as the sum of the free energy differences between intermediate states
| (64) |
where Δλi = λi+1 − λi. More generally, when the expression for the hybrid potential is not linear in λ, Δλiu in Eq. (64) is replaced by U(λi+1) − U(λi).
Because it is based on the sum of well behaved terms, the FEP stratification formula, Eq. (64), is much easier to convergence that the direct application of the FEP formula between the unbound and bound states. The procedure entails performing multiple MD or MC simulations to collect samples at each λ. The more intermediate states are employed, the fewer samples are needed to converge each term but more terms need to be evaluated. A number of techniques have been developed to optimize the λ schedule in FEP calculations and to assess the reliability if individual free energy estimates based, for example, on the analysis of neighboring distributions.[13, 49]
The thermodynamic integration (TI) formula, which is sometime used in binding free energy calculations,[51] can be considered the continuous limit of Eq. (64) for Δλi → 0
| (65) |
where the last equality follows from Eq. (62). The TI formula is formally derived from the identity
| (66) |
Eq. (64) expresses each individual free energy difference in terms of an exponential average. One limitation of the exponential average is that, as discussed above, it works well only if conformations relevant for the target state are sampled in the reference state, or in other words if the binding energy distribution in the reference state envelopes that of the target state. The result is that often one perturbation direction gives different results than the other (hysteresis), with the one going in the direction of decreasing entropy (for binding the one starting from the unbound state) usually being more accurate.[50] In some cases however neither direction may work well unless the λ spacing is made very small. In recent years more efficient free energy estimators have been developed. The Bennet acceptance ratio (BAR) formula[52, 26]
| (67) |
where f(x) = 1/[1+exp(x)] is the Fermi function and C is a constant determined iteratively, has been shown to be an optimal free energy estimator with respect to the minimization of the statistical variance. It is also symmetric with respect to the perturbation direction. The BAR formula is based on the introduction of a fictitious intermediate state whose distribution is enveloped by the distributions of both end states and peaks where they most overlap. Consequently the BAR formula requires only that the two distributions overlap to some extent, rather than requiring that one is enveloped in the other as for the exponential averaging formula. The BAR formula has for the most part replaced the exponential averaging formula in modern FEP binding free energy calculations.
A free energy perturbation approach can also be used to compute the binding free energy using the binding potential of mean force approach [Eqs. (18) and (19)]. In this case techniques to compute free energy changes along a thermodynamic path described by a structural order parameter can be considered. For example, the distance measure d(λ) of the ligand from the binding site. Samples are generated at a reference receptor-ligand distance and the potential energy changes ΔU resulting from displacing the ligand distance from the receptor by Δd = d(λi+1) − d(λi) are computed in the context of Eq. (64) or (67). More commonly however the binding potential of mean force is expressed in terms of the probability density p(d) of the receptor-ligand distance
| (68) |
where d* is some reference large distance corresponding to the solvent bulk. Because it is difficult to sample a large range of distances in one simulation, multiple simulations are conducted each employing a different auxiliary confining potential designed to bias sampling in one limited range of distances.[18] In this technique, generally known as umbrella sampling, each simulation generates a biased distribution. The data from all of the simulations is then combined and unbiased using reweighting techniques such as the weighted histogram analysis method (WHAM).[53, 54, 55] The WHAM equations in this case are expressed as
| (69) |
where, P(di) = p(di)di is the unbiased probability to find the system at distance bin i of size Δdi centered at di, n(di) is the number of samples collected from all simulations in this bin. The denominator is a sum over the simulations, each at a different value of λ. nλ is the total number of samples collected at the simulation at λ, ωλ(di) is the value of the biasing potential at λ corresponding to bin i, and, finally
| (70) |
is a normalization factor related to the free energy, kT ln fλ, of the system at λ relative to the unbiased system. Eqs. (69) and (70) are solved iteratively until convergence. The binding free energy is then computed by integrating the binding PMF over the binding site region [Eq. (18)].
The usefulness of WHAM as a binding free energy estimator extends to alchemical methods as well. As further described below, WHAM has been used to implement Eq. (23) by choosing the binding energy u as thermodynamic path parameter and setting as biased potential ωλ(u) = λu.[21] From Eq. (62), the unbiased system at λ = 0 is the unbound state and λ = 1 corresponds to the bound system, and consequently Eq. (70) evaluated at λ = 1 yields the interaction component of the binding free energy:
| (71) |
More recently the multistate Bennett acceptance ratio (MBAR) method as been developed,[56, 57] which, in a way, unifies the BAR and WHAM free energy estimators. Like WHAM it combines in an statistically optimal way data from multiple values of λ to compute the overall binding free energy [rather than from a sum of pairwise terms as in the FEP equation (64)]. It also resembles WHAM in terms of formulation. In fact, it is equivalent to WHAM in the limit that bin sizes are made so small so to contain only one sample, or none. On the other hand, MBAR reduces to the BAR estimator when only two states are considered. The MBAR free energy estimator is preferable to WHAM because it does not require the definition of an histogram grid, and it’s preferable to BAR because it more efficiently utilizes the samples generated at each λ so that all of them contribute to free energy differences. Because in addition it combines the generality of both methods the MBAR is expected to become a widely employed estimator in binding free energy calculations.
3.2 Double decoupling
The double-decoupling method[14, 11, 10] is an alchemical approach to the calculation of standard binding free energies (often referred to as absolute binding free energies in the literature). It implements Eq. (13), where the computations of the free energies of transfer, ΔG1 and ΔG2, of the ligand from the gas phase to, respectively, the solution and receptor environments, form the core of the method. The name double-decoupling comes from thinking of the two opposite processes of decoupling the ligand from the solution and receptor environments. Eqs. (12) and (10) are implemented using either the TI [Eq. (65)] or staged FEP/BAR [Eqs. (64) and (67)] free energy estimators.
Double decoupling has been used recently to compute the standard binding free energies of a variety of protein-ligand complexes. The L99A and L99A/M102Q mutants of T4-lysozyme[58, 59] have been the most studied systems; the small size of the ligands, the relative simplicity of the binding sites, and the availability of high quality structural and thermodynamic data,[60, 61] have made these systems particularly well suited for testing the validity of various computational protocols.[62, 63, 37] A number of double decoupling studies[64, 35] have also targeted a series of inhibitors of the FKBP12 receptor.[65] Applications to the trypsin[66, 67] and the ribosomal peptidyl-transferase receptors[68] have also been recently reported.
From a computational perspective the three main issues in double decoupling simulations are: (i) the extent of conformational sampling (discussed in detail in Section 3.6), (ii) the definition of the binding site volume by restraining potentials, and (iii) the use of soft-core hybrid potentials.
As discussed above the definition of the complexed state and the concentration dependence of the standard state is formally introduced by a binding site indicator function I(ζL). As discussed,[14, 15] I(ζL) can be defined in terms of a continuous function which interpolates from values near 1 within the binding site region to values near 0 outside it. A common choice is to set
| (72) |
where Urestr is a suitable restraining potential that depends only on the external coordinates of the ligand. This definition is computationally convenient because it is differentiable and, as we can see by inserting Eq. (72) in Eq. (10) or Eq. (23), the indicator function can be implemented by means of restraining potentials easily included in potential energy routines of MD packages. Note that, because the restraining potential is present in both the unbound states, it does not contribute to the binding energy [Eqs. (11) and (24)]. Also note that the definition above makes the definition of the complexed state temperature dependent, potentially affecting in unwanted ways the temperature dependence of binding free energies. This dependence can be removed by adjusting the strength of Urestr according to the simulation temperature.
Some early absolute binding free energy calculations,[69] as well as more recent ones,[70] did not account properly for the standard state definition. Moreover ligand restraints are sometime described as a convenient computational device to enhance convergence by not letting the ligand wander into the whole simulation volume when it is uncoupled from the receptor.[11] But, as discussed above, they are in fact a necessary input of the method; they implicitly provide a definition of the complexed state without which it is not possible to define its free energy. Boresch et al.[15] have introduced a general framework to define the six external degrees of freedom ζL of the ligand based on the positions (expressed in spherical polar coordinates) of three reference atoms of the ligand relative to three reference atoms of the receptor. This leads to three coordinates that specify the overall translation of the ligand (one distance and two angles) and another set of three coordinates (three angles) that determine the orientation of the ligand in the binding site. Restraining potentials can be applied only on the translational coordinates or also on the orientational coordinates. For harmonic, or flat-bottom harmonic restraints the binding site volume VsiteΩsite in Eq. (7) can be evaluated analytically. In other circumstances the integration of the indicator function can be obtained numerically with high accuracy since it involves at most six coordinates. Some early studies[71] employed multiple distance restraints between ligand atoms and receptor atoms, which, as pointed out by Boresch et al.,[15] is incorrect based on this formalism, since it would introduce couplings between the external ligand coordinates and internal coordinates of the receptor and the ligand.
It has been observed that the a hybrid potential linear in λ as in Eq. (62) leads to instabilities in the calculations of free energies near λ = 0,[72, 51] when the ligand and the receptor are nearly uncoupled. Under these conditions conformations are generated in which receptor and ligand atoms interpenetrate each other and yielding very large values of the binding energies. These cause instabilities in Eq. (63) which are difficult to overcome unless the λ spacing is very fine (small Δλ). These difficulties have led to the development of so-called soft core hybrid potentials which avoid large perturbation energies near the end point of the transformation. A popular class of soft core potential employ a λ-dependent modified distance function in the evaluation of Lennard-Jones and Coulombic interactions. For example
| (73) |
is a soft core version of the Lennard-Jones pair potential. Note that uLJ(r|λ) above is finite for any non-zero value of λ allowing particles to interpenetrate each other. This functional form also “grows” particles gradually, reducing the fluctuations of the free energy estimator at small λ. Decomposing the decoupling steps such that electrostatic interactions are turned off before Lennard-Jones has also been shown to improve convergence.
3.3 Binding energy distribution analysis method
The binding energy distribution analysis method (BEDAM)[21] is an absolute binding free energy alchemical method based on an implicit description of the solvent. It computes the binding free energy by means of Eq. (26) where the distribution of binding energies p0(u) is computed numerically. The numerical difficulties application of Eq. (26) is illustrated in Fig. 2. Because low binding energies are very rarely sampled when the ligand is not guided by the interactions with the receptor, the accurate calculation of the important low energy tail of p0(u) can not be accomplished by brute-force collection of binding energy values from a simulation of the complex in the uncoupled state. Instead, samples are collected from a series of biased MD simulations of the complex with biasing potential λu. In going from λ = 0 to λ = 1 the system progressively samples more and more favorable binding energies. The replicas collectively sample a wide range of unfavorable, intermediate and favorable binding energies which are unbiased and combined together by means of the weighted histogram analysis method (WHAM) to yield the unbiased probability density p0(u),[55] which is then used in Eq. (26) to compute the binding free energy. The ladder of λ values is chosen so that uniform coverage of the range of binding energies important for binding is achieved. In particular, the low binding energy tail of p0(u), although small in magnitude, is reliably estimated because the relative precision of the binding energy distribution p0(u) computed by WHAM depends mainly on the number of samples collected at binding energy u, rather than the value of p0(u) itself.
Although, as discussed in Section 2.4.1, the binding energy distribution formalism on which BEDAM is based is valid in general, in practice it is only applicable with implicit solvation. This is because in BEDAM the effective binding energy is part of the potential energy of the system, requiring fast evaluation of u and its gradients for MD conformational sampling. With explicit solvation however each evaluation of the effective binding energy would entail a costly and impractical binding free energy calculation [see discussion near Eq. (24)].
In a recent study[21] using the OPLS force field with the AGBNP2[46] solvation model, BEDAM was shown to accurately identify ligand binders from non-binders in a challenging set of candidate ligands to T4 lysozyme receptors (Fig. 3) failed by docking programs. In addition, the standard binding free energies of the binders were found to be in good agreement with experimental measurements. In contrast, energy-only estimators, which do not include entropic and energy reorganization effects, did not correctly reproduce the experimental rankings. As with other full free energy models of binding, BEDAM implicitly incorporates entropic and reorganization effects. In this study the reorganization free energies were evaluated using Eq. (46) and shown to be large and in many cases the discriminating factors between binders and non-binders. Analysis of the binding energy distributions, as described in Section 2.6.3, allowed the decomposition of the binding free energies into conformational contributions based on the orientation of the ligand within the binding pocket. It was found that in many cases several binding modes contributed nearly equally to the total binding free energy.
There are clear parallelisms between BEDAM and conventional binding free energy methods such as double decoupling. They are both alchemical methods that utilize a hybrid potential of the form in Eq. (62) to build a thermodynamic path between the unbound and bound states. The binding energies collected in BEDAM can yield directly the binding free energy by means of the f-factors [Eq. (70)] returned by WHAM or MBAR. One advantage of BEDAM over double-decoupling is that BEDAM estimates the binding free energy from a single perturbation leg rather than from the difference of two separate free energy calculations with double decoupling. This feature is potentially advantageous for more rapid convergence of the binding free energies of highly polar and charged ligands, which, in double decoupling and endpoint approaches discussed below, are the result of a nearly complete cancellation between the large free energies of the unbound and bound states.[11]
The challenges in BEDAM calculations are similar to those discussed above in the context of double-decoupling. In addition, BEDAM relies on the quality of the implicit solvent potential. To obtain accurate binding free energies care should be taken to achieve the correct balance between direct interaction and hydration forces.[46] As discussed below to further enhance the conformational sampling of ligand-receptor conformations BEDAM employs a λ-hopping replica exchange algorithm. The problem of the convergence of free energy differences near λ = 0 is evidenced by the long tail of the p0(u) distribution at large energies which is difficult to estimate accurately. Recent versions of BEDAM employ a soft-core hybrid potential of the form U(λ) = U0 + λf(u), with f(u) = umax tanh(u/umax), where umax is some maximum ceiling for the binding energy, which has been shown to improve convergence without appreciably affecting free energy estimates.
3.4 Potential of mean force approach
The binding potential of mean force (PMF) approach described in Section 2.3 is an example of a non-alchemical transformation to the calculation of absolute binding free energies. Numerical applications of the PMF formula have a long history in the study of dimerization of simple solutes,[16, 73] and few applications have been reported for protein-ligand binding free energy estimation.[18, 19, 11] The main advantage of PMF calculations is that they can be conducted with explicit solvation, but, unlike double-decoupling methods, they do not suffer from the large cancellation between the solvation and binding components [ΔG1 and ΔG2 in Eqs. (12) and (10)]. PMF calculations are therefore easier to converge for the binding between between charged ligands and receptors whose solvation free energies can be of the order of ~ 100 kcal/mol. The disadvantage of the PMF approach is that it relies on the presence of a physical unobstructed path for the ligand to reach the binding site from solution. This limitation basically prevents the application of the method to buried binding sites.
Computationally it is impractical to obtain the PMF along all of the six external ligand coordinates. Typically only one coordinate is used corresponding to a displacement distance d along an approach path from the bulk solution to the binding site. The other coordinates are either fixed[18] or averaged[19]. In the former case the work necessary to restrain the angular position and orientation of the ligand relative to the receptor is computed separately.[18] The PMF is computed along the approach coordinate by biased sampling and reweighting, as discussed above. In the reported applications[18, 19] harmonic biasing potentials were employed.
3.5 Relative binding free energies
Often in pharmaceutical applications[74] we are interested in the difference of binding free energy between two related compounds to the same receptor. Computational methods designed to compute directly relative binding free energies, rather than the corresponding standard binding free energies, have been developed and resulted in some of the first applications of free energy methods to protein-ligand binding.[75] Relative binding free energy calculations [commonly referred to as free energy perturbation (FEP) calculations] constitute the majority of protein-ligand binding calculations conducted in academic and industrial settings, and a variety of techniques have been developed to improve their efficiency and accuracy. This body of work has been thoroughly reviewed.[13, 76, 77, 78, 79, 51] In this section we sketch out the foundations of the method based on the statistical mechanics theory presented above and point out connections between relative and absolute binding free energy calculations.
The difference of standard binding free energies, , between two ligands B and A is equivalently expressed as the ratio of the corresponding binding constants [Eq. (2)]. Using Eq. (4), and assuming that both ligands bind to the same binding site of the receptor R, we arrive at the following expression
| (74) |
Where ΔΔGR(BA) is the difference in free energy of complexes RB and RA and ΔΔGslv(BA) is the difference in solvation free energies between ligands B and A. We see that the relative free energy of binding is independent from the standard state concentration. Also, the ratios of partition functions in Eq. (74) can be expressed as averages, similar to those in Eq. (10) and (12),4 based on the difference in potential energy between the ligands averaged over the ensembles of one of the ligands in the binding site and in solution, without resorting to intermediate gas phase state for the ligands. Given a suitable λ-dependent interpolation potential connecting the potential energies of the two ligands, these averages can be computed with the alchemical free energy estimators discussed in Section 3.1. Two main mutation techniques, single topology and dual topology,[51] exist to map the potential energy of one ligand to the other.
Relative binding free energy calculations are expected to be more efficient than computing the difference of the corresponding absolute binding free energies when the two ligands are similar to each other. Conversely it is difficult to set up an interpolation potential and converge the relative binding free energy when the two ligands have very different chemical structures. However, ligand similarity alone is not a sufficient condition for obtaining reliable relative binding free energies. As in absolute binding free energy calculations one of the main challenges is the extent of conformational sampling. It has been observed for example[37, 21] that even slight ligand modifications can cause large changes in the main ligand binding mode. In these cases the sampling of both binding modes is required to yield reliable results, thereby reducing the computational advantage of relative binding free energy calculations over absolute ones. Relative binding free energies calculations are also considered less suitable than absolute ones to assess the reliability of algorithms and force fields against experimental data.[80, 12]
3.6 Replica Exchange Conformational sampling
Conformational equilibria relevant for the binding process occur on time scales which are unattainable with conventional MD even with the fastest supercomputers available. A commonly employed strategy to enhance sampling involves the application of biasing forces, and, as we discussed above, alchemical free energy methods employing hybrid potentials and potential of mean force approaches employing umbrella potentials can be considered as belonging to this general class of methods. It has been shown in many contexts[81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 21, 94, 95, 96] that generalized ensemble conformational sampling methods based on parallel replica exchange (RE) algorithms[97] can speed up by orders of magnitude the convergence of biased simulations. The key aspect of parallel RE algorithms as applied to alchemical calculations is that simulations at different values of λ, which are executed in parallel, periodically exchange λ values thereby allowing conformational transitions to occur at the value λ at which they are more likely to do so and, by so doing, to achieve more efficient exploration of conformational space. Some binding-induced conformational changes are more likely to occur at large λ’s, when the interaction between the ligand and the receptor is stronger, while others, such as reorientation of the ligand as a whole, are more likely to occur at small λ’s when motion is less restricted. With RE both kinds of conformational changes occur more easily in each individual replica causing a larger variety of conformations to appear at each λ, as opposed to, for example, conventional MD at fixed λ = 1 which is likely to explore only one or at most few conformations. Methods such as RETI,[81] FEP/REMD,[92] and BEDAM[21] are examples of binding free energy methods that employ this λ-hopping strategy.
3.7 Mining minima
Unlike the thermodynamic path methods discussed above, the mining minima (MM) binding free energy method[98] is one of two examples of end point methods (the other being the MM/PBSA method below) that will be discussed in this review. The MM free energy estimator is unique in that it does not rely on MD/MC importance sampling of conformations. Instead, the method estimates configurational integrals by unweighted sampling of conformations around a set of selected low energy states of the molecular system.[99] This feature constitute both the main advantage and main limitation of the method. On one hand MM does not suffer from slow rates of conformational transitions typical of importance sampling algorithms. On the other hand, this advantage is counterbalanced by the challenge of performing a sufficiently complete enumeration of the important stable minima of the system. Consequently the method has been applied with implicit solvation and it has been most useful in the study of association equilibria, such as host guest systems,[98, 33, 100, 101] with manageable number of degrees of freedom. Applications to protein-ligand binding equilibria have been also recently reported.[102]
MM seeks to compute the binding free energy in the implicit solvent representation by explicitly computing each of the configurational integrals ZRL and ZR+L in Eq. (22) and expressing the standard binding free energy in terms of the end point of the equilibrium as the difference of the free energies of the binding partners:
| (75) |
where GRL is the free energy of the complex and the binding partners, where
| (76) |
and similarly for GR and GL. Given a set of minima j, located by conformational sampling,[103] the configurational partition function, , of each state is approximated as the sum of local configurational partition functions zj corresponding to each minimum defined schematically as
| (77) |
where x represent the system coordinates and the integral is considered limited to the macrostate in the vicinity of the minimum. Local integrals are then computed by normal mode analysis assuming harmonic behavior augmented by numerical treatment of anharmonic deviations.[104, 98] As mentioned above the validity of the MM approach has been confirmed in several numerical applications.[98, 33, 100, 101, 102]
The MM method leads naturally to the study of the enthalpic and entropic components of the binding affinity.[33, 30] As described in Section 2.6.1 the binding free energy in the implicit solvent representation is decomposable into the change of average effective potential energy ΔUeff and the change in configurational entropy ΔSconf [Eq. (45)]. These can be expressed in terms of the average energies and entropies of the end point states computed as sums over minima. For example,
| (78) |
where pj = zj/Z is the population of the macrostate corresponding to minimum j and is its average potential energy. Similarly, it can be shown from Eq. (44) that the configurational entropy can be expressed as[30]
| (79) |
where Sj is the configurational entropy of macrostate j, which can be estimated from the harmonic approximation discussed above. From Eq. (79) we see that contributions to the configurational entropy of binding come from both narrowing of energy well (changes in Sj upon binding) as well as redistribution of populations among the stable states [the second term in r.h.s. of Eq. (79)], with both being important, and, often, determinant factors in ligand binding.[33, 8]
3.8 MM/PBSA and MM/GBSA approaches
The molecular mechanics-Poisson Boltzmann plus surface area (MM/PBSA) method,[105, 106, 107] and its generalized Born variant (MM/GBSA), are, like the MM method above, an example of an end point approach to the calculation of binding free energies. Unlike the MM method, however, it is based on MD to sample conformational space. MD, like any other importance sampling-based method, is not suitable for computing directly configurational integrals, as in the MM method. Instead MM-PBSA computes the binding free energy from using the enthalpy/entropy decomposition approach [Eq. (45)] with implicit solvation [the Poisson-Boltzmann (PB) model for MM/PBSA[108] and the generalized Born (GB) model for MM/GBSA[43, 45]]. In principle a decomposition of this kind also applies to explicit representations of the solvent [see for example Eqs (33) and (36)], however given the challenge of converging entropy and enthalpy changes with explicit solvation,[32] in practice the method is limited to implicit solvent representations.
In MM/PBSA the enthalpic term ΔUeff is computed as the difference between the average total potential energies in the bound and unbound states, collected from MD trajectories of the the free ligand, free receptor, and their complex, which can be obtained from either explicit or implicit solvent MD simulations. The same approaches discussed above in the context of the MM method are applicable to the calculation of configurational binding entropies. So, while in principle MM/PBSA is a rigorous formulation of the free energy of binding limited in principle only by the accuracy of the potential energy model, in practice MM/PBSA applications have implemented the theory with varying degree of rigor.
Partly due to the limited extent of conformational sampling afforded by MD, the change in configurational entropy is often estimated from one of few conformational macrostates[105, 109] possibly neglecting contributions to the entropy change resulting from changes in populations of stable states [Eq. (79)]. The quasiharmonic approximation[110] has also been employed to estimate the configurational entropy change, however its accuracy for systems with multiple occupied energy wells has been questioned.[111, 19] In some MM/PBSA applications the entropic terms have been neglected.[112]
Difficulties in converging potential energy differences due to noise originating from the bulk of receptor-receptor interactions have led to single-trajectory approaches[19, 112] in which the conformational ensembles for the free ligand and receptor are taken from the ensemble of the bound complex. This effectively replaces ΔUeff in Eq. (40) with the average binding energy neglecting therefore reorganization energy contributions [Eq. (48)]. When, in addition, entropic effects are neglected, the binding free energy is equated to the average binding energy.[113] At this level of theory all entropic and reorganization effects are neglected potentially leading to gross overestimation of binding affinities and lack of ability to discriminate binders from non-binders.[21]
3.9 Studies of Ligand and Receptor reorganization
The binding free energy [Eq. (46)] is often the result of a large cancellation between the favorable work, , of forming receptor-ligand interactions and the unfavorable work ΔGreorg, to localize and reorganize the conformational ensembles of the ligand and receptor to their bound conformational states. While drug design is often concerned with strengthening receptor-ligand interactions, the reorganization component can play a fundamental role in regulating binding specificity in cases where variations of binding energies are expected to be small. In such cases optimization of binding affinity can proceed by strategies aimed at preorganizing the ligand for binding, that is by minimizing ΔGreorg.
For example, reorganization has been successfully used as the design principle for the optimization of the presentation of HIV epitopes for vaccine development.[114] This particular application was concerned with identifying modes of display of an HIV epitope on the surface of a rhinovirus vaccine vehicle in such a way that it would bind strongly to a known neutralizing antibody. Because the displayed epitope needs to necessarily reproduce the interaction of the antibody with HIV target, the binding interface between the epitope and the antibody is biologically restrained. In thermodynamic terms the binding energy can be regarded as fixed and therefore preorganization of the epitope to the bound conformation is the only viable route for optimizing the binding affinity. Based on these reorganization concepts, molecular simulations were conducted which identified those presentation constructs with the highest fraction of epitope conformations compatible with antibody complexation.[115] Subsequent biochemical work confirmed the computational prediction and, remarkably, yielded some of the most antigenic vaccine constructs of this kind to date.[114]
In another recent example[116] optimization of a class of inhibitors was achieved by chemical rigidification of the ligands into their bound conformations. In this case structural analysis indicated that enhanced binding was indeed solely due to smaller reorganization penalties rather than stronger receptor-ligand interactions. Interestingly, in this work it was regarded as paradoxical the fact that enhanced binding was not due to a reduced entropic penalty as expected, but rather to a more favorable enthalpic gain. However, this should not be regarded as surprising considering that [see Eq. (47)] reorganization has both entropic as well enthalpic signatures. Evidently, before rigidification the ligands had to surmount an energetic penalty to form their bound conformations from their predominant solution conformations. The rigidified ligands instead did not suffer this penalty to the same extent, resulting in a more favorable binding enthalpy.
A number of recent studies have focused on ligand reorganization, which is simpler to model than receptor reorganization. Both Yang et al.[117] and, on a more extensive set of systems, Gao et al.,[118] observed better correlation with experimental affinities when singletrajectory MM/GBSA scores were combined with ligand reorganization free energy estimates. As discussed above, the single-trajectory MM/GBSA model approximates the binding free energy with the ligand-receptor average binding energy, , which, although easier to converge, omits sometimes critical reorganization free energy components [Eq. (46)]. By introducing the ligand reorganization free energy, some of these effects are recaptured without substantially compromising the quality of the convergence, since most of the fluctuations in the MM/GBSA estimators come from the much more numerous degrees of freedom of the receptor. The ligand reorganization is defined as the sum of the ligand reorganization defined as [see Eq. (48)]
| (80) |
and the change of ligand configuration entropy −TΔSconf(L). The latter is evaluated using the harmonic and quasi-harmonic approaches discussed above. Gao et al.,[118] adopted a particularly rigorous entropic model incorporating both multiple minima [Eq. (79)] and anharmonic corrections.[119, 98] It has been recently confirmed[120] that MD sampling aided by temperature replica exchange can also be used to accurately compute ligand reorganization free energies. Interestingly it is observed[117] that the ligand configurational entropy does not always oppose binding. In a number of cases there is a gain of entropy [positive ΔSconf(L)] counterbalanced by an unfavorable reorganization energy. The same conclusion is suggested by the experimental work of DeLorbe et al.[116] discussed above. This phenomenon might be quite general as it is known[121] that ligands tend to form more extended, and possibly more flexible, conformations when bound to the receptor[121] than in solution, where hydrophobicity causes them to adopt more compact conformations.
Binding modeling studies explicitly incorporating receptor reorganization effects are also beginning to appear. Major challenges exist due to the size of conformational space and the rarity of conformational transitions. Some recent studies have focused on the role of protein sidechain motion. Mobley et al.[34] have introduced a confine and release method to model the free energy associated with the conformation variability of a selected set of sidechains in the binding site region. The technique consists of evaluating the binding free energy with the receptor sidechains placed in various rotamer states. These are then combined, based on Eq. (51), with the free energy differences between rotamer states with and without the ligand present to yield the total binding free energy. In a number of cases it was shown that including these terms improved the accuracy of binding affinity predictions.[34, 63, 37] Similarly, a two-dimensional Hamiltonian replica exchange free energy perturbation approach has been proposed to soften sidechain torsional barriers.[93]
4 Conclusions
The accurate estimation of protein-ligand affinities remains one of the most difficult problem in computational biophysics. Atomistic free energy models of binding are progressively improving and will continue to represent important tools to further our understanding of molecular recognition phenomena and contribute to pharmaceutical research. Better potential models, more efficient computational algorithms, and faster computers are driving this progress forward. As this is happening it is important that the relationships between theory and calculations remain clear and well understood. We have reviewed the statistical mechanics theory of binding, and we have shown how current computational methods and applications relate to the fundamental theory. These models have different features and limitations, and their ranges of applicability vary correspondingly. Yet their origins can all be traced back to a single fundamental theory. It is our hope that finding these commonalities will be useful to novices and experts alike to help them navigate the expanding universe of binding free energy methodologies, and find novel ways to use them to study complex molecular recognition problems.
Acknowledgments
This work has been supported in part by a research grant from the National Institute of Health (GM30580).
Footnotes
The separation of the overall translations is exact, while the separation of rotational degrees of freedom neglects vibrational-rotational couplings. The latter is generally a valid approximation at physiological temperature.
However, note that integration over the external degrees of the freedom ζL for the solvation free energy calculation [Eq. (12)] is unnecessary and has been explicitly indicated only for consistency with the thermodynamic cycle indicated below; both the solution and gas phases are homogeneous and isotropic, and therefore integration over the translational and rotational degrees of freedom ζL yields a canceling factor of VsiteΩsite in both the numerator and the denominator of Eq. (12).
In principle Eq. (44) should include an additional constant term corresponding to the multiplicative factor necessary to make the classical partition function dimensionless. This term, which cancels the dimensions of the distribution function within the logarithm in Eq. (44), is omitted here for brevity because it cancels out when taking differences between the quantities corresponding to the unbound and bound states.
Note that these averages still contain the I(ζL) indicator functions (assumed to be the same for the two ligands). Like absolute binding free energies, therefore, relative binding free energies are dependent on the definition of the complexed state. This aspect is often overlooked in the literature.
References
- [1].Jorgensen William L. The many roles of computation in drug discovery. Science. 2004 Mar;303(5665):1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- [2].Guvench Olgun, MacKerell Alexander D. Computational evaluation of protein-small molecule binding. Curr. Opin. Struct. Biol. 2009 Feb;19(1):56–61. doi: 10.1016/j.sbi.2008.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Mobley DL, Shirts MR, Brown SP. Structure Based Drug Discovery, chapter Free energy calculations in structure-based drug design. Cambridge University Press; 2010. [Google Scholar]
- [4].Brooijmans Natasja, Kuntz Irwin D. Molecular recognition and docking algorith. Annu. Rev. Biophys. Biomol. Struct. 2003;32:335–373. doi: 10.1146/annurev.biophys.32.110601.142532. [DOI] [PubMed] [Google Scholar]
- [5].McInnes Campbell. Virtual screening strategies in drug discovery. Curr. Opin. Chem. Biol. 2007 Oct;11(5):494–502. doi: 10.1016/j.cbpa.2007.08.033. [DOI] [PubMed] [Google Scholar]
- [6].Shoichet Brian K. Virtual screening of chemical libraries. Nature. 2004 Dec;432(7019):862–865. doi: 10.1038/nature03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zhou Zhiyong, Felts Anthony K, Friesner Richard A, Levy onald M. Comparative performance of several flexible docking programs and scoring functions: enrichment studies for a diverse set of pharmaceutically relevant targets. J. Chem. Inf. Model. 2007;47(4):1599–1608. doi: 10.1021/ci7000346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Gilson Michael K, Zhou Huan-Xiang. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct. 2007;36:21–42. doi: 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- [9].Shirts MR, Mobley DL, Chodera JD. Alchemical free energy calculations: ready for prime time? Ann. Rep. Comput. Chem. 2007;3:41–59. [Google Scholar]
- [10].Mobley David L, Dill Ken A. Binding of small-molecule ligands to proteins: “what you see” is not always “what you get”. Structure. 2009 Apr;17(4):489–498. doi: 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Deng Yuqing, Roux Benoît. Computations of standard binding free energies with molecular dynamics simulations. J. Phys. Chem. B. 2009 Feb;113(8):2234–2246. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Chodera John D., Mobley David L., Shirts Michael R., Dixon Richard W., Branson Kim, Pande Vijay S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Op. Struct. Biol. 2011 doi: 10.1016/j.sbi.2011.01.011. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Chipot Christophe, Pohorille Andrew., editors. Theory and Applications in Chemistry and Biology. Springer Series in Chemical Physics; Springer, Berlin Heidelberg, Berlin Heidelberg: 2007. Free Energy Calculations. [Google Scholar]
- [14].Gilson MK, Given JA, Bush BL, McCammon JA. The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys. J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Boresch S, Tettinger F, Leitgeb M, Karplus M. Absolute binding free energies: A quantitative approach for their calculation. J. Phys. Chem. B. 2003;107(35):9535–9551. [Google Scholar]
- [16].Jorgensen William L. Interactions between amides in solution and the thermodynamics of weak binding. Journal of the American Chemical Society. 1989 May;111(10):3770–3771. [Google Scholar]
- [17].Luo Hengbin, Sharp Kim. On the calculation of absolute macromolecular binding free energies. Proceedings of the National Academy of Sciences of the United States of America. 2002;99(16):10399–10404. doi: 10.1073/pnas.162365999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Woo Hyung-June, Roux Benoît. Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. USA. 2005 May;102(19):6825–6830. doi: 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Lee Michael S, Olson Mark A. Calculation of absolute protein-ligand binding affinity using path and endpoint approaches. Biophys. J. 2006 Feb;90(3):864–877. doi: 10.1529/biophysj.105.071589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Roux B, Simonson T. Implicit solvent models. Biophys. Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- [21].Gallicchio Emilio, Lapelosa Mauro, Levy Ronald M. Binding energy distribution analysis method (BEDAM) for estimation of protein-ligand binding affinities. J. Chem. Theory Comput. 2010 Sep;6(9):2961–2977. doi: 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Widom B. Potential-distribution theory and the statistical mechanics of fluids. J. Phys. Chem. 1982 Mar;86(6):869–872. [Google Scholar]
- [23].Beck Tom L., Paulaitis Michael E., Pratt Lawrence R. The Potential Distribution Theorem and Models of Molecular Solutions. Cambridge University Press; New York: 2006. [Google Scholar]
- [24].Pohorille A, Pratt LR. Cavities in molecular liquids and the theory of hydrophobic solubilities. J. Am. Chem. Soc. 1990;112(13):5066–5074. doi: 10.1021/ja00169a011. [DOI] [PubMed] [Google Scholar]
- [25].Widom B. Some topics in the theory of fluids. J. Chem. Phys. 1963 Dec;39(11):2808–2812. [Google Scholar]
- [26].Lu Nandou, Singh Jayant K., Kofke David A. Appropriate methods to combine forward and reverse free-energy perturbation averages. J. Chem. Phys. 2003 Feb;118(7):2977–2984. [Google Scholar]
- [27].Mihailescu Mihail, Gilson Michael K. On the theory of noncovalent binding. Biophys. J. 2004 Jul;87(1):23–36. doi: 10.1529/biophysj.103.031682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Groot Robert D. The association constant of a flexible molecule and a single atom: Theory and simulation. J. Chem. Phys. 1992 Sep;97(5):3537–3549. [Google Scholar]
- [29].Barbieri Christopher M., Kaul Malvika, Pilch Daniel S. Use of 2-aminopurine as a fluorescent tool for characterizing antibiotic recognition of the bacterial rrna a-site. Tetrahedron. 2007 Apr;63(17):3567–3574. doi: 10.1016/j.tet.2006.08.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Zhou Huan-Xiang, Gilson Michael K. Theory of free energy and entropy in noncovalent binding. Chem. Rev. 2009 Sep;109(9):4092–4107. doi: 10.1021/cr800551w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Serdyuk Igor N., Zaccai Nathan R., Zaccai Giuseppe. Methods in Molecular Biophysics: Structure, Dynamics, Function. Cambridge University Press; Cambridge ; New York: 2007. [Google Scholar]
- [32].Levy RM, Gallicchio E. Computer simulations with explicit solvent: Recent progress in the thermodynamic decomposition of free energies and in modeling electrostatic effects. Annu. Rev. Phys. Chem. 1998;49:531–67. doi: 10.1146/annurev.physchem.49.1.531. [DOI] [PubMed] [Google Scholar]
- [33].Chang Chia-en A, Chen Wei, Gilson Michael K. Ligand configurational entropy and protein binding. Proc. Natl. Acad. Sci. USA. 2007 Jan;104(5):1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Mobley David L, Chodera John D, Dill Ken A. The confine-and-release method: Obtaining correct binding free energies in the presence of protein conformational change. J. Chem. Theory Comput. 2007;3(4):1231–1235. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Jayachandran Guha, Shirts Michael R, Park Sanghyun, Pande Vijay S. Parallelized-over-parts computation of absolute binding free energy with docking and molecular dynamics. J. Chem. Phys. 2006 Aug;125(8):084901. doi: 10.1063/1.2221680. [DOI] [PubMed] [Google Scholar]
- [36].Mobley David L, Chodera John D, Dill Ken A. On the use of orientational restraints and symmetry corrections in alchemical free energy calculations. J. Chem. Phys. 2006 Aug;125(8):084902. doi: 10.1063/1.2221683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Boyce Sarah E, Mobley David L, Rocklin Gabriel J, Graves Alan P, Dill Ken A, Shoichet Brian K. Predicting ligand binding affinity with alchemical free energy methods in a polar model binding site. J. Mol. Biol. 2009 Dec;394(4):747–763. doi: 10.1016/j.jmb.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Cornell Wendy D., Cieplak Piotr, Bayly Christopher I., Gould Ian R., Merz Kenneth M., Ferguson David M., Spellmeyer David C., Fox Thomas, Caldwell James W., Kollman Peter A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. Journal of the American Chemical Society. 1995 May;117(19):5179–5197. [Google Scholar]
- [39].Jorgensen WL, Maxwell DS, Tirado-Rives J. Developement and testing of the opls all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- [40].MacKerell AD, Bashford D, Bellott, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. The Journal of Physical Chemistry B. 1998 Apr;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- [41].Schuler Lukas D., Daura Xavier, van Gunsteren Wilfred F. An improved gromos96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 2001;22(11):1205–1218. [Google Scholar]
- [42].Lazaridis T, Karplus M. Ėective energy function for protein in solution. Proteins. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- [43].Bashford D, Case DA. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- [44].Wagoner J, Baker NA. Assessing implicit models for nonpolar mean solvation forces: The importance of dispersion and volume terms. Proc. Natl. Acad. Sci. 2006;103:8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Chen J, Brooks CL, III, Khandogin J. Recent advances in implicit solvent based methods for biomolecular simulations. Curr. Opin. Struct. Biol. 2008;18:140–148. doi: 10.1016/j.sbi.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Gallicchio Emilio, Paris Kristina, Levy Ronald M. The agbnp2 implicit solvation model. J. Chem. Theory Comput. 2009 Sep;5(9):2544–2564. doi: 10.1021/ct900234u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Swanson Jessica M J, Henchman Richard H, Andrew McCammon J. Revisiting free energy calculations: a theoretical connection to mm/pbsa and direct calculation of the association free energy. Biophys J. 2004 Jan;86(1 Pt 1):67–74. doi: 10.1016/S0006-3495(04)74084-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Zwanzig Robert W. High-temperature equation of state by a perturbation method. i. nonpolar gases. J. Chem. Phys. 1954 Aug;22(8):1420–1426. [Google Scholar]
- [49].Pohorille Andrew, Jarzynski Christopher, Chipot Christophe. Good practices in free-energy calculations. J Phys Chem B. 2010 Aug;114(32):10235–10253. doi: 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
- [50].Lu Nandou, Kofke David A. Accuracy of free-energy perturbation calculations in molecular simulation. i. modeling. J. Chem. Phys. 2001 May;114(17):7303–7311. [Google Scholar]
- [51].Michel Julien, Essex Jonathan W. Prediction of protein-ligand binding affinity by free energy simulations: assumptions, pitfalls and expectations. J Comput Aided Mol Des. 2010 Aug;24(8):639–658. doi: 10.1007/s10822-010-9363-3. [DOI] [PubMed] [Google Scholar]
- [52].Bennett Charles H. Efficient estimation of free energy differences from monte carlo data. Journal of Computational Physics. 1976 Oct;22(2):245–268. [Google Scholar]
- [53].Ferrenberg AM, Swendsen RH. Optimized monte carlo data analysis. Phys. Rev. Lett. 1989;63:1195–1198. doi: 10.1103/PhysRevLett.63.1195. [DOI] [PubMed] [Google Scholar]
- [54].Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. i. the method. J. Comp. Chem. 1992;13:1011–1021. [Google Scholar]
- [55].Gallicchio E, Andrec M, Felts AK, Levy RM. Temperature weighted histogram analysis method, replica exchange, and transition paths. J. Phys. Chem. B. 2005;109:6722–6731. doi: 10.1021/jp045294f. [DOI] [PubMed] [Google Scholar]
- [56].Tan Zhiqiang. On a likelihood approach for monte carlo integration. Journal of the American Statistical Association. 2004;99(468):1027–1036. [Google Scholar]
- [57].Shirts Michael R, Chodera John D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008 Sep;129(12):124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Eriksson AE, Baase WA, Wozniak JA, Matthews BW. A cavity-containing mutant of t4 lysozyme is stabilized by buried benzene. Nature. 1992 Jan;355(6358):371–373. doi: 10.1038/355371a0. [DOI] [PubMed] [Google Scholar]
- [59].Graves Alan P, Brenk Ruth, Shoichet Brian K. Decoys for docking. J. Med. Chem. 2005 Jun;48(11):3714–3728. doi: 10.1021/jm0491187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Morton A, Baase WA, Matthews BW. Energetic origins of specificity of ligand binding in an interior nonpolar cavity of t4 lysozyme. Biochemistry. 1995 Jul;34(27):8564–8575. doi: 10.1021/bi00027a006. [DOI] [PubMed] [Google Scholar]
- [61].Wei Binqing Q, Baase Walter A, Weaver Larry H, Matthews Brian W, Shoichet Brian K. A model binding site for testing scoring functions in molecular docking. J. Mol. Biol. 2002 Sep;322(2):339–355. doi: 10.1016/s0022-2836(02)00777-5. [DOI] [PubMed] [Google Scholar]
- [62].Deng Yuqing, Roux Benoît. Calculation of standard binding free energies: Aromatic molecules in the t4 lysozyme l99a mutant. J. Chem. Theory Comput. 2006 Sep;2(5):1255–1273. doi: 10.1021/ct060037v. [DOI] [PubMed] [Google Scholar]
- [63].Mobley David L, Graves Alan P, Chodera John D, McReynolds Andrea C, Shoichet Brian K, Dill Ken A. Predicting absolute ligand binding free energies to a simple model site. J. Mol. Biol. 2007 Aug;371(4):1118–1134. doi: 10.1016/j.jmb.2007.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Wang Jiyao, Deng Yuqing, Roux Benoît. Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials. Biophys. J. 2006 Oct;91(8):2798–2814. doi: 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Holt Dennis A., Luengo Juan I., Yamashita Dennis S., Ja Oh Hye, Konialian Arda L., Kwo Yen Hwa, Rozamus Leonard W., Brandt Martin, Bossard Mary J. Design, synthesis, and kinetic evaluation of high-affinity fkbp ligands and the x-ray crystal structures of their complexes with fkbp12. Journal of the American Chemical Society. 1993 Nov;115(22):9925–9938. [Google Scholar]
- [66].Jiao Dian, Golubkov Pavel A, Darden Thomas A, Ren Pengyu. Calculation of protein-ligand binding free energy by using a polarizable potential. Proc Natl Acad Sci U S A. 2008 Apr;105(17):6290–6295. doi: 10.1073/pnas.0711686105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Jiao Dian, Zhang Jiajing, Duke Robert E., Li Guohui, Schnieders Michael J., Ren Pengyu. Trypsin-ligand binding free energies from explicit and implicit solvent simulations with polarizable potential. J. Comput. Chem. 2009;30(11):1701–1711. doi: 10.1002/jcc.21268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Ge Xiaoxia, Roux Benoit. Absolute binding free energy calculations of sparsomycin analogs to the bacterial ribosome. J Phys Chem B. 2010 Jul;114(29):9525–9539. doi: 10.1021/jp100579y. [DOI] [PubMed] [Google Scholar]
- [69].Jorgensen WL, Buckner JK, Boudon S, Tirado-Rives J. Efficient computation of absolute free energies of binding by computer simulations. application to the methane dimer in water. J. Chem. Phys. 1988;89(6):3742. [Google Scholar]
- [70].Fujitani Hideaki, Tanida Yoshiaki, Ito Masakatsu, Jayachandran Guha, Snow Christopher D, Shirts Michael R, Sorin Eric J, Pande Vijay S. Direct calculation of the binding free energies of fkbp ligands. J Chem Phys. 2005 Aug;123(8):084108. doi: 10.1063/1.1999637. [DOI] [PubMed] [Google Scholar]
- [71].Miyamoto S, Kollman PA. Absolute and relative binding free energy calculations of the interaction of biotin and its analogs with streptavidin using molecular dynamics/free energy perturbation approaches. Proteins. 1993 Jul;16(3):226–245. doi: 10.1002/prot.340160303. [DOI] [PubMed] [Google Scholar]
- [72].Steinbrecher Thomas, Mobley David L, Case David A. Nonlinear scaling schemes for lennard-jones interactions in free energy calculations. J Chem Phys. 2007 Dec;127(21):214108. doi: 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
- [73].Payne VA, Matubayasi N, Reed Murphy L, Levy RM. Monte carlo study of the effect of pressure on hydrophobic association. J. Phys. Chem. B. 1997;101:2054–2060. [Google Scholar]
- [74].Reddy MR, Erion MD, editors. Free Energy Calculations in Rational Drug Design. Springer-Verlag; 2001. [Google Scholar]
- [75].Tembe BL, McCammon JA. Ligand-receptor interactions. Computers & Chemistry. 1984;8(4):281. [Google Scholar]
- [76].Oostenbrink Chris, van Gunsteren Wilfred F. Free energies of ligand binding for structurally diverse compounds. Proc Natl Acad Sci U S A. 2005 May;102(19):6750–6754. doi: 10.1073/pnas.0407404102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Jorgensen William L., Thomas Laura L. Perspective on free-energy perturbation calculations for chemical equilibria. J. Chem. Theory Comput. 2008 Jun;4(6):869–876. doi: 10.1021/ct800011m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Jorgensen William L. Efficient drug lead discovery and optimization. Acc Chem Res. 2009 Jun;42(6):724–733. doi: 10.1021/ar800236t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Knight Jennifer L, Brooks Charles L. Lambda-dynamics free energy simulation methods. J Comput Chem. 2009 Aug;30(11):1692–1700. doi: 10.1002/jcc.21295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Shirts Michael R., Mobley David L., Brown Scott P. Free-energy calculations in structure-based drug design. Cambridge University Press; 2010. Drug Design - Structure- and Ligand-Based Approaches; pp. 61–86. [Google Scholar]
- [81].Woods Christopher J., Essex Jonathan W., King Michael A. The development of replica-exchange-based free-energy methods. J. Phys. Chem. B. 2003 Dec;107(49):13703–13710. [Google Scholar]
- [82].Woods Christopher J., Essex Jonathan W., King Michael A. Enhanced configurational sampling in binding free-energy calculations. J. Phys. Chem. B. 2003 Dec;107(49):13711–13718. [Google Scholar]
- [83].Murata Katsumi, Sugita Yuji, Okamoto Yuko. Free energy calculations for dna base stacking by replica-exchange umbrella sampling. Chemical Physics Letters. 2004 Feb;385(1-2):1–7. [Google Scholar]
- [84].Liu P, Kim B, Friesner RA, Berne BJ. Replica exchange with solute tempering: A method for sampling biological systems in explicit solvent. Proc. Natl. Acad. Sci. USA. 2005;102:13749–13754. doi: 10.1073/pnas.0506346102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Bussi Giovanni, Luigi Gervasio Francesco, Laio Alessandro, Parrinello Michele. Free-energy landscape for β hairpin folding from combined parallel tempering and metadynamics. Journal of the American Chemical Society. 2006 Oct;128(41):13435–13441. doi: 10.1021/ja062463w. [DOI] [PubMed] [Google Scholar]
- [86].Liu Pu, Huang Xuhui, Zhou Ruhong, Berne BJ. Hydrophobic aided replica exchange: an efficient algorithm for protein folding in explicit solvent. J Phys Chem B. 2006 Sep;110(38):19018–19022. doi: 10.1021/jp060365r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Piana Stefano, Laio Alessandro. A bias-exchange approach to protein folding. The Journal of Physical Chemistry B. 2007 May;111(17):4553–4559. doi: 10.1021/jp067873l. [DOI] [PubMed] [Google Scholar]
- [88].Roitberg Adrian E, Okur Asim, Simmerling Carlos. Coupling of replica exchange simulations to a non-boltzmann structure reservoir. J Phys Chem B. 2007 Mar;111(10):2415–2418. doi: 10.1021/jp068335b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Hritz Jozef, Oostenbrink Chris. Hamiltonian replica exchange molecular dynamics using soft-core interactions. J. Chem. Phys. 2008 Apr;128(14):144121. doi: 10.1063/1.2888998. [DOI] [PubMed] [Google Scholar]
- [90].Neale Chris, Rodinger Tomas, Pomès Régis. Equilibrium exchange enhances the convergence rate of umbrella sampling. Chemical Physics Letters. 2008 Jul;460(1-3):375–381. [Google Scholar]
- [91].Yeh In-Chul, Olson Mark A., Lee Michael S., Wallqvist Anders. Free-energy profiles of membrane insertion of the m2 transmembrane peptide from influenza a virus. Biophysical Journal. 2008 Dec;95(11):5021–5029. doi: 10.1529/biophysj.108.133579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Jiang Wei, Hodoscek Milan, Roux Benoît. Computation of absolute hydration and binding free energy with free energy perturbation distributed replica-exchange molecular dynamics. J. Chem. Theory Comput. 2009 Oct;5(10):2583–2588. doi: 10.1021/ct900223z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Jiang Wei, Roux Benoît. Free energy perturbation hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J. Chem. Theory Comput. 2010 Jul;6:2559–2565. doi: 10.1021/ct1001768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Mitsutake Ayori, Mori Yoshiharu, Okamoto Yuko. Multi-dimensional multicanonical algorithm, simulated tempering, replica-exchange method, and all that. Physics Procedia. 2010;4:89–105. [Google Scholar]
- [95].Khavrutskii Ilja V., Wallqvist Anders. Computing relative free energies of solvation using single reference thermodynamic integration augmented with hamiltonian replica exchange. Journal of Chemical Theory and Computation. 2010 Nov;6(11):3427–3441. doi: 10.1021/ct1003302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Meng Yilin, Roitberg Adrian E. Constant ph replica exchange molecular dynamics in biomolecules using a discrete protonation model. J Chem Theory Comput. 2010 Apr;6(4):1401–1412. doi: 10.1021/ct900676b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- [98].Chang Chia-En, Gilson Michael K. Free energy, entropy, and induced fit in host-guest recognition: calculations with the second-generation mining minima algorithm. J. Am. Chem. Soc. 2004 Oct;126(40):13156–13164. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- [99].Head Martha S., Given James A., Gilson Michael K. Mining minima: Direct computation of conformational free energy. The Journal of Physical Chemistry A. 1997 Feb;101(8):1609–1618. [Google Scholar]
- [100].Rekharsky Mikhail V, Mori Tadashi, Yang Cheng, Ho Ko Young, Selvapalam N, Kim Hyunuk, Sobransingh David, Kaifer Angel E, Liu Simin, Isaacs Lyle, Chen Wei, Moghaddam Sarvin, Gilson Michael K, Kim Kimoon, Inoue Yoshihisa. A synthetic host-guest system achieves avidin-biotin affinity by overcoming enthalpy-entropy compensation. Proc Natl Acad Sci U S A. 2007 Dec;104(52):20737–20742. doi: 10.1073/pnas.0706407105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Moghaddam Sarvin, Inoue Yoshihisa, Gilson Michael K. Host-guest complexes with protein-ligand-like affinities: computational analysis and design. J Am Chem Soc. 2009 Mar;131(11):4012–4021. doi: 10.1021/ja808175m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Chen I-Jen, Foloppe Nicolas. Drug-like bioactive structures and conformational coverage with the ligprep/confgen suite: comparison to programs moe and catalyst. J Chem Inf Model. 2010 May;50(5):822–839. doi: 10.1021/ci100026x. [DOI] [PubMed] [Google Scholar]
- [103].Chang Chia-En, Gilson Michael K. Tork: Conformational analysis method for molecules and complexes. J Comput Chem. 2003 Dec;24(16):1987–1998. doi: 10.1002/jcc.10325. [DOI] [PubMed] [Google Scholar]
- [104].Chang Chia-En, Potter Michael J., Gilson Michael K. Calculation of molecular configuration integrals. The Journal of Physical Chemistry B. 2003 Jan;107(4):1048–1055. [Google Scholar]
- [105].Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000 Dec;33(12):889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- [106].Gouda Hiroaki, Kuntz Irwin D, Case David A, Kollman Peter A. Free energy calculations for theophylline binding to an rna aptamer: Comparison of mm-pbsa and thermodynamic integration methods. Biopolymers. 2003 Jan;68(1):16–34. doi: 10.1002/bip.10270. [DOI] [PubMed] [Google Scholar]
- [107].Chong Lillian T, Pitera Jed W, Swope William C, Pande Vijay S. Comparison of computational approaches for predicting the effects of missense mutations on p53 function. J. Mol. Graph. Model. 2009;27(8):978–982. doi: 10.1016/j.jmgm.2008.12.006. [DOI] [PubMed] [Google Scholar]
- [108].Baker NA. Improving implicit solvent simulations: a poisson-centric view. Curr. Opin. Struct. Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- [109].Foloppe N, Hubbard R. Towards predictive ligand design with free-energy based computational methods? Curr Med Chem. 2006;13(29):3583–3608. doi: 10.2174/092986706779026165. [DOI] [PubMed] [Google Scholar]
- [110].Levy Ronald M., Karplus Martin, Kushick Joseph, Perahia David. Evaluation of the configurational entropy for proteins: Application to molecular dynamics simulations of an α-helix. Macromolecules. 1984;17:1370–1374. [Google Scholar]
- [111].Chang Chia-En, Chen Wei, Gilson Michael K. Evaluating the accuracy of the quasiharmonic approximation. Journal of Chemical Theory and Computation. 2005 Sep;1(5):1017–1028. doi: 10.1021/ct0500904. [DOI] [PubMed] [Google Scholar]
- [112].Brown Scott P, Muchmore Steven W. Rapid estimation of relative protein-ligand binding affinities using a high-throughput version of mm-pbsa. J. Chem. Inf. Model. 2007;47(4):1493–1503. doi: 10.1021/ci700041j. [DOI] [PubMed] [Google Scholar]
- [113].Brown Scott P, Muchmore Steven W. High-throughput calculation of protein-ligand binding affinities: modification and adaptation of the mm-pbsa protocol to enterprise grid computing. J Chem Inf Model. 2006;46(3):999–1005. doi: 10.1021/ci050488t. [DOI] [PubMed] [Google Scholar]
- [114].Lapelosa Mauro, Ferstandig Arnold Gail, Gallicchio Emilio, Arnold Eddy, Levy Ronald M. Antigenic characteristics of rhinovirus chimeras designed in silico for enhanced presentation of HIV-1 gp41 epitopes. J Mol Biol. 2010 Apr;397(3):752–766. doi: 10.1016/j.jmb.2010.01.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Lapelosa Mauro, Gallicchio Emilio, Ferstandig Arnold Gail, Arnold Eddy, Levy Ronald M. In silico vaccine design based on molecular simulations of rhinovirus chimeras presenting hiv-1 gp41 epitopes. J Mol Biol. 2009 Jan;385(2):675–691. doi: 10.1016/j.jmb.2008.10.089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].DeLorbe John E, Clements John H, Teresk Martin G, Benfield Aaron P, Plake Hilary R, Millspaugh Laura E, Martin Stephen F. Thermodynamic and structural effects of conformational constraints in protein-ligand interactions. entropic paradoxy associated with ligand preorganization. J. Am. Chem. Soc. 2009 Nov;131(46):16758–16770. doi: 10.1021/ja904698q. [DOI] [PubMed] [Google Scholar]
- [117].Yang Chao-Yie, Sun Haiying, Chen Jianyong, Nikolovska-Coleska Zaneta, Wang Shaomeng. Importance of ligand reorganization free energy in protein-ligand binding-affinity prediction. J. Am. Chem. Soc. 2009 Sep;131(38):13709–13721. doi: 10.1021/ja9039373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Gao Cen, Park Min-Sun, Stern Harry A. Accounting for ligand conformational restriction in calculations of protein-ligand binding affinities. Biophys J. 2010 Mar;98(5):901–910. doi: 10.1016/j.bpj.2009.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Kolossvary Istvan. Evaluation of the molecular configuration integral in all degrees of freedom for the direct calculation of conformational free energies: Prediction of the anomeric free energy of monosaccharides. The Journal of Physical Chemistry A. 1997 Dec;101(51):9900–9905. [Google Scholar]
- [120].Okumura Hisashi, Gallicchio Emilio, Levy Ronald M. Conformational populations of ligand-sized molecules by replica exchange molecular dynamics and temperature reweighting. J. Comput. Chem. 2010;31:1357–1367. doi: 10.1002/jcc.21419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Perola Emanuele, Charifson Paul S. Conformational analysis of drug-like molecules bound to proteins: an extensive study of ligand reorganization upon binding. J Med Chem. 2004 May;47(10):2499–2510. doi: 10.1021/jm030563w. [DOI] [PubMed] [Google Scholar]