A Tetrahedral Representation of the Genetic Code Emphasizing Aspects of Symmetry

Abstract

The genetic code is a mapping of 64 codons to 22 actions, including polypeptide chain initiation, termination, and incorporation of the twenty amino acids. The standard tabular representation is useful for looking up which amino acid is encoded by a particular codon, but says little about functional relationships in the code. The possibility of making sense of the code rather than simply enumerating its codon-to-action pairings therefore is appealing, and many have attempted to find geometric representations of the code that illuminate its functional organization. Here, I show that a regular tetrahedron with each of its four faces divided into sixteen equilateral triangles (for a total of 64 triangular ‘cells’) is a particularly apt geometry for representing the code. I apply five principles of symmetry and balance in order to assign codons to the triangular cells of the tetrahedral faces. These principles draw on various aspects of the genetic code and the twenty amino acids, making the final construct a positional balance of the amino acids and their functions rather than a re-analysis of them. The potential significance of this exercise, and others like it, is that this way of organizing the biological facts may provide new insights into them.

INTRODUCTION

The genetic code maps the 64 possible nucleotide triplets, or codons, to 22 distinct ribosomal operations (including the 20 amino acid specifications and chain initiation and termination). The most familiar representations of the code are tables organized by the identity of the nucleotides at each of the three-codon positions. These tables are convenient representations of the raw facts of correspondence, but they also point to underlying order within the code. Most notably, the sixteen codons with uracil (U) at the middle position all encode hydrophobic amino acids. If this is an organizing principle, might there be others as well? That possibility, coupled with the idea that some geometric representations of the code might display the code’s underlying organization better than others has generated interest in functional representations—ways of displaying the basic mapping that emphasize possible principles of organization rather than ease of looking up the mapped pairs. If the genetic code can be represented in ways that offer important insights into the biological properties of its components, these representations may be of use both in education and in bioinformatics.

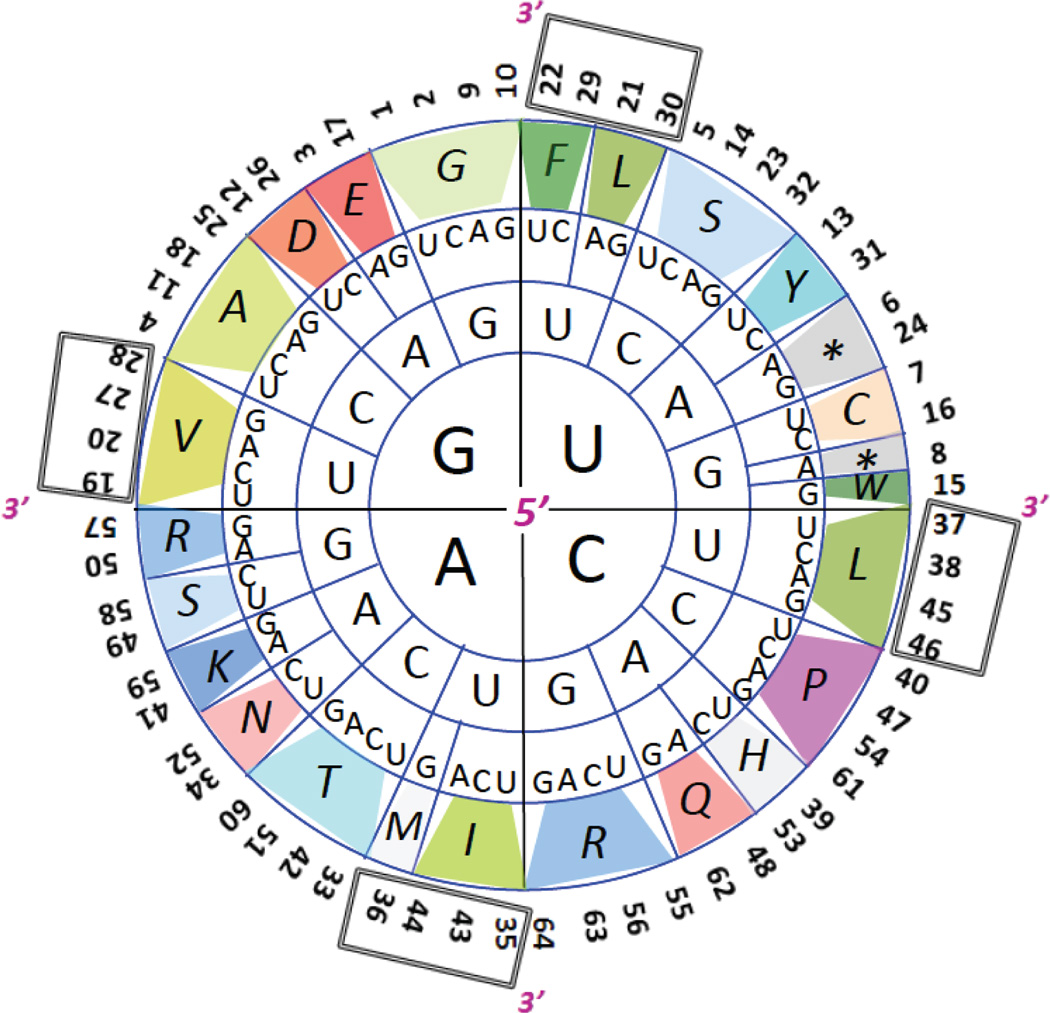
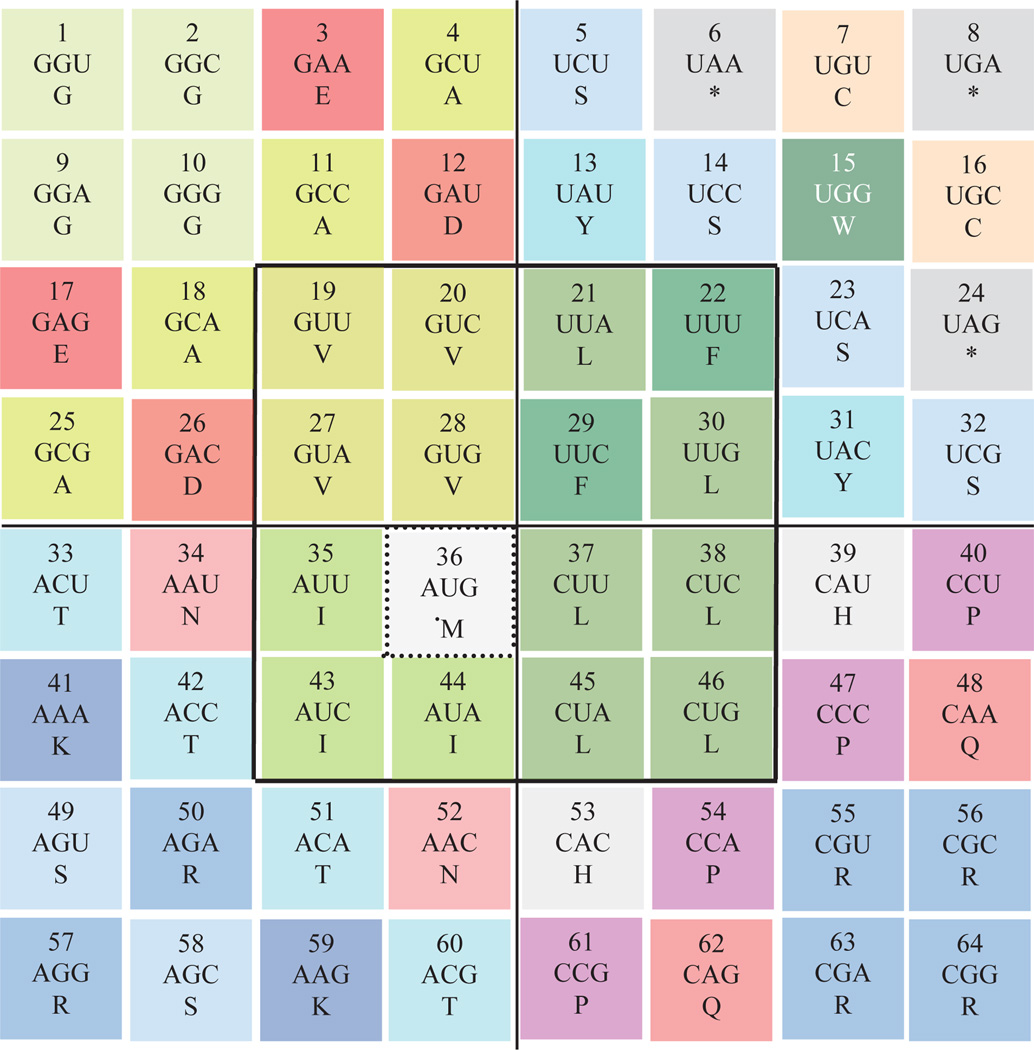
The earliest known tabular representation of the 64 codons was sketched out by Nirenberg in 1965 but left unpublished [1]. Since then several two-dimensional representations of the code have been in common use, including the classic circular one of Figure 1 [2–6]. That particular representation emphasizes the periodicity of the code, in that there is a clear hydrophobic to hydrophilic cycle in the character of the encoded amino acids within each quadrant of the circle [4–5]. Rectangular grid representations can likewise capture this periodicity (Fig. 2) [6].

Figure 1. The classic circular genetic code.

Codons specifying hydrophobic amino acids are spaced at 90° as part of the design of the circular representation, and their numerical assignments are enclosed in boxes (see Fig. 2 legend for explanation of numerical assignments). Codons are read from inside (5′) to outside (3′) of the circle. Amino acids are identified by their single letter codes, and are assigned colors in this and all figures based on aspects of their chemical properties, in order to facilitate comparison of different code representations. Hydrophobic amino acids Leu (L), Ile (I), Val (V), Phe (F) and Trp (W) are colored green; basic amino acids Lys (K), Arg (R), and His (H) are blue or gray; acidic amino acids Asp (D) and Glu (E), and their respective amides Asn (N) and Gln (Q) are orange to salmon in color; amino acids with hydroxyl groups—Ser (S), Tyr (Y) and Thr (T)—are light blue or teal; Cys (C), Pro (P), Gly (G) and Ala (A) are beige, fuschia, or light green; Met (M) (the initiation code) and the termination codons (indicated by *) are colored gray. doi:10.5048/BIO-C.2012.2.f1

Figure 2. An 8 × 8 square representation of the genetic code.

Adapted from reference 6, this representation places the hydrophobic amino acids within the central square. Asterisks indicate stop codons, as before, with a dashed square marking the start codon. The order of appearance of codons in this representation is indicated by a number in each square—these numbers appear in other figures for comparison. doi:10.5048/BIO-C.2012.2.f2

A number of three-dimensional representations of the genetic code have also been proposed, including a dodecahedral version [7], and multiple tetrahedral ones [8–17]. Most of these latter ones either divide the tetrahedron into twenty parts representing the amino acids, or divide each of the four faces into nine triangular subdivisions, with the inner vertices or intersections representing the codons.

Although the use of a third dimension opens the possibility of representing more complex symmetries and periodicities, current three-dimensional representations of the code have not taken full advantage of this, as most of them lack the natural periodicity and/or the geometric simplicity of the classic circular representation in two dimensions. The dodecahedral version, for example, assigns three pentagonal faces to each of the four nucleotide bases, with each of these pentagons representing ten codons. The mismatch between the 120 codons represented in this way and the 64 actual ones can be deemed as redundant, making the model as a whole less compelling than it might otherwise be. Extreme geometric complexity can likewise detract from a model representation, at least for practical applications, by making it harder to use. For example, fractal-like multi-level tetrahedral representations also have numerical mismatches [9–15]. One described by Trainor [11] has 108 geometric locations (27 for each face of the enclosing tetrahedron) being mapped to the 64 codons.

Others [13, 16] have constructed much simpler tetrahedral representations by dividing the shape into twenty locations to represent the amino acids. These benefit from being much easier to visualize, but since the genetic code maps 64 codons to 22 operations (polypeptide chain initiation and termination, as well as amino-acid addition), these models are too simple to represent the actual code.

Here I propose a new tetrahedral representation of the genetic code that aims for both simplicity and full inclusion of the actual 64-to-22 mapping. The aim is to incorporate the most informative aspects of the classical circular representation (Fig. 1) into a new representation that benefits from an additional spatial dimension without becoming too complicated for easy visual and educational use.

APPROACH

The idea motivating this work is that a geometric representation of the code will only be as compelling as the harmony between the chosen geometry and the biological reality. The tetrahedron (meaning the regular tetrahedron in this work) is a simple solid shape with four identical faces (each in the shape of an equilateral triangle), four vertices, and six edges. A tetrahedral representation of the genetic code should fit naturally within this geometry if it is to illustrate real underlying order. Otherwise it would merely be an instance of displaying the code on a shape that does not fit it in any compelling sense.

The five principles of symmetry used to build the new representation are described next, beginning with the ones that most clearly justify using a tetrahedral shape, and then continuing with successive principles for representing details of the code within that shape.

1. Triangles within triangles

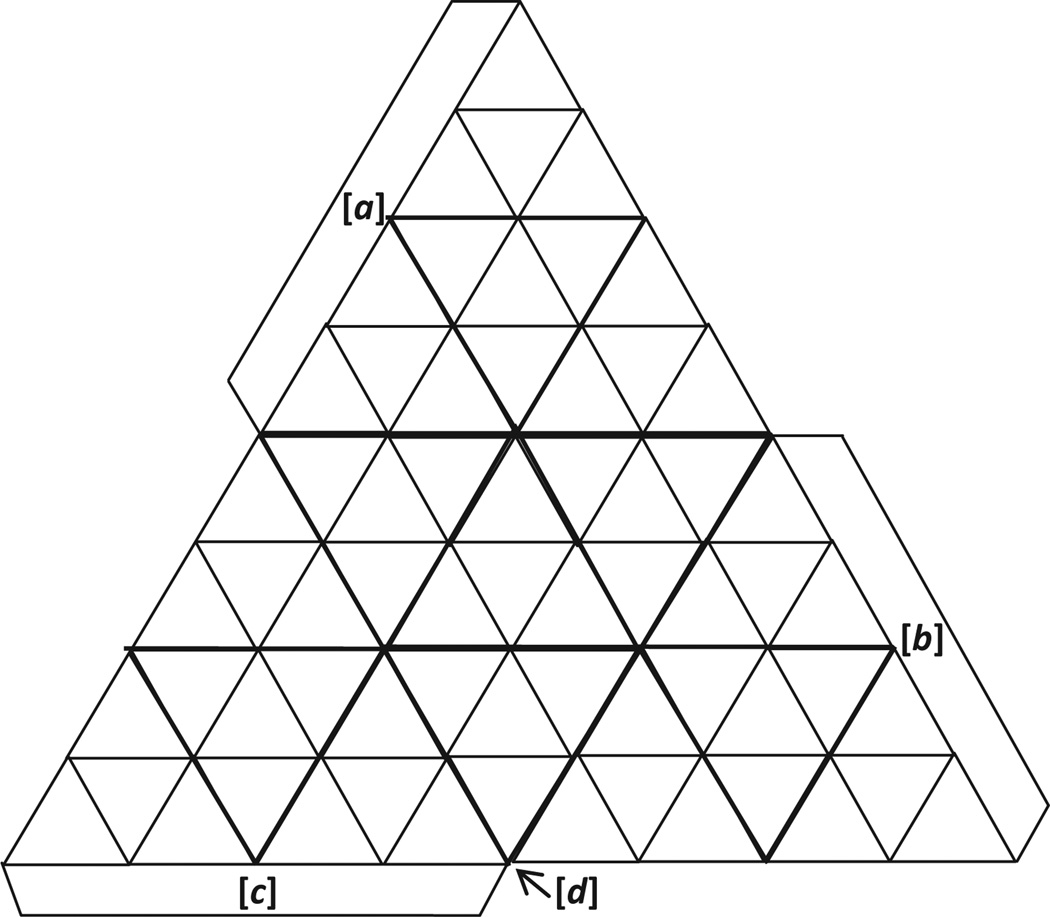
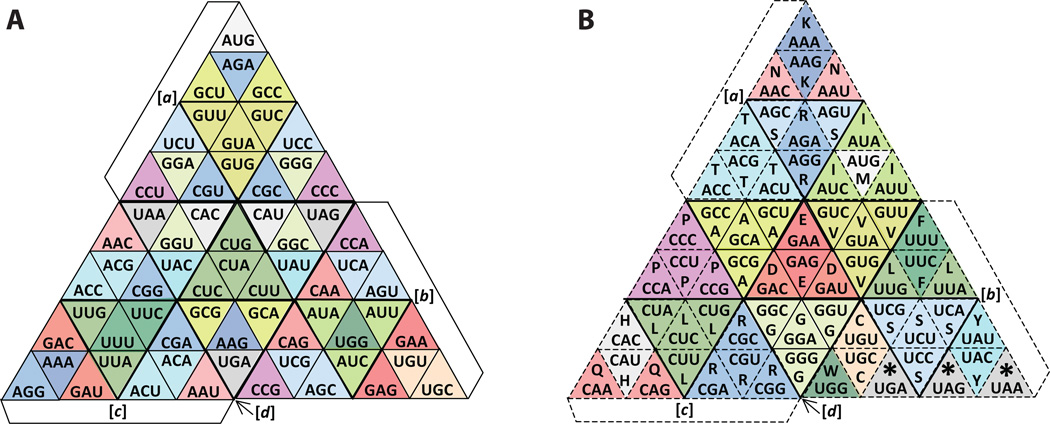
The number of codons (64) divided by the number of faces of the tetrahedron (4) is sixteen. In considering how best to represent sixteen codons per face, we note that equilateral triangles (such as those forming the faces) can be divided into rows of smaller equilateral triangles, with the top row always consisting of one small triangle and subsequent rows each having two more than the prior row. By dividing the tetrahedral faces into four rows of triangular ‘cells’, we have therefore 1 + 3 + 5 + 7 = 16 triangular cells per face for a total of 64 cells. Each cell can therefore represent one of the codons. Equivalently, we can think of dividing each face of the tetrahedron into four triangular sections (1 + 3 = 4), and then repeating that division for each of these sections (Fig. 3).

Figure 3. The proposed geometry represented as a “cut-and-fold” tetrahedron.

Each of the four faces of the tetrahedron has been divided into four triangular sections, with each section subdivided into four triangular cells. doi:10.5048/BIO-C.2012.2.f3

2. Vertices to represent endpoints

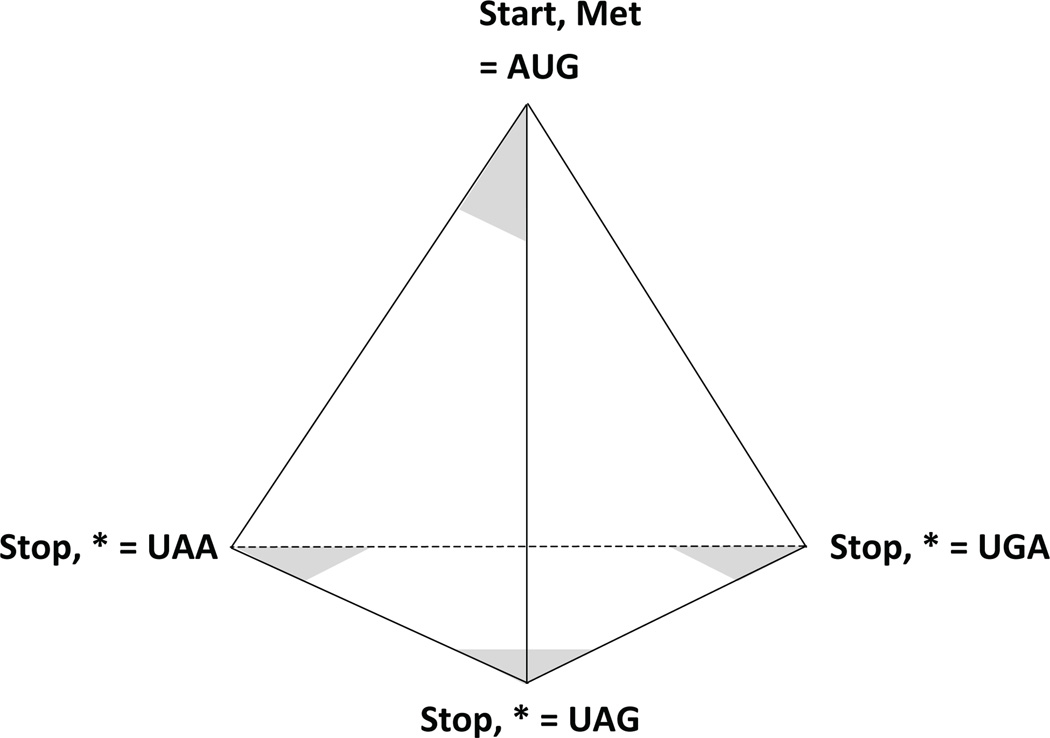
The four points of the tetrahedron most distant from its center are the vertices. Similarly, the genetic code uses four codons to mark the boundaries of open reading frames, AUG being the codon that initiates polypeptide chain elongation, and UAA, UAG, and UGA being the codons that terminate elongation. These four functional codons therefore divide it into two subsets: the initiation codon (1 member), and the termination codons (3 members). If we define one face of the tetrahedron to be the base, we have a similar division of its vertices into two subsets: the apical vertex (1 member) and the non-apical vertices (3 members). As shown in Figure 4this correspondence between tetrahedral vertices and initiation/termination codons provides a starting point for using the 64 triangular cells described above in order to build a full representation of the code.

Figure 4. Placement of start and stop codons at vertices.

By defining one of the tetrahedral faces to be the base (thereby making one of the vertices the apex) we have three cells at the vertices on the base and three at the apex (on different faces). The start codon (AUG) is placed in one of these apical cells with the three stop codons occupying the cells on the base. doi:10.5048/BIO-C.2012.2.f4

3. Balance of synonymous codon groups across faces

The geometric symmetry of the divided tetrahedron (four equilateral triangular faces, each divided into sixteen equilateral triangular cells) suggests that codons should be assigned to cells in a way that achieves balance among the four faces. Because the goal here is a functional representation, the emphasis should be on balancing what the codons encode rather than on balancing their nucleotide compositions. Using functional distinctions and principles of symmetry, I propose the following assignment of codons to the four tetrahedral faces, whereby each of the faces has one encoded function that is represented just once, one that is represented three times, one that is represented four times, and four that are represented twice:

• For tetrahedral face a:

  • 1 codon for: Met (M), Start
  • 3 codons for: Arg (R)
  • 4 codons for: Val (V)
  • 2 codons for: Gly (G), Ala (A), Ser (S), and Pro (P)
• For tetrahedral face b:

  • 1 codon for: Trp (W)
  • 3 codons for: Ile (I)
  • 4 codons for: Ser (S)
  • 2 codons for: Glu (E), Gln (Q), Cys (C), and Pro (P)
• For tetrahedral face c:

  • 1 codon for: Lys (K)
  • 3 codons for: Arg (R)
  • 4 codons for: Thr (T)
  • 2 codons for: Asp (D), Asn (N), Leu (L), and Phe (F)
• For tetrahedral face d (the base):

  • 1 codon for: Lys (K)
  • 3 codons for: Stop
  • 4 codons for: Leu (L)
  • 2 codons for: His (H), Gly (G), Ala (A), and Tyr(Y)

4. Hydrophobic amino acids in central triangular sections

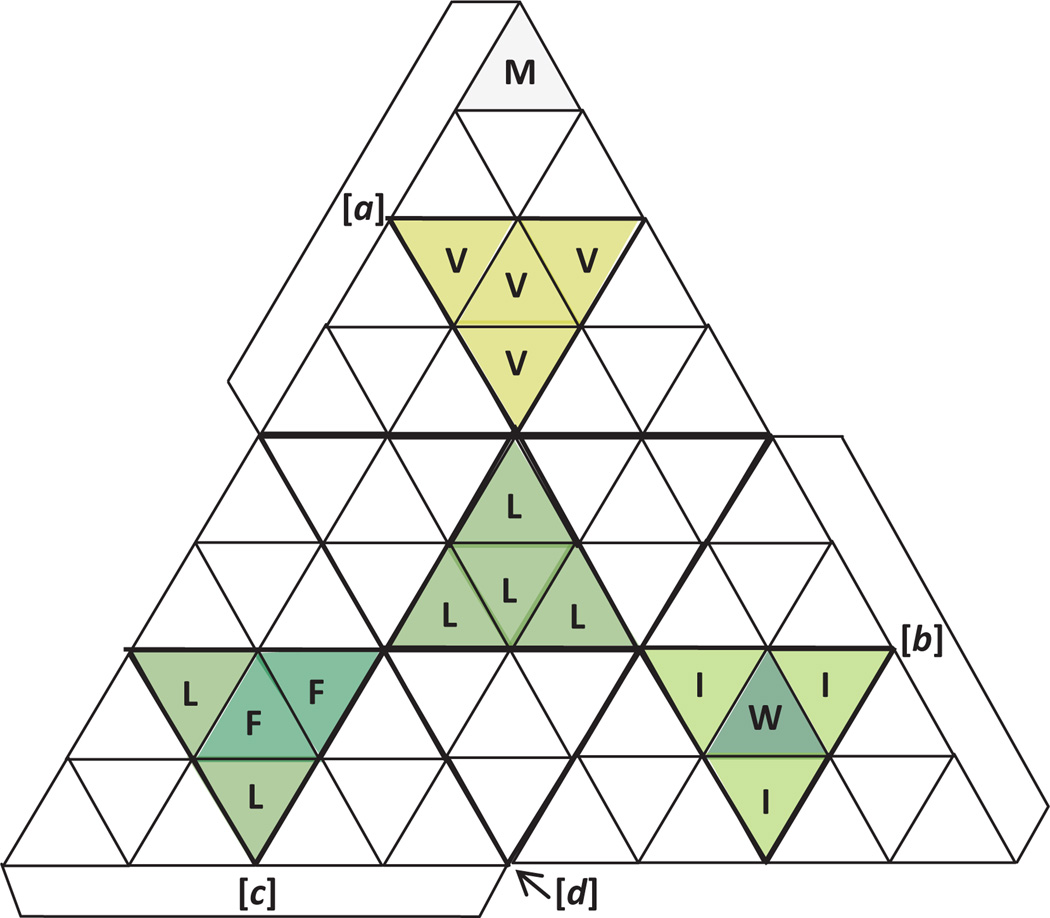
Considering the important role of hydrophobicity in the determination of protein structure [18], the assignment of codons to triangular cells within the faces of the tetrahedron starts with hydrophobic amino acids. Since methionine has already been assigned according to Principle 2 above, we are left with five hydrophobic amino acids, Trp, Phe, Ile, Val, and Leu, which are encoded by one, two, three, four, and six codons, respectively. With attention to balance and symmetry, this whole set of sixteen codons can be divided among the four faces by assigning the codons to the central triangular sections (each with four cells) of each face, as shown in Figure 5.

Figure 5. Placement of hydrophobic amino acids in central sections of each tetrahedral face.

The single codon for Met occupies an apical cell, as shown in Figure 4. doi:10.5048/BIO-C.2012.2.f5

5. Extending the themes of balance and symmetry

With the above principles providing the overall framework for representing the genetic code, we next fill in the remaining details by making continued use of the themes of balance and symmetry. The resulting representation is shown in Figure 6.

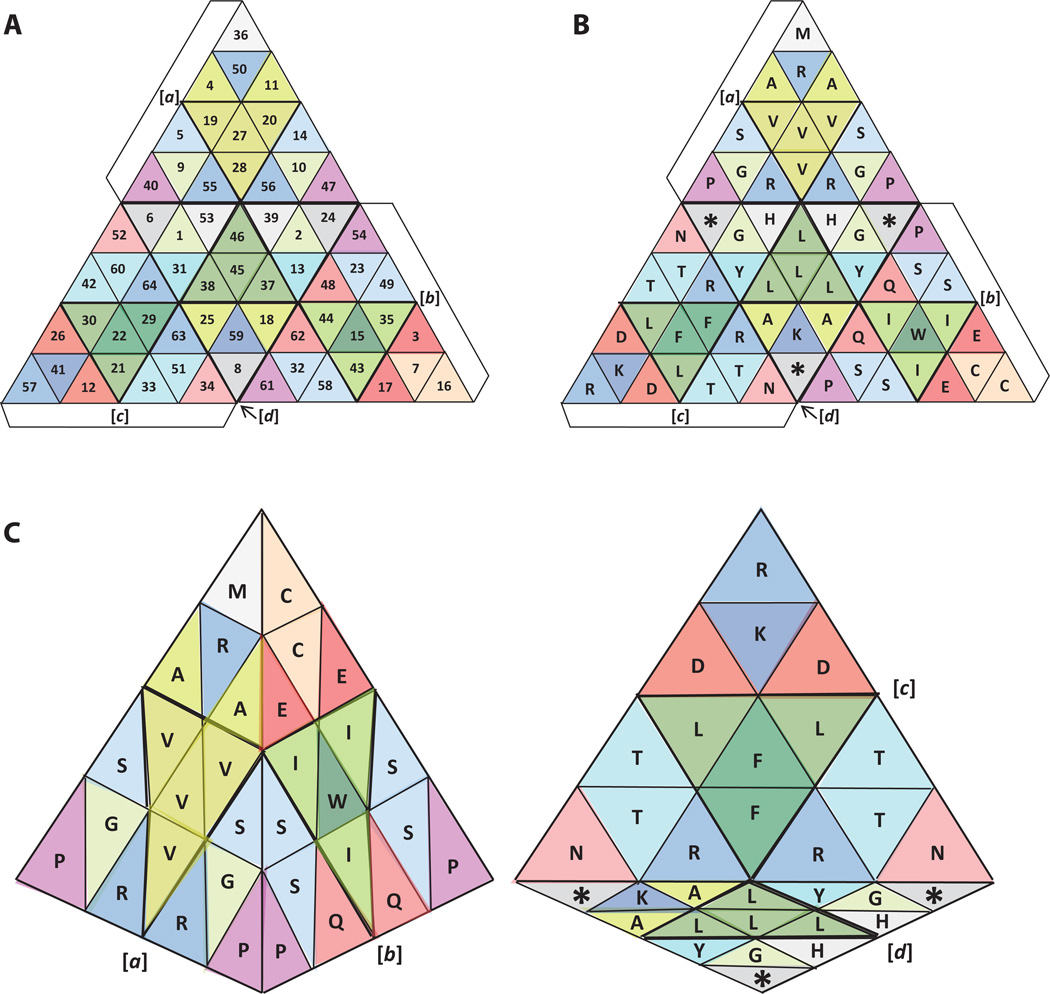
Figure 6. The proposed tetrahedral representation of the genetic code, based on symmetry and periodicity.

A) Placement of amino acids within the tetrahedral framework outlined in Figures 3 and 4. B) Placement of amino acid codons (numbered according to Figures 1 and 2). C) Two views of the folded representation. doi:10.5048/BIO-C.2012.2.f6

Although some of the codon assignments in this model are analogous to the two-dimensional representations of Figures 1 and 2, the new geometry has called for some deviations from those prior models. The codon for Met, for example, is now located at the top (see Principle 2) whereas in the two-dimensional representations it was placed with the three codons for Ile [2–6]. Among the other changes, the three Ile codons have been placed around the single Trp codon (located at the center of the hydrophobic section of tetrahedral face b); the six Arg codons have been placed on two faces (a and c), with similar placement on each face, except for one Arg (in a) that is matching the two Lys codons that are separated likewise (one on face c and the other on face d); the Pro codons have been placed in pairs at corresponding vertices of faces a and b; codons for the small amino acids Ala and Gly have likewise been placed in pairs in corresponding cells of faces a and d.

DISCUSSION

I have here attempted to construct a geometric representation of the genetic code that emphasizes the natural patterns of symmetry and periodicity. As discussed in the Introduction, several other tetrahedral representations exist. In addition to the ones already mentioned, one described by Fujimoto [17] places sixteen codons on each tetrahedral face, as does the present representation. Beyond this basic structural similarity, however, there is little resemblance between the two (see Fig. 7). In particular, Fujimoto’s representation does not aim to represent the kind of underlying order that has been the focus here, namely the natural patterns of symmetry and periodicity.

Figure 7. Comparison of the proposed representation (left) to Fujimoto’s tetrahedral representation (right) [17].

Amino acids are identified by codon and single letter abbreviation in B, since that is the way Fujimoto’s patent was formulated. doi:10.5048/BIO-C.2012.2.f7

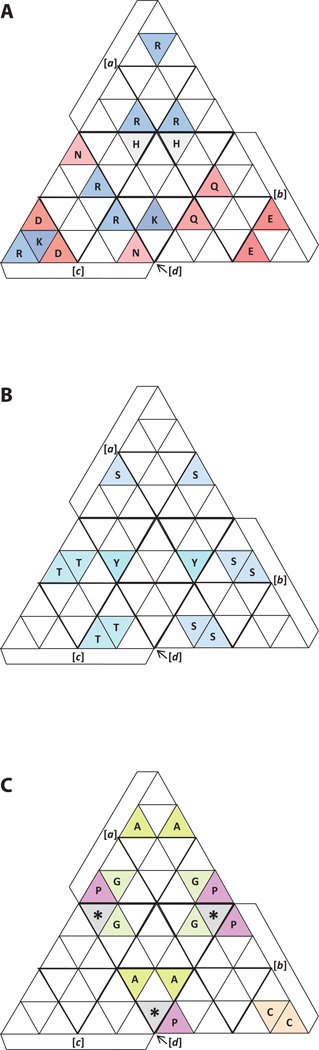
With the start and stop codons placed at the four vertices and the hydrophobic amino acids placed at the center of each tetrahedral face, as shown in Figures 4 and 5, respectively, the proposed location for the rest of the amino acids is as shown in Figure 8. Where possible, amino acids are grouped by salient properties, and the principle of balance is applied to each group. Accordingly, I have grouped the acidic amino acids—Glu (E) and Asp (D)—and placed them in balanced arrangement on faces b and c while their respective amides—Gln (Q) and Asn (N)—are located on the same tetrahedral faces with them. The basic amino acids Lys (K), Arg (R), and His (H) form another group. These are balanced on faces a, c and d (Fig. 8A), with His (H) being located at the bottom of the tetrahedron. The three amino acids with hydroxyl groups—Ser (S), Thr (T), and Tyr (Y)—can also be placed in a balanced way. As shown in Figure 8B, Ser and Thr have a positional balance on faces b and c, respectively, while Tyr is at the bottom of the tetrahedron, matching Ser on face a by position, and also the remaining Ser and Thr already mentioned. Gly and Ala are grouped according to their small size and placed in balanced positions as shown in Figure 8C.

Figure 8. Placement of non-hydrophobic amino acids.

A) Hydrophilic 10:75–83. amino acids. B) Amino acids with hydroxyl groups. C) The remaining amino acids. doi:10.5048/BIO-C.2012.2.f8

The unique properties of Pro and Cys suggest that they should not be grouped. Pro is the only amino acid with a side chain that is bonded to the backbone nitrogen, which makes it uniquely able to constrain the geometry of the protein backbone. Cys is the only amino acid whose side chain forms covalent inter-chain or intra-chain links. Since there are four Pro codons, these are placed in balanced positions at the bottom vertices of faces a and b, as shown in Figure 8C. Cys, on the other hand, has only two codons. One of these is placed at the top (apical) position of face b, with the other placed immediately below it (Fig. 8C).

With the current representation of the genetic code having now been described, I return briefly to the question of its possible significance. Many different representations of the genetic code will continue to find use in multiple applications. That being so, the suitability of any particular representation has to be judged in relation to the needs at hand. Even when those needs are clear, the choice of which code representation to use has an element of subjectivity. Real properties of the code and of the encoded amino acids were drawn upon to construct the representation described here, but that exercise also depended on subjective decisions regarding both the choice of organizing principles and the details of their implementation. The final tetrahedral representation presented here is therefore offered not as a demonstration of any new facts, but rather as an application of existing facts, the potential significance being that this way of organizing them may provide new insights.