Approximate-model closed-loop minimal sampling method for HIV viral-load minima detection

Abstract

We present a closed-loop method for determining the minimum of a viral rebound curve for an HIV patient undergoing a therapy transition. This method fits the parameters for a reduced approximate solution to the viral load measurements using a Simulated Annealing direct search algorithm. Gaussian white noise is added, and a family of fits is obtained. A safety tolerance measure is applied to the family of fits to obtain the next sample time. Using parameters identified from HIV data, we show that this method exhibits robust performance on noisy data generated from identified patient models, while greatly reducing the number of samples needed compared to a fixed-interval sampling approach.

I. INTRODUCTION

HIV infection is a potentially deadly disease. The virus is well-controlled by the application of Highly-Active Antiretroviral Therapy (HAART), but the emergence of drug-resistant strains is common, and forces a therapy change [1].

In order to reduce the risk of subsequent virological failures immediately following the introduction of a new antiviral regimen, we have previously proposed a family of optimal treatment scheduling algorithms [2], [3], [4], [5]. These algorithms utilize treatment interruptions and permuted antiviral drug regimens in an optimal manner to create transient crashes in the total viral load. Because the drugs being used in these optimized schedules are from regimens to which resistant virus has already emerged, the crash is always followed by a viral rebound. By switching at the viral load minimum, before rebound, it is theoretically possible to reduce the risk of subsequent virlogical failure by an order of magnitude or more [6], [3].

Model uncertainty due to interpatient parameter variation makes a priori calculation of the minimum time impossible. Frequent sampling makes it possible to find the minimum, but the samples are expensive and invasive, so this should be avoided. In a previous paper, we have introduced a simple algorithm for finding the viral load minimum [7]. In this paper, we improve the algorithm through the use of Simulated Annealing-based parameter identification and test the model’s performance against noisy data generated from models identified from experimental HIV patient data..

II. MODEL

A. Viral strain competition model

The dynamics of HIV infection by two competing strains is well described by Equation 1

$$\begin{array}{c}\dot{x}=\lambda -\mathit{\text{dx}}-{\beta }_w(1-u_1)(1-u_2){\mathit{\text{xv}}}_w-{\beta }_r(1-u_2){\mathit{\text{xv}}}_r\hfill \\ {\dot{y}}_w={\beta }_w(1-u_1)(1-u_2){\mathit{\text{xv}}}_w-a_w{y}_w+{\lambda }_w\hfill \\ {\dot{y}}_r={\beta }_r(1-u_2){\mathit{\text{xv}}}_r-a_r{y}_r+{\lambda }_r\hfill \\ {\dot{v}}_w={\gamma }_w{a}_w{y}_w-{\omega }_w{v}_w\hfill \\ {\dot{v}}_r={\gamma }_r{a}_r{y}_r-{\omega }_r{v}_r\hfill \end{array}$$ (1)

where v_w, y_w are the populations of virus and infected cells, respectively, susceptible to drug regimens u₁ and u₂, v_r and y_r the populations of virus and infected cells resistant to u₁, respectively, and x is the uninfected target cell population. The parameters of this model were identified from viral load data from six patients subjected to a series of treatment interruptions and reintroductions [8], using modified Markov-Chain Monte-Carlo methods as described in [3], [5] The parameters used for the plots generated in this paper are shown in Table I.

TABLE I.

Identified parameter values for each patient

Parameters	Patient A	Patient B
λ	123	51.7
d	0.108	0.113
βw	5.51 * 10−6	5.40 * 10−6
βr	5.51 * 10−6	5.40 * 10−6
aw	0.476	0.528
ar	0.952	1.06
λw	3.00 * 10−4	3.00 * 10−4
λr	3.00 * 10−4	3.00 * 10−4
γw	167	275
γr	167	275
ωw	0.569	0.549
ωr	0.569	0.549

B. Approximate Solution

Equation 1 has twelve parameters and five state variables, which would require at least seventeen measurements before closed-loop parameter estimation could begin. However, under the conditions induced by the switching algorithms described in [2], [3], [4], [5], the total viral load v(t) = v_w(t) + v_r(t) can be well approximated by the equation:

$$\widehat{v}(t)={\widehat{v}}_w(0)e^{-k_{w}t}+{\widehat{v}}_r(0)e^{k_{r}t}$$ (2)

which has only one state and three unknown parameters, if the total initial viral load is assumed to be known.

III. ALGORITHM

A. Simulated Annealing-based parameter estimation

Once we have three measurements, we can perform non-linear least-squares estimation. To overcome problems with local minima in the fit encountered while using steepest-descent based methods, we used a simulated annealing algorithm to obtain our parameter fits [9]. We used the built-in MATLAB implementation simulannealbnd with default settings, enforcing upper and lower bounds on the parameters 0.95 * y(0) ≤ ŷ_w(0) ≤ y(0), 0.1 ≤ k_w ≤ 1, 0.1 ≤ k_r ≤ 1 and a terminal function value tolerance of 10⁻²⁰. A parameter set θ = [v_w0 k_w k_r] is found to minimize the cost function ln(∑_i|v(t_i) − v̂(t_i)|) for the set of samples {t_i}.

B. Closed-loop sampling criterion

In order to avoid either sampling too frequently or overshooting the minimum, we implement a closed-loop algorithm. A minimum interval T_min = 3 days and a maximum interval T_max = 7 days are defined. After three initial samples spaced at T_min, parameter estimation is performed as described above. This step is repeated J = 100 times with proportional gaussian random noise added to the sampled data y(t_i), with standard deviation equal to 5% of the nominal measured value, and J estimated viral-load minimum times $t_j=\frac{1}{k_r(j)+k_w(j)}\mathit{\text{ln}}(\frac{k_w(j){\widehat{v}}_{w0}(j)}{k_r(j){\widehat{v}}_{r0}(j)})$ are calculated. The worst-case (earliest) rebound time $t_{\mathit{\text{min}}}^{~}={\text{inf}}_{j\in J}\{t_j\}$ is calculated. If $t_{\mathit{\text{min}}}^{~}>t_S+T_{\mathit{\text{max}}}$, where t_S is the current sample time, the next sample is taken at t_S + T_max. If $t_{\mathit{\text{min}}}^{~}<t_S+T_{\mathit{\text{min}}}$, the next sample is taken at t_S + T_min. If $t_S+T_{\mathit{\text{min}}}<t_{\mathit{\text{min}}}^{~}<t_S+T_{\mathit{\text{max}}}$, the next sample is taken at $t_{\mathit{\text{min}}}^{~}$. The algorithm terminates when $t_{\mathit{\text{min}}}^{~}\ge t_S$ for the set of samples {t_i}.

IV. Simulations

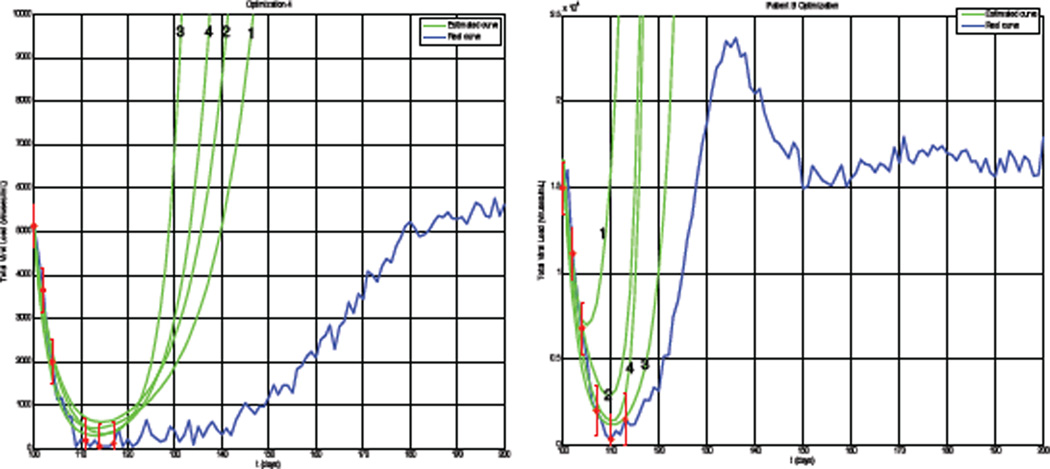
Equation 1 was used to generate data using identified parameter values from a number of patients. The system was allowed to settle for 100 days, simulating the initial emergence of a resistant strain. These data were corrupted by proportional Gaussian white noise with standard deviation equal to 3% of the measurement value. Overall, we saw a reduction in the required number of samples of approximately 50% compared to a fixed 3-day sampling interval while maintaining a ±3-day accuracy. Figure 1 show the results for two example patients. The blue curve is the actual noise-corrupted viral load generated by Equation 1, the red circles are the measurements with error bars showing the range of values considered by the estimation algorithm, and the numbered green curves are the successive estimate curves following Equation 2 generated by the algorithm.

Fig. 1.

Patient A and B Data.

V. CONCLUSIONS AND FUTURE WORKS

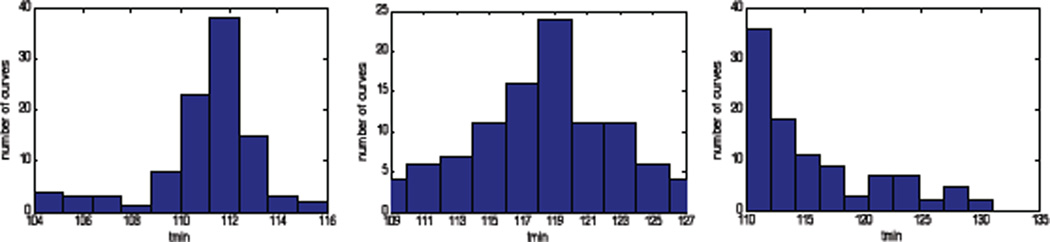
We have demonstrated a closed-loop sampling algorithm which robustly finds a viral load minimum despite the presence of measurement noise. This algorithm uses an approximate solution method, and employs a Simulated Annealing algorithm for robust parameter identification. The algorithm consistently reduces the number of samples required to find the minimum compared to a frequent sampling approach. In future work, we will explore other direct search methods such as Genetic Algorithms, as the Simulated Annealing method is quite slow for this problem. A faster algorithm will allow us to explore a less-conservative approach where the next sample time is taken to be one standard deviation before the mean, instead of the earliest. Histograms of the estimated minimum times obtained from the algorithm for Patient A show a roughly normal distribution, implying that this is feasible. A much larger number of fits will be necessary to generate a sufficiently smooth distribution, however, and this will require a faster algorithm.

Fig. 2.

Distribution of estimates of rebound time for Patient A after 3, 4, and 5 measurements respectively.