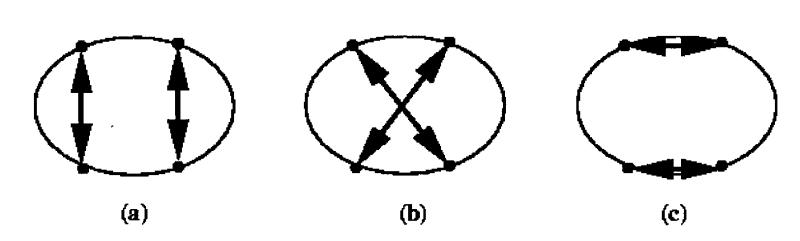Combining Geometric and Probabilistic Reasoning for Computer-based Penetrating-Trauma Assessment

Abstract

Objective: To ascertain whether three-dimensional geometric and probabilistic reasoning methods can be successfully combined for computer-based assessment of conditions arising from ballistic penetrating trauma to the chest and abdomen.

Design: The authors created a computer system (TraumaSCAN) that integrates three-dimensional geometric reasoning about anatomic likelihood of injury with probabilistic reasoning about injury consequences using Bayesian networks. Preliminary evaluation of TraumaSCAN was performed via a retrospective study testing performance of the system on data from 26 cases of actual gunshot wounds.

Measurements: Areas under the receiver operating characteristics (ROC) curve were calculated for each condition modeled in TraumaSCAN that was present in the 26 cases. The comprehensiveness and relevance of the TraumaSCAN diagnosis for the 26 cases were used to assess the overall performance of the system. To test the ability of TraumaSCAN to handle limited findings, these measurements were calculated both with and without input of observed findings into the Bayesian network.

Results: For the 11 conditions assessed, the worst area under the ROC curve with no observed findings input into the Bayesian network was 0.542 (95% CI, 0.146–0.937), the median was 0.883 (95% CI, 0.713–1.000), and the best was 1.00 (95% CI, 1.000–1.000). The worst area under the ROC curve with all observed findings input into the Bayesian network was 0.835 (95% CI, 0.602–1.000), the median was 0.941 (95% CI, 0.827–1.000), and the best was 0.992 (95% CI, 0.965–1.000). A comparison of the areas under the curve obtained with and without input of observed findings into the Bayesian network showed that there were significant differences for 2 of the 11 conditions assessed.

Conclusion: A computer-based method that combines geometric and probabilistic reasoning shows promise as a tool for assessing ballistic penetrating trauma to the chest and abdomen.

Research on penetrating trauma has shown that the early administration of expert care to victims would considerably reduce the number of deaths due to these injuries.¹ In actual medical practice, confusion about the spatial relationships among different anatomic structures sometimes arises in the treatment of patients with penetrating trauma. (A description of such a situation is given in Ogunyemi et al.²) Tools or knowledge aids that reinforce an understanding of these relationships for patients presenting with penetrating injury may be of value in enhancing patient care. A computer program that integrates anatomic and diagnostic reasoning in assessing a patient could serve as such a tool or knowledge aid.

To be successful, computer-based assessment of penetrating trauma requires a model that 1) reflects the relationships among human anatomy, physiology and physical manifestations of injury, and 2) can take into account uncertainty about the region of damage produced by a mechanism of injury and variability in the amount of information about available patient findings.

Accordingly, the research question we are investigating is as follows: Can three-dimensional geometric and probabilistic reasoning methods be successfully combined for computer-based assessment of conditions arising from ballistic penetrating trauma to the chest and abdomen? To address this issue, we have developed a prototype computer system, TraumaSCAN,³ that assesses the effects of ballistic penetrating trauma to the chest and abdomen. TraumaSCAN reasons about injured anatomic structures on the basis of information about surface wounds and bullet locations, and uses the results of this geometric reasoning process to drive diagnostic reasoning about the consequences of injury. The system is designed to take into account uncertainty about the extent of damage caused by a mechanism of injury and variability in information available about patient signs, symptoms, and test results.

In this paper, we describe the methods used for penetrating trauma assessment in TraumaSCAN and present the results of retrospective testing of the system using data from 26 actual gunshot wound cases.

Background

Penetrating trauma is responsible for a large number of civilian deaths in the United States and is also a major cause of battlefield fatalities. Injury mortality statistics from the Centers for Disease Control and Prevention (CDC) for the United States as a whole show that over a 9-year period (1989–97), penetrating trauma from firearms accounted for more than 32,000 deaths each year. The average death rate from firearm injuries was 12.55 percent over this period.⁴

Research efforts on assessment of the effects of penetrating trauma from firearms include the approach of Wind et al., by which three-dimensional graphics methods were used to determine ballistic penetration paths⁵; research by Eisler et al. on estimating human incapacitation from different projectiles,⁶ ballistic casualty reduction,⁷ and simulation and modeling of penetrating wounds to the extremities⁸; research by Fackler et al. on missile–tissue interaction⁹; and the examination by Yoganandan et al. of the wounding mechanics of different low-velocity projectiles, using high-speed video photographic analysis.¹⁰

These different approaches attempt to simulate the effects of projectiles on tissue in order to increase understanding of the damage they cause. The results from these methods shed light on the problem of assessing ballistic penetration paths. However, these methods use knowledge about the types of projectiles, their velocities, directions of entry, and so on.

In embarking on this study, we decided to approach the penetrating trauma assessment problem from a perspective that is closer to that of a health care provider presented with patient with trauma. Thus, our solution has to incorporate methods for reasoning under uncertainty. Assessment of the consequences of injury is designed to proceed in the absence of detailed information about projectile characteristics.

The TraumAID^11,12 project is an example of previous work on computer-assisted diagnosis of penetrating trauma in the absence of information about the projectile, such as type and velocity. TraumAID is a validated rule-based expert system designed to assist physicians with the diagnosis and treatment of penetrating trauma to the chest and abdomen. The system integrates diagnostic reasoning, planning, and action. TraumAID's rule-base relates information about patient findings to diagnoses (for example, one rule specifies that an observable injury to the left lower chest, in conjunction with certain patient findings, should lead a clinician to suspect that a patient has pericardial tamponade).

The reasoning modules of TraumAID identify diagnostic and therapeutic goals appropriate to the state of a particular patient (as determined from information requested by, and provided to, the system about patient findings). The rule-based reasoner uses three-valued logic (true, false, unknown) to handle uncertainty in reasoning about diagnostic or therapeutic goals. Some potential limitations of TraumAID are as follows:

• It provides little information about the anatomic structures involved in injury—for example, there is no attempt to relate directly the region covered by the designation “left lower chest” to the set of anatomic structures that may have been injured.

• It does not take into account the fact that when a patient has multiple gunshot wounds, there are different plausible hypotheses for the paths that the projectiles may have taken (since information about direction of entry may not be available), such that each hypothesis corresponds to a different set of injuries.

• The ability to make a diagnosis depends on the availability of information about those patient findings that the system requires to perform its reasoning.

Work on TraumaSCAN began as an attempt to provide a framework for deeper anatomic reasoning in TraumAID. The system provides information about the involvement of anatomic structures in injury, takes into account different possible injury hypotheses when making a diagnosis, and is able to perform diagnostic reasoning under uncertainty. (That is, unlike TraumAID, TraumaSCAN can come up with a diagnosis given information about surface wound or bullet locations and no other details about patient findings).

TraumaSCAN also provides a means of quantifying the uncertainty associated with diagnoses. We have not found evidence of previous attempts in this domain to use the output of geometric reasoning as the driving mechanism for probabilistic reasoning about injury consequences (as is the case in TraumaSCAN). In earlier publications, we discussed our initial approaches for generating different penetration path hypotheses for cases involving multiple gunshot wounds,¹³ estimating the probability of injury to anatomic structures for a given hypothesis¹⁴ and incorporating Bayesian networks^15–17 for diagnostic reasoning.² We have also shown that TraumaSCAN is more sensitive and specific than TraumAID, given the same input on a set of penetrating trauma cases.¹⁸ A comprehensive and in-depth description of the methods used in developing the TraumaSCAN system can be found in Ogunyemi.³

Methods

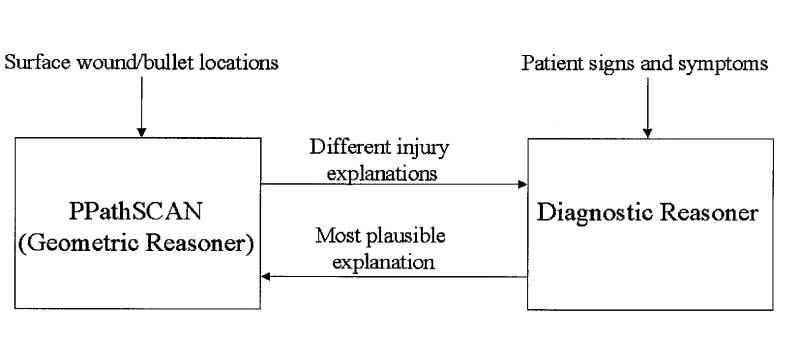
TraumaSCAN consists of a geometric reasoner (PPathSCAN), a diagnostic reasoner based on Bayesian networks, and bi-directional communications between the geometric and diagnostic reasoners (Figure 1▶). PPathSCAN makes use of both three-dimensional models of the human anatomy and three-dimensional models of the estimated region of damage caused by a mechanism of injury in calculating the probability of injury to anatomic structures. The diagnostic reasoner expresses the causal relationships among anatomic structure injuries and diagnoses and among diagnoses and patient findings. It also quantifies uncertainty about the degree of dependency encoded in each causal relationship by means of conditional probabilities. Connections between PPathSCAN and the diagnostic reasoner come from probabilities of injury to specific structures calculated by PPathSCAN and fed to the diagnostic reasoner as input, and from probabilities of injury to specific structures revised by the diagnostic reasoner on the basis of observed physiologic manifestations of injury and passed back to PPathSCAN.

Figure 1 .

TraumaSCAN system architecture.

Geometric Reasoning about Anatomic Structure Injury

Our approach to reasoning about penetrating injury attempts to take into consideration the mechanism of injury and available information about the role (entry, exit, or unknown) of ballistic surface wounds. The geometric reasoner requires, as input, the locations of surface wounds and of any bullets lodged in the body. Assessment of anatomic structure injury involves creating three-dimensional models corresponding to the region of damage associated with a projectile. We then determine which anatomic structures in a three-dimensional model of a human torso intersect with these three-dimensional models of damage. We use a three-dimensional polygonal surface model of a female torso with internal organs (developed at Viewpoint DataLabs, Viewpoint Corp., New York, New York) for this purpose.

Once a list of possibly injured anatomic structures is generated in this manner, we compute the probability of injury to each structure by casting rays from one end of the model of damage to another. The probability of injury to the structure, or hit probability, is given by the total number of rays that hit the structure, divided by the total number of rays cast. This approach is described in more detail elsewhere.³

Several factors complicate reasoning about damage to organs from multiple gunshots: 1) it is not always possible to tell whether a wound is an entry wound or an exit wound, and 2) many different pairings are possible among entry wounds and exit wounds or entry wounds and bullets lodged in the body. Different pairings for the same set of external wounds and bullets may indicate injury to different sets of anatomic structures, possibly yielding dissimilar diagnoses in the absence of information that helps clarify the situation.

For a patient presenting with two entry wounds and two bullets lodged in the body, there are two possible hypotheses about which bullet is linked by a path to each entry wound. Figure 2▶ shows the hypotheses about external wound connections for a case involving two through-and-through paths (a total of four external wounds).

Figure 2 .

Three wound connection hypotheses for four external wounds.

In general, if there are i external wounds, and j through-and-through paths, the total space of hypotheses to consider is:

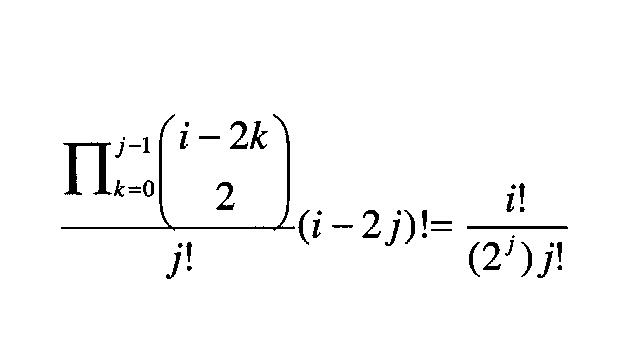The equation shows that the number of hypotheses to consider increases exponentially as the number of external wounds increases. Thus, an approach that involves generating the possible hypotheses for a given set of wounds and bullets and assessing damage to anatomic structures for each of these hypotheses is intractable in general.

To deal with this, in TraumaSCAN we generate hypotheses when assessing four or fewer external wounds (a maximum of 24 hypotheses) and use techniques from computational geometry to create an approximate solution when the number of external wounds is greater than four. The approximate solution involves computing the convex hull¹⁹ of points corresponding to external wounds and bullets in order to create a three-dimensional region of damage.

Once the set of possibly injured anatomic structures and their probabilities of injury are calculated for each hypothesis, this information is passed to the diagnostic reasoner to determine possible injury consequences.

Diagnostic Reasoning about Injury Consequences

The diagnostic reasoning system is based on Bayesian networks and updates probabilities of injury diagnoses when provided with evidence regarding:

• Injury probabilities for different anatomic structures from the geometric reasoner;

• Information about patient findings (e.g., distended neck veins, muffled heart sounds)

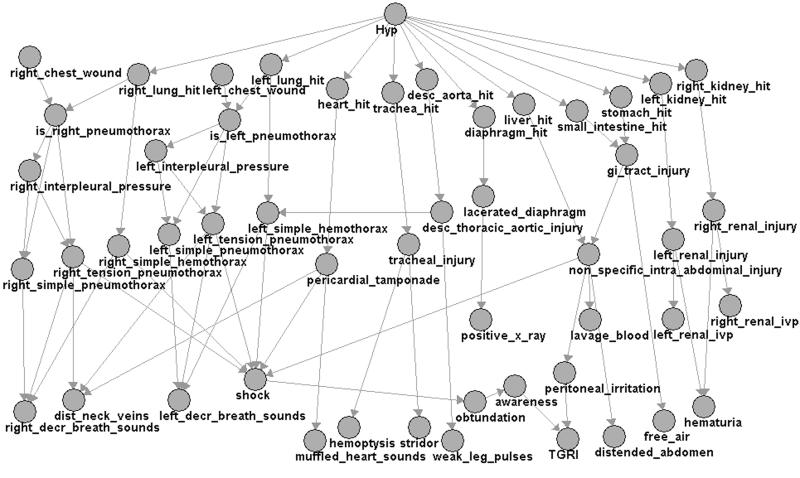
The Bayesian network software used in TraumaSCAN is JavaBayes (www.cs.cmu.edu/~javabayes/), developed by Fabio Cozman at Carnegie Mellon University. Figure 3▶ shows the directed acyclic graph of TraumaSCAN's Bayesian network model for chest and abdominal injuries. The model covers the most common subset of possible chest and abdominal injuries and comprises 51 variables.

Figure 3 .

Bayesian network model for penetrating trauma to chest and abdomen.

The penetrating injury network model for the chest and abdomen was created by examining the rules from TraumAID's rule base and clarifying organ injury–diagnosis–findings relationships through consultations with a trauma surgeon (Dr. John R. Clarke). Conditional probabilities of anatomic structure injury given an injury hypothesis are obtained automatically from the geometric reasoner.

Since we had limited access to large amounts of actual patient data, conditional probabilities of diagnoses given anatomic structure injury and of findings given diagnoses were based on estimates provided by the trauma surgery expert. Some studies have shown that subjective probabilities derived from experts may not be best for diagnosis.^20–22 Neapolitan¹⁵ shows a way of augmenting the estimates of an expert with empirical data as it becomes available over time.

The random variable corresponding to the root node Hyp in the Bayesian network has several mutually exclusive values. These values represent the different hypotheses identified by the geometric reasoner as well as the value “other,” which captures the fact that the geometric reasoner may not have covered all injury possibilities. Hypotheses originating from the geometric reasoner are assumed to be equally likely, whereas “other” is considered less likely and has a low fixed prior probability of 1 percent.^*

The Bayesian network has nodes that represent injury to the left and right lungs, heart, trachea, descending thoracic aorta, diaphragm, liver, intestine, stomach, and left and right kidneys. Table 1▶ lists the different diagnoses and findings modeled as nodes in the network.

Table 1 .

Diagnoses and Patient Findings Modeled in the Bayesian Network

Diagnoses:

Left simple pneumothorax

Left tension pneumothorax

Left hemothorax

Right simple pneumothorax

Right tension pneumothorax

Right hemothorax

Pericardial tamponade

Tracheal injury

Lacerated diaphragm

Descending thoracic aortic injury

Nonspecific intra-abdominal injury

Gastrointestinal tract injury

Left renal injury

Right renal injury

Patient findings:

Left decreased breath sounds

Right decreased breath sounds

Distended neck veins

Shock

Muffled heart sounds

Weak leg pulses

Hemoptysis

Stridor

Distended abdomen

Lavage results blood

Positive x-ray for lacerated diaphragm

Free air in abdomen

Positive left renal injury on ivp

Positive right renal injury on ivp

Hematuria

Tenderness, guarding, rebound-tenderness, and ileus (TGRI)

Using the geometric reasoner's anatomic structure hit probabilities for a set of hypotheses (and information about patient findings modeled in the network, if provided), the Bayesian network computes posterior probabilities for each variable corresponding to network nodes. The computed values determine the final probabilities of anatomic structure injury and of each diagnosis for a penetrating trauma case.

The different hypotheses identified for the case can be ranked according to their calculated posterior probabilities. The probabilities of anatomic structure injury calculated by the geometric reasoner are unique for each trauma case. The Bayesian network is able to perform diagnostic reasoning for a trauma case given only the hit probabilities computed by the geometric reasoner. Further information about the presence or absence of patient findings provided as input to the Bayesian network helps refine the diagnostic reasoning process.

Geometric Reasoner–Diagnostic Reasoner Interface

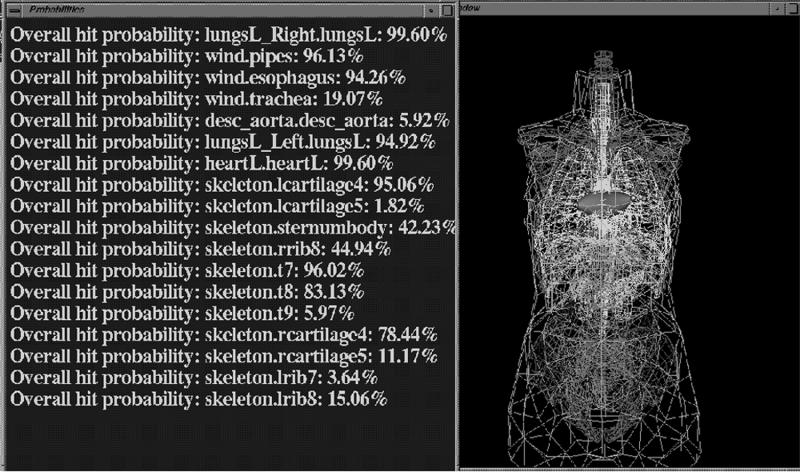
Communication between the geometric and the diagnostic reasoner is achieved by updating data repositories of organ injury probabilities. After assessing, for a given number of gunshot wounds, the probability that anatomic structures are injured, the geometric reasoner updates the conditional probabilities of anatomic structure injury used by the Bayesian network. Figure 4▶ shows a partial screen shot of the system display (with anatomic structures displayed in wireframe mode) after the geometric reasoning process has occurred.

Figure 4 .

Partial screen shot of TraumaSCAN geometric reasoner graphical user interface.

Once inferences are made about injury consequences, the posterior probabilities of injury to anatomic structures as well as the posterior probabilities of each modeled diagnosis are transferred to the geometric reasoner.

Preliminary Evaluation

To test the diagnostic ability of TraumaSCAN, we used 26 gunshot wound cases involving penetrating injury to the chest and abdomen (collected for assessment of TraumAID). The cases were from the Medical College of Pennsylvania Trauma Center and represent a portion of the actual gunshot wound cases seen over 15 months, from November 1989 to January 1991. The data were collected for gunshot wound patients with chest and abdominal injuries seen during this period for whom wound and bullet site information were available. Each case also included a written set of findings observed by the trauma team at the time a patient was cared for and the set of injuries and diseases were diagnosed.

Information about external wound locations for each case was marked (by a physician or research assistant) on paper diagrams, each depicting anterior, posterior, left lateral, and right lateral views of a male torso, with the skeleton showing through as a landmark in each view. The external wound markings represented the physician's or research assistant's approximate transcription of the surface wound on the body of an actual patient to the paper diagram of the torso.

Bullet information was given mainly in terms of text descriptions of anterior-posterior and lateral x-ray results, although in two cases the bullet was palpable (its position was apparent to physicians by feeling a particular region of the torso). The external wound locations given on the paper diagrams were transcribed to the three-dimensional torso model of TraumaSCAN, also using anterior, posterior and left or right lateral views of the torso with the skeleton showing through as a landmark.

It should be noted that this transcription would necessarily entail some error, further compounding the initial error in the physician's or nurse's transcriptions from the actual patient to the paper diagram.

Of the 26 gunshot wound cases, 18 involved a single external wound with a bullet lodged in the body, 7 were single through-and-through wounds involving two external gunshot wounds, and 1 consisted of two through-and-through wounds involving four external gunshot wounds. No information about surface wound type (entry or exit) was given in any of the cases, but this was relevant only for the one case involving four external wounds. The gold standards for the 26 cases were based on care provider reports for patients who survived and autopsy reports for those who did not. Table 2▶ lists the occurrence of diseases and conditions based on the gold standard diagnoses.

Table 2 .

Areas under the Receiver Operating Characteristics (ROC) Curve for TraumaSCAN

Diagnosis	No. of Occurrences	AUC Without BNet Findings (95% CI)	AUC with BNet Findings (95% CI)
Non-specific intra-abdominal injury	13	0.899 (0.755–1.000)	0.941 (0.827–1.000)
Descending aortic injury	1	1.000 (1.000–1.000)	0.920 (0.814–1.000)
Gastrointestinal-tract injury	5	0.914 (0.802–1.000)	0.895 (0.773–1.000)
Lacerated diaphragm	7	0.883 (0.713–1.000)	0.835 (0.602–1.000)
Left simple hemothorax*	11	0.752 (0.545–0.985)	0.955 (0.878–1.000)
Left simple pneumothorax	4	0.977 (0.924–1.000)	0.977 (0.924–1.000)
Pericardial tamponade*	6	0.758 (0.517–1.000)	0.942 (0.854–1.000)
Right renal injury	2	0.542 (0.146–0.937)	0.958 (0.878–1.000)
Right simple hemothorax	6	0.879 (0.690–1.000)	0.992 (0.965–1.000)
Right simple pneumothorax	2	0.958 (0.878–1.000)	0.854 (0.623–1.000)
Right tension pneumothorax	1	0.880 (0.753–1.000)	0.840 (0.696–0.984)
Left tension pneumothorax	0	–	–
Left renal injury	0	–	–
Tracheal injury	0	–	–

*The AUC (area under the ROC curve) values with and without findings are statistically different (p<0.05).

The area under the ROC curve²³ for each diagnosis was calculated using the nonparametric method for constructing curves, as described by Beck and Schultz.²⁴ For each condition evaluated, two areas under the curve were obtained, one corresponding to the TraumaSCAN diagnosis before information about patient findings were input into the Bayesian network, and the other corresponding to the TraumaSCAN diagnosis after information about patient findings were input into the Bayesian network. The areas under the curve for the TraumaSCAN diagnoses of the same condition were compared by the Hanley and McNeil method.²⁵

The methods require that the tests are not highly correlated (i.e., the Pearson's correlation coefficient, r, should be less than 0.9) and that the area under the curve ranges between 0.7 and 0.975. As a result, we were not able to compare the before and after areas under the ROC curves for some of the conditions. The statistical calculations were performed using Analyse-it! (statistical analysis add-in software for Microsoft Excel developed by Analyse-it Software Ltd., Leeds, United Kingdom).

The different areas under the ROC curve give an indication of the system performance in diagnosing individual diseases or conditions. However, there is also a need to rate the ability of the system ability to identify all or most conditions that are relevant for a particular patient.

Our assessment of the overall performance of TraumaSCAN is based on the comprehensiveness and relevance of the system diagnosis for each patient. These measures were developed to assess the performance of diagnostic systems that can generate multiple diagnoses.²⁶ Comprehensiveness and relevance of the TraumaSCAN diagnoses were calculated using a modification of the method described by Berner et al.²⁷

Comprehensiveness is a measure of how broad or inclusive a system is in diagnosing all appropriate conditions for a specific patient. It is defined as the ratio of the number of correct diagnoses for a specific case as determined by the system to the number of diagnoses in the gold standard for the case. Comprehensiveness is somewhat related to sensitivity of the system. Relevance captures whether the system came up with only appropriate diagnoses or whether it includes additional inappropriate diagnoses for a particular case (analogous to specificity of the system). It is calculated as the number of correct diagnoses made by the system divided by the total number of diagnoses made by the system. We calculated comprehensiveness and relevance at different thresholds (from 0.0 to 1.0) for the presence of diseases and conditions. For each patient, all conditions for which system's posterior probability of occurrence was greater than or equal to the threshold were considered to be conditions diagnosed by the system for the patient.

Results

Sensitivities and specificities obtained for the 26 cases were used to calculate areas under the ROC curve for the 11 (of a possible 14) conditions found in the 26 cases. The three conditions modeled in the Bayesian network that were not present in any of the 26 patients were left renal injury, left tension pneumothorax, and tracheal injury. For each condition, the areas under the ROC curve before and after the Bayesian network was given information on findings modeled in the Bayesian network are presented, along with 95 percent confidence intervals (95% CI). These results are given in Table 2▶.

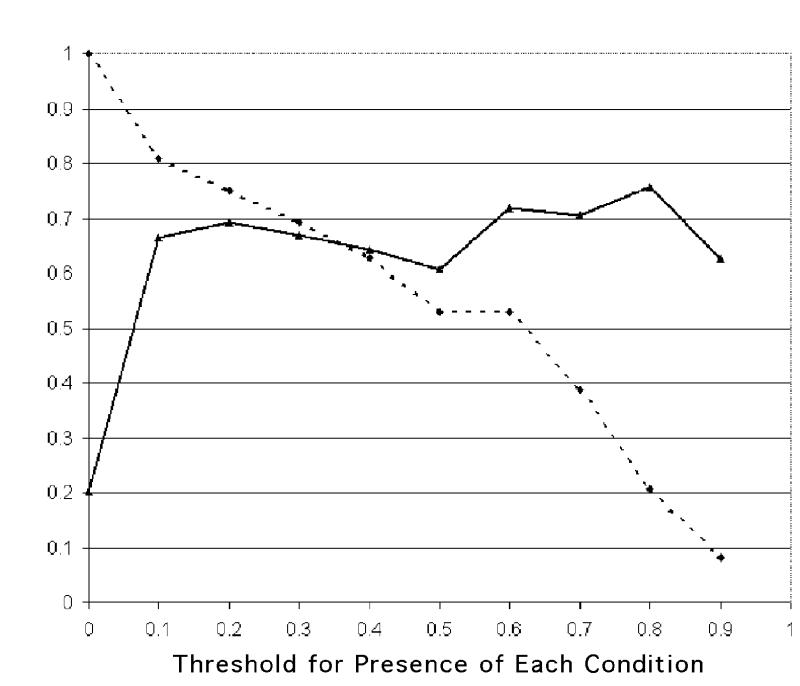
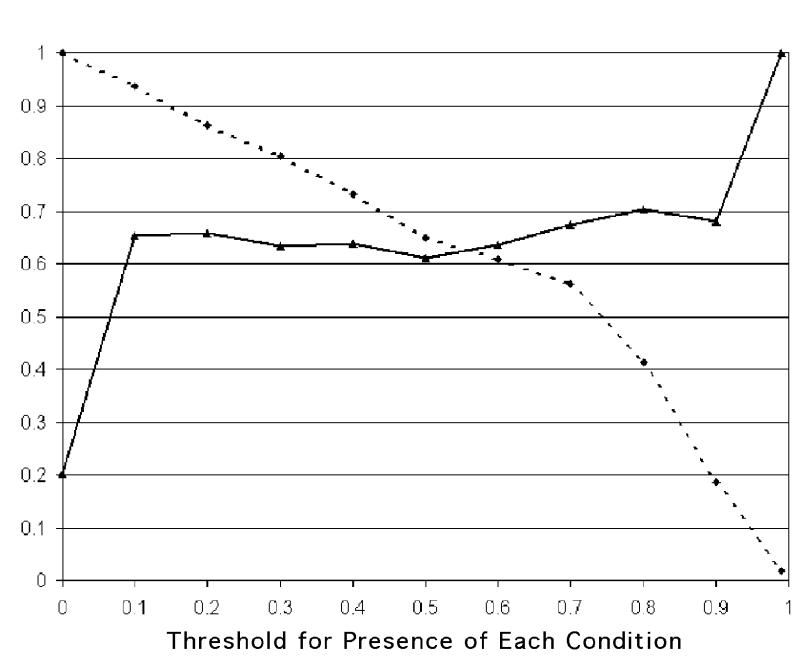
The comprehensiveness and relevance of the system diagnoses are graphed in Figures 5 and 6▶▶. The x axis gives the different thresholds used for presence of each condition. The comprehensiveness of the system is high using small thresholds (the system considers more conditions as being present), and lowers steadily as the threshold is elevated. The relevance is low using small thresholds; it grows as the threshold is raised but stays steady above 60 percent for most threshold values.

Figure 5 .

Relevance (solid line) and comprehensiveness (staggered line) before BNet findings are used.

Figure 6 .

Relevance (solid line) and comprehensiveness (staggered line) after BNet findings are used.

Discussion

The results obtained from measuring areas under the ROC curve indicate that for the 26 cases tested, TraumaSCAN performed well in general, both when provided with information on variables corresponding to findings in the Bayesian network and when no information about these findings were provided. However, in light of the small number of cases used for evaluation, no general statistical conclusions can be drawn about the diagnostic abilities of the system.

In five of the conditions evaluated, the area under the ROC curve was smaller (although not significantly smaller) after information about patient findings was entered. This can be explained in part by the fact that findings were entered into the Bayesian network as given in the reports and notes provided by the trauma team, and some of these were misleading. (An example of this was an observation of decreased breath sounds on the right side of the chest for a case with left lung injury only). These observations highlight the sensitivity of the Bayesian network model to findings: Erroneous findings are likely to throw the system off (although the same problem would probably hold true for experts presented with such erroneous information retrospectively).

With respect to descending thoracic aortic injury, an error in the Bayesian network model itself was found. Although the finding “weak leg pulses” was modeled, the finding “weak arm pulses” was not (see Table 1▶). The presence of weak leg pulses greatly increases the Bayesian network's posterior probability of descending thoracic aortic injury. However, the combined presence of weak leg pulses and strong arm pulses is a better indication of this condition, as weak arm and leg pulses in combination more likely suggest hemodynamic shock. As none of the cases involved five or more external wounds, we were not able to test the system's diagnoses based on approximate solutions derived for more than than four wounds.

Figures 5 and 6 ▶▶show that use of different thresholds for presence of conditions produces different values of comprehensiveness and relevance. When the thresholds are smaller than 0.1, comprehensiveness is very high, while relevance is intermediate, less than 60 percent (i.e., the system has the tendency to over-diagnose). It should be noted that there is no single measure that summarizes the relationship between relevance and comprehensiveness in the way that the area under the ROC curve relates sensitivity and specificity.

We did not attempt to compute the “additional diagnoses” score of Berner et al., which reflects the average number of additional diagnoses suggested by an expert system that medical experts would consider relevant.^26,27 In this analysis, we used the same fixed thresholds for disease presence across all diseases and conditions. However, it is not clear that use of the same fixed threshold for all diseases is the best way to measure relevance and comprehensiveness, since a unique “optimal” diagnostic threshold exists for each disease (as can be ascertained from the graph of the area under the ROC curve).

A better approach for a single measurement of overall relevance and comprehensiveness for the system would be to use the optimal clinical threshold for each diagnosis, as derived from the individual ROC curves. This would require randomly partitioning the total number of cases to be analyzed into two sets, calculating the areas under the ROC curve for one set, as above, and then assessing TraumaSCAN's comprehensiveness and relevance for the second set using the optimal thresholds from the ROC curves obtained for the first set of cases. The number of cases available were too few to pursue this strategy for analysis, but it will be adopted in the future.

Patients vary with respect to their body proportions and the size and placement of their internal organs. This means that people with similar external wounds have potential differences in the scope of damage. However, TraumaSCAN makes use of one three-dimensional model of the torso, as mentioned above, and the results we obtained are from use of this same torso model for all cases. Modeling differences in individuals with respect to the body volume occupied by their chest or abdominal cavities could be done by making use of statistical three-dimensional models of anatomy using an approach similar to that suggested by Mazziota et al.²⁸ Although statistical anatomic models have been developed for the human brain using data from different persons,²⁹ there are fewer examples of this type of research for other parts of the anatomy. The purpose of the work by Mazziota et al. on statistical modeling of the human brain is to map an individual's brain scans to the reference brain atlas created from analysis of numerous brains, in this way taking advantage of what is already known about structure and functionality in each area of the brain.

Another issue is that the geometric reasoner does not directly address the problems of bullet ricochet or secondary projectiles, such as bits of bone or bullet fragments. The hope was that patient findings for these cases would point to conditions other than those that would arise from pure geometric reasoning, an example of the goal of using the strengths of each reasoning method to bolster the other.

Future work on TraumaSCAN includes learning the Bayesian network probabilities from patient data, retrospectively testing a large set of trauma cases, and assessing TraumaSCAN's value in aiding spatial reasoning skills for emergency department residents at different stages of training. A Web-based Java three-dimensional version will be created for this purpose, since it will facilitate easier dissemination of the system. (The prototype system runs only on Silicon Graphics machines.) Also, viable approaches for the assessment of stab wounds will be addressed in future versions of the system.

Actual use of a system like TraumaSCAN in a clinical setting would require analysis of the workflow for that particular setting. For example, when TraumAID was tested at the Medical College of Pennsylvania over a 15-month period, it was found that scribe nurses could perform the data entry into the system as they would normally do for the medical and legal record.

Conclusion

We have described a computer-based approach for reasoning about possible consequences of ballistic penetrating trauma in the face of uncertainty. Our prototype system, TraumaSCAN, uses knowledge about the geometry and spatial relationships between anatomic structures and general knowledge about mechanisms of injury in its reasoning process. Uncertainty arises because the extent of damage produced by a mechanism of injury for a particular patient is not precisely known, and only partial information may be available about patient manifestations of injury, which can give valuable information about injuries and diseases that may be present. Using probabilities as a means of quantifying uncertainty, TraumaSCAN integrates anatomic and physiologic knowledge with information about patient manifestations of injury by combining geometric reasoning with probabilistic reasoning based on Bayesian networks. A system like TraumaSCAN could help providers decide what to attend to first, by indicating which condition has the greatest urgency.

Results obtained by testing TraumaSCAN on 26 real gunshot wound cases to the chest and abdomen are encouraging and indicate that the approach for combining geometric and probabilistic reasoning holds promise. It would be instructive to see how TraumaSCAN fares on a larger set of penetrating trauma cases. TraumaSCAN shows that probabilities offer a natural means of mediating between the different reasoning methods, since they both involve uncertainty. It may be useful in aiding reasoning about the spatial relationships among anatomic structures involved in injury.