Symmetries in bacterial motility

Abstract

Descriptions are given of three kinds of symmetries encountered in studies of bacterial locomotion, and of the ways in which they are circumvented or broken. A bacterium swims at very low Reynolds number: it cannot propel itself using reciprocal motion (by moving through a sequence of shapes, first forward and then in reverse); cyclic motion is required. A common solution is rotation of a helical filament, either right- or left-handed. The flagellar rotary motor that drives each filament generates the same torque whether spinning clockwise or counterclockwise. This symmetry is broken by coupling to the filament. Finally, bacterial populations, grown in a nutrient medium from an inoculum placed at a single point, usually move outward in symmetric circular rings. Under certain conditions, the cells excrete a chemoattractant, and the rings break up into discrete aggregates that can display remarkable geometric order.

Biology is an historical science. Nature fiddles around and figures out how to build something, and then it improves upon it in a cut-and-try fashion. The rule is: if a perturbation (or mutation) works, keep it; if it does not, throw it away. Physics tells you about the design constraints and whether the solution found is nearly optimum, but it does not tell you what the actual solution must be. Once the latter is known, it is fun to say, “Gee, this symmetry was met and that was broken.” But this is after the fact. Symmetries do not help you solve problems in quite the profound way that they do, for example, in theoretical physics. Having said that, I probably should sit down or go home. Instead, I am going to describe three symmetries encountered in studies of the motile behavior of bacteria.

Cyclic Motion

The bacterium that most of us study is Escherichia coli, a species that lives in an aqueous medium, including your gut. It is very small, about 1 μm in diameter by about twice as long. It is propelled by the rotation of several left-handed helical filaments that extend out into the external medium. They have a wavelength of about 2.5 μm, a helix diameter of about 0.5 μm, and they can be up to 10-μm long (see ref. 1 for review). When these filaments turn counterclockwise (CCW, when viewed along the helical axis looking toward the cell body) they coalesce into a bundle that pushes the cell forward, at speeds of order 30 μm/s.

The Reynolds number, R = lvρ/η, is a dimensionless parameter indicating the relative importance, in the equations of motion of a fluid, of inertial as compared with viscous forces. Here l is the size of the swimming organism, v its velocity, ρ the specific gravity of the fluid, and η its viscosity. For E. coli in water, l ∼ 10⁻⁴ cm, v ∼ 3 × 10⁻³ cm/s, ρ ∼ 1 g/cm³, and η ∼ 10⁻² g/cm·s, so R ∼ 3 × 10⁻⁵. Motion of a bacterium is completely dominated by viscous forces.

Viscous drag on a thin filament is asymmetric. If you drop a thin metal rod in molasses, it falls straight down twice as fast when oriented vertically than when oriented horizontally. However, if you drop it slantwise, it falls slantwise. This is because the component of force (due to gravity) parallel to the rod carries the rod farther in that direction in a given time than the component of force normal to the rod carries it in the perpendicular direction. Segments of a rotating helical filament move slantwise through the medium. Components of viscous drag in a direction parallel to the helical axis add up and, thus, generate thrust (see figure 6.3 of ref. 2). Rotation of the helix is cyclic: after each revolution the filament looks the same, but if left-handed and turning CCW, the wave crests always travel from base to tip.

Sir Geoffrey Taylor is often credited with the first theoretical work showing how microorganisms generate thrust at low Reynolds number (3, 4). However, that credit should go to Wilhelm Ludwig who wrote a monumental paper on the subject in 1930 (ref. 5, a journal of comparative physiology, not read by applied mathematicians). Ludwig realized that the relevant equations of motion do not depend explicitly on time: if a microscopic organism moves its appendages one way and then moves them back, retracing their steps in a reciprocal manner, then it does not go anywhere (see figure 2 of ref. 5, or its reprint, figure 2 of ref. 6). Ludwig’s organism is shown in Fig. 1. A simpler organism, one with a single hinge connecting two rigid parts, was envisaged by Edward M. Purcell; he called it a scallop (see figure 6 of ref. 7). If macroscopic, the scallop could swim by opening its shell slowly and closing it rapidly. It would coast further after the power stroke than after the recovery stroke and, thus, progress hinge first. However, if microscopic, it would just return to its initial position. After discussing the “Scallop Theorem,” namely that at low Reynolds number reciprocal motion does not work, Purcell noted that a microscopic organism with two hinges could swim if it strokes, instead, in a cyclic manner (figure 7 of ref. 7). Ludwig’s organism could do this by moving its oars independently, in the manner described in Fig. 1b. Purcell argued that such an organism would swim to the right, but he left the proof as an exercise for the student. Another way that Ludwig’s organism could swim would be to feather its oars on the return stroke (i.e., change their shape, so that on the return stroke, they are closer to the cell body). This is, in fact, how many ciliated organisms swim, as noted by Ludwig, e.g., Chlamydomonas. Finally, to set the record straight, a real scallop does not swim hinge first, as Purcell imagined, but hinge last (Charles W. McCutchen, letter to Purcell dated February 28, 1977)! So a real scallop is more complicated.

Figure 1.

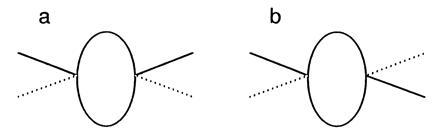
An organism propelled by two rigid oars. (a) If the organism strokes reciprocally, pulling both oars rapidly downwards, then returning them slowly upwards, and repeating this motion, it could swim upwards if macroscopic but not if microscopic (5). The position of the oars at the beginning of the power stroke is shown by the solid lines. Their position at the end of the power stroke is shown by the dotted lines. (b) If, instead, the organism stroked cyclically by moving its oars one by one, in the sequence right down, left down, right up, left up, and repeating this motion, it could swim, even if microscopic (7). The position of the oars at the end of the first step of the cycle is shown by the solid lines.

The most dramatic way I know of illustrating the Scallop Theorem is by stirring and then unstirring a viscous fluid, e.g., glycerol, contained between two concentric cylinders, Fig. 2. Taylor demonstrated this experiment in a movie (now a video) on low Reynolds-number flows, using an inner cylinder of relatively small diameter and viewing the assembly from the top (8). It is more devious to use an inner cylinder of relatively large diameter and to view the assembly from the side, where one cannot see what is really going on, Fig. 2a. What happens when one rotates the inner cylinder is that the stripe of dye (Fig. 2b) gets spread out into a spiral. The end of the stripe at the Pyrex wall stays put, while the end at the lucite wall gets dragged around with the inner cylinder. After three revolutions, say, the spiral has three turns. Seen from above, the dye layer is razor thin, rolled up like toilet paper on a roll. Seen from the side, the solution looks homogeneous. When one rotates the inner cylinder back the other way, retracing one’s steps, the spiral unrolls, and the stripe of dye returns to its original configuration. Seen from the side, it appears that the solution has been mixed and then unmixed, an unexpected result! The experiment works, not simply because of low Reynolds number, but because the dye, in a highly viscous medium, has a small diffusion coefficient and, thus, accurately tracks bulk flow.

Figure 2.

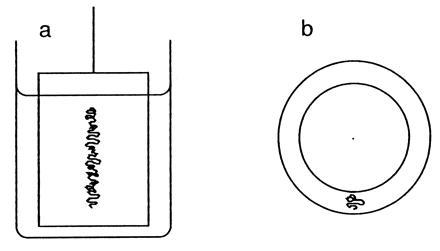
Two concentric cylinders used to stir a viscous medium. (a) Viewed from the side. (b) Viewed from the top. The inner cylinder can be rotated about its long axis. The space between the cylinders is filled with a viscous medium (e.g., glycerol), marked with a dyed sample of the same medium (e.g., glycerol containing amido black), as shown by the squiggly line. The cylinders actually used in the demonstration were a 400 ml Pyrex beaker (7 cm i.d., 10 cm high) and a closed lucite pipe (5 cm o.d., 7 cm high) mounted on the shaft of an old double-ended potentiometer, fixed to a delrin cap, fitted to the beaker. An access hole cut through the cap allowed the dyed sample to be added with the aide of a hypodermic syringe. In this set up l ∼ 1 cm, v ∼ 3 cm/s (at ∼5 s per revolution), ρ ∼ 1.3 g/cm³, and η ∼ 14 g/cm·s, so R ∼ 0.3.

Rotary Motor

The motor that drives the helical filament is at its base, embedded in the cell wall and cytoplasmic membrane, Fig. 3. This figure shows 20 or so components identified according to the names of genes by which they are encoded (named, in turn, from the phenotypes of defective products). The component of largest diameter (about 50 nm) is the C-ring (FliG, M, and N), located in the cytoplasm. Next comes the MS-ring (FliF), embedded in the cytoplasmic membrane. Then comes the rod or drive shaft (FlgB, C, F, and G) that passes through a bushing (the P- and L-rings, FlgI and FlgH) and connects to a flexible coupling (the hook, FlgE) and thence to the flagellar filament (FliC). Note the other components of the Gram-negative cell wall (peptidoglycan layer and outer membrane). It’s the peptidoglycan that provides the rigid framework.

Figure 3.

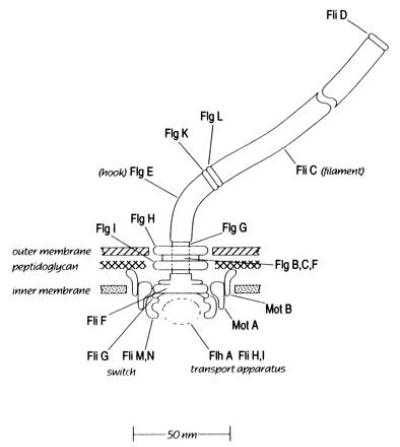
A scale drawing of the bacterial flagellar motor. Structural components are named after their genes, which fall in classes flg, flh, fli (originally called fla). Null mutants in the fla class are nonflagellate. Null mutants in the mot class are flagellate but nonmotile. The switch controls the direction of rotation. It interacts with certain cytoplasmic proteins, part of the cell’s sensory system (not shown). The transport apparatus (as yet poorly defined) controls the excretion of axial motor components. The motor is assembled from the inside-out, with new components added at its distal end (1).

Torque is thought to be generated by the interaction of the transmembrane components MotA and MotB, linked to the peptidoglycan, with proteins attached to the MS-ring, probably FliG (ref. 9; see ref. 10 for review). This interaction is coupled to translocation of protons (or hydronium ions) across the cytoplasmic membrane from the outside to the inside of the cell. Force generation does not involve hydrolysis of ATP (11).

The simplest way to study flagellar rotation is to fix one flagellar filament to a microscope slide or coverslip and watch the motion of the cell body: it spins alternately clockwise (CW) or CCW (12). The torque-speed relationship is symmetric, i.e., the same whether the motor turns CW or CCW (see figure 2b of ref. 13). If one watches a cell spin, writes down the time intervals during which it turns CW or CCW, and plots the corresponding interval-length distributions (not worrying about very short intervals, that are hard to study) they prove to be exponential, with decay times of order 1 s (see figure 2 of ref. 14). The motor of a wild-type cell behaves as a two-state system, with constant probabilities per unit time of changing from one state to the other. The dwell times in these states are approximately equal.

These symmetries are broken when motors are coupled to flagellar filaments. Swimming cells execute a random walk. They swim steadily forward (or run) for a period averaging about 1 s, then move erratically in place (or tumble) for a period averaging about 0.1 s, and then run again, choosing a new direction approximately at random (15). Both run and tumble intervals are exponentially distributed. This asymmetry arises for the following reason. The flagellar filaments rotate synchronously and form a bundle when the motors spin CCW: the bundle pushes the cell steadily forward. The bundle flies apart when the motors spin CW: the different filaments not only pull the cell in different directions, they also change their shape (snap from a left- to a right-handed conformation, with half the pitch) making the motion even more chaotic (16). For a discussion of bundle dynamics, see (17).

If a tethered cell is exposed to a chemical attractant (e.g., an exponentially increasing temporal gradient of the amino acid aspartate), the rate constant for the CCW → CW transition shifts to a lower value, while the rate constant for the CW → CCW transition shifts to a higher value. As a consequence, the motor spends more time spinning CCW (see figure 5 of ref. 14). The reverse is not true unless gradients are very large, i.e., a decreasing temporal gradient of an attractant is usually ignored.

Thus, if a swimming cell is exposed to an increasing temporal gradient of an attractant, e.g., if a run happens to carry the cell up a spatial gradient of an attractant, that run is extended. If, on the other hand, a run happens to carry a cell down a spatial gradient of an attractant, then the run interval reverts to a zero-stimulus value. Therefore, the cell drifts up a spatial gradient following a biased random walk. The bias is positive, not negative; runs are lengthened, not shortened (ref. 15; for a review, see ref. 18).

Pattern Formation

The final part of my story concerns the migration of populations of cells. If cells are inoculated in a Petri plate containing agar that is soft enough to allow them to migrate through the gel but hard enough to suppress convection, and if the medium contains a metabolizable attractant (or a mixture of such attractants), the cells grow and divide, consume one attractant after another, and spread out across the plate in a series of symmetric circular chemotactic rings (19). The cells generate spatial gradients of attractants by uptake and metabolism, and then they pursue these gradients (19, 20). One set of cells exhausts the first attractant, a second set the second, and so on. Regions of high cell density scatter light, so chemotactic rings are easy to see. Just illuminate the plate from behind and view it against a dark background.

Elena O. Budrene found something different: if cells are grown on relatively high concentrations of substances that are components of the tricarboxylic-acid cycle, e.g., fumarate, malate, or succinate (at best weak attractants), they excrete the amino acid aspartate, a strong attractant (21, 22). What happens depends on the concentration of the substrate (e.g., succinate), which determines both the final cell density and the rate of excretion of aspartate: one goes from a single ring, to radial arrays of spots, to spots on intersecting spirals, to similar spots with tails, and finally to macroscopic ensembles that we call slugs. The most elaborate patterns have been observed with Salmonella typhimurium, a cousin of E. coli, that is chemotactic toward (moves up gradients of) citrate, another component of the tricarboxylic-acid cycle. In mixtures of succinate and citrate, both mechanisms apply. The cells consume citrate and chase the spatial gradient thus formed. They also consume succinate and excrete aspartate. The patterns formed are unexpectedly complex and remarkably beautiful. Examples are shown in Fig. 4.

Figure 4.

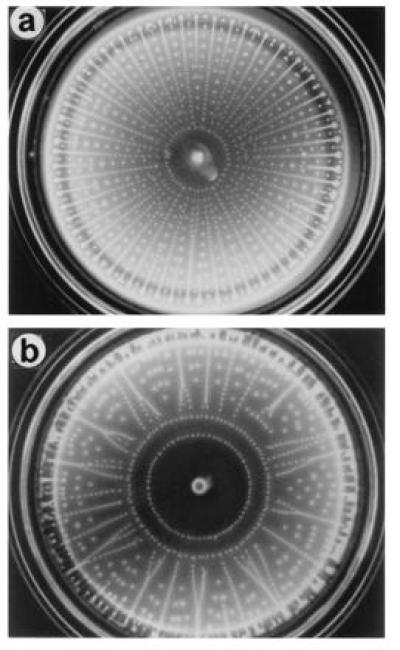
Petri plates (8.5 cm i.d.) containing aggregates of S. typhimurium wild-type strain LT2 grown in M9 succinate, citrate for 72 h at 25°C: (a) 5 mM succinate and 1.5 mM citrate. (b) 5 mM succinate and 1.7 mM citrate. The inoculum, a remnant of which can be seen at the center of each plate, was 5 μl of a stationary-phase culture grown on M9 glycerol. For other details, see figure 1 of ref. 21 or 22. Photographs courtesy of E. O. Budrene (Harvard University).

When S. typhimurium is grown on succinate alone, elements of the patterns no longer line up on spokes of a wheel (23). This alignment requires interactions between aggregates and an advancing ring, from which they were spawned (22). In the absence of metabolizable attractants, this ring appears with wild-type cells of E. coli but not with S. typhimurium.

Summary

Flagellated bacteria swim at low Reynolds number, where reciprocal motion is futile, by rotating thin helical filaments. Each filament is driven at its base by a rotary motor that works equally well whether turning CCW or CW. When several filaments on the same call are driven CCW, they coalesce to form a bundle that pushes the cell steadily forward. When they are driven CW, the bundle flies apart, and the cell moves erratically in place. By measuring the concentrations of chemical attractants and extending CCW intervals when these concentrations increase with time, a cell is able to move up a spatial gradient of an attractant. When these gradients are generated by metabolism of attractants, populations of growing cells migrate outwards in circular rings. However, when the cells themselves excrete an attractant, rings can break up into discrete aggregates. The symmetry of the ring is broken, but higher-order symmetries appear.