Abstract
Integrins are transmembrane adhesion receptors that bind extracellular matrix (ECM) proteins and signal bidirectionally to regulate cell adhesion and migration. In many cell types, integrins cluster at cell-ECM contacts to create the foundation for adhesion complexes that transfer force between the cell and the ECM. Even though the temporal and spatial regulation of these integrin clusters is essential for cell migration, how cells regulate their formation is currently unknown. It has been shown that integrin cluster formation is independent of actin stress fiber formation, but requires active (high-affinity) integrins, phosphoinositol-4,5-bisphosphate (PIP2), talin, and immobile ECM ligand. Based on these observations, we propose a minimal model for initial formation of integrin clusters, facilitated by localized activation and binding of integrins to ECM ligands as a result of biochemical feedback between integrin binding and integrin activation. By employing a diffusion-reaction framework for modeling these reactions, we show how spatial organization of bound integrins into clusters may be achieved by a local source of active integrins, namely protein complexes formed on the cytoplasmic tails of bound integrins. Further, we show how such a mechanism can turn small local increases in the concentration of active talin or active integrin into integrin clusters via positive feedback. Our results suggest that the formation of integrin clusters by the proposed mechanism depends on the relationships between production and diffusion of integrin-activating species, and that changes to the relative rates of these processes may affect the resulting properties of integrin clusters.
Introduction
Precise control over integrin function is important to such diverse cellular processes as cell migration, hemostasis, wound healing, angiogenesis, and development (1). In many cell types, integrins form clusters upon which numerous cytoplasmic proteins gather to form a link between the extracellular matrix (ECM) and the cell cytoskeleton. Integrin cluster formation is critical not only for creating contact points where many integrin-ECM bonds distribute adhesive force, but also for creating a signaling platform where protein-protein interactions occur in discrete spatial locations to influence integrin-related cell signaling systems (2–4).
Despite the importance of integrin clustering for cell adhesion, migration, and signaling, the mechanisms responsible for integrin clustering remain poorly understood. Computational modeling has shown that a favorable energetic interaction between two bound integrins can result in integrin clustering, but does not identify the source of such an interaction (5). It has been suggested, based on in vitro data, that interactions between integrin transmembrane domains may give rise to integrin subunit homodimerization (6), but it is not clear whether this mechanism is responsible for integrin cluster formation in adherent cells.
Increases in integrin affinity for ECM ligands, which shift integrins into an active conformation and prime them for binding to ECM, result from binding of an effector molecule to integrin cytoplasmic tails or by binding of the integrin extracellular domain to ECM ligand (7). Integrin affinity also influences integrin clustering (8) and integrin affinity modulation plays a key role in dynamic cell adhesion processes by providing reversible control over integrin binding (9). By regulating integrin affinity precisely in both time and space, cells can use integrin binding as an adhesive switch that facilitates migration in many cell types (10). Despite the importance of integrin affinity regulation for integrin clustering, it is not known how integrin affinity modulation may be spatially regulated to produce small, localized regions where high concentrations of bound integrins are grouped to form integrin clusters.
Here, we present a minimal model for how initial formation of integrin clusters may occur based on known biochemical interactions between molecules associated with integrin clusters. We evaluate the feasibility of such a mechanism for generating integrin clusters by simulating the proposed reactions and model analysis is used to suggest how the rates of reaction and diffusion of molecules that affect integrin affinity may affect the properties of newly formed integrin clusters.
Materials and Methods
Details of the experimental and computational methods employed in this work, as well as the methodology for estimating the baseline model parameter values (Table 1) and initial species concentrations, may be found in the Supporting Material.
Table 1.
Baseline parameter set
| Model parameter | Description | Baseline model value∗ | Reference |
|---|---|---|---|
| k1f | Active talin binding integrin | 3.3 | (22,23) |
| k1r | Talin-integrin dissociation | 0.0042 | (22,23) |
| k2f | Active integrin binding ECM | 1.5 | (44,46–49) |
| k2r | Active integrin-ECM dissociation | 0.1 | (50) |
| k3f | Inactive integrin binding ECM | 0.34 | (44,46–49) |
| k3r | Inactive integrin-ECM dissociation | 3.4 | (50) |
| k4f | Active talin binding inactive integrin-ECM | 495 | (22,23) |
| k4r | Active talin-integrin-ECM dissociation | 0.0042 | (22,23) |
| k5f | PIP kinase binding active integrin-ECM | 100 | — |
| k5r | PIP kinase-active integrin-ECM dissociation | 0 | — |
| k6 | PIP phosphorylation | 0.92 | (51) |
| k7 | PIP2 degradation | 2.4 | (51) |
| k8f | Talin activation by PIP2 | 50 | (19) |
| k8r | Talin deactivation | 0.1 | (19,53) |
| DI | Integrin diffusivity | 0.01 | (5,54–56) |
| DI∗ | Active integrin diffusivity | 0.01 | (5,54–56) |
| DT | Talin diffusivity | 1 | (19,57) |
| DT∗ | Active talin diffusivity | 0.01 | (57,58) |
| DPIP | PIP diffusivity | 0.01 | (59,60) |
| DPIP2 | PIP2 diffusivity | 0.01 | (59,60) |
| DPIPKIγ | PIP kinase diffusivity | 1 | (57) |
Units are [1/s] for reaction rate and [μm2/s] for diffusivity.
Results
A spatial model for the biochemical events leading to integrin clustering
Although binding of the talin head domain is sufficient to activate integrins in phospholipid vesicles (11), cells minimally require integrin, talin, PIP2, and immobile ECM ligand to form integrin clusters, but do not require polymerized actin (8). These observations suggest that the production and activation of two species involved in activating integrins, namely PIP2 and talin, must be regulated to control integrin clustering. If integrin clustering is controlled by these molecules, then how do cells coordinate their production and activation to regulate integrin clustering temporally and spatially?
We propose that local increases in integrin-activating molecules create a region within which integrins are activated and then immobilized by binding ECM as a function of increased integrin affinity. The conceptual reactions involved in this mechanism are illustrated in Fig. 1. According to this model for integrin clustering, low-affinity integrins are shifted into the high-affinity state by binding to active talin. High-affinity integrins bind to ECM and undergo conformational changes that reveal a site for protein docking on the integrin cytoplasmic tail (12), and phosphoinositol kinase (PIPKIγ) localizes to these bound integrins via talin (13–16). After associating with the bound integrin complex, PIPKIγ begins phosphorylating phosphoinositol phosphate (PIP) to create PIP2 (13,17). PIP2 is free to diffuse away from the immobile integrin-ECM-kinase complex, creating a concentration gradient of PIP2 surrounding the immobilized complex. Within this region, PIP2 binds to and activates additional talin molecules (18,19), resulting in local increases in active talin (20). Active talin binds inactive integrin, creating active integrin (21) that binds to ECM and creates another immobilized binding site for PIPKIγ on the talin/integrin complex (22,23).
Figure 1.
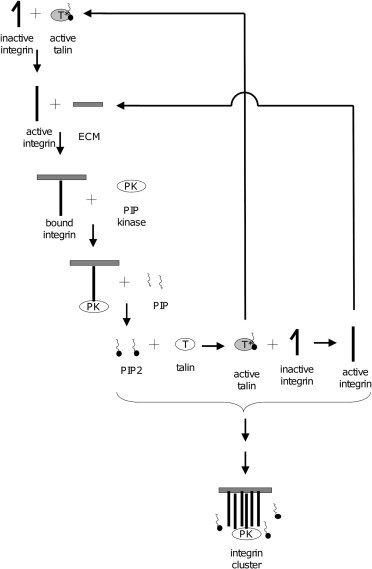
Proposed reaction cascade responsible for integrin clustering. Integrin activation by talin yields high-affinity integrin that binds to ECM, becomes immobilized, and creates a binding site for PIP kinase. PIP kinase produces PIP2, which activates talin and produces more high-affinity integrin. Cluster growth is facilitated by diffusion of active integrin or integrin-activating species (i.e., active talin, PIP2) away from the site of initial activation on the tails of bound integrins.
This reaction cascade creates a positive feedback mechanism that is capable of producing high local concentrations of PIP2, talin, and active integrins; these active integrins can subsequently bind ECM and become immobilized, creating a region with high bound integrin concentration, which we take to be indicative of an integrin cluster.
The mathematical representations of these reactions, shown in Eqs. 1–8, are based on mass-action kinetics of the bimolecular interactions and unimolecular decomposition or dissociation reactions:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
In these equations, I represents the concentration of inactive, unbound integrin, IT represents the concentration of active integrin, T represents the concentration of inactive talin, T∗ represents the concentration of active talin, E represents the concentration of ECM binding sites, K represents the concentration of PIPKIγ, PIP represents the concentration of PIP, and PIP2 represents the concentration of PIP2. Because full-length, unactivated talin has a low affinity for integrin tails, we assume that only active talin can activate integrin (24).
Model simulation without a nucleation event does not result in formation of a discernible integrin cluster; therefore, all simulations shown here were performed with a small nonzero concentration of an integrin-activating species at a discrete location in simulation space ([T]o = 0.001, unless otherwise indicated). How the magnitude and molecular identity of this nucleation event affect integrin clustering via the proposed mechanism is quantified in Magnitude and Identity of the Nucleation Event, below.
Based on this reaction network, material balances yield the partial differential equations shown in Eqs. 9–18. Initial formation of nascent integrin clusters seems to occur within a very thin region of an advancing lamellipod and in a radially symmetric fashion with respect to each cluster (25). Thus, we consider a one-dimensional model for this investigation, with the single spatial dimension representing the cross section of a single circular nascent integrin cluster:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
All reaction rate constants and species diffusivities were determined from published experimental and computational studies as described in the Parameter Estimation section of the Supporting Material.
An adherent cell exhibiting several small, presumably nascent, adhesions is shown in Fig. 2, and the bound integrin concentration profile of the integrin cluster indicated in Fig. 2 b is shown in Fig. 2 c (additional experimental cluster profiles are shown in Fig. S1 of the Supporting Material). A simulation of the proposed integrin clustering mechanism produces a similar pattern of bound integrin concentration, as shown in Fig. 2 d. All of the integrin clusters shown in Fig. 2, a and b, are not necessarily nascent adhesions and the larger clusters may have experienced anisotropic growth due to additional growth and remodeling mechanisms that are beyond the intended scope of this work. Additionally, a nonzero concentration of bound integrin far from the cluster nucleation site is present in simulation results shown in Fig. 2 d but absent from the experimental measurement in Fig. 2 c, due to considerations discussed in the Supporting Material. To focus on clustered integrins, all subsequent plots and analysis employ the bound integrin concentration that is greater than the concentration due to basal low-affinity integrin binding.
Figure 2.
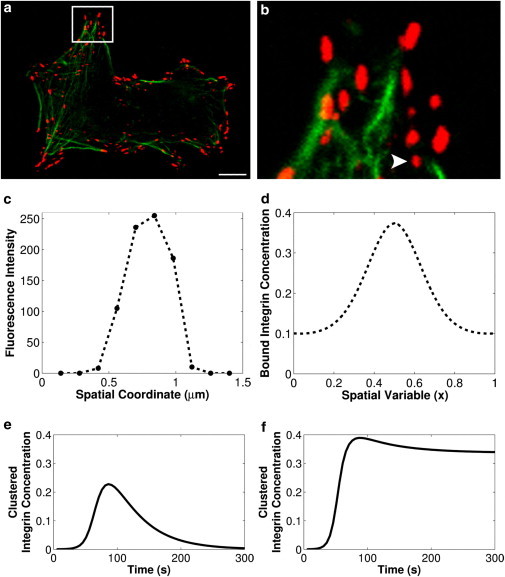
Comparison of measured bound integrin concentration and simulated bound integrin concentration. (a) Confocal microscope image of adherent cells showing bound integrin (red, color online), and actin cytoskeleton (green, color online). Scale bar is 10 μm. (b) Higher magnification of the portion of the cell indicated in panel a; (arrow) nascent integrin cluster analyzed in panel c. (c) Example concentration profile of bound integrin in the nascent integrin cluster indicated in panel b. (d) Simulated bound integrin concentration, calculated as [B] = [IE] + [IET] + [IETK]. The simulation was initiated with a small pulse of active talin at x = 0.5 ([T]∗o = 0.001) as the nucleation event; model parameter values are as given in Table 1. (e and f) Dynamics of integrin cluster formation and turnover under conditions representing: (e) cluster turnover (k5r = 1 s−1) and (f) cluster stabilization (k5r = 0).
Integrin clustering dynamics and cluster turnover
The mechanisms by which integrin cluster turnover is regulated are only just being discovered but it is clear that various focal adhesion proteins affect the relative rate of cluster turnover. In the proposed model, integrin cluster turnover occurs via sequential unbinding of integrins that reside in a complex with talin, ECM, and PIPKIγ. The effect of proteins that initiate cluster turnover is represented by dissociation of PIPKIγ from the integrin-ECM-talin complex, because this is the final reaction in the cluster formation cascade. A nonzero value for PIPKIγ dissociation results in transient formation of an integrin cluster, as shown in Fig. 2 e; such transient integrin clustering may occur, for example, when integrin clusters form but fail to mature into focal adhesions (25). The timescales for formation and dispersion of an integrin cluster predicted by the proposed model match the experimentally observed timescales for formation and dispersion of nascent adhesions quite well (25). A different temporal profile would result when integrin clusters are stabilized by association with the actin cytoskeleton and thus experience no PIPKIγ dissociation, as shown in Fig. 2 f. Because the focus of this work is the initial formation of integrin clusters, we restrict the following analysis to the latter case; all subsequent simulations are performed with the rate constant for PIPKIγ dissociation set to zero.
Analysis of the proposed integrin clustering mechanism
To facilitate quantitative comparison of the effects of changes to different diffusion and reaction rates on integrin clustering, we calculate the bound integrin concentration center-of-mass (COM), defined as
| (19) |
where [B] represents the concentration of bound integrin, given by [B] = [IE] + [IET] + [IETK]. This metric was chosen to quantify the density of bound integrin within a spatial region; higher cluster COM indicates more densely clustered integrins with respect to spatial location, whereas lower cluster COM indicates loosely clustered integrins.
Effects of molecular perturbations and species concentrations on integrin clustering
Use of computational modeling to investigate cellular systems enables analysis of perturbations that may be difficult or impossible to implement experimentally, but which nonetheless provide valuable theoretical insight into the system. When comparing such model simulations with experiments it is important to consider that a change to a chemical species’ theoretical properties may have compound effects on the related experimental measurement. For example, in the case of integrin clustering, changes to integrins’ biochemical properties may influence cluster nucleation, initial formation, cluster maturation, and/or turnover—all of which may in turn influence the integrin cluster properties observed in adherent cells. In this work, our focus is solely on the initial formation of nascent adhesions, and therefore our predictions are not directly comparable to measurements of populations of integrin clusters in adherent cells. For these reasons, all of the simulations shown in this work are predictions describing how the proposed clustering mechanism would affect the properties of nascent integrin clusters that are devoid of many of the confounding mechanisms that influence observable cluster size.
As shown in Fig. 3, a and b, the proposed clustering model predicts that increases in the rate of active integrin binding to ECM (k2f) and the rate of inactive integrin-binding ECM (k3f) result in integrin clusters that are more densely packed with integrins, although changes to the values of these two different rate constants result in different changes to the spatial properties of integrin clusters. Whether expressed or implied, measures of integrin cluster size determined from fluorescence images or related concentration profiles require definition of an intensity or concentration value above which a region is defined as an integrin cluster, and the value of such a threshold affects measured integrin cluster sizes (26). As shown in Fig. 3 a, any appropriate concentration threshold results in increasing cluster size as a function of increases in the rate of active integrin binding to ECM (k2f); however, the cluster profiles shown in Fig. 3 b would suggest inverse relationships between the rate of inactive integrin binding ECM (k3f) and cluster size, depending on whether the concentration threshold is above or below 0.1.
Figure 3.
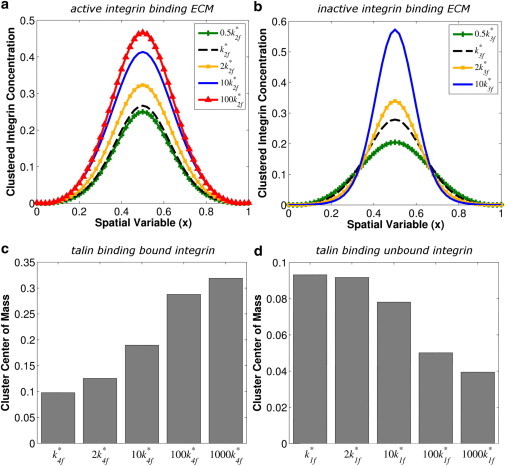
Effects of altered reaction rates on the concentration profile and COM of clustered integrin. The parameter k∗2f represents the baseline value for the reaction of active integrin with ECM; k∗3f represents the baseline value for the reaction of inactive integrin with ECM; k∗4f represents the baseline value for the reaction of bound integrin with active talin; and k∗1f represents the baseline value for the reaction of unbound integrin with active talin.
We will now discuss how changes to the model parameters may be related to reported amino-acid mutations that result in constitutive activation of the αIIbβ3 heterodimer (27). If we assume that such a constitutively active integrin mutant exhibits a faster rate of association between inactive integrins and ECM (i.e., increased k3f), such mutant integrins are predicted to cause formation of more densely packed clusters than wild-type integrins, as shown in Fig. 3 b. Amino-acid mutations that alter integrin-talin affinity may also affect integrin clustering (28), and model simulations predict that increases in the rate of talin binding to bound integrin (k4f) increase the density of clustered integrin (as measured by cluster COM, Fig. 3 c). In contrast, increases in the rate of talin binding to unbound integrin (k1f) decrease cluster COM (Fig. 3 d), suggesting that the rate of talin binding integrin will have different effects on integrin clustering depending on the state of the integrin exhibiting the altered integrin-talin affinity. Increases in the rate of PIPKIγ binding to bound, active integrin, or increases in the rate of PIP2 production by PIPKIγ are not predicted to have dramatic effects on nascent adhesion cluster COM (data not shown). Amino-acid mutations that result in observable changes to integrin clustering have also been described (29); based on the simulation results shown here, we predict that such integrin amino-acid mutations may influence integrin clustering by altering the interactions of integrin with either ECM or talin, but that the context for these interactions determines the effect on integrin clustering.
As shown in Fig. 4 a, model simulations predict that increases in ECM concentration will increase cluster COM, and predicted changes to integrin cluster size depend on how integrin clusters are defined. For example, a concentration threshold of 0.05 yields the prediction that integrin cluster size is unchanged by increasing ECM concentration, but a concentration threshold of 0.2 would yield the prediction that integrin cluster size increases with increasing ECM concentration. The focus of this study is initial cluster formation, excluding any mechanisms of cluster regulation that act on clusters after their initial formation. The observation that cells adhering to higher concentrations of ECM proteins exhibit smaller integrin clusters (30) may underscore the importance of these additional mechanisms for regulating cluster growth and turnover as a function of ECM density.
Figure 4.
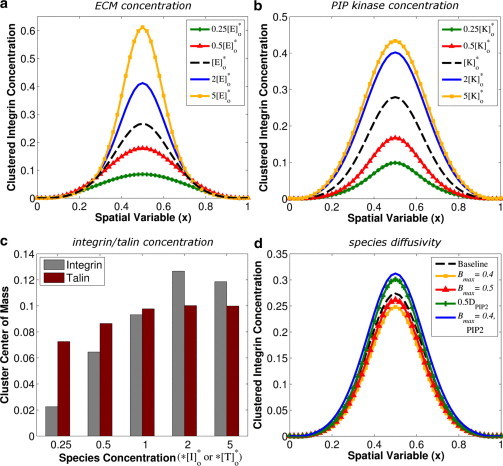
(a–c) Effects of initial species concentrations on the concentration profile and COM of clustered integrin. The values in the legends (a and b) or x axis (c) indicate the initial species concentrations as a function of the baseline initial species concentrations, which are [E]∗o, [K]∗o, [I]∗o, and [T]∗o for ECM, PIPKIγ, integrin, and talin, respectively. (d) Effects of altered diffusivity on the concentration profile of clustered integrin. [B]max = 0.5 and [B]max = 0.4 indicate simulations for which all species diffusivities were calculated as shown in Eq. 20. The legend entry 0.5DPIP2 indicates a simulation for which the diffusivity of PIP2 was one-half the baseline value. The legend entry [B]max = 0.4, PIP2 indicates a simulation for which the diffusivity of PIP2 was calculated as shown in Eq. 20 and the diffusivities of all other species were set to baseline values.
Model simulations predict that increases in the concentration of PIPKIγ increase COM (Fig. 4 b), and a concentration threshold of 0.05 would yield the prediction that integrin cluster size increases with increasing PIPKIγ. Experimental observations indicate that overexpression of full-length talin does not affect integrin clustering (29), and model simulations show that increases in the concentration of full-length talin above the baseline value do not affect integrin cluster COM, although decreases in talin concentration from baseline do decrease cluster COM (Fig. 4 c). Model simulations predict that increases in the integrin concentration increase cluster COM, but only if [I] < [ECM]; if [I] > [ECM], the cluster COM is predicted to decrease slightly (Fig. 4 c).
Effects of altered diffusivity on integrin clustering
The local state of the cytoskeleton or the cell membrane may affect the diffusivity of membrane proteins and phospholipids (31–34). Furthermore, the local density of transmembrane proteins within integrin clusters is presumably greater than the density of transmembrane proteins within the surrounding plasma membrane; therefore, it seems plausible that transmembrane proteins may exhibit reduced diffusion within an integrin cluster. To simulate the effect of molecular crowding on local diffusivity within the integrin cluster, the diffusivity for each mobile species was scaled as
| (20) |
where [B](x) is the local concentration of bound integrin, [B]max is the theoretical maximum concentration of bound integrin, and D∗i is the diffusivity of species i in the absence of bound integrin. The value for the parameter [B]max represents the bound integrin concentration above which potentially mobile species are unable to diffuse due to molecular crowding; lower values for [B]max increase the effect that [B](x) will have on diffusion. Simulation results in Fig. 4 d show the effects of altered diffusivity on integrin clustering.
Because diffusion of mobile species capable of activating integrins causes cluster growth in the spatial dimension, reducing the diffusivity of PIP2 is expected to increase cluster COM, as shown in Fig. 4 d. This effect is balanced by diffusion of precursors to these integrin-activating species into the integrin cluster. Reducing the diffusivities of all mobile species as a function of local bound integrin concentration will decrease cluster COM slightly, as shown in Fig. 4 d. The effects of concentration-dependent changes to PIP2 diffusivity on integrin clustering are similar to those changes caused by global reduction in PIP2 diffusivity. Thus, we conclude that the observed differences between the effects of concentration-dependent changes to PIP2 diffusivity and concentration-dependent changes to the diffusivities of all mobile species are due to reduced diffusion of precursors to integrin-activating species (i.e., inactive integrins and PIP) into the integrin cluster.
Sensitivity analysis of the model parameters
To assess the relative influence of each reaction on the proposed integrin clustering mechanism, we performed local sensitivity analyses as follows. For each parameter j, the baseline parameter value, pj (Table 1), was changed, the resulting model was simulated, and the perturbed COMj,k was calculated from the simulation result. The change to the COM value as a result of changes to each parameter was calculated as
| (21) |
where COMb is the COM calculated from simulation of the baseline parameter set in Table 1, and Δpk is the fractional change to the baseline parameter value pj (i.e., −0.1, 0.1, 0.2). This procedure was repeated independently for each parameter value shown in Table 1.
Fig. 5 a shows the sign and magnitude of the change in cluster COM when the model is simulated with an increase or decrease in a model parameter. The magnitude of the change in COM indicates the relative influence of a particular reaction on integrin clustering as measured by the cluster COM, and the sign of the change indicates whether an increase in a specific reaction rate increases or decreases the cluster COM. As shown in Fig. 5 a, most of the model parameters influence integrin clustering univariately, and the sign and magnitude of a change to a model parameter affects how the change to a given parameter influences the cluster COM. The lack of a simple relationship between reaction rates and integrin clustering suggests that integrin clustering via the proposed mechanism may not be regulated by any single reaction or set of reactions that limits the kinetics of integrin clustering, but rather by the collective balance among production, immobilization, and diffusion of integrin-activating species.
Figure 5.
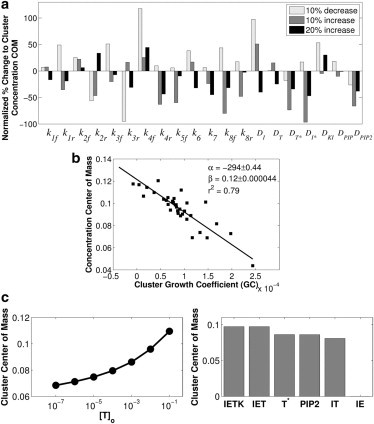
(a) Parameter sensitivity analysis. The relative change in cluster concentration COM was calculated based on a simulation implementing a 10% increase, or 10% decrease, or 20% increase in a given parameter value. The percentage change to the baseline cluster COM was normalized by the sign and magnitude of the change to the parameter value as described in Sensitivity Analysis of the Model Parameters (see main text). (b) Relationship between GC and cluster COM. Parameter sets described in Table 2 were simulated and the resulting bound integrin concentration profile was characterized by the concentration COM. The GC was calculated from the reaction rates and species diffusivities as described in A Metric for Summarizing the Mechanisms Driving Changes to Integrin Clustering (see main text), at a spatial location nine nodes away from the cluster nucleation point. A linear model, y = α∗GC + β, was fitted to the simulation data, and estimates for α and β are shown along with 95% confidence intervals on the parameter estimates. (c) Effect of the magnitude and identity of the nucleation event on cluster COM. (Left panel) Demonstration of how the cluster COM changes as a function of the magnitude of the pulse of active talin used to initiate clustering. (Right panel) The COM of each cluster initiated by a concentration pulse of equal magnitude (0.001) for each of the indicated species.
A metric for summarizing the mechanisms driving changes to integrin clustering
For the proposed reaction network to produce integrin clusters, integrins must be activated and bound within a small region surrounding other bound integrins. If active integrins, active talin, or PIP2 diffuse away from their activation site before becoming immobilized themselves, this diffusion of integrin-activating species results in spreading out of the integrin cluster and decreased bound integrin concentration within the cluster. Changes to reaction rates or diffusion coefficients of mobile species can increase or decrease the cluster COM depending on whether the changes decrease or increase dispersion of integrin-activating species, respectively. Thus, the rate of production of active integrin (or integrin-activating species), combined with the rate of consumption and the diffusivity of that species, determine how far and how quickly a cluster grows. To characterize this phenomenon, we introduce the cluster growth coefficient (GC),
| (22) |
where D is diffusivity, i indicates a given species, x is spatial location, and t is time. The notation GC is used to describe general properties of the metric, which apply to both individual species GCi values and aggregate GC values. A species GCi was determined by calculating the rate of each species’ production and consumption at each point in time and each spatial location using Eqs. 1–8. The GCi of each mobile integrin-activating species was calculated using the following reactions for the rates of production and consumption: Eq. 6–Eq. 8, Eq. 8–Eq. 1, and Eq. 1–Eq. 2 for PIP2, active talin, and active integrin, respectively.
To determine whether the GC is related to the degree of integrin clustering, the model was used to produce values of the aggregate GC and COM using 38 different parameter sets shown in Table 2 as deviations from the baseline parameter set (Table 1). The GCi (x) for each simulation was calculated at each node in the simulation space by summing GCi (x,t) over the entire time course at that node. Because integrin cluster spread results from dispersion of any species capable of activating integrins, we reasoned that an aggregate GC, which incorporates cluster dispersion by more than one species, should be used to characterize the cluster COM. Fig. 5 b shows the simulated cluster COM plotted against the mean of the active talin, active integrin, and PIP2 GCs calculated at locations near but not directly at the nucleation site, indicating that smaller GC values are associated with integrin clusters that are more densely packed with integrins. The aggregate GC values measured at locations far from the cluster nucleation site (or directly upon it) do not show any apparent correlation with the cluster COM (results not shown). Because the GC is measured at a point in space that is close to but not directly upon the nucleation site, the GC accounts for initial diffusion of the reactants that form an integrin-activating species to the measurement point, creation of the integrin activating species by reaction at that point, and the ensuing diffusion away from the measurement point.
Table 2.
Deviations from baseline parameter set used for calculation of GC
| Model parameter | k1f | k1r | k2f | k2r | k3f | k3r | k5f | k6 | k7 | k8f | k8r | DI∗ | DT | DT∗ | DPIP2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Values | 3 | 2 | 1 | 0.005 | 0.15 | 1.5 | 25 | 0.45 | 0.5 | 10 | 0.01 | 0.0025 | 0.5 | 0.0025 | 0.0025 |
| 3.5 | 5 | 5 | 0.15 | 0.7 | 7 | 200 | 1.5 | 5 | 20 | 0.05 | 0.005 | 2 | 0.005 | 0.005 | |
| 200 | 0.2 | 0.02 | 0.02 | 0.02 | |||||||||||
| 0.4 | 0.04 | 0.04 |
Units are [1/s] for reaction rate and [μm2/s] for diffusivity.
The observed relationship between the calculated GC and the simulated cluster COM suggests that the GC may be used to summarize how the relationships between reaction rates and diffusivities affect the properties of integrin clusters formed by the proposed mechanism. If the number of bound integrins remains constant, binding of integrins far away from where integrin-activating species are produced results in a more dispersed cluster with reduced bound integrin density within that cluster. Thus we can use the principles guiding formulation of the GC to predict how changes to the reaction cascade not investigated here, such as additional integrin activation mechanisms, may affect initial integrin clustering. An increase in the rate of production of an integrin-activating species is predicted to increase the local density of bound integrins only if the relative mobility of this species is low enough that these integrin-activating species do not diffuse away before becoming immobilized, otherwise such an increase in the production rate of an integrin-activating species would increase cluster dispersion.
Magnitude and identity of the nucleation event
A critical feature of the proposed integrin clustering mechanism is the ability of the reaction network to amplify a very small increase in the concentration of an integrin-activating species, called a cluster nucleation event, into an integrin cluster. Here, we investigate how the magnitude and molecular identity of the nucleation event may influence integrin clustering. As shown in Fig. 5 c, the proposed positive feedback loop is capable of amplifying even very small increases in the concentration of an integrin-activating species, and the observation that increasing the magnitude of the nucleation pulse increases the cluster COM suggests that cluster dispersion may be related to the amplification kinetics of the nucleation species. Small local increases in the concentration of active talin, active integrin, active integrin bound to ECM, PIPKIγ bound to the integrin-ECM complex, and PIP2 were sufficient to induce integrin clustering at the site of the concentration increase. All the species that are capable of nucleating integrin clustering are involved in the proposed positive feedback mechanism responsible for integrin clustering, suggesting that a local increase in the activity of any species whose activity is amplified by the proposed positive feedback mechanism may initiate cluster formation.
Discussion
Formation of the integrin clusters that nucleate nascent adhesions is independent of myosin II activity (25), and the traction force sustained by nascent adhesions in the very front of the cell is lower than that maintained by more mature adhesions located farther from the cell edge (35). Thus, initial formation of nascent adhesions appears to be independent of the stress-induced mechanisms that may be responsible for anisotropic growth of larger adhesions (36), and the dynamic changes in integrin cluster size observed in migrating cells are most likely influenced by such force-dependent adhesion remodeling mechanisms (37). In this work, we have proposed and evaluated a minimal mechanism for formation of nascent integrin clusters that is independent of force; application of force to nascent adhesions apparently causes their maturation and thus the properties of mature adhesions measured in adherent cells are presumably subject to additional forms of regulation not considered here.
An attractive means for removing the effects of myosin contractility on cluster growth and turnover would be to employ blebbistatin to inhibit myosin-induced contractility; however, it should be noted that such a treatment may not deter all of the processes that affect integrin cluster size after initial cluster formation. Additionally, the small size, fast formation and turnover dynamics, and limited spatial location of nascent adhesions make it difficult to quantify their size with conventional microscopy techniques. We expect that ad hoc experimental studies will be necessary to quantify how the properties of these unique adhesion structures are affected by the biochemical processes explored in this work.
Any biochemical or mechanical mechanism that results in positive feedback between integrin binding and integrin activation could potentially result in integrin clustering. We have presented one possible mechanism based on a minimal set of components necessary for integrin clustering. Theoretical studies have suggested that integrin clustering may result from pairwise interactions between bound integrins (5,38,39). Additionally, mechanical considerations such as membrane fluctuations (38), deformation of the cell membrane and ECM (40), or strain-induced changes in integrin properties (41) may also influence integrin clustering. Integrin activation may also occur by additional signaling mechanisms that cooperate to activate integrins (42,43), and these signaling mechanisms may be subject to mechanisms of spatial regulation different from talin-induced integrin activation. Both chemical and mechanical regulatory mechanisms may work in tandem to control integrin clustering, especially during the force-induced growth and remodeling processes exhibited by integrin clusters.
Recent theoretical work suggests that occupation of a large fraction of available binding sites by integrins requires both talin and an additional positive feedback mechanism between integrin binding and integrin activation (44). The results presented here indicate that interactions between membrane and focal adhesion proteins are indeed capable of producing such a feedback mechanism, and that initial integrin clustering may be regulated by the protein-protein interactions that underlie the mechanism proposed here. A small local increase in the concentration of an integrin-activating species is capable of initiating integrin clustering, and although the exact molecular nature of such events is currently unknown, experimental evidence suggests that any reactions that result in active integrin or bound integrin, including active talin or PIP2, may be capable of initiating integrin cluster formation (8,45) and that such events may be affected by the local rate of protrusion of a spreading or migrating cell (25).
Given the infrequency of cluster nucleation relative to the concentration of these species, cluster nucleation may require assembly of several of these components into a complex. The reactions underlying the proposed clustering mechanism could create a discrete integrin cluster from each occurrence of such a rare nucleation event, thus producing the apparent random spacing of integrin clusters underneath a protruding lamellipod (25). Further experimental work will be required to determine the molecular composition, spatial distribution, and temporal occurrence of such nucleation events.
Acknowledgments
We thank Marc Birtwistle and Jason Haugh for helpful discussion.
We gratefully acknowledge the National Science Foundation-Integrative Graduate Education and Research Traineeship (DGE-0221651), the National Institutes of Health ( HL63960), and the Department of Chemical Engineering at the University of Delaware for financial support.
Supporting Material
References
- 1.Hynes R.O. Integrins: bidirectional, allosteric signaling machines. Cell. 2002;110:673–687. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 2.Goffin J.M., Pittet P., Hinz B. Focal adhesion size controls tension-dependent recruitment of α-smooth muscle actin to stress fibers. J. Cell Biol. 2006;172:259–268. doi: 10.1083/jcb.200506179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shi Q., Boettiger D. A novel mode for integrin-mediated signaling: tethering is required for phosphorylation of FAK Y397. Mol. Biol. Cell. 2003;14:4306–4315. doi: 10.1091/mbc.E03-01-0046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wiseman P.W., Brown C.M., Horwitz A.F. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 2004;117:5521–5534. doi: 10.1242/jcs.01416. [DOI] [PubMed] [Google Scholar]
- 5.Irvine D.J., Hue K.-A., Griffith L.G. Simulations of cell-surface integrin binding to nanoscale-clustered adhesion ligands. Biophys. J. 2002;82:120–132. doi: 10.1016/S0006-3495(02)75379-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li R., Mitra N., Bennett J.S. Activation of integrin αIIbγ3 by modulation of transmembrane helix associations. Science. 2003;300:795–798. doi: 10.1126/science.1079441. [DOI] [PubMed] [Google Scholar]
- 7.Leisner T.M., Yuan W., Parise L.V. Tickling the tails: cytoplasmic domain proteins that regulate integrin αIIbγ3 activation. Curr. Opin. Hematol. 2007;14:255–261. doi: 10.1097/MOH.0b013e3280dce543. [DOI] [PubMed] [Google Scholar]
- 8.Cluzel C., Saltel F., Wehrle-Haller B. The mechanisms and dynamics of αvγ3 integrin clustering in living cells. J. Cell Biol. 2005;171:383–392. doi: 10.1083/jcb.200503017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Luo B.-H., Springer T.A. Integrin structures and conformational signaling. Curr. Opin. Cell Biol. 2006;18:579–586. doi: 10.1016/j.ceb.2006.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Webb D.J., Parsons J.T., Horwitz A.F. Adhesion assembly, disassembly and turnover in migrating cells—over and over and over again. Nat. Cell Biol. 2002;4:E97–E100. doi: 10.1038/ncb0402-e97. [DOI] [PubMed] [Google Scholar]
- 11.Ye F., Hu G., Ginsberg M.H. Recreation of the terminal events in physiological integrin activation. J. Cell Biol. 2010;188:157–173. doi: 10.1083/jcb.200908045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wegener K.L., Campbell I.D. Transmembrane and cytoplasmic domains in integrin activation and protein-protein interactions (Review) Mol. Membr. Biol. 2008;25:376–387. doi: 10.1080/09687680802269886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ling K., Doughman R.L., Anderson R.A. Type Iγ phosphatidylinositol phosphate kinase targets and regulates focal adhesions. Nature. 2002;420:89–93. doi: 10.1038/nature01082. [DOI] [PubMed] [Google Scholar]
- 14.Barsukov I.L., Prescot A., Critchley D.R. Phosphatidylinositol phosphate kinase type 1γ and β1-integrin cytoplasmic domain bind to the same region in the talin FERM domain. J. Biol. Chem. 2003;278:31202–31209. doi: 10.1074/jbc.M303850200. [DOI] [PubMed] [Google Scholar]
- 15.Kong X., Wang X., Qin J. Structural basis for the phosphorylation-regulated focal adhesion targeting of type Iγ phosphatidylinositol phosphate kinase (PIPKIγ) by talin. J. Mol. Biol. 2006;359:47–54. doi: 10.1016/j.jmb.2006.02.048. [DOI] [PubMed] [Google Scholar]
- 16.Di Paolo G., Pellegrini L., De Camilli P. Recruitment and regulation of phosphatidylinositol phosphate kinase type 1γ by the FERM domain of talin. Nature. 2002;420:85–89. doi: 10.1038/nature01147. [DOI] [PubMed] [Google Scholar]
- 17.Kanaho Y., Kobayashi-Nakano A., Yokozeki T. The phosphoinositide kinase PIP5K that produces the versatile signaling phospholipid PI4,5P2. Biol. Pharm. Bull. 2007;30:1605–1609. doi: 10.1248/bpb.30.1605. [DOI] [PubMed] [Google Scholar]
- 18.Ling K., Doughman R.L., Anderson R.A. Tyrosine phosphorylation of type Iγ phosphatidylinositol phosphate kinase by Src regulates an integrin-talin switch. J. Cell Biol. 2003;163:1339–1349. doi: 10.1083/jcb.200310067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martel V., Racaud-Sultan C., Albiges-Rizo C. Conformation, localization, and integrin binding of talin depend on its interaction with phosphoinositides. J. Biol. Chem. 2001;276:21217–21227. doi: 10.1074/jbc.M102373200. [DOI] [PubMed] [Google Scholar]
- 20.Smith A., Carrasco Y.R., Hogg N. A talin-dependent LFA-1 focal zone is formed by rapidly migrating T lymphocytes. J. Cell Biol. 2005;170:141–151. doi: 10.1083/jcb.200412032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Calderwood D.A. Talin controls integrin activation. Biochem. Soc. Trans. 2004;32:434–437. doi: 10.1042/BST0320434. [DOI] [PubMed] [Google Scholar]
- 22.Wegener K.L., Partridge A.W., Campbell I.D. Structural basis of integrin activation by talin. Cell. 2007;128:171–182. doi: 10.1016/j.cell.2006.10.048. [DOI] [PubMed] [Google Scholar]
- 23.Calderwood D.A., Yan B., Ginsberg M.H. The phosphotyrosine binding-like domain of talin activates integrins. J. Biol. Chem. 2002;277:21749–21758. doi: 10.1074/jbc.M111996200. [DOI] [PubMed] [Google Scholar]
- 24.Calderwood D.A., Zent R., Ginsberg M.H. The talin head domain binds to integrin β-subunit cytoplasmic tails and regulates integrin activation. J. Biol. Chem. 1999;274:28071–28074. doi: 10.1074/jbc.274.40.28071. [DOI] [PubMed] [Google Scholar]
- 25.Choi C.K., Vicente-Manzanares M., Horwitz A.R. Actin and α-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 2008;10:1039–1050. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Welf E.S., Ogunnaike B.A., Naik U.P. Quantitative statistical description of integrin clusters in adherent cells. IET Syst. Biol. 2009;3:307–316. doi: 10.1049/iet-syb.2009.0009. [DOI] [PubMed] [Google Scholar]
- 27.Kashiwagi H., Tomiyama Y., Shattil S.J. A mutation in the extracellular cysteine-rich repeat region of the β3 subunit activates integrins αIIbβ3 and αVβ3. Blood. 1999;93:2559–2568. [PubMed] [Google Scholar]
- 28.Anthis N.J., Wegener K.L., Campbell I.D. Structural diversity in integrin/talin interactions. Structure. 2010;18:1654–1666. doi: 10.1016/j.str.2010.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Saltel F., Mortier E., Wehrle-Haller B. New PI4,5P2- and membrane proximal integrin-binding motifs in the talin head control β3-integrin clustering. J. Cell Biol. 2009;187:715–731. doi: 10.1083/jcb.200908134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Welf E.S., Naik U.P., Ogunnaike B.A. Probabilistic modeling and analysis of the effects of extra-cellular matrix density on the sizes, shapes, and locations of integrin clusters in adherent cells. BMC Biophys. 2011;4:15. doi: 10.1186/2046-1682-4-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Klann M.T., Lapin A., Reuss M. Stochastic simulation of signal transduction: impact of the cellular architecture on diffusion. Biophys. J. 2009;96:5122–5129. doi: 10.1016/j.bpj.2009.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jacobson K.A., Moore S.E., Walsh F.S. Cellular determinants of the lateral mobility of neural cell adhesion molecules. Biochim. Biophys. Acta. Biomembr. 1997;1330:138–144. doi: 10.1016/s0005-2736(97)00128-4. [DOI] [PubMed] [Google Scholar]
- 33.Yechiel E., Edidin M. Micrometer-scale domains in fibroblast plasma membranes. J. Cell Biol. 1987;105:755–760. doi: 10.1083/jcb.105.2.755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Weisswange I., Bretschneider T., Anderson K.I. The leading edge is a lipid diffusion barrier. J. Cell Sci. 2005;118:4375–4380. doi: 10.1242/jcs.02551. [DOI] [PubMed] [Google Scholar]
- 35.Gardel M.L., Sabass B., Waterman C.M. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. J. Cell Biol. 2008;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nicolas A., Geiger B., Safran S.A. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stricker J., Aratyn-Schaus Y., Gardel M.L. Spatiotemporal constraints on the force-dependent growth of focal adhesions. Biophys. J. 2011;100:2883–2893. doi: 10.1016/j.bpj.2011.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhao T., Li Y., Dinner A.R. How focal adhesion size depends on integrin affinity. Langmuir. 2009;25:1540–1546. doi: 10.1021/la8026804. [DOI] [PubMed] [Google Scholar]
- 39.Brinkerhoff C.J., Linderman J.J. Integrin dimerization and ligand organization: key components in integrin clustering for cell adhesion. Tissue Eng. 2005;11:865–876. doi: 10.1089/ten.2005.11.865. [DOI] [PubMed] [Google Scholar]
- 40.Paszek M.J., Boettiger D., Hammer D.A. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLoS Comput. Biol. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ali O., Guillou H., Fourcade B. Cooperativity between integrin activation and mechanical stress leads to integrin clustering. Biophys. J. 2011;100:2595–2604. doi: 10.1016/j.bpj.2011.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ma Y.-Q., Qin J., Plow E.F. Kindlin-2 (Mig-2): a co-activator of β3 integrins. J. Cell Biol. 2008;181:439–446. doi: 10.1083/jcb.200710196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Reedquist K.A., Ross E., Bos J.L. The small GTPase, Rap1, mediates CD31-induced integrin adhesion. J. Cell Biol. 2000;148:1151–1158. doi: 10.1083/jcb.148.6.1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Iber D., Campbell I.D. Integrin activation—the importance of a positive feedback. Bull. Math. Biol. 2006;68:945–956. doi: 10.1007/s11538-005-9049-5. [DOI] [PubMed] [Google Scholar]
- 45.Banno A., Ginsberg M.H. Integrin activation. Biochem. Soc. Trans. 2008;36:229–234. doi: 10.1042/BST0360229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Faull R.J., Kovach N.L., Ginsberg M.H. Affinity modulation of integrin α5β1: regulation of the functional response by soluble fibronectin. J. Cell Biol. 1993;121:155–162. doi: 10.1083/jcb.121.1.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Suehiro K., Gailit J., Plow E.F. Fibrinogen is a ligand for integrin α5β1 on endothelial cells. J. Biol. Chem. 1997;272:5360–5366. doi: 10.1074/jbc.272.8.5360. [DOI] [PubMed] [Google Scholar]
- 48.Kuo S.C., Lauffenburger D.A. Relationship between receptor/ligand binding affinity and adhesion strength. Biophys. J. 1993;65:2191–2200. doi: 10.1016/S0006-3495(93)81277-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Moy V.T., Jiao Y., Sano T. Adhesion energy of receptor-mediated interaction measured by elastic deformation. Biophys. J. 1999;76:1632–1638. doi: 10.1016/S0006-3495(99)77322-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Vitte J., Benoliel A.-M., Pierres A. Beta-1 integrin-mediated adhesion may be initiated by multiple incomplete bonds, thus accounting for the functional importance of receptor clustering. Biophys. J. 2004;86:4059–4074. doi: 10.1529/biophysj.103.038778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xu C., Watras J., Loew L.M. Kinetic analysis of receptor-activated phosphoinositide turnover. J. Cell Biol. 2003;161:779–791. doi: 10.1083/jcb.200301070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Reference deleted in proof.
- 53.Cho H., Kim Y.A., Ho W.K. Low mobility of phosphatidylinositol 4,5-bisphosphate underlies receptor specificity of Gq-mediated ion channel regulation in atrial myocytes. Proc. Natl. Acad. Sci. USA. 2005;102:15241–15246. doi: 10.1073/pnas.0408851102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chan P.Y., Lawrence M.B., Springer T.A. Influence of receptor lateral mobility on adhesion strengthening between membranes containing LFA-3 and CD2. J. Cell Biol. 1991;115:245–255. doi: 10.1083/jcb.115.1.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Panorchan P., Thompson M.S., Wirtz D. Single-molecule analysis of cadherin-mediated cell-cell adhesion. J. Cell Sci. 2006;119:66–74. doi: 10.1242/jcs.02719. [DOI] [PubMed] [Google Scholar]
- 56.Gaborski T.R., Clark A., Jr., McGrath J.L. Membrane mobility of β2 integrins and rolling associated adhesion molecules in resting neutrophils. Biophys. J. 2008;95:4934–4947. doi: 10.1529/biophysj.108.132886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Arrio-Dupont M., Foucault G., Cribier S. Translational diffusion of globular proteins in the cytoplasm of cultured muscle cells. Biophys. J. 2000;78:901–907. doi: 10.1016/S0006-3495(00)76647-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ohsugi Y., Saito K., Kinjo M. Lateral mobility of membrane-binding proteins in living cells measured by total internal reflection fluorescence correlation spectroscopy. Biophys. J. 2006;91:3456–3464. doi: 10.1529/biophysj.105.074625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Haugh J.M., Codazzi F., Meyer T. Spatial sensing in fibroblasts mediated by 3′ phosphoinositides. J. Cell Biol. 2000;151:1269–1280. doi: 10.1083/jcb.151.6.1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.van Rheenen J., Jalink K. Agonist-induced PIP2 hydrolysis inhibits cortical actin dynamics: regulation at a global but not at a micrometer scale. Mol. Biol. Cell. 2002;13:3257–3267. doi: 10.1091/mbc.E02-04-0231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ward M.D., Hammer D.A. A theoretical analysis for the effect of focal contact formation on cell-substrate attachment strength. Biophys. J. 1993;64:936–959. doi: 10.1016/S0006-3495(93)81456-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Goksoy E., Ma Y.-Q., Qin J. Structural basis for the autoinhibition of talin in regulating integrin activation. Mol. Cell. 2008;31:124–133. doi: 10.1016/j.molcel.2008.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Goldmann W.H., Senger R., Isenberg G. Determination of the affinity of talin and vinculin to charged lipid vesicles: a light scatter study. FEBS Lett. 1995;368:516–518. doi: 10.1016/0014-5793(95)00678-3. [DOI] [PubMed] [Google Scholar]
- 64.Hirata H., Ohki K., Miyata H. Mobility of integrin α5β1 measured on the isolated ventral membranes of human skin fibroblasts. Biochim. Biophys. Acta. 2005;1723:100–105. doi: 10.1016/j.bbagen.2005.01.014. [DOI] [PubMed] [Google Scholar]
- 65.Keselowsky B.G., García A.J. Quantitative methods for analysis of integrin binding and focal adhesion formation on biomaterial surfaces. Biomaterials. 2005;26:413–418. doi: 10.1016/j.biomaterials.2004.02.050. [DOI] [PubMed] [Google Scholar]
- 66.Wouwer A., Saucez P., Thompson S. A MATLAB implementation of upwind finite differences and adaptive grids in the method of lines. J. Comput. Appl. Math. 2005;183:245–258. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


