Quantitative Characterization of Local Protein Solvation To Predict Solvent Effects on Protein Structure

Abstract

Characterization of solvent preferences of proteins is essential to the understanding of solvent effects on protein structure and stability. Although it is generally believed that solvent preferences at distinct loci of a protein surface may differ, quantitative characterization of local protein solvation has remained elusive. In this study, we show that local solvation preferences can be quantified over the entire protein surface from extended molecular dynamics simulations. By subjecting microsecond trajectories of two proteins (lysozyme and antibody fragment D1.3) in 4 M glycerol to rigorous statistical analyses, solvent preferences of individual protein residues are quantified by local preferential interaction coefficients. Local solvent preferences for glycerol vary widely from residue to residue and may change as a result of protein side-chain motions that are slower than the longest intrinsic solvation timescale of ∼10 ns. Differences of local solvent preferences between distinct protein side-chain conformations predict solvent effects on local protein structure in good agreement with experiment. This study extends the application scope of preferential interaction theory and enables molecular understanding of solvent effects on protein structure through comprehensive characterization of local protein solvation.

Introduction

Cosolvents such as denaturants, salts, amino acids, polyols, and sugars play an important role in many protein processes involving protein folding, stabilization, and association (1–3). This is because the addition of cosolvents to aqueous protein solutions commonly alters the equilibrium between protein conformations (4–6). Over the past decades, a rigorous thermodynamic framework has been developed that relates cosolvent effects on protein conformations with solvent preferences of the protein surface (4,7–19). This framework—which is often referred to as “preferential interaction theory”—stipulates that adding cosolvent to a protein solution will shift the protein toward conformations with a greater degree of preferential solvation by the cosolvent. Preferential solvation of a protein is quantified by the preferential interaction coefficient Γ_XP (4,20). Because every solvent molecule at the protein surface contributes to Γ_XP (7,11,21), detailed characterization of protein solvation is required for molecular understanding of solvent effects on protein conformations.

Preferential interactions reflect relative preferences of the protein surface for either cosolvent or water, and are manifested in local concentration ratios of cosolvent and water that are either greater (preferential solvation), smaller (preferential hydration), or equal (neutral solvation) with respect to the bulk solvent (4). Because protein surfaces comprise physically and chemically distinct surface loci, protein solvation in a mixed solvent can be conceived of as an ensemble of preferentially hydrated, solvated, and neutral solvent regions near the protein surface (4,22). Just like a protein displays a mosaic of heterogeneous surface loci to the solvent, the solvent surrounding a protein is expected to form a mosaic of solvent regions with varying degrees of preferential interactions.

Unfortunately, characterization of the protein solvation mosaic has remained elusive to this day. Although various spectroscopy- and NMR-based techniques have revealed many aspects of protein solvation, these techniques do not allow quantifying local solvation preferences (23–25). On the other hand, equilibrium techniques such as vapor pressure osmometry and dialysis-densitometry allow the measurement of the preferential interaction coefficient Γ_XP of the ensemble-average of all protein conformations in a solvent mixture (4,26,27). However, equilibrium techniques cannot quantify differences of Γ_XP between distinct protein conformations and are unable to resolve local preferential interactions at distinct protein surface loci.

One approach to understand solvent effects on protein conformations was pioneered by Tanford (22), who quantified thermodynamic solvent effects on smaller constituent groups of a protein molecule and hypothesized the additivity of individual contributions of the constituent groups. Group additivity has proven to be a useful assumption for quantifying the effects of a number of cosolvents on protein folding (28–30); however, other studies reported solvent effects on proteins for which group additivity is not valid (31–33). Hence, more research is needed to determine the range of cosolvents and the extent of conformational changes for which group additivity holds.

Solvent effects on protein (un)folding events have been directly observed from extended molecular-dynamics (MD) simulations (34–38), and solvent effects on the free energy landscape of peptides and mini-proteins have been quantified through advanced sampling techniques (39–41). These techniques have provided a wealth of information on the folding mechanisms of proteins, but they have also generated widely differing views on the molecular mechanisms by which cosolvents alter protein conformations. Perhaps the most prevalent reason for this disagreement is the difficulty to differentiate cause and effect between concurrent changes of protein structure and protein solvation. Another reason for the longstanding disagreement on the molecular mechanisms of cosolvent effects on protein conformations could be that these studies provide no or limited insight in local solvent preferences at distinct loci of the protein surface.

An alternative approach for obtaining detailed molecular understanding of solvent effects on protein conformations is by quantifying differences of Γ_XP values between specific protein conformations. Γ_XP of a specific protein conformation can be calculated from MD simulations of a single protein conformation with well-defined atom coordinates or an ensemble of protein conformations corresponding to a particular protein state (21,42–46). The solvent-induced equilibrium shift between two protein conformations can then be quantified from the difference of Γ_XP values between the respective protein conformations (42,46). Because Γ_XP values are calculated by summing up solvent molecules at all loci of the protein surface (21), this approach could, in principle, elucidate the role of individual solvent molecules and protein surface loci in solvent-induced conformational changes. However, even though previous studies have shown that Γ_XP values calculated from MD simulations—when run for tens of nanoseconds—are generally in good agreement with experiment (21,42–45), simulation times in this range turned out to be insufficient to quantify local preferential interactions coefficients (47).

Convergence of local preferential interaction coefficients from MD simulations is perceived as a formidable challenge because Γ_XP is intrinsically “a fluctuation difference and is prone to large levels of noise” (48) and because “dissection of the influence of different protein group contributions is not straightforward” (49). Key issues that hinder convergence are limitations in computational power and lacking insight on pertinent timescales of protein solvation. To this day, these issues continue to curtail the potential of computational studies of solvent effects on biomolecules, and molecular insight has been mostly limited to inferences from nonconverged protein simulations and simulations of smaller model compounds such as amino acids and peptides (49–53).

In this study, key issues that have curtailed the potential of computational studies of solvent effects on proteins are addressed. We demonstrate that the protein solvation mosaic can be characterized over the entire protein surface from MD simulations that are sufficiently longer than the longest intrinsic solvation timescale, which is ∼10 ns. Local preferential interaction coefficients are quantified for all protein residues of two proteins (lysozyme and antibody fragment D1.3) in 4 M glycerol, and cosolvent effects on local protein conformations are predicted from changes in local preferential interactions between distinct protein side-chain conformations.

Methods

Molecular-dynamics simulations

All-atom molecular simulations are performed for two proteins, Hen Egg-white Lysozyme (HEL) and the antibody fragment Fv D1.3 (54), which are explicitly solvated in a box of water with 4 M glycerol (see Table S1 in the Supporting Material). The CHARMM22 parameter set (55) is used to model protein atoms, water is modeled by the TIP3-model (56), and force-field parameters for glycerol are based on the carbohydrate hydrate parameters developed by Ha et al. (57). Crystallographic structures for HEL and D1.3 are taken from PDB:1VFB (54) and the setup of each simulation is carried out with CHARMM version c32b2 (58). Simulations of the solvated proteins are run for 1.3 μs at constant pressure and temperature (1 atm and 298 K) with NAMD version 2.7 (59), as described previously in Vagenende et al. (47).

In a previous study, we pointed out that conformational changes of the backbone generally occur within nanoseconds along divergent trajectories and result in protein conformations with significantly different preferential interaction coefficients (42). Because this study aims to determine converged characteristics of the protein solvation mosaic, coordinates of the protein backbone are constrained with respect to the crystal structure. To investigate effects of side-chain motions, an additional simulation whereby all protein atom coordinates are constrained is performed for HEL (see Table S1). Unless indicated otherwise, the results in this study are based on the simulations with constrained backbone coordinates and free side-chain motions.

Computation of preferential interaction coefficients

The global preferential interaction coefficient Γ_XP can be calculated from MD simulations by counting water and cosolvent molecules within a distance R from the protein surface (21,47):

$${\Gamma }_{XP}\left(R\right)={\langle n_{XP}\left(r<R\right)-\frac{n_X-n_{XP}\left(r<R\right)}{n_W-n_{WP}\left(r<R\right)}{n}_{WP}\left(r<R\right)\rangle }_{{\tau }_{run}}$$ (1)

In the above equation, brackets 〈⋅〉τ_run refer to the time average over the entire simulation time τ_run; n_X and n_W are the total number of cosolvent and water molecules in the simulation box; and n_XP(r < R) and n_WP(r < R) are the number of cosolvent and water molecules for which the center of mass falls within a radial distance R from the protein van der Waals surface. The global preferential interaction coefficient Γ_XP(R) reaches a plateau from 5 Å onwards (see Fig. S1 in the Supporting Material). This indicates that preferential interactions of a protein in a mixture of water and glycerol are confined to the solvent region within 5 Å from the protein van der Waals surface.

Residue-based preferential interaction coefficients Γⁱ_XP are calculated by assigning each solvent molecule within 5 Å from the protein surface to its closest protein residue i (21):

$${\Gamma }_{XP}^i={\langle n_{XP}^i\left(r<5\AA \right)-\frac{n_X-n_{XP}\left(r<5\AA \right)}{n_W-n_{WP}\left(r<5\AA \right)}{n}_{WP}^i\left(r<5\AA \right)\rangle }_{{\tau }_{run}}$$ (2)

In the above equation, nⁱ_XP (r < 5 Å) and nⁱ_WP (r < 5 Å) are the number of cosolvent and water molecules within 5 Å from the protein surface that are closer to residue i than to any other residue of the protein. Residues with, on average, less than 1 water molecule and less than 0.1 glycerol molecule are considered to have limited solvent accessibility. Because each solvent molecule is assigned to only one residue, residue-based preferential interaction coefficients are additive and the following equation is automatically met:

$$\sum _i{\Gamma }_{XP}^i={\Gamma }_{XP}$$ (3)

The additivity of residue-based preferential interaction coefficients implies that an independent change of Γⁱ_XP for any of the protein residues results in an identical change of the global preferential interaction coefficient Γ_XP, and therefore codetermines the effect of cosolvent on the chemical potential of the protein.

To quantify local solvation preferences of groups of residues, we calculate regional preferential interaction coefficients by assigning solvent molecules to a particular residue group if the residue that is closest to the solvent molecule belongs to that residue group. For a residue group consisting of residues [a, b,…], we get:

$${\Gamma }_{XP}^{\left[a,b,\dots \right]}={\langle \sum _{i\in \left[a,b,\dots \right]}{n}_{XP}^i\left(r<5\AA \right)-\frac{n_X-n_{XP}\left(r<5\AA \right)}{n_W-n_{WP}\left(r<5\AA \right)}\sum _{i\in \left[a,b,\dots \right]}{n}_{WP}^i\left(r<5\AA \right)\rangle }_{{\tau }_{run}}$$ (4)

The prime symbol (′) is used to refer to all protein residues excluding residues [a, b,…], and we get

$${\Gamma }_{XP}^{\left[a,b,\mathrm{\dots }\right]}+{\Gamma }_{XP}^{{\left[a,b,\mathrm{\dots }\right]}^{\prime }}={\Gamma }_{XP}$$ (5)

Although regional preferential interaction coefficients of a residue group are simply the sum of the residue-based preferential interaction coefficients of the residues of that group, they can be determined with higher precision because solvent fluctuations near neighboring residues are generally negatively correlated.

Statistical analysis

Statistical analysis of any property A is performed based on plots of p(τ_B) (47,60):

$$p\left({\tau }_B\right)=\frac{{\tau }_B}{{\tau }_{rec}}\frac{{\sigma }^2{\langle A\rangle }_{{\tau }_B}}{{\sigma }^2{\langle A\rangle }_{{\tau }_{rec}}}$$ (6)

In the above equation, τ_rec and τ_B are the trajectory recording period and the variable block time, respectively, and σ²〈A〉τ_rec and σ²〈A〉τ_B are the variances calculated for the respective times. The block time τ_B for which p(τ_B) reaches a plateau indicates the correlation time beyond which block time averages 〈A〉τ_B become statistically independent (60). If p(τ_B) remains at the plateau value for all block times, the standard error σ〈A〉 is estimated from the average plateau value. If this is not the case, an upper limit of σ〈A〉 is obtained from the average of σ〈A〉τ_B for the four largest block times after it has been verified that σ〈A〉τ_B continually decreases for increasing bock times.

Local concentration maps and characteristic residence times

Local concentrations are calculated based on the solvent occupancy of a three-dimensional grid with grid size 1.5 Å and visualized with the software VMD 1.9 (61), as described previously in Vagenende et al. (47). Cutoff values are selected such that local concentration maps depict all solvent regions with local solvent concentrations $c_{\alpha }\left(\overrightarrow{r}\right)$ greater than the respective bulk solvent concentrations c_{α, bulk}.

Residence times of solvent molecules near the protein surface (r < 5 Å) and survival functions for glycerol and water, i.e., N_XP(t) and N_WP(t), are calculated as described previously (47). Characteristic residence times are obtained by fitting N_XP(t) and N_WP(t) to the following function:

$$N_{ZP}\left(t\right)\cong n_1{e}^{-\frac{t}{{\tau }_1}}+n_2{e}^{-\frac{t}{{\tau }_2}}+n_3{e}^{-\frac{t}{{\tau }_3}}+c$$ (7)

Equation 7 allows for good fitting of N_XP(t) and N_WP(t) for both HEL and D1.3 (see Fig. S2).

To estimate the surface density of specific surface loci, protein solvent-accessible surface areas are calculated with VMD 1.9 (61) using a probe radius of 1.4 Å. The average solvent-accessible surface areas of HEL and D1.3 are 7248 Å² and 11,118 Å², respectively.

Results

Global protein solvation

Molecular-dynamics simulations of two proteins, HEL and D1.3, in a mixture of water and 4 M glycerol are run for 1.3 μs and subjected to extensive statistical analyses. For both proteins, the global preferential interaction coefficient Γ_XP has a distinctive correlation time of ∼10 ns (Fig. 1). This time corresponds with the longest characteristic residence time of glycerol (Table 1). Glycerol molecules with characteristic residence times of ∼10 ns reside at specific protein surface loci that form multiple hydrogen bonds with glycerol (47), such as near HEL-residues Lys¹³ and Asp¹⁸ (Fig. 2). This surface locus is occupied by glycerol for approximately half of the time, and, within a time period of 200 ns, there are three instances whereby glycerol stays longer than 5 ns at this locus (Fig. 2 and see Movie S1 in the Supporting Material). Because each glycerol molecule increases Γ_XP by nearly one unit (Eq. 1), temporal changes in glycerol occupancy of such loci cause proportional fluctuations of Γ_XP on a timescale of ∼10 ns. We conclude therefore that the distinctive correlation time of Γ_XP at ∼10 ns (Fig. 1) results from temporal changes of solvent occupancy of protein surface loci that form multiple hydrogen bonds with glycerol.

Figure 1.

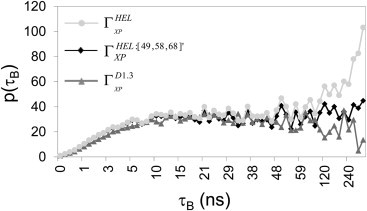
Statistical analysis of the global preferential interaction coefficient for HEL and D1.3 and the regional preferential interaction coefficient for all HEL residues except residue 49, 58, and 68. Values of p(τ_B) reach a plateau at ∼10 ns, which indicates the correlation time of Γ_XP. For ${\Gamma }_{XP}^{HEL}$ (but not for ${\Gamma }_{XP}^{HEL:{\left[49,58,68\right]}^{\prime }}$), values of p(τ_B) increase from 100 ns onwards, indicating that Γ_XP for HEL is affected by local solvation changes near residues 48, 58, and 68 on timescales >100 ns.

Table 1.

Characteristic residence times of water and glycerol molecules at the protein surface

	Protein	Constraint	n1 [−]	τ1 [ns]	n2 [−]	τ2 [ns]	n3 [−]	τ3 [ns]	c [−]
Glycerol	D1.3	Backbone	21.5	0.3	91.7	1.4	10.3	8.6	0.8
	HEL	Backbone	15.1	0.3	66.1	1.3	2.3	10.3	0.9
	HEL	All	14.4	0.3	62.5	1.4	3.1	11.3	0.3
Water	D1.3	Backbone	1200.9	0.4	67.7	2.0	9.2	22.5	2.0
	HEL	Backbone	831.6	0.3	16.0	2.0	3.4	17.1	2.4
	HEL	All	781.5	0.3	30.6	2.0	5.3	8.7	3.5

Parameters obtained by fitting N_XP(t) and N_WP(t) according to Eq. 7.

Figure 2.

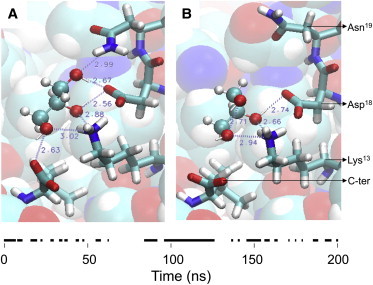
Glycerol at the protein surface of HEL near Lys¹³ and Asp¹⁸ at 107 ns (A) and at 118 ns (B). (Bottom line) Times when this surface locus is occupied by glycerol.

If the slowest timescale of protein solvation is 10 ns, preferential interaction coefficients could be quantified with statistical significance based on MD simulations that are at least 10 times longer, i.e., 100 ns (44). Although this is the case for D1.3, block time averages of Γ_XP for HEL are correlated over time intervals exceeding 100 ns (Fig. 1). Long correlation times of Γ_XP for HEL are also reflected in the increasing number of glycerol molecules near the protein surface at simulation times >700 ns (see Table S2 and Fig. S3). Nevertheless, variances σ〈Γ_XP〉_τB for HEL continue to decrease for larger block times (see Fig. S4) and an upper limit of the standard deviation of Γ_XP can be determined (see Table S1).

Local protein solvation

The protein solvation mosaic—which is the ensemble of preferentially solvated, preferentially hydrated and neutral solvent regions at the protein surface—can be visualized by local concentration maps. Unlike previous studies using shorter simulations (47), convergence of local concentration maps is obtained from 100 ns trajectories (see Fig. S5). Local concentration maps from microsecond simulations reveal that most solvent regions near the protein surface of HEL are either preferentially hydrated or preferentially solvated, and very few solvent regions do not have any preference for either solvent (Fig. 3 A). The majority of the mapped solvent regions rapidly vanish for increasing cutoff-values (Fig. 3, B and C), which indicates that solvent preferences of most protein surface loci are weak. A limited number of solvent regions have a significantly higher degree of preferential interactions (Fig. 3 B) and the highest degree of preferential interactions is found for glycerol in the catalytic binding pocket of HEL (Fig. 3 C). Similar observations are made for local concentration maps of D1.3 (see Fig. S6).

Figure 3.

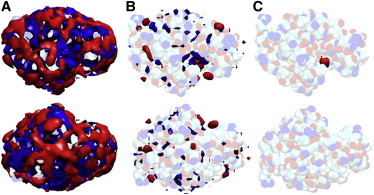
Local concentration maps for glycerol (red) and water (blue) at the surface of HEL (top and bottom view) for increasing cutoff values: $c_{\alpha }\left(\overrightarrow{r}\right)$ > c_{α, bulk} (A), $c_{\alpha }\left(\overrightarrow{r}\right)$ > 1.5 c_{α, bulk} (B), and $c_{\alpha }\left(\overrightarrow{r}\right)$ > 3 c_{α, bulk} (C).

Local protein solvation is further characterized by quantifying local preferential interaction coefficients Γⁱ_XP for all residues of HEL (Fig. 4 and see Fig. S7) and D1.3 (see Fig. S8). Local preferential interaction coefficients Γⁱ_XP of solvent-accessible protein residues differ widely and range from significantly negative values (i.e., strong preferential hydration) to significantly positive values (i.e., strong preferential solvation by glycerol). For most protein residues, correlation times of Γⁱ_XP are smaller than 100 ns, but for ∼10% of the residues, correlation times are significantly longer (Fig. 4 and see Fig. S8). Interestingly, slow convergence of Γ_XP for HEL is caused by local solvation changes near three of the 13 residues with slow convergence, i.e., Gly⁴⁹, Ile⁵⁸, and Arg⁶⁸ (Fig. 1). Moreover, slow local solvation changes disappear and Γ_XP converges in 10 ns when protein side-chain motions are constrained (see Fig. S9). We conclude, therefore, that slow solvation changes affecting Γ_XP of HEL on timescales exceeding 100 ns are related to protein side-chain motions near Gly⁴⁹, Ile⁵⁸, and Arg⁶⁸.

Figure 4.

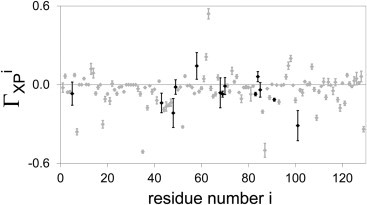
Residue-based preferential interaction coefficients Γ_XPⁱ for HEL. Data points for residues with correlation times <100 ns (gray) and >100 ns (black).

Interdependence of protein solvation and side-chain motions

A single instance whereby side-chain motions affect protein solvation is observed near Gly⁴⁹ and Arg⁶⁸ of HEL. At the start of the simulation, the side chain of Arg⁶⁸ quickly changes from conformation A with its guanidinium-group contacting the carboxyl group of Gly⁴⁹ (Fig. 5 A) to conformation B with its guanidinium-group separated from Gly⁴⁹ by Arg⁴⁵ (Fig. 5 B). At 860 ns, Arg⁶⁸ switches again from conformation B to conformation A. This conformational change coincides with an increase of Γⁱ_XP for both Arg⁶⁸ and Gly⁴⁹ (Fig. 5 C). Changes in protein solvation near these residues are also evident from local concentration maps: when Arg⁶⁸ adopts conformation A, solvent region 1 is preferentially hydrated and solvent region 2 is preferentially solvated by glycerol (Fig. 5 D), but when Arg⁶⁸ adopts conformation B, both solvent regions 1 and 2 are preferentially hydrated near the protein surface and preferentially solvated by glycerol further from the protein surface (Fig. 5 E). Thus, local preferential interaction coefficients and concentration maps concordantly confirm that side-chain motions of Arg⁶⁸ affect local protein solvation.

Figure 5.

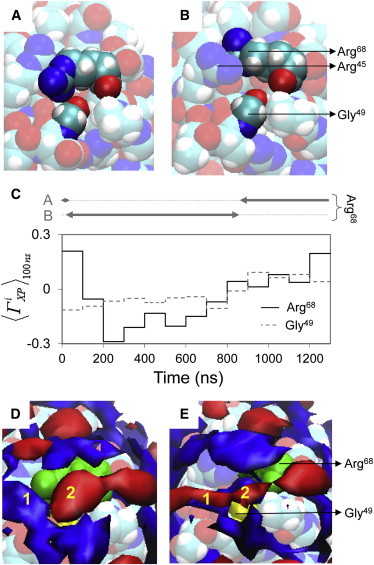
Arg⁶⁸ side-chain conformation A and B (A and B, respectively), local preferential interaction coefficients for Gly⁴⁹ and Arg⁶⁸ (C), and local concentration maps for glycerol (red) and water (blue) near Arg⁶⁸ conformation A and B (D and E, respectively). In panels D and E, distinct solvent regions near Gly⁴⁹ (yellow) and Arg⁶⁸ (green) are numbered.

The sum of Γⁱ_XP for Arg⁶⁸ and Gly⁴⁹ is significantly larger for Arg⁶⁸ conformation A (0.17 ± 0.06) than for conformation B (−0.23 ± 0.07). Based on the thermodynamic principles of preferential interactions applied to aqueous glycerol solutions (42), a difference of Γⁱ_XP between conformation A and B of 0.4 results in a glycerol-induced shift of the relative free energies of conformation A and B in favor of conformation A by ∼1 kJ/mol. This prediction is in good agreement with the range of free energy shifts between local protein conformations in aqueous glycerol solutions derived from hydrogen-exchange experiments (62).

Similar to Gly⁴⁹ and Arg⁶⁸, local preferential interaction coefficients of 10 other residues of HEL have long correlation times (>100 ns) because of slow side-chain motions (Fig. 4). However, unlike Gly⁴⁸ and Arg⁶⁸, side-chain motions near these residues only affect the proximity to distinct solvent regions without affecting local protein solvation. The corresponding changes of Γⁱ_XP values of these residues are consequently such that their overall contributions to the global preferential interaction coefficient Γ_XP cancel out (Eq. 3). That most side-chain motions do not considerably affect protein solvation is also evidenced by the limited effects of constraining side-chain motions on 1), characteristic residence times of solvent at the protein surface (Table 1); 2), the global preferential interaction coefficient (see Table S1); and 3), local concentration maps (see Fig. S10).

Solvation of a protein-binding pocket

A unique case of local protein solvation is observed in the catalytic binding pocket of HEL near Ile⁵⁸. When protein side chains are constrained, this binding pocket contains only water. However, for the simulation of HEL with unconstrained side-chain coordinates, a glycerol molecule enters the binding pocket at 80 ns and it remains there for ∼500 ns before leaving the binding pocket (Fig. 6). Consecutively, several other glycerol molecules populate the binding pocket with residence times of ∼100 ns, and the binding pocket is occupied by glycerol for >90% of the simulation time (Fig. 6 C, and see Movie S2). Glycerol in the binding pocket adopts two major binding orientations: orientation A is such that its O-atoms are in contact with the protein and its C-atoms point toward the solvent (Fig. 6 A), whereas for orientation B the direction of O- and C-atoms is reversed (Fig. 6 B). The switch from glycerol orientation A to orientation B around the middle of the simulation coincides with the increase of residue-based preferential interaction coefficient Γⁱ_XP for Ile⁵⁸ (Fig. 6 C). This indicates that local solvation preferences of a protein can be affected by slow (>100 ns) orientational changes of cosolvent molecules at unique binding pockets.

Figure 6.

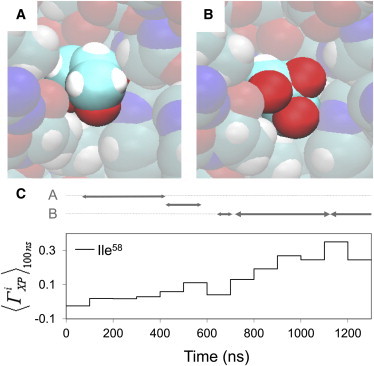
Major glycerol orientations in the catalytic pocket of HEL (A and B) and corresponding local preferential interaction coefficients for Ile⁵⁸ (C).

Discussion

In this study we have characterized the protein solvation mosaic—i.e., the ensemble of preferentially hydrated, preferentially solvated, and neutral solvent regions—over the entire surface of a specific protein conformation in a mixed solvent. This was achieved by performing extended (1.3 μs) classical all-atom MD simulations of a protein in a mixed solvent with constrained protein coordinates. We found that correlation times of preferential interaction coefficients are governed by the longest characteristic residence time of glycerol of ∼10 ns, which arises from glycerol molecules forming multiple hydrogen bonds with specific protein surface loci. Solvation timescales of ∼10 ns were also reported for proteins in mixtures of water and other cosolvents such as urea (63) and arginine (43). This suggests that the slowest intrinsic timescale for protein solvation in mixed solvents is generally ∼10 ns. As a corollary, simulations need to be sufficiently longer than 10 ns to obtain multiple statistically independent block-time averages of Γ_XP, and we find that a minimum simulation time of ∼100 ns is needed to quantify global and local preferential interactions of a specific protein conformation with statistical significance.

Interestingly, Ma et al. (51) found that the minimum simulation time to obtain convergence of Γ_XP for a triglycine peptide in aqueous urea solutions was also ∼100 ns. These authors used multiple 2–3 ns simulations, whereas we used a single extended simulation per protein. Although both simulation schemes appear equally effective for quantifying local preferential interaction coefficients and equally efficient in their use of computational resources, multiple shorter simulation times can arguably be completed in a shorter time. This apparent advantage loses much of its significance when one considers that a 100 ns simulation of a medium-size protein (∼25 kDa) in a solvent box only takes ∼5 days on a standard high-performance computing cluster with ∼100 CPUs. However, an important difference between both simulation schemes is that only continuous extended simulations allow characterizing residence of solvent molecules at the protein surface. This is a considerable advantage because characteristic residence times determine convergence times of preferential interactions and reveal pertinent protein solvation characteristics (42,47).

Specific protein-surface loci forming multiple hydrogen bonds with the cosolvent have a surprisingly low affinity for cosolvent. For example, a specific protein surface locus that forms up to six hydrogen bonds with a single glycerol molecule is only occupied by glycerol for half of the time (Fig. 2). Assuming a Langmuir binding model, this surface locus binds glycerol with a dissociation constant K_d of ∼4 M. Thus, multiple hydrogen-bonding at this surface-locus results in specific glycerol orientations without pronounced increases of the binding affinity. This is in agreement with empirical observations that hydrogen bonds in molecular recognition processes primarily convey specificity rather than affinity (33). Taking into account the average number of glycerol molecules with long characteristic residence times (i.e., n₃ in Table 1), the solvent-accessible surface areas of the simulated proteins, and an average locus occupancy by glycerol of 50%, we find that the surface density of specific loci that form multiple hydrogen bonds with glycerol is typically in the range 0.5–2.0 × 10⁻³/Ų. This corresponds with several specific surface loci for smaller proteins and tens of specific surface loci for larger proteins. Specific surface loci forming multiple hydrogen bonds with a cosolvent molecule will therefore significantly contribute to Γ_XP, and local solvation preferences at such loci are expected to affect overall cosolvent effects on protein processes.

Most protein surface loci have a similar affinity for glycerol as for water (Fig. 3). However, several protein surface loci, including loci forming multiple hydrogen bonds with glycerol, have a higher affinity for glycerol with dissociation constants K_d as low as 2 M. By far the greatest binding affinity for glycerol is found in the catalytic binding pocket of HEL, which is occupied by glycerol for ∼90% of the time (Fig. 6 C). The high occupancy of the binding pocket by glycerol, which is in good agreement with crystal structures of HEL that resolve glycerol in the binding pocket (64), corresponds with a dissociation constant K_d of ∼0.4 M. The clear distinction in timescales and binding affinities between the catalytic binding pocket of HEL and the rest of the protein surface prompts us to differentiate between general protein solvation, which is determined by low binding affinities (K_d > 2 M) and characteristic solvent residence times <20 ns, versus high-affinity protein solvation, which is determined by substantially higher binding affinities (K_d < 0.5 M) and residence times >100 ns.

Despite the high binding-affinity of the catalytic binding pocket of HEL, glycerol only enters this pocket for the first time after 80 ns. This clearly demonstrates that shorter simulation times and simulations that fail to demonstrate convergence behavior of local preferential interactions may lead to erroneous conclusions on local solvation preferences of proteins. Hence, careful evaluation is needed of local protein solvation data from shorter simulations or simulations during which the protein undergoes large conformation changes. This is especially critical when using classical MD simulations to identify binding pockets and estimate the affinity of druglike molecules (65).

After entering the binding pocket, glycerol predominantly adapts two distinct binding orientations and repeatedly undergoes orientational changes on timescales in the order of ∼100 ns. Such slow orientational changes obviously do not converge within microsecond classical molecular dynamics simulations and other computational methods such as 3D-RISM based methods (66) could be more appropriate to characterize solvent orientations in high-affinity binding pockets. By constraining cosolvent molecules at high-affinity sites with respect to predominant binding orientations, local solvation preferences of the binding pocket could then be characterized by classical MD simulations. In this manner, the structural and dynamical properties of the protein solvation mosaic could be determined over the entire protein surface, even near high-affinity pockets. Alternatively, if the protein process of interest does not involve the binding pocket, high-affinity binding pockets could be excluded by considering regional preferential interaction coefficients of all protein residues outside of the binding pockets.

Local preferential interaction coefficients may differ for protein residues of the same amino-acid type. For example, Lys¹³ of HEL is preferentially solvated by glycerol (Γⁱ_XP = 0.12 ± 0.04) whereas Lys¹¹⁶ of HEL is preferentially hydrated (Γⁱ_XP = −0.05 ± 0.03) (Fig. 4). Local preferential interaction coefficients of these two residues differ because of adjacent residues: Lys¹³ and its adjacent residues cooperatively bind glycerol (Fig. 2), whereas protein residues near Lys¹¹⁶ do not cooperatively interact with the solvent. Cooperative interactions of adjacent protein groups with solvent molecules depend on the size and nature of the constituent groups that partition the protein surface. Although smaller constituent groups allow characterization of local protein solvation at higher resolution, local preferential interaction coefficients of smaller protein constituent groups become increasingly dependent on solvent interactions with adjacent groups and information on solvent interactions of individual constituent groups becomes more convoluted.

Results from our simulations of two proteins (lysozyme and antibody fragment D1.3) in 4 M glycerol agree well with available experimental data on 1), characteristic residence times of solvent molecules at the protein surface; 2), the high occupancy of the catalytic cleft of HEL by glycerol; and 3), the glycerol-induced shift of the free energy between local protein conformations. Previously, we also demonstrated quantitative agreement of Γ_XP values for lysozyme in aqueous glycerol between simulation and experiment (42). This indicates that force fields used in this study are appropriate for characterizing local protein solvation in aqueous glycerol solutions.

Conclusions

We have shown that local solvation preferences can be quantified over the entire protein surface from extended MD simulations of specific protein conformations in mixed solvents. This has been achieved by combining analysis methods with gradually increasing resolution, starting with the statistical analysis of the global preferential interaction coefficient Γ_XP and the identification of protein solvation timescales, followed by the characterization of local concentration maps and residue-base preferential interaction coefficients, and complemented with the inspection of the trajectories of specific solvent molecules and protein surface loci. This methodology allows quantifying the contribution of individual solvent molecules and protein residues to Γ_XP, and therefore expands the scope of preferential interaction theory by directly linking atom-level details of local protein solvation with thermodynamic solvent effects on protein processes.

From the statistical analysis of solvent fluctuations at the protein surface, we derived that the slowest intrinsic solvation timescale of a protein in a mixture of water and cosolvent is determined by long residence times of cosolvent molecules at specific protein surface loci that enable multiple hydrogen-bonding with a cosolvent molecule. The slowest intrinsic solvation timescale is generally ∼10 ns, and simulation times to quantify local solvation preferences of a constrained protein conformation need to be longer than 100 ns. Most protein side-chain motions do not significantly affect protein solvation, although slow (>100 ns) side-chain motions of a single protein residue can lead to significant changes of local solvent preferences. Another singular event that affects local solvation preferences is the slow reorientation of cosolvent molecules at protein surface loci with high cosolvent affinity, such as observed for glycerol in the catalytic binding pocket of lysozyme.

Because convergence of local solvent preferences of proteins in mixed solvents can be achieved on standard high-performance clusters, computational characterization of local protein solvation emerges as an accessible high-resolution technique for studying solvent effects on proteins. Granted the availability of accurate force fields, this technique enables direct identification of physicochemical properties that determine solvent preferences without assuming group additivity. Even for a relatively simple cosolvent like glycerol, solvent preferences are remarkably heterogeneous at distinct protein residues. Detailed characterization of local protein solvation, therefore, appears indispensable to further understanding of the molecular mechanisms by which solvents affect protein structure.