Interfacial Tension and Surface Pressure of High Density Lipoprotein, Low Density Lipoprotein, and Related Lipid Droplets

Abstract

Lipid droplets play a central role in energy storage and metabolism on a cellular scale. Their core is comprised of hydrophobic lipids covered by a surface region consisting of amphiphilic lipids and proteins. For example, high and low density lipoproteins (HDL and LDL, respectively) are essentially lipid droplets surrounded by specific proteins, their main function being to transport cholesterol. Interfacial tension and surface pressure of these particles are of great interest because they are related to the shape and the stability of the droplets and to protein adsorption at the interface. Here we use coarse-grained molecular-dynamics simulations to consider a number of related issues by calculating the interfacial tension in protein-free lipid droplets, and in HDL and LDL particles mimicking physiological conditions. First, our results suggest that the curvature dependence of interfacial tension becomes significant for particles with a radius of ∼5 nm, when the area per molecule in the surface region is <1.4 nm². Further, interfacial tensions in the used HDL and LDL models are essentially unaffected by single apo-proteins at the surface. Finally, interfacial tensions of lipoproteins are higher than in thermodynamically stable droplets, suggesting that HDL and LDL are kinetically trapped into a metastable state.

Introduction

Lipid droplets play an important role in many physiological processes such as metabolism, energy storage, and lipid transportation. Consequently, the role they play in health is also quite profound, because dysfunction of lipid droplets is related to several diseases such as atherosclerosis and diabetes.

Lipid droplets are small particles made up of a hydrophobic core covered by a surface monolayer. The hydrophobic core typically contains neutral lipids like triacylglycerols, diacylglycerols, and sterol esters. The surface monolayer surrounding the core has a mixture of amphipathic phospholipids, glycolipids, and sterols. Quite often, the biological function of these droplets is further complemented by one or more proteins adsorbed to the surface of the droplet. The diameter of droplets varies from 10 nm to 200 μm (1).

Despite the biological relevance of lipid droplets, even their basic properties and functions have remained rather elusive. This is highlighted by the limited understanding of, for instance, the stability of droplets against coalescence (i.e., fusion) (2,3), adsorption of enzymes to their surface (4–7), and their shape (8,9). Interestingly, all of these phenomena are likely related to surface pressure.

High (HDL) and low (LDL) density lipoprotein particles are especially interesting from this point of view because they are essentially nanosized lipid droplets covered by specific proteins. Their dysfunctions are related to atherosclerosis, which is among the leading causes of death among the Western countries. The emergence of atherosclerosis is related to the coalescence of LDL particles, which has been shown to depend on surface layer modifications, though a proper physical explanation is still lacking (2,3). On the other hand, the decrease in surface pressure (increase in interfacial tension) is rather generally considered to render membranes more fusogenic (11–13). Thus, the changes in surface pressure due to surface modifications could provide a plausible explanation for coalescence of LDL particles. However, more studies are needed because the molecular mechanism of membrane fusion is still under discussion (11,14,15).

Surface pressure is also associated with adsorption of enzymes and proteins (such as lecithin-cholesterol acyltransferase, cholesteryl ester transfer protein, and apolipoproteins) to the surface of HDL and LDL particles (4,16–19). These adsorption phenomena are important for metabolism and lipoprotein structure (20). The connection between adsorption and surface pressure is understandable as the work required to incorporate an object into another body depends on local pressure. Previously this has been demonstrated for membrane proteins and other inclusions (21–23). Importantly, a high surface pressure (low interfacial tension) can also lead to nonspherical shapes of droplets found in both LDL (8) and HDL (9,20).

To clarify the issues discussed above, it is necessary to determine the surface pressure and interfacial tension of lipid droplets and related particles. Unfortunately, surface pressure cannot be experimentally measured directly for nanosized droplets because contemporary technology can only provide estimates based on measurements at macroscopic interfaces (4,18,19). These results must be interpreted with caution because the dependence of interfacial tension (and surface pressure) on curvature is still a debated topic (24,25). A single protein at a highly curved interface may also behave differently compared to a case with many proteins adsorbed at a macroscopic interface (16).

To elucidate these issues, we used coarse-grained molecular-dynamics (MD) simulations to calculate interfacial tensions and surface pressures for flat and highly curved lipid-protein-water interfaces with physiologically relevant lipid compositions. The systems we consider include lipid droplets and HDL and LDL lipoproteins and their variants, as well as flat membrane systems that enable comparison with experimental data.

We were able to estimate when the curvature dependence of surface pressure is significant, although the model used in this work for lipid droplets seems to give somewhat lower surface pressures compared to recent experimental data (26). We also calculated interfacial tensions for the recently developed HDL and LDL models (27,28) whose lipid and protein compositions are close to those of lipoproteins under physiological conditions. The results for HDL and LDL were compared to protein-free droplets having the same lipid compositions but without the proteins, and the results indicated that protein inclusion did not essentially change the interfacial tension. This suggests that the interfacial tension (surface pressure) for these droplets cannot be determined directly by considering just the area covered by different molecular components from macroscopic interfaces (4,16). Relatively high interfacial tensions also suggest that HDL and LDL are kinetically trapped into a metastable state.

Models and Methods

Simulated systems

We consider a number of different model systems: flat membranes, lipid droplets, and lipoproteins, and all of them with a variety of different molecular compositions. The molecules included in the models are free (unesterified) cholesterol (CHOL), cholesteryl ester (CHES), triglyceride (TG) with oleate tails, palmitoyloleoylphosphatidylcholine (POPC), dilinoleoylphosphatidylcholine (DLPC), and lysophosphatidylcholine (lysoPC). The system topologies are visualized in Fig. 1, and the molecular compositions with the numbers of lipids in each system are listed in Table 1. Note that POPC has been replaced by polyunsaturated DLPC in the Flat2 system.

Figure 1.

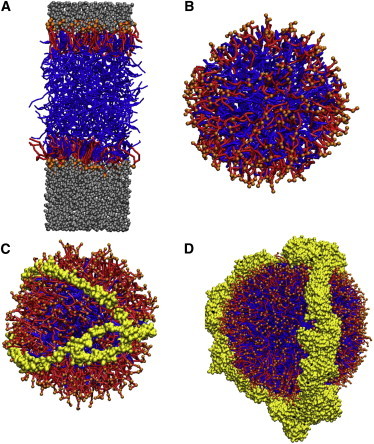
Simulated system topologies. (A) Trilayer structure, (B) lipid droplet, (C) HDL particle, and (D) LDL particle. Note that the pictures are not in scale, as for example LDL is in practice larger than HDL. (Red) Surfactant lipids (POPC, lysoPC); (orange) PC headgroup beads; (blue) other lipids (CHOL, TRIOL, CHES); and (yellow) protein. For clarity, water beads (gray) are depicted only in the trilayer system.

Table 1.

Molecular compositions with number of molecules in the systems studied in this work

	CHES	TG	CHOL	POPC	LysoPC	Water
Flat1	—	100	—	62	—	2514
Flat2	—	100	—	62∗	—	2514
Flat3	245	26	86	62	10	2514
Droplet1	245	26	86	297	41	28,687†
Droplet2	245	26	86	239	36	28,687†
Droplet3	245	26	86	172	26	28,687†
Droplet4	245	26	86	114	17	28,687†
Droplet5	245	26	86	60	8	28,687†
HDL‡	122	39	49	260	10	27,664
HDL-Droplet	122	39	49	260	10	78,655
HDL-Core	122	39	—	—	—	78,655
HDL-Core-Large	1342	429	—	—	—	101,004†
HDL-Core-Flat	150	50	—	—	—	1331†
LDL‡	1600	180	600	630	80	96,060
LDL-Droplet	1600	180	600	630	80	80,613
LDL-Core	1600	180	—	—	—	80,613
LDL-Core-Small	144	16	—	—	—	63,154†
LDL-Core-Flat	180	20	—	—	—	1089†
TG-Small	—	39	—	—	—	78,655
TG-Large	—	180	—	—	—	83,957†
TG-Flat	—	92	—	—	—	1996†

Systems that contain the abbreviation “Flat” are planar as in Fig. 1A). Systems that contain the abbreviation “Droplet” are spherical lipid droplets with core and monolayer lipids, but without a protein. Systems that contain the abbreviation “Core” possess hydrophobic core lipids only.

^∗Flat2 system contains DLPC instead of POPC.

^†Number contains ∼10% of antifreeze particles (34).

^‡In addition to lipids, the HDL model contains two apoA-I proteins and the LDL model one apoB-100 protein (27,28).

The systems Flat1-Flat3 were used to calculate surface pressure and interfacial tension-area isotherms for flat interfaces. In practice, we simulated a planar layer of hydrophobic molecules, which was covered by a monolayer on both sides, and the whole complex was embedded in water (see Fig. 1 A). A similar setup has been previously used elsewhere (29,30). Then, the box area was varied and surface pressure with different areas per PC was calculated to reproduce surface pressure-area isotherms. This was done for flat interfaces with three different molecular compositions: triolein-POPC-water (Flat1), triolein-DLPC-water (Flat2), and an interface with lipoprotein-droplet lipids (Flat3). By lipoprotein-droplet lipids in Flat3, we mean that the oil phase consists of CHES and TG, and the surface layer is comprised of POPC and lysoPC lipids, whereas free cholesterol is both in oil and in the interface. Area per PC was calculated by dividing the area of the layer by the total number of POPC and lysoPC lipids in a single leaflet.

The systems Droplet1-Droplet5 were used to calculate interfacial tension-area isotherms for small droplets with highly curved interfaces. In contrast to the flat interfaces, areas per PC in the surface monolayer were here varied by changing the number of molecules.

The systems without surfactants (HDL-Core, HDL-Core-Large, HDL-Core-Flat, LDL-Core, LDL-Core-Large, LDL-Core-Flat, TG-Small, TG-Large, TG-Flat) were used to calculate interfacial tension as a function of curvature for pure oil-water interfaces. From these simulations, we get the interfacial tensions for interfaces with three different molecular composition in oil (HDL, LDL, and pure TG) having three different curvatures (flat, small droplet, and large droplet).

The HDL, HDL-Droplet, HDL-Core, LDL, LDL-Droplet, and LDL-Core systems were used to study interfacial tension in lipoprotein droplet models for HDL and LDL as presented in previous studies (27,28). By comparing results from particles containing all the elements (core, monolayer, and protein (HDL, LDL)) to the ones lacking proteins (HDL-Droplet, LDL-Droplet), and to the ones with only core left (HDL-Core, LDL-Core), we can decompose the influence of different elements on interfacial tension. The relative numbers of molecules in HDL are based on the study of Maldonado et al. (31) and for LDL on the average LDL particle composition (32).

The coarse-grained MARTINI model (33–35) and the GROMACS simulation package (36–41) were used in all simulations. Force-field description, simulation details, construction of initial structures, and simulation times are described in the Supporting Material.

Surface pressure and interfacial tension in lipid droplets

In lipid droplets, as in all droplets, the interfacial tension acts as to minimize the contact area between the core and the solvent. This typically results in spherical particles as it is the shape that minimizes the interfacial area. In simple droplets, like large oil droplets in water, the radius R, interfacial tension γ, and pressure difference between the inside and the outside ΔP, can be connected by the Laplace equation

$$\Delta P=\frac{2\gamma }{R}.$$

A surfactant monolayer at an interface reduces the interfacial tension due to repulsion between surfactants. This reduction is usually called the surface pressure Π, which is defined as the difference between interfacial tension without (γ₀) and with (γ (A)) surfactant:

$$\Pi \left(A\right)={\gamma }_0-\gamma \left(A\right).$$ (1)

Note that in this description the interfacial tension with surfactant (and surface pressure) depends on the area per surfactant A. This corresponds to a situation where the number of surfactant molecules at the interface is constant whereas the area may change. This is the case in Langmuir-Blodgett and droplet tensiometer experiments, where the timescale for area change is faster than the timescale of transferring molecules from interface to bulk. The latter process is especially slow—several hours—for phospholipids with tails longer than 12 carbons (42). It is obvious that the conditions in MD simulations are similar. In physiological droplets, changes in surfactant concentration at the interfacial region, resulting from equilibration, may be slower than other processes such as enzymatic modifications.

In this work, we refer to the “surface pressure-area isotherm” when we deal with surface pressure described as a function of area per molecule. Correspondingly, interfacial tension described in terms of area per molecule is called the “interfacial tension-area isotherm”.

In addition to the pure surface pressure, the surface layer may have also other elastic properties such as a preferred (spontaneous) curvature, and resistance to bending (bending modulus). In this case, the surface energy depends on curvature as well as area. This dependence can be handled either by defining a curvature-dependent interfacial tension σ_s(R) or by using an interfacial tension for a flat interface γ with curvature correction, which can be related to the monolayer elastic coefficients (43–45). The first approach is used in this work, yet the second approach should provide an equivalent picture.

Interfacial tensions γ₀ and γ(A) were calculated from trilayer simulations by using standard procedures (see the Supporting Material).

Interfacial tension calculations for spherical droplets

To calculate the interfacial tension for spherical lipid droplets, we used its connection to the pressure tensor (45–47). In spherical symmetry, the pressure tensor can be written as

$$\mathbf{P}\left(\mathbf{r}\right)=\left({\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+{\mathbf{e}}_{\varphi }{\mathbf{e}}_{\varphi }\right)p_T\left(r\right)+{\mathbf{e}}_{\mathbf{r}}{\mathbf{e}}_{\mathbf{r}}{p}_{rr}\left(r\right)$$ (2)

(45,47,48), where r is the distance from the origin of the coordinate system. From spherical symmetry it follows that p_T(r) = p_θθ(r) = p_ϕϕ(r) depends only on r (45). If p_T(r) and p_rr(r) are known, then the Laplace interfacial tension can be calculated by

$${\sigma }_s=-\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left(\frac{r}{R_s}\right)}^2\left[p_T\left(r\right)-p_{rr}\left(r\right)\right]\text{d}r$$ (3)

(45,46), where R_s is called the Laplace radius given by

$$R_s^3=\frac{\underset{0}{\overset{\mathrm{\infty }}{\int }}{r}^2\left[p_T\left(r\right)-p_{rr}\left(r\right)\right]\text{d}r}{\underset{0}{\overset{\mathrm{\infty }}{\int }}{r}^{-1}\left[p_T\left(r\right)-p_{rr}\left(r\right)\right]\text{d}r}.$$ (4)

Tension σ_s and radius R_s are defined such that the Laplace equation holds with these values, i.e., ΔP = 2σ_s/R_s. This means that σ_s deviates from the value of a flat interface and R_s from the physical radius, if the interfacial energy depends on curvature. Similar equations have previously been used to calculate surface tensions for Lennard-Jones models of liquid drops (25,49,50) and interfacial tensions in coarse-grained models of vesicles (48,51).

In this work, we calculated p_T(r) and p_rr(r) from MD simulation data as described in Ollila et al. (48). Briefly, we divided the system into a grid (with a spacing of 0.3 nm), calculated the local pressure tensor in each cube in the grid, transformed the tensor in every cube to spherical coordinates, and then averaged over angular coordinates to find p_T(r) and p_rr(r). We then applied these in Eqs. 3 and 4 to find the Laplace radius and the interfacial tension.

As an example, Fig. 2 depicts the components of the pressure tensor, and the density distributions of the different components for Droplet3 as a function of distance from the particle center.

Figure 2.

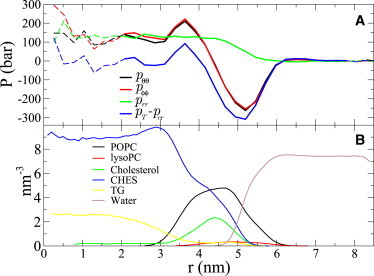
(A) Angular p_θθ(r), p_ϕϕ(r), and radial p_rr(r) components of the pressure tensor as a function of distance from the center of the particle r for Droplet3. Also the difference p_T(r) − p_rr(r) (integrand of Eqs. 3 and 4 is shown here. The pressure tensor data in core region (dashed line) are ignored in the interfacial tension calculation as explained in the text. (B) Density distributions of different molecules for the same droplet.

The droplet needs to have a bulk region both inside and outside to have a reasonable definition for the interfacial tension. In the bulk region, by definition p_θθ(r) = p_ϕϕ(r) = p_rr(r), thus p_rr(r) − p_T(r) = 0. This means that the integrand in Eq. 3 is zero in bulk and integration is needed only over the nonbulk interfacial region.

In the Supporting Material, we justify that the bulk region can be assumed to exist also in the core of small droplets, and hence it can be neglected when integrating Eqs. 3 and 4 to calculate interfacial tensions. This is equal to the assumption that p_T(r) − p_rr(r) = 0 in this region. For this purpose, the region where the density of pure core lipids is roughly constant and the density of surfactant lipids is zero is defined to be the core region. In Fig. 2 A for Droplet3, the neglected part of the pressure profile is shown by a dashed line and the part used in the integration by a solid one. The interfacial tension values somewhat depend on the starting point of the integration due to pressure fluctuations in the core region. The error bars for interfacial tension values are determined by varying the integration starting point by roughly 0.5 nm.

To calculate the interfacial tension for the lipid monolayer region in HDL and LDL particles (with proteins), we divided the interface into lipid and protein regions. To begin, we defined a coordinate system for each frame such that the angular location of the protein, with respect to the droplets center, did not change. This coordinate frame rotates with the particle. Next, we determined fixed angles from the center of the particle for the locations occupied by the protein and calculated the local pressure tensor in this frame. Then we averaged the pressure profile over those solid angles that the protein never occupied during the simulation and used this profile to calculate the interfacial tension for the lipid region. This method could potentially be used to calculate line tensions from particles with arbitrary shapes. The relative area coverage was calculated by using similar solid angles for locations occupied by the protein.

Nakamura et al. (52) recently introduced a method to calculate the spherical pressure tensor, which is numerically more efficient compared to our method. This method would likely reduce pressure fluctuations in the core region discussed above. However, their method would not allow separate calculations for the lipid and protein regions.

In interfacial tension-area isotherm calculations, the area for each droplet was calculated assuming them to maintain a spherical shape and then using the Laplace radius. The area per PC in the surface monolayer was calculated by dividing the area by the total number of POPC and lysoPC lipids.

Results and Discussion

Comparison between measured and simulated surface pressure-area isotherms

Although the surface pressure cannot be directly measured for small droplets, the surface pressure as a function of area per PC (surface pressure-area isotherm) can be determined for an essentially flat oil-monolayer-water interface by combining droplet tensiometer and Langmuir trough results (26). These results can be compared to the simulated isotherms calculated from trilayer systems as described in Models and Methods.

We calculated the interfacial tension for a water-TG interface from the TG layer in water (TG-Flat). The tension was found to be 31 ± 2 mN/m, in good agreement with the experimental value of 32 mN/m (5).

In Fig. 3 we show the isotherms calculated from simulations for the interfaces of TG-POPC-water (Flat1), TG-DLPC-water (Flat2), and lipoprotein droplet-lipid systems (Flat3). The experimental isotherm for the triolein-eggPC-water interface from Mitsche et al. (26) is also shown in Fig. 3.

Figure 3.

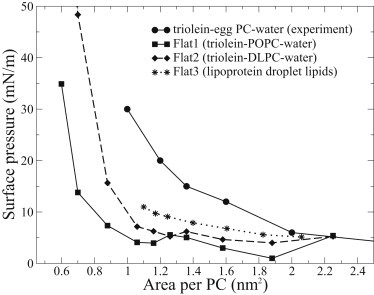
Surface pressure-area per PC isotherm for the triolein-POPC-water interface measured by Mitsche et al. (26) compared to isotherms calculated from simulations of several different interfacial systems. Error bars are of the same size as the size of symbols.

We see that the surface pressures determined from simulations are systematically smaller than the experimental values with corresponding area per PC. However, qualitatively the behavior is similar in the sense that the surface pressure curve is essentially flat with large areas per molecule, and the surface pressure starts to increase when the area per molecule decreases. Mitsche et al. (26) explained this by the idea that decreasing the area per molecule decreases the number of triolein molecules in the monolayer. This is noted both in simulations and experiments, but in simulations the increase starts at a lower area per molecule compared to experiments.

The lipid compositions are not exactly the same in any of the simulations as in experiments, which could, in principle, explain the differences. However, if the systems with different compositions are compared with one another, only rather minor deviations are found (see Fig. 3). Areas per molecule are slightly larger with monolayers containing polyunsaturated DLPC compared to the ones with monounsaturated POPC, and the largest areas are found with lipoprotein droplet lipids. These results make sense because polyunsaturated lipids are known to increase the area per molecule (53), and with the lipoprotein-droplet lipid composition, some cholesterol molecules are also located in the surface region, increasing the area per PC. However, the differences are not large enough to explain the discrepancy between simulations and experiments.

Considering these views, it seems that the used simulation model gives surface pressures that are too low (i.e., the interfacial tension is too high) for oil-water interfaces covered by a phospholipid monolayer. For comparison, the isotherms for an air-water interface calculated from the same model have recently been compared to experiments (54,55). The difference compared to our case is that the MARTINI model predicts a too-low surface tension between air and water, whereas the interfacial tension for the triolein-water interface is in good agreement with experimental values. Baoukina et al. solved this issue by fitting the isotherm to an experimental one (54), whereas Duncan and Larson (55) used experimental values for the air-water interfacial tension. Importantly, a surface pressure comparable to our result would be obtained by using the interfacial tension of the air-water interface from the MARTINI model. If this analysis were done, results in both of the above-mentioned studies would also produce a too low surface pressure for a monolayer (54,55).

Altogether, it seems that the effective intermolecular repulsion between lipid molecules is too low in this model, although it correctly reproduces the area per molecule in a lipid bilayer under zero tension. The results in this work could be explained by inaccuracies in triolein-phospholipid interactions, but this would not apply to the monolayers at air-water interfaces. In general, it is very difficult to build a model that would correctly reproduce tensions in a wider range of conditions due to a delicate balance between opposing components in the total tension (56).

Effect of curvature on interfacial tension

In general, interfacial tension measurements can be done only for macroscopic droplets. For example, the volume of a droplet ranges between 25 and 45 mm³ in droplet tensiometer measurements (26). However, physiologically relevant lipid droplets are often much smaller. For instance, the diameters of HDL and LDL are usually between 10 and 25 nm (1), highlighting the importance of understanding the role of particle curvature. The curvature dependence of interfacial tension has been under extensive discussion since its formulation by Tolman (24), but many aspects even for simple droplets without surfactants are still not understood (25). The general opinion is that the curvature correction becomes significant for droplets without surfactants when the radius approaches the size of molecules forming the droplet (25). The correction is likely larger for droplets covered by a monolayer due to the larger bending energy compared to a pure interface. Hence, the curvature correction might be important when measurements with an essentially flat monolayer (e.g., a Langmuir monolayer and droplet tensiometer) are used to gauge properties of microscopic droplets covered by a highly curved monolayer, as done in Weinberg et al. (4), Ibdah et al. (18), and Slotte and Grönberg (19). In this section, we calculate interfacial tensions for pure and surfactant covered oil-water interfaces with different curvatures.

For pure interfaces between oil and water, we simulated oil droplets in water having three different lipid compositions: TG (triolein) droplet, HDL-Core, and LDL-Core (compositions shown in Table 1). For each composition, three different simulations were made: a flat interface and two nanoscale droplets having different radii.

The interfacial tensions for pure interfaces with different curvatures are shown in Fig. S1 in the Supporting Material. The variations in the interfacial tension as a function of curvature are of the order of error bars and significant curvature dependence for pure interfaces is not found. This is expected because the studied droplets are larger than the size of a single molecule.

Interfaces covered with a surfactant monolayer are more complicated because the bending modulus is expected to depend on area per molecule (packing) in the interface. To study the curvature dependence of interfacial tension with an excess amount of surfactants, we should simulate interfaces with equilibrium surface concentrations. However, the timescale for this equilibration is several hours for phospholipids with long acyl tails (42), which is far too long for molecular simulations. Instead, we compare the interfacial tension-area per molecule isotherms between flat interfaces and nanoscale droplets. For a flat interface, the isotherm is generated by changing the area of the simulation box. For a droplet, the number of PC molecules is varied whereas the number of core lipids is fixed (Droplet1-Droplet5). With this procedure, the Laplace radius for a droplet is roughly constant, varying between 4.7 and 5.7 nm.

The interfacial tension versus area per PC curves for a droplet and a flat interface are shown in Fig. 4. Interfacial tensions for small droplets are generally lower compared to flat interfaces with corresponding areas per molecule. The difference becomes more pronounced with a smaller area per PC, which is expected because the monolayer bending becomes more difficult with higher packing. For droplets with a radius of ∼5 nm, and with a lipid composition as in the Droplet1-Droplet5 systems, the curvature correction for interfacial tension becomes significant with areas smaller than roughly 1.4 nm² per PC. As discussed in the next section, this would be the case, for example, with HDL droplets.

Figure 4.

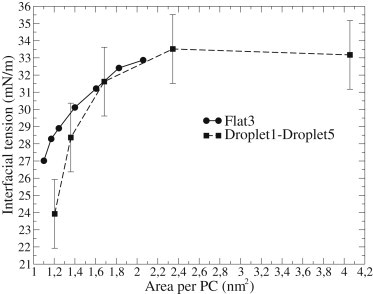
Interfacial tension as a function of area per PC for a flat interface (Flat3 with different box sizes) and a droplet of radius 4.7–5.7 nm containing lipoprotein-droplet-like substances (Droplet1–Droplet5). Error bars for flat interfaces are of the same size as the size of symbols.

Due to the semiquantitative nature of the MARTINI model, the result is not guaranteed to be quantitatively accurate. If quantitatively reliable results were desired, then the bending energy of a monolayer should be correctly described by the used model. For lipid bilayers, the bending modulus in the MARTINI model has been calculated by several groups and the results vary between 5.5 and 16 × 10⁻²⁰ J (57–59), whereas experimental values are 5 ± 2 × 10⁻²⁰ J (60). Whereas the experimental and simulated values have the same order of magnitude, the quantitative agreement is unclear due to large variations in the calculated values.

In the previous section, we reported that monolayer surface pressures in this model were somewhat underestimated. This does not affect the curvature correction of interfacial tension, if the underestimation is similar for both flat and curved interfaces. What remains to be explored in future studies is whether the dependence of bending energy on the area per molecule is given correctly by MARTINI-related models, as it may have some influence on our results.

Concluding, we predict that the interfacial tension of a curved oil-monolayer-water interface is significantly smaller than for a flat interface, when the radius of curvature and the area per molecule are small enough. However, quantitative predictions for the limits might not be accurate due to the nature of the used model.

Interfacial tension of HDL and LDL particles

Although surface pressure cannot be directly measured for small lipid droplets, it has been estimated for HDL and LDL particles by using results for macroscopic interfaces (4,16,18,19). Generally, the idea is to combine surface pressure-area isotherms for lipids and adsorption isotherms for proteins or enzymes, both determined at macroscopic interfaces. Estimates for surface pressure of HDL particles vary between 20 and 33 mN/m (4,18,19), whereas 25 mN/m was estimated for LDL (19).

To calculate the surface pressure for HDL and LDL models, we subtracted interfacial tensions of full lipoprotein droplets with a protein (HDL and LDL) from the interfacial tension of droplets consisting only of the core lipids (HDL-Core and LDL-Core). We also calculated surface pressures for HDL-Droplet and LDL-Droplet without proteins to decompose the protein contribution to the surface pressure. The pressure tensor components are shown in Fig. 5 for HDL- and LDL-related systems. The interfacial tensions and Laplace radii calculated from these are shown in Table 2.

Figure 5.

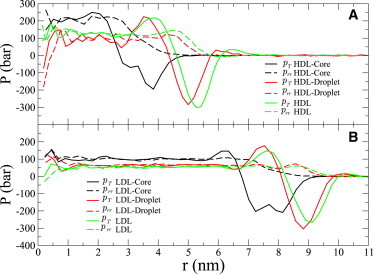
Tangential p_T(r) and radial p_rr(r) components of pressure tensor as a function of distance from the center of the particle r for (A) HDL- and (B) LDL-related systems. The systems are labeled as in Table 1.

Table 2.

Interfacial tension and Laplace radius calculated for HDL- and LDL-related systems

	HDL-Core	HDL-Droplet	HDL	LDL-Core	LDL-Droplet	LDL
Interfacial tension (mN/m)	38 ± 2	24 ± 2	26 ± 1	40 ± 1	27 ± 1	26 ± 1
Laplace radius (nm)	3.5 ± 0.1	5.1 ± 0.1	5.4 ± 0.1	7.7 ± 0.1	9.1 ± 0.1	9.2 ± 0.1

The difference between interfacial tensions of core droplets and full lipoprotein particles gives a surface pressure of ∼12 mN/m for HDL and ∼14 mN/m for LDL. The results are significantly lower than experimental estimates of 20–33 mN/m (4,18,19), which is expected because the monolayer surface pressure for flat interfaces is underestimated in simulations, as discussed above. In flat monolayers, for surface pressure with area per molecule corresponding to HDL (1.2 nm²) and LDL (1.5 nm²) models, the difference between experiments and simulations can be estimated from Fig. 3. We estimate the differences to be ∼15 mN/m for HDL and ∼10 mN/m for LDL. Adding these values to the calculated surface pressures, we would get surface pressures of ∼27 mN/m for HDL and ∼24 mN/m for LDL, which are close to the experimental values. Thus, the somewhat too-low surface pressure in the HDL and LDL models probably arises from the used model. Similarly, the corrected interfacial tensions would be 11 mN/m for HDL and 16 mN/m for LDL.

From Table 2 we see that the interfacial tensions, and also surface pressures, are essentially the same for droplets with (HDL, LDL) and without protein (HDL-Droplet, LDL-Droplet). This is unexpected because the protein penetrates into the monolayer and covers roughly 30% of the surface in both cases. If we assume that the protein conquers all of this area by pushing the surfactant lipids aside and that the droplet is incompressible, the tighter packing of a monolayer should lead to an increase in the surface pressure. The area per PC in LDL-Droplet (LDL without the surrounding apoB-100 protein) is ∼1.5 nm². Squeezing this by ∼30% due to protein inclusion would lead to an area per PC of ∼1.1 nm² in the lipid monolayer region of a LDL particle. According to the interfacial tension-area isotherm from Fig. 4, this area decrease would correspond to a decrease of at least 4 mN/m in the interfacial tension, and even more for a highly curved surface. Correspondingly for HDL, the area per PC would decrease from 1.2 to 0.8 nm². Extrapolating the curve in Fig. 4 we see that the change in interfacial tension should be even bigger than in LDL. The idea of this analysis is essentially similar as in Weinberg et al. (4) and Ibdah and Phillips (16).

According to this analysis, the interfacial tension should decrease in the lipid monolayer region in HDL and LDL particles. However, the interfacial tensions shown in Table 2 are calculated for the whole particles including proteins. To ensure that this does not cause unexpected results, we calculated the interfacial tension separately only for the lipid monolayer region of HDL and LDL. To do this, we averaged the pressure distribution in spherical coordinates only over the solid angle corresponding to the monolayer region and used this profile in the interfacial tension calculation (see Models and Methods). The pressure tensor components calculated for the monolayer regions of HDL and LDL are shown in Fig. S2, A and B, respectively. The pressure tensor components for the droplets without proteins are also shown (HDL-Droplet and LDL-Droplet).

The interfacial tension and Laplace radius calculated from the distributions of the nonprotein region of HDL are 24 mN/m and 5.6 nm, and 26 mN/m and 9.2 nm for LDL. The results are essentially the same as for droplets without proteins.

Our results suggest that a single protein adsorbed to the monolayer at the surface of a lipid droplet does not simply push surfactant lipids aside and increase surface pressure (decrease interfacial tension). A more plausible explanation for the observation would be that the attraction between lipids and proteins would concentrate lipid molecules next to the proteins such that the area per molecule does not essentially decrease. This would be a similar phenomenon as the interfacial tension antagonism described in Rosen (61). To analyze this, we calculated the surface density of PC groups in spherical coordinates for HDL and LDL systems. The results are illustrated in Fig. S3. We clearly see a higher headgroup concentration next to the protein regions, which suggests that the lipids rather pack next to proteins than decrease the monolayer area.

Some experimental results also indicate a possibility of nontrivial lipid-protein interactions in apolipoprotein systems (6,16), although the effects seem to be smaller than in our results. Thus, we suggest that the interfacial tension in HDL and LDL particles cannot be estimated by assuming that lipids are simply pushed aside by proteins, although this effect may be overestimated in this model.

A very low interfacial tension is needed to stabilize nanoscale lipid droplets. A simple relation σ∼k_BT/R ≈ 0.04 mN/m can be used to estimate the interfacial tension σ, which would produce thermodynamically stable droplets with a radius of R ∼ 10 nm (62). Our results suggest clearly higher interfacial tensions in HDL and LDL droplets, with and without proteins. Even the complete coverage of the interface by proteins in droplet tensiometer experiments would not decrease the interfacial tension enough for thermodynamically stable nanoscale droplets (5,6). Thus, our results suggest that HDL and LDL droplets are in a metastable state, stabilized by a kinetic barrier with respect to the interfacial energy. Apolipoproteins covering the droplets have previously been suggested to be in a similar state (63,64). In conclusion, we suggest that one has to concentrate on these kinetic barriers to understand the physiologically relevant destabilization of LDL (2).

Conclusions

We calculated interfacial tensions and surface pressures for oil-monolayer-water interfaces with physiologically relevant lipid compositions by using the coarse-grained MARTINI model and MD simulations. The shape of the surface pressure-area isotherm for a flat interface agrees qualitatively with experimental data, being essentially flat with large areas per molecule but increasing with lower areas per molecule (26). However, quantitatively surface pressures calculated from simulations are lower compared to the experimental values for flat interfaces (26), and HDL and LDL particles (4,18,19). The differences are roughly 15 mN/m and 10 mN/m with areas per molecule corresponding to HDL and LDL droplets, respectively. Our results indicate that the MARTINI model gives a too low surface pressure (too high interfacial tension) also for the oil-monolayer-water interface, as found previously for air-monolayer-water interfaces with the same model (54,55).

We also studied curvature dependence of interfacial tension by comparing results between flat interfaces and small droplets. For oil-water interfaces without surfactant, we studied small droplets with a radius as small as ∼2.7 nm, but we did not find significant dependence on curvature. However, the situation changed in interfaces that contained a surfactant monolayer. The comparison of interfacial tension-area isotherms between flat interfaces and lipid droplets (without proteins, with HDL/LDL lipid compositions) having a radius of 4.7–5.7 nm predicts that the interfacial tension is significantly lower in a droplet, when the area per PC is lower than ∼1.4 nm². The results suggest that the curvature dependence would be significant, for example, in HDL droplets having a radius of ∼5 nm and area per molecule of 1.2 nm². However, the quantitative accuracy of the predicted numbers is uncertain due to the nature of the used model.

Furthermore, we determined the interfacial tensions and surface pressures for recently published HDL and LDL models (27,28). The calculated surface pressures were ∼12 mN/m for HDL and ∼14 mN/m for LDL, which are smaller than experimental estimates that vary between 20–33 mN/m (4,18,19). The difference between simulations and experiments is similar as in a flat interface with a corresponding area per molecule. Our results suggest that the interfacial tensions of HDL and LDL are relatively high, ∼26 mN/m (or 11 mN/m and 16 mN/m, taking into account the discrepancy between simulations and experiments).

Surprisingly, we found essentially similar surface pressures for droplets with and without proteins. This observation can be explained by lipid-protein attraction, which packs lipids next to the protein rather than decreasing area per molecule in a bulk monolayer. This is similar to the interfacial tension antagonism effect (61). Indications of this kind of behavior were also seen in recent experiments, where different proteins covering the same area led to a different decrease in surface pressure (6).

In conclusion, we suggest that: 1), Specific lipid-protein interactions play a major role in the adsorption and in the behavior of individual apolipoproteins at lipid-droplet interfaces by concentrating lipids next to proteins. 2), Due to this effect, apolipoproteins do not essentially decrease the interfacial tension in HDL and LDL. 3), Relatively high interfacial tensions indicate that HDL and LDL are not thermodynamically stable microemulsion droplets but, instead, are stabilized by a kinetic barrier. Apolipoproteins at the surface of lipid droplets have also been suggested to be kinetically stabilized (63,64). Thus, we propose that one has to concentrate on the kinetic barrier of metastable lipid droplet fusion processes to understand physiologically relevant changes in HDL and LDL stability (2).