Conditional and Marginal Estimates in Case-Control Family Data - Extensions and Sensitivity Analyses

Abstract

This work considers two specific estimation techniques for the family specific proportional hazards model and for the population-averaged proportional hazards model. So far, these two estimation procedures were presented and studied under the gamma frailty distribution mainly because of its simple interpretation and mathematical tractability. Modifications of both procedures for other frailty distributions, such as inverse Gaussian, positive stable and a specific case of discrete distribution, are presented. By extensive simulations, it is shown that under the family specific proportional hazards model, the gamma frailty model appears to be robust to frailty distribution misspecification in both bias and efficiency loss in the marginal parameters. The population-averaged proportional hazards model, is found to be robust under the gamma frailty model misspecification only under moderate or weak dependency within cluster members.

1. Introduction

In family studies correlated failure times arise frequently in the form of ages at onset or ages at diagnosis for a disease. Many diseases such as coronary heart disease or cancer, are known to be correlated within families due to common genetic and environment factors that contribute to the occurrences of the disease. For the same reason, family studies have been frequently used in discovering novel genes or characterizing candidate genes for their involvement in diseases.

In our work we will focus on population-based case-control studies, where a number of cases and controls are sampled randomly from a well-defined population and an array of risk factors is collected on the cases and controls and their relatives [1]. We refer these cases and controls as probands to indicate that they are the index subjects because of whom the families are ascertained.

Our work is motivated by a recent breast cancer study conducted at the Fred Hutchinson Cancer Research Center [2]. In this study, the cases were incident breast cancer cases ascertained from a set of geographically defined, population based cancer registries in the United States. The controls were selected by random digit dialing, and matched with cases based on age at diagnosis and country of residence. Each subject (case or control proband) was asked to enumerate all their first-degree (mother, sister, daughters) and second-degree (aunts and grandmothers) female blood relatives. For each relative enumerated, the interviewer asked for the birth year, vital status, death year, history and type of cancer, and laterality (if breast cancer). Blood samples were collected on the probands to determine the presence or absence of BRCA1/2 mutations. One of the study objectives was to estimate the effects of BRCA1/2 mutation and other risk factors on the age at breast cancer diagnosis. It was also desired to estimate the baseline hazard function for obtaining absolute risk for a woman given her risk profile.

Case-control family studies, involve a cluster structure with potential correlations between the outcomes within a cluster. There are two main approaches for dealing with the dependence induced by the cluster effects: the conditional (or family-specific) model [3, 4] and the marginal (or population-averaged) model [5, 6]. In the conditional model, the hazard function takes into account the cluster effects and is used to compare between the risk of failure of members within the same cluster (family). Extensive reviews and discussions on the shared frailty models can be found in [7] and [8], and references therein. In the marginal approach, the risk of failure does not take into account the cluster effects. It represents the averaged hazard in the population and is used to compare the risk of failures of members in the population.

Estimation in the frailty model, has received much attention under various frailty distributions, including gamma [9–11], positive stable [12], inverse gaussian [11, 13], compound Poisson [13] and log-normal [14, 15]. Among many frailty distributions considered, gamma, or equivalently the Clayton-Oakes model [16, 17], is most commonly used due to its appealing interpretation and mathematical convenience. Despite its popularity, it is of concern that misspecification of gamma frailty distribution may invalidate the inference. Model diagnostic procedures, for cohort data, have been developed for that purpose [18–22]. However, in reality it may not be always easy to check the goodness-of-fit of the model because there is a lack of sufficient data to distinguish between various models. Hence, it is of practical importance that one should first examine to what extent the misspecification of the frailty distribution may affect the regression coefficients and baseline hazard function estimation in terms of bias and efficiency.

Some work has been done on the misspecification of frailty distribution in cohort family studies. It is found by simulation [23] that the regression coefficient estimates under the assumed gamma frailty model appeared to be minimally affected when the true frailty distribution is inverse Gaussian or positive stable. However, they did not study the effect of misspecified frailty distribution on the hazard functions. Hsu et al. [4] studied, under cohort and case-control settings, how the misspecification of the frailty distribution affects the estimation of the fitted marginalized hazard function for individuals with a particular risk profile. They assumed gamma distribution when the true distributions were inverse Gaussian, positive stable and specific case of the discrete distribution. They showed that the gamma distribution appears to be robust to frailty distribution misspecification and that the biases are generally 10% and lower, even when the true frailty distribution deviates substantially from the assumed gamma distribution. Note that both works concentrated on wrongly assuming gamma frailty model.

While family-specific hazard function is useful in genetic counseling, population-averaged marginal hazard functions are also of interest from the public health perspective for devising effective strategies for preventing diseases and treating the general population. Under the frailty model, the population-averaged hazard functions can be obtained by integrating out the frailty. However it may likely be affected by the frailty distribution assumption, as the integrated function involves not only the regression coefficients but also the dependence parameter. To overcome this undesired property, Hsu et al. [5] proposed a population-averaged marginal hazard frailty-based model for the case-control study design, while the marginal hazard functions are free of the frailty distribution. They showed by simulations, that the efficiency gain by the proposed method, in contrast to the generalized estimating equation approach, is most pronounced with high degree of correlation and with large family size.

Both works, [3, 5], only considered the gamma frailty distribution with scale and shape parameters θ⁻¹. Hence, the main goals of this work are: (1) extending and applying the estimation procedures of [3, 5] for different frailty distributions for case-control family data; and (2) studying the bias and particularly the efficiency loss of gamma frailty distribution misspecification on the regression estimates and marginal hazard functions. We investigated the following frailty distributions: inverse Gaussian, positive stable and a specific case for the discrete distribution. The discrete distribution is such that the frailty variate takes one of only two possible values, 1 − θ or 1 + θ, where the constraint (1 + θ + 1 − θ)/2 = 1 is set to allow for a unique identification of the baseline hazard function. Each distribution is a function of a parameter which quantifies differently the heterogeneity in risks among families and allow for a unique identification of the baseline hazard function. Each frailty distribution yields a different association between survival times of cluster (family) members. Table 1 gives the density functions (f), the first and second moments (μ₁, μ₂), Laplace transforms (ϕ) and cross-ratio (C) for the above distributions. We use here the popular cross ratio function [16] as a measure of dependency for bivariate survival times when comparing between the distributions. Hougaard [7] provides a comprehensive review of the properties of the various frailty distributions.

Table 1.

Density functions (f), first and second moments (μ₁, μ₂), Laplace transforms (ϕ) and cross-ratio (C) for the distributions: gamma, inverse Gaussian, positive stable and discrete.

Gamma

f(t) = θ–1/θt(1–θ)/θ exp(–t/θ)/γ(1/θ), θ > 0

μ1 = 1, μ2 = θ + 1

ϕ(s) = (1 + θs)–1/θ

C(t1, t2) = θ + 1

Inverse Gaussian

f(t) = (πθ)–1/2 exp(2/θ)t–3/2 exp{–t/θ – 1/(tθ)}, θ ≥ 0

μ1 = 1, μ2 = θ/2

$\varphi \left(s\right)=\text{exp}\left[2\{\frac{1}{\theta }-{(\frac{1}{{\theta }^2}+\frac{s}{\theta })}^{1∕2}\}\right]$

$C(t_1,t_2)=1+\frac{\theta }{2-\theta \text{log}{S}^m(t_1,t_2)}$

Sm(t1, t2) = P(T1 ≥ t1, T2 ≥ t2) = ϕ(H1(t1) + H2(t2)) where Hi(ti) = Λ0(ti) exp(βTZi)

Positive Stable

$f\left(t\right)=-{\left(\pi t\right)}^{-1}{\Sigma }_{k=1}^{\infty }\gamma (k\theta +1){(k!)}^{-1}{(-t^{-\theta })}^k\text{sin}\left(\theta \pi k\right),,0<\theta <1$

μ1, μ2 does not exist for θ < 1

ϕ(s) = exp(–sθ)

$C(t_1,t_2)=1+\frac{1-\theta }{-\theta \text{log}{S}^m(t_1,t_2)}$

Discrete

Pr(ω = 1 + θ) = 0.5, and Pr(ω = 1 – θ) = 0.5, –1 ≤ θ < 1

μ1 = 1, μ2 = 1 + θ2

ϕ(s) = 0.5 exp {–s(1 – θ)} + 0.5 exp {–s(1 + θ)}

C(t1, t2) = 1 + 4θ2[(1 + θ){G(t1, t2)}–θ + (1 – θ){G(t1, t2)}θ]–2

G(t1, t2) = exp{H1(t1) + H2(t2)}

The rest of the article is organized as follows. In Section 2 we provide the conditional modeling approach along with an estimation procedure based on [3]. Simulation results for this modeling are presented in Section 3. Section 4 consists of the marginal modeling approach and an estimation procedure based on [5], and its simulation study is presented in Section 5. A data set of a case-control breast cancer family study is being analyzed under the above two models, in Section 6. A discussion is provided in Section 7.

2. Conditional modeling - notation and the model under consideration

Let T and C be the failure and censoring times, respectively, and let Z be a p × 1 vector of covariates. We assume that the failure time support is [0, τ], for some time point τ < ∞. Denote the random effect by ω. We postulate the Cox proportional hazards model [24] for the effects of Z and ω on the failure time T for each individual. Under this model, the conditional hazard function given the vector of covariates Z and the frailty variate ω is defined by

$${\lambda }^c(t\mid \mathbf{Z},\omega )=\omega {\lambda }_0^c\left(t\right)\text{exp}\left({\beta }^{c^T}\mathbf{Z}\right)$$ (1)

where ${\lambda }_0^c\left(t\right)$ is an unspecified baseline hazard function and β^c is a p × 1 vector of unknown regression parameters.

In what follows, we derive the marginal hazard and joint survival function based on model (1). Denote the Laplace transform function by ϕ_θ(s) = E{exp(−sY)}, for a random variable Y, where θ is the parameter of the distribution of Y. Now, consider a family of size m and let T = (T₁, ..., T_m)^T and $\mathbf{Z}={({\mathbf{Z}}_1^T,\dots ,{\mathbf{Z}}_m^T)}^T$. Assume that the covariates’ effect is subject specific, namely P(T_i ≤ t|ω, Z) = P(T_i ≤ t|ω, Z_i) for i = 1, . . . , m and also assume that the family frailty variate ω is independent of ${\left\{{\mathbf{Z}}_i\right\}}_{i=1}^m$. Then, under model (1), the multivariate survival function of T given Z, becomes

$$S_{\mathbf{T}}^M(t_1,\dots ,t_m\mid \mathbf{Z})={\varphi }_{\theta }\left\{\sum _{i=1}^m{H}_i\left(t_i\right)\right\}$$ (2)

where $H_i\left(t_i\right)={\Lambda }_0^c\left(t_i\right)\text{exp}\left({\beta }^{c^T}{\mathbf{Z}}_i\right)$, ${\Lambda }_0^c\left(t\right)={\int }_0^t{\lambda }_0^c\left(u\right)du$ and θ is the parameter of the frailty distribution. Also, we get the marginal survival function for each family member, for example, S^m(t₁|Z₁) = S^m(t₁, 0, ..., 0|Z) = ϕ_θ{H₁(t₁)} for the first subject. By some algebra, we express the marginal hazard function, λ^m(t_i|Z_i), in terms of the conditional hazard function, as follows

$${\lambda }^m(t_i\mid {\mathbf{Z}}_i)={\lambda }_0^c\left(t_i\right)\text{exp}\{{\beta }^{C^T}{\mathbf{Z}}_i+\text{log}\left(U_i\right)\},i=1,\dots ,m$$ (3)

where U is determined by the frailty distribution and H_i(t). It is well known that proportional hazards model for λ^c generally does not yield a proportional hazards model for λ^m unless the frailty distribution is positive stable.

2.1. Conditional modeling - the likelihood function

Consider a matched case-control family study where one case proband is matched in age with one control proband (age of disease onset for cases and age at censoring for controls), and an array of risk factors is collected on the case and control probands and their relatives. Each matched set contains one case family and one control family, and there are a total of n matched sets. For each family member i of family k we define X_ki = min(T_ki, C_ki) and δ_ki = I(T_ki ≤ C_ki), k = 1, ..., 2n, i = 0, ..., m_k, where i = 0 corresponds to the proband. Furthermore, define X_k = (X_k1, ..., X_kmk), δ_k = (δ_k1, ..., δ_kmk) and ${\mathbf{Z}}_k={({\mathbf{Z}}_{k1}^T,\dots ,{\mathbf{Z}}_{k{m}_k}^T)}^T$. In addition, we associate with family k an unobserved frailty variate ω_k, k = 1, ..., 2n, which induces dependence among family members. We assume ω_k k = 1, . . . , 2n are independent identical distributed according to a known distribution with unknown parameter θ. This work centers on the estimation of β^c, ${\Lambda }_0^c$ and θ.

In what follows, we review the construction of the likelihood function for case-control family study as presented in [3], so that this paper will be self contained. We make the following common assumptions: (1) Given ω_k, the failure times of the family members are independent. (2) Conditional on ${\left\{{\mathbf{Z}}_{ki}\right\}}_{i=0}^{m_k}$ and ω_k, the censoring times are independent of the failure times and noninformative for ω_k, β^c and ${\Lambda }_0^c$. (3) The frailty ω_k is independent of ${\left\{{\mathbf{Z}}_{ki}\right\}}_{i=0}^{m_k}$. (4) The effect of covariates on the failure time is subject specific. Then, the likelihood function can be written as

$$\mathcal{L}=\prod _{k=1}^{2n}f({\mathbf{X}}_k,{\delta }_k\mid {\mathbf{Z}}_k,X_{k0},{\delta }_{k0},{\mathbf{Z}}_{k0})\times f({\mathbf{Z}}_{k0}\mid X_{k0},{\delta }_{k0})\times f({\mathbf{Z}}_k\mid {\mathbf{Z}}_{k0}).$$

The last factor f(Z_k|Z_k0) is the conditional distribution of the covariates. It does not contain information on β^c, ${\Lambda }_0^c\left(t\right)$ and θ and will therefore be ignored. In what follows we treat each of the other two factors, separately.

The likelihood function of the probands’ data, ${\prod }_{k=1}^{2n}f({\mathbf{Z}}_{k0}\mid X_{k0},{\delta }_{k0})$, is a retrospective likelihood for the usual case-control study and it can be replaced by the conditional logistic regression model [25] where cases and controls are matched on age. Hence, under the hazard function (3) it can be written as

$${\mathcal{L}}_P=\prod _{k=1}^n\frac{\text{exp}\{{\beta }^{C^T}{\mathbf{Z}}_{k0}+\text{log}\left(U_{k0}\right)\}}{\text{exp}\{{\beta }^{c^T}{\mathbf{Z}}_{k0}+\text{log}\left(U_{k0}\right)\}+\text{exp}\{{\beta }^{c^T}{\mathbf{Z}}_{(k+n)0}+\text{log}\left(U_{(n+k)0}\right)\}}$$ (4)

where without loss of generality we let the first n families to be the case families, and the kth case family k = 1, ..., n be matched with the (n + k)th control family. Note that Z_k0 and Z_(k+n)0 are the respective covariate vectors of the case-proband and control-proband of the kth matching set and log(U_k0) and log(U_(n+k)0) are of these same individuals, respectively. Table 2 presents U_j0, j = 1, ..., 2n for each frailty distribution discussed in this work.

Table 2.

U_j0 under gamma, inverse Gaussian, positive stable and discrete.

Gamma	Uj0 = {1 + θHj0(t)}–1
Inverse Gaussian	$U_{j0}=\frac{1}{\theta }{\{\frac{1}{{\theta }^2}+\frac{H_{j0}\left(t\right)}{\theta }\}}^{-1∕2}$
Positive stable	Uj0 = θ{Hj0(t)}θ–1
Discrete	$U_{j0}=\frac{(1+\theta )\text{exp}\{-H_{j0}\left(t\right)(1+\theta )\}+(1-\theta )\text{exp}\{-H_{j0}\left(t\right)(1-\theta )\}}{\text{exp}\{-H_{j0}\left(t\right)(1+\theta )\}+\text{exp}\{-H_{j0}\left(t\right)(1-\theta )\}}$

The likelihood function ${\prod }_{k=1}^{2n}f({\mathbf{X}}_k,{\delta }_k\mid {\mathbf{Z}}_k,X_{k0},{\delta }_{k0},{\mathbf{Z}}_{k0})$ is a function of the relatives’ data conditional on the probands’ data. As noted in [3], this likelihood would be greatly simplified if the family members were independent. This motivates us to consider the joint distribution of the relatives given the unobserved frailty variate ω_k and (Z_k, Z_k0, X_k0, δ_k0). Namely, we consider

$${\mathcal{L}}_R=\prod _{k=1}^{2n}f({\mathbf{X}}_k,{\delta }_k\mid {\omega }_k,{\mathbf{Z}}_k,{\mathbf{Z}}_{k0},X_{k0},{\delta }_{k0})=\prod _{k=1}^{2n}\prod _{i=1}^{m_k}f(X_{ki},{\delta }_{ki}\mid {\omega }_k,{\mathbf{Z}}_{ki}).$$ (5)

Based on (1) and assuming the frailty variates ${\left\{{\omega }_k\right\}}_{k=1}^{2n}$ are known, the right-hand side of (5) can be fitted by using the usual partial likelihood function with offset term log(ω_k). Specifically,

$${\mathcal{L}}_R\propto \prod _{k=1}^{2n}\prod _{i=1}^{m_k}{\left[\frac{\text{exp}\{{\beta }^{c^T}{\mathbf{Z}}_{ki}+\text{log}\left({\omega }_k\right)\}}{\sum _{l\in R\left(X_{ki}\right)}\text{exp}\{{\beta }^{c^T}{\mathbf{Z}}_l+\text{log}\left({\omega }_l\right)\}}\right]}^{{\delta }_{ki}}$$ (6)

where R(t) is the risk set consists of all the relatives who are at risk at time t.

2.2. Conditional modeling - an estimation procedure

The following is a summary of the estimation procedure of [3] which is extended to fit any frailty distribution. If ${\left\{U_{k0}\right\}}_{k=1}^{2n}$ and ${\left\{{\omega }_k\right\}}_{k=1}^{2n}$ were known, an estimator of β^c can be easily obtained by maximizing the product of ${\mathcal{L}}_R$ and ${\mathcal{L}}_P$ by the usual stratified Cox proportional hazards model with the offset terms log(U_k0) and log(ω_k). Since ${\left\{U_{k0}\right\}}_{k=1}^{2n}$ and ${\left\{{\omega }_k\right\}}_{k=1}^{2n}$ are unknown, we need to estimate them from the data. The estimators ${\left\{{\widehat{U}}_{k0}\right\}}_{k=1}^{2n}$ are defined as ${\left\{U_{k0}\right\}}_{k=1}^{2n}$ after replacing the unknown parameters by their estimates. For ${\widehat{\omega }}_k$ we use the posterior mean E(ω_k|X_k, δ_k, Z_k, X_k0, δ_k0, Z_k0) that can be written bas a function of the d_kth and (d_k + 1)th order differentiations of the Laplace transform ϕ_θ where $d_k={\sum }_{i=0}^{m_k}{\delta }_{ki}$. Specifically, let $H_{k.}\left(\tau \right)={\sum }_{i=0}^{m_k}{H}_i\left(X_{ki}\right)$, and note $f({\mathbf{X}}_k,{\delta }_k,{\mathbf{Z}}_k,X_{k0},{\delta }_{k0},{\mathbf{Z}}_{k0}\mid {\omega }_k)\propto {\omega }_k^{d_k}\text{exp}\{-{\omega }_k{H}_{k.}\left(\tau \right)\}$. Hence, we get

$$E({\omega }_k\mid {\mathbf{X}}_k,{\delta }_k,{\mathbf{Z}}_k,X_{k0},{\delta }_{k0},{\mathbf{Z}}_{k0})=\frac{{(-1)}^{(d_k+1)}{\varphi }_{\theta }^{(d_k+1)}\left(s\right){\phantom{\mid }\mid }_{s=H_{k.}\left(\tau \right)}}{{(-1)}^{\left(d_k\right)}{\varphi }_{\theta }^{\left(d_k\right)}\left(s\right){\phantom{\mid }\mid }_{s=H_{k.}\left(\tau \right)}}.$$

In Table 3 we present the posterior mean for each frailty distribution of Table 1. For simplicity of presentation, we assume that there is only one relative for each proband. However, the posterior mean for other family sizes can be obtained similarly.

Table 3.

The posterior mean E(ω_k|X_k, δ_k, Z_k, X_k0, δ_k0, Z_k0) under gamma, inverse Gaussian, positive stable and discrete.

Gamma

{1+ θHk.(t)}–1/θ

inverse Gaussian

$\{\begin{array}{cc}\frac{1}{\theta }{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}\hfill & \text{if}{d}_k=0\hfill \\ \frac{1}{\theta }{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}[1+\frac{1}{2}{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}]\hfill & \text{if}{d}_k=1\hfill \\ \frac{1}{\theta }{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}[\{1+{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}\}+\frac{1}{4}{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-1}{\{1+\frac{1}{2}{(\frac{1}{{\theta }^2}+\frac{H_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}\}}^{-1}]\hfill & \text{if}{d}_k=2\hfill \end{array}\phantom{\}}$

Positive Stable

$\{\begin{array}{cc}\theta H_{k.}{\left(t\right)}^{\theta -1}\hfill & \text{if}{d}_k=0\hfill \\ \theta H_{k.}{\left(t\right)}^{\theta -1}-(\theta -1)H_{k.}{\left(t\right)}^{-1}\hfill & \text{if}{d}_k=1\hfill \\ \frac{{\theta }^2{H}_{k.}{\left(t\right)}^{2\theta }{\left(t\right)}^{2\theta }-3\theta (\theta -1)H_{k.}{\left(t\right)}^{\theta }+(\theta -1)(\theta -2)}{H_{k.}\left(t\right)(\theta H_{k.}{\left(t\right)}^{\theta }-\theta +1)}\hfill & \text{if}{d}_k=2\hfill \end{array}\phantom{\}}$

Discrete

$\frac{{(1+\theta )}^{d_k+1}\text{exp}\{-(1+\theta )H_{k.}\left(t\right)\}+{(1-\theta )}^{d_k+1}\text{exp}\{-(1-\theta )H_{k.}\left(t\right)\}}{{(1+\theta )}^{d_k}\text{exp}\{-(1+\theta )H_{k.}\left(t\right)\}+{(1-\theta )}^{d_k}\text{exp}\{-(1-\theta )H_{k.}\left(t\right)\}}$

For estimating the baseline hazard function, we use a Breslow-type estimator with jumps only at the observed failure times of the relatives. Namely, given the estimators $\widehat{{\beta }^c}$ and ${\left\{{\widehat{\omega }}_k\right\}}_{k=1}^{2n}$, a Breslow-type estimator at time t is defined as a step function with jump-size at time s by

$$\Delta {\widehat{\Lambda }}_0^c\left(s\right)=\frac{\sum _{k=1}^{2n}\sum _{i=1}^{m_k}I(X_{ki}=s){\delta }_{ki}}{\sum _{k=1}^{2n}\sum _{i=1}^{m_k}I(X_{ki}\ge s)\text{exp}\left\{{\widehat{{\beta }^c}}^T{\mathbf{Z}}_{ki}+\text{log}\left({\widehat{\omega }}_k\right)\right\}}.$$ (7)

Finally, the estimation of the dependence parameter is done based on a pseudo likelihood function consists of the marginal distribution of the relatives’ data given the probands’ data and $(\widehat{{\beta }^c},{\widehat{\Lambda }}_0^c)$. For simplicity of presentation, we consider the case in which each proband has only one relative. The general case can be derived similarly.

Let $S_k^m(t_{k1}\mid t_{k0},{\delta }_{k0}=j,{\mathbf{Z}}_k)$ and $f_k^m(t_{k1}\mid t_{k0},{\delta }_{k0}=j,{\mathbf{Z}}_k),j=0$, 1 be the respective survival and density functions of the relative given its probands’ disease status, δ_k0, and age at onset or age at censoring t_k0, of the kth family. Also, let ${\mathcal{L}}_k^{\ast }$ be the contribution of family k to the likelihood function ${\mathcal{L}}_{\theta }^{\ast }={\prod }_{k=1}^{2n}{\mathcal{L}}_k^{\ast }$. Then, for each k = 1, ..., 2n we get

$${\mathcal{L}}_k^{\ast }={\left[S_k^m(t_{k1}\mid t_{k0},{\delta }_{k0}=0,{\mathbf{Z}}_k\right]}^{(1-{\delta }_{k1})(1-{\delta }_{k0})}{\left[S_k^m(t_{k1}\mid t_{k0},{\delta }_{k0}=1,{\mathbf{Z}}_k))\right]}^{{\delta }_{k0}(1-{\delta }_{k1})}{\left[f_k^m(t_{k1}\mid t_{k0},{\delta }_{k0}=0,{\mathbf{Z}}_k)\right]}^{{\delta }_{k1}(1-{\delta }_{k0})}{\left[f_k^m(t_{k1}\mid t_{k0},{\delta }_{k0}=1,{\mathbf{Z}}_k))\right]}^{{\delta }_{k0}{\delta }_{k1}}.$$

Table 4 presents log ${\mathcal{L}}_k^{\ast }$ under each distribution listed in Table 1. The proposed estimator of θ, denoted by $\widehat{\theta }$, is the value of θ which maximizes ${\mathcal{L}}_{\theta }^{\ast }$ after replacing β^c and ${\Lambda }_0^c$ by their estimates. It should be noted that under the gamma frailty model the cross-ratio is constant and equals θ + 1. Therefore, under this specific frailty model, it is easier to estimate the dependence parameter by using a stratified Cox regression model [3] instead of using the above likelihood approach.

Table 4.

log ${\mathcal{L}}_k^{\ast }$ for the distributions: gamma, inverse Gaussian, positive stable and discrete.

Gamma

$\text{log}{\mathcal{L}}_k^{\ast }\propto {\theta }^{-1}\text{log}\left\{\frac{1+\theta H_{k0}\left(t_0\right)}{1+\theta H_{k.}\left(t\right)}\right\}-({\delta }_{k0}+{\delta }_{k1})\text{log}\{1+\theta H_{k.}\left(t\right)\}+(2{\delta }_{k0}{\delta }_{k1}-{\delta }_{k0})\text{log}\{1+\theta H_{k0}\left(t_0\right)\}-{\delta }_{k1}\text{log}\theta +{\delta }_{k0}{\delta }_{k1}\text{log}(1+\theta )$

Inverse Gaussian

$\text{log}{\mathcal{L}}_k^{\ast }\propto \frac{2}{\eta }\{{(1+\eta H_{k0}\left(t_0\right))}^{1∕2}-{(1+\eta H_{k.}\left(t\right))}^{1∕2}\}+\frac{1}{2}{\delta }_{k0}\text{log}\{1+\eta H_{k0}\left(t_0\right)\}-\frac{1}{2}({\delta }_{k1}+{\delta }_{k0})\text{log}\{1+\eta H_{k.}\left(t\right)\}+{\delta }_{k0}{\delta }_{k1}\text{log}\{1+\frac{\eta }{2{(1+\eta H_{k.}\left(t\right))}^{1∕2}}\}$

Positive Stable

$\text{log}{\mathcal{L}}_k^{\ast }\propto H_{k0}^{\theta }\left(t_0\right)-H_{k.}{\left(t\right)}^{\theta }+{\delta }_{k1}(1-{\delta }_{k0})\text{log}\theta +\{(\theta -1)({\delta }_{k0}+{\delta }_{k1})-\theta {\delta }_{k0}{\delta }_{k1}\}\text{log}\left\{H_{k.}\left(t\right)\right\}-{\delta }_{k0}(\theta -1)\text{log}\left\{H_{k0}\left(t_0\right)\right\}+{\delta }_{k0}{\delta }_{k1}\text{log}\{\theta H_{k.}{\left(t\right)}^{\theta }-\theta +1\}$

Discrete

$$\begin{gathered} \text{log}{\mathcal{L}}_k^{\ast }\propto (\theta -1)\text{log}\left\{\frac{G(t_0,t_1)}{G\left(t_0\right)}\right\}+({\delta }_{k0}-1)\text{log}\{1+G^{-2\theta }\left(t_0\right)\}+(1-{\delta }_{k1})(1-{\delta }_{k0})\text{log}\{1+G^{-2\theta }(t_0,t_1)\}++({\delta }_{k0}+{\delta }_{k1}-2{\delta }_{k0}{\delta }_{k1})\text{log}\{(1-\theta )+(1+\theta )G^{-2\theta }(t_0,t_1)\}-{\delta }_{k0}\text{log}\{(1-\theta )+(1+\theta )G^{-2\theta }\left(t_0\right)\} \\ +{\delta }_{k0}{\delta }_{k1}\text{log}\{{(1-\theta )}^2+{(1+\theta )}^2{G}^{-2\theta }(t_0,t_1)\} \end{gathered}$$

where G(t0, t1) = exp{Hk.(t)},G(t0) = exp{Hk0(t0)}

The following is a summary of the above estimation procedure of $({\beta }^c,{\Lambda }_0^c,\theta )$, under the conditional proportional hazards model (1):

1. Set initial values for $({\beta }^c,{\Lambda }_0^c)$ by fitting a Cox proportional hazards model assuming independence among relatives, and let θ be the value corresponds to independence among family members.

2. Given $(\widehat{{\beta }^c},{\widehat{\Lambda }}_0^c,\widehat{\theta })$ obtain ${\left\{{\widehat{\omega }}_k\right\}}_{k=1}^{2n}$ and ${\left\{{\widehat{U}}_{k0}\right\}}_{k=1}^{2n}$.

3. Given $\widehat{\theta }$ and ${\left\{{\widehat{\omega }}_k\right\}}_{k=1}^{2n}$ and ${\left\{{\widehat{U}}_{k0}\right\}}_{k=1}^{2n}$, obtain $\widehat{{\beta }^c}$ and ${\widehat{\Lambda }}_0^c$ by fitting a Cox model with the offset terms $\text{log}\left({\widehat{U}}_{k0}\right)$ and $\text{log}\left({\widehat{\omega }}_k\right)$.

4. Given $(\widehat{{\beta }^c},{\widehat{\Lambda }}_0^c)$ obtain $\widehat{\theta }$ by maximizing the pseudo likelihood function based on ${\mathcal{L}}_{\theta }^{\ast }$.

5. Iterate between Steps (2)-(4) until convergence is reached with respect to all the parameters.

As mentioned, [3] presented the above estimation procedure under the gamma frailty model with expectation 1 and variance θ. By simulation study they showed that the method performs very well under finite sample sizes, in terms of bias. In addition, [4] studied the effect of frailty distribution misspecification in terms of bias under the assumed gamma distribution. Hence, they only estimated the parameters under the gamma model. The performance of the above estimation procedure under other frailty distributions, and, more importantly, the bias and efficiency loss under the misspecification of the gamma model will be studied, by simulation, in the next section.

3. Conditional modeling - a simulation study

We conducted a simulation study for matched case-control family study design under the conditional hazard function (1), and each of the frailty distributions of Table 1, where each proband has one relative. To allow for comparability across various frailty models, we used a fixed value of the Kendall's τ coefficient of concordance [26] as a measure of dependency of survival times within a family. We set τ to be 0.33 or 0.45 corresponding to moderate and strong dependency, respectively, between paired failure times. Since the results are similar for these two values of Kendall's τ , results of τ = 0.33 are omitted. Table 5 provides the Kendall's τ coefficient in terms of the frailty distribution's parameter and the parameter value under τ = 0.45, for each distribution.

Table 5.

The Kendall's τ function for gamma, inverse Gaussian, positive stable and discrete, and the parameter value under τ = 0.45.

Gamma	$\tau =\frac{\theta }{\theta +2}$	θ = 1.64
Inverse Gaussian	$\tau =0.5-2∕\theta +8∕{\theta }^2\text{exp}(4∕\theta ){\int }_{4∕\theta }^{\infty }{u}^{-1}\text{exp}(-u)du$	θ = 30.55
Positive Stable	τ = 1 – θ	θ = 0.55
Discrete	τ = θ2/2.	θ = 0.95

We assumed one covariate such that Z ~ Bernoulli(0.5). For sampling n = 500 matched case-probands with control-probands, we generated N = 20,000 independent failure times T|Z, ω ~ Exponential (ωexp(β^cZ)) and N independent censoring times C ~ Uniform(0, b). Taking b = 0.3 or 3 yields 60%-80% (high censoring rates) or 30%-40% (medium censoring rates) censoring rate, respectively. As expected, the censoring rates can vary under different frailty distributions. Evaluation of the observed times and the case/control status of each subject, yields N₁ case-probands and N₂ control-probands, N₁ + N₂ = N. Finally, we randomly selected n cases out of the N₁ case-probands and matched each case with one control-proband. For each selected proband (case and control), its relative data were generated, given the observed frailty value. The regression coefficient was chosen to be β = log(2) = 0.693. We used 1000 simulated data sets for each configuration. Note that instead of presenting simulation results for different sample sizes, we present simulation results for different censoring times since the efficiency in survival analysis is mostly determined by the number of events in the sample.

In order to compare between the marginalized hazard function under the true frailty distribution versus the misspecified frailty distribution we used Λ^m(t|Z) = −log ϕ_θ{H(t)}, presented in Table 6 for the various frailty distributions.

Table 6.

The cumulative marginal hazard function given Z = 0 or Z = 1 for gamma, inverse Gaussian, positive stable and discrete.

Gamma

${\Lambda }^m(t\mid Z=0)=\frac{1}{\theta }\text{log}\{1+\theta {\Lambda }_0^c\left(t\right)\}$

${\Lambda }^m(t\mid Z=1)=\frac{1}{\theta }\text{log}\{1+\theta {\Lambda }_0^c\left(t\right)\text{exp}\left({\beta }^{C^T}\right)\}$

Inverse Gaussian

${\Lambda }^m(t\mid Z=0)=-2\{\frac{1}{\theta }-{(\frac{1}{{\theta }^2}+\frac{{\Lambda }_0^c\left(t\right)}{\theta })}^{1∕2}\}$

${\Lambda }^m(t\mid Z=1)=-2\{\frac{1}{\theta }-{(\frac{1}{{\theta }^2}+\frac{{\Lambda }_0^c\left(t\right)\text{exp}\left({\beta }^{C^T}\right)}{\theta })}^{1∕2}\}$

Positive Stable

${\Lambda }^m(t\mid Z=0)={\left\{{\Lambda }_0^c\left(t\right)\right\}}^{\theta }$

${\Lambda }^m(t\mid Z=1)={\left\{{\Lambda }_0^c\left(t\right)\text{exp}\left({\beta }^{C^T}\right)\right\}}^{\theta }$

Discrete

${\Lambda }^m(t\mid Z=0)=-\text{log}[0.5\text{exp}\{-{\Lambda }_0^c\left(t\right)(1-\theta )\}+0.5\text{exp}\{-{\Lambda }_0^c\left(t\right)(1+\theta )\}]$

${\Lambda }^m(t\mid Z=1)=-\text{log}[0.5\text{exp}\{-{\Lambda }_0^c\left(t\right)\text{exp}\left({\beta }^{C^T}\right)(1-\theta )\}+0.5\text{exp}\{-{\Lambda }_0^c\left(t\right)\text{exp}\left({\beta }^{C^T}\right)(1+\theta )\}]$

The simulation results are summarized in Tables 7-9. Table 7 provides means and standard errors of the estimates of the conditional cumulative baseline hazard function at t = 0.05, 0.1, 0.15 and 0.2, for each frailty distribution, under the true frailty distribution and under the misspecified gamma model. Tables 8-9 provide the estimates of the regression coefficient and of the marginalized hazard function for Z=0 and Z=1 when the censoring rate is heavy (68%-80%) and moderate (30%-40%), respectively. Each case was studied under the true frailty distribution and under the misspecified gamma model. For each frailty model we present the true parameter values (first row); the empirical means (and standard errors in parentheses) under the true frailty distribution (second row) and under the misspecified gamma model (third row); the mean squared error (MSE) (×100) under the true frailty distribution (fourth row) and under the misspecified gamma model (fifth row), and the relative efficiency (RE) which is the variances’ ratio of the true model to the misspecified model (sixth row).

Table 7.

Simulation results: empirical mean (standard error) of ${\widehat{\Lambda }}_0^c\left(t\right)$

	${\Lambda }_0^c\left(0.05\right)=0.05$	${\Lambda }_0^c\left(0.1\right)=0.1$	${\Lambda }_0^c\left(0.15\right)=0.15$	${\Lambda }_0^c\left(0.2\right)=0.2$
60% – 80% censoring rate
True frailty distribution: inverse Gaussian (IG)
Used: IG	0.055(0.012)	0.110(0.022)	0.164(0.033)	0.218(0.044)
Used: gamma	0.045(0.009)	0.082(0.015)	0.116(0.022)	0.149(0.028)
True frailty distribution: positive stable (PS)
Used: PS	0.057(0.013)	0.113(0.023)	0.168(0.033)	0.221(0.041)
Used: gamma	0.278(0.047)	0.505(0.090)	0.743(0.141)	0.998(0.203)
True frailty distribution: discrete (Disc)
Used: Disc	0.052(0.007)	0.106(0.012)	0.159(0.017)	0.212(0.023)
Used: gamma	0.051(0.007)	0.105(0.014)	0.161(0.020)	0.219(0.027)
30% – 40% censoring rate
True frailty distribution: inverse Gaussian (IG)
Used: IG	0.067(0.041)	0.137(0.085)	0.208(0.130)	0.279(0.176)
Used: gamma	0.035(0.006)	0.062(0.010)	0.087(0.013)	0.110(0.016)
True frailty distribution: positive stable (PS)
Used: PS	0.050(0.010)	0.101(0.018)	0.151(0.025)	0.201(0.032)
Used: gamma	0.192(0.031)	0.326(0.054)	0.452(0.078)	0.578(0.105)
True frailty distribution: discrete (Disc)
Used: Disc	0.050(0.006)	0.100(0.011)	0.151(0.015)	0.201(0.019)
Used: gamma	0.055(0.008)	0.114(0.015)	0.176(0.022)	0.241(0.023)

Table 9.

Simulation results: empirical mean (standard error), mean squared error ×100 (MSE) and the relative efficiency (RE) of the regression coefficient and the marginalized hazard function estimates for 30%-40% censoring rate

		Λm(0.05)		Λm(0.1)		Λm(0.15)		Λm(0.2)
	βC	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l
True frailty distribution: inverse Gaussian (IG)
True value	0.693	0.039	0.066	0.066	0.109	0.089	0.143	0.109	0.172
mean(SE): IG	0.703(0.128)	0.041(0.011)	0.069(0.015)	0.069(0.015)	0.113(0.020)	0.092(0.017)	0.147(0.023)	0.113(0.019)	0.177(0.026)
mean(SE): gamma	0.690(0.129)	0.034(0.006)	0.065(0.011)	0.058(0.008)	0.110(0.016)	0.079(0.011)	0.146(0.019)	0.097(0.013)	0.177(0.022)
MSE: IG	1.648	0.012	0.023	0.023	0.041	0.029	0.054	0.037	0.070
MSE: gamma	1.665	0.006	0.012	0.013	0.026	0.022	0.037	0.031	0.050
RE	0.984	3.361	1.859	3.515	1.560	3.388	1.465	2.136	1.396
True frailty distribution: positive stable (PS)
True value	0.693	0.192	0.282	0.282	0.413	0.352	0.516	0.413	0.604
mean(SE): PS	0.685(0.108)	0.187(0.028)	0.274(0.038)	0.276(0.034)	0.404(0.046)	0.345(0.039)	0.506(0.052)	0.405(0.043)	0.594(0.056)
mean(SE): gamma	0.695(0.124)	0.165(0.022)	0.293(0.035)	0.257(0.031)	0.434(0.045)	0.332(0.037)	0.542(0.052)	0.398(0.042)	0.632(0.058)
MSE: PS	1.172	0.080	0.151	0.119	0.219	0.157	0.280	0.191	0.323
MSE: gamma	1.538	0.121	0.134	0.158	0.246	0.177	0.338	0.199	0.415
RE	0.758	1.612	1.178	1.202	1.045	1.111	1.000	1.048	0.932
True frailty distribution: discrete (Disc)
True value	0.693	0.049	0.095	0.095	0.182	0.140	0.260	0.182	0.329
mean(SE): Disc	0.702(0.105)	0.049(0.006)	0.096(0.011)	0.096(0.010)	0.185(0.017)	0.141(0.013)	0.266(0.021)	0.184(0.016)	0.339(0.025)
mean(SE): gamma	0.678(0.114)	0.052(0.007)	0.099(0.014)	0.103(0.012)	0.186(0.021)	0.152(0.017)	0.265(0.027)	0.197(0.021)	0.335(0.032)
MSE: Disc	1.110	0.003	0.012	0.010	0.029	0.017	0.047	0.026	0.072
MSE: gamma	1.322	0.005	0.021	0.021	0.045	0.043	0.075	0.066	0.106
RE	0.848	0.734	0.617	0.694	0.655	0.584	0.604	0.580	0.610

Table 8.

Simulation results: empirical mean (standard error), mean squared error ×100 (MSE) and the relative efficiency (RE) of the regression coefficient and the marginalized hazard function estimates for 60%-80% censoring rate

		Λm(0.05)		Λm(0.1)		Λm(0.15)		Λm(0.2)
	βC	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l
True frailty distribution: inverse Gaussian (IG)
True value	0.693	0.039	0.066	0.066	0.109	0.089	0.143	0.109	0.172
mean(SE): IG	0.700(0.136)	0.041(0.007)	0.072(0.013)	0.071(0.012)	0.118(0.020)	0.095(0.016)	0.154(0.026)	0.117(0.019)	0.185(0.030)
mean(SE): gamma	0.663(0.127)	0.039(0.007)	0.067(0.013)	0.064(0.012)	0.106(0.020)	0.084(0.015)	0.134(0.026)	0.101(0.019)	0.156(0.030)
MSE: IG	1.854	0.005	0.020	0.017	0.048	0.029	0.079	0.042	0.107
MSE: gamma	1.702	0.005	0.017	0.015	0.041	0.025	0.075	0.042	0.115
RE	1.146	1.000	1.000	1.000	1.000	1.130	1.000	1.000	1.000
True frailty distribution: positive stable (PS)
True value	0.693	0.192	0.282	0.282	0.413	0.352	0.516	0.413	0.604
mean(SE): PS	0.681(0.130)	0.197(0.026)	0.290(0.038)	0.290(0.033)	0.426(0.049)	0.363(0.039)	0.533(0.057)	0.425(0.043)	0.624(0.064)
mean(SE): gamma	0.666(0.139)	0.175(0.021)	0.263(0.032)	0.253(0.029)	0.358(0.041)	0.312(0.034)	0.425(0.047)	0.361(0.040)	0.478(0.053)
MSE: PS	1.704	0.070	0.151	0.115	0.257	0.164	0.353	0.199	0.445
MSE: gamma	2.005	0.073	0.138	0.168	0.470	0.275	1.049	0.430	1.868
RE	0.874	1.532	1.410	1.294	1.428	1.315	1.410	1.155	1.490
True frailty distribution: discrete (Disc)
True value	0.693	0.049	0.095	0.095	0.182	0.140	0.260	0.182	0.329
mean(SE): Disc	0.691(0.103)	0.051(0.007)	0.101(0.012)	0.102(0.011)	0.194(0.020)	0.150(0.015)	0.281(0.027)	0.196(0.021)	0.359(0.036)
mean(SE): gamma	0.711(0.110)	0.050(0.007)	0.099(0.014)	0.099(0.013)	0.192(0.023)	0.148(0.018)	0.280(0.032)	0.196(0.024)	0.362(0.042)
MSE: Disc	1.061	0.005	0.018	0.017	0.054	0.032	0.117	0.063	0.219
MSE: gamma	1.242	0.005	0.021	0.018	0.063	0.038	0.142	0.077	0.285
RE	0.876	1.000	0.734	0.715	0.756	0.694	0.712	0.765	0.734

As expected, we see that the estimation procedures which we extended for inverse Gaussian, positive stable and the discrete distributions perform very well. When we used the gamma distribution when the true frailty distribution is not, the bias in ${\widehat{\Lambda }}_0^c$ is moderate for inverse Gaussian, substantial for positive stable, and very small for discrete, under heavy censoring (60%-80%). Under moderate censoring rate (30%-40%), the bias becomes substantial for inverse Gaussian and remains the same for positive stable and the discrete distributions. In general, ${\Lambda }_0^c$ is underestimated for inverse Gaussian but overestimated for positive stable. Under the inverse Gaussian distribution, the standard errors that we get under misspecification of the frailty distribution are lower than those under the true distribution. Whereas, the standard errors we get for the positive stable distribution are higher under the misspecified gamma model than under the true distribution. Under the discrete distribution, the differences between the standard errors are relatively low. This can be explained by the fact that the variances are functions of the mean estimates.

Table 8 indicates that the bias in ${\widehat{\Lambda }}_0^m$ under misspecification of the frailty distribution is relatively small for all the three distributions (up to 10%). The most surprising results are that for the inverse Gaussian and the positive stable distributions there is no efficiency loss. The RE is higher than 1 and could be of 1.532 for the positive stable distribution. Under the discrete distribution we observed some efficiency loss (RE around 0.7). In Table 9, which consists of lower censoring rate, the bias is again small under all the frailty distributions (up to 11% for the inverse Gaussian and up to 8% for the positive stable and the discrete distributions), similar to the case of high censoring. Moreover, for the inverse Gaussian and positive stable distributions, there is even a gain in efficiency while using the misspecified gamma model: RE up to 3.388 for the inverse Gaussian distribution and up to 1.612 for the positive stable distribution. In contrast, under the discrete distribution, we observed efficiency loss (RE around 0.6), which is probably due to the lack of fit of the continuous gamma approximation for the discrete frailties. The bias and efficiency losses in $\widehat{{\beta }^c}$ in both censoring rates were quite minimal under all the frailty distributions investigated in this work (up to 4% and RE around 0.8). For the inverse Gaussian distribution with the high censoring rate, there is a gain in efficiency in $\widehat{{\beta }^c}$ (RE equals 1.146). These results suggest that the gamma frailty model can serve as a good practical choice in real data analysis if the marginal parameters are of primary interest since the “price” to be paid in bias is small, and the efficiency loss is minimal, if any.

4. Marginal modeling - notation and the model under consideration

Now we focus on the multivariate survival model proposed by [5], with the marginal hazard function following the Cox proportional hazards model. Under this model, the marginal hazard function, given the vector of covariates Z, is defined by

$${\lambda }^m(t\mid \mathbf{Z})={\lambda }_0^m\left(t\right)\text{exp}\left({\beta }^{m^T}\mathbf{Z}\right)$$ (8)

where β^m and ${\lambda }_0^m\left(t\right)$ are the marginal regression coefficient vector and the unspecified marginal baseline hazard function, respectively. The conditional hazard function, under a multiplicative effect of ω on the hazard function, takes the form of

$${\lambda }^c(t\mid \mathbf{Z},\omega )=\alpha \left(t\right)\omega .$$ (9)

The relationship between α and λ^m can be derived as follows. Write ${\Lambda }^m(t\mid \mathbf{Z})=-\text{log}{S}^m(t\mid \mathbf{Z})={\Lambda }_0^m\left(t\right)\text{exp}\left({\beta }^{m^T}\mathbf{Z}\right)$ and ${\Lambda }^c(t\mid \mathbf{Z},\omega )=-\text{log}{S}^c(t\mid \mathbf{Z},\omega )=\omega {\int }_0^t\alpha \left(s\right)ds$. Then, we get

$$S^m(t\mid \mathbf{Z})={\int }_0^{\infty }\text{exp}\left\{-\omega {\int }_0^t\alpha \left(s\right)ds\right\}dF\left(\omega \right),$$

where F(·) is the cumulative distribution function of the frailty variate. Let $A\left(t\right)={\int }_0^t\alpha \left(s\right)ds$. Hence, the function α should satisfy the constraint

$${\Lambda }_0^m\left(t\right)\text{exp}\left({\beta }^{m^T}\mathbf{Z}\right)=-\text{log}{\varphi }_{\theta }\left\{A\left(t\right)\right\}.$$ (10)

Note that based on (10), α(t) can be written as ${\lambda }_0^m\left(t\right){\alpha }^{\ast }\left(t\right)$ as long as the inverse function ${\varphi }_{\theta }^{-1}$ exists. Table 10 presents the “baseline” function α(t) for the frailty distributions gamma, inverse Gaussian and positive stable of Table 1. Hence, α* can be deduced easily. In the case of the discrete distribution, there is no close analytical form of α(t). Hence, we will not consider this distribution under the marginal modeling.

Table 10.

The function α under gamma, inverse Gaussian and positive stable models.

Gamma	$\alpha \left(t\right)={\lambda }_0^m\left(t\right)\text{exp}\{{\beta }^{M^T}Z+\theta \text{exp}\left({\beta }^{M^T}Z\right){\Lambda }_0^m(t-)\}$
Inverse Gaussian	$\alpha \left(t\right)={\lambda }_0^m\left(t\right)\text{exp}\left({\beta }^{M^T}Z\right)\{\frac{\theta }{2}{\Lambda }_0^m(t-)\text{exp}\left({\beta }^{M^T}Z\right)+1\}$
Positive Stable	$\alpha \left(t\right)={\lambda }_0^m\left(t\right)\frac{1}{\theta }{\left\{{\Lambda }_0^m(t-)\right\}}^{1∕\theta -1}\cdot \text{exp}\left(\frac{1}{\theta }{\beta }^{M^T}Z\right)$

4.1. Marginal modeling - the likelihood function

As in [5], assume that the effect of covariates on the age at onset is subject specific. Then, similarly to (4), the likelihood is partitioned into ${\mathcal{L}}^m\propto {\mathcal{L}}_P^m\times {\mathcal{L}}_R^m$ where ${\mathcal{L}}_P^m={\prod }_{k=1}^{2n}f({\mathbf{Z}}_{k0}\mid X_{k0},{\delta }_{k0})$ and ${\mathcal{L}}_R^m={\prod }_{k=1}^{2n}f({\mathbf{X}}_k,{\delta }_k\mid {\mathbf{Z}}_k,{\mathbf{Z}}_{k0},X_{k0},{\delta }_{k0})$.

The likelihood function ${\mathcal{L}}_P^m$ of the probands’ data, is a retrospective likelihood for the usual case-control study. Assume cases and controls are one-to-one matched and there are n matched sets. Then, ${\mathcal{L}}_P^m$ can be replaced by a conditional logistic regression model of [25]

$$\prod _{k=1}^n\frac{\text{exp}\left({\beta }^{m^T}{\mathbf{Z}}_{k0}\right)}{\text{exp}\left({\beta }^{m^T}{\mathbf{Z}}_{k0}\right)+\text{exp}\left({\beta }^{m^T}{\mathbf{Z}}_{(k+n)0}\right)}$$ (11)

where without loss of generality, the first n families are the case families and the kth family, k = 1, . . . , n, is matched with the (k + n)th control family.

In principle, we can follow the estimation procedure of Section 2.2 to obtain estimators of β^m, ${\Lambda }_0^m$ and θ with the conditional model (9) and the appropriate α(t). However, α(t) has a complicated structure and does not factor in the form as in the Cox model. Thus we can not use standard statistical packages for estimating β^m and ${\Lambda }_0^m$. Alternatively, we use an estimation procedure that is based on the innovation theorem. The following is an extension of [5] to address any frailty distribution.

Let N_k(t) = (N_k1(t), ..., N_kmk(t)) and Y_k(t) = (Y_k1(t), ..., Y_kmk(t)) be the event and at-risk processes where N_ki(t) = δ_kiI(X_ki ≤ t) and Y_ki(t) = I(X_ki ≥ t), and let ${\mathcal{F}}_t$ denote the entire observed history up to time t, that is

$${\mathcal{F}}_t=\{X_{k0},{\delta }_{k0},{\mathbf{Z}}_{k0},{\mathbf{N}}_{ki}\left(s\right),{\mathbf{Y}}_{ki}\left(s\right),{\mathbf{Z}}_{ki},s\in [0,t],k=1,\cdots ,2n;i=1,\cdots ,m_k\}$$

which includes the history of relatives up to time t, and the history of probands up to time τ , the end of the study. By the innovation theorem [27] we get that the ${\mathcal{F}}_{t-}$ stochastic intensity process of N_ki(t) is given by replacing ω_k by its conditional expectation with respect to the history ${\mathcal{F}}_{t-}$. Namely ${\lambda }_{ki}^{{\mathcal{F}}_t}\left(t\right)={\alpha }_{ki}\left(t\right)E({\omega }_k\mid {\mathcal{F}}_{t-})Y_{ki}\left(t\right)$, and the function α_ki(t) depends on t only up to t−, beside ${\lambda }_0^m\left(t\right)$, as shown in Table 10. Hence, we get [28]

$${\mathcal{L}}_R^m\propto \prod _{k=1}^{2n}\prod _{i=1}^{m_k}\left[\prod _{u\ge 0}{\left\{{\lambda }_{ki}^{{\mathcal{F}}_u}\left(u\right)\right\}}^{\Delta N_{ki}\left(u\right)}\right]\text{exp}\left\{-{\int }_0^{\tau }{\lambda }_{ki}^{{\mathcal{F}}_u}\left(u\right)Y_{ki}\left(u\right)du\right\}.$$ (12)

For writing the likelihood (12) explicitly for each frailty distribution, note that for any given t ∈ [0, τ]

$$E({\omega }_k\mid {\mathcal{F}}_t)=\frac{{(-1)}^{{\delta }_{k0}+N_{k.}\left(t\right)+1}{\varphi }^{{\delta }_{k0}+N_{k.}\left(t\right)+1}\left(s\right){\phantom{\mid }\mid }_{s=A_{k.}\left(t\right)}}{(-1){}^{{\delta }_{k0}+N_{k.}\left(t\right)}{\varphi }^{{\delta }_{k0}+N_{k.}\left(t\right)}\left(s\right){\phantom{\mid }\mid }_{s=A_{k.}\left(t\right)}}$$

where $N_{k.}\left(t\right)={\sum }_{i=1}^{m_k}{N}_{ki}\left(t\right)$ and $A_{k.}\left(t\right)={\sum }_{i=1}^{m_k}{A}_{ki}\left(t\right)$. In Table 11 we present $E({\omega }_k\mid {\mathcal{F}}_t)$ for each of the investigated frailty distribution and for simplicity of presentation, we assume one relative for each proband. Finally, we get ${\mathcal{L}}_R^m$ explicitly, for each frailty distribution, by plugging the functions α_ki(t) and $E({\omega }_k\mid {\mathcal{F}}_{t-})$ for all t ∈ [0, τ].

Table 11.

$E({\omega }_k\mid {\mathcal{F}}_t)$ for the distributions: gamma, inverse Gaussian and positive stable.

Gamma

$\frac{{\theta }^{-1}+{\delta }_{k0}+N_{k1}\left(t\right)}{{\theta }^{-1}+A_{k0}\left(T_{k0}\right)+A_{k1}(T_{k1}\wedge t)}$

Inverse Gaussian

$\{\begin{array}{cc}\frac{1}{\theta }{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}\hfill & \text{if}{d}_k=0\hfill \\ \frac{1}{\theta }{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}[1+\frac{1}{2}{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}]\hfill & \text{if}{d}_k=1\hfill \\ \frac{1}{\theta }{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}[\{1+{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}\}+\frac{1}{4}{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-1}{\{1+\frac{1}{2}{(\frac{1}{{\theta }^2}+\frac{A_{k.}\left(t\right)}{\theta })}^{-\frac{1}{2}}\}}^{-1}]\hfill & \text{if}{d}_k=2\hfill \end{array}\phantom{\}}$

Positive Stable

$\{\begin{array}{cc}\theta A_{k.}{\left(t\right)}^{\theta -1}\hfill & \text{if}{d}_k=0\hfill \\ \theta A_{k.}{\left(t\right)}^{\theta -1}-(\theta -1)A_{k.}{\left(t\right)}^{-1}\hfill & \text{if}{d}_k=1\hfill \\ \frac{{\theta }^2{A}_{k.}{\left(t\right)}^{2\theta }-3\theta (\theta -1)A_{k.}{\left(t\right)}^{\theta }+(\theta -1)(\theta -2)}{A_{k.}\left(t\right)(\theta A_{k.}{\left(t\right)}^{\theta }-\theta +1)}\hfill & \text{if}{d}_k=2\hfill \end{array}\phantom{\}}$

4.2. Marginal modeling - an estimation procedure

We start with the baseline hazard function. The structure of the ${\mathcal{F}}_{t-}$ stochastic intensity process suggests a Breslow-type estimator for the cumulative baseline hazard function estimator denoted by ${\widehat{\Lambda }}_0^m\left(t\right)$. Specifically, the intensity function ${\lambda }_{ki}^{{\mathcal{F}}_t}\left(t\right)$ can be expressed as ${\lambda }_0^m\left(t\right){\alpha }_{ki}^{\ast }(t-)E({\omega }_k\mid {\mathcal{F}}_{t-})Y_{ki}\left(t\right)$ as evident from Tables 10-11. Then,

$$\Delta {\widehat{\Lambda }}_0^m\left(s\right)=\frac{\sum _{k=1}^{2n}\sum _{i=1}^{m_k}I(X_{ki}=s){\delta }_{ki}}{\sum _{k=1}^{2n}\sum _{i=1}^{m_k}I(X_{ki}\ge s){\widehat{\alpha }}_{ki}^{\ast }(s-)\widehat{E}({\omega }_k\mid {\mathcal{F}}_{s-})}.$$

where in ${\widehat{\alpha }}_{ki}^{\ast }$ and $\widehat{E}({\omega }_k\mid {\mathcal{F}}_{t-})$ we replace all the unknown parameters by their estimates. Note that $E({\omega }_k\mid {\mathcal{F}}_t)$ involves ${\Lambda }_0^m$ of the probands’ observation times, T_k0, that can be greater than time t. Therefore, an iterative procedure is required.

Estimation of the dependence parameter θ and the regression coefficient β^m is straightforward once we know ${\Lambda }_0^m$. We construct a profile likelihood based on ${\mathcal{L}}_P^m\times {\mathcal{L}}_R^m$ in (11) and (12) by replacing ${\Lambda }_0^m$ with ${\widehat{\Lambda }}_0^m$, so $\widehat{{\beta }^m}$ and $\widehat{\theta }$ are those the values that maximize the profile likelihood. The final estimates of ${\Lambda }_0^m$ and (β^m, θ) are given by iterating between ${\widehat{\Lambda }}_0^m$ and $(\widehat{{\beta }^m},\widehat{\theta })$ until convergence is reached with respect to all the parameters.

Hsu et al. [5] presented and studied the above estimation procedure only under the gamma frailty model. The performance of the above estimation procedure under other frailty distributions was not examined. More importantly, the efficiency loss under the misspecification of the gamma model is not clear. These will be studied, by simulation, in the next section.

5. Marginal modeling - a simulation study

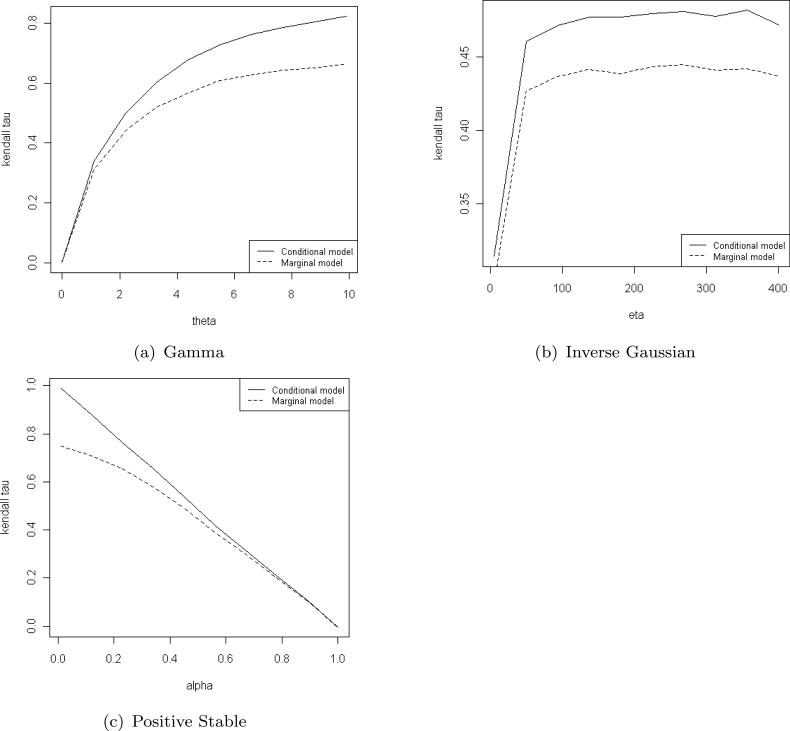
We conducted a simulation study for matched case-control family study design under the marginal hazard function (8). Table 12 provides the frailty distribution parameter value corresponds to τ = 0.33 and 0.45. In Figure 1 we present the Kendall's τ coefficient as a function of the dependence parameter θ for the conditional model (1) and the marginal model (8) under various frailty distributions. From these figures we see that under these three frailty distributions, for the same strength of Kendall's τ , the marginal modeling requires higher variability of the frailty variate, when compared to that of the conditional model. Moreover, this variability increases in τ. This is an important fact for understanding the following simulation results and for comparing them to those of the conditional modeling.

Table 12.

The frailty distribution parameter value used in the simulation study

Kendall's τ	0.33	0.45
Gamma	1.25	2.20
Inverse Gaussian	8.50	380
Positive Stable	0.63	0.50

Figure 1.

Kendall's τ as a function of θ under gamma, inverse Gaussian and positive stable frailty models. Solid line - conditional model, dotted line - marginal model.

For sampling under (8) and (9), write $S_{ki}^c(t\mid Z_{ki},{\omega }_k)=\text{exp}\{-{\omega }_k{A}_{ki}\left(t\right)\}$, so if U ~ Uniform(0, 1), we get $T_{ki}=A_{ki}^{-1}\{-\text{log}(1-U)∕{\omega }_k\}$, given that A⁻¹ exists. Table 13 provides the inverse function A⁻¹ for each frailty distribution, under ${\Lambda }_0^m\left(t\right)=t$. The rest of the sampling scheme is similar to that of Section 3.

Table 13.

The inverse function A^–1 (x).

Gamma	$A^{-1}\left(x\right)=\frac{\text{log}(1-\theta x)}{\theta \text{exp}\left({\beta }^{M^T}Z\right)}$
Inverse Gaussian	$A^{-1}\left(x\right)=\frac{-1+\sqrt{1-\theta x}}{\frac{\theta }{2}\text{exp}\left({\beta }^{M^T}Z\right)}$
Positive Stable	$A^{-1}\left(x\right)={(-x)}^{\theta }\text{exp}(-{\beta }^{M^T}Z)$

Tables 14-16 provide results of τ = 0.45 and 30%-50% censoring rate, τ = 0.33 and 60%-80% censoring rate, and τ = 0.33 and 30%-40% censoring rate, respectively. It is evident that the estimation procedures for all the three distributions, when they are true, perform very well in terms of bias with respect to all the parameters. Under high dependence (τ = 0.45) and low censoring rate (30%-50%), the bias in ${\widehat{\Lambda }}_0^m$ due to misspecification of the frailty distribution is very substantial for all the distributions (Table 14). Therefore, the MSE and the RE are omitted. Similar results were observed for high censoring rate (60%-80%) with τ = 0.45, and hence these results are not shown. For moderate dependence (τ = 0.33) with high censoring rate, the bias in ${\widehat{\Lambda }}_0^m$ under misspecification of the frailty distribution is relatively small for the inverse Gaussian distribution (up to 7%) and more substantial for the positive stable distribution (Table 15). For the inverse Gaussian distribution there is no efficiency loss (the RE is around 1.3). Under lower censoring rate (30%-40%) and moderate dependence (τ = 0.33), the bias is small under both frailty distributions (up to 2% for the inverse Gaussian and up to 10% for the positive stable distribution) (Table 16). Moreover, for the inverse Gaussian and positive stable distributions, there is even a gain in efficiency while using the misspecified gamma model (RE around 1.25 for the inverse Gaussian distribution, and around 2.3 for the positive stable distribution). The bias in β^m is quite minimal for the high and moderate dependence in both distributions (up to 4%). The difference in the results between the high dependence (τ = 0.45) and the moderate dependence (τ = 0.33) can be explained by the fact that the variability in the frailty variate for high dependency is much greater than that of the moderate dependence. So, as expected, under high variance of the frailty variate, the effect of misspecification of the frailty distribution can not be negligible.

Table 14.

Simulation results: empirical mean (standard error) of the dependence parameter, regression coefficient and the marginal hazard functions with τ = 0.45 and 30%-50% censoring rate.

			Λm(0.05)		Λm(0.1)		Λm(0.15)		Λm(0.2)
	θ	βm	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l
True frailty distribution: gamma
True value	2.2	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
Used: gamma	2.26(0.486)	0.696(0.096)	0.049(0.008)	0.099(0.015)	0.099(0.014)	0.198(0.027)	0.148(0.021)	0.295(0.04)	0.186(0.029)	0.372(0.055)
True frailty distribution: inverse Gaussian (IG)
True value	380	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
Used: IG	407(222)	0.691(0.094)	0.053(0.018)	0.104(0.031)	0.104(0.031)	0.205(0.051)	0.153(0.041)	0.302(0.068)	0.190(0.049)	0.376(0.083)
Used: gamma	-	0.695(0.084)	0.022(0.012)	0.043(0.024)	0.038(0.021)	0.076(0.042)	0.051(0.028)	0.103(0.057)	0.061(0.034)	0.121(0.068)
True frailty distribution: positive stable (PS)
True value	0.5	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
Used: PS	0.526(0.057)	0.696(0.080)	0.051(0.012)	0.099(0.021)	0.105(0.019)	0.207(0.031)	0.159(0.028)	0.314(0.046)	0.209(0.033)	0.413(0.055)
Used: gamma	-	0.661(0.077)	0.032(0.010)	0.065(0.021)	0.057(0.018)	0.115(0.037)	0.078(0.026)	0.157(0.052)	0.096(0.032)	0.192(0.064)

Table 16.

Simulation results: empirical mean (standard error), mean squared error ×100 (MSE) and the relative efficiency (RE) of the dependence parameter, the regression coefficient and the marginal hazard function estimates with τ = 0.33 and 30%-40% censoring rate.

			Λm(0.05)		Λm(0.1)		Λm(0.15)		Λm(0.2)
	θ	βm	Z=0	Z=1	Z=0	Z=1	Z=0	Z=1	Z=0	Z=1
True frailty distribution: gamma
True value	1.25	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
mean(SE): gamma	1.250(0.148)	0.690(0.059)	0.050(0.007)	0.099(0.013)	0.099(0.011)	0.199(0.019)	0.150(0.015)	0.299(0.025)	0.201(0.019)	0.400(0.032)
True frailty distribution: inverse Gaussian (IG)
True value	8.5	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
mean(SE): IG	8.860(2.080)	0.684(0.064)	0.051(0.008)	0.101(0.016)	0.102(0.014)	0.201(0.023)	0.153(0.018)	0.302(0.030)	0.203(0.022)	0.402(0.036)
mean(SE): gamma	-	0.667(0.061)	0.048(0.007)	0.094(0.013)	0.099(0.012)	0.193(0.020)	0.151(0.017)	0.293(0.027)	0.202(0.021)	0.394(0.033)
MSE: IG	-	0.417	0.006	0.025	0.020	0.053	0.033	0.090	0.049	0.130
MSE: gamma	-	0.439	0.005	0.019	0.014	0.045	0.029	0.077	0.044	0.112
RE	-	1.100	1.306	1.514	1.361	1.322	1.121	1.234	1.097	1.190
True frailty distribution: positive stable (PS)
True value	0.63	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
mean(SE): PS	0.650(0.037)	0.704(0.062)	0.046(0.012)	0.093(0.021)	0.095(0.018)	0.193(0.031)	0.145(0.022)	0.292(0.037)	0.195(0.027)	0.393(0.042)
mean(SE): gamma	-	0.665(0.060)	0.046(0.007)	0.090(0.012)	0.096(0.012)	0.188(0.019)	0.148(0.016)	0.287(0.026)	0.200(0.020)	0.389(0.032)
MSE: PS	-	0.396	0.015	0.048	0.035	0.101	0.054	0.14	0.075	0.187
MSE: gamma	-	0.438	0.006	0.020	0.016	0.050	0.026	0.084	0.042	0.114
RE	-	1.067	2.890	3.121	2.351	2.662	2.030	2.036	1.701	1.780

Table 15.

Simulation results: empirical mean (standard error), mean squared error ×100 (MSE) and the relative efficiency (RE) of the dependence parameter, the regression coefficient and the marginal hazard function estimates with τ = 0.33 and 60%-80% censoring rate.

			Λm(0.05)		Λm(0.1)		Λm(0.15)		Λm(0.2)
	θ	βm	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l	Z=0	Z=l
True frailty distribution: gamma
True value	1.25	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
mean(SE): gamma	1.260(0.304)	0.702(0.091)	0.049(0.007)	0.100(0.013)	0.099(0.012)	0.200(0.021)	0.149(0.018)	0.3(0.033)	0.198(0.024)	0.398(0.048)
True frailty distribution: inverse Gaussian (IG)
True value	8.5	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
mean(SE): IG	8.450(2.220)	0.686(0.094)	0.050(0.008)	0.099(0.014)	0.102(0.015)	0.201(0.028)	0.151(0.023)	0.299(0.040)	0.188(0.028)	0.373(0.052)
mean(SE): Gamma	-	0.695(0.098)	0.050(0.007)	0.099(0.013)	0.097(0.013)	0.194(0.023)	0.142(0.019)	0.285(0.032)	0.186(0.024)	0.371(0.041)
MSE: IG	-	0.888	0.006	0.019	0.022	0.078	0.053	0.160	0.092	0.343
MSE: gamma	-	0.960	0.005	0.017	0.017	0.056	0.042	0.125	0.077	0.252
RE	-	0.920	1.306	1.159	1.331	1.482	1.465	1.562	1.361	1.608
True frailty distribution: positive stable (PS)
True value	0.63	0.693	0.05	0.1	0.1	0.2	0.15	0.3	0.2	0.4
mean(SE): PS	0.641(0.036)	0.700(0.083)	0.050(0.008)	0.101(0.015)	0.101(0.013)	0.202(0.025)	0.150(0.018)	0.302(0.036)	0.200(0.022)	0.402(0.048)
mean(SE): gamma	-	0.719(0.092)	0.042(0.007)	0.086(0.015)	0.075(0.013)	0.155(0.028)	0.105(0.019)	0.216(0.041)	0.132(0.025)	0.271(0.055)
MSE: PS	-	0.693	0.006	0.024	0.019	0.062	0.035	0.129	0.052	0.239
MSE: gamma	-	0.914	0.011	0.043	0.079	0.283	0.238	0.879	0.524	1.965
RE	-	0.814	1.306	1.039	1.126	0.768	0.979	0.741	0.831	0.793

These results suggest that, only in cases of moderate dependence, using the gamma frailty model with models (8) and (9) can serve as a good practical choice in real data analysis if the marginal parameters are of primary interest, since the “price” to pay in terms of bias could be substantial under strong dependence.

6. Example - A case-control family study of breast cancer

We now apply the above two models and methods of estimation, to the breast cancer study mentioned in the Introduction. Various risk factors were measured on probands and their relatives. For illustrative purposes we consider age at first fullterm pregnancy as the covariate and the relatives of the probands being the mothers. The covariate takes the value of 1 if a women experienced first live birth before age 20, and 0 otherwise. The following analysis is based on 437 breast cancer case probands matched with 437 control probands and a total of 874 mothers. The number of mothers who had breast cancer was 70 among the case families and 35 among the control families. The number of women whose first live birth occurred before age 20 was 142 among the probands and 181 among the mothers. For estimating the standard errors, we used the bootstrap approach using case-family and its matched control-family as the sampling unit, and 200 bootstrap samples.

Tables 17 and 18 summarize the results of the parameter estimates for each frailty distribution under the conditional and marginal modeling, respectively. In Table 17, the regression coefficient $\widehat{{\beta }^c}$ describes the effect of age at full-term pregnancy conditional on the family frailty variate. Therefore, this model allows for the comparison of the breast cancer risks of women in the same family. Specifically, our results imply that women who had first full-term pregnancy before age 20, has about half the risk of developing breast cancer, compared with her relative without full-term pregnancy before age 20. The estimated regression coefficients under the various frailty distributions are very similar except for the positive stable distribution which yielded a slightly higher covariate effect. In Table 18, the regression coefficient $\widehat{{\beta }^m}$ describes the effect of age at full-term pregnancy in the general population, and therefore is expected to be lower than $\widehat{{\beta }^c}$. The results are also very similar for all the distributions and the covariate effect is indeed slightly lower from the one we observed for the conditional modeling. The cumulative baseline hazard estimates are similar under all the distributions, and are also similar to the results of the conditional modeling.

Table 17.

Analysis of a case-control family study of breast cancer under the conditional modeling

	Gamma		Inverse Gaussian		Positive Stable		Discrete
	estimate	Bootstrap SE	estimate	Bootstrap SE	estimate	Bootstrap SE	estimate	Bootstrap SE
${\widehat{\beta }}^C$	-0.484	0.216	-0.485	0.226	-0.595	0.247	-0.477	0.203
$\widehat{\theta }$	0.889	0.443	1.835	0.924	0.984	0.006	0.947	0.216
${\widehat{\Lambda }}_0^C\left(40\right)$	0.005	0.002	0.005	0.002	0.002	0.001	0.005	0.002
${\widehat{\Lambda }}_0^C\left(50\right)$	0.023	0.006	0.023	0.005	0.016	0.008	0.023	0.005
${\widehat{\Lambda }}_0^C\left(60\right)$	0.051	0.010	0.050	0.009	0.044	0.016	0.050	0.009
${\widehat{\Lambda }}_0^C\left(70\right)$	0.095	0.016	0.095	0.016	0.097	0.026	0.092	0.016
${\widehat{\Lambda }}_0^m\left(40\right)$	0.005	0.002	0.005	0.002	0.002	0.002	0.005	0.002
${\widehat{\Lambda }}_0^m\left(50\right)$	0.023	0.005	0.022	0.006	0.017	0.008	0.022	0.005
${\widehat{\Lambda }}_0^m\left(60\right)$	0.049	0.009	0.049	0.009	0.046	0.016	0.048	0.009
${\widehat{\Lambda }}_0^m\left(70\right)$	0.090	0.016	0.091	0.016	0.100	0.027	0.087	0.016

Table 18.

Analysis of a case-control family study of breast cancer under the marginal modeling

	Gamma		Inverse Gaussian		Positive Stable
	estimate	Bootstrap SE	estimate	Bootstrap SE	estimate	Bootstrap SE
${\widehat{\beta }}^m$	-0.470	0.187	-0.471	0.182	-0.554	0.182
$\widehat{\theta }$	0.970	0.444	2.058	0.936	0.986	0.006
${\widehat{\Lambda }}_0^m\left(40\right)$	0.004	0.002	0.004	0.002	0.001	0.001
${\widehat{\Lambda }}_0^m\left(50\right)$	0.021	0.005	0.020	0.006	0.015	0.006
${\widehat{\Lambda }}_0^m\left(60\right)$	0.046	0.008	0.046	0.009	0.045	0.010
${\widehat{\Lambda }}_0^m\left(70\right)$	0.085	0.014	0.085	0.015	0.098	0.014

In both tables, we can not compare the estimates of the dependence parameter θ directly because they quantify differently the risk among families for each distribution. However, we can see that under both models, the estimates of θ correspond to moderate dependency between paired failure times and therefore, the results provided by the marginal model can also be regarded as reliable results.

7. Discussion

In this work, we focused on case-control family setting and considered the two estimation procedures of [3] under the family specific proportional hazards functions, and of [5] under the population averaged proportional hazards functions. We presented these estimation procedures for different frailty distributions, such as inverse Gaussian, positive stable and a specific case of a discrete distribution.

We showed, by simulations, that when the conditional hazard function follows a Cox proportional hazards model multiplied by the frailty variate, the gamma frailty model appears to be robust to frailty distribution misspecification in terms of bias and efficiency loss in the marginal parameters. Considering the mathematical convenience of the gamma distribution, we conclude that the gamma frailty can be a useful choice in a real data analysis when the marginal parameters are of primary interest and the true underlying distribution is unknown.

However, in the population-averaged proportional hazard model, our results suggest that, only in cases of moderate dependence, the gamma frailty model could serve as a useful choice, if the true frailty distribution is unknown, since the “price” to be paid in terms of bias could be too high. Another disadvantage of this modeling approach is the lack of unique representation of the baseline function α(·) under some frailty models, such as the discrete model discussed in this work.

The main difference between the conditional and the marginal modeling, in terms of the frailty distribution, is that for the same strength of Kendall's τ, the marginal modeling requires higher variability of the frailty variate in compare to that of the conditional model. This explains the observation that the marginal modeling was found to be robust to the gamma frailty model misspecification only under moderate or weak dependency, since under very high variance of the frailty distribution, the effect of frailty distribution misspecification is not expected to be negligible. In our real data analysis we found that both models provide similar results. This is due to the fact that the dependence within family, given the age at first full term pregnancy, is moderate. These results indicate that when analyzing data of this type, both models are expected to be robust.

This work is concentrated on estimation of the marginal parameters. It is of practical importance to investigate the performances of hypothesis testing and confidence intervals under misspecification of the frailty distribution. However, this is beyond the scope of this work.

Obviously, the ideal situation is when the frailty distribution is known. However, since the frailty variates are unobservable, it is difficult to extract information from the observed data about the underlying frailty distribution. There are tests and graphical procedures for checking the dependence structure for cohort data [18–22]. These procedures, however, are not directly applicable to the case-control family data, and extension of these procedures to our setting is a potential problem for future work.

While this work is mainly concerned about the regression coefficients and marginal hazard functions, the dependencies among failure times sometimes are of interest in family studies. In these cases, an approximated correct frailty distribution is crucial in obtaining unbiased estimates of these quantities and assuming a gamma distribution, when it is not, can yield misleading results.