Optimization-based Reconstruction of Sparse Images from Few-view Projections

Abstract

In this work, we investigate optimization-based image reconstruction from few-view (i.e., <10 views) projections of sparse objects such as coronary-artery specimens. Using optimization programs as a guide, we formulate constraint programs as reconstruction programs and develop algorithms to reconstruct images through solving the reconstruction programs. Characterization studies are carried out for elucidating the algorithm properties of “convergence” (relative to designed solutions) and “utility” (relative to desired solutions) by using simulated few-view data calculated from a discrete FORBILD coronary-artery phantom, and real few-view data acquired from a human coronary-artery specimen. Study results suggest that carefully designed reconstruction programs and algorithms can yield accurate reconstructions of sparse images from few-view projections.

I. Introduction

In computed tomography (CT) imaging, projections are acquired typically at a large number (300-1000) of angular views from the imaged object. Such densely sampled projection data are required by current analytic-based algorithms for yielding accurate reconstruction of the imaged object. In CT imaging of biological specimens considered in this work, data collection at a large number of projection views may limit system throughput, and may result in radiation-induced object deformation. It is thus of practical interest to develop imaging techniques capable of yielding accurate reconstructions from projection data acquired at less than 10 views, which we refer to as few-view data.

Conventional, analytic-based algorithms such as the FDK algorithm [1] are not suitable for image reconstruction from few-view data [2], because they are derived from a continuous imaging model and implicitly assume densely sampled projections over the scanning angular range. In recent years, sparse-view image reconstruction has been investigated with the guide of different optimization-program formulations some of which use an image total variation (TV) constraint [3-9]. The investigation suggests that optimization-based reconstruction employing discrete imaging models can be, in general, more effective than analytic-based reconstruction in dealing with sparsely sampled projections.

Despite the fact that previous works exist [10-13] on image reconstruction from few-view projections for objects with sparse structures such as coronary-artery specimens [14], this problem of practical significance remains largely unexplored. In particular, because extremely few data are available in the present few-view problem, they generally lead to a reconstruction problem with a high degree of under-determinedness that may require considerations different from those for sparse-view reconstruction problems involving projection views substantially more than 10.

Optimization programs and algorithms can be developed for addressing the reconstruction problem. Such formulations are useful, because they succinctly describe a design for specifying a particular reconstructed image, and because a number of algorithmic tools are available to solve such problems. However, due to the large scale of CT systems, a number of theoretical and practical issues in the development of optimization programs and algorithms may not be always practically addressable. For example, for an optimization program involving a number of constraints of practical interest, it can be challenging, if not impossible, to characterize the solution set specified by the optimization program.

Additionally, in a practical scenario of solving an optimization problem, even if an algorithmic solver is available, issues of practical implication can be identified: (a) because the algorithm generally takes infinite, instead of finite, iterations to converge truly to the optimization solution, it cannot achieve the solution, as only finite iterations can be performed in practice; and (b) because of limited computer numerical precision, the algorithm cannot be guaranteed to achieve the optimization solution in a realistic, practical study. Also, with current computational technology and demands of practical CT application, iterative reconstruction algorithms are often desired to be truncated at iteration numbers on the order of 10 – well short of convergence to the solution set specified by the optimization program.

Some research efforts in iterative image reconstruction do a better job in terms of converging a particular program, but even in these cases there can be choices of optimization programs of interest where numerical convergence is not practical. While true convergence is probably not necessary from a utility viewpoint, one is left with the problem as to how one would talk about algorithms that do not converge the problem that they are designed to solve, and as to how one would characterize the resulting reconstructions.

We have found it useful to employ a set-theoretic picture [15] of iterative image reconstruction as a process of finding an image in the intersection of multiple sets, defined by various image properties. This view leads to a practical algorithmic approach to solving constraint programs, which are designed with the guide of optimization programs. Throughout the paper, we also refer to a constraint program as a reconstruction program and use both interchangeably for presentation convenience. The various constraints involved specify the “borders” of the various descriptive sets. An algorithm solving a reconstruction program consists of “projection” operations onto some of these sets, and the final reconstruction is described by constraints specifying the sets that it belongs to. Furthermore, as the constraints can be non-convex, the sets are not necessarily convex, thus the approach is more general than convex optimization. Nevertheless, we still refer to a constraint reconstruction as optimization-based, because they are designed with a particular optimization program in mind.

It is often the case that metrics describing the utility of an image are not the same as quantities formulated in a mathematical imaging model and program [16]. Because of this dichotomy, we make a clear distinction in the work between desired and designed solutions (i.e., the desired and designed reconstructions.) The concepts of desired and designed solutions takes an added level of importance in the development of reconstruction programs and algorithms of task-based value: it is possible, and often the case, that the set of images satisfying the designed reconstruction program (i.e., a constraint program) have similar desirability for the particular imaging task [7, 8].

In this work, we focus on investigating and characterizing optimization-based reconstruction from few-view projections for sparse objects such as coronary-artery specimens. Using optimization programs as guides, we formulate reconstruction programs that specify solutions with designed properties. We then describe algorithms to solve the reconstruction programs through achieving numerically the designed solutions (i.e., reconstructions.) Using simulated- and real-data, we carry out quantitative studies to validate and characterize properties of the designed solutions and algorithms.

The paper is organized as follows. We discuss the design of optimization-based reconstructions from few-view data in Sec. II, followed by the presentation of experimental designs and quantitative studies involving simulated and real data in Secs. III, IV, and V. Final discussion and remarks are given in Sec.VI.

II. Reconstruction programs and algorithms

A. Imaging model and data divergence

A linear system is used often for modeling the CT-imaging process and can be written as

$${\text{g}}_0=\mathcal{H}\mathbf{f},$$ (1)

where g₀ denotes the model-data vector of size M that expand the data function, f the image vector of size N that expand the underlying image function, and the M-by-N matrix $\mathcal{H}$ models the discrete X-ray transform, which depends upon the choice of basis functions for expanding data and image functions and of schemes for computing the discrete X-ray transform. In this work, we use M pixels and N voxels to expand the data and image functions, and the intersection length of an X-ray with an image voxel to represent an element of system matrix $\mathcal{H}$.

We denote g the measured data in a simulated- or real-data study and consider

$$D\left(\mathbf{f}\right)=\mid \mathcal{H}\mathbf{f}-\text{g}\mid ∕M,$$ (2)

i.e., the average Euclidean data divergence per detector pixel between measured data and imaging model, in the formulation of optimization/constraint programs below. The data divergence can be zero only in a simulation study in which “data” are generated by use of the imaging model. Simulated data can also be generated with components inconsistent with the imaging model, and measured data in a real-data study unavoidably contain inconsistencies with respect to the imaging model. In these situations, the data divergence necessarily are non-zero. Other forms of data divergence can also be used in the design of optimization-based reconstructions.

B. Reconstruction programs and designed solutions

With the imaging model and data divergence defined, reconstruction (i.e., constraint) programs and algorithms can be designed. We discuss four reconstruction programs below that are formulated based upon optimization programs, as described in Appendix A.

1) Reconstruction program 1

Considering the data divergence and image positivity, we design reconstruction program 1 in Appendix A as

$$D\left(\mathbf{f}\right)\le ∊\text{and}{f}_j\ge 0,$$ (3)

where ∊ > 0 is a selected parameter for accommodating possible inconsistency between data and imaging model, and f_j indicates the value at voxel j of image f, and j = 1, 2, …, N. This reconstruction program specifies a convex set of solutions. For a few-view data set, it is highly likely that reconstruction program 1 can be satisfied by multiple solutions, and additional constraints can be used to reduce the solution space.

2) Reconstruction program 2

In an attempt to narrow the solution space of reconstruction program 1, we add an imagesparsity constraint to Eq. (3), thus obtaining reconstruction program 2 in Appendix A as [17]:

$$D\left(\mathbf{f}\right)\le ∊,f_j\ge 0,\text{and}{\parallel \mathbf{f}\parallel }_0\le s,$$ (4)

where ∥f∥₀ denotes the l₀-norm of the image, and sparsity parameter s is the number of non-zero voxels imposed on the image. Because of the image-sparsity constraint, this program specifies a non-convex set of solutions that is likely to be tighter than that specified by reconstruction program 1.

3) Reconstruction program 3

For an image with a high degree of sparsity, such as those under consideration, its discrete gradient magnitude image is likely to be sparse. The l₁-norm of the gradient magnitude image (or, equivalently, the total variation (TV) of the image) has been exploited as a sparsity constraint for potentially narrowing the solution space. By incorporating the TV constraint in program 2, we form in Appendix A reconstruction program 3

$$D\left(\mathbf{f}\right)\le ∊,{\parallel \mathbf{f}\parallel }_{TV}\le t_0,f_j\ge 0,\text{and}{c}_{\alpha }\left(\mathbf{f}\right)\le \gamma ,$$ (5)

where ∥f∥_TV denotes the image TV (see, e.g., Eq. (9) of Ref.[5]), parameter t₀ constrains TV of the reconstructed image, c_α(f) is defined below, and γ is a negative number larger than −1 discussed below. Reconstruction program 3 determines a non-convex set of solutions because constraint c_α(f) ≤ γ can be non-convex.

4) Reconstruction program 4

Finally, an image with a small TV may not be sparse. Therefore, including a sparsity constraint in Eq. (5), we arrived in Appendix A at reconstruction program 4 [18]

$$D\left(\mathbf{f}\right)\le ∊,{\parallel \mathbf{f}\parallel }_{TV}\le t_0,f_j\ge 0,{\parallel \mathbf{f}\parallel }_0\le s,\text{and}{c}_{\alpha }\left(\mathbf{f}\right)\le \gamma ,$$ (6)

which specifies a non-convex set of solutions due to the non-convex sparsity and c_α f) ≤ γ constraints. Again, because of the sparsity constraint, the set of solutions is likely to be tighter than that specified by reconstruction program 3.

In Eqs. (5) and (6), c_α(f) is given by

$$c_{\alpha }\left(\mathbf{f}\right)=\frac{{\mathbf{d}}_{TV}\cdot {\mathbf{d}}_{data}}{\mid {\mathbf{d}}_{TV}\mid \mid {\mathbf{d}}_{data}\mid },$$ (7)

${\mathbf{d}}_{TV}={\stackrel{‒}{\nabla }}_{\mathbf{f}}{\parallel \mathbf{f}\parallel }_{TV}$, ${\mathbf{d}}_{data}={\stackrel{‒}{\nabla }}_{\mathbf{f}}{D}^2\left(\mathbf{f}\right)$, and ${\stackrel{‒}{\nabla }}_{\mathbf{f}}$ indicates a gradient operator that excludes zero elements of f [5]. A heuristic algorithm, referred to as the adaptive steepest-descent and projection-onto-convex-set (ASD-POCS) algorithm [3], has been developed for solving a related optimization program specified by Eq. (11) in Appendix A. It can be shown [3] that c_α(f) = −1 provides a necessary condition on the convergence of the ASD-POCS algorithm when it is applied to solving the optimization program. Despite the fact that it may be challenging to achieve this condition precisely, previous studies [7, 8] indicate that ASD-POCS reconstructions with c_α(f) in the range (−1.0, −0.5] often show insignificant visual differences. Therefore, parameter γ is selected in this range in the numerical studies below.

5) Designed solutions

As discussed above, each of the reconstruction programs in Eqs. (3)-(6) specifies a set of solutions, which we refer to as the “designed solutions” determined by the reconstruction program. While reconstruction program 1 specifies a convex set of solutions, reconstruction programs 2-4 yield non-convex sets due to non-convex constraints ∥f∥₀ ≤ s and c_α(f) ≤ γ. Because the constraints in Eqs. (3)-(6) are explicit, they can be used for monitoring and guiding an algorithm to reach numerically a designed solution, and a final reconstruction of an algorithm would necessarily be a designed solution as long as it satisfies the constraints. The properties of the solution set specified by a reconstruction program relies upon numerous factors involved in the formulation of the program. For example, in general, the tighter the constraints, the tighter the solution set. When the constraints are too tight, it is possible that they have no intersection, thus resulting in an empty set. In this case, the constraints can be relaxed so that a tight but non-empty set of solutions can be designed.

6) Program-specification parameters

The complete specification of reconstruction programs in Eqs. (3)-(6) involves not only explicit parameters (i.e., ∊, t₀, s, and γ) on the right-hand sides of the inequalities but also implicit attributes such as the basis sets spanning the image and data spaces and the calculation method for system matrix $\mathcal{H}$. We refer to these parameters and attributes as program-specification parameters. Selections of different program-specification parameters necessarily lead to different sets of solutions (or, equivalently, designed solutions.) As mentioned above, we employ voxels and pixels to span the image and data spaces, and the intersection lengths of X-rays with image voxels to model the elements of system matrix $\mathcal{H}$. The adequate selection of parameters, such as ∊, t₀, s, and γ, is reconstruction-task specific and can be determined adaptively, as discussed in the real-data studies below.

7) Physical interpretation of constraints

In reconstruction programs 1-4, two types of constraints are considered. The first type is based directly upon the expected physical properties of designed solutions, such as positivity (i. e. f_j ≥ 0), sparsity(i.e., ∥f∥₀ ≤ s), and gradient sparsity (i.e., ∥f∥_TV ≤ t₀). On the other hand, the second type of constraints concerns he properties of the transforms of designed solutions: data-divergence constraint D(f) ≤ ∊ represents a physical “distance” of a designed solution relative to data measurements, whereas constraint c_α(f) ≤ γ reflects a property unique to the specific design of reconstruction programs 3 and 4. Of course, additional reconstruction programs can be designed that may include constraints of both types differing from those discussed.

C. Algorithms for reconstruction programs

Once designed solutions are specified by reconstruction programs in Eqs. (3)-(6), algorithms are needed to solve the reconstruction programs for achieving the designed solutions. We focus on investigating heuristic algorithms for image reconstruction through solving numerically the reconstruction programs with finite iteration numbers. Some of the constraints in each of the programs are used also for monitoring and adjusting the algorithm behavior, as demonstrated in the numerical studies in Sec. IV.

1) P-POCS algorithm for reconstruction program 1

The projection-onto-convex-set (POCS) algorithm can minimize the data divergence in Eq. (2) in the absence of data inconsistencies. For reconstruction program 1, we use a variant of the POCS algorithm, referred to as the P-POCS algorithm, in which the positivity constraint is imposed by setting negative voxel values to zero in the reconstruction at a particular POCS iteration. This algorithm is not intended for obtaining reconstruction of practical utility. Instead, we use it only for the purpose of demonstrating reconstruction differences from different algorithms.

2) IT-P-POCS algorithm for reconstruction program 2

We consider another variant of the POCS algorithm in which, following the exercise of the positivity constraint, an iterative thresholding (IT) technique is applied to setting all voxel values to zero except for a given number of voxels with the largest values in the reconstruction at a particular POCS iteration [17, 19]. As the image sparsity is a non-convex constraint, in an attempt to avoid being trapped outside the solution set, we start out with a large sparsity number and then reduce it gradually to the preset sparsity parameter s as iteration number increases. Again, we are not proposing the IT-P-POCS as an algorithm for yielding image reconstruction of practical utility. Instead, it is used only for estimating sparsity parameter s in the absence of truth in a real-data study [17].

3) ASD-POCS algorithm for reconstruction program 3

The ASD-POCS algorithm [5] was developed previously for solving optimization program 3 in Eq. (11). As reconstruction program 3 is derived based upon the optimization program defined in Eq. (11) of Appendix A, the ASD-POCS is also chosen as the algorithm for achieving the set specified by reconstruction program 3. The algorithm uses steepest descent (SD) for lowering image TV, and the POCS for reducing the discrepancy between data and imaging model, along with the enforcement of the positivity constraint after the TV and POCS steps at an iteration. The balance between the reductions of image TV and data divergence is maintained by adaptive adjustment of relative reduction-step sizes. Implementation details and pseudo code of the ASD-POCS algorithm can be found in [5]. Clearly, one can replace SD and POCS with other methods in the ASD-POCS for achieving desired computational efficiency and accuracy, and previous studies [5, 7, 8] indicate that the ASD-POCS algorithm solves numerically the optimization program specified by Eq. (11) in Appendix A. and that c_α(f) = −1 provides a necessary condition on its convergence. We select parameter γ in the range (−1.0, −0.5] in numerical studies. When the ASD-POCS algorithm is applied to solving reconstruction program 3, the constraints on data divergence, image TV, and c_α(f) are computed following the execution of the positivity constraint at an iteration.

4) IT-ASD-POCS algorithm for reconstruction program 4

For reconstruction program 4, we consider a heuristic algorithm, which is referred to as the iterative thresholding (IT)-ASD-POCS algorithm because it combines the IT technique [19] with the ASD-POCS algorithm. In terms of implementation, the IT-ASD-POCS is identical to the ASD-POCS only with an additional exercise of setting all image-voxel values to zero except for the s voxels with the largest values [17, 19]. When the IT-ASD-POCS algorithm is used for solving the optimization program specified by Eq. (12) in Appendix A, it can be shown that c_α(f) = −1 also provides a necessary condition on its convergence, and we select γ ∈ (−1.0, −0.5] in numerical studies. Similar to the IT-P-POCS algorithm, one can start out with a large sparsity parameter and then shrink it gradually to the preset s as iteration number increases.

The ASD-POCS and IT-ASD-POCS algorithms are the focus of numerical reconstruction studies in the work. As discussed above, they are not established as mathematic solvers for reconstruction programs 3 and 4. However, the constraints themselves in the programs can be exploited as necessary conditions for monitoring and validating numerically the convergence of the algorithms to their respective sets. In particular, conditions

$$D\left(\mathbf{f}\right)\le ∊,{\parallel \mathbf{f}\parallel }_{TV}\le t_0,\text{and}{c}_{\alpha }\left(\mathbf{f}\right)\le \gamma$$ (8)

are used for assessing numerically the convergence properties of the ASD-POCS and IT-ASD-POCS algorithms. The first condition has been used widely for validating algorithm convergence, whereas the third condition has been shown to provide a sensitive check on the ASD-POCS and IT-ASD-POCS convergence [7, 8].

5) EM algorithm

Variants of the expectation maximization (EM) algorithm have been used for image reconstruction. In the work, we also perform reconstructions by using the generic EM algorithm, with the intention of demonstrating reconstruction differences of different algorithms. The EM algorithm is a mathematic solver for an optimization program in which the Kullback-Leibler (KL) divergence is minimized.

6) Algorithm-specification parameters

Numerical properties of algorithms depend upon not only explicit parameters such as step sizes of the SD or POCS used in algorithm design and implementation but also implicit attributes such as the order of enforcement of different constraints. Moreover, some of the algorithm components such as the SD and POCS can be replaced with other methods/schemes for enhanced computation accuracy and efficiency [7, 8]. We refer to these parameters, attributes, and selections of methods/schemes as algorithm-specification parameters, which differ fundamentally from program-specification parameters. Any change in program-specification parameters would necessarily result in different reconstruction programs (or, equivalently, designed solutions). Conversely, algorithm-specification parameters can affect the numerical performance of algorithms and thus the selection of a specific solution within the set, but they have no effect on the specification of designed solutions.

III. Quantitative study design

We focus on characterizing the performance of the ASD-POCS and IT-ASD-POCS algorithms in image reconstruction from few-view data. The P-POCS and EM algorithms are also considered for demonstrating reconstruction differences. As the IT-P-POCS algorithm yields reconstructions comparable to the P-POCS reconstruction, we use it to estimate sparse parameter s only in the real-data study below. We generated simulation data from a discrete FORBILD coronary-artery phantom [20] and acquired real data from a human coronary-artery specimen.

In the studies, we validate whether the algorithm for a reconstruction program under consideration can achieve a designed solution determined by the reconstruction program, and how “different” a designed solution numerically achieved is than a “desired” solution of particular utility. Therefore, the studies have two purposes: (a) to numerically demonstrate, in terms of necessary conditions in Eq. (8), that the ASD-POCS and IT-ASD-POCS algorithms can achieve numerically the designed solutions of reconstruction programs in Eqs. (5) and (6); and(b) to quantitatively assess differences between the designed solutions achieved numerically and desired solutions.

For purpose (b), desired solutions are needed. In the simulated-data study, the desired solution is the (known) truth image that is used to generate the data. In the real-data study, however, the “truth” image is generally unknown. Instead, because the FDK image reconstructed from data collected at a large number of views is used generally in current practical applications, we use the FDK reconstruction as the “desired” solution and refer to it and the data as the FDK-reference image and full data, respectively. One can select an image obtained with an algorithm other than the FDK as the desired solution, and different “desired” images can result in different “distances” between the designed and “desired” reconstructions.

A. Simulated-data Study

1) Rationale

We first carried out a simulation study in which the imaging model in Eq. (1) is used for data generation and in the reconstruction programs/algorithms. This constitutes an inverse-crime study [21-23] that permits the characterization of the reconstruction programs and algorithms in the absence of data inconsistencies except for computer precision error. Under certain data condition, if a reconstruction program and algorithm are appropriately designed, they should lead to an exact recovery (within computer precision) of the desired solution (i.e., the discrete truth image that yields the data.) Therefore, the value of an inverse-crime study lies in that it can be used for verifying how well the designed solution determined by a reconstruction program agrees with the desired solution, and to validate whether the algorithms can achieve the designed solution. It is not unreasonable to assume that, if a reconstruction program and algorithm fail to perform in an inverse-crime scenario, it is unlikely that they would perform well in studies in which data contain inconsistencies. Because real-data studies are performed below in which the measured data are necessarily inconsistent with the imaging model, we consider in the work no study using simulated data containing inconsistencies.

2) Study setup and data

The discrete FORBILD coronaryartery phantom [20] mimics the blood-vessel branches and is represented by a 256×256×256 array of voxels each of which has a size of 82 m. In the generation of simulated data, a flat-panel detector, composing of 512×512 pixels each of which with a size of 41 m, was used to collect data from a source over a circular scanning trajectory identical to that used in the real-data study below. Using the scanning information described above, we calculated the system matrix $\mathcal{H}$ and generated data from the phantom at a total of 721 views. In the inverse-crime study, the exactly same system matrix $\mathcal{H}$ is also used in the imaging model, reconstruction program, and algorithm. This 721-view data are referred to as the full data from which few-view data sets are extracted. The FORBILD coronary-artery phantom has sparse structures. For example, among the total 65,535 pixels within the central, transverse slice, only 671 have non-zero values, i.e. ∥f∥₀ = 671.

B. Real-data Study

1) Rationale

We also carried out a real-data study to demonstrate and characterize reconstruction programs 3 and 4 and the associated ASD-POCS and IT-ASD-POCS algorithms. Unlike the simulated-data study in which data are consistent with the imaging model, the measured data in the real-data study contain physical factors and thus are generally inconsistent with any imaging model. Therefore, the real-data study provides an characterization of the robustness and utility of reconstruction programs and algorithms under realistic imaging conditions.

Again, in the study, we first demonstrate numerically that, in terms of necessary conditions described in Eq. (8), the ASD-POCS and IT-ASD-POCS reconstructions yield numerically solutions within the sets determined by reconstruction programs 3 and 4. Secondly, using the FDK-reference image as the desired solution, we show that the ASD-POCS and IT-ASD-POCS reconstructions indeed converge to the desired solution, in terms of some measure of the discrepancy between the reconstructions and desired solution. We also employ visual inspection of reconstruction details for assessing the reconstruction programs and algorithms.

2) Study setup and data

Using a custom made micro cone-beam CT scanner [24], data were acquired from a human coronary-artery specimen with a circular scanning geometry. The flat-panel detector in the micro-CT system consists of 1024×673 square bins of size 20.5 m. The distances from the source to the system center of rotation and to the detector surface are 59.7 cm and 61.0 cm. Additional details for the micro-CT system can be found in Ref. [24]. The image is represented by a 512×300×272 array of cubic voxels each of which has a size of 41 m. For the given scanning geometry and detector and image arrays, we calculate the system matrix and use it in the imaging model, reconstruction program, and reconstruction algorithm. In the study, full data were acquired at 721 views from which few-view data sets were extracted. The FDK-reference image reconstructed from the full-data set is used as the desired solution in the characterization of the reconstruction programs and algorithms when they are applied to reconstructing images from the few-view data sets.

IV. Results of simulated-data study

In this inverse-crime study, we first perform image reconstruction from a 4-view data set. The 4-view case is selected as a focused study, because it represents a severely under-sampling situation, which can thus provide a challenging test of the programs and algorithms. We use this case study to illustrate the validation of algorithm convergence and characterization of reconstruction accuracy with respect to the desired solution(i.e., the known truth image in this case.) We also show results of studies on other few-view cases, including cases with view numbers ranging from 3 to 9. In the simulated-data study, 2D and 3D reconstructions have been performed. For the sake of illustrating the study in detail, including experimental design, parameter selection, and convergence analysis, 2D results are presented, while similar results and observations can be made for 3D reconstructions.

A. A focused case study: 4-view reconstruction

As displayed in Fig. 1, a 4-view data set was extracted from the full-data set at angles 0°, 72°, 144°, and 216°, which were selected to avoid forming conjugate views. For the purpose of illustration, we show in Fig. 2 the central, transverse slice of the FORBILD phantom, with zoomed-in views of two selected square-shaped regions of interest (ROIs).

Figure 1.

Projection images of the FORBILD phantom at (a) 0°, (b) 72°, (c) 144°, and (d) 216°, respectively.

Figure 2.

(a) Truth image and (b) 4-view FDK reconstruction within a transverse slice of the FORBILD phantom. The square regions enclosed by dotted lines are re-displayed in a zoomed-in view in the corresponding square regions enclosed by solid lines. Display window: [0, 1] cm⁻¹.

1) Selection of reconstruction-program parameters

In the inverse-crime study, data and imaging model are completely consistent, and thus data divergence should be mathematically zero. However, we choose ∊ = 5×10⁻⁷ in the study for practical reasons to be discussed below. Also, the central slice of the FORBILD phantom has ∥f∥_TV = 483.78 and ∥f∥₀ = 671, which are selected as the TV parameter t₀ and the sparsity parameter s. Finally, we choose γ = −0.99 so that it is close to −1 but remains numerically achievable within a finite number of iterations. With data and imaging model described and parameters ∊, t₀, s, and γ selected, reconstruction programs 3 and 4 in Eqs. (4) and (5) (or, equivalently, designed solutions) are completely determined. Images are reconstructed through solving the two programs by use of the ASD-POCS and IT-ASD-POCS algorithms, respectively.

2) Algorithm convergence

We first determine whether the algorithms are achieving the corresponding sets of designed solutions by validating their convergence based upon the necessary conditions in Eq. (8). In Fig. 3, we show D(f) and c_α(f) as functions of iteration numbers for the ASD-POCS and IT-ASD-POCS algorithms. As it can be observed, both algorithms satisfy numerically the conditions in Eq. (8), suggesting that the algorithms are converging numerically to the designed solutions specified by reconstruction programs 3 and 4.

Figure 3.

Parameters D(f) (top) and c_α(f) (bottom) as functions of iteration numbers for ASD-POCS (solid curve) and IT-ASD-POCS (dashed curve) algorithms for reconstructions from the 4-view data set.

3) Designed solutions relative to desired solutions

Having shown that the algorithms converge to the designed solutions, we turn our attention to characterization of the “distances” of the designed solutions to the desired solution (i.e., the FORBILD phantom image). The significance of this characterization lies in that it reveals whether the reconstruction programs are adequately designed to yield solutions close to the desired solution.

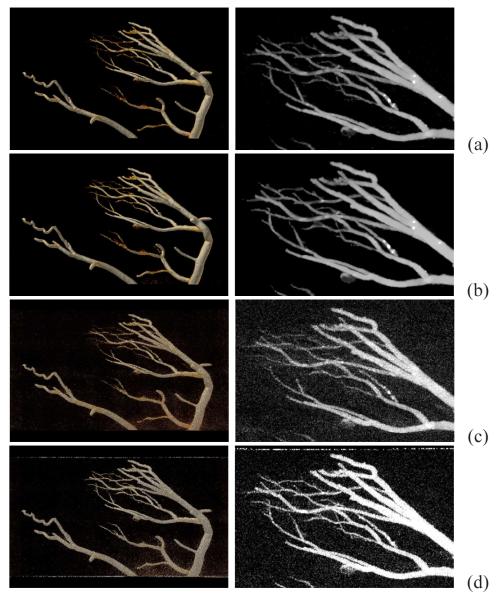
We first carried out visual inspection of reconstructions in Fig. 4, and compare them to the desired solution displayed in Fig. 2a. In an attempt to reveal reconstruction details, zoomed-in views of selected ROIs are also included in Fig. 4. Clearly, under the display condition, little visual difference can be observed between the reconstructions and desired solution. We also display in Figs. 4c and 4d 4-view reconstructions obtained by use of the P-POCS and EM algorithms at iterations with D(f) reaching 5 × 10⁻⁷.

Figure 4.

Images within a transverse slice of the FORBILD phantom reconstructed, respectively, by use of (a) ASD-POCS, (b) IT-ASD-POCS, (c) P-POCS, and (d) EM algorithms from the 4-view data set. Square regions display the zoomed-in views of square-shaped ROIs defined in Fig. 2a. Display window: [0, 1] cm⁻¹.

For visualization of difference details between the reconstructions and desired solution, we show in Fig. 5 the corresponding absolute-difference images, which suggest that reconstruction programs 3 and 4 and the corresponding algorithms (i.e., ASD-POCS and IT-ASD-POCS) yield reconstructions close to the desired solution throughout the image space, whereas the P-POCS and EM reconstructions differ from the desired solution more significantly. We also calculated a similarity-based metric, the root-mean-square error (RMSE), between reconstructions and the desired solution within two ROIs defined in Fig. 2a. The results are shown in Tab. I, which further confirm quantitatively the observation that reconstruction programs 3 and 4 and the corresponding algorithms yield reconstructions close to the desired solution.

Figure 5.

Absolute-difference images between the truth image and (a) ASD-POCS, (b) IT-ASD-POCS, (c) P-POCS, and (d) EM reconstructions from the 4-view data set. RMSEs(×10⁻³) of these difference images are 8.3, 0.2, 31.6, and 37.7, respectively. Display window: [0, 0.1] cm⁻¹.

Table I.

RMSEs(×10⁻⁴) of forbild-phantom reconstructions

ROI	ASD-POCS	IT-ASD-POCS	P-POCS	EM
ROI 1	1.67	0.06	6.46	7.68
ROI 2	2.31	0.05	7.55	9.46

4) “Utility” of intermediate solutions

We show a plot of RMSEs, calculated over the entire image array, against c_α(f) for images at iterations reconstructed by use of the ASD-POCS and IT-ASD-POCS algorithms. This plot is interesting in that its abscissa and ordinate represent difference measures of a reconstruction at a particular iteration, respectively, from the designed and desired solutions. The designed solutions achieved numerically by the ASD-POCS and IT-ASD-POCS algorithms are indicated by points A (at iteration 219,500) and B (at iteration 155,000), with c_α(f) < γ, and RMSEs(×10⁻³) 8.3 and 0.2, respectively.

The discussion above focuses on reconstructions at numerically convergent points A and B in Fig. 6. If the hypothetic utility of a reconstruction is defined as inversely proportional to the RMSE relative to the desired solution, reconstructions at points between A and A’ (at iteration 80,000) or between B and B’ (at iteration 80,000) on the curves in Fig. 6 can be of some utility, even though they are not convergent (i.e., c_α(f) > γ.)

Figure 6.

Reconstruction RMSEs, as functions of c_α(f), obtained with ASD-POCS (solid curve) and IT-ASD-POCS (dashed curve) algorithms from the 4-view data set. The abscissa and ordinate of the plot represent differences of a reconstruction measured, respectively, from the designed and desired solutions. Two filled circles marked by A (at iteration 219,500) and B (at iteration 155,000) indicate the designed solutions, whereas the two open circles marked by A’ (at iteration 80,000) and B’(at iteration 80,000) indicate two intermediate solutions that have not reached the corresponding designed solutions.

B. Selection of ∊ in an inverse-crime study

The results shown above obtained by use of the ASD-POCS and IT-ASD-POCS algorithms represent the designed solutions determined by reconstruction programs 3 and 4 specified with parameter ∊ = 5 × 10⁻⁷ in Eqs. (4) and (5). In the inverse-crime study, ∊ should theoretically be set to 0, because data g generated are perfectly consistent with the imaging model, and because the imaging model is used for reconstruction. However, the choice of ∊ = 0 poses practical issues: (a) in general, an infinite number of iterations, and hence an infinite amount of time, is required for an algorithm to achieve ∊ = 0; (b) the convergence metric c_α(f) becomes undefined in this case and thus cannot be employed for checking algorithm convergence; and (c) because the numerical precision of any computer is limited, ∊ = 0 is practically unreachable. Instead, we study the asymptotic properties of the designed solutions determined by reconstruction programs 3 and 4 in Eqs. (4) and (5) with a descending series of ∊ from 5 × 10⁻⁷ down to 5 × 10⁻⁹. The trends of the results may reveal some properties of the designed solutions specified by ∊ = 0. In Fig. 8, we plot RMSEs of ASD-POCS and IT-ASD-POCS reconstructions as functions of ∊. For both algorithms, reconstructions with lower RMSEs are achieved for a smaller ∊. Also, reconstruction program 4 and the IT-ASD-POCS algorithm appear to yield reconstructions with RMSEs lower than those yielded by reconstruction program 3 and the ASD-POCS algorithm for the cases under study.

Figure 8.

Reconstruction RMSEs, as functions of parameter ∊, obtained with the ASD-POCS (Δ) and IT-ASD-POCS (○) algorithms from the 4-view data set.

C. Reconstructions from different view numbers less than 10

In addition to the 4-view study, we also investigated reconstructions from 3-, 5-, 7-, and 9-view data sets extracted from the full-data set, respectively, representing different levels of data under-sampling. In each case, the views are uniformly distributed over 2π. For each data set, in addition to ASD-POCS and IT-ASD-POCS reconstructions, we also include the P-POCS and EM reconstructions to demonstrate reconstruction difference. The study focuses on how varying degree of under-sampling impacts on reconstructions. For these data sets, values for total data divergence (i.e., m∊), t₀, s, and γ identical to those for the 4-view case were used, and both ASD-POCS and IT-ASD-POCS reconstructions satisfy numerically conditions in Eq. (8).

In an attempt to reveal differences in reconstructions relative to the desired solution, we show in Figs. 9 and 10 the absolute-difference images between the desired solution and ASD-POCS and IT-ASD-POCS reconstructions. From the difference images, we also calculated the RMSEs as functions of the view number, and display them in Fig. 11, along with the corresponding RMSEs of the P-POCS and EM reconstructions. The results indicate, as expected, that the algorithms yield increasingly accurate reconstructions as data at more views become available. Inspection of Fig. 11 also reveals that RMSEs appear to start flatting out as the view number increases, suggesting that, for the phantom under study, difference in algorithm performance (in terms of RMSE) diminishes as the view number grows. It can also be observed that difference in algorithm performance narrows for the 3-view data set, as the reconstruction task becomes equally challenging for all algorithms in 3-view case.

Figure 9.

Absolute-difference images between the truth image and ASD-POCS reconstructions, respectively, from (a) 3-, (b) 5-, (c) 7-, and (d) 9-view data sets. Display window: [0, 0.005] cm⁻¹.

Figure 10.

Absolute-difference images between the truth image and IT-ASD-POCS reconstructions, respectively, from (a) 3-, (b) 5-, (c) 7-, and (d) 9-view data sets. Display window: [0, 0.005] cm⁻¹.

Figure 11.

Reconstruction RMSEs, as functions of the view number, obtained by use of ASD-POCS (Δ), IT-ASD-POCS (○), P-POCS (+), and EM (*) algorithms, respectively.

Performance difference can, however, be identified for cases between 3- and 9-view cases. The results indicate that the IT-ASD-POCS outperforms ASD-POCS algorithm for all of the cases under study, though their difference varies as a function of the view number: it starts out small when view number is 3, grows larger at 5 views, then shrinks again beyond that. This reflects the fact that, when data are extremely sparse and/or become more available, performance difference among different reconstruction algorithms diminishes; whereas within a certain range between the two extremes, algorithms may show a more noticeable performance difference. However, it should be reminded that the analysis above hinges upon the performance metrics used. When the inspection is based on visualization, differences in reconstructions of the ASD-POCS and IT-ASD-POCS algorithms become minimum. While the general trend of improved RMSE with increased view number can also be observed for P-POCS and EM reconstructions, both algorithms yield visually and quantitatively less accurate reconstructions than that of the ASD-POCS and IT-ASD-POCS algorithms.

V. Results of real-data study

Real-data studies allow one to assess the effectiveness and robustness of reconstruction programs and algorithms in the presence of data inconsistencies. In the real-data study, from the full-data set of a human coronary-artery specimen, we extract 5- and 9-view data sets in which the 5 or 9 views are also distributed uniformly over 2π. As discussed above, because no truth about the specimen is available in the study, we use the FDK-reference image as the desired image and display it in Fig. 12 within a transverse and sagittal slices and in Fig. 13 in a volume-rendered view. For revealing detailed structures in the desired solution (i.e., the FDK-reference image,) we also display zoomed-in views of square-shaped ROIs 1 and 2, enclosed by dotted lines, in Fig. 12 and a zoomed-in, maximum-intensity-projection (MIP) view of the ROI, enclosed by dashed-lines, in Fig. 13a. It can be observed from the desired image that the specimen has sparse structures, which can be exploited for its reconstruction by use of the reconstruction programs and algorithms discussed above. The gross vasculature geometry and details of some fine vessels, as highlighted in these images, are compared with images reconstructed from few-view data sets by use of the ASD-POCS and IT-ASD-POCS algorithms.

Figure 12.

Images within (a) a coronal slice and (b) a sagittal slice of the FDK-reference reconstruction for the coronary-artery specimen. The square regions enclosed by dotted lines are re-displayed in a zoomed-in view in the corresponding square regions enclosed by the solid lines. Display window:[0.05, 0.6] cm⁻¹.

Figure 13.

(a) A volume-rendered view of the FDK-reference image of the coronary-artery specimen and (b) a zoomed-in, MIP view of the region enclosed by the dashed lines in (a).

A. Reconstructions from 5-view data

1) Selection of reconstruction-program parameters

We determine adaptively the parameters specifying the reconstruction programs below. For reconstruction program 3, we apply the P-POCS algorithm to the 5-view data set to obtain a residual data divergence when successive iterations result in little change in D(f), and we then select ∊ around the residual data divergence. Using the selected ∊, we then run the ASD-POCS algorithm over the 5-view data, calculate reconstruction TV, and select t₀ around the calculated TVs that are flatting out as a function of iterations. Similarly, applying the IT-P-POCS algorithm to the 5-view data set, we determine the residual data divergence and select ∊ around it to specify reconstruction program 4. Subsequently, using the selected ∊, we apply the IT-ASD-POCS algorithm to the 5-view data to determine t₀ as described above for reconstruction program 3. For determining sparsity parameter s, we carried out reconstructions by using the IT-P-POCS algorithm to empirically estimate a sparsity parameter: Using sparsity parameters in a range that amounts to 0.001 to0.5 of the total voxels of the image array, we carry out IT-P-POCS reconstructions from 5-view data set and then determine the residual data divergence. As shown in Fig. 14, a considerable rise of the residual data divergence can be observed as the sparsity parameter decreases, because the sparsity constraint becomes too stringent to be satisfied by images in close agreement with the measured data. We therefore select sparsity parameter s before, but close to, the considerable rise of residual data divergence. As previous studies [7, 8] indicate, c_α(f) ≤ −0.5 generally result in insignificant visual differences in real-data studies. Therefore, we select γ = −0.5.

Figure 14.

Residual data divergence, D_res, as a function of the sparsity fraction, which is the ratio of the selected sparsity parameter and the total number of voxels in the image array, imposed on IT-P-POCS reconstructions from the 5-view data set.

2) Algorithm convergence

We have validated algorithm convergence in terms of achieving the designed solutions specified by the conditions in Eq. (8) and the selected parameters ∊, t₀, s, and γ. The calculation of D(f) and c_α(f) as functions of the iteration number suggests that in terms of conditions in Eq. (8), both ASD-POCS and IT-ASD-POCS algorithms converge numerically to the set of solutions specified by reconstruction programs 3 and 4. In Figs. 15 and 16 we display images(i.e., the numerically achieved designed solutions) within two slices, as well as a volume-rendered and a zoomed-in MIP view, reconstructed by use of the two algorithms, along with the P-POCS and EM reconstructions.

Figure 15.

Images within a coronal slice (left) and a sagittal slice (right) of the coronary-artery specimen reconstructed from the 5-view data set, respectively, by use of (a) ASD-POCS, (b) IT-ASD-POCS, (c) P-POCS, and (d) EM algorithms. Display window: [0.05, 0.6] cm⁻¹. The square regions enclosed by the white lines display the zoomed-in view of the ROI defined in Fig. 12.

Figure 16.

Volume-rendered views (column 1) of the coronary-artery specimen images and zoomed-in, MIP views (column 2) of the ROI defined in Fig. 13a reconstructed from the 5-view data set, respectively, by use of (a) ASD-POCS,(b) IT-ASD-POCS, (c) P-POCS, and (d) EM algorithms.

3) Designed solutions relative to desired solution

Visual comparison of reconstructions in Figs. 15 and 16 can be made with the desired solution in Figs. 12 and 13: (a) the overall appearance of the ASD-POCS and IT-ASD-POCS reconstructions is similar to that of the desired solution, whereas zoomed-in ROI views reveal some differences; and (b) although the P-POCS and EM reconstructions can recover the major vessel structures, considerable artifacts can be observed in the structures and background, which obscure smaller vessel structures and some contrast differences within vessels. In particular, the rather noisy EM reconstruction may be perceived in the MIP image to have a high visual “contrast” because noise can be interpreted as signal in the creation of an MIP image. However, careful comparison with the FDK-reference in Fig. 13 suggests that no additional fine vessels were revealed by the EM reconstruction, and, moreover, that no calcification can be observed in the EM reconstruction, which can clearly be identified in ASD-POCS and IT-ASD-POCS reconstructions. In an attempt to reveal reconstruction details within the two ROIs, we calculated RMSEs of reconstructions relative to the desired solution within the two ROIs defined in Fig. 12. The results are shown in Tab. II, which indicate that both ASD-POCS and IT-ASD-POCS are capable of yielding accurate reconstructions of the specimen against the desired solution, i.e., the currently used FDK reconstruction from full data. Therefore, the 5-view reconstruction may be of usefulness for applications in which the overall branch geometry is of interest. Close inspection also suggests that the IT-ASD-POCS reconstructions show a cleaner background than the ASD-POCS reconstructions. For tasks of determining details of finer vessel structures, the algorithms under consideration are likely to require data more than 5 projections.

Table II.

RMSEs(×10^×2) of specimen reconstructions

# of views	ROI	ASD-POCS	IT-ASD-POCS	P-POCS	EM
5	ROI 1	3.8	3.4	6.3	7.7
5	ROI 2	4.7	4.1	10.4	11.2
9	ROI 1	3.5	1.8	6.1	6.3
9	ROI 2	4.6	2.7	6.4	7.2

4) “Utility” of intermediate solutions

We also plot RMSEs in Fig. 17, calculated over the entire image array, against c_α(f). The algorithms take different paths to achieve their designed solutions indicated by points A (at iteration 10,000) and B (at iteration 3,000). Again, if the RMSE-based utility is of practical interest, reconstructions at points between A and A’ (at iteration80) or between B and B’ (at iteration 80) can be of some utility even though they are not satisfying the condition c_α(f) ≤ γ.

Figure 17.

Reconstruction RMSEs, as functions of c_α(f), obtained with ASD-POCS (solid curve) and IT-ASD-POCS (dashed curve) algorithms from the 5-view data set. Two filled circles marked by A (at iteration 10,000) and B (at iteration 3,000) indicate the designed solutions, whereas the two open circles marked by A’ (at iteration 80) and B’(at iteration 80) indicate two intermediate solutions that have not reached the corresponding designed solutions.

B. Reconstructions from 9-view data

Using the methods discussed above for the 5-view case, we determine the reconstruction-program parameters and specify reconstruction programs 3 and 4 in Eqs. (4) and (5) for the 9-view case. Using the ASD-POCS and IT-ASD-POCS algorithms, we reconstruct images from the 9-view data through solving reconstruction programs 3 and 4, and make sure that the reconstructions satisfy numerically the conditions in Eq. (8). In Figs. 18 and 19 we display images within two transverse slices, as well as in a volume-rendered and a zoomed-in MIP view, reconstructed by use of the two algorithms, along with the P-POCS and EM reconstructions. Observations similar to those for the 5-view case can be made. We also compute the RMSEs within the two ROIs of the reconstructions relative to the desired solution for characterizing the “distances” of the achieved designed solutions from the desired solution, and show the result in Tab. II. Detailed examination of the reconstructions within the two ROIs reveals that the ASD-POCS and IT-ASD-POCS algorithms appear to be able to recover some of the fine vessels observed in the FDK-reference image, suggesting that images reconstructed with the algorithms from 9-view data can be of some practical utility for applications in which detailed structures of the fine vessels are of interest.

Figure 18.

Images within a coronal slice (left) and a sagittal slice (right) of the coronary-artery specimen reconstructed from the 9-view data set, respectively, by use of (a) ASD-POCS, (b) IT-ASD-POCS, (c) P-POCS, and (d) EM algorithms. Display window: [0.05, 0.6] cm⁻¹. The square regions enclosed by the white lines display the zoomed-in view of the ROI defined in Fig. 12.

Figure 19.

Volume-rendered views (column 1) of the coronary-artery specimen images and zoomed-in, MIP views (column 2) of the ROI defined in Fig. 13a reconstructed from the 9-view data set, respectively, by use of (a) ASD-POCS,(b) IT-ASD-POCS, (c) P-POCS, and (d) EM algorithms.

VI. Discussion

As mentioned in Sec. I, the idea of developing constraint programs and algorithms is not new, as they can be identified in e.g., the general POCS approach to achieving a solution set specified by a convex constraint program, provided that projectors are available [15, 25, 26]. However, existing algorithms for convex constraint programs may not be applied to non-convex constraint programs discussed. Additional algorithmic power and flexibility comes from allowing this projection process solving a constraint program to be adaptive; that is, fixing some sets while iteratively and adaptively shrinking others to uncover desired information.

The advantages of this constraint-based approach also come at a price. Traditional ideas of a mathematically well-posed problem are given up, and in particular, the solution uniqueness is not guaranteed. In fact, it is unlikely a property at all of a given constraint program. For practical applications such as medical imaging, giving up uniqueness in a mathematical program describing an image may not be a large sacrifice, because the utility of a particular image is based on the imaging task for which it is used [16].

In general, a designed solution may, or may not, be a desired solution of practical utility. Therefore, for a given desired solution in an imaging task, it is of importance to formulate a reconstruction program such that it can yield designed solutions close to the desired solution, and to develop algorithms that can achieve the designed solutions. A focus of the work is to characterize how different designed solutions are than the corresponding desired solutions of particular interest, and whether the developed algorithms can achieve the designed solutions determined by the reconstruction programs. Using simulated data and real data, we demonstrated and characterized quantitatively the reconstruction programs in terms of certain distances between designed and desired solutions and the algorithms in terms of their convergence to the designed solutions.

Results of the quantitative studies suggest that, for a sparse object, one may design appropriate reconstruction programs and algorithms for accurate image reconstruction from few-view projections of the object. However, it should be reminded that few-view reconstruction is object dependent, as demonstrated in previous work [27] that accurate image reconstruction from few-view data for an object with complex structure generally requires projection views considerably more than what is considered for sparse objects in the work [7, 8]. Also, characterization results of reconstruction utility depends on tasks and metrics involved. We have considered image utility based upon the RMSEs between a selected desired solution and reconstructions. One may choose a different desired solution, which can result in quantitatively different characterization results and even alter possibly algorithm-performance ranks.

For a given reconstruction program and algorithm, the determination of a practical iteration number is a tricky issue, as it is reliant on specific tasks (i.e., desired solutions), object complexity, data quality, and algorithm design and implementation. For example, because a tiny ∊ used in the inverse-crime study described above specifies a very tight set of solutions, it takes a considerably large number of iterations for an algorithm to achieve the designed solution. However, in the study involving real data (or data containing components inconsistent with the imaging model), a larger ∊ generally is needed for accommodating data inconsistency. As such, the reconstruction programs specify larger sets of solutions, and the algorithms may take iterations on the order of 10 to 10³ for arriving at solutions of potential practical utility or designed solutions [7, 8, 18].

As illustrated in Sec. II, the complete specification of a reconstruction program (or, equivalently, designed solutions) involves numerous program-specification parameters, including the type and number of basis sets expanding the underlying data and image functions, calculation of the system matrix, data-error tolerance ∊, image TV upper bound t₀, image sparsity s, and convergence parameter γ. Other parameters can also be selected for designing a reconstruction program. For example, blobs instead of voxels can be used as image-basis functions [28-31]; and/or other methods [32-35] can be used for generating different system matrices $\mathcal{H}$. Different choices of the parameters result necessarily in different reconstruction programs (or, equivalently, designed solutions.)

In contrast to the program-specification parameters, algorithm-specification parameters specify the design and implementation of algorithms for solving a reconstruction program. These parameters include the selection of methods/schemes such as POCS and SD for use in an algorithm to reduce data divergence and image TV, the numbers and sizes of SD/POCS steps, and the order of enforcement of different constraint conditions. Different selections of the parameters result in different paths in the solution space and can thus affect considerably the numerical behavior of an algorithm. However, the algorithm-specification parameters play no role in specifying a reconstruction program (or, equivalently, designed solutions.) If an algorithm is known to solve a reconstruction program, it should achieve designed solutions within the set even when different, but appropriately selected, algorithm-specification parameters are used. Numerically, these reconstructions are likely to be somewhat different due to the finite size of the set and the finite numerical precision of a computer.

We investigated and characterized optimization-based image reconstruction from few-view data sets. The objective of the work is not to promote the discussed reconstruction programs and algorithms such as the ASD-POCS and IT-ASD-POCS, as the only, or ultimate, solutions to the few-view reconstruction problem. Instead, recognizing that, in principle, infinite optimization/constraint programs and algorithms can be designed some of which may be superior, in terms of certain characterization metrics, to those studied in the work, we thus accent the illustration and demonstration of the design, implementation, and characterization of optimization/constraint programs and algorithms for image reconstructions, with the hope to generate insights into the identification and development of such superior programs and algorithms for image reconstruction from reduced data in general.

VII. Conclusion

In this work, we have investigated optimization-based reconstruction of sparse images from few-view (i.e., <10) data by considering reconstruction programs (or, equivalently, designed solutions) and algorithms for achieving the designed solutions. We have formulated reconstruction programs with the guides of optimization programs, and have used them to design solutions that can be achieved numerically by the algorithms. Results showed that accurate reconstruction could be achieved from few-view data under conditions of potentially practical interest, through appropriately designed optimization-based algorithm. Evaluation of the potential clinical-task-specific utilities of the few-view reconstruction remains to be carried out in future studies.

Figure 7.

Intermediate reconstructions at the two open circles marked by A’ and B’ in Fig. 6, obtained with (a) ASD-POCS and (b) IT-ASD-POCS algorithms. Square regions display the zoomed-in views of square-shaped ROIs defined in Fig. 2a. Display window: [0, 1] cm⁻¹.

Appendix A

Recent work on various optimization algorithms [36-39] show promise for convex optimization programs. As discussed in Sec. I, however, issues exist in a practical scenario of solving an optimization problem, even if an algorithmic solver is available. It should also be pointed out that these algorithms may not apply to non-convex optimization programs. Despite the recent research effort in solving non-convex optimization problems [40, 41], this remains a largely unexplored area of challenging research that is beyond the scope of the work. Furthermore, at present it is desirable to have the flexibility for obtaining and analyzing algorithms, with finite iterations, of potential practical utility. Therefore, we consider constraint programs that can be designed with the guide of optimization programs. Using optimization programs as guides, we formulate below four constraint programs (or, equivalently, reconstruction programs.) Mathematical notations used below are defined in Secs. II-A and II-B.

A. Reconstruction (or constraint) program 1

We first consider an optimization program that seeks to minimize the data divergence in Eq. (2) subject to (s.t.) an image-positivity constraint:

$${\mathbf{f}}^{\ast }=\text{argmin}D\left(\mathbf{f}\right)\text{s}.\text{t}.f_j\ge 0.$$ (9)

Using the optimization program above as the guide, we design reconstruction program 1 as

$$D\left(\mathbf{f}\right)\le ∊\text{and}{f}_j\ge 0,$$

which is also given in Eq. (3).

B. Reconstruction (or constraint) program 2

The second optimization program can be obtained by adding an image-sparsity constraint to Eq. (9) [17]:

$${\mathbf{f}}^{\ast }=\text{argmin}D\left(\mathbf{f}\right)\text{s}.\text{t}.f_j\ge 0\text{and}{\parallel \mathbf{f}\parallel }_0\le s.$$ (10)

Using this optimization program as the guide, we obtain reconstruction program 2:

$$D\left(\mathbf{f}\right)\le ∊,f_j\ge 0,\text{and}{\parallel \mathbf{f}\parallel }_0\le s,$$

which is also written in Eq. (4).

C. Reconstruction (or constraint) program 3

We obtain another optimization program by including a sparsity constraint on the image TV in Eq. (9):

$${\mathbf{f}}^{\ast }=\text{argmin}{\parallel \mathbf{f}\parallel }_{TV}\text{s}.\text{t}.D\left(\mathbf{f}\right)\le ∊\text{and}{f}_j\ge 0,$$ (11)

which has been studied extensively in recent years [3-5]. Again, guided by the optimization program, we arrive at reconstruction program 3

$$D\left(\mathbf{f}\right)\le ∊,{\parallel \mathbf{f}\parallel }_{TV}\le t_0,f_j\ge 0,\text{and}{c}_{\alpha }\left(\mathbf{f}\right)\le \gamma ,$$

as expressed in Eq. (5).

D. Reconstruction (or constraint) program 4

The final optimization program can be obtained by adding a sparsity constraint to Eq. (11) [18]:

$${\mathbf{f}}^{\ast }=\text{argmin}{\parallel \mathbf{f}\parallel }_{TV}\text{s}.\text{t}.D\left(\mathbf{f}\right)\le ∊f_j\ge 0,\text{and}{\parallel \mathbf{f}\parallel }_0\le s.$$ (12)

Based upon this optimization program, we design reconstruction program 4 as

$$D\left(\mathbf{f}\right)\le ∊,{\parallel \mathbf{f}\parallel }_{TV}\le t_0,{\parallel \mathbf{f}\parallel }_0\le s,f_j\ge 0,\text{and}{c}_{\alpha }\left(\mathbf{f}\right)\le \gamma ,$$

which is given also in Eq. (6).

We summarize the optimization and reconstruction programs in Table A, along with the reconstruction algorithms discussed in Sec. II-C.

E. Optimization and constraint programs

In a constraint program, all of the constraints are specified by pre-selected parameters (e.g., the parameters on the righthand sides of the inequalities in constraint programs 1-4.) In contrast, in an optimization program, only some of the constraints are specified by pre-selected parameters, whereas the others are realized through an optimization process. For example, constraint programs 3 and 4 use parameter t₀ for imposing a constraint on the maximally allowable image TV, whereas the same constraint in the corresponding optimization programs is achieved through minimizing the image TV without invoking any pre-selected parameter. It is interesting to note that identical constraint programs can be designed with the guide of different optimization programs. For example, an optimization program

$${\mathbf{f}}^{\ast }=\text{argmin}D\left(\mathbf{f}\right)\text{s}.\text{t}.{\parallel \mathbf{f}\parallel }_{TV}\le t_0\text{and}{f}_j\ge 0,$$ (13)

has been considered previously [42]. It can be observed that, although this optimization program differs than optimization program in Eq. (11), it can also be used as the guide for designing constraint program 3.

Table A.

Optimization programs, constraint programs, and iterative algorithms

#	Optimization Program	Constraint Program	Iterative Algorithm
1	f* = argmin D(f) s.t. fj ≥ 0	D(f) ≤ ε and fj ≥	0 P-POCS
2	f* = argmin D(f) s.t. fj ≥ 0 and ∥f∥0 ≤ s	D(f) ≤ ε, and fj ≥ 0, ∥f∥0 ≤ s	IT-P-POCS
3	f*= argmin∥f∥TV s.t. D(f) ≤ ε and fj ≥ 0	D(f) ≤ ε, ∥f∥TV ≤ t0, fj ≥ 0, and cα(f) ≤ γ	ASD-POCS
4	f*=argmin∥f∥TV s.t. D(f)≤ε, fj ≥0, and ∥f∥0≤s	D(f)≤ε, ∥f∥TV≤t0, fj ≥0, ∥f∥0≤s, and cα(f)≤ γ	IT-ASD-POCS