Abstract
The role of symmetry in the folding of proteins is discussed using energy landscape theory. An analytical argument shows it is much easier to find sequences with funneled energy landscape capable of fast folding if the structure is symmetric. The analogy with phase transitions of small clusters with magic numbers is discussed.
The role of symmetry in the physics of atoms, nuclei, and elementary particles is different from its role in the biological world. In microphysics, it has been fruitful to postulate symmetry as being fundamental, thereby severely constraining the form of the underlying laws (1). Furthermore, the consequences of symmetry for dynamics and stability are profound in the subatomic world. General treatment of these symmetry effects, based on group theory, allows a nearly complete classification of states and transitions (2, 3). Indeed, even the deviations from exact symmetry have their own quantifiable consequences. In the biological world, symmetry exists too, but it often appears to be an accident (4). While accidents still can have significant consequences, rationalizable on a case-by-case basis, there has been no general unifying theory of symmetry in biology. Exact symmetry in biology would even seem to be antithetical to the notions of complexity, variety, and metamorphosis that are central to the idea of life as we know it. Nevertheless, as in microphysics, life requires stability and sameness as well as change. The apparent conflict of these notions was captured in Schrödinger’s metaphor of life as an “aperiodic crystal” (5). Since Schrödinger’s time, numerous studies of biological macromolecules have revealed their structure and, thereby, the aptness of his aphorism. X-ray diffraction and nuclear magnetic resonance have led to a view of proteins and nucleic acids as complex three-dimensional structures with some precision (6, 7). At the same time, dynamical studies show that the situation is much more complex than the static models alone suggest (8) and that the proteins fluctuate through a variety of conformational substates whose average is represented by the beautiful pictures now in biology textbooks. This complexity is reflected in the notion of the energy landscape (9).
In this paper, we discuss the role that symmetry plays in the structure and dynamics of biomolecules. Some of this discussion is speculative, but we shall see that the origin and importance of symmetry for biomolecules can be made much clearer in the light of a joint consideration of evolution and biomolecular energy landscapes. We will argue that, while the relationship between symmetry, stability, and dynamics is different for biological physics than for the subatomic world, there are deep similarities.
Symmetry and Evolution
Two extreme points of view can be taken in thinking about biomolecular symmetry from an evolutionary standpoint. Symmetry of its biomolecules may provide some essential advantage to an organism and thus may reflect some important constraint on function. Alternatively, biomolecular symmetry may be a “frozen accident” of natural history. An example of thinking along the first lines was provided by Jordan (10, 11) long before a structure of any biological macromolecule was known. Jordan argued that heredity required the duplication of a molecular structure and that this duplication could be specifically carried out through the formation of a symmetric dimer in which like parts of a molecule would be attracted to like parts of its dimeric counterpart through a quantum mechanical resonance interaction. The attraction, according to Jordan, arises through the combined thermal and quantum fluctuations of the electronic structure of the molecule. These attractions are stronger if the two molecules have the same excitation spectrum. Despite the beauty of the idea, the analysis was mathematically flawed. Pauling and Delbrück (12) soundly trounced it by showing the weakness of the difference in force and argued instead that heredity and biological specificity in general arose through precise shape complementarity, so that symmetry was not necessary for these functions. The history of structural molecular biology has many times over confirmed the fruitfulness of the Pauling and Delbrück point of view.
Biomolecular symmetry may be advantageous and therefore adaptive on other grounds, however. Duplication of parts from the same instructions means less expenditure of energy and material in carrying forward genetic information. On these grounds, Crick and Watson (13) predicted that the coats of viruses would be made of repeating subunits and thus exhibit the symmetry of closed polyhedra. This beautiful symmetry of viruses was later revealed when their structures were solved by electron microscopy and x-ray diffraction (14). Larger organisms are not so constrained by the cost of passing on genetic information. Indeed, there is a tremendous amount of “noncoding DNA” in eukaryotes (15), so this cannot be the entire explanation for symmetry in more complex living things.
As the study of DNA sequence confirms in the higher organisms, gene duplication is quite common and provides a route to symmetry. A fair fraction of enzymes and other functional molecules are oligomers (4). The most famous example is hemoglobin (see Fig. 1). The tetrameric hemoglobin molecule has a two-fold symmetry, as revealed by x-ray diffraction. The oligomerization allows the possibility of cooperative binding with all of the concomitant functional advantages. The natural historians tell us that this function evolved ≈600 million years ago, and the missing link between the monomeric and oligomeric form can be seen fixed in the genes of the sea lamprey whose hemoglobin subunits are monomeric but associate upon binding oxygen (16). The similarity between the α and β subunits is so close that we can be quite confident that this gene duplication occurred as a historical fact. In this scenario, the actual symmetry of the oligomer would seem to be a kind of accident, and the differences between the α and β chains, which prevent a full 222 symmetry from being exact, is a fossilized mark of this history.
Figure 1.
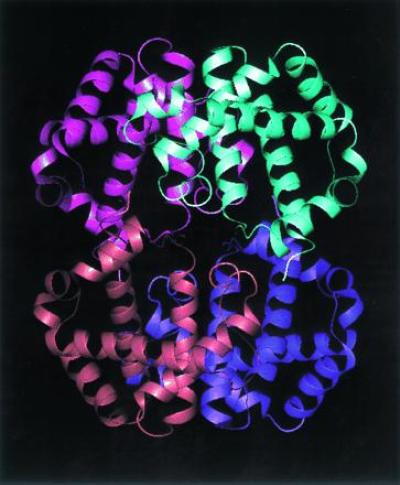
The hemoglobin molecule is a tetramer α2β2. If the subunits were identical it would have 222 symmetry.
It is the inexact symmetries of biological molecules that are most striking. At the tertiary fold level, a single nonoligomeric biomolecule can show symmetry in its overall structure, even though the sequences of the approximate symmetrically related portions of the chains are not the same. An example of this type is shown in Fig. 2. The overall chain traces of the residues from 1 to 88 and from 89 to 174 of the γ crystallin clearly have the same shape, but their sequences are not identical. The symmetry is therefore not exact; furthermore, the similarity in sequence is sufficiently small that we might not realize the two sequences are related by evolution at first. Nevertheless, each section of the molecule is so large that, again, we can be fairly confident after seeing the structure that, in fact, this approximate symmetry arose through gene duplication and fusion followed by genetic drift for a very long period of time.
Figure 2.
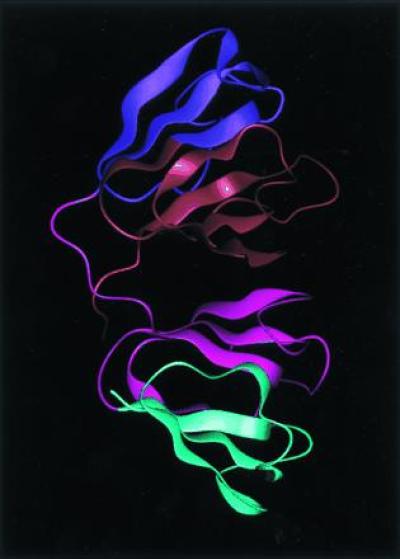
γ crystallin is a monomeric protein, but clearly its structure arises from gene duplication and drift. The two modules are similar but not identical in sequence.
The most striking examples of approximate biomolecular symmetry arise, however, for smaller proteins that lack any obvious subunit structure or symmetry in sequence. In Fig. 3, we show a four-helix bundle protein, cytochrome b562. There is no obvious exact symmetry in sequence, but the tertiary fold is easily described using the language of symmetry. The molecule is made of four helices of nearly the same length. (One has a poorer hydrogen bonding, so it actually appears to be shorter than it really is.) There is also a twist ultimately due to chirality, which is important, but, ignoring this, it is a symmetric bundle of four cylinders. It is at this crude level of approximation that a symmetry is apparent.
Figure 3.
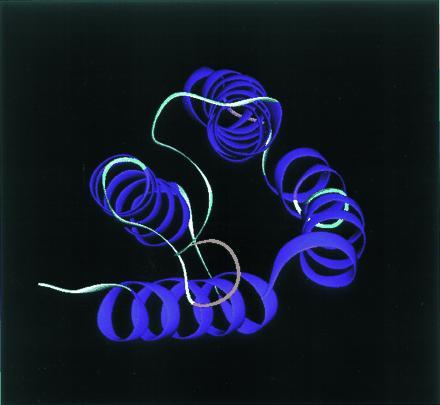
A four-helix bundle molecule, cytochrome b562. The ribbon diagram actually exaggerates the dissymmetry because of the demanding algorithm for secondary structure assignment.
Protein folds generally can be described as belonging to families (48). Many, but not all, of these families exhibit simple approximate symmetries when we idealize them, ignoring the fine details of the chirality of the helices—e.g., approximate mirror symmetries, like the four-helix bundle, or approximate polyhedral symmetries, like the globins (see Fig. 3). The hemoglobin subunit, when the helices are rendered as cylinders, looks like a polyhedron. Symmetry is not universal, since some families do not exhibit even this approximate symmetry. Why are these approximately symmetric structures so prevalent? Again it is possible that the approximate symmetry is an accident of natural history tracing back to primordial proteins. It has been hypothesized that the original proteins were much shorter than most present day proteins and that the larger proteins were later assembled from these units (17, 18). This attractive hypothesis was made soon after the discovery of split genes or exons in eukaryotes, which could have encoded these folding units. The hypothesis remains a bit controversial, but, if correct, even the symmetry of these smaller proteins would be an accidental result of gene duplication and drift. An alternate view, we pursue below is that this kind of approximate biomolecular symmetry in smaller proteins arises not from duplication and drift but from some kind of convergence in evolution. In this view, the symmetry conferred an advantage even for organisms possessing the primordial proteins and/or symmetry continues to be reinvented during evolutionary history. Under this view, in any event, we must explain why such approximate symmetry of tertiary structure should persist and be prevalent in the absence of obvious symmetry in sequence. An explanation lies in the energy landscape of foldable proteins.
The Energy Landscape of Foldable Proteins and the Minimal Frustration Principle
To function efficiently, most proteins must fold. Much recent theoretical work suggests that achieving a folded structure spontaneously is not trivial (ref. 19; ref. 20 and references therein; refs. 21–23). Foldability requires a specially shaped energy landscape resembling a funnel (20, 21). Not all protein sequences possess an obviously “funneled” landscape and certainly not all sequences have surfaces funneled to the same degree. A heteropolymer with a completely random sequence generically possesses a rugged energy landscape without a funnel, because bringing together two segments of a random sequence will usually give rise to conflicting interactions between the connected side chains, and, therefore, many alternative local minima of the energy can be found. We therefore say a random heteropolymer typically is “frustrated” [a term from solid state physics (24, 25)], because these conflicts make the search through the landscape very difficult. At temperatures low enough to stabilize the ground state conformational dynamics is sluggish or “glassy.” States that are geometrically globally different can be nearly ground states and can act as traps slowing the folding process.
Fast-folding proteins can access their thermodynamically stable organized (folded) structure at temperatures where glassy dynamics and traps can be avoided. To do this, the interactions in the folded structure must act in concert more effectively than expected in the most random case. This idea is called the “principle of minimal frustration” (19) and is a generalization of many older notions, such as the idea of Gō (26) that local secondary and nonlocal tertiary interactions must be consistent with each other.
The principle of minimal frustration can be made quantitative using energy landscape theory. Using the simplest approximations of the statistical mechanics of disordered systems, it can be shown to be equivalent to the assertion that the ground state energy of the protein is significantly (i.e., many standard deviations of the energies in the rugged part of the landscape) lower than the bulk of the collapsed states of the protein (27, 28). Such an energy landscape allows folding into the correct state at temperatures where glassy traps are unimportant. When the ground state energy is very low, structures similar to the ground state will also be low in energy, thus leading to a funnel structure of the energy landscape as shown in Fig. 4. Many analytical and simulation studies of model heteropolymer problems confirm the outlines of the energy landscape description quickly summarized above. The quantitative form of these ideas can also be used to find and evaluate energy functions for protein structure prediction (27, 28) and to design foldable protein sequences (29) if one is given exact energy functions. The most rapidly foldable proteins have the most pronounced funnel structure to their landscape and are quite stable.
Figure 4.
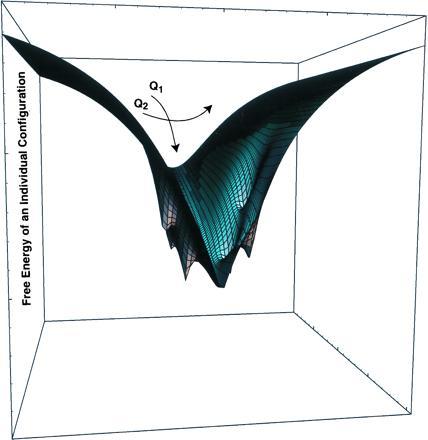
A protein folding funnel. The width of the funnel represents configurational entropy. The depth is the free energy of an individual configuration. The funnel is shown as anisotropic. The coordinate Q1, which destroys the symmetry rapidly, changes the energy, while Q2, preserving symmetry gives smaller energy changes.
Again we must emphasize that minimal frustration does not mean no frustration. The symmetry and apparent uniqueness of the folded configuration is only approximate, leading to a large number of distinct conformational substates with different reaction characteristics in the overall folded state.
Symmetry and Minimally Frustrated Energy Landscapes
It is natural to suppose that symmetry, minimal frustration, and the funneled nature of the landscape are somehow connected. The consistency of geometry in symmetric structures suggests some preselection and consistency of interaction—i.e., an argument for the validity of the minimal frustration principle (30). This connection is easily understandable when one deals with systems with precisely symmetric interactions between identical particles, such as those in nuclei or atomic clusters. In fact, the notion of funneled landscapes has been taken over to the world of the thermodynamics and kinetics of simple (nonbiological) clusters of atoms (31). For atomic clusters, an especially stable ground state, removed in energy from the bulk of the states allowing a crisp and rapid melting transition, can be achieved only when highly symmetric arrangements of the atoms are possible (32). This property is related to the phenomenon of the “magic numbers” for the stability of van der Waals clusters. Ar13, which is capable of forming a close packed icosahedron, has a funneled landscape easily accessible upon cooling. On the other hand, Ar8 has a much rougher landscape and the ground state is not easily accessed kinetically. We must unfortunately admit the current lack of a deep understanding or mathematical proof of why symmetric arrangements are always so stable for such systems with symmetric (and therefore minimally frustrated) interactions. But the observation of extra stability through symmetry is nevertheless not only very plausible for systems of equal particles but also a fact. Admitting this fact, there still remains a significant puzzle for heteropolymers, since the interactions within proteins are far from symmetric. Indeed, an explanation based on the symmetries of a homopolymer seems out of the question on several thermodynamic grounds. Soluble homopolymers of amino acids are either in a random coil state or helical fibers. Simulations of homopolymers on lattices usually give nearly degenerate ground states and insufficient driving force toward the native structure when it is unique. It can also be demonstrated that even for highly complex nonsymmetric structures, there are sequences capable of giving a protein with a funneled landscape that leads to an asymmetric structure but where the frustration has nevertheless been minimized (29).
In answering this last puzzle, the symmetry of heteropolymers, it is important to recall that the observation requiring explanation is not that symmetrical protein folds are universal but that they are prevalent. Several studies suggest all shapes are not equally easy to design by a random process like evolution (33–36). In the context of RNA secondary structure folding where the secondary structural folding problem can be explicitly solved, Schuster et al. (34) have shown that some shapes have many sequences that can code for them while others have few (34). In the more difficult computational problem of protein tertiary folding, Yue and Dill (35), using lattice models of proteins with two-letter codes, both hydrophobic and hydrophilic, have shown that symmetric patterns giving nondegenerate ground states are easy to design and have argued that this is the origin of the symmetry prevalence. Govindarajan and Goldstein (36) have not discussed the symmetry issue explicitly but have tried to quantify the statistical distribution of designable proteins using landscape theory and recently lattice models. Using some ideas from statistical mechanics of energy landscapes, we now can make the connection between symmetry and designability of funnel landscapes more precise and explicit.
For concreteness, consider an ensemble of heteropolymers of fixed length N and average composition. For purposes of illustration, the energy function for this heteropolymer can be taken to have the pairwise additive form:
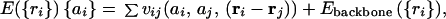 |
1 |
where {ri} is the set of polymer subunit locations and {ai} represents the sequence information. The pair potential vij depends on the distance between and identity of the residues. The potential Ebackbone ({ri}) maintains chain connectivity and those backbone effects inherent to poly-amimo acids that allow α-helices and β-sheets to form. We now consider the designability of a specific structure {ri}. If the landscape is to be funneled, this structure must have an energy considerably below that for the typical random structure. The latter quantity, according to the simplest theories, should be a function only of the composition but not the “sequence order.” Thus, to ensure a funneled landscape, we must ask that the energy of that configuration with locations of residues at {Ri}, E({Ri}) ☰ EF({ai}) must reach some desired low value. The folded energy EF is a function now only of the sequence {ai}. The actual value of the energy difference needed depends on the biological constraint for the time scale of folding. This involves the physics of the stability folding time correlation. Finding the most designable structures by a random process corresponds with finding the structures such that the number of sequences corresponding to them is the largest. This can be thought of equivalently as the entropy of a statistical mechanics problem (29), where the sequence is the variable rather than the locations, {Ri}.
Elementary statistical thermodynamics (37) argues that for large enough systems, maximizing the entropy, given an energy constraint, is equivalent to minimizing the free energy for a specific value of a pseudotemperature T* chosen in such a way that the Boltzmann average energy of the structures at that pseudotemperature is equal to that selected energy value. In fact, just such a pseudo-Boltzmann ensemble is the basis of some formal approaches to the statistical mechanics of polymers satisfying the minimal frustration principle (38, 39). To be consistent with a low energy ground state, T* must be lower than physiological temperature and the glass transition temperature.
For a specific structure, this free energy can be written using a partition sum:
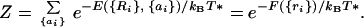 |
2 |
This partition sum is an average over possible sequences with a given average composition. Thus we can see that the effective free energy governing the prevalence of sequences for a given structure is a Hamiltonian lacking disorder. The sequence dependence is per force averaged over! The effective free energy function contains only equivalent sites. The energy corresponds to what is known as the “annealed” average of the partition function for the originally disordered system. The connection to symmetry and the simple cluster system can be made especially transparent when the number of types of amino acids is large. In this case, the individual pairs of interactions or bonds are nearly independent and the energy of a given pair and the average over sequence used to compute pseudo-Boltzmann probability for a structure is just a product of the average Boltzmann factors for each pair. This approximation, while exact for large numbers of amino acid types, is not a bad approximation even when there are few. It is equivalent to the quasichemical or Bethe and Kirkwood approach used in the statistical mechanics of magnetic systems (37). The sequence averaged energy function, appropriate for determining the designability of this sequence, is in fact identical with the energy function of an equivalent homopolymer. The interactions of this homopolymer are attractive (and may be much stronger than those presenting any actual homopolymer of amino acids). If the pair interactions were precisely Gaussian in their distribution, they would give a free energy of the form:
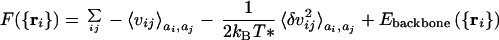 |
3 |
Here δvij = vij −
〈vij〉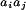 is the fluctuating part of the interaction representing the fact that
an individual protein is a heteropolymer. We see the most easily
designable structures (i.e., the most numerous in a random sampling
with the minimal frustration constraint) are the minimum energy
structures for an effectively homoattractive polymer with some specific
backbone interactions (the expression in Eq. 3). Just as for
atomic clusters, we would expect the most stable arrangements of the
equivalent homopolymer to correspond with symmetrical arrangements. If
the backbone interactions were entirely isotropic and very weak, the
resulting highly symmetric structures would in fact be the same as
those corresponding with the magic numbers of van der Waals clusters.
is the fluctuating part of the interaction representing the fact that
an individual protein is a heteropolymer. We see the most easily
designable structures (i.e., the most numerous in a random sampling
with the minimal frustration constraint) are the minimum energy
structures for an effectively homoattractive polymer with some specific
backbone interactions (the expression in Eq. 3). Just as for
atomic clusters, we would expect the most stable arrangements of the
equivalent homopolymer to correspond with symmetrical arrangements. If
the backbone interactions were entirely isotropic and very weak, the
resulting highly symmetric structures would in fact be the same as
those corresponding with the magic numbers of van der Waals clusters.
Two effects will change the preferred symmetries from those of atomic clusters. First, the inadequacy of the independent pair or quasichemical approximation would imply that the actual sequence-averaged free energy would not be additive as in Eq. 3, but would have nonadditive interactions. Nevertheless, it would still be symmetrical between the particles. The favored symmetries for nonadditive forces may be different from additive ones. This is what occurs for metallic clusters in contrast to van der Waals clusters. More important, however, is that the backbones of proteins favor linear hydrogen bonded arrangements such as α-helices, so one really must consider the most symmetrical arrangements of α helices or β sheets but with homoattractive interactions. Just such a route to understanding the families of protein folds was undertaken by Murzin and Finkelstein (40) a rather long time ago when they discussed the bundle and polyhedral packings of helices, neglecting the heteropolymeric aspect (41). Similar ideas have been used for the homoattractive β-sheets by Chothia et al. (42). We see that the validity of those crystallographically inspired approaches can be based on the combination of the minimal frustration principle for the energy landscape providing a force for convergence in evolution with the assumption of otherwise sufficient neutrality and time for drift so that the most common adaptive sequences are those that are observed.
It is amusing that the evolutionarily averaged potential that
gives rise to the symmetry, according to this view, is very much
analogous to the quantum mechanical van der Waals force. The term
〈vij〉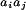 contributes too but is partially canceled by the fact that it is also
present in the disordered molten globule, as is a fraction
T*/T of the fluctuation part. Indeed, it is the
average interaction over evolutionary fluctuations in sequence as
opposed to quantum mechanical or thermal fluctuations in electronic
structure that enters the probability of finding an abundant structure.
Despite the validity of the Pauling and Delbrück viewpoint for
each individual biomolecule, in a sense, a ghost of Jordan’s mechanism
for biomolecular symmetry resurfaces through an analogy involving the
statistical mechanics of evolution and minimally frustrated energy
landscapes.
contributes too but is partially canceled by the fact that it is also
present in the disordered molten globule, as is a fraction
T*/T of the fluctuation part. Indeed, it is the
average interaction over evolutionary fluctuations in sequence as
opposed to quantum mechanical or thermal fluctuations in electronic
structure that enters the probability of finding an abundant structure.
Despite the validity of the Pauling and Delbrück viewpoint for
each individual biomolecule, in a sense, a ghost of Jordan’s mechanism
for biomolecular symmetry resurfaces through an analogy involving the
statistical mechanics of evolution and minimally frustrated energy
landscapes.
Consequences of Symmetry for the Biomolecular Energy Landscape
For a particular protein, biomolecular symmetry will not be exact unless it is the result of gene duplication. It is a quantitative issue how much the forces leading to minimal frustration, partially determined by symmetry considerations, are dominant over the aspects of the landscape arising from randomness. For protein folding itself, and even more so for function, much needs to be done to address these issues, but we will make here a few observations and speculations.
First, the convergent evolution viewpoint on biomolecular symmetry could be most directly investigated by combinatorial synthesis experiments in which random or partially random proteins are produced through genetic engineering. Two efforts along this line already give some information. Sauer’s group at the Massachusetts Institute of Technology has synthesized random amino acid chains from a small library (43). They showed that a small fraction (0.5%) showed the two-state-like thermodynamics associated with a funneled energy landscape. It is very interesting that of this fraction many of the species were oligomers and, therefore, may be taking advantage of symmetry to fold. On the other hand, Hecht and coworkers (44) has synthesized a random library of proteins whose hydrophobic pattern were forced to obey the exact symmetries of the four-helix bundle, and, in this case, the fraction of sequences with apparently funneled energy landscapes for the monomer is considerably higher. These studies in combinatorial synthesis of proteins, however, point out the complexity in applying quantitatively the statistical mechanical analysis described earlier. Clearly, specific packing forces involving side chains need to be taken into account to achieve fully protein-like behavior.
While the symmetry is approximate for any given native protein, it will contribute to the overall shape of the energy landscape. We might expect there to be a tendency for the symmetry to be preserved in the most important routes to folding and for breaking of symmetry along such a route to be more costly. Again, there is some anecdotal evidence of symmetry preservation along the dominant folding routes when we examine folding of systems such as triosphosphate isomerase. This molecule has an overall three-fold symmetry, but, on the long time scales, it seems to fold in two steps. In the first a two-fold symmetry is preserved and the final third unit is added last (49). The statistical mechanical analysis of folding for symmetrical proteins may also show some correlation of the typical barrier heights with the degree of symmetry of the molecules. The landscape or funnel geometry for a specific minimally frustrated protein will have a strong correlation to the landscape of the sequence averaged effective homopolymer and the energy (see Fig. 4) should vary differently along collective coordinates preserving symmetry from those breaking it.
The individuality of proteins with a common symmetric fold arises from the fluctuations away from the ideal average landscape. It is interesting that the magnitude of these fluctuations is again dependent on the δv2 interaction that enters the annealed average. For quenched disorder, according to spin glass theory, however, the relevant disorder averaged force is scaled by the actual temperature, not T*, and is therefore weaker. Different heteropolymers exhibit non-self-averaging behavior when δv2/kBT is sufficiently strong to cause a glass transition. In the formal statistical mechanics of disordered systems, the glass transition corresponds to “broken replica symmetry” (45). In the language used by the particle physicists, we can restate the minimal frustration principle as “the folding transition that breaks the isotropic symmetry of the globule down to the point symmetry of the folded state occurs at higher temperature than the temperature of broken replica symmetry in order for fast folding to occur.”
The arguments presented here have focused on symmetry and the energy landscape involved in folding, but there may be important consequences for function as well as for folding. It is important to remember that Monod, Wyman, and Changeux proposed their two-state model for the allostery of hemoglobin on the basis that the dyadic symmetry of the molecule had to be preserved (46, 47). Since that time, especially in the kinetics, other nonsymmetric states have been invoked and found to be important in the dynamics. We can see the present arguments would, however, be consistent with the Monod, Wyman, and Changeux perspective. Clearly, if one wishes to have an allosteric protein, it must have two different structures. By the same counting arguments that make single symmetric structures more easily designable, pairs of symmetric structures should be an easier design goal if one needs two-state-like switching behavior. It is striking that Eaton has recently described the multistate complex kinetics of hemoglobin allostery using the basic Monod, Wyman, and Changeux symmetry-derived notion of two symmetric R and T states with a simple superposition of multistate relaxation through an energy landscape superimposed on these two basic structures (E. R. Henry, J. Hofrichter, and W. Eaton, personal communication).
We see that the beautiful symmetries of biomolecules may indeed reflect basic principles about the energy landscape in biology, just as symmetry relations do in particle physics. The extra key, however, is the notion of evolution, which can reconcile the symmetry of a family and the diversity of individuals. Whether the powerful mathematical machinery describing symmetry via group theory used in field theory and condensed matter theory will also help understand the biomolecular energy landscape through the choice of collective coordinates and by describing the nature of defects in biomolecular structure is a question for future development.
Note Added in Proof.
Several papers relevant to the theme of this paper have appeared recently. These should be consulted for alternate viewpoints and approaches (50–52).
Acknowledgments
I am indebted to Hans Frauenfelder, both for his long-term inspiration of this work through his conviction that fundamental physics is to be found in the biomolecular world and for the initial discussions that specifically motivated me to write this for the National Academy of Sciences Colloquium on Symmetry in the Sciences. I also thank him for graciously presenting the work at that meeting. I thank William Eaton and Hans Frauenfelder for critically reading the manuscript and Zan Luthey-Schulten for her extraordinary help providing the figures. This paper was completed while I was a Scholar-in-Residence at the Fogarty International Center for Advanced Study in the Health Sciences, National Institutes of Health, Bethesda.
Footnotes
The present paper was started as a collaboration between P.G.W. and Hans Frauenfelder. As the paper progressed, it became clear that the crucial ideas were entirely those of P.G.W. Hans Frauenfelder therefore removed his name, but nevertheless presented the paper at the conference that P.G.W. was unable to attend.
References
- 1.Frauenfelder H, Henley E. Subatomic Physics. 2nd. Ed. Englewood Cliffs, NJ: Prentice–Hall; 1991. [Google Scholar]
- 2.Wigner E. Gruppentheorie und ihre Anwendung unf die Quantenmechanik der Atomspektren. Braunschweig, Germany: Vieweg; 1932. [Google Scholar]
- 3.Gell-Mann M, Neeman Y. The Eightfold Way. New York: Benjamin; 1964. [Google Scholar]
- 4.Monod J. In: Symmetry and Function of Biological Systems at the Macromolecular Level. Engstrom A, Strandbert B, editors. New York: Wiley; 1969. pp. 15–29. [Google Scholar]
- 5.Schrödinger E. What is Life? Cambridge, U.K.: Cambridge Univ. Press; 1949. [Google Scholar]
- 6.Perutz M. Protein Structure: New Approaches to Disease and Therapy. New York: Freeman; 1992. [Google Scholar]
- 7.Branden C, Tooze J. An Introduction to Protein Structure. New York: Garland; 1991. [Google Scholar]
- 8.Frauenfelder H, Parak F, Young R D. Annu Rev Biophys Biophys Chem. 1988;17:451–479. doi: 10.1146/annurev.bb.17.060188.002315. [DOI] [PubMed] [Google Scholar]
- 9.Frauenfelder H, Wolynes P G. Phys Today. 1994;47:58–64. [Google Scholar]
- 10.Jordan P. Phys Z. 1938;39:711–714. [Google Scholar]
- 11.Jordan P. Z Phys. 1939;113:431. [Google Scholar]
- 12.Pauling L, Delbrück M. Science. 1940;92:77–79. doi: 10.1126/science.92.2378.77. [DOI] [PubMed] [Google Scholar]
- 13.Crick F, Watson J D. Nature (London) 1956;177:473–475. doi: 10.1038/177473a0. [DOI] [PubMed] [Google Scholar]
- 14.Caspar D L D, Klug A. Cold Spring Harbor Symp Quant Biol. 1962;27:1–24. doi: 10.1101/sqb.1962.027.001.005. [DOI] [PubMed] [Google Scholar]
- 15.Darnell J, Lodish H, Baltimore D. Molecular Cell Biology. New York: Freeman; 1986. [Google Scholar]
- 16.Dickerson R E, Geis I. Hemoglobin: Structure, Function, Evolution and Pathology. Menlo Park, CA: Benjamin; 1983. [Google Scholar]
- 17.Gilbert W. Nature (London) 1978;271:501. doi: 10.1038/271501a0. [DOI] [PubMed] [Google Scholar]
- 18.Blake C C F. Nature (London) 1978;273:267. [Google Scholar]
- 19.Bryngelson J D, Wolynes P G. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bryngelson J D, Onudic J, Socci N, Wolynes P. Proteins Struct Funct Genet. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 21.Leopold P E, Montal M, Onuchic J. Proc Natl Acad Sci USA. 1992;89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dill K A, Bromberg S, Yue K, Fiebig K M, Yee D P, Thomas P D, Chan H S. Protein Sci. 1995;4:561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shakhnovich E, Gutin A M. Proc Natl Acad Sci USA. 1993;90:7195–7199. doi: 10.1073/pnas.90.15.7195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Anderson P W. J Less Common Met. 1978;62:291–294. [Google Scholar]
- 25.Toulouse G. Commun Phys (London) 1977;2:115–126. [Google Scholar]
- 26.Gō N. Annu Rev Biophys Bioeng. 1983;12:183–210. doi: 10.1146/annurev.bb.12.060183.001151. [DOI] [PubMed] [Google Scholar]
- 27.Goldstein R A, Luthey-Schulten Z A, Wolynes P G. Proc Natl Acad Sci USA. 1992;89:4818–4822. doi: 10.1073/pnas.89.19.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goldstein R A, Luthey-Schulten Z A, Wolynes P G. Proc Natl Acad Sci USA. 1992;89:9029–9033. doi: 10.1073/pnas.89.19.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shakhnovich E, Gutin A. Protein Eng. 1993;6:793–800. doi: 10.1093/protein/6.8.793. [DOI] [PubMed] [Google Scholar]
- 30.Wolynes P G. In: Spin Glasses and Biology. Stein D, editor. Singapore: World Scientific; 1992. pp. 225–259. [Google Scholar]
- 31.Ball K D, Berry R S, Kunz R E, Li F-Y, Proykova A, Wales D J. Science. 1996;271:963–965. [Google Scholar]
- 32.Hoare M R, Pal P. Adv Phys. 1975;24:645–678. [Google Scholar]
- 33.Finkelstein A, Gutin A, Badredtinov A. FEBS Lett. 1993;325:23–28. doi: 10.1016/0014-5793(93)81407-q. [DOI] [PubMed] [Google Scholar]
- 34.Schuster P, Fontana W, Stadler P, Hofecker I. Proc R Soc London Ser B. 1994;255:279–284. doi: 10.1098/rspb.1994.0040. [DOI] [PubMed] [Google Scholar]
- 35.Yue K, Dill K. Proc Natl Acad Sci USA. 1995;92:146–150. doi: 10.1073/pnas.92.1.146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Govindarajan S, Goldstein R A. Proc Natl Acad Sci USA. 1996;93:3341–3345. doi: 10.1073/pnas.93.8.3341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hill T L. Introduction to Statistical Thermodynamics. Reading, PA: Addison–Wesley; 1962. [Google Scholar]
- 38.Ranganathan S, Shakhnovich E. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top. 1994;50:1303–1312. doi: 10.1103/physreve.50.1303. [DOI] [PubMed] [Google Scholar]
- 39.Pande V, Grossberg A, Tanaka T. J Phys. 1994;4:1771–1784. [Google Scholar]
- 40.Murzin A, Finkelstein A. J Mol Biol. 1988;204:749. doi: 10.1016/0022-2836(88)90366-x. [DOI] [PubMed] [Google Scholar]
- 41.Chirgadze Y N. Acta Crystallogr A. 1987;43:405. [Google Scholar]
- 42.Chothia C, Levitt M, Richardson D. Proc Natl Acad Sci USA. 1977;73:3793. doi: 10.1073/pnas.74.10.4130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Davidson A R, Sauer R T. Proc Natl Acad Sci USA. 1994;91:2146. doi: 10.1073/pnas.91.6.2146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kamtekar S, Schiffer J M, Xiong H, Babik J M, Hecht M H. Science. 1993;262:1680–1685. doi: 10.1126/science.8259512. [DOI] [PubMed] [Google Scholar]
- 45.Mezard M, Parisi G, Virasoro M. Spin Glass Theory and Beyond. Singapore: World Scientific; 1986. [Google Scholar]
- 46.Monod J, Changeux J P, Jacob F. J Mol Biol. 1963;6:306–329. doi: 10.1016/s0022-2836(63)80091-1. [DOI] [PubMed] [Google Scholar]
- 47.Monod J, Wyman J, Changeaux J P. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 48.Richardson J. Adv Protein Chem. 1981;34:167. doi: 10.1016/s0065-3233(08)60520-3. [DOI] [PubMed] [Google Scholar]
- 49.Mathews C R. Annu Rev Biochem. 1993;62:653–683. doi: 10.1146/annurev.bi.62.070193.003253. [DOI] [PubMed] [Google Scholar]
- 50.Li H, Helling R, Tang C, Wingreen N. Science. 1996;273:666–669. doi: 10.1126/science.273.5275.666. [DOI] [PubMed] [Google Scholar]
- 51.Lindgard P A, Bohr H. Phys Rev Lett. 1996;77:779–782. doi: 10.1103/PhysRevLett.77.779. [DOI] [PubMed] [Google Scholar]
- 52.Kellman M. J Chem Phys. 1996;105:2500–2508. [Google Scholar]


