Breast Ultrasound Image Classification Based on Multiple-Instance Learning

Abstract

Breast ultrasound (BUS) image segmentation is a very difficult task due to poor image quality and speckle noise. In this paper, local features extracted from roughly segmented regions of interest (ROIs) are used to describe breast tumors. The roughly segmented ROI is viewed as a bag. And subregions of the ROI are considered as the instances of the bag. Multiple-instance learning (MIL) method is more suitable for classifying breast tumors using BUS images. However, due to the complexity of BUS images, traditional MIL method is not applicable. In this paper, a novel MIL method is proposed for solving such task. First, a self-organizing map is used to map the instance space to the concept space. Then, we use the distribution of the instances of each bag in the concept space to construct the bag feature vector. Finally, a support vector machine is employed for classifying the tumors. The experimental results show that the proposed method can achieve better performance: the accuracy is 0.9107 and the area under receiver operator characteristic curve is 0.96 (p < 0.005).

Introduction

Breast cancer is the most common cancer found in women both in the developed and developing countries. One of ten new cancers diagnosed worldwide each year is breast cancer [1]. Breast cancer is also the principal cause of death from cancer for the female population globally [1, 2].

Ultrasound examination, which is noninvasive and nonradioactive, is more convenient and suitable for palpable tumors in daily clinical practice [3]. Differential diagnosis of breast lesions can be acquired from ultrasound images. However, ultrasonography is operator-dependent, and reading breast ultrasound (BUS) images requires well-trained radiologists. Even experts may have inter-observer variation; therefore, computer-aided diagnosis (CAD) system is needed to help radiologists in breast cancer detection and classification [4]. CAD system acts as a second reader that assists radiologists in medical decision-making process to reduce diagnosis error. For breast ultrasound CAD systems, the tumor region is located as a region of interest (ROI), and the features are extracted from the ROI; finally, the tumor is classified as benign or malignant. The most predictive features of a benign mass image are oval or round shape, circumscribed margins, and homogeneous internal echoes. The most predictive features of a malignant mass image are speculated or microlobulated margins, irregular shape, ill-defined margins, and heterogeneous internal echoes [5, 6].

Segmentation is a key step for most of CAD systems. There are some problems in ultrasound (US) images such as attenuation, speckle, shadows, and signal dropout. In addition, the contrast of BUS images is very low. These characteristics make auto-segmentation of BUS images very difficult and cause large difference between the auto-segmented result and real ROI [7]. Such difference will directly affect the final classification accuracy because the features (shape, margin, etc.) are dependent on correctly located ROIs.

Diseases tend to change tissue scatter properties which reflected by texture variations in BUS images. Different tissues have different textures; therefore, the texture of BUS image is an effective feature for differentiating benign and malignant breast tumors [3, 8]. Auto-covariance [9], fractal dimension [10], co-occurrence matrix [11], run-length matrix [12], and wavelet coefficients [13] have been widely utilized to derive discriminant features.

In method of [14], the local texture features of the subregions in roughly segmented ROIs were used to characterize lesions. The experiments demonstrated that such strategy was robust to segmentation result. But when modeling ROIs with local features, traditional supervised learning methods are not suitable, since in learning phase, we only know the label of ROI, while the labels of the subregions in ROI are unknown. It is not appropriate to simply assign the label of the ROI to its subregions. For solving such problem, ROI can be considered as a bag and its subregions can be viewed as the instances of the bag. Then, the problem is transformed to a multiple-instance learning problem [15].

Multiple-instance learning (MIL) was proposed to solve learning problems with incomplete information about the labels of the data. For traditional supervised learning, each training example is represented by a fixed-length vector of the features with known label. However, in MIL, each example is called a bag and represented by multiple instances. The number of instances in each bag can be different. In other words, bags are represented by variable-length vectors. Labels are only provided for the training bags, and the labels of instances are unknown. The MIL task is to learn a model to classify new bags [16, 17].

MIL was introduced by Dietterich et al. [15] when they were investigating the problem of drug activity prediction. After that, many MIL methods have been studied for wide applications, such as axis-parallel rectangle for drug activity prediction [15], diverse density (DD) for stock market prediction [18], natural scene classification [19], content-based image retrieval [20], MIL support vector machine for image classification [21], Citation-k-nearest neighbor (kNN) for web mining [22], etc. The paper presents a novel method for automatic breast tumor detection and classification of BUS images based on local texture features and multiple-instance learning method.

Previous Work Review

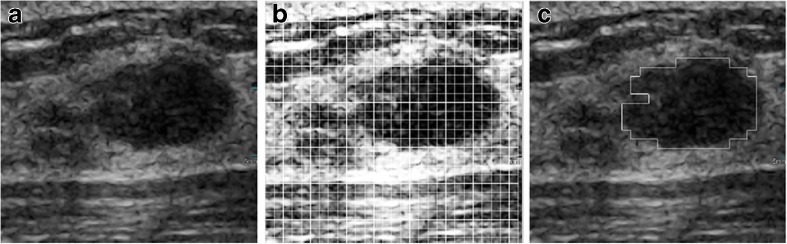
In our previous work [14], the image is enhanced in fuzzy domain [23]. The S-function is used as the fuzzy membership function [24]. Then, the enhanced image is divided into non-overlapping subregions. The co-occurrence matrix [25] was utilized to describe the texture information of subregions. A support vector machine (SVM) was applied to classify subregions into tumor or normal tissues. And the prior knowledge about BUS images was used to obtain a rough ROI. An example was shown in Fig. 1.

Fig. 1.

a Original image. b Enhanced and divided image. c Rough ROI

In Fig. 1, the original BUS image (Fig. 1a) was enhanced and divided (Fig. 1b). When the classifier was applied to subregions, the rough location of the tumor was segmented (Fig. 1c). For extracting the local features of the ROI, the points evenly distributed in the ROI were selected as the checkpoints, and their neighborhood windows were constructed as shown in Fig. 2.

Fig. 2.

Classification point and neighborhood window

For each checkpoint, five distances (d = 1, 2, 3, 4, and 8), four directions (θ = 0°, 45°, 90°, and 135°), and five windows (W = 0, 1, 2, 3, and 4) are used to establish the co-occurrence matrices. From a co-occurrence matrix, four descriptors are calculated: entropy, contrast, sum average, and sum entropy [25]. These descriptors are employed to represent the local texture features of the checkpoints.

Finally, an SVM classifier is trained to classify the checkpoints. A threshold is selected according to the experiments. When the ratio of the checkpoints in a ROI classified as malignant is higher than the threshold (50 %), the tumor is classified as malignant.

The problem is more suitable for MIL which views the ROI as bag and its subregions as instances. The traditional MIL assumes that the positive bag has at least one positive instance and the negative bag has no positive instance. However, such assumption is not suitable for classifying breast cancers. A malignant tumor is a group of cancer cells that may grow into surrounding tissues or spread to distant areas of the body. Invasive ductal carcinoma is the most common type of breast cancer. About 80 % of all breast cancers are invasive ductal carcinomas. It starts from a milk duct of the breast, breaks through the wall of the duct, and grows into the fatty tissue of the breast. It also may spread to other parts of the body through the lymphatic system and bloodstream [26]. That is to say, the tumor not only contains tumor cells, but also includes other kind of tissues, such as fatty tissue, connective tissue, blood vessel, etc. The difference of their echoic properties causes texture variation in BUS images. It makes BUS images to have complex textures. Here, the bag is an ROI and the instances are the checkpoints in the ROI. Due to the complex nature of BUS images, we cannot simply consider that the checkpoints in a benign mass are all negative; and if only one checkpoint is positive, then the mass is malignant.

Proposed Method

The image database used in this research contains 168 cases (72 malignant and 96 benign). The average size of the tumors was 2.74 ± 1.3 cm (range, 0.77–5.64 cm). The ultrasound images were acquired by the Department of Ultrasound, Second Affiliated Hospital of Harbin Medical University. All images were collected by using a VIVID 7 with a 5–14-MHz linear probe and captured directly from the video signals. Pathologic validation was used for cancers and biopsy was used for benign lesions. Informed consents to the protocol were obtained from all patients in this study. Among malignant nodules, there were 61 invasive duct carcinomas, 7 invasive lobular carcinomas, 2 ductal carcinomas in situ, 1 mucinous carcinoma, and 1 medullar carcinoma. Among benign nodules, there were 83 mammary fibroadenomas, 8 intraductal papillomas, 3 mammary lipomas, and 2 benign phyllodes tumors. The privacy of the patients has been well protected. The original BI-RADS ratings of these lesions are assessed by experienced radiologists according to [27] and are listed in Table 1.

Table 1.

Original BI-RADS ratings

Pathology	BI-RADS rating
	Categories—2	Categories—3	Categories—4	Categories—5	Categories—6	Total
Benign	17	58	19	2	0	96
Malignant	1	4	22	38	7	72

The MIL task is to build a model based on the given images (bags) and predict the class labels of future images (bags) [17]. Formally, let χ denote the bag space and γ be the set of class labels. In traditional supervised learning case, the training data consist of examples 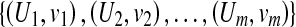, where U_i ∊ χ is a bag and v_i ∊ γ is the label of U_i. The goal is to train a function f:χ → γ to predict label y for new bag U.

However, in MIL, the training data consist of bags and bag labels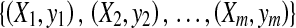, where 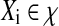is a bag which has a set of instances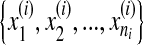, ,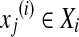, 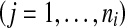n_i is the number of instances of the bag X_i and y_i ∊ {− 1, + 1} is the known label of X_i [28]. The key challenge of MIL is the ambiguity in the labels of the instances.

The standard assumption of MIL is that the positive bag has at least one positive instance and the negative bag has no positive instance [17]. The generalized multiple-instance learning (GMIL) was proposed. It extends the assumption of how a bag's label is determined by its instances. In GMIL, a set of underlying concepts are considered; each concept may contribute to the classification. It assumes that a number of instances in each concept could determine the bag's label [29].

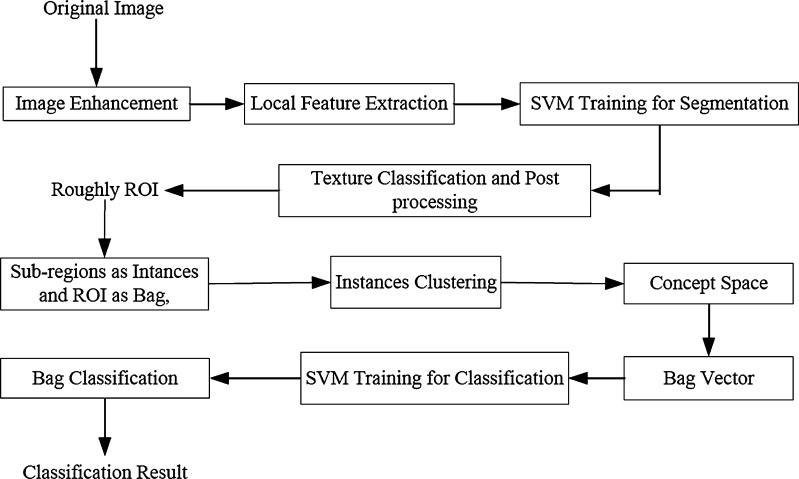
For our proposed approach, the GMIL idea was adopted. First, the concepts were learned from the instance space. Then, the bag was projected to the concept space and the projection could be used to construct the bag features. Finally, a trained SVM is employed to classify bags. The flowchart of the proposed approach is presented in Fig. 3.

Fig. 3.

Flowchart of the proposed method

When a rough ROI is obtained and the local features of subregions are extracted, the classification task can be converted into an MIL task. The subregions of ROI can be viewed as the instances and the ROI can be considered as a bag. The key difficulty of MIL is the ambiguity of the instance labels. One method is to find which instance is like positive most by learning from instances statistically, such as DD algorithm [19]. The other method is to map the instance space to other spaces in which traditional learning algorithms can be employed, such as Citation-kNN algorithm [22].

In our proposed algorithm, to learn concepts from instances, the instances of all the bags are put together and clustered. Each cluster can be viewed as a concept in the concept space. The clusters can also reflect the distribution pattern of the instances. All the clusters can be considered as the concept space constructed from the instance space, i.e., by clustering, the instance space can be transformed to the concept space.

Each instance of an ROI can be mapped to a concept in the concept space. Then, a bag can be represented by a fixed-length vector in the concept space. The element of the vector can be represented by the number of instances in a concept normalized by the number of instances of the bag. It reflects the distribution characteristics of a bag in the concept space. After transformation, traditional supervised learning algorithm can be employed in concept space.

Formally, the steps can be defined as follows:

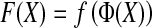1

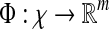2

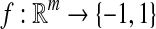3

where F maps the instance space to the concept space and projects the bag in this space to obtain 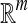Euclidean space; and f is a traditional supervised classifier learned from 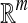which is used to classify the bags.

When a new bag is input, each instance of the bag is assigned to a concept (cluster) in the concept space learned from the training bags. Then, the bag can be represented by a vector whose length is equal to the number of concepts (clusters). And the vector is input to the classifier learned using training bags to classify new bags.

A cluster method can be used to construct the concept space. In this paper, self-organizing map (SOM), or K-means, or fuzzy C-means is employed to transfer the instance space to the concept space, and their corresponding results will be compared. We will briefly discuss them below.

• Self-organizing map

SOM [30] is an unsupervised learning method. SOM represents input data by a small number of neurons and still preserves the topology of input data. The goal of SOM is to map arbitrary dimension input data to a one- or two-dimensional discrete map [31].

• K-means

K-means clustering algorithm is one of the simplest unsupervised learning algorithms to partition a data set into k groups. Given a set of instances (x₁, x₂, .., x_n), where each instance is a d-dimensional vector, k-means clustering aims to partition n instances into k sets (k < n) and S = {S₁, S₂, …, S_k} to minimize the within-cluster sum of squares [32].

• Fuzzy C-means

In fuzzy C-means (FCM) algorithm [33], each instance has a degree of belonging to clusters, rather than completely belonging to just one cluster. It iteratively classifies the data into optimal c partitions. All the instances of training bags can be mapped to the concept space by using SOM, or K-means, or fuzzy C-means.

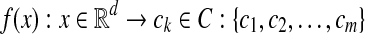4

where x is an instance of a bag, c_k is the kth concept in the concept space, and m is the number of clusters.

For our proposed method, the concepts can be considered as visual words [26, 33] which reflect the local patterns of the tumor. A bag can be represented by a vector in the concept space .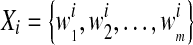

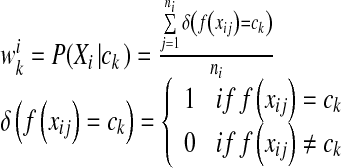5

where n_i is the total number of instances in the ith bag, and 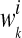is the conditional probability of the bag X_i with the kth concept.

Then, each bag can be represented by a vector in 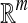Euclidean space. And the MIL problem is transformed to a traditional supervised learning problem.

The SVM is used to train and classify the bags in this paper. The radius basis function (RBF) is chosen as the kernel.

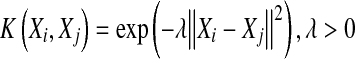6

where K(X_i, X_j) is the RBF kernel function, X_i and X_j are the bag feature vectors, and λ is the kernel parameter, λ > 0.

• Citation-KNN and EM-DD

For comparing with other MIL algorithms, the Citation-KNN [22] and expectation maximization methods with diverse density (EM-DD) [34] algorithms are implemented as well. Citation-kNN is an improved kNN algorithm suitable for MIL. It is a kind of lazy learning method which defers processing the training data until a query needs to be answered [35]. It borrows the concepts of citation and reference from scientific literatures. Citation-kNN achieves robustness by taking into account the impact of citers, but it is still sensitive to the structure of local data. In our proposed method, the concepts (clusters) reflect the global distribution characteristics of instances and our method is more robust than the Citation-kNN.

The DD algorithm [19] tries to learn “true” concept from feature space. EM-DD is an improved DD algorithm. It considers the label of the instance as a missing attribute and estimates the label by using EM approach [34]. EM-DD algorithm is still under the assumption of traditional MIL, i.e., there is at least one positive instance in a positive bag and there are all negative instances in a negative bag. But this assumption is not suitable for BUS image classification.

Experimental Results

In experiments, k-fold cross-validation approach is used. All the images are randomly divided into ten groups. Each time, one group is chosen for testing and the others are used for training.

The performance of the proposed feature extraction and classification strategy is evaluated by the classification accuracy. Define the number of correctly and incorrectly classified malignant tumors as true positive (TP) and false negative (FN), and the number of correctly and incorrectly classified benign tumors as true negative (TN) and false positive (FP), respectively; the classification accuracy (ACC) is defined as: (TP + TN) / (TP + TN + FP + FN).

For comparison, the number of clusters in SOM, or K-means, or fuzzy C-means is chosen from 4 to 100. For determining the parameters C and λ, the grid search method is used [36]. C = 8 and λ = 4 are determined by experiments. The results are shown in Table 2.

Table 2.

Performance comparing with that of [14]

Method	TP	TN	SE (%)	SP (%)	ACC (%)
[14]	58	77	80.56	80.21	80.36
SOM (4 neurons)	55	78	76.39	81.25	79.17
k-means (4 clusters)	52	82	72.22	85.42	78.42
FCM (4 clusters)	51	77	70.83	80.21	76.19
SOM (9 neurons)	61	80	84.72	83.33	83.93
k-means (9 clusters)	57	82	79.17	85.42	82.74
FCM (9 clusters)	58	76	80.56	79.17	79.76
SOM (16 neurons)	62	77	86.11	80.21	82.74
k-means (16 clusters)	64	79	88.89	82.29	85.12
FCM (16 clusters)	54	79	75.00	82.29	79.17
SOM (25 neurons)	62	80	86.11	83.33	84.52
k-means (25 clusters)	63	81	87.50	84.38	85.71
FCM (25 clusters)	56	78	77.78	81.25	79.76
SOM (36 neurons)	62	84	86.11	87.50	86.90
k-means (36 clusters)	59	86	81.94	89.58	86.31
FCM (36 clusters)	53	75	73.61	78.13	76.19
SOM (49 neurons)	62	91	86.11	94.79	91.07
k-means (49 clusters)	62	85	86.11	88.54	87.50
FCM (49 clusters)	48	82	66.67	85.42	77.38
SOM (64 neurons)	54	91	75.00	94.79	86.31
k-means (64 clusters)	58	86	80.56	89.58	85.71
FCM (64 clusters)	51	80	70.83	83.33	77.98
SOM (81 neurons)	58	88	80.56	91.67	86.98
k-means (81 clusters)	62	84	86.11	87.50	86.90
FCM (81 clusters)	57	74	79.17	77.08	77.98
SOM (100 neurons)	61	87	84.72	90.63	88.10
k-means (100 clusters)	61	86	84.72	89.58	87.50
FCM (100 clusters)	58	74	80.56	77.08	78.57

From Table 2, we can see that, in most cases, the method proposed by this paper has better performance than that of [14]. And the best performance is reached when 49 neurons were employed by SOM. The difference of ACCs between SOM and fuzzy C-means is significant (p < 0.001). But the difference of ACCs between SOM and k-means is not significant (p > 0.05). This confirms that the local features can be used to classify the tumors into benign and malignant well. When local features are modeled and extracted, the problem is more suitable for utilizing MIL than utilizing traditional supervised learning as described in [14]. The receiver operator characteristic (ROC) curves are also utilized to evaluate the performance of the proposed method as shown in Fig. 4.

Fig. 4.

The ROC curves of the proposed method and the one in [14]

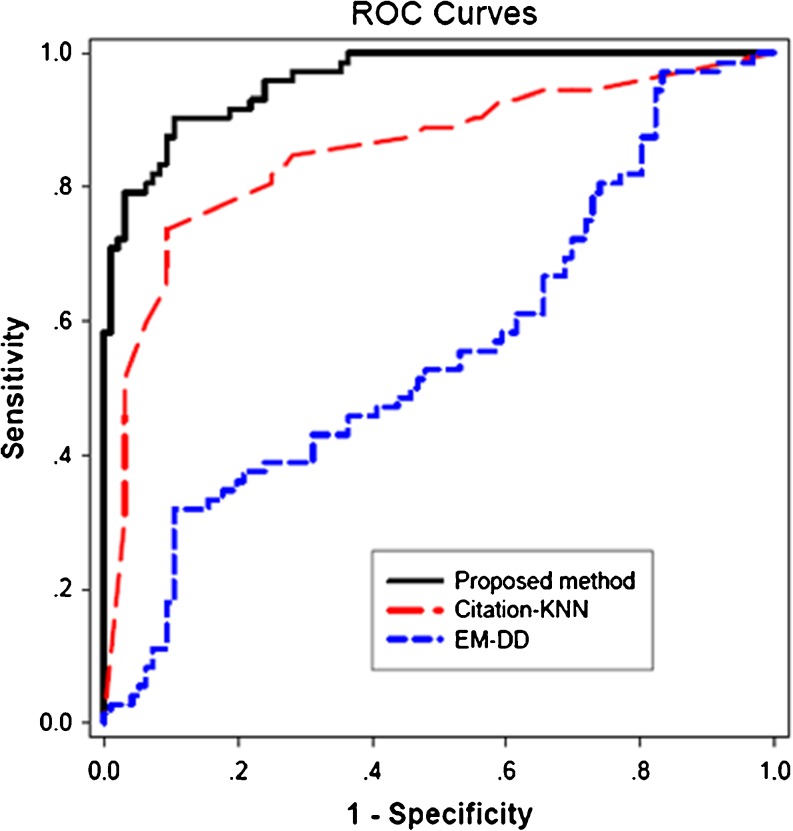
The area under curve (AUC) of the proposed method is higher than that of the method in [14] (0.96 vs. 0.87, p < 0.005). The ROC curves compared with that of Citation-KNN and EM-DD are shown in Fig. 5. The AUC of the proposed method is higher than that of Citation-KNN (0.96 vs. 0.85, p < 0.0001) and EM-DD (0.96 vs. 0.56, p < 0.0001).

Fig. 5.

The ROC curves of the proposed method, Citation-KNN, and EM-DD

Discussions and Conclusions

US imaging becomes an important diagnostic tool for breast cancer detection. CAD system can help radiologists in making decision objectively and quantitatively. Segmentation is an important step for most of CAD systems. The global features of lesions such as shape and margin can be extracted from segmented results. But due to low quality of the BUS images, the auto-segmentation is very difficult [7].

The local texture features are also effective in differentiating benign and malignant breast tumors [8–14]. When these features are used to describe the lesion, the lesion can be viewed as a bag and the subregions of the lesion can be viewed as instances of the bag. The classification problem can be transformed from traditional supervised learning to MIL.

The proposed novel MIL method is utilized to classify tumors into benign and malignant. The tumor region is located by rough segmentation and the local features are used to describe tumors. The instance space is mapped to the concept space and a classifier is trained to differentiate the tumors. The experimental results show that the proposed method has much better performance, and it will be useful for CAD systems of BUS images. The AUC of the proposed method is higher than that of the method in [14] (0.96 vs. 0.87, p < 0.005). The AUC of the method is also higher than that of Citation-KNN (0.96 vs. 0.85, p < 0.0001) and EM-DD (0.96 vs. 0.56, p < 0.0001).

There are two limitations in this study. First, we just concentrated on local texture features. The global features (such as shape, margin, etc.) are also important. The combination of global features and local features will be studied in the future. Second, most cases in our study are invasive duct carcinomas mammary fibroadenomas which are more common. Other types should be studied in future research.