Symmetry arguments in chemistry

Abstract

The use (and misuse) of symmetry arguments in constructing molecular models and in the interpretation of experimental observations bearing on molecular structure (spectroscopy, diffraction, etc.) is discussed. Examples include the development of point groups and space groups for describing the external and internal symmetry of crystals, the derivation of molecular symmetry by counting isomers (the benzene structure), molecular chirality, the connection between macroscopic and molecular chirality, pseudorotation, the symmetry group of nonrigid molecules, and the use of orbital symmetry arguments in discussing aspects of chemical reactivity.

Because of the preoccupation with shapes and properties of atoms, molecules, and crystals, symmetry considerations have been involved in chemistry ever since its beginnings. Even in pre-Socratic Greece, Democritus taught that the material world around (and even including) us is composed of very tiny particles in constant motion, the so-called atoms. These atoms were purely mental constructs, invisible, intangible, so that, unhampered by any need or even possibility of experimental verification, one could give them any shapes and properties one liked. The properties of substances were supposed to be determined in some way by the shapes of these atoms. Thus, atoms of water were supposed to be round and smooth, able to roll over one another, while atoms of iron were rough and uneven in shape so that they were able to cling together and form a solid body. Roughly about the same time, an alternative model was proposed by Empedocles, according to which there are only four primary substances or elements—fire, air, earth, and water—all the other substances being made up of these elements in different proportions. As is well known, Plato took the step of associating each of these elements with one of the first four regular polyhedra (known ever since as the platonic solids): fire = tetrahedron, air = octahedron, earth = cube, water = icosahedron. Plato drew far-reaching conclusions. From the fact that the tetrahedron, octahedron, and icosahedron all have equilateral triangular faces, he deduced that fire, air, and water could be transformed into one another. On the other hand, since the cube, the symbol for the element earth, could not be decomposed into equilateral triangles, he concluded that earth could not be transformed into fire, air, or water. The dodecahedron with its pentagonal faces was regarded as something special—the fifth essence, the quintessence—of a purer quality than the other four. The quintessence was supposed to have been formed at the creation of the Universe, when it flew upwards to form the stars. Thus, unrestricted by the need to check hypotheses with brutal facts, the Greeks found in the platonic solids a theory of chemistry, of fundamental particles, and even of cosmology; a classical theory of everything!

Crystal Shapes

We jump two millennia to the year 1611, when Kepler (1) drew a connection between the macroscopic symmetry of a crystal and the packing of elementary, invisible building blocks. The example Kepler chose was the hexagonal symmetry of snowflakes, which he explained in terms of the close packing of spherical elementary particles. Kepler explained not only the shapes of snowflakes but also the shapes of honeycombs and pomegranate seeds. In this he made an important discovery. Space-filling can be achieved by packing identical triangular, square, and hexagonal prisms as well as parallelepipeds, but Kepler found that this could also be done with the rhombic dodecahedron, the figure obtained from the cubic close-packed arrangement of spheres if each sphere is separated from its 12 neighboring spheres by plane faces.

In three dimensions, there are two regular ways of stacking close packed nets of spheres: cubic and hexagonal close packing, as well as an infinity of irregular ways. It is a remarkable fact that about 30 elements, including most of the metals, crystallize in one of the two regular patterns, and some in both. Thus these ridiculously simple symmetry arguments lead to mostly correct although not infallible predictions for the structure of metals.

It is remarkable that so many of the early arguments for the particulate nature of matter came from speculations about the beautifully symmetric shapes of crystals, not only snowflakes. By the middle of the 18th century it had been recognized that although crystals of a given substance grow in different shapes, the shapes have something in common: they show the same interfacial angles. To explain this constancy Haüy (2) suggested that crystals were built by regular repetition of fundamental units—molécules intégrantes—which could have any arbitrary shape. Hessel (3) showed that if crystals are built by regular repetition on a lattice, their external symmetry is restricted to only 32 possible point groups, the so-called crystal classes. In particular, the only possible rotation axes are of order 2, 3, 4, and 6 (5-fold symmetry being forbidden). The next step was to enumerate all ways in which such units could be arranged in repeating patterns, a purely geometric problem that was solved by the end of the century. There are exactly 230 ways of combining elements of point symmetry and translational symmetry to form space groups, as was found independently and almost simultaneously by Federow, Schoenflies, and Barlow (4). Thus, by 1912, when von Laue discovered x-ray diffraction, the mathematical theory of crystal symmetry was essentially complete, although nothing was known about the actual structure of the molécules intégrantes.

By now, the atomic structures of more than 150,000 crystals have been established by x-ray and neutron diffraction, providing an enormous library of information on the structures of molecules and their mutual interactions. Space group theory has been an invaluable aid in this endeavour. It therefore came somewhat as a surprise when in 1984 certain Al/Mn alloys were found to give diffraction patterns with supposedly forbidden icosahedral symmetry, so-called quasicrystals, based on quasiperiodic structures. These are not a “new form of matter,” as was asserted in some of the earlier, more sensational accounts, but can be accommodated with minor modifications within the existing conceptual framework, as will be discussed in other papers in this colloquium (5, 6).

Counting Isomers

But symmetry arguments also entered chemistry from a quite different direction. Well before the elucidation of molecular structure by physical methods became possible in this century, structural formulas for thousands of compounds had been inferred by purely chemical methods, that is to say, by an intricate, characteristically chemical chain of reasoning based on simple experimental facts. Substances were weighed, dissolved, allowed to react, and the products of reaction were isolated, purified, and subjected to elemental analysis. The structure assigned to a compound was initially a kind of summary of the reactions that the compound could undergo. Thus, as a simple example, the formula CH₃·CO·OH for acetic acid was a concise expression of the facts: (i) that one H atom behaves differently from the other three, (ii) that the two oxygen atoms behave differently (e.g., one can be replaced by another atom or grouping while the other is retained), and (iii) that the two carbon atoms behave differently, one being detachable as carbon dioxide, the other as methane or a methyl derivative. In this way, each compound could be associated with a formula, and each formula with a compound. Slowly, by the 1860s, such formulas began to be considered as actual atomic arrangements in which the atoms were linked by “bonds,” subject to certain rules: valency rules. Each type of atom was imagined to form a definite number of bonds—e.g., four for carbon, three for nitrogen, two for oxygen, and only one for hydrogen or for chlorine. A given set of atoms could be joined into different patterns corresponding to different molecules, known as isomers, each corresponding to a different substance. Once the molecular concept had established itself, symmetry arguments began to flower.

I mention two examples. It was known by 1860 that the benzene molecule consists of six atoms of carbon and six of hydrogen, C₆H₆. By standard chemical methods, these hydrogens can be replaced, one at a time, by chlorine atoms to give a quite definite number of isomers. Thus, there is only one monosubstituted compound, which, on further chlorination, yields a mixture of three disubstituted isomers. When the chlorination process is carried a stage further, one of these isomers gives a mixture of three trisubstituted compounds, one gives a mixture of two such compounds, and one gives a single pure product (Fig. 1).

Figure 1.

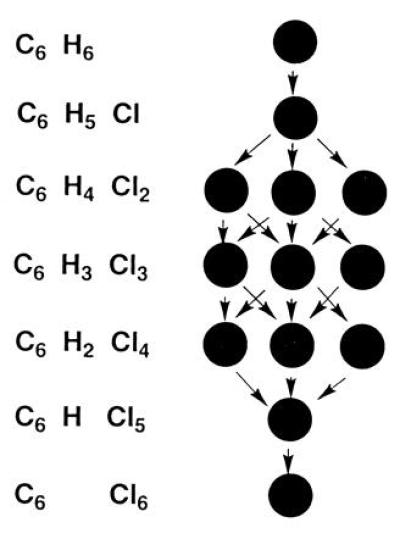
Relationships among the chloro-substituted benzenes, C₆H_6-nCl_n, n = 0–6.

The solution of this problem was provided by Kekulé (7), who proposed a cyclic structure with 6-fold symmetry for the benzene molecule. This gives the correct number of isomers of the chlorinated compounds and explains their inter-relationships (Fig. 2) but it cannot be reconciled with the valency rule, four bonds per carbon atom, that had been propounded by Kekulé himself only a few years earlier. This rule would demand a less symmetric molecule, with only a 3-fold rather than a 6-fold rotation axis (Fig. 3). At the time there was no way of determining the atomic arrangement in molecules directly; the structures in question were purely intellectual constructions designed to explain the chemical facts, and one essential fact was that there were only three disubstituted benzenes and not four, as would be required by the lower symmetry model. Kekulé’s proposal was to keep the cyclic formula but with the proviso that the single and double bonds change place rapidly—the molecule was supposed to be a kind of hybrid of two structures that maintained the valency rules, a concept that was to recur a couple of generations later in the guise of mesomerism and resonance theory. The hexagonal structure was not the only one that was proposed at the time to explain the facts but it is the one that endured.

Figure 2.

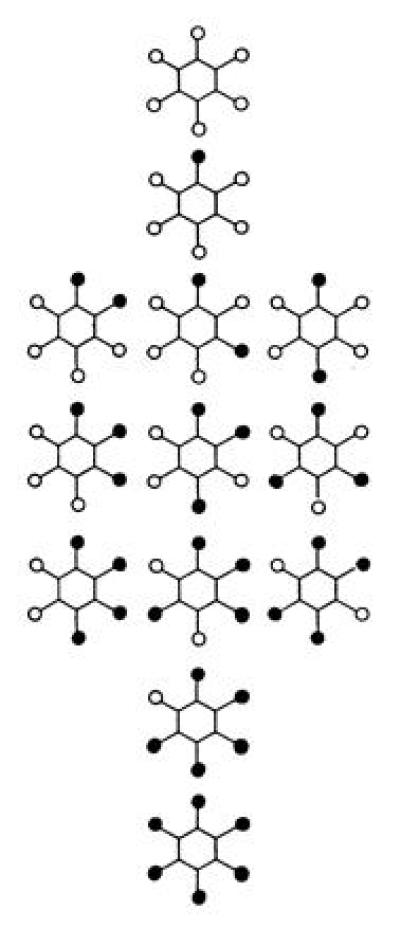
Isomers of chloro-substituted benzenes, C₆H_6-nCl_n, n = 0–6, based on hexagonal symmetry of the benzene molecule.

Figure 3.

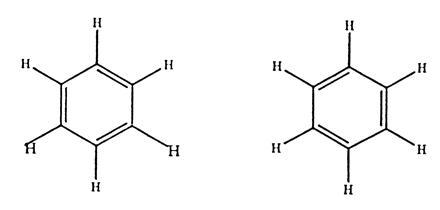
Structure of benzene that satisfies the quadrivalency of carbon. Kekulé assumed that the single and double bonds interchange rapidly.

Extrapolation from the successful benzene formula might lead to the expectation that the molecules of the analogous eight-membered ring compound C₈H₈, cyclooctatetraene, would have an analogous octagonal planar hybrid structure. However, as was established many years later, the molecules of C₈H₈ have a nonplanar structure with alternating double and single bonds. The reason why the six-membered ring molecule of benzene has its highest possible symmetry, while the eight-membered ring of cyclooctatetraene has a lower symmetry than its maximum possible became clear only with the development of quantum chemistry.

Symmetry arguments sometimes led to the right conclusion, as with benzene, but sometimes to the wrong conclusion, as in the early controversy about the molecular structure of cyclohexane, C₆H₁₂. As there is only one monosubstituted isomer C₆H₁₁Cl, the cyclohexane molecule could be assumed to have D_6h symmetry, with all valency rules satisfied and all hydrogen atoms equivalent (8). On the other hand, the concept of the tetrahedral carbon atom requires a nonplanar carbon ring with bond angles of around 109.5° instead of 120°, as in a planar hexagon (9). The nonplanar structure (D_3d symmetry) has two kinds of hydrogen atom (called equatorial and axial) and it should therefore give rise to two monosubstituted isomers (Fig. 4). But only one compound could be isolated. For many years, therefore, the planar structure was generally accepted. What the early investigators did not know was that at room temperature the cyclohexane molecule undergoes rapid ring inversion, which interchanges the equatorial and axial substituents. This inversion process can now be followed by nuclear magnetic resonance spectroscopy. Around −90°C there are two distinct signals from the hydrogen nuclei, corresponding to the two kinds of environment; at this temperature the inversion frequency is so slow that the two kinds of hydrogen retain their identity during the characteristic time resolution of the experiment. As the temperature is raised, however, the inversion frequency increases, the signals broaden and finally coalesce, corresponding to a set of “averaged” hydrogens. At room temperature, molecules with a substituent in an axial position and those with a substituent in an equatorial position are in rapid equilibrium, so that only the more stable of the two isomers is isolable. Rapid ring inversion was responsible for the failure to isolate more than one monosubstituted isomer.

Figure 4.

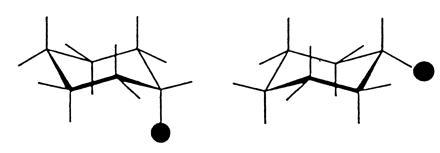
Axial and equatorial isomers expected of a monosubstituted cyclohexane with a nonplanar carbon skeleton with bond angles close to the tetrahedral angle of 109.47°. Ring inversion interchanges the axial and equatorial positions.

Molecular Chirality

Starting from observations on the morphology of ammonium sodium tartrate crystals deposited from wine, Pasteur found that tartaric acid can occur as two chemically indistinguishable compounds that differ with respect to their effect in rotating the plane of linearly polarized light: solutions of one compound rotate it to the left, solutions of the other to the right, by equal amounts (10). Unhampered by the lack of a detailed theory of molecular structure, Pasteur postulated that the molecules of the two “optical antipodes” were related as nonsuperimposable mirror images. He went even further and proposed that the ability to produce substances in a single “dissymmetric” form is an intrinsic property of living systems. Today we know that achiral molecules are the exception; the vast majority of molecules are chiral, that is to say, they lack improper symmetry elements and hence are not superimposable on their mirror images. Normal laboratory syntheses based on achiral or racemic (optically inactive, containing equal amounts of the two mirror-image forms, so-called enantiomers) starting materials lead to racemic products, while the molecules involved in living systems occur almost always only as a single chiral form, as Pasteur foresaw. This means that the physiological effects of enantiomers can be very different, a matter of life and death, and one of great concern in the pharmacological industry, where considerable efforts are made to obtain products in a single chiral form, either by separation of the racemic mixture or by “chiral” synthesis leading to the desired form.*

For many years it was not known which of the two possible enantiomers for any optically active compound corresponded to the dextrorotatory isomer and which to the levorotatory. All that the then available chemical methods could do was to relate the various spatial configurations of compounds among one another, i.e., to establish the configuration of a given molecule relative to some standard, usually taken as (+)-glyceraldehyde. This was arbitrarily assigned the spatial configuration I and conventionally represented by the projection formula II (Fischer projection). Within this system, for example, the configuration of (+)-tartaric acid was known to be III and that of the naturally occurring amino acids to be IV, but there was no way to establish whether the actual configuration of the reference molecule was I or its mirror image. When I was a student I was told that it was impossible to answer this question, even by x-ray diffraction.

The crux of the problem lay in Friedel’s Law, which stated essentially that x-ray diffraction effects are centrosymmetric, whether the diffracting crystal itself has a center of symmetry or not. In other words, the diffraction patterns from a pair of enantiomorphic crystals are indistinguishable. Friedel’s Law rests on the assumption that the intrinsic phase change during the scattering of x-rays is the same for every atom. If this is true, then phase differences between different beams diffracted by a crystal depend only on differences in path length. For a noncentrosymmetric crystal, the structure factors F(h) and F(−h) for propagation of x-rays along two opposite directions are then related as a pair of complex conjugates, and the corresponding diffracted intensities I(h) and I(−h) are equal. In fact, as was already known by 1930 (11), Friedel’s Law is not strictly true because the assumption on which it is based is only approximately valid. If the x-ray wavelength is close to an absorption edge of some of the atoms in the crystal, these atoms do not scatter exactly in phase with the others. There is a slight “phase lag.” For propagation along two opposite directions, the phase differences due to the arrangement of the atoms in space are simply reversed, but the same phase lag applies to both. For noncentrosymmetric crystals, this leads to a difference between the intensities of pairs of reflections propagated in opposite directions: I(h) ≠ I(−h). In 1951, Bijvoet showed (12) that this difference could be used to make the connection between macroscopic and molecular chirality. The arbitrarily assigned spatial configuration I assigned to (+)-glyceraldehyde turned out to be correct after all.

The absolute configuration of organic compounds is usually described by means of the CIP system, so-named after the initials of its inventors (13). It consists of a series of rules for putting the four groups around a tetrahedral center into a priority sequence: a, b, c, and d, where a > b > c >d. The first rule involves the atomic number of the directly bonded atoms; high atomic number takes precedence over low. If this is not enough to determine the sequence one proceeds to the second rule, which involves atomic mass, and if this is still not enough one proceeds outwards to the next set of atoms and applies these and other, more complicated rules. The chirality sense of the central atom is then assigned by the following convention: view the chiral center from the direction opposite to the group d of lowest priority. If the sense of rotation of the other three groups, from a to b to c is clockwise, then the chirality sense is designated as R (rectus). If it is anticlockwise, then the chirality sense is S (sinister)†. Thus, the central carbon atom in I (and II) is R, the tartaric acid molecule in III is R, R, and the amino acid in IV is S.

We now know that the amino acids of proteins all have the S configuration (as in IV), and that the ribose units in nucleic acids all have the R configuration (as in II), and thus we know on which side of the mirror plane the molecules in our bodies, and those of all other forms of life on this earth, exist. There is no problem in explaining the Darwinian advantage of bioactive polymers containing only one set of homochiral monomers. A polypeptide made by random condensation of R- and S-amino acids from a racemic mixture would have no chance of folding into the kind of definite pattern characteristic of an enzyme, and a polynucleotide built from a random sequence of R- and S-ribose molecules could not achieve the regular repeating helical structure required for genetic information storage and retrieval. In the primitive pre-biotic world, once one sense of chirality or the other gained a slight dominance as a result of chance fluctuations in any autocatalytic process, the other would be rapidly eliminated.

However, this kind of argument leaves the question of the original choice of one or the other set of enantiomers open. Was it simply a matter of chance, or was there an underlying physical reason for the preference? Several possibilities have been proposed over the years, such as the role of electric and magnetic fields (14) and especially that of parity nonconservation and the electroweak interaction (15). The enantiomeric energy difference due to the electroweak interaction is very small, of the order of 10⁻¹⁴ J·mol⁻¹, corresponding to an excess of about 10⁶ molecules of the more stable enantiomer per mol of racemate in thermodynamic equilibrium at 300 K (note that the expected excess of R or S molecules from random “heads or tails” selection would be of the order of 10¹² molecules for one mol of substance!). Inclusion of the electroweak interaction into quantum mechanical ground state energy calculations is indeed reported to show a slight preference for the R-sugars and the S-amino acids, the ones selected in the course of evolution. However, the significance of this for autocatalytic and other chemical reactions is not clear. There is still no consensus on the matter, nor is there likely to be.

Teaching Symmetry Concepts

Until about 30 years ago, the role of formal symmetry arguments in chemical thought was almost negligible. Few chemists found any use for symmetry concepts in their everyday thinking, and those few were mostly at the physical end of the science - spectroscopists, crystallographers, theoreticians. The practical chemist, engaged in making new compounds, in isolating, purifying and identifying them, in unraveling the mechanistic details of chemical reactions, was more likely to be aware of symmetry considerations in art than in his own science. And this was reflected in chemical textbooks and in the teaching of the subject. Symmetry was hardly mentioned; only, perhaps, in the explanation of “optical activity,” as discussed above, but even there the emphasis was on the easily grasped concept of the “asymmetric carbon atom” rather than on the distinction between superposable and nonsuperposable mirror-images in terms of fundamental symmetry properties.

Today the situation is very different. Books that purport to explain group theory to chemists appear every year. Even elementary textbooks now contain mandatory chapters dealing at least with point group symmetry and often more. Along similar lines, many chemistry courses include explanations and discussions of symmetry at very early stages. In the general chemistry course that I taught in the 1980s, elementary symmetry ideas were introduced around the third week, immediately following the fundamental concept of the molecule. I must admit that some students had initial difficulty in seeing the point of learning about symmetry. While I chose highly symmetric molecules such as benzene or methane to make my point, many students were aware such molecules are quite atypical. Only a tiny fraction of the millions of known compounds are built from molecules with any symmetry whatsoever. “Learn now, understand later,” was my advice, and I hope it benefited them in the end.

Why did this change in the cultural background of chemists take place? There are probably many contributory factors; the intrusion of orbital symmetry arguments, the increased importance of physical methods, such as NMR spectroscopy and x-ray crystallography in molecular structure determination, the discovery of the so-called fullerenes, mentioned elsewhere in this colloquium (6), and probably others. For further reflections on this topic see ref. 16.

In my own undergraduate and doctoral work, I learned a little about point groups and space groups in connection with the external and internal symmetry elements of crystals but I had never heard of group theory. My first exposure came when I was a postdoctoral student at Caltech. Around 1950, Bryce Crawford came to Pasadena to give a course on molecular vibrations and told us how the normal vibrations of simple molecules could be nicely classified by group theory. I was impressed. We also learned that this method could be useful in many other applications, such as the classification of molecular wave functions in quantum mechanics. When I met Linus Pauling in the corridor one day I told him how impressed I was with Crawford’s lectures and asked why he, Pauling, had almost nothing to say about group theory in his Nature of the Chemical Bond or his Introduction to Quantum Mechanics. “Jack” he said, “if you need group theory to solve the kind of problems you’re tackling, then you’re in the wrong line of business.” The point was that Pauling could see the relationships in his head, he did not need this elementary group theory, and he couldn’t be bothered by the formalism.

Pseudorotation

A beautiful and simple application of this kind of group theory led to the concept of pseudorotation (17). The carbon skeleton of cyclopentane C₅H₁₀ is an equilateral pentagon. If the internal angles were all exactly 108° then, of course, the pentagon would be planar, but this arrangement was known from chemical strain theory to be energetically less stable than one in which the pentagonal ring is nonplanar. The relative positions of N points in space are defined by 3N-6 independent coordinates, of which 2N-3 can be chosen in an arbitrary plane, leaving N-3 coordinates to describe the deviation from planarity; for n = 5, there are thus 2 coordinates to describe the puckering of the ring. With the use of symmetry coordinates (linear combinations of the initial coordinates with special properties when transformed according to the symmetry operations of some reference structure), it could be shown (17) that: “… the ring puckering motions are: first, an ordinary vibration in which the amount of puckering oscillates about a most stable value, and second, a pseudo one-dimensional rotation in which the phase of the puckering rotates around the ring. This is not a real rotation since the actual motion of the atoms is perpendicular to the direction of rotation and there is no angular momentum about the axis of rotation.” The pseudo one-dimensional path runs along a circle in the sub-space spanned by the doubly degenerate E₂" symmetry displacement coordinates of the regular pentagon with D_5h point group symmetry.

Other molecular processes that run along almost isoenergetic pathways involving pairs of degenerate deformation coordinates include the twist-boat conformational change of cyclohexane and several Jahn-Teller type deformations of symmetric molecular frameworks; see ref. 18 for examples.

Use of Symmetry Coordinates

Although the vast majority of molecules occurring in nature or created by synthetic chemistry have no symmetry, point group symmetry nevertheless provides a useful classification scheme for simple molecules. For such molecules, it is most convenient to use symmetry coordinates for describing displacements of the atoms from the equilibrium structure, e.g., molecular vibrations. This is because in harmonic approximation, i.e., if the potential energy is expressed as a sum of quadratic terms in the various displacement coordinates, vibrations belonging to different irreducible representations of the molecular point group are not coupled—there are no crossterms between them. Those that belong to the same irreducible representation are coupled and thus cannot be treated separately from one another. The symmetry classification of more-or-less rigid molecules, i.e., those where the atomic displacements are small, is fairly straightforward, but, for nonrigid molecules, the problem becomes more difficult and the choice of a reference point group may not be clear cut.

Nonrigid Molecules

As a simple example we take the molecule of ethane, H₃C—CH₃, two methyl groups linked by a carbon—carbon bond. For our purposes, we regard the methyl groups as rigid units with 3-fold symmetry. An arbitrary mutual orientation of the methyl groups then corresponds to a molecule with D₃ symmetry, order 6 (Fig. 5), so that there are six symmetry equivalent arrangements of the same figure. If we now allow rotation about the central bond, new possibilities arise. Arrangements R and R² show the result of rotating the distal methyl group by 120° and by 240° (rotation by 360° produces the initial arrangement E). Arrangements R and R² are isometric with E, and each of them also gives rise to six symmetry equivalent arrangements, making 18 in all. Moreover, since the initial arrangement E is chiral, there is another matching set of 18 isometric structures that are enantiomorphic to E. Thus the order of the isometric symmetry group of ethane is 36. Note that rotation of one methyl group with respect to the other is not a point group symmetry operation of the ethane molecule regarded as a rigid figure but it is a symmetry operation of the isometric group of the molecule.

Figure 5.

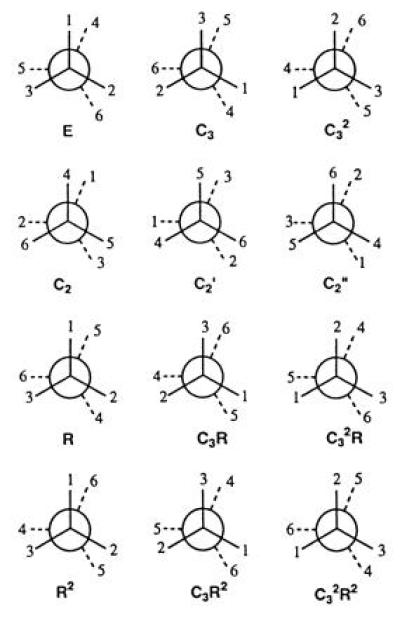
A set of 18 isometric structures of the ethane molecule, obtained by symmetry operations of the D₃ point group and by rotation of one methyl group with respect to the other. There is a matching set of 18 isometric enantiomorphic structures, so the order of the isometric group is 36.

Special conformations of the ethane molecule have higher symmetry than D₃; there is a set of D_3h conformations (with the hydrogen atoms eclipsing one another) and one of D_3d conformations (with the hydrogen atoms perfectly interposed). The latter set is the one of lowest potential energy. At normal temperature ethane molecules undergo torsional oscillation about a D_3d conformation, and a considerable fraction accumulate sufficient energy in the torsional mode to undergo internal rotation from one D_3d conformation to another. In the analogous molecule dimethyl acetylene H₃C—C☰C—CH₃ the barrier is so small that internal rotation is virtually unhindered.

Problems of this type, first taken up by Longuet-Higgins (19), can be quite complex, especially when large displacements occur in several degrees of freedom, and have given rise to considerable controversy (20–23). In spite of their abstract nature, they are important in determining selection rules for electric dipole type transitions and in the analysis of atomic motion in isomerization reactions.

As an alternative to thinking about such problems in terms of the feasible internal motions of a flexible molecule, one can describe the isometric group in terms of the symmetry properties of the many-dimensional energy hypersurface relevant to the dynamics of all possible molecular isomerizations (24). Every possible atomic arrangement corresponds to a representative point in the many-dimensional space, and since isometric structures must be energetically equivalent, the energy hypersurface must be invariant to all symmetry operations of the isometric group. It is difficult to visualize symmetry operations in many-dimensional space, and it is sometimes helpful to restrict the discussion to particular subspaces of the (3N-6)-dimensional internal coordinate space (20, 25). Note than when cyclic coordinates (torsion angles) are used as internal coordinates to describe atomic displacements in a finite molecule, the relevant sub-space corresponds to an infinite group containing elements of translational symmetry—i.e., to a space group rather than a point group.

Orbital Symmetry Arguments

One of the main reasons for the intrusion of symmetry arguments into the culture of modern chemistry is undoubtedly the concept of the “Conservation of Orbital Symmetry,” as introduced by Woodward and Hoffmann some 30 years ago (26). In the language of quantum chemistry, orbitals are one-electron wave functions; the molecular orbitals of interest here are linear combinations of atomic orbitals, in the so-called LCAO approximation. Simple arguments based on the symmetry behavior of the molecular orbitals involved—i.e., the Woodward–Hoffmann rules, permit certain classes of chemical reactions to be classified as being symmetry-allowed or symmetry-forbidden.

As an example, we look at the molecular p orbitals (MOs) of butadiene, H₂C=CH—CH=CH₂, built from the atomic p orbitals (AOs) of the four carbon atoms; four AOs, four linear combinations, shown in Fig. 6. The AO is antisymmetric, i.e., it changes its sign at the atomic nucleus, and the MOs are, correspondingly, antisymmetric with respect to the plane in which the four carbon atoms are assumed to lie. The symmetry behavior of the MOs is indicated by the different shading. It is seen that the MO Ψ₁, the one of lowest energy, is constructed so that the four AOs have the same sign; all the lobes on one side of the plane are positive, all those on the opposite side are negative. One condition on the AOs that has to be satisfied in constructing the MOs is that the latter must be mutually orthogonal. Each additional change of sign corrresponds to an increase in the orbital energy, so that the next MO Ψ₂ must have one change of sign, Ψ₃ two such changes, and Ψ₄ three. Each of the carbon atoms contributes one electron to the p system so there are four electrons to be accommodated. Since, according to the Pauli principle, only two electrons may be housed in the same orbital, the state of lowest energy is the one in which the two lowest energy orbitals Ψ₁ and Ψ₂ contain two electrons each.

Figure 6.

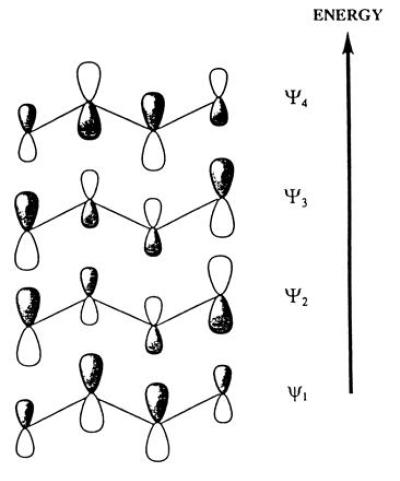
Molecular orbitals of butadiene, built from the AOs of the four carbon atoms.

The chemical behavior of a molecule is determined largely by the properties of the highest lying occupied MO, the one in which the most loosely bound electrons are found (the so-called HOMO or “frontier orbital”). In our butadiene example this is Ψ₂. The symmetry properties of this orbital should therefore determine the course of the chemical reactions of butadiene, at least as long as the molecule is supposed to remain in its electronic ground state.

We now apply this kind of reasoning to follow the course of a simple reaction of butadiene, the ring-closure leading to cyclobutene. For identification purposes, we start with an unsymmetrically 1,4-disubstituted butadiene; call one of the substituents P, the other Q. If we now form a new bond between the outer carbon atoms to form a closed ring, there are two possible outcomes; the substituents can end up on the same side of the ring plane, or on opposite sides. On the basis of orbital symmetry arguments, which do we expect to occur? The lower drawing of Fig. 7 shows the frontier orbital Ψ₂ in the molecular conformation in which the outer carbon atoms approach one another on the way to the ring-closure reaction. According to the Woodward–Hoffmann rules, based on orbital symmetry conservation, the orbital components at the two outer atoms must come together in such a way that lobes of the same sign match. This is only possible if the two end groups are rotated in the same sense—i.e., both clockwise or both anticlockwise. The term “conrotatory” is used to describe this kind of coupled motion. The two substituents P and Q must therefore end up on opposite sides of the ring plane. Thus, as long as the ring-closure reaction proceeds via the electronic ground state of the molecule, we expect to get the transisomer.

Figure 7.

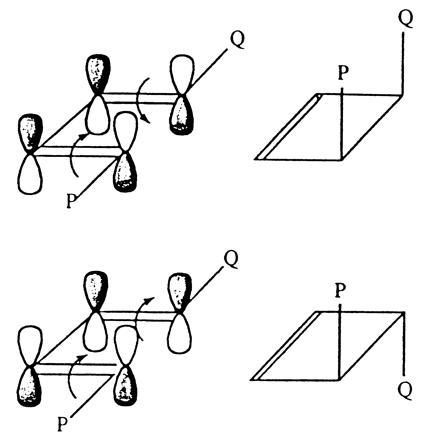
Conrotatory and disrotatory motions leading to different cyclization products of a disubstituted butadiene.

By absorption of a suitable photon, molecules can be made to exist in an electronically excited state involving the promotion of an electron from a low-lying occupied orbital to a higher-lying unoccupied one. In the butadiene example, light absorption could lead to promotion of an electron from Ψ₂ to Ψ₃. In this case Ψ₃ would become the frontier orbital and its symmetry behavior would be decisive in influencing the outcome of the ring-closure reaction. As seen from the upper drawing in Fig. 7, the lobe-overlapping condition now requires that the two end-groups be rotated in opposite senses—i.e., one clockwise and the other anticlockwise (known as “disrotatory” motion). As a result, in a photochemically activated ring closure reaction, the end groups P and Q should end up on the same side of the ring plane. Thus, the thermally activated reaction is expected to lead to one isomer, the photochemically activated one to another.

This presentation is greatly simplified and it has ignored the fact that, for thermodynamic reasons, butadiene derivatives do not undergo ring-closure reactions to form cyclobutene derivatives. It would be an uphill reaction in energy terms. In the real world, it is the other way round; cyclobutene derivatives can be transformed into butadienes, both thermally and photochemically, and the two modes of reaction indeed lead to different products in accord with expectations based on the rules. Similar arguments can be applied to several types of chemical reactions: ring-closure and ring-opening reactions, skeletal rearrangements, and others. The rules that emerge from orbital symmetry arguments help to systematize and rationalize a vast amount of experimental results and are enormously useful in planning the synthesis of complex molecules and in overcoming the stereochemical problems that arise there. They have become an essential part of the intellectual equipment of the practicing chemist.