Abstract
High dynamic range optical-to-near-infrared transmission measurements for different parts of human body in the spectral range from 650 to 950 nm have been performed. Experimentally measured spectra are correlated with Monte Carlo simulations using chromaticity coordinates in CIE 1976 L*a*b* color space. Both a qualitative and a quantitative agreement have been found, paving a new way of characterizing human tissues in vivo. The newly developed experimental and computational platform for assessing tissue transmission spectra is anticipated to have a considerable impact on identifying favorable conditions for laser surgery and optical diagnostics, while providing supplementary information about tissue properties.
OCIS codes: (170.6510) Spectroscopy, tissue diagnostics; (170.3660) Light propagation in tissues; (170.6935) Tissue characterization; (200.4960) Parallel processing; (300.6550) Spectroscopy, visible; (330.1730) Colorimetry
1. Introduction
The spectral and colorimetric studies of biological tissues are of a considerable interest from the point of view of potential development of new techniques for non-invasive in vivo imaging and spectroscopic characterization of biological and human tissues and monitoring variations of their properties without amending their physiological state [1–3]. This is especially important for a number of practical applications including medical diagnostics [4], plastic surgery [5], face recognition for security needs [6], as well as for the optical design of a particular diagnostic system. It is especially critical for success of many therapeutic procedures when the exact knowledge of laser fluence delivered to a specific organ is essential [7,8], as well as for determination of the optimal laser excitation conditions for maximum depth tissue probing [1–3,9]
Spectral composition of light penetrating through biological tissues depends on the concentration and spatial distribution of chromophores within the given tissue, as well as on particular experimental conditions, including the probe geometry and multiple parameters of the incident optical radiation. In the past, there were numerous attempts to evaluate optical tissue properties by assessing both scattering and absorption properties of tissues (see, for example [4,10,11]; however, when it comes to the practical aspects, i.e., what is the fraction of the incident light radiation, which reaches a certain depth of a tissue, it creates a challenging computational problem of combining all the data collected in different ways [10,11], and, to the best of our knowledge, no data on the light transmission through thick tissues is available in support of such calculations.
In this report, we present a computational technique specially developed for simulation of the visible/near-IR transmittance and/or reflectance spectra of human skin and skin color calculation. The computational data are compared with the experimental data obtained using high-dynamic range spectral transmission measurements through different parts of a human body, which are easily accessible through those measurements.
2. Materials and method
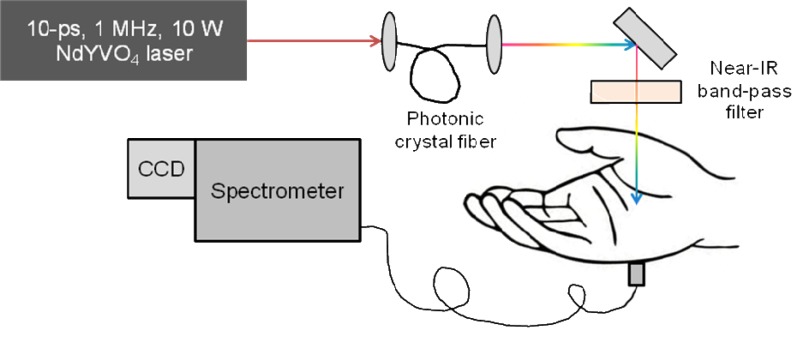
The principles of optical spectroscopy are well known and widely described in details elsewhere, see, e.g., [12]. The optical spectroscopy experimental set up, used in current study, is schematically presented in Fig. 1 . To perform high dynamic-range optical transmission measurements a high spectral brightness optical source, which could be directed to a specific part of a tissue, is required. White-light continuum generated in an optical fiber provides rather high spectral intensity and focus ability [13]; however, short- and long-term stability of this continuum is rather limited. Thus, we used a modified approach employing high-energy picosecond laser pulses and large area photonic crystal fiber [14,15]. A broadband super-continuum was generated through a cascade of stimulated Raman scattering and wave-mixing processes and extended from 600 nm to 2200 nm; however, only a portion of this radiation from 650 nm to 950 nm was utilized in the experiment mentioned above. In order to avoid tissue damage and discomfort during long-exposure measurements, only 50% of the total laser power (roughly, 350 mW) was used for tissue irradiation. A multimode optical fiber bundle with an 0.6-mm2-area was employed to collect the transmitted light through a part of the body. The input end of the fiber was gently pressed against the opposite side of the body, and the output of the fiber served as an input slit of a 1/2–meter imaging spectrometer (Horiba, Inc.) with the attached TE-cooled CCD camera (iDus-401-BRDD; Andor, Inc.). A portion of the incident light was reflected off by the front surface of a glass slide and directed to a spectrometer for reference measurements. The reference spectrum was accumulated in the same time by using simultaneous input from two identical fiber ports at the entrance slit of the imaging spectrometer. The accuracy of this approach was validated by letting the incident beam entering the signal path without passing through the sample. For all the described measurements, the signal was corrected for a background, normalized to the incident light and averaged over 100-s to maximize the signal-to-noise-ratio.
Fig. 1.
Schematic presentation of the experimental system used in current study.
The above measurements were taken at different locations of human hand, including fingertip (through the fingernail), finger, palm wrist and forearm. Transmittance spectra measurements for a biceps were limited due to the sensitivity of the detection system. To avoid artifacts associated with spontaneous motions during the long-exposure measurements a hand of a volunteer was placed in specially designed holder.
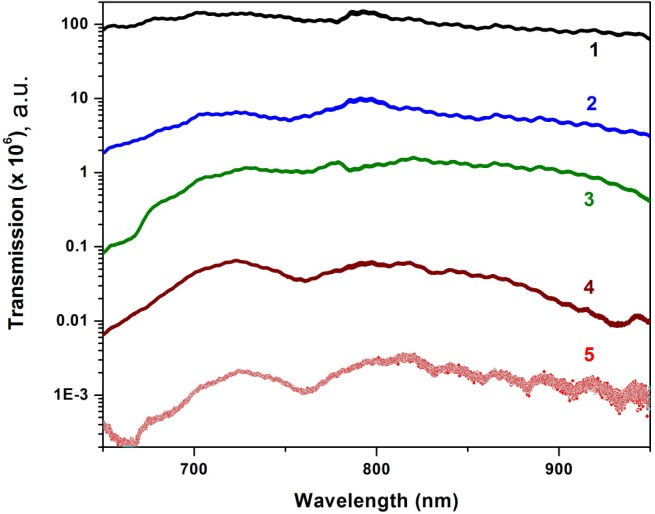
The measured transmittance spectra are displayed in Fig. 2 . The variations in the spectral transmission are clearly observed for different parts of human arm that can be explained with the computational modeling in terms of the variation of the photons’ pathlength in the tissue.
Fig. 2.
Near-IR spectral transmission measured in vivo for fingernail (1), finger (2), palm (3), wrist (4) and forearm (5).
3. Computational modeling
Owing to a wide range of actual probing conditions and a very complex composite structure of tissues considered in the current study, no general analytical solution is available that can simulate the detected scattered optical radiation and its interaction with tissues, their structural malformations and/or physiological changes. Therefore, stochastic Monte Carlo (MC) modeling was employed. We utilized a recently developed object oriented MC model [16,17] that allows description of photons and tissue structural components as objects, which interact each other. Thus, an object photon propagates through an object medium (or medium layer) and interacts with its constituents, such as cells, blood vessels, collagen fibers, etc. Such representation of the medium by objects makes it possible to develop realistic tissue models presenting 3D spatial variations of a biological structure. To achieve the most optimal simulation performance, a parallel computing framework known as Computer Unified Device Architecture (CUDA), introduced by NVIDIA Corporation, was employed. This capability enables simulation of thousands of photons simultaneously speeding up the process of simulation more than 103 times.
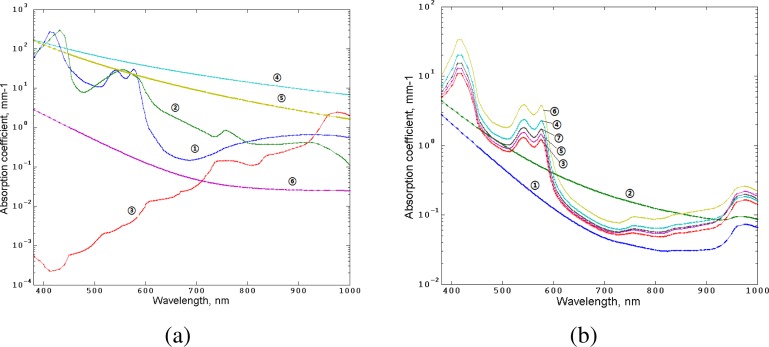
To simulate transmission spectra we applied a multilayered tissue model. This model, originally developed in Refs. [19–21], was extended to 17 layers by including muscles and bone structures. In this model, the absorption coefficients of each layer (Fig. 3 ) take into account the concentration of blood (Cblood) in various vascular beds, oxygen saturation (S), water content (CH2O), melanin fraction (Cmel) and are defined as
Fig. 3.
Absorption properties of skin tissues used in the simulation. Left, absorption coefficients of key skin tissues chromophores: 1, oxy-hemoglobin; 2, deoxy-hemoglobin; 3, water; 4, eumelanin [18]; 5, pheomelanin [18]; 6, baseline [18]. Right, absorption coefficients of the human skin layers counted by Eqs. (1)-(3).
| (1) |
| (2) |
| (3) |
Here μamel(λ) is the absorption coefficient of eumelanin, μaph.mel(λ) is the absorption coefficient of pheomelanin, Bmel is the volume fraction of the blend between two melanin types, μaoxy(λ) is the absorption coefficient of oxy-hemoglobin, μadeoxy(λ) is the absorption coefficient of deoxy-hemoglobin, μabaseline(λ) is the absorption coefficient of other water-free tissues (see Fig. 3). The actual values of the hematocrit index (Ht), volume fraction of hemoglobin (FHb), fraction of erythrocytes (FRBC), concentration of blood, oxygen saturation and water content are presented in Table 1 .
Table 1. Parameters used for assessment of the absorption coefficients of the layers. Layers 10–17 are the same as layers 1–7 in the reverse order.
| Name of Layer | CBlood | S | Ht | FHt | FRBC | CH20 | |
|---|---|---|---|---|---|---|---|
| 1 | Stratum corneum | 0 | 0 | 0 | 0 | 0 | 0.05 |
| 2 | Living epidermis | 0 | 0 | 0 | 0 | 0 | 0.2 |
| 3 | Papillary dermis | 0.04 | 0.6 | 0.45 | 0.99 | 0.25 | 0.5 |
| 4 | Upper blood net dermis | 0.3 | 0.6 | 0.45 | 0.99 | 0.25 | 0.6 |
| 5 | Reticular dermis | 0.04 | 0.6 | 0.45 | 0.99 | 0.25 | 0.7 |
| 6 | Deep blood net dermis | 0.1 | 0.6 | 0.45 | 0.99 | 0.25 | 0.7 |
| 7 | Subcutaneous fat | 0.05 | 0.6 | 0.45 | 0.99 | 0.25 | 0.7 |
| 8 | Muscles | 0.2 | 0.6 | 0.45 | 0.99 | 0.25 | 0.6 |
| 9 | Bone | 0.02 | 0.6 | 0.45 | 0.99 | 0.25 | 0.1 |
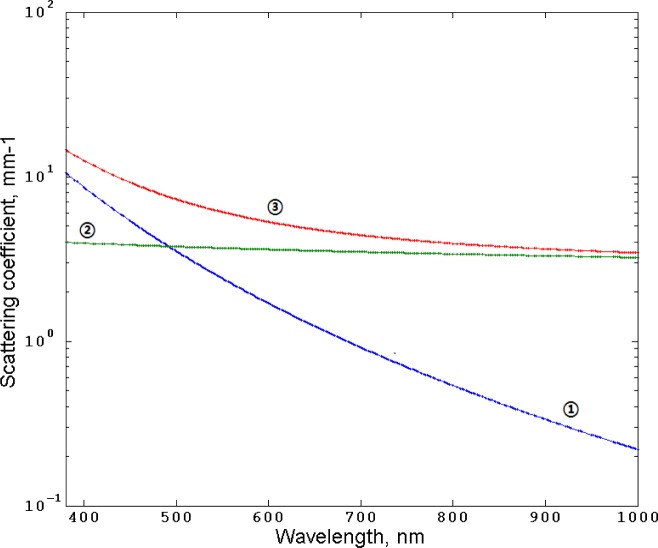
The scattering coefficients of the layers are approximated based on combination of Mie and Rayleigh scattering (Fig. 4 ) suggested in [22]:
Fig. 4.
Rayleigh scattering (1), Mie scattering (2), and combined Rayleigh and Mie scattering (3) by Eqs. (4), (5), and (6), respectively.
| (4) |
| (5) |
| (6) |
where N is the coefficient (in a range 1 to10) depending on the scattering properties of tissue.
The MC simulations were performed for the actual probe geometry used in the experiment (see Fig. 1) utilizing 1010 of the detected photon packets. The conversion of the spectral power distribution to the CIE XYZ (CIE 1976 L*a*b*) coordinates [23], as well as to the RGB-gamut color values, was performed using the standard CIE 2° observer and tristimulus values utilizing D65 illuminant.
4. Results and discussion
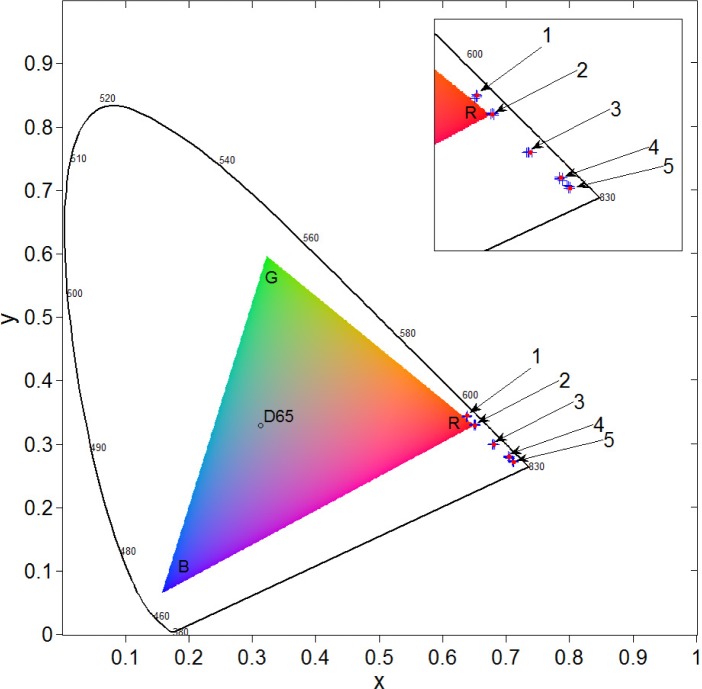
Figure 5 displays the experimental results shown in Fig. 2 for different parts of a human body in chromaticity coordinates plotted in the CIE 1931 color space in comparison to the results of the MC simulation. It is clear that the experimental and computational results are in a good agreement with each other.
Fig. 5.
Chromaticity coordinates for fingernail (1), finger (2), palm (3), wrist (4) and forearm (5): crosses display experimental data and circles—the results of computer MC simulations.
The design of the CIE 1931 color space splits the concept of color into brightness and chromaticity. The black contour in Fig. 5 is the spectral locus with the corresponding wavelengths. D65 is the standard daylight illuminant used in the MC model. The triangle represents a color gamut that can be reproduced by a standard computer monitor. As one can see, the modeled tissue colors outside the gamut cannot be displayed properly on a standard color reproduction device and require a conversion procedure. Moreover, the above diagram does not allow displaying the actual brightness (luminance) of those colors. However, the actual colors are observed by a naked eye during the experiment.
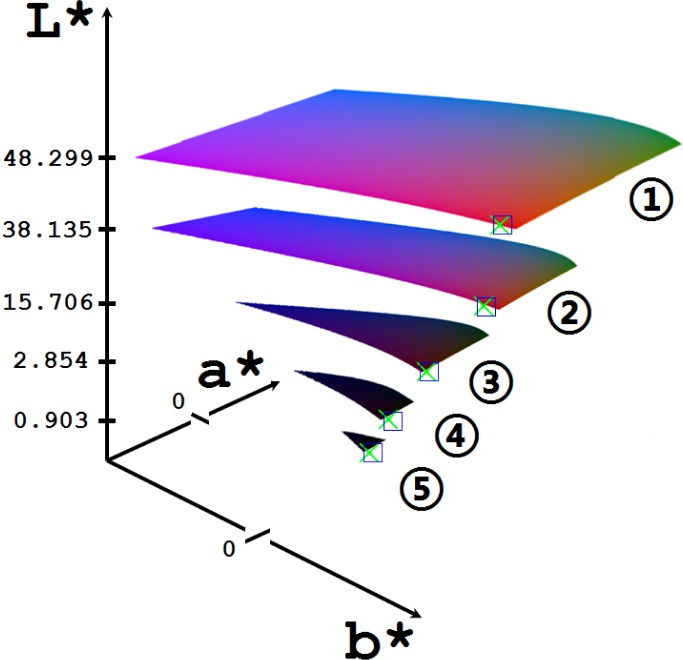
To make the luminance visible we converted the modeled CIE chromaticity coordinates into the Lab color space. Figure 6 shows experimentally observed and computer simulated the near-IR transmission colors of different parts of a human arm, presented in CIE 1976 L*a*b* color space. The simulation was done for the actual experimental geometry and the fiber probe position used to collect the data. The simulated CIE 1976 L*,a*,b* coordinates in the color space, plotted in Fig. 6, are presented in Table 2 with the converted sRGB colors.
Fig. 6.
The changes of human skin color presented in CIE 1976 L*a*b* color space simulated by the developed MC model (crosses) compared with the results of measurements/observations in vivo (squares) for near-IR light transmitted through the various parts of human body: 1,fingernail; 2, finger; 3, palm; 4, wrist; 5, forearm.
Table 2. Results of the MC simulation of skin color CIE coordinates in L*,a*,b* color spacea.
| Sample | L* | a* | b* | Standard deviation | sRGB Color |
|---|---|---|---|---|---|
| Fingernail | 48.299 | 67.372 | 68.396 | 0.001 | |
| Finger | 38.135 | 62.883 | 54.705 | 0.001 | |
| Palm | 15.706 | 44.938 | 24.774 | 0.001 | |
| Wrist | 2.854 | 19.824 | 4.601 | 0.001 | |
| Forearm | 0.930 | 7.024 | 1.532 | 0.001 |
aThe standard deviation is calculated between the experimental data and the modeling output. CIE xyY coordinates converted to sRGB values are presented the resulting color in sRGB column.
Observing the effect of the changes of tissues color due to, for example, changes of blood and/or melanin content, and variations in blood oxygenation, is of a potential use for the practical diagnostic purpose and bioengineering applications. These changes can be quantified and characterized with the developed MC model. Figures 7 and Fig. 8 show the examples of the results of the human skin spectra and skin color modeling for varying the melanin and blood contents in skin, respectively.
Fig. 7.
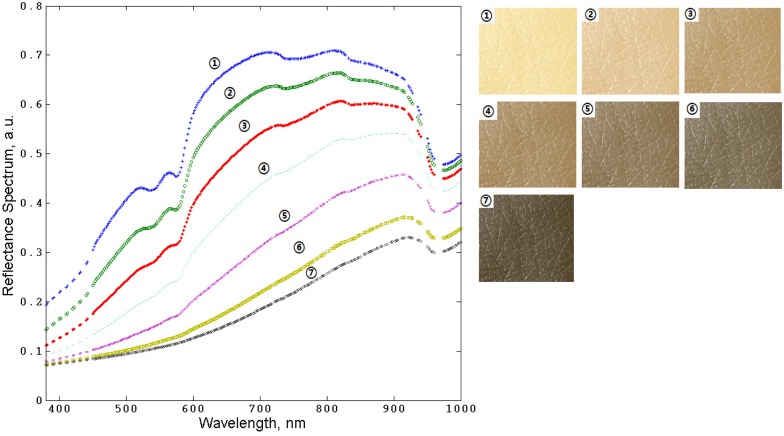
The results of MC simulation of human skin spectra (left) and corresponding colors (right) while varying the melanin content in living epidermis: (1), 0%; (2), 2%; (3), 5%; (4), 10%; (5), 20%; (6), 35%; (7), 45%; fraction between eumelanin and pheomelanin is 1:3.
Fig. 8.
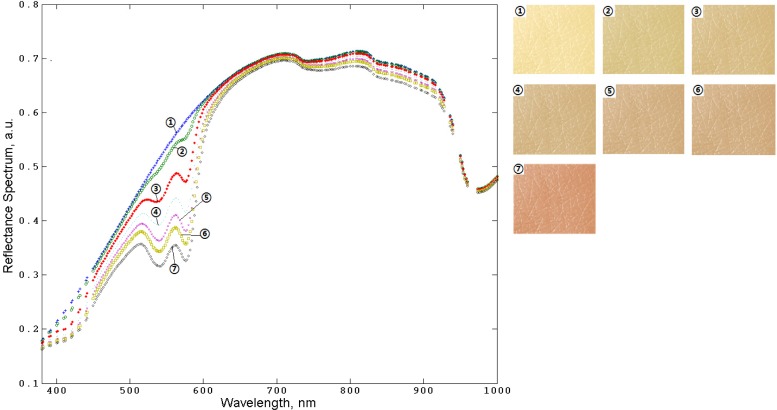
The results of MC simulation of human skin spectra (left) and corresponding colors (right) while varying the blood concentration in the layers from papillary dermis to subcutaneous tissue: (1), 0%; (2), 2%; (3), 5%; (4), 10%; (5), 20%; (6), 35%; (7), 70%, respectively. The melanin concentration is 2% and fraction between eumelanin and pheomelanin is 1:3.
The results presented in Figs. 7–8 demonstrate the changes of spectra and color of human skin resulting from the melanin or blood content variations that can be characterized by combining spectral measurements with the results of MC modeling.
5. Summary and Conclusions
We performed the pilot experimental studies of the near-IR spectral transmission measurements through a bulk tissue samples in vivo. Those results provide a quantitative measure of the light transmitted through a certain body area as a function of the incident wavelength in the biologically significant optical transmission window. Those experimental results are compared with the results of computer simulations, and a good quantitative agreement is found when the data are presented in CIE 1976 L*, a*, b* color space. The chromaticity coordinates are calculated and the regularities of color variation are analyzed by MC simulation in the context of functional properties of human tissues. The spectral color composition of human skin and other biological tissues presented in a particular color space can be used for express-analysis of their functional physiological condition and identification of optimal conditions for optical diagnostics.
We expect that in a similar manner the regularities of human body color variation associated with the changes of optical properties of biological tissues due to optical clearing, melanin content changes and physiological changes (e.g., blood oxy-/deoxy-genation) can be observed and presented.
Acknowledgments
This work was partially supported by the University of Otago, New Zealand, and Texas A&M University, USA. Authors also acknowledge the support of University of Otago (New Zealand) 2010-2011 PBRF Research Output Publishing Grant,, the NIH (R21EB011703) and the NSF (ECS Grant 0925950, DBI Grant 0964225, and CBET Grant 1066562).
References and links
- 1.Ntziachristos V., Ripoll J., Wang L. V., Weissleder R., “Looking and listening to light: the evolution of whole-body photonic imaging,” Nat. Biotechnol. 23(3), 313–320 (2005). 10.1038/nbt1074 [DOI] [PubMed] [Google Scholar]
- 2.Helmchen F., Denk W., “Deep tissue two-photon microscopy,” Nat. Methods 2(12), 932–940 (2005). 10.1038/nmeth818 [DOI] [PubMed] [Google Scholar]
- 3.Ntziachristos V., “Going deeper than microscopy: the optical imaging frontier in biology,” Nat. Methods 7(8), 603–614 (2010). 10.1038/nmeth.1483 [DOI] [PubMed] [Google Scholar]
- 4.Key H., Davies E. R., Jackson P. C., Wells P. N. T., “Optical attenuation characteristics of breast tissues at visible and near-infrared wavelengths,” Phys. Med. Biol. 36(5), 579–590 (1991). 10.1088/0031-9155/36/5/002 [DOI] [PubMed] [Google Scholar]
- 5.Sarwer D. B., Wadden T. A., Whitaker L. A., “An investigation of changes in body image following cosmetic surgery,” Plast. Reconstr. Surg. 109(1), 363–369, discussion 370–371 (2002). 10.1097/00006534-200201000-00060 [DOI] [PubMed] [Google Scholar]
- 6.Li H. Y. S., Qiao Y., Psaltis D., “Optical network for real-time face recognition,” Appl. Opt. 32(26), 5026–5035 (1993). 10.1364/AO.32.005026 [DOI] [PubMed] [Google Scholar]
- 7.Dolmans D. E. J. G. J., Fukumura D., Jain R. K., “Photodynamic therapy for cancer,” Nat. Rev. Cancer 3(5), 380–387 (2003). 10.1038/nrc1071 [DOI] [PubMed] [Google Scholar]
- 8.Eells J. T., Henry M. M., Summerfelt P., Wong-Riley M. T., Buchmann E. V., Kane M., Whelan N. T., Whelan H. T., “Therapeutic photobiomodulation for methanol-induced retinal toxicity,” Proc. Natl. Acad. Sci. U.S.A. 100(6), 3439–3444 (2003). 10.1073/pnas.0534746100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yakovlev V. V., Zhang H. F., Noojin G. D., Denton M. L., Thomas R. J., Scully M. O., “Stimulated Raman photoacoustic imaging,” Proc. Natl. Acad. Sci. U.S.A. 107(47), 20335–20339 (2010). 10.1073/pnas.1012432107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Patterson M. S., Chance B., Wilson B. C., “Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties,” Appl. Opt. 28(12), 2331–2336 (1989). 10.1364/AO.28.002331 [DOI] [PubMed] [Google Scholar]
- 11.Cheong W. F., Prahl S. A., Welch A. J., “A review of the optical properties of biological tissues,” IEEE J. Quantum Electron. 26(12), 2166–2185 (1990). 10.1109/3.64354 [DOI] [Google Scholar]
- 12.N. V. Tkachenko, Optical Spectroscopy: Methods and Instrumentations (Elsevier Science, 2006). [Google Scholar]
- 13.Ranka J. K., Windeler R. S., Stentz A. J., “Visible continuum generation in air-silica microstructure optical fibers with anomalous dispersion at 800 nm,” Opt. Lett. 25(1), 25–27 (2000). 10.1364/OL.25.000025 [DOI] [PubMed] [Google Scholar]
- 14.Petrov G. I., Yakovlev V. V., Minkovski N. I., “Broadband nonlinear optical conversion of a high-energy diode-pumped picosecond laser,” Opt. Commun. 229, 441–445 (2004). 10.1016/j.optcom.2003.11.009 [DOI] [Google Scholar]
- 15.Petrov G. I., Yakovlev V. V., “Enhancing red-shifted white-light continuum generation in optical fibers for applications in nonlinear Raman microscopy,” Opt. Express 13(4), 1299–1306 (2005). 10.1364/OPEX.13.001299 [DOI] [PubMed] [Google Scholar]
- 16.Doronin A., Meglinski I., “Online object oriented Monte Carlo computational tool for the needs of biomedical optics,” Biomed. Opt. Express 2(9), 2461–2469 (2011). 10.1364/BOE.2.002461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.I. Meglinski and A. Doronin, “Online Monte Carlo for biomedical optics,” SPIE Newsroom, Nov.7, 2011, http://spie.org/x57619.xml [DOI] [PMC free article] [PubMed]
- 18.G. Donner, H. W-Jensen, “A spectral BSSRDF for shading human skin,” EGSR Symposium (2006). [Google Scholar]
- 19.Meglinski I. V., “Modeling the reflectance spectra of the optical radiation for random inhomogeneous multi-layered highly scattering and absorbing media by the Monte Carlo technique,” Quantum Electron. 31, 1101–1107 (2001). [Google Scholar]
- 20.Meglinski I. V., Matcher S. J., “Computer simulation of the skin reflectance spectra,” Comput. Methods Programs Biomed. 70(2), 179–186 (2003). 10.1016/S0169-2607(02)00099-8 [DOI] [PubMed] [Google Scholar]
- 21.Doronin A., Fine I., Meglinski I., “Assessment of the calibration curve for transmittance pulse-oximetry,” Laser Phys. 21(11), 1972–1977 (2011). 10.1134/S1054660X11190078 [DOI] [Google Scholar]
- 22.Saidi I. S., Jacques S. L., Tittel F. K., “Mie and Rayleigh modeling of visible-light scattering in neonatal skin,” Appl. Opt. 34(31), 7410–7418 (1995). 10.1364/AO.34.007410 [DOI] [PubMed] [Google Scholar]
- 23.D. H. Brainard, “Color appearance and color difference specification,” In The Science of Color, S. K. Shevell, ed. (Elsevier, 2003). [Google Scholar]