Application of non-negative matrix factorization to multispectral FLIM data analysis

Abstract

Existing methods of interpreting fluorescence lifetime imaging microscopy (FLIM) images are based on comparing the intensity and lifetime values at each pixel with those of known fluorophores. This method becomes unwieldy and subjective in many practical applications where there are several fluorescing species contributing to the bulk fluorescence signal, and even more so in the case of multispectral FLIM. Non-negative matrix factorization (NMF) is a multivariate data analysis technique aimed at extracting non-negative signatures of pure components and their non-negative abundances from an additive mixture of those components. In this paper, we present the application of NMF to multispectral time-domain FLIM data to obtain a new set of FLIM features (relative abundance of constituent fluorophores). These features are more intuitive and easier to interpret than the standard fluorescence intensity and lifetime values. The proposed approach, unlike several FLIM data analysis methods, is not limited by the number of constituent fluorescing species or their possibly complex decay dynamics. Moreover, the new set of FLIM features can be obtained by processing raw multispectral FLIM intensity data, thereby rendering time deconvolution unnecessary and resulting in lesser computational time and relaxed SNR requirements. The performance of the NMF method was validated on simulated and experimental multispectral time-domain FLIM data. The NMF features were also compared against the standard intensity and lifetime features, in terms of their ability to discriminate between different types of atherosclerotic plaques.

1. Introduction

Despite several studies showing the potential of multispectral FLIM as a promising clinical optical imaging modality [1–4], its utility has not yet been fully established. One of the main reasons for this is the element of subjectivity involved in interpreting multispectral FLIM images. Existing methods of interpreting multispectral FLIM images are based on a qualitative comparison of spectral intensity and lifetime values at each pixel in a FLIM image with those of known fluorophores. Such comparison-based interpretation of FLIM images is satisfactory only when the fluorescence decay at each pixel can be attributed to just one fluorophore. However, in most practical applications, there are often more than one fluorescing species contributing to the bulk fluorescence signal. In such cases, it becomes imperative to develop a method that can quantitatively characterize the type and relative abundance of fluorophores present in a sample. This is of particular interest in the context of biomedical diagnosis, since the progression from normal to pathological tissue is often characterized by changes in the relative abundance of tissue fluorophores.

Several studies reported in the literature that attempt to quantify the contributions of constituent fluorophores to bulk fluorescence signal are based on lifetime measurements [5, 6]. In the general approach, it is assumed that the constituent fluorophores have mono-exponential decay dynamics with known lifetimes, and consequently the mixture fluorescence dynamics is modeled as multi-exponential decay wherein each exponential component corresponds to a specific fluorophore. The sample fluorescence decay at each pixel is thus fitted to the corresponding multi-exponential model, and the estimated pre-exponential weights are used as surrogates for the relative contributions of the constituent fluorophores to the bulk signal. When the lifetime values of the fluorophores are not known a priori, the global analysis approach is applied, in which the global fluorophore lifetimes are also estimated from the complete FLIM data [5].

Although generally used, these methods suffer from several limitations. First, the assumption of mono-exponential decay for each fluorophore is quite often inaccurate, since many exogenous and endogenous fluorophores show more complex decay profiles. For instance, Flavin Adenine Dinucleotide (FAD), which is an important cofactor in many enzymatic reactions, is known to have a non-exponential decay [7]. Similarly, for a single tryptophan protein, the distribution of protein conformations results in a complex decay profile [8]. Second, most of these methods are restricted to two-component models [5,9]; thus, they can only handle experimental FLIM data in which at most two fluorescent species are being simultaneously monitored. These two major limitations have been identified in a number of publications. In particular, Veerver et al. have addressed these issues in [5], where the authors have stated that the “resolution of fluorophores with complex decays and separation of more than two fluorophores continues to be a topic of research”. Third, from a computational aspect, accurate fitting of fluorescence decay data to a multi-exponential model requires signal-to-noise levels that are in many cases impractical for FLIM measurements [7]. Fourth, unless extremely short excitation light pulses are used, time deconvolution of the instrument response from the fluorescence decay data is required prior to lifetime estimation, which results in an additional computational burden. Lastly, all these methods are applicable to single spectral channel FLIM data and are thus unable to exploit the spectral information contained in the multispectral FLIM data [6, 10].

In this study we present the application of non-negative matrix factorization (NMF) to multispectral FLIM data analysis. NMF is a multivariate data analysis technique that aims at extracting non-negative signatures and relative contributions of pure components from an additive mixture of those components; a process commonly referred to as unmixing [11]. In the context of FLIM data analysis, unmixing amounts to expressing the bulk fluorescence signal obtained from a sample as a weighted sum of fluorescence signals of the constituent fluorophores present in that sample, where the weights correspond to the relative contribution of each constituent fluorophore to the bulk fluorescence signal. Unlike most other approaches mentioned earlier that make assumptions about the functional form of the constituent fluorophore decay profiles and are restricted to two-component models, NMF is able to handle more than two fluorescent species showing complex decay dynamics (i.e. non-monoexponential decay). Another important advantage of the proposed method is that NMF can be directly applied to raw multispectral FLIM intensity data obviating the need to perform time deconvolution, resulting in lesser computational time and relaxed SNR requirements.

In the present study, the following two specific aims were accomplished. First, we proposed a new set of features to characterize multispectral FLIM images. This feature set (henceforth referred to as NMF FLIM features) comprises the relative abundance of constituent fluorophores derived via NMF of multispectral FLIM data. We also showed how these features are more intuitive and easier to interpret than the standard bulk intensity and lifetime features (henceforth referred to as standard FLIM features), which are currently used to characterize multispectral FLIM data. Second, we compared the performance of the NMF FLIM features against the standard FLIM features derived from multispectral FLIM data obtained by imaging of human coronary arteries, in terms of their ability to discriminate between three types of atherosclerotic plaques.

2. Materials and methods

2.1. FLIM instrumentation

The coronary segments were imaged using an in-house built high speed bench-top multispectral FLIM system reported in [12]. Briefly, the scanning FLIM system was implemented following a direct pulse-recording scheme, in which the pixel rate could be equal to the laser repetition rate. A frequency tripled Q-switched Nd:YAG laser was used as the excitation source (355 nm, 30 kHz max. repetition rate, 1 ns pulse FWHM). The fluorescence emission was separated into three spectral channels using a set of dichroic mirrors and filters (390±20 nm for collagen, 452±22.5 nm for elastin, and 550±20 nm for lipids). The emission from each channel was launched into fibers with different lengths (1 m, 10 m and 19 m) chosen to provide 45 ns interval between each emission band decay. The three consecutive decays were detected with a MCP-PMT (rise time: 150 ps) and sampled with a high bandwidth digitizer (1.5 GHz, 4 GS/s). The system’s lateral resolution was measured to be 100 μm. Each multispectral FLIM image (FOV: 2×2 mm² at 60×60 pixels) was acquired in ∼7 s.

2.2. Tissue sample preparation and histopathological evaluation

Fresh human coronary artery tissues were obtained within 48 hours of autopsy after 6 postmortem examinations, according to a protocol approved by the Texas A&M University Institutional Review Board. The arterial tissues were segmented and longitudinally opened to acquire multispectral FLIM images. In total, 58 segmented tissues were imaged over a 2×2 mm² area. During the experiment, each tissue specimen was placed on a quartz slide with the internal lumen directly facing the microscope objective. Imaged region of the specimen tissue was immediately marked for histopathological processing after imaging. Each tissue specimen was then sectioned every 500 μm and the sections were stained with Movat Pentachrome for histopathological evaluation. Based on the histopathological evaluation, each section was classified as: intimal thickening (IT), pathological intimal thickening (PIT), fibroatheroma (FA), thin-cap fibroatheroma (TCFA), calcified plaque (CA), and/or plaque with significant foam-cell (FC) infiltration [13]. A total of 21 segments showing similar and uniform histopathological characteristics in all consecutive sections were selected and grouped either as High-Collagen (HC; including FA and PIT), High-Lipids (HL; including TCFA and PIT with significant foam-cell infiltration or FC-PIT) or Low-Collagen/Lipids (LCL; including IT and CA). We shall refer to these datasets as the homogeneous datasets while the remaining 37 datasets shall be called the heterogeneous datasets.

2.3. Problem statement: multispectral FLIM data in NMF framework

Before setting out to describe the problem statement, the following notations are in order. We shall denote the multispectral fluorescence intensity decay measured at a given pixel (x, y) as a function of time (t) and wavelength band (λ_i) by I(x, y, t; λ_i). If we linearly index, say N pixels in a multispectral FLIM image as i = 1, 2,...,N, such that the ith. index corresponds to the pixel (x, y), and if we denote the spectro-temporal FLIM profile at the ith. pixel by x_i, then we define this spectro-temporal decay as a concatenation in time of the fluorescence decays for all emission bands; i.e., x_i ≡ I(x, y, t; λ₁, λ₂,..., λ_P) = [I(x, y, t; λ₁), I(x, y, t; λ₂),..., I(x, y, t; λ_P)], where P denotes the number of emission bands. Let us also assume that in a sample there are K fluorophores, termed end-members having multispectral time resolved fluorescence decays denoted by s_k ∈ ℝ^T, for k = 1, 2,..., K, where T denotes the length of the spectro-temporal signals. In accordance with the hyperspectral imaging terminology, we shall interchangeably refer to these end-member profiles as end-member signatures. If we denote the multispectral time resolved fluorescence signal recorded at a given pixel (say nth. pixel) in a FLIM image by x_n, then under the linear mixing assumption, x_n can be expressed as a linear combination of the K end-member signatures, i.e.

$${\mathbf{x}}_n=a_{1,n}{\mathbf{s}}_1+a_{2,n}{\mathbf{s}}_2+\cdots +a_{K,n}{\mathbf{s}}_K\iff {\mathbf{x}}_n=\mathbf{S}{\mathbf{a}}_n,$$ (1)

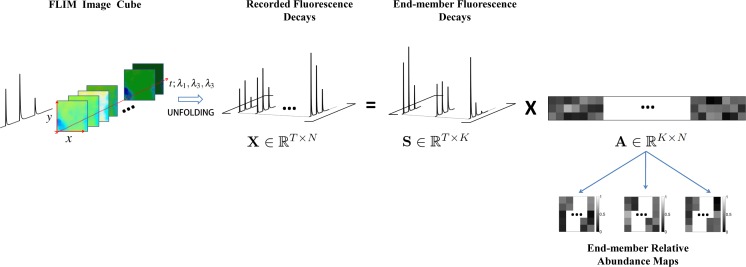
where S ≡ [s₁, s₂, ⋯ , s_K] ∈ ℝ^T×K and a_n ≡ [a_1,n, a_2,n, ⋯ , a_K,n]^T ∈ ℝ^K. In such a case, the weights: a_1,n, a_2,n,..., a_K,n represent the contributions or abundances of the K end-members at the nth. pixel. We we can then express the data matrix: X ≡ [x₁, x₂, ⋯ , x_N] ∈ ℝ^T×N, containing the recorded spectro-temporal fluorescence decays from N pixels along its columns (henceforth referred to as data vectors) in matrix notations as X = SA. We shall call: S ≡ [s₁, s₂, ⋯ , s_K] the mixing matrix, which holds the K end-member signatures in its columns, and A ∈ ℝ^K×N shall be referred to as the abundance matrix, which contains the contributions of K end-members (along rows) for each of the N pixels (along columns). Taking into account the fact that matrices X, S and A contain non-negative elements (denoted by: X, S, A ≽ 0), the problem we attempt to address can be stated as follows: Given a non-negative data matrix X and the number of fluorophores: K contributing to the bulk fluorescence signal, find the mixture and the abundance matrices S, A ≽ 0 such that the product SA best approximates X; i.e. X ≈ SA. This problem is more generally known as non-negative matrix factorization and appears in several research areas under different names, most notably, spectral unmixing or blind source separation in hyperspectral image analysis and multivariate curve resolution in chemometrics [14, 15].

2.4. Geometrical interpretation, preprocessing and NMF algorithms

2.4.1. Geometrical interpretation

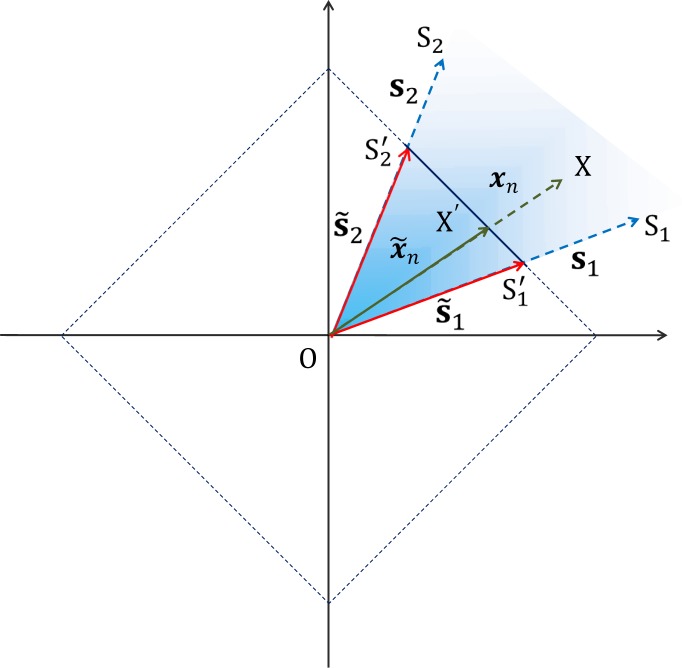
The solution to the NMF problem stated in the previous section can be better understood by resorting to a geometrical interpretation of NMF [17]. For meaningful interpretation, the rows of A are interpreted to represent the relative abundance of different end-members, in which case they are assumed to follow a full-additivity constraint, i.e. ${\sum }_{k=1}^K{a}_{k,n}=1$ for n = 1, 2,...,N (in the following section, we discuss how a simple normalization procedure can be employed to make sure that the data always follows the full-additivity constraint). Under the non-negativity, linear mixing and full-additivity constraints, it then follows that the set 𝔛 ≡ {x_n ∈ ℝ^T : x_n=Sa_n, 1^T a_n = 1, n = 1, 2,..., N} represents a K − 1 dimensional simplex and estimating S amounts to finding the vertices of such a simplex. This is shown in Fig. 1 and Fig. 2 for the case when K = 2 and K = 3, respectively.

Fig. 1:

All possible non-negative linear combinations of s₁ and s₂ lie in the blue shaded unbounded area contained within s₁ and s₂. x_n represents one such data vector. Normalizing data vectors to unit L₁-norm length amounts to rescaling them such that the tip of the rescaled data vectors lie on the portion of the unit L₁ norm circle (shown in dotted lines) contained between the normalized end-member signatures s̃₁ and s̃₂, i.e. on the line S′₁S′₂, which represents a 1-D simplex.

Fig. 2:

In the general case, all possible non-negative linear combinations of s₁ s₂ and s₃ lie in the blue shaded unbounded volume enclosed by s₁ s₂ and s₃. On imposing the full-additivity constraint all possible non-negative linear combinations of s₁ s₂ and s₃ are constrained to lie on the triangle S₁S₂S₃, which represents a 2-D simplex.

2.4.2. Data preprocessing

The full-additivity constraint described in the previous paragraph is not always satisfied in many practical situations. This may happen when either the imaged area is large or in situations where it is desired to use data acquired from different imaging sessions. In the former case it is mainly the variations in physical and chemical conditions, while in the the latter case, it is the differences in experimental conditions that results in the violation of the full-additivity constraint. This effect is commonly referred to as signature variability in hyperspectral imaging literature and is characterized by what is called spectral shape invariance, which means that although the shapes of the end-member signatures do not vary much across different pixels, their scaling or amplitude vary significantly over the imaged area [16]. In such a case, instead of being contained on a K −1 dimensional simplex, the data lies within a region of the positive orthant of the T dimensional space enclosed by a convex polygonal cone spanned by K columns of S. This is shown in Fig. 1 and Fig. 2 for the case when K = 2 and K = 3, respectively, where the data vectors lie within the cone (shown as blue shaded region) spanned by the end-member signatures, as opposed to lying on a line (K = 2) and a triangular plane (K = 3), respectively.

In cases like these, a normalization technique inspired from the dark point fixed transform (DPFT) can be performed to ensure that the normalized data satisfies the full-additivity constraint [17,18]. This normalization involves scaling the data vectors x_n to have unit length in the L₁-norm sense, i.e. if x̃_n denotes the normalized data vector, then x̃_n = x_n/||x_n||₁, where ||x||₁ for a vector x = (x₁, x₂,..., x_n) is defined as: ||x||₁ := |x₁| + |x₂| + ⋯ + |x_n|. The linear mixing model stated in Eq. (1) can then be reformulated as:

$${\tilde{\mathbf{x}}}_n={\frac{{\mathbf{x}}_n}{\Vert {\mathbf{x}}_n\Vert }}_1=\frac{{\sum }_{k=1}^K{a}_{k,n}{\mathbf{s}}_k}{{\Vert {\mathbf{x}}_n\Vert }_{\mathbf{1}}}=\sum _{k=1}^K\left(a_{k,n}\frac{{\Vert {\mathbf{s}}_k\Vert }_1}{{\Vert {\mathbf{x}}_n\Vert }_1}\right)\left(\frac{{\mathbf{s}}_k}{{\Vert {\mathbf{s}}_k\Vert }_1}\right)=\sum _{k=1}^K{\tilde{a}}_{k,n}{\tilde{\mathbf{s}}}_k,$$ (2)

where, s̃_k = s_k/||s_k||₁ denotes the rescaled end-member signatures and ã_k,n = a_k,n||s_k||₁/||x_n||₁ denotes the corresponding rescaled contributions. Observing that ${\Vert {\mathbf{x}}_n\Vert }_1={\sum }_{k=1}^K{a}_{k,n}{\Vert {\mathbf{s}}_k\Vert }_1$, it follows immediately that ${\sum }_{k=1}^K{\tilde{a}}_{k,n}=1$. The meaning of the term “relative abundance” can now be better understood if we reconsider the NMF problem: X = SA, where it is assumed that the row entries of a given column of S sum to 1; an assumption that follows from the preceding discussion on normalization. In this case, the relative abundance of an end-member (say kth.) at a given pixel (say nth.) is a kind of a weighting factor interpreted to signify the relative contribution of its signature signal (kth. column of A) to the possibly normalized signal measured at the nth. pixel (nth. column of X).

The aforementioned normalization technique can be understood intuitively by considering a simple case where we have a mixture of 2 end-members (K = 2), for which the end-member signatures s₁ and s₂ are represented as vectors OS₁ and OS₂ in Fig. 1. In 2-D space, the unit L₁-norm circle (set of vectors of norm 1) is a square, which is shown in dotted lines in Fig. 1. Now, under the non-negativity and linear mixing assumptions, a data vector x_n, denoted by OX lies inside the blue shaded region spanned by OS₁ and OS₂. The effect of normalizing a vector to unit length in L₁-norm sense can be thought of as scaling the length of that vector so that the tip of the vector falls on the unit L₁-norm circle, without changing the direction of that vector. Thus, the normalized vector x̃_n is simply a scaled version of the original vector x_n and is denoted by OX′. By similar reasoning, the normalized end-member signatures, s̃₁ and s̃₂ (denoted by vectors OS′₁ and OS′₂) also lie on the unit L₁-norm circle, whence it follows that any vector expressed as a non-negative linear combination of s₁ and s₂ (or lying in the blue shaded region) upon normalization will fall on the line joining S′₁ and S′₂, which represents a 1-D simplex.

2.4.3. NMF algorithms

A class of algorithms to perform NMF is based on the above mentioned geometrical interpretation of linear mixing model. These algorithms can be broadly grouped into two categories. The first category includes algorithms that are based on the assumption that the set containing the end-member signatures 𝔖 ≡ {s_k ∈ ℝ^T, k = 1, 2,..., K} is a subset of the set 𝔛 ≡ {x_n ∈ ℝ^T, n = 1, 2,..., N} containing the data vectors. This means that there are at least K pixels denoted by n₁, n₂,..., n_K such that x_ni = s_i, for i = 1, 2,..., K. This assumption is commonly referred to as the pure pixel assumption and it simply means that the vertices of the simplex described by the set of points in 𝔛 are contained in 𝔛. The problem of estimating end-member signatures is then reduced to finding the data vectors that form the vertices of the simplex. Some popular algorithms based on this assumption are Vertex Component Analysis (VCA), Pixel Purity Index (PPI) and N-FINDR [19–21]. The second category of NMF algorithms deal with a more realistic and difficult situation where the end-members appear rarely as pure pixels or in other words, the observed pixels are mostly a mixture of end-members. In such a case, the data does not span the entire simplex and not many observed pixels are found at the vertices of the simplex. The basic idea behind these algorithms is that even in the absence of pure pixels, it may be possible in many cases to deduce the simplex structure of the data. This idea was described in [22], where the author introduced a Minimum Volume Transform (MVT) to infer the simplex structure in the absence of pure pixels. Following the idea of MVT, several unmixing algorithms based on the same idea have been proposed in the literature [18, 23, 24]. In this research, we present the application of Simplex Identification via Split Augmented Lagrangian (SISAL) [25] to find the vertices of a minimum volume simplex that encloses the multispectral FLIM data subject to the non-negativity and full-additivity constraints. To state this condition mathematically, let us assume that the T dimensional data vectors are represented in a K dimensional subspace. If we denote the lower dimensional analogues for matrices X and S by 𝒳 and 𝒮, then the volume of the K − 1 dimensional simplex embedded in K dimensions is |det (𝒮)|. Furthermore, if we define 𝒬 ≡ 𝒮⁻¹, then the optimization problem that SISAL attempts to address can be mathematically expressed as:

$$\begin{array}{ll}\underset{𝒬}{\text{arg}\hspace{0.17em}\text{max}}\hfill & \hfill -\mathit{log}\hspace{0.17em}\left|\mathit{det}(𝒬)\right|\hfill \\ \text{subject}\hspace{0.17em}\text{to}\hfill & 𝒬𝒳\succcurlyeq \mathbf{0},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{1}}_K^T𝒬𝒳={\mathbf{1}}_N^T.\hfill \end{array}$$ (3)

In order to account for outliers and noise in the data, the full-additivity hard constraint is replaced by a soft constraint which results in the following modified optimization problem:

$$\begin{array}{ll}\underset{𝒬}{\text{arg}\hspace{0.17em}\text{max}}\hfill & -\mathit{log}\hspace{0.17em}\left|\mathit{det}(𝒬)\right|+\lambda {\Vert 𝒬𝒳\Vert }_h\hfill \\ \text{subject}\hspace{0.17em}\text{to}\hfill & \hfill {\mathbf{1}}_K^T𝒬𝒳={\mathbf{1}}_N^T,\hfill \end{array}$$ (4)

where ||Y||_h ≡ ∑_ij max{−[Y]}_ij, 0} and λ > 0 is the regularization parameter. The optimization problem stated in Eq. (4) is solved using a set of sequential quadratic programming problems as discussed in [25]. An efficient MATLAB implementation of SISAL algorithm is made publicly available by the authors of [25] on their website.

2.5. Feature extraction and classification

2.5.1. Feature extraction

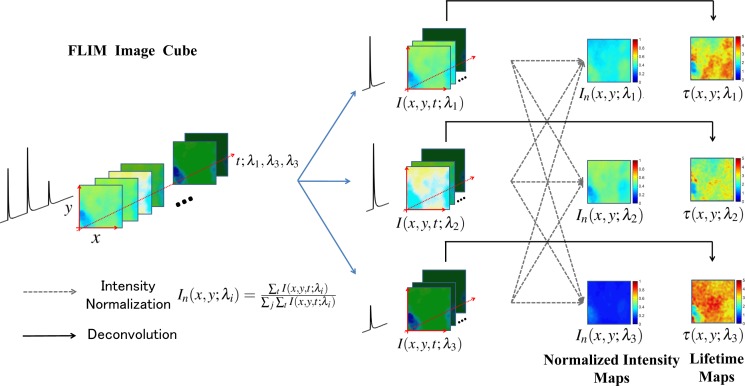
A total of 58 arterial tissue samples were imaged over 2 mm × 2 mm field of view by the multispectral FLIM system described earlier, generating a database of 58 multispectral FLIM data cubes of size 60 × 60 × 768 (x × y × t; λ₁, λ₂, λ₃). The 3-D multispectral FLIM image cubes were then processed to obtain two sets of 2-D feature maps, namely, the standard FLIM features and the NMF FLIM features. The process of obtaining these features from multispectral FLIM images is outlined in Fig. 3 and Fig. 4 respectively. The normalized intensity and lifetime maps constitute the first set of features (standard FLIM features). In order to obtain these features, the first step was splitting the spectro-temporal FLIM data cube into different temporal FLIM cubes, one for each wavelength band. These temporal FLIM data cubes are denoted by I(x, y, t; λ₁), I(x, y, t; λ₂) and I(x, y, t; λ₃) in Fig. 3; where the process of extracting standard FLIM features is illustrated for the case of a 3 wavelength multispectral FLIM data cube. Next, intensity map for each wavelength band was obtained by integrating in time, the measured fluorescence decay signals in the temporal FLIM data cube for a given wavelength. The normalized intensity maps were then obtained by dividing the intensity value at each pixel in an intensity map by the sum of the intensity values at that pixel in the intensity maps for each wavelength band. This process of normalization is illustrated by dashed arrows in Fig. 3. Finally, to obtain lifetime maps for each wavelength band, the measured temporal decays in a FLIM data cube for each wavelength band was deconvolved from the instrument response using the Laguerre deconvolution method and the lifetime was estimated by finding the expected value of the deconvolved decay [26]. The deconvolution process is illustrated by solid black arrows in Fig. 3. The set of normalized intensity and lifetime maps, denoted by I_n(x, y; λ₁), I_n(x, y; λ₂), I_n(x, y; λ₃) and τ(x, y; λ₁), τ(x, y; λ₂), τ(x, y; λ₃) respectively in Fig. 3 comprise the standard FLIM features.

Fig. 3:

Schematic illustrating the process of obtaining the normalized intensity maps and lifetime maps from a 3 channel multispectral FLIM data cube. The first step in this process is splitting the spectro-temporal cube into three temporal cubes: one cube per wavelength channel, shown in blue arrows. The normalized intensity and lifetime maps are then obtained from the temporal cubes by a normalization procedure (dashed lines, also see legend) and time deconvolution (solid lines) respectively. These maps constitute the standard FLIM features.

Fig. 4:

Schematic showing the process of performing NMF on a multispectral FLIM data cube. The 3-D spectro-temporal cube is unfolded and normalized to obtain a 2-D data matrix X. The data matrix is then factorized to yield the mixing matrix S and the relative abundance matrix A, columns of which are reshaped to obtain end-member relative abundance maps. These abundance maps constitute the NMF FLIM features.

The process of obtaining the second set of features (NMF FLIM features) is shown in Fig. 4. To perform NMF on multispectral FLIM data, the first step was “unfolding” the multispectral FLIM data cube, which involved reshaping the 3-D data cube (x × y × t; λ₁, λ₂, λ₃) to form a 2-D data matrix (t; λ₁, λ₂, λ₃ × xy). The data matrix thus obtained was then normalized by using the DPFT and subsequently factorized using the SISAL algorithm to yield a mixing matrix that contains the end-member signatures and an abundance matrix, rows of which were reshaped to yield relative abundance maps for the end-members as shown in Fig. 4. The relative abundance maps for the end-members constitute the NMF FLIM features.

The performance of the two sets of features was evaluated in terms of their ability to characterize multispectral FLIM images by training and testing a multinomial logistic regression classification model (described in the next section) on a subset of 21 out of 58 multispectral FLIM datasets (homogeneous datasets). Furthermore, to obtain pixel level classification, each pixel of a FLIM image was considered to be a data-point, yielding a labeled data set of 21 × 60 × 60 data-points. The classification performance for the logistic regression model obtained from each set of features was compared by estimating the 10 fold cross-validation misclassification error.

2.5.2. Multinomial logistic regression

Supervised classification is the problem of deriving a set of rules from a set of pre-classified data and using that rule to classify a new data-point. The set of pre-classified data-points along with the class for each data-point is called the training set 𝒯 = {(z₁, y₁), (z₂, y₂),..., (z_N, y_N)}, where z_n is referred to as the feature vector for the n th. data point and y_n = [y_n,1, y_n,2,..., y_n,C] is a 1 × C vector such that y_n,c = 1 if the n th. data point belongs to c th. class and 0 otherwise. Multinomial logistic regression is one such supervised classification method that models the posterior probability of a data point belonging to one of the C possible classes as a linear function of z [27, 28]. By fixing one of the classes as the baseline class, the conditional log-odds of other classes with respect to the baseline class have the form:

$$\text{log}\frac{\text{Pr}\left(\text{Class}=c|\mathbf{Z}=\mathbf{z}\right)}{\text{Pr}\left(\text{Class}=C|\mathbf{Z}=\mathbf{z}\right)}={\beta }_{c,0}+{\mathit{\beta }}_c^T\mathbf{z},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}c=1,2,\dots C-1,$$ (5)

where the C th. class is assumed to be the baseline class. The special form of logistic regression model ensures that the posterior probabilities sum to 1, i.e. ∑_c Pr (Class = c|Z = z) = 1. The problem of fitting a logistic regression model amounts to solving the maximum likelihood problem defined as:

$$\ell (\mathit{\beta })=\sum _{n=1}^N\sum _{c=1}^{C-1}{y}_{n,c}\text{log}\frac{\text{exp}\left({\beta }_{c,0}+{\mathit{\beta }}_c^T{\mathbf{z}}_n\right)}{1+{\sum }_c\text{exp}\left({\beta }_{c,0}+{\mathit{\beta }}_c^T{\mathbf{z}}_n\right)},$$ (6)

where the maximum likelihood estimate for the model parameter β ≡ (β_1,0, β₁, β_2,0, β₂,..., β_C−1,0, β_C−1) is obtained through an iterative optimization procedure like Newton-Raphson method [28,29]. The model thus obtained is then used to predict the posterior probability of a given data point belonging to one of the C classes and consequently assigning it to the class with the maximum probability.

3. Results

3.1. Validation on simulated data

The proposed method was first validated on simulated multispectral FLIM data, to which effect 10000 data vectors (N = 10000) representing artificial mixtures of collagen, lipids and elastin (K = 3) were generated. Collagen, lipids and elastin are the dominant endogenous fluorophores in artery tissue and are thus relevant to the present study. The end-member profiles for collagen, lipids and elastin (T = 510) were simulated based on the expected intensity and lifetime values for these fluorophores obtained from a time resolved fluorescence study [30]. These profiles constituted the S matrix and are referred to as the “true end-member profiles”. To form the relative abundance matrix A, values for relative abundances were obtained by sampling from a uniform distribution and subsequent normalization to enforce full-additivity. To ensure that the data does not contain any pure pixel, data vectors having relative abundance greater than 0.7 for any end-member were discarded. Finally, an additive white Gaussian noise was added to obtain a SNR of 15 dB. To quantify the performance of the algorithm on simulated data, 5 realizations of the noisy data were generated and the weighted mean absolute percent error (WMAPE), defined as:

$$\text{WMAPE}=\frac{\sum _{n=1}^N\left|\frac{x_n-{\tilde{x}}_n}{x_n}\right|\cdot x_n}{\sum _{n=1}^N{x}_n}\times 100\%$$ (7)

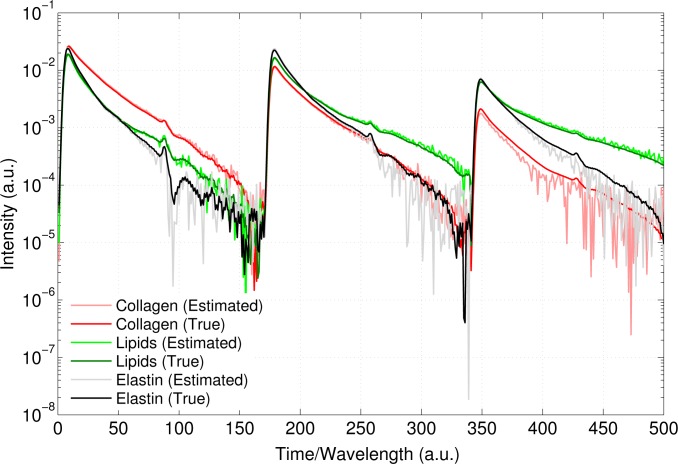
was calculated for S and A for each realization. The WMAPE in estimating A and S was found to be 15.81±0.42 and 9.67±0.81 (mean ± standard error) respectively, indicating a good agreement between the actual and estimated values. Figure 5 shows the true end-member pro-files plotted along with the estimated profiles for one of the realizations of the noisy data. The profiles are plotted on a semilog (y axis) graph to highlight the differences between the two profiles that were not evident on a linear scale. The plot indicates good agreement between the two profiles. Likewise, a scatter plot shown in Fig. 6 also indicates good match between the estimated and true relative abundances. To further compare the estimated profiles with the true profiles, the normalized intensity and lifetimes in the three channels estimated from the profiles are plotted in Fig. 7(a) and (b) respectively. These plots suggest a good match between the spectro-temporal characteristics of the true and estimated end-members. The large mismatch between collagen’s lifetime in the third channel is possibly a result of the sensitivity of lifetime estimation to SNR which is a consequence of low signal level in collagen’s spectro-temporal profile in the third channel.

Fig. 5:

True end-member profiles (dark shade) plotted over estimated profiles (light shade) for the simulation study discussed in the text. The profiles are plotted on a semilog (y) axis to highlight the differences between the two profiles that were indistinguishable on a linear scale

Fig. 6:

Scatter plot showing good agreement between the estimated and true relative abundances. Black dashed line represents the line of perfect fit (y = x).

Fig. 7:

(a) Normalized intensity and (b) lifetimes in the three channels for the true and estimated end-member profiles. Results indicate good agreement between the spectro-temporal characteristics of the two profiles

3.2. Validation on experimental data: feature extraction

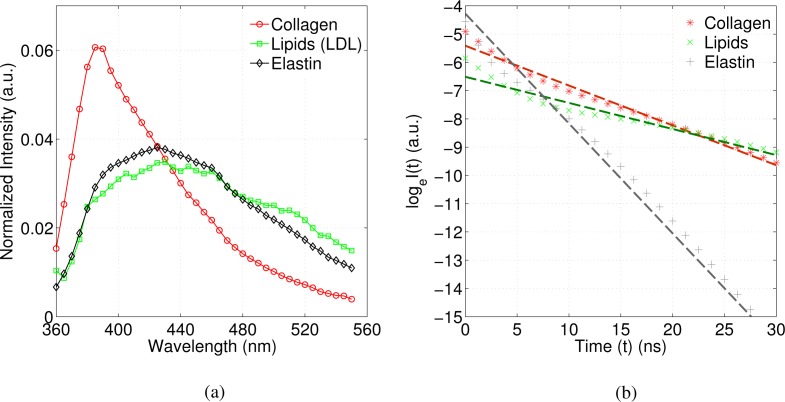
The method was also validated on experimental multispectral FLIM data obtained from fresh human postmortem atherosclerotic coronary plaques. Standard and NMF FLIM features were extracted from the multispectral FLIM database through the procedure outlined in the methods section. The end-member profiles obtained via NMF are shown in Fig. 8. The profile in red (solid line) has maximum emission intensity in the first channel followed by a relatively lower intensity in the second channel and least intensity in the last channel. This intensity trend is characteristic of collagen. Likewise, the green (dotted line) and black (dashed line) profiles have relatively same intensity in the first two channels but a lower intensity in the third channel, which is characteristic of both lipids and elastin as shown in the steady state spectra in Fig. 10(a) (see also [30]). To identify the end-members, we deconvolved the decay profile corresponding to the dominant emission band for each end-member and estimated the average lifetime from the deconvolved decays. This is shown in Fig. 10(b), where the log-transformed deconvolved profiles, log_e(I(t)) are plotted against time, t. In the case of a simple mono-exponential decay, the log-transformed plots would be straight lines. Deviation from a straight line indicates complex nature of decay kinetics. To estimate average lifetime from such a plot, a straight line fit based on least squares estimation was obtained and the average lifetime was estimated by calculating −1/slope of the best fit line. Based on the intensity trends and lifetime values, the three end-member profiles were identified as collagen (red, τ_avg= 7.1 ns), lipids (green, τ_avg= 10.8 ns) and elastin (black, τ_avg= 2.6 ns).

Fig. 8:

End-member signatures obtained from the artery multispectral FLIM data. Based on the spectro-temporal characteristics, the end-members were identified as collagen (red, solid line), lipids (green, dotted line) and elastin (black, dashed line)

Fig. 9:

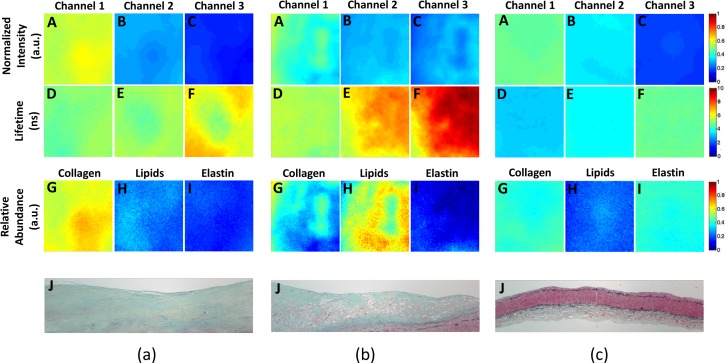
Standard FLIM features: normalized intensity and lifetime maps (A–C & D–F resp.) and NMF FLIM features: relative abundance maps (G–I) for three homogeneous samples, one from each (a) High Collagen, (b) High Lipids and (c) Low Collagen/Lipids class. Also shown are the representative histology sections for each class (J).

The two sets of features corresponding to a representative HC, HL and LCL plaque from the homogeneous datasets are shown in Fig. 9. In each sub-figure, the top row (A)–(C) shows the normalized fluorescence intensity maps for the three spectral channels. Likewise, the second row (D)–(F) shows the lifetime maps for the three channels. The relative abundance maps of the three end-members, namely, collagen, lipids and elastin, constitute the NMF FLIM features that are shown in the third row (G)–(I). Representative histopathological sections for each plaque type are also shown in the last row (J) of each sub-figure.

Fig. 10:

(a) Steady state spectra for collagen, lipids (LDL) and elastin obtained from time-resolved measurements (b) log-transformed fluorescence decays for collagen, lipids and elastin fitted to straight lines, where the negative inverse slope is equal to a fluorophore’s average lifetime. Deviation from a straight line indicates the non-mono-exponential nature of the decay.

For the HC plaque (Fig. 9(a)) the fluorescence intensity was stronger in channel 1 than in channels 2 and 3, and the average lifetime varied between ∼5–6 ns, which resembles the fluorescence emission characteristics of collagen. In the histopathological section, the light blue stain color indicates the presence of collagen. The relative abundance maps in this case, showed higher abundance of collagen (0.61±0.04) as compared to that of lipids (0.25±0.04) and elastin (0.17±0.02). For the HL plaque (Fig. 9(b)), the fluorescence intensity, as compared to the HC plaque, was lower in channel 1, similar in channel 2 and higher in channel 3. The averaged lifetime gradually increased from ∼5 ns in channel 1 to ∼8 ns in channel 3. In the histopathological section empty areas indicate lipids. The relative abundance maps in this case showed the largest abundance of lipids (0.57±0.09) along with some collagen (0.33±0.09) but significantly lower amount of elastin (0.10±0.05). Lastly, for the LCL plaque (Fig. 9(c)), the fluorescence intensity had a similar trend in channels 1 and 2 as HL plaque (due to the similar emission intensity profiles for elastin and lipids, see Fig. 10(a)). However, unlike HL, the lifetime maps in the case of LCL were similar in the three channels (between ∼3–4 ns). The relative abundance maps for LCL type of plaque suggested presence of collagen (0.41±0.02) and elastin (0.40±0.02) but a significantly lower amount of lipids (0.21±0.03).

3.3. Classification performance on homogeneous dataset

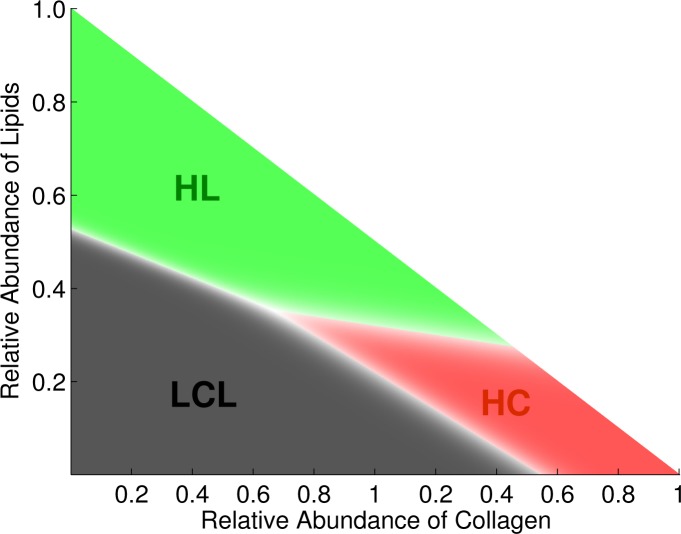
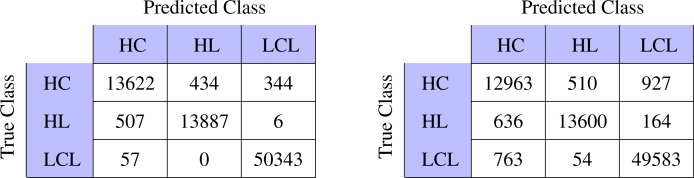
To compare the performance of the two sets of features (standard FLIM vs. NMF features) in terms of their ability to discriminate between the three plaque types (HC, HL, LCL), two multinomial logistic regression models, one from each feature set, were trained and tested on the homogeneous dataset. In the case of standard FLIM features, the decision boundaries are hypersurfaces in a 5 dimensional feature space and cannot be visualized. However, in the case of NMF features, the decision boundaries are lines in a 2-D feature space as shown in Fig. 11. As can be seen in Fig. 11, the classifier partitions the feature space into 3 regions corresponding to the three classes. In order to quantify the classification performance of the classifier trained and tested on the two sets of features, we computed the confusion matrices via 10 fold stratified cross validation shown in Fig. 12. The overall classification accuracy for the standard FLIM features was estimated to be 98.3% and 96.1% for the NMF features.

Fig. 11:

The multinomial logistic regression classifier for the NMF features partitions the feature space into three regions corresponding to the three classes: High Collagen (HC), High Lipids (HL) and Low Collagen/Lipids (LCL) seperated by linear decision boundaries (white region)

Fig. 12:

Confusion matrix for the standard FLIM features (left) and the NMF FLIM features (right). The diagonal entries indicate the number of pixels that were correctly classified, while the off-diagonal entries indicate the misclassified pixels.

3.4. Validation on heterogeneous plaques

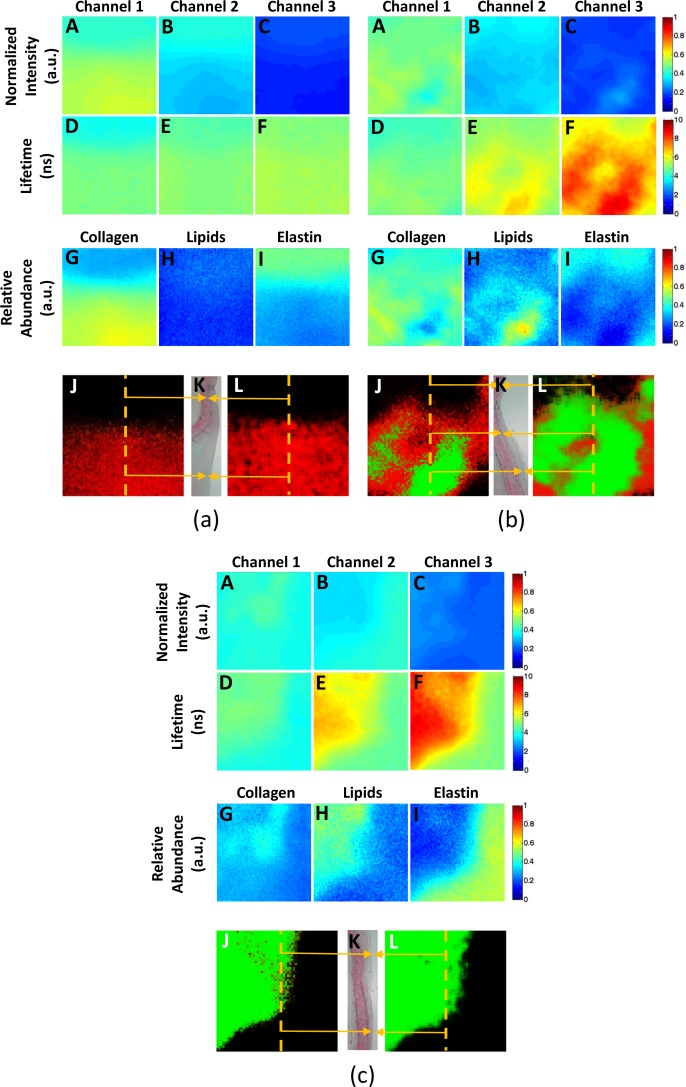
We also compared the performance of the two classifiers trained on the standard FLIM and NMF features extracted from the homogeneous datasets by testing them on datasets of plaques showing heterogeneous histopathology. Three examples of such validation are shown in Fig. 13(a)–(c). The first two rows: (A)–(C) & (D)–(F) in each sub-figure show the normalized intensity and lifetime maps respectively. The abundance maps for collagen, lipids and elastin are shown in the third row (G)–(I). The classification maps for classifier trained on standard FLIM and NMF features are shown in panel (J) and (L) respectively. For both classification maps, the probability of each FLIM image pixel belonging to HC or HL class is color coded in red and green, respectively. We also display a matching histology section for each plaque in panel (K) of each sub-figure.

Fig. 13:

Standard FLIM features: normalized intensity and lifetime maps (A–C & D–F resp.) and NMF FLIM features: relative abundance maps (G–I) for three heterogeneous samples with regions of: (a) HC and LCL (b) HC, HL and LCL, and (c) HL and LCL. Also shown are the histology sections from the center of the sample (K) with matching regions in the classification maps obtained from the NMF features (J) and the standard FLIM features (L) shown in orange arrows. Pixels in the classification maps are color coded as red for HC, green for HL and black for LCL

Fig. 13(a) shows the feature and classification maps for a plaque with regions of LCL (top) and HC (bottom). The matching histology section for this sample confirmed that the LCL region was IT and the HC region was fibrotic PIT. A plaque showing regions of HC, HL and LCL is shown in Fig. 13 (b); a histology section corresponding to the middle of the plaque confirmed that the HC region was fibrotic PIT, the HL region showed foam cell infiltration, and the LCL region was IT. Finally, a plaque showing regions of HL (top-left) and LCL (bottom-right) is shown in Fig. 13 (c); a histology section corresponding to the middle of the plaque confirmed that the HL region was PIT highly infiltrated by foam cells, and the LCL region was IT.

4. Discussion

In this study, we presented an application of NMF to identify the type of constituent fluorophores and their relative contributions to the bulk multispectral FLIM signal measured from a sample. We also demonstrated the potential application of the proposed method for multi-spectral FLIM based tissue characterization using the coronary atherosclerotic plaques as a test model. In the following, we discuss the main advantages and limitations of the proposed method over the standard methods of interpreting multispectral FLIM images.

The conventional method of interpreting multispectral FLIM images is based on comparing the average spectral intensity and lifetime values of a sample with a set of possible known fluorophores. This method is in most cases very subjective, especially when there are more than one fluorescing species contributing to the bulk fluorescence signal. In contrast, the NMF features provide a more direct and intuitive way of interpreting FLIM images, because fluorophore abundance maps can be directly related to tissue biochemistry. The application of NMF to the multispectral FLIM data from human coronary plaques clearly demonstrated this aspect of the proposed method, where it was shown how the NMF approach was not just able to identify the main endogenous tissue fluorophores (i.e. elastin, collagen and lipids), but was also able to quantify their relative abundance maps, allowing for direct biochemical characterization of the atherosclerotic plaques.

To provide quantitative interpretation of FLIM images based on the intensity and lifetime values, the most commonly used method assumes that all the constituent fluorophores in a sample have mono-exponential decay kinetics. The sample fluorescence decay is then expressed as a multi-exponential model, in which each exponential component is associated to each constituent fluorophore. The sample fluorescence decay at each pixel is thus fitted to the multi-exponential model, and the estimated normalized pre-exponential weights are interpreted as the relative contribution of each constituent fluorophore to the bulk fluorescence signal [6, 31]. While such an interpretation of FLIM images can be more informative than the analysis based on single average lifetime value, it is restricted in a way, because many fluorophores are known to exhibit non-monoexponential decays thereby violating the assumption of a mono-exponential decay associated to each constituent fluorophore. This is even more pertinent when analyzing endogenous multispectral FLIM data, because many endogenous fluorophores show non-monoexponential decay dynamics [7]. This however, is not a problem with the NMF approach, because it does not make any assumption about the functional form of the end-member profiles (i.e. decay dynamics of the constituent fluorophores). This is evident from the log-transformed fluorescence decay profiles for collagen, lipids and elastin retrieved via NMF and shown in Fig. 10 (b), where the deviation of these plots from straight lines (dashed lines) indicate the complex nature of the decay dynamics.

Kremers et al. recently proposed a method capable of handling fluorophores showing non-monoexponential decays; however, its application was limited to two species [6], like many other earlier studies [5,9]. This is mainly because the SNR requirement for fitting a multiexponential model with more than two lifetimes is very demanding. Thus, these methods can handle experimental FLIM data where only two molecules can be simultaneously monitored. Moreover, in most of these studies only the fluorescence lifetime but not the spectral information is used in the unmixing process [6, 10]; e.g. in the method proposed by Kremers et al., only one emission band was considered. Schlachter et al. recently proposed a method capable of handling multispectral FLIM data; however, its application was limited to mono-exponential fluorescence decays and to two species [10]. The NMF approach, on the other hand, can handle multispectral FLIM data originating from more than two constituent fluorophores that is measured across an arbitrary number of emission spectral bands. This can facilitate the identification of the underlying constituent fluorophores, since the end-member profiles obtained via NMF contain both spectral and temporal information which makes it possible to identify them with adequate confidence. This was clearly demonstrated in our analysis of the multispectral FLIM data from the human atherosclerotic plaques, where the three fluorophores were correctly identified as elastin, collagen and lipids, as expected based on the well characterized histopathology of atherosclerosis [30]. In this case, the identification of the constituent fluorophores was performed based on both the spectral and lifetime values of the estimated end-member profiles at three different emission bands. This is in contrast to the standard FLIM analysis method, where only one lifetime value is available for making such an identification. In such a case, unless guided by strong evidence derived from tissue biochemistry, the identification of the latent fluorophores can at best be only hypothesized.

Another advantage of the NMF approach over the standard FLIM data analysis methods is that the NMF features (abundance maps) can be obtained directly from the spectro-temporal FLIM intensity data in a computationally efficient manner without the need for time deconvolution. The time complexity of SISAL algorithm is estimated to be of the order O(NK) in [25], wherein the authors have also compared the time performance of SISAL against other NMF algorithms. Furthermore, once the end-member profiles have been derived from a pre-recorded dataset, the abundance maps for a new sample can be obtained quickly by performing a simple inversion. This is unlike in the case of standard FLIM features, where unless extremely short excitation light pulses are used, time-deconvolution of the instrument response from the fluorescence decay data is required to obtain lifetime maps [7]. The deconvolution coupled with multi-exponential model fitting involve iterative optimization, which is both computationally expensive and time consuming. This advantage of the proposed method, however, necessitates that the data is recorded by the same system, i.e. the instrument response for all the data is the same.

The above stated advantages of the NMF method however, come with the need of having enough diversity in data such that the simplex formed by the data vectors is filled adequately to enable the inference of the underlying simplex structure. It is only in such a case, that NMF algorithms are able to estimate the end-member profiles and the corresponding relative abundances with confidence.

An important aspect of the proposed technique is the estimation of the number of components (end-members) present in the linear mixing model. Several methods for determining the number of end-member are reported in the literature, ranging from relatively simple techniques like principal component and independent component analysis to more complicated techniques like virtual dimensionality [32], maximum noise fraction [33] and noise adjusted principal components [34] and many more. While these techniques have been applied with varying degrees of success in different applications, there is no single approach generally accepted to work in all cases. In our case, the choice of three end-members (K = 3) was primarily based on the biochemical understanding of the underlying tissue. However, in cases where there is no prior knowledge about the possible number of end-members, any or more than one of the above techniques can be used in conjugation with the interpretation of the end-member signatures obtained by NMF to decide on an appropriate number of end-members.

Finally, we also validated the performance of the new set of FLIM features in terms of their ability to discriminate between three types of atherosclerotic plaques. The classification maps and the confusion matrices presented in the results section, suggested that the NMF features are comparable to the standard FLIM features in terms of their discriminatory power to differentiate between the three plaque types. With the added advantage of ease of interpretation, we believe that the NMF features can facilitate the translation of multispectral FLIM from predominantly a lab imaging modality to clinical setting.

5. Conclusions

To summarize, we presented the application of NMF to multispectral FLIM data to derive a set of NMF features that provides an intuitive and objective way of characterizing latent tissue fluorophores and their abundances. The method presented in this study made no assumption about the functional form of decay kinetics of the fluorophores under study and was applied directly from the recorded multispectral FLIM intensity data thereby obviating the need for deconvolution. As discussed earlier, several studies on the application of FLIM to tissue diagnosis use the difference in lifetime values to distinguish normal tissue from a pathological tissue; however, the scope of such studies has been severely restricted to those two ends of the disease-progression spectrum. We believe that this is mainly due to the absence of techniques that can objectively characterize the latent tissue fluorophores and quantify the changes in their abundance during the pathogenesis of a disease. The method proposed in this study is an attempt in this direction, which would expand the scope of FLIM in clinical graded diagnosis by providing an easy and objective way of interpreting multispectral FLIM data. More generally, the method detailed in this study can also be helpful in advancing the field of molecular imaging and may find broad applicability in basic, pre-clinical and clinical research.