Variable-sized bar targets for characterizing three-dimensional resolution in OCT

Abstract

Resolution is an important figure of merit for imaging systems. We designed, fabricated and tested an optical phantom that mimics the simplicity of an Air Force Test Chart but can characterize both the axial and lateral resolution of optical coherence tomography systems. The phantom is simple to fabricate, simple to use and functions in versatile environments.

1. Introduction

Optical resolution is an important characteristic that describes the quality and utility of an imaging system. The 1951 United States Air Force Test Chart (AFTC) has long been used as a simple and reliable way to characterize the lateral resolution of optical systems like optical coherence tomography (OCT): a major advantage of the bar chart layout of the AFTC is its simplicity and ease of interpretation. However, the traditional AFTC is incapable of characterizing axial resolution, which is important in OCT. A simple-to-use optical phantom for characterizing both the lateral and axial resolutions of OCT systems could serve as a powerful calibration standard for this technique.

The recent proliferation of optical techniques for medical imaging has generated new interest in optical phantoms to evaluate imaging systems [1–4]. In particular, several new phantoms have been developed specifically for OCT, including phantoms with embedded scattering particles [5], layered phantoms [6,7], and embossed phantoms [8]. Problems associated with these phantoms include the complexity of the measurement [5], the limited range of operation across multiple devices [6], and the use of complicated fabrication processes requiring many steps [7] or layouts that do not permit simple readout of results [8]. We describe the use of soft lithography to fabricate a phantom that combines the advantages of embossed polydimethylsiloxane (PDMS) structures (e.g., rapid prototyping, variable optical properties) with the simple readout characteristics of the AFTC. After fabrication, we validated the performance of the phantom by imaging it with a commercial OCT system.

2. Methods and experimental design

2.1. Design of the phantom

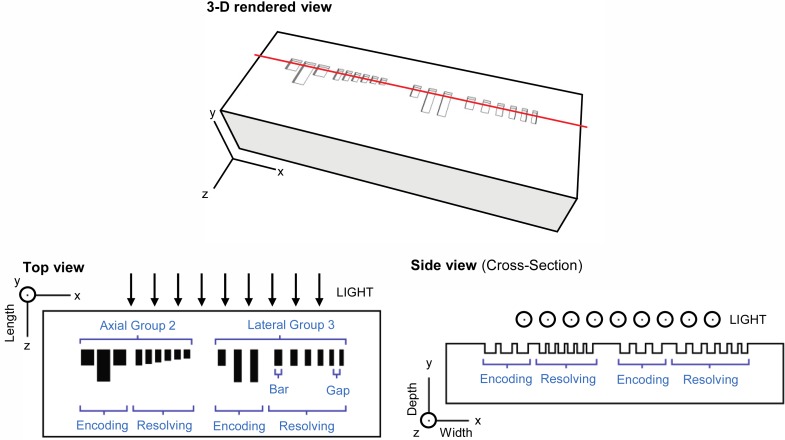
Our goal was to design a phantom with the following features: (1) simple bar patterns that mimic the AFTC; (2) operability over a range of devices with different resolutions; (3) rapid correlation of visible features with their sizes; (4) dual-purpose patterns for measuring axial and lateral resolution. We describe here the general layout of our design, which comprises bars arranged in “groups” of similarly sized features. Each axial resolving group contains nine bars: three binary-formatted “encoding” bars, all having the same width but quantized length, indicate the group number; six “resolving” bars, all having the same width and varying length, are provided to measure the axial resolution. The lateral resolving groups are similarly structured, having three binary-formatted “encoding” bars to indicate the group number and six “resolving” bars, all having the same length and varying width, to measure lateral resolution. The dimensions of the varying parameter of the resolving bars match the widths of the line pairs of a commercial AFTC (e.g., the group 3 lateral resolving bars range in width from 125.0 μm to 70.2 μm, logarithmically). For the lateral resolving bars, the five gaps (spaces between bars) are also important for finding the resolution and have the same widths as the bars immediately to their left. The design is illustrated schematically in Fig. 1 below.

Fig. 1.

3-D rendered (above) and schematic (below) layouts of the optical phantom. Submerged structures (bars) are shown in black in the schematic top view. The location of the side-view cross section is shown by the red line in the 3-D rendered view. Axes map to definitions of depth, width and length referred to throughout this paper. Within each group, only one dimension (either width or length) varies between the six resolving bars; these are listed in Table 1. Dimensions are not to scale.

Table 1 describes the encoding scheme for the group numbers and the sizes of the largest and smallest bars in each group. The width of the axial resolving bars is the same for all groups (100 μm). We chose this width to ensure that the bars would be visible in any OCT system (most systems have a lateral resolution less than 100 μm). The encoding bars are 200 μm wide to differentiate them from the resolving bars, and their length is either one or two times the length of the longest resolving bar in a given group. This ensures that the encoding bars are always visible for the group number that characterizes the resolution of the phantom. Hence, the inability to resolve the group number for a particular set of resolving bars suggests that this group does not contain structures that are within the resolution of the system, and the next largest group should be imaged instead. The lateral resolving bars are the same length for all groups (250 μm) but vary in width based on the size of the AFTC bars for that group. The width of the encoding bars is the width of the largest resolving bar in that group. Thus, the encoding structure is always visible for the group that characterizes the lateral resolution. The length of the encoding bars is one or two times the length of the resolving bars, depending on the binary representation of the group number.

Table 1. Scheme for encoding the group number and dimensions of the resolving bars.

Group Number				Resolving Structure
Decimal	Binary	Encoding		Max. size	Min. size
2	010			250 μm	140.3 μm
3	011			125 μm	70.2 μm
4	100			62.5 μm	35.1 μm

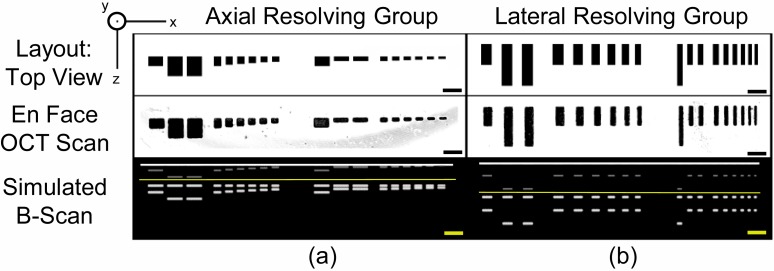
Figure 2 shows the designed layout of the group 3 axial and group 4 lateral resolving bars we fabricated along with acquired en-face OCT scans of groups 3 and 4, which clearly resemble the intended layout. The third row shows MATLAB simulations [9] of the B-scans we expected to obtain based on parameters of the commercial system we used for imaging. The simulation accounts for the expected appearance of self-interference due to autocorrelation artifacts, shown as faint structures appearing above the solid yellow line. From this simulation it can be seen that each individual bar generates two bright lines in the B-scan, which is sufficient to observe cross-talk; this mimics the functionality of the three-bar structure of the AFTC. This is in contrast to using a single mirror to measure the axial resolution, as is typically done, which can only provide one peak of strong reflectivity and thus cannot be used to observe crosstalk.

Fig. 2.

Layout, en face OCT scans and simulated B-scans of the axial resolving group and lateral resolving group of the optical phantom. Reflectivity (in dB) is mapped to inverted brightness or brightness of the image for the en face scans or simulations, respectively. The en face OCT scan was acquired at the y = 0 plane of the phantom. Note that the view of the simulated B-scan (x-z plane) is perpendicular to that of the phantom layout and en face OCT scans. Scale bars = 250 μm.

2.2. Fabrication of the phantom

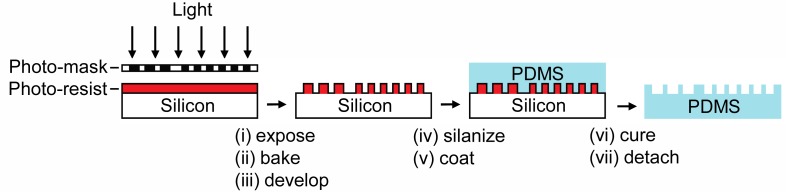
We used PDMS to fabricate the phantom using replica molding [10]. We chose to use PDMS because it is optically transparent, cheap, non-toxic and stable over long time periods. A diagram of the fabrication process is shown in Fig. 3 . In brief, a patterned photo-mask (CAD/Art Services) was transferred to a silicon wafer using a negative photoresist process; the bar chart features appeared raised in the patterned wafer. After silane treatment, liquid PDMS was made to flow over the mold and cured thermally. The bar chart features of the final PDMS phantom appeared submerged relative to the thickness of the PDMS substrate. The depth of all bars on the phantom was 50 μm: this is larger than the expected lateral resolution of most OCT systems and facilitated locating the phantom while mitigating diffraction. This depth was controlled by the thickness of the photoresist layer applied to the bare silicon wafer. The maximum allowable aspect ratio of the available photolithography equipment (1.5:1.0, width:depth) limited the minimum achievable bar size but is not a hard limit: with better equipment one can fabricate PDMS structures with larger ratios (> 5:1) using the same process [10]. The phantom we fabricated included groups 2 through 4; the width and length of the features range from 250 μm to 35.1 μm. As needed, groups with larger and smaller dimensions can be fabricated on the same phantom, and the number of designs to be fabricated simultaneously on a single phantom is easily scalable.

Fig. 3.

Representative steps in the soft lithography process used to fabricate phantom. The figures show schematic representations of the phantom as cross-sections viewed from the side. Dimensions are not to scale.

2.3. Validation and imaging

We used a commercial, spectral-domain OCT system (Telesto, Thorlabs) to validate the expected output of the phantom. The axial and lateral resolutions (full-width at half-maximum of the point-spread function) of the system were 10.6 μm and 12 μm, measured experimentally using a mirror and standard AFTC, respectively. We built a mount for the phantom with standard optomechanical components to allow six degrees of freedom for alignment. The phantom was oriented in the system such that light traveled along the z axis. The reference mirror was positioned to prevent corruption of the peaks of the bars [11] due to overlap with the self-interference patterns. To test the performance of the phantom in different reflectivity or scattering conditions, we imaged the phantom in air, water, and milk.

3. Results and discussion

3.1. Performance of the phantom for assessing resolution

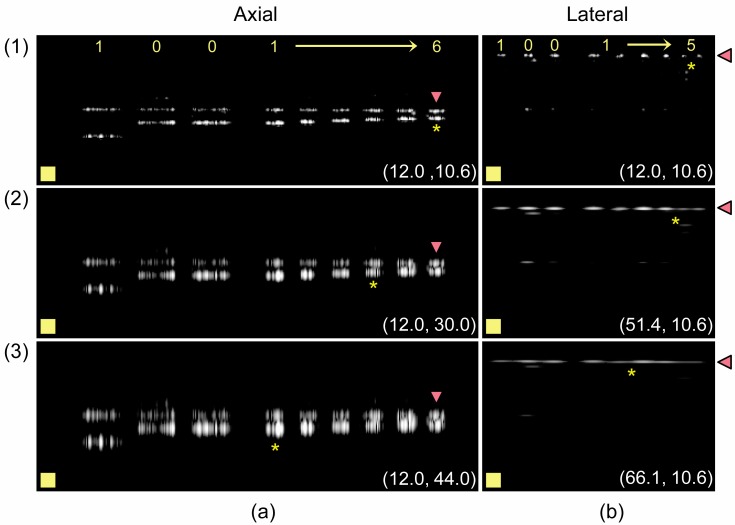
The first row of Fig. 4 shows actual B-scans of the group 4 axial (Fig. 4(a)) and lateral (Fig. 4(b)) resolving bars acquired in air. Notably, the positions of the bars in the B-scans agree with the simulations and the design (Fig. 2). The dynamic range of the B-scans is 24 dB; hence a drop in reflectivity of −6 dB corresponds to a drop in brightness of 25%. The labels at the top of the image identify the group 4 encoding bars and assign numbers to the six bars or five gaps in the group (in the case of the axial or lateral resolving structures, respectively). We have labeled the gaps of the lateral resolving structures instead of the bars because the overlap between the reflectivity of neighboring bars that occurs in the gap is the metric of interest for determining the lateral resolution.

Fig. 4.

B-scans of the axial (a) and lateral (b) resolving bars in air (row 1). Rows 2 and 3 show simulated cases for the reduced axial and lateral resolutions given as ordinate pairs: (lateral, axial). Asterisks denote the smallest resolvable structures. Scale box = 100 μm x 100 μm.

It is clear that even the smallest features of group 4 (bar 6 and gap 5) are resolvable in our system, which makes sense because the native resolution of our OCT system was better than the smallest resolving bars we fabricated. Thus, we simulated the effect of imaging the phantom in an OCT system with worse resolution by modifying the experimental data as follows. In Fig. 4(a), the bandwidth of each interferogram was artificially reduced by multiplying it with a Gaussian function with a full-width at half-maximum (FWHM) bandwidth of 25.2 nm or 17.2 nm to produce the modified images in rows 2 and 3, respectively. This degraded the effective axial resolution of the system from 10.6 μm to 30.0 μm and 44.0 μm, respectively; these latter values are within the range of sizes of the resolving bars in group 4. We similarly modified the lateral resolution of the original data in Fig. 4(b) by convolving the B-scan laterally with Gaussians with FWHM of 50.0 μm and 65.0 μm to yield the data in rows 2 and 3, respectively, which caused the lateral resolution to worsen from 12 μm to 51.4 μm and 66.1 μm, respectively.

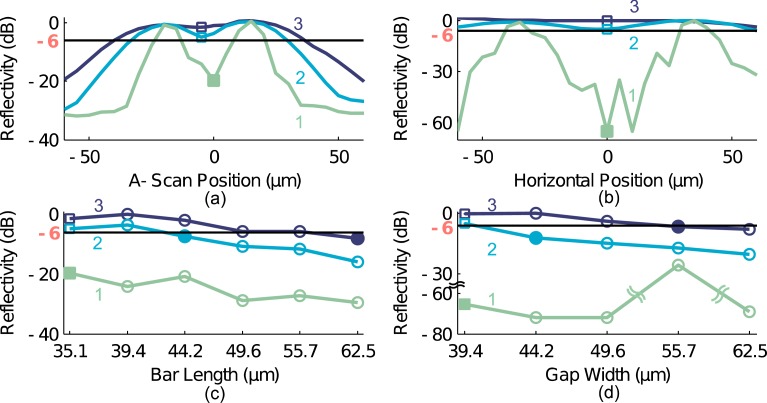
Figure 5(a) plots A-scans of bar 6 from each of the rows in Fig. 4(a); the centers of the bars are aligned at 0 μm, the maximum reflectivity was normalized to 0 dB, and the minimum reflectivity in each case is indicated with a square marker. Similarly, Fig. 5(b) plots the reflectivity profile across the smallest gap (gap 5) for each row of Fig. 4(b); the minimum reflectivity is also marked (squares). As is clear from Figs. 5(a) and 5(b), every bar in the unmodified B-scan (row 1) is resolvable, and the minimum reflectivity within or between the bars is less than −6 dB (solid line) for all bars. Thus, the smallest features we fabricated provides an upper bound for the axial and lateral resolutions of the Telesto OCT system.

Fig. 5.

Reflectivity profile along the smallest (squares) axial bar (a) or lateral gap (b) from the numbered rows in Fig. 4 at the location of the red arrows. The −6dB line marks the threshold for resolvability. Minimum reflectivity between all bars (c) and gaps (d) in Fig. 4; the smallest resolvable structure in each row is denoted by filled markers.

Theoretically, the reflectivity of the surface of the bars in the axial dimension is the convolution of the index mismatch (modeled as a delta function) with the Gaussian PSF of the source spectrum. The smallest bar size d that would yield a drop of 6 dB between the surfaces of the bars is related to the axial resolution of the system z_fwhm by $d=1.41z_{fwhm}^{}$; this relation can be found by solving Eq. (1):

$$20{\log }_{10}^{}\left(\frac{\min \left[\left({\delta }_{-d/2}^{}(z)+{\delta }_{d/2}^{}(z)\right)\ast \exp \left(-4\ln (2)z_{}^2/z_{fwhm}^2\right)\right]}{\max \left[\left({\delta }_{-d/2}^{}(z)+{\delta }_{d/2}^{}(z)\right)\ast \exp \left(-4\ln (2)z_{}^2/z_{fwhm}^2\right)\right]}\right)=-6\text{ dB,}$$ (1)

where min and max denote the local minimum and maximum of the contained function with respect to z, and _* denotes convolution. From this we expect to resolve bars larger than 42.3 μm and 62.0 μm, given the axial resolutions we simulated in rows 2 and 3 of Fig. 4(a). Thus, the smallest bars on our phantom that we would expect to resolve are bars 4 (44.2 μm) and 1 (62.5 μm) respectively, which is what we observe. The smallest resolvable bar for each row in Fig. 4(a) is indicated by a yellow asterisk, and by a filled marker in Fig. 5(c).

Reflectivity along the lateral dimension is given by convolution of the shape of the lateral bars (rectangle functions) with the PSF of the incident Gaussian beam. The minimum gap size g that we would expect to resolve is related to the lateral resolution of the system x_fwhm through Eq. (2):

$$20{\log }_{10}^{}\left(\frac{\min \left[\left(\Pi (\frac{x-g/2}{g})+\Pi (\frac{x+g/2}{2_{}^{1/6}g})\right)\ast \exp \left(-4\ln (2)x_{}^2/x_{fwhm}^2\right)\right]}{\max \left[\left(\Pi (\frac{x-g/2}{g})+\Pi (\frac{x+g/2}{2_{}^{1/6}g})\right)\ast \exp \left(-4\ln (2)x_{}^2/x_{fwhm}^2\right)\right]}\right)=-6\text{ dB,}$$ (2)

where min and max denote the local minimum and maximum of the contained function with respect to x, and * denotes convolution. From this we expect to resolve gaps (with a 6 dB drop) larger than 43.0 μm and 54.7 μm for the lateral resolutions we simulated in rows 2 and 3 of Fig. 4(b). Thus the smallest gaps in our phantom that we would expect to resolve are gaps 4 (44.2 μm) and 2 (55.7 μm), respectively. Indeed, this is what we observe. The smallest resolvable gap for each row in Fig. 4(b) is indicated by a yellow asterisk, and by a filled marker in Fig. 5(d).

Clearly, degrading the resolution of the system changes which is the smallest resolvable bar, as expected. The maximum drop in reflectivity between the surfaces of all bars in Fig. 4(a) is plotted in Fig. 5(c). Similarly, the largest drop in reflectivity for all gaps between the lateral resolving bars in Fig. 4(b) is plotted in Fig. 5(d). For each bar (gap), a drop in reflectivity of more than −6 dB from the maximum reflectivity of the bars indicates that such bars (gaps) are “resolvable.”

3.2. Demonstration of use of the phantom in various media

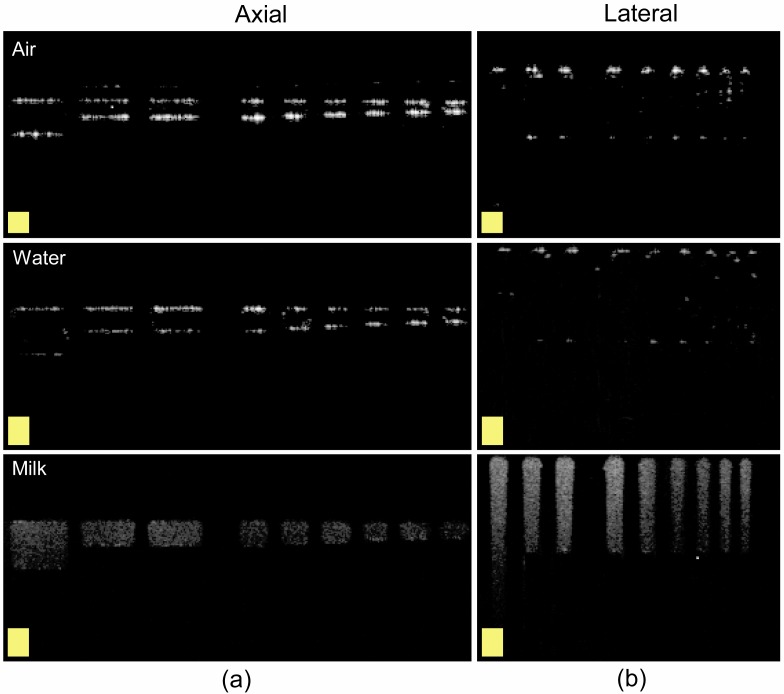
Figure 6 shows B-scans of the group 4 axial and lateral resolving groups in air, water and milk. These B-scans show the versatility of the phantom for imaging media with different optical properties. The axial distance between surfaces of the bars in the B-scan is greater when the phantom is in water (row 2) compared to when it is in air: the distance increases by a factor of 1.33 ± 0.07. This is in line with our expected results, given the actual refractive index of water. Lateral resolution is unaffected. The overall brightness of the bars also decreases by approximately 10 dB when the phantom is submerged in water, indicative of the smaller index mismatch between the PDMS and the surrounding media.

Fig. 6.

B-scans of the axial (a) and lateral (b) resolving bars when submerged in various liquid media. Scale boxes = 75 μm x 75 μm.

In milk (a scattering medium), a brightly speckled rectangle replaces the bars seen in air and water. Since the index of refraction of milk (n = 1.35 [12]) is close to that of water, the lengths of the rectangles are nearly the same as the lengths of the bars in water. Note that the largest lateral encoding bar is longer than the mean free scattering path of the milk (500 μm vs. 300 μm [12]), and the bottom of the bar is not visible because of attenuation due to scattering. However, this does not affect measurement of the lateral resolution.

4. Conclusion

We have fabricated a phantom that mimics the functionality of the AFTC for characterizing axial and lateral optical resolution. Our phantom has many advantages: (1) no prior knowledge of the characteristics of the OCT system is necessary to use it; (2) the size of the smallest resolvable features in the B-scan can be easily determined; (3) the axial and lateral resolutions can be obtained from the same phantom; (4) the phantom can be created using single-layer photolithography; (5) the construction material is versatile – the phantom (or its surroundings) can be easily modified to characterize the performance of OCT systems on absorbing and scattering samples. We demonstrated the versatility of the phantom to characterize the resolution in different environments that mimic properties of tissue (e.g., refractive index contrast, scattering).

The phantom we created is illustrative of a general design for a phantom – for OCT or other confocal imaging systems – that can characterize optical resolution in three dimensions. Due to limitations in available photolithographic equipment, the smallest features we created were 35.1 μm. However, a similarly designed phantom with smaller features could be easily created with better equipment or a different fabrication process (e.g., chemical etching). With newly-developed techniques, one could in principle create features smaller than 0.1 μm [13], which is notably below the expected resolution of any OCT system. More conventionally, features as small as 1 μm have been achieved by a number of groups [14,15] using techniques known since the introduction of soft lithography.

We anticipate that the design for our phantom could be converted into a commercial calibration standard. As future work, one could also consider modifying the phantom to fabricate different sections of the phantom with different scattering properties; this would allow for simultaneous characterization of the system performance for samples with different optical properties.