On the use of photoacoustics to detect red blood cell aggregation

Abstract

The feasibility of detecting red blood cell (RBC) aggregation with photoacoustics (PAs) was investigated theoretically and experimentally using human and porcine RBCs. The theoretical PA signals and spectra generated from such samples were examined for several hematocrit levels and aggregates sizes. The effect of a finite transducer bandwidth on the received PA signal was also examined. The simulation results suggest that the dominant frequency of the PA signals from non-aggregated RBCs decreases towards clinical frequency ranges as the aggregate size increases. The experimentally measured mean spectral power increased by ~6 dB for the largest aggregate compared to the non-aggregated samples. Such results confirm the theoretical predictions and illustrate the potential of using PA imaging for detecting RBC aggregation.

1. Introduction

The aggregation of red blood cell (RBC) refers to the phenomenon during which individual cells stack face-to-face against one another forming structures that are known as rouleaux (due to their resemblance to a stack of coins) or spherical clusters. Aggregation occurs in the presence of an elevated concentration of macromolecules in the suspending medium and decreased blood flow [1]. The degree and the time kinetics of aggregation depend on the properties of the suspending medium as well as the in vivo RBC age or surface charge density [2].

RBC aggregation has significantly affected blood rheology and hemodynamics. Shear forces created due to blood flow velocity gradients decrease when blood flow decreases, thus enhancing aggregate formation. As a result, the viscosity of aggregated blood increases more than 4 times compared to non-aggregated blood at shear rates lower than 20 s⁻¹ [3]. Increased blood viscosity affects the passage of the RBCs through micro-vessels thus impairing the adequate exchange of gases in tissue [4]. Although it is difficult to determine the “normal” extent of aggregation in human circulation due to how aggregation is assessed (predominantly ex vivo), enhanced RBC aggregation has been observed in a variety of disorders [5]. In addition to being a good marker for acute phase reactions such as sepsis and septic shock, RBC aggregation has been used to monitor the inflammatory response in cardiovascular conditions such as atherosclerosis and cerebral ischemia as well as metabolic conditions such as diabetes and obesity [6–8].

1.1. Current methods for assessing aggregation

Quantification of the extent and time kinetics of aggregation has been shown to be clinically important leading to the development of several methods and instruments to assess RBC aggregation [1]. Each technique attempts to quantify RBC aggregation based on several different physical principles, but currently there is no widely accepted practice for the clinical detection and characterization of aggregation.

Observing the phase separation of blood remains the oldest technique for the diagnosis of hemorheological diseases. The erythrocyte sedimentation rate (ESR) attempts to assess RBC aggregation by measuring the rate at which RBCs sediment from the plasma of whole blood. Deviations from the normally accepted ranges of ESR (10-12 mm/h) serve as non-specific indicators of inflammation which suggests the presence of RBC aggregation [9]. ESR is however a time consuming technique with a strong hematocrit dependence which makes it difficult to differentiate the presence of aggregation from other hematocrit-dependent such as anemia.

A more direct way of demonstrating the effect of RBC aggregation on blood flow is to measure the viscosity of aggregated samples as a function of the shear rate [5]. Various viscometers are commercially available and capable of supplying shear rates lower than 1 s⁻¹ by either a rotating cylinder (Couette flow) or a stationary wall arrangement. This method is commonly used as an independent assessment of RBC aggregation. Correlations between the sample viscosity and other methods of assessing aggregation often provide a means of evaluating the feasibility of the technique being studied [1]. This technique works well when the biochemical agents to promote RBC aggregation do not affect the morphology and deformability of RBCs. Time-dependent sedimentation effects have been shown to affect the measurement since the separation of the RBCs from the plasma can change the torque of the measuring element at low shear rates where the aggregation is typically assessed [10].

Photometric methods monitor the intensity of backscattered or transmitted light during the time course of RBC aggregation [11]. Samples are initially sheared by rotating cylinders at high rates in order to disrupt aggregates. The abrupt stoppage of the rotating cylinder allows the RBCs to aggregate. The time course of the reflected or transmitted light intensity during aggregation is used to assess both the magnitude of RBC aggregation as well as the aggregation kinetics by computing the indexes of aggregation. Although many instruments have been developed for assessing RBC aggregation using photometric methods, the technical requirements of each apparatus (i.e., the temperature of measurement, disaggregation protocol or sample’s oxygenation status) render the results laboratory dependent [1]. There have been reports that data obtained in different laboratories using instruments by the same manufacturer have a wide distribution range thus limiting direct comparisons [12].

Ultrasound (US) backscattering (BSC) methods have been proposed to assess the presence of RBC aggregation in situ. The aggregation of RBCs significantly alters the spatial organization of the cells that in turn produces detectable changes in US BSC [13]. The formation of aggregates causes the relationship between the BSC amplitude of individual RBCs to no longer be depended on the 4th power of the interrogating US frequency as predicted by Rayleigh scattering theory (for clinical US frequencies). However, US methods are not well established for assessing RBC aggregation in vivo. A limiting factor remains the inability of in vivo US imaging to provide robust quantitative aggregation parameters that could be utilized for making clinical decisions. Additionally, BSC as a function of hematocrit reaches a peak at a certain hematocrit level (depending on the US frequency) and decreases thereafter [14]. Since RBC aggregation is depended on the hematocrit level, assessing the changes in RBC aggregation using US BSC might prove to be difficult due to the complexity of the BSC-hematocrit relationship.

1.2. Photoacoustics and its potential for detecting RBC aggregation

In this paper we propose using photoacoustics (PA) for the noninvasive detection of RBC aggregation. PA has led to the development of an imaging modality which probes the optical and thermo-mechanical properties of tissue by optically illuminating samples noninvasively and detecting the ultrasonic waves produced. This is based on the PA effect where the absorption of the illuminating light by the sample is partially converted to heat giving rise to pressure waves via the thermo-elastic expansion of the medium. The pressure transient propagates through the medium as ultrasonic waves which can then be detected with commonly used US transducers operating in receive-only mode [15]. PA imaging contrast is primarily due to optical absorption but the spatial resolution (and to some degree the penetration depth) is controlled by the ultrasonic detection thus allowing imaging in the optical diffusive regime [16]. By probing the oxygen-dependent absorption of blood, PA imaging is capable of forming high resolution functional maps of the vasculature of small animal brains by differentiating the oxygenation state the hemoglobin [17].

It is well known that the size of the optical absorbers in PA dictates the frequency content of the PA waves [18]. We postulate that analysis of PA radiofrequency (RF) signals produced from RBC aggregates will provide information about the RBC aggregate size.

2. Theoretical model

The theoretical model used in this study was originally reported in two recent publications by our group [19,20]. In order to compute the PA pressure field from non-aggregating (NAG) and aggregating (AG) RBCs (approximated as spheres), the analytical solution for the time-independent wave equation for spheres was solved in the frequency domain [18]. The solution to this equation assumes uniform optical irradiation with intensity I₀ which propagates along the x axis and varies sinusoidally with time. The frequency-domain pressure for the uniform illumination of a single spherical absorber at a distance r in the surrounding medium is given by

$$P_{s\text{ingle}}(\widehat{q})=\frac{i\mu \beta I_0{v}_s{a}^2\left[\sin \widehat{q}-\widehat{q}\cos \widehat{q}\right]\exp (i{k}_f(r-a))}{C_{P}r{\widehat{q}}^2\left[(1-\widehat{\rho })(\sin \widehat{q}/\widehat{q})-\cos \widehat{q}+i\widehat{\rho }\widehat{v}\sin \widehat{q}\right]},$$ (1)

where, $\widehat{q}=\varpi a/v_s$is the dimensionless frequency and a is the radius of the absorbing sphere. The dimensionless quantities $\widehat{v}=v_s/v_f$and $\widehat{\rho }={\rho }_s/{\rho }_f$ represent the ratios of the speed of sound (v) and density (ρ) for the spherical absorber (s) and surrounding fluid medium (f), respectively. Moreover, k_f is the wave number in the fluid medium for a pressure wave with frequency ω, β is the isobaric thermal expansion coefficient, C_P is the heat capacity per unit mass, v_s is the speed of sound in the illuminated region and µ is the optical absorption coefficient of the illuminated absorbers. In order to compute the PA pressure field from multiple absorbers, the superposition of spherical waves generated by the RBCs was calculated. Such approach has been implemented for light and ultrasound scattering problems in random media. In particular, Yu and colleagues have successfully used a similar approach to investigate the dependence of US BSC on RBC aggregation [21,22]. In the current study it is assumed that all the absorbers (RBCs) within the region of interest (ROI) are simultaneously illuminated irrespective of their spatial positions within the optical field with multiple US scattering being negligible. The non-band-limited (NBL) pressure field from a collection of N absorbers can be written as

$$P_{\text{collection}}^{\text{NBL}}(\widehat{q})=\frac{i\mu \beta I_0{v}_s{a}^2\left[\sin \widehat{q}-\widehat{q}\cos \widehat{q}\right]}{C_P{\widehat{q}}^2\left[(1-\widehat{\rho })(\sin \widehat{q}/\widehat{q})-\cos \widehat{q}+i\widehat{\rho }\widehat{v}\sin \widehat{q}\right]}\times {\displaystyle \sum _{n=1}^N\frac{\exp (i{k}_f(\left|\overrightarrow{r}-{\overrightarrow{r}}_n\right|-a)}{\left|\overrightarrow{r}-{\overrightarrow{r}}_n\right|}}.$$ (2)

Here, ${\overrightarrow{r}}_n$is the position vector of the nth absorber, If the observation distance ${\overrightarrow{r}}_{}$is large compared to the size of the ROI, the term $k_f\left|\overrightarrow{r}-{\overrightarrow{r}}_n\right|$can be approximated as $k_{f}r-{\overrightarrow{k}}_f\cdot {\overrightarrow{r}}_n$and the term $\left|\overrightarrow{r}-{\overrightarrow{r}}_n\right|$can be approximated as r. The final expression is given by

$$P_{\text{collection}}^{\text{NBL}}(\widehat{q})=\frac{i\mu \beta I_0{v}_s{a}^2\left[\sin \widehat{q}-\widehat{q}\cos \widehat{q}\right]\exp (i{k}_f(r-a))}{C_{P}r{\widehat{q}}^2\left[(1-\widehat{\rho })(\sin \widehat{q}/\widehat{q})-\cos \widehat{q}+i\widehat{\rho }\widehat{v}\sin \widehat{q}\right]}\times {\displaystyle \sum _{n=1}^N\exp (-i{\overrightarrow{k}}_f\cdot {\overrightarrow{r}}_n)}.$$ (3)

The above expressions do not take into account the finite nature of ultrasonic transducers used in PA experiments. In this model the finite bandwidth of the transducer was modeled as a Gaussian function modeling the frequency response of typical ultrasound transducers [23]. The band-limited (BL) pressure then becomes

$$P_{\text{collection}}^{\text{BL}}(\widehat{q})=p_{collection}^{NBL}(\widehat{q})\times \exp \left[-{(\varpi -{\varpi }_0)}^2/2{\sigma }^2\right],$$ (4)

where ω₀ is the center frequency of a transducer with the width of the Gaussian function σ related to the −6 dB receiving bandwidth of the transducer (chosen to be 60%) by $2\sigma \sqrt{2\log (2)}=0.6{\varpi }_0$. The time-dependent PA pressure can be obtained by the Fourier transform of Eq. (3) for the NBL case and Eq. (4) for the BL case.

For this study, 2D simulations were performed to determine the dependence of PA RF power spectra on NAG and AG human and porcine RBCs, h-RBCs and p-RBCs, respectively. The spatial organization of the RBCs had to be calculated using specialized algorithms. NAG RBC samples were generated using a Monte Carlo method known as the random sequential adsorption technique. This allowed the coordinates of the cells to be randomly chosen within the ROI with the restriction that the cells must be separated by a distance equal to or more than their diameters and was repeated until the coordinates of all RBCs at a particular hematocrit (defined in this simulation as the ratio of the area occupied by the cells to the total area of the ROI) were set. Once the positioning of the RBCs within the ROI was completed, the Fourier Transform of Eq. (3) was evaluated to obtain the PA RF signal for that particular configuration. Aggregation of RBCs was simulated by employing a hexagonal close packing scheme [24]. RBC clusters (representing an aggregate) were formed by positioning individual RBCs in a hexagonal packing arrangement relative to one another. The aggregate was then randomly and repeatedly placed within the ROI and the coordinates of each RBC with respect to the center of the cluster were stored in order to evaluate the PA signal from Eq. (3). For each cluster, the radius of gyration (Rg) was computed to quantify the mean cluster size. This was determined by using the square of the distances of the cells from the center of the cluster. This approach has been used successfully to model the effects of aggregation on US backscattering [20,21].

The physical constants and simulation parameters associated with NAG and AG conditions for h-RBCs and p-RBCs used in this study are summarized in Table 1 :

Table 1. Physical constants and simulation parameters.

				Simulation Parameters
	Physical Constants			h-RBC			p-RBC
	h-RBC	p-RBC		NAG	AG		NAG	AG
a (µm)	2.75	2.53	H (%)	2-50	40		5-50	40
ρf (kg/m3)	1005	1005	N (#)	34-842	674		99-994	795
ρs (kg/m3)	1092	1078	Cl (#)	-	54.8-11.8		-	50.2-12.1
vf (m/s)	1498	1498	NCl (#)	-	11.8-57.1		-	15.2-65.3
vs (m/s)	1639	1628	Rg(µm)	2.13	7.6-15.4		1.96	7.7-15.4

The physical constants were used to evaluate Eqs. (3) and (4) for a 200 µm x 200 µm ROI. In the simulation parameters column, H stands for the hematocrit, N is the number of total RBCs at the given hematocrit, Cl is the number of clusters, N_Cl is the number of RBCs per cluster.

3. Experimental methods

3.1. Sample preparation

Proof of concept experiments were conducted using h-RBCs purchased from Innovative Research (Novi, MI). The RBCs were extracted from a single donor. Gentle centrifugation (1800 rpm, 6 minutes) was applied to remove any remaining plasma. Upon isolation, the RBCs were washed twice with phosphate buffered saline (PBS) and suspended in PBS at 40% hematocrit. The RBCs were aggregated using Dextran-70, a fibrinogen mimicking macromolecule (70,000 kDa molecular weight, Sigma-Aldrich Co., St. Louis, MO). This was achieved by suspending the RBCs in solutions of varying Dextran-PBS concentrations ([Dextran-PBS]). [Dextran-PBS] of 1, 3 and 8% (wt/vol) were used to suspend the RBCs in order to induce varying aggregation levels at 40% hematocrit. The presence of aggregation (i.e., aggregation protocol) was assessed by measuring the viscosity of each [Dextran-PBS] using a low-shear viscometer (Contraves LS30, Zurich, Switzerland).

The validity of the technique was assessed using porcine blood extracted from the femoral vein of Yorkshire pigs (Comparative Research, Toronto, ON). The blood was collected into K₂-EDTA vacutaners (Becton, Dickinson and Company, Franklin Lakes, NJ). RBCs were separated from the plasma and white cells by centrifugation (2500 rpm, 6 minutes) and careful aspiration. The cells were then washed twice with PBS before being suspended in the same medium at 10, 20 and 40% hematocrit. For each hematocrit level, the NAG RBCs were suspended at 1, 3 and 8% [Dextran-PBS] solution in order to induce aggregation. All experiments were completed within 4 hours of blood collection at room temperature.

3.2. PA measurements

PA measurements were performed using the Imagio small animal PA imaging device (Seno Medical Instruments Inc., San Antonio, TX) shown in Fig. 1 .

Fig. 1.

Imagio PA imaging device components.

This device consisted of a Q-switched Nd:YAG laser delivered through an articulated arm and a transducer mounted 60 mm coaxially to the laser for raster scanning the ROI. The pulsed laser (emitting at 1064 nm) had a 9 mm beam diameter, 6 ns pulse width, 10 Hz pulse repetition rate and 25 mJ/cm² energy fluence per pulse. The transducer used to record the PA signals was a 4-channel annular array with center frequency of 5 MHz and a 60% −6dB bandwidth. The RBC samples were loaded into cylindrical tubes. For the h-RBCs, a 14 mm plastic Beral transfer pipette was used as a sample holder while a 0.5 mm inner diameter tygon tube (Norton Performance Plastic, Akron, OH) served as the sample holder for the p-RBC experiments. Both sample holders were placed at the focus of the ultrasonic transducer. A vertical raster scan was performed for each sample while the laser emitted 4 pulses at each location which were then averaged to generate 1 RF signal. A total of 20 RF signals were recorded for each solution exposed corresponding to a total of 80 laser pulses that illuminated each RBC sample.

3.3. Signal analysis

For each PA signal recorded, the PA signal amplitude was calculated by integrating the envelope of each signal which was calculated by taking the magnitude of the Hilbert Transform of the signal. The average amplitude of 250 simulated and 20 measured PA signals was computed along with the standard deviation for each sample. The Fast Fourier Transform algorithm was used to compute the power spectrum of each PA RF signal. In order to minimize spectral leakage, a Hamming window was used. For each spectrum, the frequency at which the maximum peak of the RF power spectrum occurred was found. The mean spectral power in a −6 dB region around that peak was also computed. The average of the power spectra was then computed for both simulated and experimentally measured signals. The normality of the data was confirmed with a Shapiro-Wilk test the criterion for normality being W > 0.05. Statistical significance between two measurements was determined using an unpaired t-test. A p value of 0.05 or less was considered statistically significant.

For the experimental h-RBC data, the correlation between the PA signal amplitude and viscosity was computed for all samples (for the different [Dextran-PBS]). The PA signal amplitude of each sample was plotted as a function of viscosity at the 0.05 s⁻¹ shear rate. The correlation coefficient R² and the statistical significance of the correlation (p value) were computed using the corrcoef function in Matlab 2010b (The Mathworks, Natick, MA). A p value of less than 0.05 was considered statistically significant.

4. Results

4.1. Simulation results

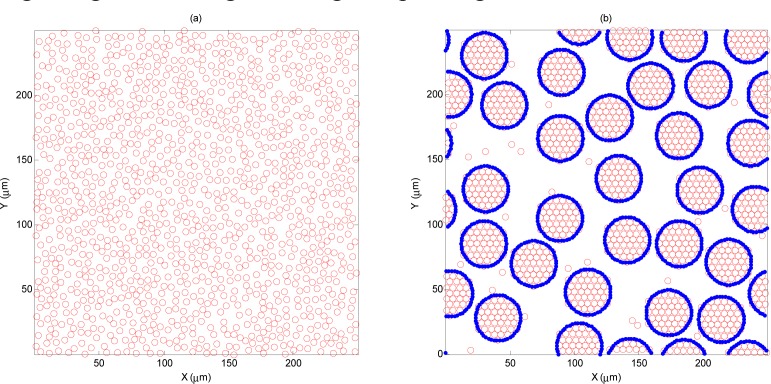
Figure 2 shows a representative plot of the 2D spatial organization of (a) NAG and (b) AG p-RBCs. In Fig. 2b each spherical cluster (representing an aggregate) is composed of individual RBCs arranged together through a hexagonal packing scheme.

Fig. 2.

Representative (a) NAG and (b) AG p-RBC configurations simulated in this study. For both cases the hematocrit is 40% and for the aggregated case, Rg is 12.24 µm.

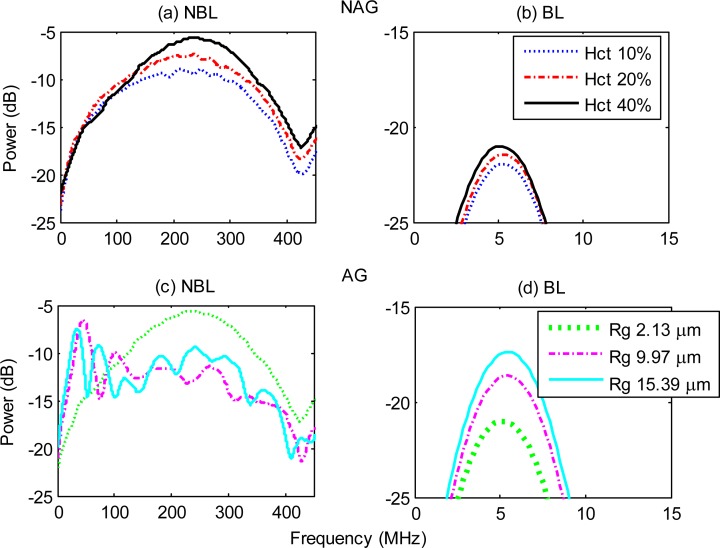
The average of simulated PA RF power spectra for 250 different h-RBCs configurations is shown in Fig. 3 . For the NBL, NAG RBCs (Fig. 3a), the spectral power generally increased over all frequencies with increasing hematocrit. The peak of the RF power spectrum occurred at ~230 MHz for all hematocrit levels. The NBL power spectra for AG RBCs are shown in Fig. 3c. As the size of the aggregate increases (as characterized by Rg), the peak frequency of the power spectra shifted towards the low frequency regime (< 30 MHz). Specifically, the peak frequency for the largest h-RBC aggregate (Rg = 15.39 µm) was ~195 MHz lower than the non-aggregated case (Rg = 2.13 µm). The RF spectral power for the largest aggregate was ~9 dB higher than the NAG RBCs at 15 MHz.

Fig. 3.

Simulated PA RF power spectra for NAG (top row) and AG (bottom row) h-RBCs. Panel (a) and (c) show the NBL spectra while panels (b) and (d) are the BL spectra. Hct stands for hematocrit and Rg represents the radius of gyration (used to denote aggregate size). The hematocrit for the AG RBCs was 40%.

When the transducer finite bandwidth was taken into account, the PA RF power spectra for both the NAG (Fig. 3b) and AG (Fig. 3d) RBCs was significantly altered compared to the NBL spectra. The BL spectra shown in Figs. 3b and 3d were obtained by filtering the NBL power spectra with a Gaussian function representing the frequency response of a 5 MHz transducer. The shape of the power spectra resembled that of the transducer frequency profile used to filter the NBL spectra (Eq. (3)). For both the NAG and AG RBCs, the peak frequency of the RF power spectra occurred at ~5 MHz. As the hematocrit increased, the mean spectral power increased monotonically for NAG RBCs (Fig. 3b). The mean spectral power of the largest aggregate was ~4 dB higher than the NAG sample (Fig. 3c).

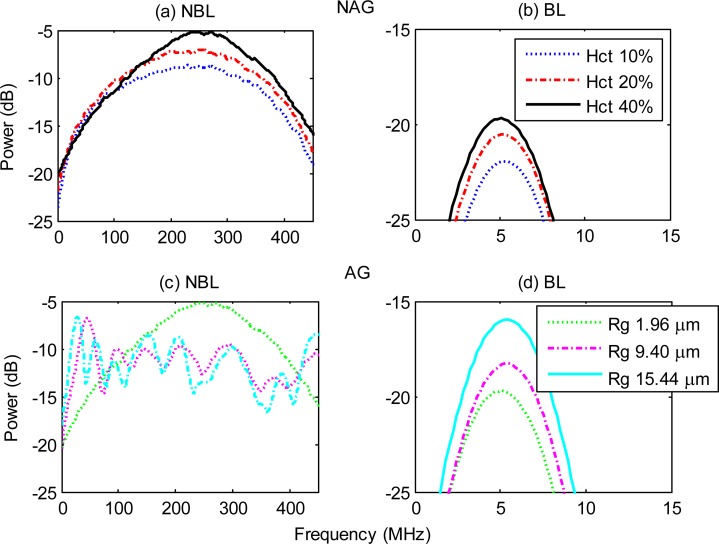
The simulated RF power spectra for p-RBCs are shown in Fig. 4 . Much like the case of h-RBCs, the NBL, NAG RF power increased with increasing hematocrit (Fig. 4a) and the peak frequency shifted towards lower frequencies (< 30 MHz) as the size of the aggregates increased (Fig. 4c). The peak frequency of the NBL, NAG p-RBC spectra was ~35 MHz higher than h-RBCs. For the largest p-RBC aggregate, the peak frequency was ~237 MHz lower than the NAG case. Both the BL spectra (Figs. 4b and 4d) resembled the transducer frequency profile and the mean spectral power increased in a very similar manner to h-RBCs.

Fig. 4.

Simulated PA RF power spectra for NAG (top row) and AG (bottom row) p-RBCs. Panels (a) and (c) show the NBL spectra while panels (b) and (d) are the BL spectra. Hct stands for hematocrit and Rg represents the radius of gyration (used to denote aggregate size). The hematocrit for the AG RBCs was 40%.

4.2. Experimental results

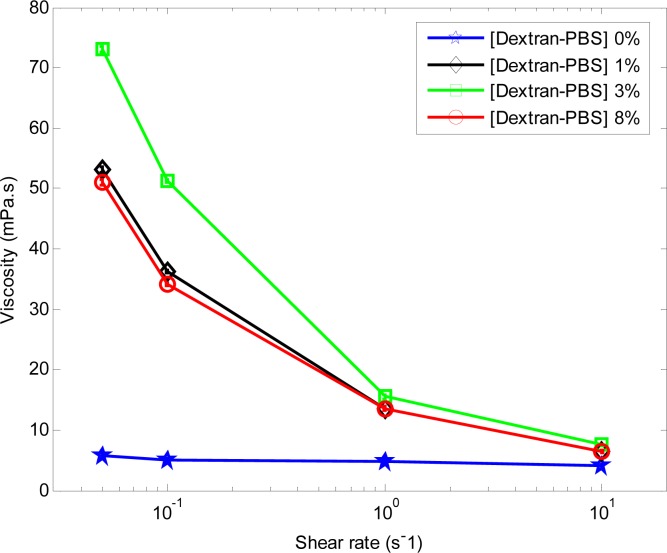
Figure 5 shows the viscosity measurements for h-RBCs at each [Dextran-PBS] used in this study. In the presence of Dextran there is a marked effect of shear rate on viscosity for RBC suspensions. The viscosity decreased with increased shear rates for each [Dextran-PBS] with the exception of the 0% suspension (i.e., RBC in PBS). At shear rates lower than 1 s⁻¹, the viscosity of the 3% [Dextran-PBS] was greater than 10 times higher than the 0% suspension and more than 1.5 times higher than the other two [Dextran-PBS] which exhibited nearly identical behavior. For shear rates higher than 1 s⁻¹ the viscosity of all suspensions converged at around 10 mPa.s.

Fig. 5.

Effect of [Dextran-PBS] on the viscosity of h-RBC samples. The error bars (too small to be seen) represent the standard deviation of the viscosity measurements taken over 1 minute at a constant shear rate. The hematocrit level of all samples is 40%.

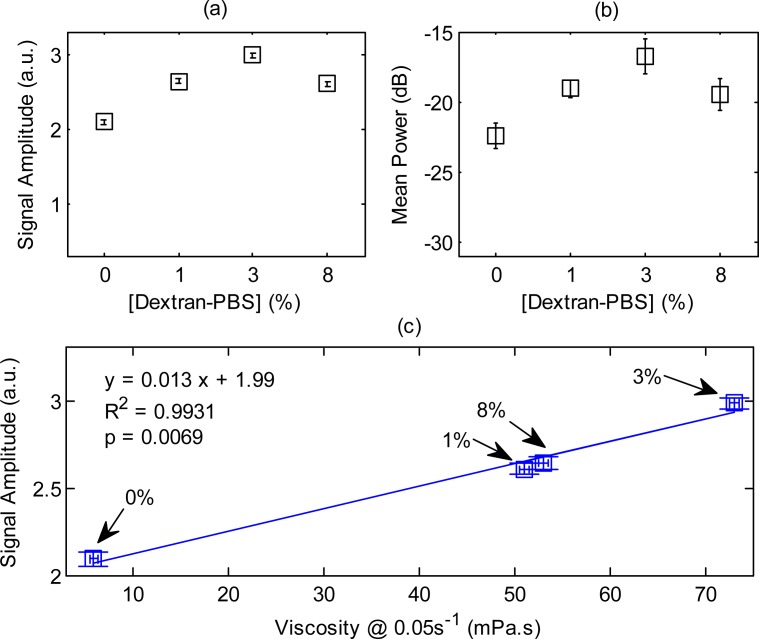
The experimentally measured PA signal amplitudes and mean RF spectral power for h-RBCs are shown in Fig. 6a and Fig. 6b, respectively. Both parameters followed a non-linear trend with increasing [Dextran-PBS]. The maximum signal amplitude was achieved at 3% [Dextran-PBS] with 1% and 8% suspensions having similar amplitude. The amplitude at the 3% [Dextran-PBS] was ~1.6 times higher than the NAG case (0% [Dextran-PBS]) (p = 0.0002) and ~1.2 and ~1.5 times higher than the 1% and 8% [Dextran-PBS] (p = 0.0009 and p = 0.001), respectively. The mean spectral power at 3% was ~2.3 dB higher than the 1% and 8% suspensions (p = 0.008) and ~5.6 dB higher than the non-aggregated case (p = 0.0003).

Fig. 6.

(a) PA signal amplitude, (b) mean spectral power and (c) correlation between the signal amplitude and viscosity for h-RBCs at 40% hematocrit. The arrows in (c) denote the [Dextran-PBS] for which the PA signal amplitude and viscosity was measured. The error bars for the PA signal amplitude and mean power denote the standard deviation of 20 PA signals and power spectra.

The correlation between the PA signal amplitude and RBC viscosity measurements as a function of [Dextran-PBS] was established by comparing the PA signal amplitudes of h-RBCs with the viscosity measured for the various [Dextran-PBS] at the lowest shear rate (0.05 s⁻¹). Figure 6c shows the PA signal amplitudes and viscosity measurements for all [Dextran-PBS] along with the linear regression line. The correlation coefficient was 0.9931 and it was statistically significant (p = 0.0069). The PA signal amplitude and viscosity was highest for the 3% [Dextran-PBS] while it was nearly identical for the 1% and 8% suspensions. The NAG sample (0%) had the lowest PA signal amplitude and viscosity.

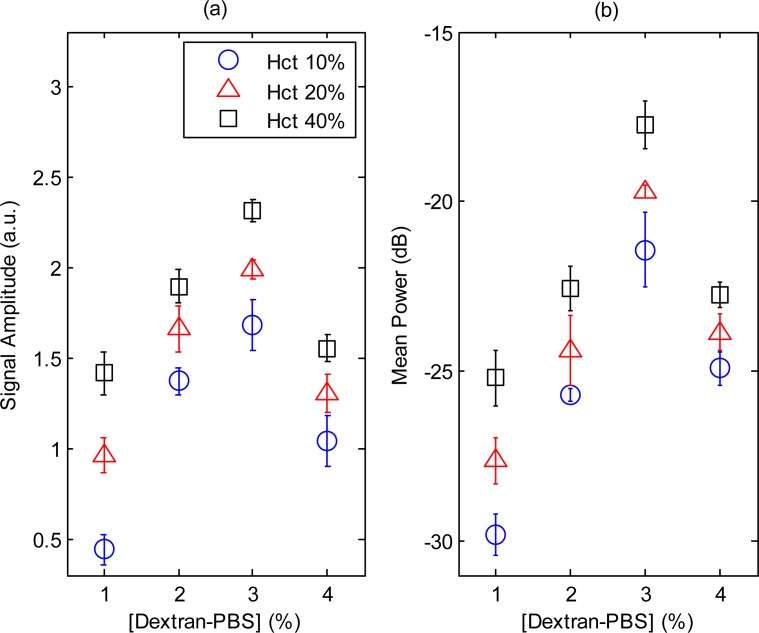
The PA signal amplitude and mean RF power spectra for p-RBCs are shown in Fig. 7 . As observed for h-RBCs, both parameters followed a non-linear trend with increasing [Dextran-PBS]. The PA signal amplitude of p-RBCs at 40% hematocrit (Fig. 7a) was ~1.5 times smaller than h-RBCs (p = 0.001) and monotonically increased with increasing hematocrit levels. The mean spectral power (Fig. 7b) at 3% [Dextran-PBS] was ~7.5 dB higher than the NAG case (p = 0.0003) and ~4.8 dB higher than the 1% and 8% suspensions (p = 0.0001) at each hematocrit level. For all [Dextran-PBS] the mean spectral power increased monotonically with increasing hematocrit.

Fig. 7.

(a) PA signal amplitude and (b) mean spectral power for p-RBCs. The error bars for the PA signal amplitude and mean power denote the standard deviation of 20 PA signals and power spectra.

5. Discussion

This study presented a theoretical and experimental investigation of the potential of PA for detecting the presence of RBC aggregation. Here we have been able to demonstrate that simulated and in-vitro RBC aggregation produces changes in the PA signals that could be used to identify the presence of varying degrees of aggregation. The results indicate that the size of RBC aggregates dictates the frequency content of the PA RF signals. In addition, it was shown that the bandwidth of the ultrasonic transducers used for PA imaging acts as band-pass filters by removing most frequencies predicted theoretically and yielding RF power spectra that closely resemble those observed experimentally. The experimentally measured PA signals (and their respective power spectra) were very well correlated to the viscosity measurements for each aggregating condition.

Our theoretical simulations for both h-RBCs (Fig. 3) and p-RBCs (Fig. 4) suggest that analysis of the PA RF power spectra could provide information about the concentration of RBCs and sizes of the aggregates. As shown from the NBL power spectra for NAG RBCs, the spectral power increased over all frequencies when the hematocrit increased (Figs. 3a and 4a). By increasing the RBC concentration, the signal amplitude and spectral power will increase linearly. This can be inferred by inspection of Eq. (3): the PA spectral amplitude is computed by the linear superposition of the pressure wavelets that each RBC emits when uniformly irradiated by a laser source. A similar trend in the amplitude of the PA signals with increasing hematocrit has been observed in other experimental [25] and theoretical studies [26]. Since the RBC aggregation is dependent on the RBC hematocrit [1], the linear PA signal amplitude – hematocrit relationship in PA imaging confers an advantage over US imaging for monitoring changes in RBC aggregation. This is due to the fact that the relationship between US BSC and hematocrit is complex [14]; determining the hematocrit from BSC measurements is difficult.

It is well established that the PA RF power spectra contain information about the size of the optical absorbers [18]. This becomes a significant advantage of PA imaging as RF power spectra could be potentially used in order to monitor the size of the source of the PA signal. During the formation of RBC aggregates, the sizes of the clusters can increase up to ~10 times the size of the individual RBCs and significantly impair the microcirculation [4]. Recently, Galanzha and colleagues have shown experimentally, by monitoring the PA signal trace dynamics obtained with PA fluctuation flow cytometry, that large increases in the PA signal are measured in vessels with pathological conditions leading to RBC aggregation [27,28]. This finding is consistent with the theoretical and experimental findings of this study. Therefore, PA imaging could potentially contribute since the RBCs are an endogenous source of strong contrast [29]. PA imaging could potentially contribute since the RBCs are an endogenous source of strong contrast [29]. The RF power spectra could be used to assess the size of RBC aggregates. As shown by the NBL AG power spectra (Figs. 3c and 4c), as the size of the aggregates increases, the peak frequency of the RF power spectra decreases by >195 MHz compared to the NAG case. In addition, the RF spectral power increased significantly (~9 dB) in the diagnostic US frequency regime (< 30 MHz). For both cell types, it appears as if it is the entire aggregate that behaves as the source of the PA signal rather than the individual RBCs. As the size of the aggregates increased, the spectral content of the PA RF signals shifted towards a range of frequencies where diagnostic PA imaging becomes more clinically relevant.

However, PA imaging much like its ultrasonic counterpart uses transducers with a finite receiving bandwidth [16]. The finite bandwidth affected the simulated RF power spectra for both NA (Figs. 3b and 4b) and AG (Figs. 3d and 4d) RBC configurations. For both cell types, the shape of the BL spectra for NA and AG RBCs resemble the shape of the transducer frequency profile centered at 5 MHz regardless of the hematocrit or aggregate size. It is possible to distinguish between the simulated samples as the mean spectral power at 5 MHz increased with increasing hematocrit and aggregate size. The ~4 dB enhancement for the largest aggregate (both h-RBCs and p-RBCs) compared to the NAG case at 5 MHz allow for detecting the presence of aggregates at diagnostic frequency ranges. The mean spectral power for p-RBC was ~1.3 dB higher than h-RBCs at all aggregation levels since there are more p-RBCs than h-RBCs for any aggregation levels, which compensates for the weaker signal due to size [18]. It is worth noting that quantitative ultrasound (QUS) techniques utilize the frequency content of the RF signals to estimate sizes of acoustic scatterers in biological tissue [30]. By taking into account the transducer frequency response (i.e., how the transducer modifies the frequency content of the ultrasound backscattered RF signals), one can relate parameters derived from fits to the normalized data, such as the midband fit and the spectral slope, to the scatterer properties. Since our theoretical results indicate that the PA RF signals are significantly affected by the size and concentration of the absorbing structures, it is then reasonable to expect that normalizing the PA RF power spectra by the transducer frequency response can provide information about absorber properties such as size. Many assumptions are made in the theoretical derivations and therefore the relation between the aggregate size and changes in the PA RF power spectrum are still speculative. Nevertheless, these quantitative techniques can be used to characterize the PA signals, irrespective of how the fit parameters derived are related to the actual aggregate size and morphology. Our group has adopted the approach utilized in QUS for monitoring the changes in the RBC aggregate size and is currently investigating its theoretical and practical implications [31].

The theoretical simulations suggest that clusters of RBC aggregates cause enhancements in the PA signals even when a finite bandwidth transducer is employed. As was shown in Fig. 6, the PA signal amplitude and mean spectral power increased as the extent (i.e., size) of aggregates was increased (by modifying [Dextran-PBS]). The aggregation protocol was confirmed by the low-shear viscometry measurements (Fig. 5). Other experimental studies have also measured almost identical viscosity-shear rate curves for h-RBCs. As shown in Fig. 6c, the PA signal amplitude and viscosity at the lowest shear rate correlated very well which suggests that the PA imaging is capable of detecting the presence of varying degrees of aggregation. The biphasic behavior with increasing [Dextran-PBS] has also been confirmed by optical aggregometry, a commonly used experimental technique for assessing aggregation [32]. The 3% [Dextran-PBS] yields the largest aggregate size since that concentration has been shown to have the largest affinity for inducing aggregates [33]. This was confirmed by the viscosity values measured at low shear rates and the excellent correlation that was recorded for the other [Dextran-PBS]. The potential of PA to detect RBC aggregation was re-enforced by the ability to distinguish between different hematocrits as shown in Fig. 7 for p-RBC. The increase in PA signal amplitude (Fig. 7a) and mean spectral power (Fig. 7b) with hematocrit for each aggregation level correlated well with the theoretical findings for p-RBCs. The monotonic increase in mean spectral power for each aggregation level as a function of hematocrit demonstrated the ability of PA to detect the presence of RBC aggregation at multiple hematocrit levels. This is a significant advantage of since the hematocrit significantly affects the aggregation measurements [5]. The hematocrit dependence of aggregation makes it nearly impossible to assess the size of aggregates through optical microscopy images since they are mostly performed at low hematocrit levels. In addition, manipulation of the aggregated blood (i.e., to prepare for optical microscopy) has been shown to affect the aggregate formation thus making it difficult to obtain accurate aggregate sizes [1]. The spectral information contained in the PA RF signals suggests that it might be possible to obtain quantitative information on the size of the aggregates at any hematocrit level.

6. Conclusions

In this study we demonstrate that PA can be used for detecting RBC aggregation. Theoretical simulations suggest that PA imaging can be used to differentiate levels of RBC aggregation and hematocrit. The feasibility of detecting these PA RF spectral changes was investigated by incorporating a finite transducer in detection of PA signals. Experimental results indicate that PA is indeed capable of assessing changes that occur during the aggregation process for the two types of RBCs used in these experiments.