Characterization of the Reaction Path and Transition States for RNA Transphosphorylation Models from Theory and Experiment

The elucidation of the chemical mechanisms whereby biological molecules control, regulate and catalyze phosphoryl transfer reactions has profound implications for processes such as transcription, energy storage and transfer, cell signalling and gene regulation.^{[1, 2]} The catalytic properties of RNA, in particular, have application in the design of new biotechnology and implications into the evolutionary origins of life itself.^[3] Of primary importance to the understanding of mechanism is the characterization of the transition state for these reactions. Kinetic isotope effects (KIEs) offer one of the most powerful and sensitive experimental probes to interrogate the chemical environment of the transition state.^[4-6] However, for complex reactions, theoretical methods are required to interpret the experimental measurements in terms of a detailed mechanistic model that traces the pathway from the reactant state through the transition state and into the product state.^{[7, 8]}

This paper presents experimental and computational results to characterize the mechanism of model phosphoryl transfer reactions that mimic RNA cleavage transesterification catalyzed by enzymes such as RNase A^[1] as well as endonucleolytic ribozymes such as the hammerhead, hairpin, hepatitis delta virus (HDV), VS and glmS ribozymes.^[9-11] Herein, secondary kinetic isotope effects are reported for the cleavage transesterification of a dinucleotide system, which, together with previously reported primary isotope effect measurements,^{[12, 13]} represent a comprehensive characterization of isotope effects for a native (unmodified) RNA system.

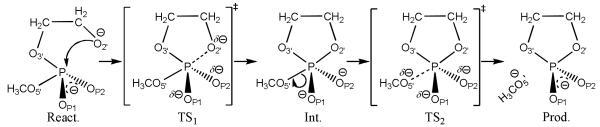
Scheme 1 illustrates the general mechanism for the reverse dianionic in-line methanolysis of ethylene phosphate, a model for base-catalysed RNA phosphate transesterification, with phosphoryl oxygen positions labelled in accord with their RNA counterparts. In this study, the free energy profiles for Scheme 1 were determined with density-functional quantum mechanical/molecular mechanical (QM/MM) simulations in explicit solvent.^[14-17] These simulations are state-of-the-art, and take into account the dynamical fluctuations of the solute and solvent degrees of freedom in determination of the free energy profiles. In addition, adiabatic reaction energy profiles were determined with solvation effects treated implicitly with a polarizable continuum model (PCM)^[18] specifically calibrated for the native and 3′ and 5′ thio-substituted compounds (Figure 1). The 3′ and 5′ thio-substituted compounds model the corresponding chemically modified RNAs that serve as valuable experimental probes of phosphoryl transfer mechanisms catalyzed by ribozymes.^[19] The S5′ substitution, for example, in the HDV ribozyme serves as an enhanced leaving group that suppresses the deleterious effect of mutation of a critical cytosine residue, which has been interpreted to support its role as a general acid catalyst.^[20] The energy values for stationary points of the native and thio-substituted reactions are in Table 1. Using our recently developed ab initio path-integral method based on Kleinert’s variational perturbation theory,^{[7, 21-23]} we also calculated kinetic isotope effects, which are shown along with the most relevant experimental values for comparison in Table 2. The agreement that is achieved between the theoretical and experimental results allows a detailed mechanistic interpretation based on the theoretical models.^{[7, 8]}

Scheme 1.

General reaction scheme for the (associative) reverse of dianionic in-line methanolysis of ethylene phosphate: a model for RNA phosphate transesterification under alkaline conditions. In the present work, the native reaction shown in the scheme is studied as well as reactions that incorporate single thio substitutions in the bridging 3′ (denoted S3′) and leaving group 5′ (denoted S5′) positions. Note: as revealed by the computational analysis herein, not all of the states shown in the scheme exist for every reaction (see text for details).

Figure 1.

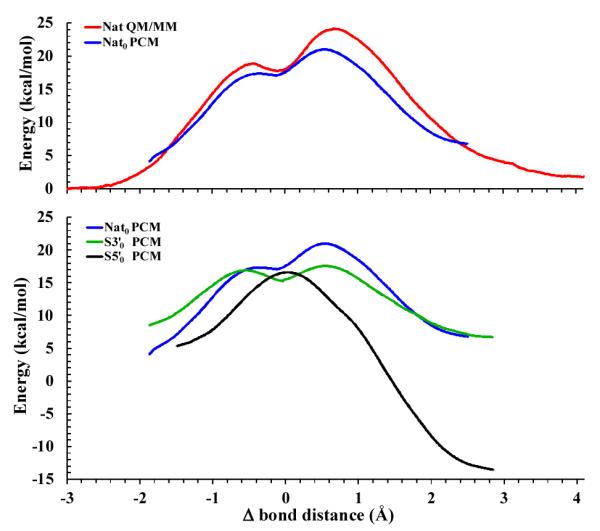
(Color online) Comparison of density-functional QM/MM free-energy and adiabatic PCM profiles for the native reaction (top), and density-functional adiabatic PCM profiles for native and thio-substituted reactions (bottom) as a function of the difference of the bond distance (Δbond distance) between the breaking bond P—X5′ (X = O for native and S3′, and X = S for S5′ reactions) and the forming bond P—O2′. The adiabatic PCM profiles are mapped from the intrinsic reaction coordinate paths and have been shifted to match the respective rate-controlling free-energy barriers calculated in the decoupled rigid-rotor harmonic-oscillator approximation^[26] at 37°C. However, aside from this shift, the adiabatic PCM profiles otherwise do not include zero-point energy or thermal corrections to the free energy, unlike the numbers listed in Table 1 at the bottom.

Table 1.

Relative free energy (kcal/mol) and reaction coordinate (Δbond) values (Å) computed for stationary points along the coordinate of the native and thio-substituted RNA phosphate transesterification reaction models shown in Scheme 1.[^[a]]

Reaction	TS1		Int.		TS2
	Δ G ‡	Δbond	Δ G	Δbond	Δ G ‡	Δbond
Nat QM/MM	18.8[[b]]	−0.43	17.7[[b]]	−0.12	24.1[[b],[c]]	0.67
Nat0 PCM	17.3	−0.36	17.0	−0.12	21.0[[b],[c]]	0.54
Nat PCM	18.6	−0.36	18.3	−0.12	21.0[[b]]	0.54
S3′ PCM	16.9	−0.55	16.0	−0.04	17.8	0.54
S5′ PCM	16.6	−0.02	n.a.[[d]]	n.a.[[d]]	n.a.[[d]]	n.a.[[d]]

^[a]Δbond (Å) is defined as the difference of the bond distance between the breaking bond P—X5′ and the forming bond P—O2′. ΔG values are in kcal/mol. Nat₀ is PCM energy (Fig. 1) shifted by the thermal corrections at TS₂. Boldface type indicates the rate controlling transition state suggested by comparison with experimental KIE measurements.

^[b]Statistical uncertainties are 1.1, 0.8, 1.4 kcal/mol for TS₁, Int., TS₂, respectively.

^[c]Experimental estimated barrier for UpG transphosphorylation is 19.9 kcal/mol.^[12]

^[d]Not applicable as Int. and TS₂ cannot be found.

Table 2.

Primary kinetic isotope effects (KIEs) on 2′ nucleophile (¹⁸k_Nu) and 5′ leaving (¹⁸k_Lg) oxygens, and secondary KIEs on O1P (¹⁸k_O1P) and O2P (¹⁸k_O2P) oxygens in aqueous solution for the TS₁ and TS₂ transition states, along with the most relevant available experimental results for comparison.[^[a]]

Reaction	TS1		TS2		Expt
	18kNu	18/34kLg	18kNu	18/34kLg	18kNu	18/34kLg
Native	1.017	1.006	0.968	1.059	0.981(3)[[b]]	1.034(4)[[b]]
S3′	1.043[[c]]	1.008[[c]]	0.992[[c]]	1.049[[c]]	1.119(6)[[d]]	1.0118(3)[[d]]
S5′	1.042[[c]]	1.002[[c]]	n.a.[[e]]	n.a.[[e]]	1.025(5)[[d]]	1.0009(1)[[d]]

Reaction	TS1		TS2		Expt
	18kO1P	18kO2P	18kO1P	18kO2P	18kO1P	18kO2P
Native	1.004	1.004	1.005	1.003	0.999(1)[[f]]	0.999(1)[[f]]
S3′	1.004[[c]]	1.004[[c]]	1.002[[c]]	1.003[[c]]	n.d.[[g]]	n.d.[[g]]
S5′	1.004[[c]]	1.004[[c]]	n.a.[[e]]	n.a.[[e]]	n.d.[[g]]	n.d.[[g]]

^[a]Temperatures used in calculations are identical to those used in the experiments that are being compared: 37°C for native reactions, and 80°C for thio-substituted reactions. All primary KIE values are computed using the second order Kleinert’s variational perturbation theory with decoupled instantaneous normal coordinate approximation, while the secondary KIE values are computed using the Bigeleisen equation in the decoupled rigid-rotor harmonic-oscillator approximation.^{[27, 28]} Boldface type represents the rate controlling KIE value as determined by comparison with experimental KIE measurements. Experimental errors in the last decimal place are given in parenthesis.

^[b]Extracted from Ref. ^[12] in which the observed ¹⁸k_Nu has been corrected for deprotonation.

^[c]To be consistent with the experiments in Ref. ^[13], the KIE values are calculated with the nucleophile O2′ protonated in the reactant state.

^[d]Extracted from Ref. ^[13], in which the nucleophile O2′ is protonated in the reactant state.

^[e]Not applicable as TS₂ cannot be found.

^[f]New experimental data given in this work; values represent an average observed for O1P and O2P positions.

^[g]Not determined yet by experiments.

All of the profiles calculated in this work correspond to associative (or concerted) mechanisms characterized by initial nucleophilic attack, as is typical of phosphate diesters.^[6] The departure of the leaving group can be concerted with nucleophilic attack (as in the S5′ substituted reaction) or can occur in a stepwise fashion resulting in the formation of a stable pentavalent phosphorane intermediate. In the stepwise mechanism, two transition states occur: one in which nucleophilic attack occurs (TS₁) and another one in which leaving group departure takes place (TS₂) as indicated in Scheme 1. These transition states themselves can be characterized as either “early” or “late”, depending on the degree of P-O2′ and P-O5′ bond formation/cleavage.

Native reaction: the late transition state is rate-controlling

The density-functional QM/MM free energy profile^{[24, 25]} and PCM adiabatic reaction profile for the native reaction are very similar (Fig. 1, top). Both profiles describe an associative mechanism, and exhibit distinct TS₁ and TS₂ transition states separated by a shallow, metastable intermediate, with TS₂ rate controlling. Comparison of the activation free energy values from the QM/MM simulations and adiabatic reaction profiles (including zero-point and thermal corrections, Table 1 bottom) indicate that the TS₁ are very similar in activation energy (18.8 and 18.6 kcal/mol, respectively), whereas the TS₂ is 3.1 kcal/mol higher in the QM/MM simulation. The rate-controlling TS₂ itself has considerable “late” character in which cleavage of the exocyclic P-O5′ bond is advanced (Δbond in Table 1). This result derives from a combination of ring strain effects and differential solvation of the cyclic versus acyclic phosphates.^{[8, 29]} The calculated density-functional free energy barrier with PCM solvation (21.0 kcal/mol) is in close agreement with that estimated from the experimental rate for UpG transphosphorylation extrapolating to the infinite pH limit in the rate expression (i.e., assuming the nucleophile is always in deprotonated form) and assuming unit transmission coefficient (19.9 kcal/mol).^[12] This result, taken together with the consistency between the PCM reaction profile and the profile derived from the QM/MM simulations with explicit solvent (Fig. 1, top), suggests that the density-functional PCM calculations sufficiently capture the essential features of the solvation effects on the profile to determine kinetic isotpe effects. The close agreement between the calculated and experimental KIEs (shown below) further supports this supposition.

The primary KIE values calculated using our ab initio path-integral method^{[7, 21-23]} are listed in Table 2, and are in good agreement with experimental results. Here, by “good agreement”, we refer to agreement within the resolution of the kinetic isotope effects as being large inverse (less than 0.97), inverse (0.97-0.99), near unity (0.99-1.01), normal (1.01-1.03) and large normal (greater than 1.03). In the experiment, the model reaction for the RNA transesterification is the base-catalyzed 2′-O-transphosphorylation of the RNA dinucleotide 5′-UpG-3′.^[12] Since both 2′OH deprotonation and 2′O-P bond formation will contribute to the observed KIE, the values reported here for ¹⁸k_Nu and ¹⁸k_Lg (at the infinite pH limit) do not include the equilibrium isotope effect on alcohol deprotonation. The inverse value of ¹⁸k_Nu (0.981) and the large normal value of ¹⁸k_Lg (1.034) measured by experiment^[12] agree well with the values calculated in the present work (0.968 and 1.059 in Table 2). In contrast to the rate-controlling TS₂ transition state, our calculated value of ¹⁸k_Nu based on the TS₁ transition state is normal (1.017), and ¹⁸k_Lg is close to unity (1.006). This lends credence to the interpretation that the measured KIE values for the native (UpG transphosphorylation) reaction are consistent with a rate-controlling transition state that is characterized by an almost fully formed P-O2′ bond and an almost fully cleaved P-O5′ bond (Table 1 and Fig 2).

Figure 2.

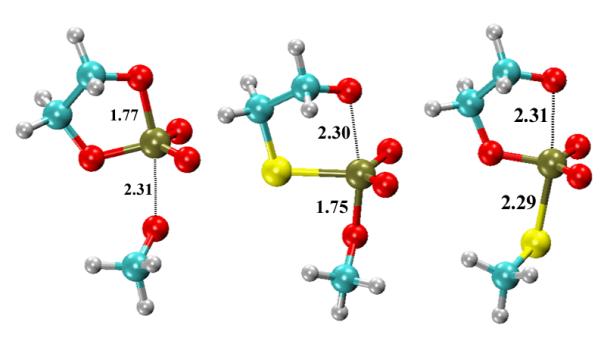
(Color online) Rate-controlling transition state structures (Scheme 1) consistent with experimental KIE values. Left: Native; Middle: S3′; Right: S5′. The bond distance values are in units of Å.

The anharmonic contributions to all primary KIE calculations estimated by our ab initio path-integral method are small in the present work (though anharmonicity has been shown to be large for some other reactions^[7]). The largest anharmonic contribution is only about 0.3%. Hence, in this study, we computed the anharmonic contributions in the KIE only for the primary isotopomers (i.e., the X2′ and X5′ atoms) listed in Table 2.

S3′ reaction: the measured KIE values correspond to an early transition state

In comparison with the native reaction, the thio effects on the 3′ position lead to a reaction profile characterized by two transition states separated by a kinetically distinct intermediate (Figure 1 bottom and Table 1). The calculated barriers of the two transition states are quite similar to one another (less than 1 kcal/mol difference), and both are lower than the rate-controlling transition state of the native reaction by 3 kcal/mol or more. This result indicates that the 3′ thio-substituted reaction rate should be faster than the native reaction, which is consistent with experimental measurements for 3′ thio-substituted dinucleotides.^{[13, 30, 31]} The lower barrier arises from a combination of stabilizing electronic effects of the soft sulfur in the equatorial position of the pentavalent transition state that is able to help delocalize charge, and partial alleviation of ring strain due the longer P-S3′ bond. Solvation effects are also present, but are less pronounced than at the non-bridge positions that carry a formal negative charge.

Despite the similarity in their barrier heights, the TS₁ and TS₂ for the S3′ reaction produce significantly different primary KIE signatures. The calculated TS₁ displays large normal and close to unity primary KIE values for the nucleophile (¹⁸k_Nu) and leaving group (¹⁸k_Lg), respectively, whereas the calculated TS₂ exhibits near unity and large normal primary KIE values, respectively (Table 2). The experimental KIE values for the reaction with a m-nitrobenzyl leaving group (pK_a=14.9)^[32-34] exhibits an anomalously large normal (¹⁸k_Nu =1.119) and moderate normal (¹⁸k_Lg =1.011) nucleophile and leaving group KIEs^[13], respectively, consistent with the signature of the TS₁ transition state (Table 1 and Fig 2). This experimental ¹⁸k_Nu value^[13] reflects a reaction from the ground state in which the 2′O is not deprotonated and includes a somewhat large normal contribution of 2-4% due to the equilibrium isotope effect on alcohol deprotonation. Accordingly, the calculated KIE values include this contribution. As in the case for the native reaction, the calculated secondary KIE values of O1P and O2P oxygens for the S3′ reaction are close to unity (Table 2).

S5′ reaction: the unimodal barrier is corresponding to the early transition state

The sulfur-substitution on the 5′ position results in a reaction profile that is unimodal, and lower in activation energy than the native and S3′ reaction profiles (Figure 1 bottom and Table 1). Although sulfur is less apicophilic than oxygen in pentavalent phosphorus compounds,^[35] this effect is not predicted to be large in the present calculations, as suggested by the free energy of formation of the TS₁ in the S5′ reaction that is only 2 kcal/mol lower than for the native reaction. The main contribution to the differences in the native and S5′ reaction profiles derives from the nature of the thiolate as an enhanced leaving group relative to the methoxide anion (the pK_a of primary alcohols being typically ~5 pK_a units higher than the corresponding thiols). This leads to the elimination of the TS₂ transition state in the profile, and a shift toward early transition state character (smaller P-O2′ bond order). The value of Δbond in Table 1 and Fig 2 for the transition state is -0.02 Å, but this value reflects the longer bond distance of P—S5′ relative to P— O5′ distances by about 0.5 Å. The rate-controlling barrier for the S5′ reaction is approximately 16.6 kcal/mol, which is the smallest of the reaction models studied here, suggesting this substitution will have the fastest rate. This result is consistent with experimental studies of 5′ substituted reaction models.^{[13, 36, 37]}

The predicted primary KIE values of both ¹⁸k_Nu (1.040) and ¹⁸k_Lg (1.002) for the S5′ model reaction (Table 2) are normal and are in good accord with the experimental results (¹⁸k_Nu: 1.025; ¹⁸k_Lg: 1.001) for the cyclization of m-nitrobenzyl ribonucleoside phosphodiester with S5′ substitution.^[13] This lends support to the notion that the rate-controlling transition state for the S5′ reaction is the TS₁.

Secondary KIEs at the non-bridge phosphoryl oxygen positions

In this work, KIEs were measured for the non-bridge phosphoryl oxygen positions for the native UpG dinucleotide reaction (Table 2). In the present model systems, we have an associative reaction involving a dianionic phosphate diester with the added complexity of coupling between the ring vibrational modes in formation of the transition state. Our measured KIE values of the non-bridge phosphoryl oxygen positions were very close to unity (0.999), and within error are in good agreement with the calculated values of 1.003-1.005 for the native reaction (Table 2). Unlike the calculated differences between the primary KIE values for the native, S3′ and S5′ reactions, the calculated secondary KIEs are all close to unity.

Conclusion

We report results of density-functional combined QM/MM simulations and solvated adiabatic reaction profiles for native and thio-substituted RNA transphosphorylation reaction models. Kinetic isotope effects were calculated using our recently-developed ab initio path-integral method^{[7, 21-23]} that takes into account treatment of internuclear quantum effects. Additionally, we report new measurements of secondary kinetic isotope effects for the native reaction of UpG, the dinucleotide sequence representing the cleavage site in the HDV ribozyme,^{[9, 12]} and make predictions of the secondary isotope effects for thio-substituted reactions. Our results provide an atomic-level picture of the reactions, including a detailed characterization of the rate-controlling transition states that are in agreement with experimental measurements of both the rates and the primary and secondary KIEs. The native reaction is characterized by a rate-controlling transition state corresponding to exocyclic bond cleavage of the leaving group with an inverse primary nucleophile KIE. The S3′ reaction is characterized by two distinct transition states, with the transition state corresponding to nucleophilic attack rather than leaving group departure giving rise to the observed large primary nucleophile KIE value. The S5′ reaction is concerted, and has a unimodal reaction profile with the lowest barrier, and large normal primary KIE values. Unlike the striking differences in the calculated primary KIE values between native and thio-substituted reaction models, all secondary KIE values are close to unity. Together, these results paint a detailed picture of the reaction mechanisms of model phosphoryl transfer reactions.