Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 May 1.
Published in final edited form as: Appl Geogr. 2012 Mar 28;34:559–568. doi: 10.1016/j.apgeog.2012.02.009

Spatially and Temporally Varying Associations between Temporary Outmigration and Natural Resource Availability in Resource-Dependent Rural Communities in South Africa: A Modeling Framework

Stefan Leyk 1,*, Galen J Maclaurin 1, Lori M Hunter 2,4, Raphael Nawrotzki 2, Wayne Twine 3, Mark Collinson 4, Barend Erasmus 3
PMCID: PMC3448370  NIHMSID: NIHMS366863  PMID: 23008525

Abstract

Migration-environment models tend to be aspatial within chosen study regions, although associations between temporary outmigration and environmental explanatory variables likely vary across the study space. This research extends current approaches by developing migration models considering spatial non-stationarity and temporal variation – through examination of the migration-environment association at nested geographic scales (i.e. whole-population, village, and subvillage) within a specific study site. Demographic survey data from rural South Africa, combined with indicators of natural resource availability from satellite imagery, are employed in a nested modeling approach that brings out distinct patterns of spatial variation in model associations derived at finer geographic scales. Given recent heightened public and policy concern with the human migratory implications of climate change, we argue that consideration of spatial variability adds important nuance to scientific understanding of the migration-environment association.

Keywords: migration models, outmigration-environment associations, spatial non-stationarity, scale, Agincourt, demographic surveillance

1 Introduction

Fueled by recognition of the world’s changing climate (IPCC, 2007 and 2012), the past several years have seen burgeoning academic interest in the environmental dimensions of human migration. The connection is logical, particularly in rural regions where daily lives are dependent on proximate natural resources, since environmental change portends dramatic shifts in livelihood options. In the face of livelihood decline, migration can be seen as an adaptive strategy (McLeman and Hunter, 2010) and, therefore, methodological advancements in the study of migration-environment associations are particularly timely.

This paper offers substantial methodological advancement in this context through systematic examination of the robustness of migration-environment associations across different spatial scales (whole-population, village, and subvillage). Since migrationenvironment associations are expected to vary under different socio-ecological conditions, models not accounting for such variations (i.e. ‘global’ statistical models) are limited in that they provide only an averaged estimation of this association across a predefined space. How to methodologically assess the robustness of such associations across different scales, and to explore the effects of inherent spatial variation of such associations with statistical rigor, remain open questions. We explore these questions here.

1.1 Environmental Dependence in Rural Regions

Recent studies document widespread use of natural resources and natural resource-based products in rural regions across the globe. Millions of households make direct use of wild resources for dietary and other household uses (Crookes, 2003), while some engage in direct trade of collected products such as fruit, mushrooms, worms (e.g. Wynberg et al., 2003). Resource-based craft trades are also common, for example producing and selling twig brooms and reed mats, represent important livelihood strategies in parts of rural South Africa (Botha et al., 2004; Gyan and Shackleton, 2005; Shackleton et al., 2008). Although cash returns to resource-based livelihoods are often quite low, many households devote time and energy to these activities to enhance livelihood security and lessen the need to seek demoralizing, insecure casual labor (Shackleton and Shackleton, 2011).

Proximate natural resources also often serve as “safety nets” for vulnerable rural households in less developed settings (Hunter et al., 2011; McSweeny, 2004). A recent study in rural South Africa found that, in the wake of a shock such as job loss or mortality, a majority of households increased use of locally-collected resources such as wild foods, fuelwood and medicinal plants (Paumgarten and Shackleton, 2011). In the wake of environmental change, the availability and variability of such natural “safety nets” may shift and households may adapt alternative strategies such as migration.

1.2 Migration as Adaptation

Human migration as an adaptive strategy is certainly nothing new, and historical analogs, such as investigation of migration from the Great Plains’ Dust Bowl, have informed recent understandings of migration potential (McLeman and Smit, 2006). Yet, what is new is the sheer number of households potentially impacted by contemporary environmental change, the magnitude of vulnerability due to widespread impoverishment, and the security concerns being articulated by policymakers and the public (Scheffran and Battaglini, 2011). Further, recent methodological advancements have provided the basis for improved scientific examination of the migration-environment association.

Aspatial empirical models have taken two key forms. First, aggregated data (such as information at the state, county or village levels) are used as units of analysis in order to estimate associations between migration rates and relevant socio-economic and environmental characteristics (e.g. Hunter, 1998 and 2000; Feng et al., 2010). Within such models, environmental factors are included as general spatially undifferentiated measures. As a logical consequence, spatial dependence and clustering effects are rarely considered, and variation in the migration-environment association within the broader study region are not explored. Second, individual- and household-level predictive models of migration have been extended to add environmental measures to the set of typical cross-sectional predictors at the individual-level such as gender, age, and education, or at the household level, such as size and compositional indicators (Findley, 1994; Meze-Hausken, 2000). Within these ‘global’ statistical approaches, factors such as estimated (regional) rainfall or general undifferentiated measures of natural resource availability can represent local or even regional environmental pressures at a particular point in time, or they can be used to analyze change within a recent temporal window (e.g., Gray, 2009; Henry et al., 2004). As a consequence, results tend to reveal that environmental factors act in concert with other migration pressures and thus differential effects within the study region, net of incorporated controls, cannot be estimated.

1.3 Needs in Modeling Migration-Environment Associations

Within the past several years, models of the migration-environment association in resource-dependent regions have become increasingly sophisticated through the use of, for example, longitudinal and/or multi-level models. These often integrate random effects (e.g., Henry et al., 2004; Barbieri and Carr, 2005; Yabiku et al., 2009; Gray, 2011) and have, therefore, advanced inclusion of general spatial effects. However, rarely has spatial variation in the migration-environment association itself nor the role of scale in the modeling approach been the content of substantive query. Exploring spatial variation raises two important connotations of scale. Geographic scale refers to the spatial extent within which the phenomenon or association is being studied (Lam and Quattrochi, 1992), and analysis scale (or resolution) refers to the size of the units at which observations were recorded or aggregated (Montello, 2001). In this study we vary the geographic scale used for modeling (i.e. the population size, or n, in the statistical model) while holding the analysis scale (i.e. the household unit) fixed. This approach allows to explore how associations (regression coefficients) change at different spatial extents of analysis (whole-population, village and subvillage). We argue that much can be learned from how migration propensity varies with changing geographic scale of the modeling approach.

Although methods to investigate spatial non-stationarity are routinely employed in the field of geography, migration-environment connections have not been studied in this context. These existing approaches usually rely on local estimations such as varying coefficient models (Cleveland et al., 1991; Hastie and Tibshirani, 1993) or geographically weighted regression (GWR) models (Brunsdon et al., 1996; Fotheringham et al., 2002) which have significant limitations that result in a lack in robustness for statistical inference (O’Sullivan and Unwin, 2010). For instance, models can suffer from local over-fitting as a result of reduced degrees of freedom and the spatial weighting of observations in each local regression can lead to patterns of induced spatial heterogeneity (Cho et al., 2010). Furthermore, the instability of coefficient estimates as a function of bandwidth (Farber and Páez, 2007) and multicollinearity of the local coefficient estimates have been identified as serious hindrances with the GWR method (Wheeler, 2007; Griffith, 2008). For modeling Poisson distributed migration data, local estimation models have not been readily extended into a Generalized Linear Model (GLM) framework. In order to improve our ability to understand existing associations between migration and environmental factors on the household level and thus improve program and policy recommendations, these limitations must be addressed. Particularly, the sensitivity of statistical models to changes in geographic scale and the variation of target associations across space (non-stationarity) have to be evaluated. Identifying sub-regions experiencing heightened vulnerability to environmental change could greatly enhance targeted interventions.

This research taps into the potential of spatially explicit demographic surveillance data from a remote rural region of South Africa, combined with indicators of both spatial and temporal variation in natural resource availability across the study site. We make use of the Normalized Difference Vegetation Index (NDVI) derived from MODIS remote sensing imagery as an indicator of natural resource availability and variability. An analytical framework is developed that overcomes the above limitations by using traditional regression approaches on nested geographic scales generated by random simulation (spatial permutation). This allows for:

  1. comparison of models across (nested) geographic scales (i.e., whole-population, village and subvillage scales) in order to systematically examine the sensitivity of the migration-environment association to changing (sub)populations used for modeling;

  2. investigation of the spatial non-stationarity of migration-environment associations estimated on a set of sub-populations (i.e. villages) at the same geographic scale within the study site. In contrast to common local estimators, each model association is estimated from an entire subpopulation and has sufficient statistical rigor without induced effects of over-fitting or multicollinearity;

  3. comparison of models for two different points in time (2002 and 2007) in order to estimate the effect of changing environmental conditions on the migration-environment models.

2 Data and data processing

The Agincourt Health and Demographic Surveillance System (AHDSS) site is located in a rural region of northeastern South Africa (Fig. 1).1 Since 1992, the AHDSS has conducted an annual census, today encompassing 24 villages including approximately 84,000 residents and 14,000 households. The area is characterized by high population densities, high levels of poverty and long standing lack of development and access to state services.

Figure 1.

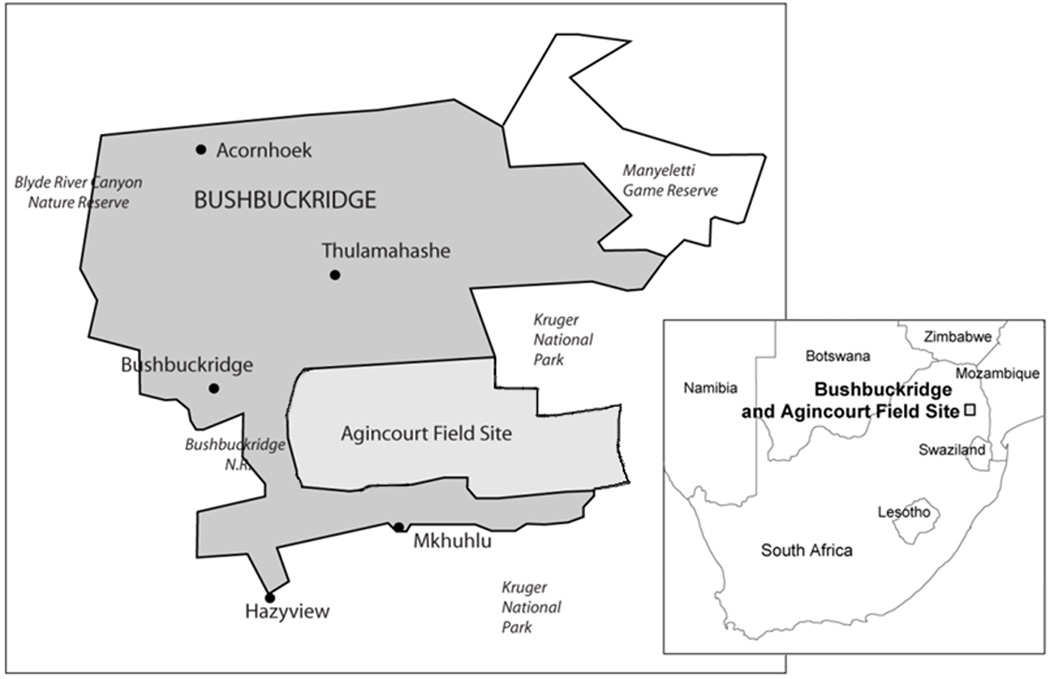
Figure 1

Open in a new tab

Bushbuckridge and Agincourt Field Site, South Africa.

Our dataset consists of 9,374 households that were sampled in both 2002 and 2007 from the 21 villages. The latitude and longitude of each household has been recorded in the dataset, and thus provides the unique opportunity to undertake spatial analyses at the household level.

Our response variable is the number of temporary migrants, older than 15 years, at the household level. A temporary migrant is defined as a person leaving a household with a temporary intention and spending at least six months of a year away from home, although still linked to the rural household. As an independent variable, we employ an additive index of household socio-economic status (SES) that combines measures of modern assets, livestock assets and information about power supply, access to water and sanitation, and dwelling structure. Household SES was identified as an important explanatory variable for migration in our preliminary analysis as well as in recent research (e.g., Mberu, 2006).

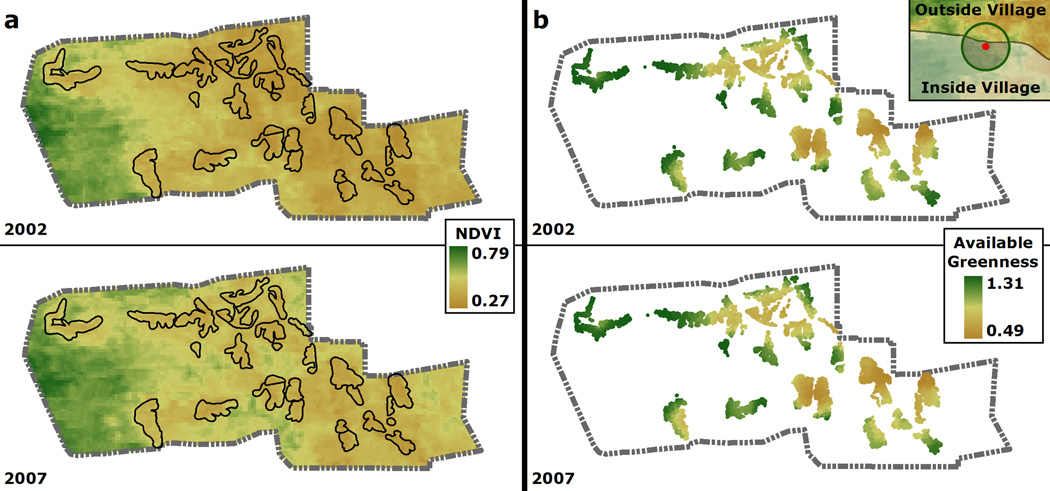
In order to incorporate an environmental independent variable, we use the Normalized Difference Vegetation Index (NDVI) to calculate a greenness metric as a surrogate for natural resource availability at the household level (Fig. 2). NDVI has been used to monitor plant growth (vigor), density of vegetation cover and biomass production (Foody et al., 2001; Wang et al., 2004) and is therefore an effective indicator of the natural resources locally used in livelihood strategies (e.g. firewood, seeds, wild foods, fencing materials, etc.).

Figure 2.

Figure 2

Open in a new tab

Mean relative greenness for periods leading up to 2002 and 2007, for (a) the Agincourt study area; (b) extracted within household collection zones (displayed at household level within the original village polygons). Inset (b) shows an example of how natural resource availability was calculated for each household.

Yearly NDVI values were calculated by taking the annual mean of 16-day composites from MODIS satellite imagery (250 meter resolution). We took the mean of the year of analysis and the two years prior to create greenness grids for 2002 and 2007 (Fig. 2a). By including the two years prior to the outcome years, we take into account the availability of natural resources leading up to 2002 and 2007.

The first time period is characterized by relatively high but slightly decreasing greenness values from 2000 to 2002 (NDVI between 0.55 – 0.49 on average); the latter period shows similar mean greenness but higher variation across the years with an increasing trend from 2005 to 2007 (NDVI between 0.45 – 0.53). Thus, on average, mean greenness values were similar in both time periods with some visible differences in the spatial distributions due to different resource availability “histories”. Investigation into the effect of refined temporal trends in resource availability will be left to future research.

From the two greenness grids, areas within village boundaries were excluded since these are not communal lands and are therefore not used for resource collection. We next created 2000-meter buffer zones around each household (top panel inset, Fig. 2b) based on the distance within which residents tend to travel to access natural resources (Giannecchini et al., 2007; Fisher et al., 2011). Finally, the sum of NDVI values within this buffer zone was calculated by household, then divided by the number of households in the buffer. The resulting metric serves as a surrogate for per household resource availability. To illustrate, the top panel inset of Fig. 2 shows the shaded within-village area on the bottom of the inset and the colored region towards the top of the buffer containing available and accessible natural resources. Fig. 2b illustrates household resource availability based on this calculation. Note that households toward village centers have lower resource availability.

In addition to SES and the NDVI greenness metric, we include control variables that attained statistical significance in the analysis at the whole-population scale. The total number of independent variables was restricted in this way in order to facilitate localized analyses while maintaining sufficient degrees of freedom. Control variables include household size, proportion working age male, gender and marital status of household head, mean educational level within household, and proportion household members currently working. Additional household-level resource variables were not available for the current study; however, prior migration work has, indeed, demonstrated the predictive value of the household-level characteristics in our model (e.g., Kok et al., 2003; White and Lindstrom, 2006; Mberu, 2006; Lindstrom and Ramirez, 2010; Massey et al., 2010).

3 Methods

3.1 Understanding the role of geographic scale: Nested regions of varying sizes

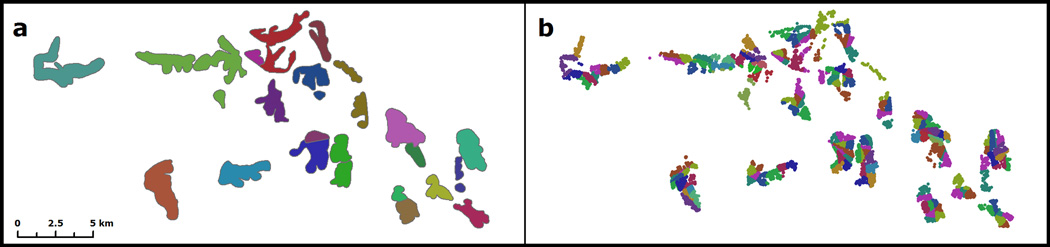
Three nested geographic scales are examined by subdividing the set of surveyed household locations. First, the migration-environment association is modeled for the whole population, making use of all 9,374 households. Next, the model is fit to each of the 21 villages separately, and finally, spatial variation within each village is examined through random generation of spatially contiguous subvillage regions which is repeated in 1000 permutations to test the stability of subvillage model associations. This repeated random regionalization is done in order to test whether the subvillage models show more robust “local” target associations and thus indicate a geographic scale at which spatial non-stationarity in such associations could be reduced or even removed.

As such, increasingly “localized” outmigration models are estimated, still based on underlying (sub-)populations of sufficient size and variability to develop relatively robust statistical models. The strength of this approach is that it fits a simple Poisson (GLM) regression model to the households of each spatially contiguous region within each village and repeats the random simulation of subvillage regions. It thus allows the use of established diagnostic techniques such as the likelihood ratio test and the variance inflation factor while objectively assessing spatial variation in the relationships of interest. The approach thus overcomes limitations of common local estimators (e.g., GWR) as described earlier and can be applied to count data.

Nested subvillage regions were randomly generated such that they subdivide villages into smaller exclusive (non overlapping), contiguous areas. Essentially, this technique constitutes a spatially constrained random permutation method. Our approach generates subvillage regions that contain a minimum of 47 and a maximum of 94 households in order to ensure that the smallest village is divided into two regions while all other subvillage regions cannot become larger than the smallest village. Thus villages are divided into subregions with a similar number of households (randomly varying between the two thresholds) while maintaining statistically acceptable sample sizes. Spatial contiguity in this regionalization process was achieved by randomly selecting two seed points (households) within each village. Regions were then generated by joining all remaining households with the closest seed point. This process was repeated until the size of all regions was between the two thresholds, creating the subvillage units (Fig. 3). We assessed the average model structure and performance over all 1000 regionalization runs in the subsequent modeling process. The same analysis was undertaken for 2002 and 2007 with the same simulated sets of subregions in order to ensure identical degrees of freedom for all models. This allows for comparison of significance levels and diagnostics between the two years.

Figure 3.

Figure 3

Open in a new tab

Different geographic scales used in this analysis to subdivide global population: (a) village scale, and (b) subvillage scale (one random regionalization outcome is shown).

3.2 Modeling, coefficient estimation and mapping

At each geographic scale (i.e., whole-population, village and sub-village), regressions (GLM) were fit for Poisson-distributed household-level temporary outmigration counts. For each model, coefficient estimates and their corresponding p-values were derived and residuals were tested for spatial autocorrelation using Global Moran’s I (Moran, 1950) as well as for spatial clustering using Local Moran’s I, a class of Local Indicators of Spatial Association (LISA) (Anselin, 1995).

At the subvillage scale, models were fit for random regions across the 1000 simulations and, for each subvillage model from each simulation, the coefficient estimates and p-values were stored. Thus, for each household, coefficient estimates were stored from model runs on 1000 different configurations of random subvillage regions. Finally, we took the mean coefficient estimates for each household across all simulations and calculated the proportion of simulations where those coefficients were significant (p < 0.05). Thus, spatial distributions of varying mean model coefficients, and proportion of significant coefficients at the household level could be created based on a series of statistical sub-village models as described below.

As for the mapping process, at the village scale we created maps of coefficient values and their statistical significance using village boundaries (polygon feature data). At the subvillage scale, we mapped mean coefficient estimates and the proportion of significant tests over 1000 model runs for each household location (point feature data). This mapping allowed us to visualize (1) changes in model structure across different geographic scales within the whole study area, (2) at each geographic scale, the spatial variation or spatial heterogeneity in the two target associations of interest (i.e., outmigration-SES and outmigration-NDVI), and (3) given the two time points (2002 and 2007), a temporal comparison of model coefficients and spatial distributions. In order to better understand the spatial structure of model performance, and thus to identify regions of potential clusters of under and over prediction, maps of LISA clusters (Anselin, 1995) on the model residuals were also created.

3.3 Diagnostics for models at different geographic scales

Finally, the goodness-of-fit is assessed at each geographic scale using the Akaike Information Criterion (AIC). Traditionally, AIC is used to compare models fit to the same population with different sets of predictor variables. Here, we compare the goodness-of-fit of two models with the same set of predictor variables but originally fit to different geographic scales (e.g., whole-population and village). AIC is generally calculated as:

AIC=−2 log(L)+2k (1)

where L is the maximum likelihood estimate and k is the number of model parameters (Akaike, 1974). For n independent observations of a Poisson model, the log-likelihood function for the model with parameters β is:

log L(β)=∑i=1n(yi log(μi)−μi) (2)

where μi is the fitted response value from the Poisson regression model for the observation yi (Rodríguez, 2007). As mentioned, AIC only allows a valid comparison between models when models are fit to the same population. Therefore, in order to compare the goodness-of-fit of models estimated on different geographic scales, we took the fitted response values μ for the subset of observations from the coarser scale regression model which corresponded to the same observations used for fitting the finer scale regression model. For example, to compare the model for village number 1 (with 971 households) to the whole-population scale model, we took the 971 corresponding fitted values of μ from the whole-population model and calculated the maximum likelihood estimate L. The AIC is then calculated using this value of L and compared to the AIC from the village model, computed with the traditional approach (Akaike, 1974). Decomposing the likelihood function of the coarser scale model in this way allows cross-scale comparisons of goodness-of-fit. This comparison was done between each village and the whole-population scale, and between each random subvillage region and the village scale for each of the 1000 simulations.

Yet, a decrease in AIC of the more ‘localized’ model does not show whether the improvement (i.e., reduction in AIC) is statistically significant since the value has no intrinsic meaning (Sayyareh et al., 2010). For this reason, we employed the Vuong likelihood ratio test (Vuong, 1989) to reliably identify where the finer scale of analysis performs more robust. Here, the comparison is between models considered overlapping i.e., (i) the two models have common distributional properties (Poisson) and (ii) neither model has a subset of parameters from the other (i.e. both models have the same independent variables) (Vuong, 1989, p. 320). In an empirical study, Genius and Strazzera (2002) showed that the Vuong test is more robust for comparing overlapping models than other tests (such as AIC or Cox test) for small sample sizes (recall that the subvillage regions have between 47 to 94 households). The Vuong test statistic for models f and g is:

υ=nLRn(θ^n,γ^n)ω^n (3)

where LRn(θn,γn) is the log-likelihood ratio of the models f and g, and ωn is the square root of the variance (i.e. standard deviation) of their point-wise log-likelihood ratios. That is:

ωn2=var⌊logf(yi|xi,θn)g(yi|xiγn⌋ (4)

A two-sided test is conducted where a critical value c from a standard normal distribution is selected based on the desired significance level, 0.05 in this case. If the test statistic v is greater than c, then model f performs better than model g. If v is less than -c, then g is preferred over f. In the case that |v| ≤ c, then the two models cannot be discriminated (Vuong, 1989, p. 318).

4 Results and Discussion

4.1 Whole-population scale models

Whole-population scale model diagnostics indicate that both explanatory variables of interest, SES and NDVI, are highly significant in 2002 and 2007 (p < 0.01) (Table 1). At increasingly localized geographic scales, however, the estimates show increasing spatial variation and increasing variance across regions (as discussed below). This suggests that the whole-population scale obscures considerable spatial variation in these associations across the study area.

Table 1.

Summary of whole-population scale model coefficient estimates (SES and NDVI).

Whole-population Scale
SES Coefficients NDVI Coefficients
Year Est. Std. Error p-value Est Std. Error p-value
2002 0.068 0.024 0.005 0.280 0.080 0.001
2007 0.162 0.025 ~0.00 0.304 0.073 ~0.00
Open in a new tab

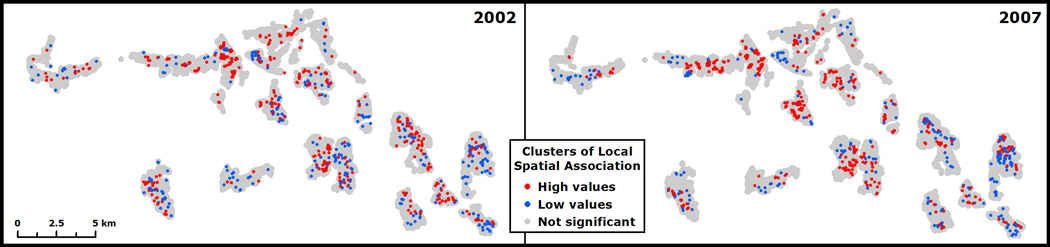
The whole-population model’s residuals reveal significant spatial autocorrelation based on global Moran’s I (p < 0.05), suggesting a non-random error structure due to spatial dependence. In both years, significant local clusters based on LISA measures of low and high residual values are well separated from each other and do not vary considerably between 2002 and 2007 (Fig. 4). Substantively, this translates to spatially clustered overand under-predictions, respectively, and suggests the need for approaches accounting for spatial non-stationarity to better understand the target associations.

Figure 4.

Figure 4

Open in a new tab

Maps of statistically significant (p < 0.05) local clusters of high and low residual values of the whole-population geographic scale model computed using LISA tests.

4.2 Village scale models

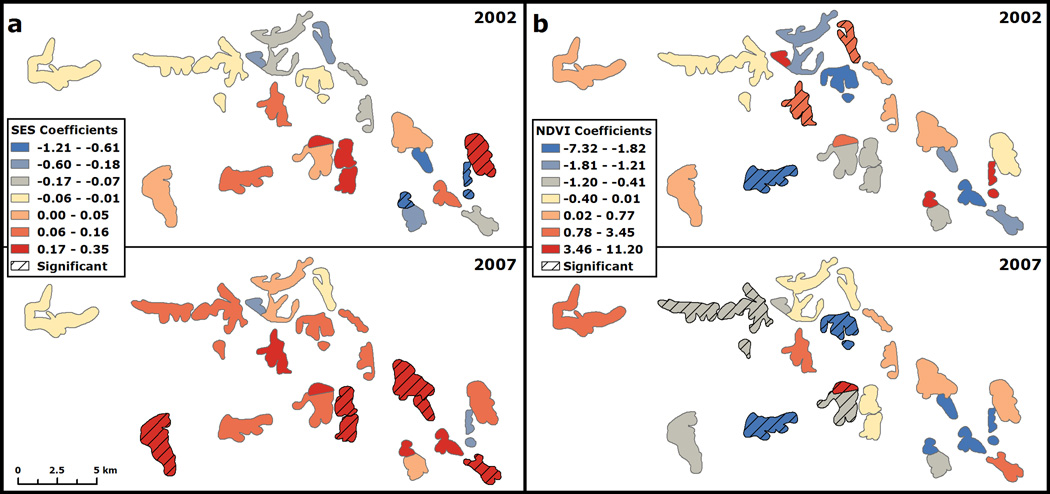
At the village scale, considerable variation emerged in coefficient estimates across villages, as well as interesting patterns of change between the two years (Fig. 5). The overall outmigration-SES association on the village scale was stronger in 2007 compared to 2002 and showed higher spatial variation in 2002 (i.e., more stable in the later time period) (Fig. 5a). This indicates that households with higher SES were more likely to send migrants in 2007 relative to 2002.

Figure 5.

Figure 5

Open in a new tab

Village scale model coefficients for target associations (a) SES-outmigration and (b) NDVI-outmigration for 2002 and 2007. If coefficients were tested significant (p < 0.05) they appear hashed in the figure.

As for the NDVI greenness metric, there are high degrees of spatial variation that result in positive and negative relationships in both years with a slight trend of decreasing coefficient values (2002 to 2007). As such, no generalized statement as to the migration-environment association accurately characterizes the Agincourt study site as a whole.

4.3 Sub-village scale models

The subvillage scale reveals more refined spatial patterns of associations (Fig. 6). Within village boundaries, considerable spatial variation exists in both SES and NDVI coefficient estimates, indicating considerable local variation in their association with outmigration not reflected by village scale models.

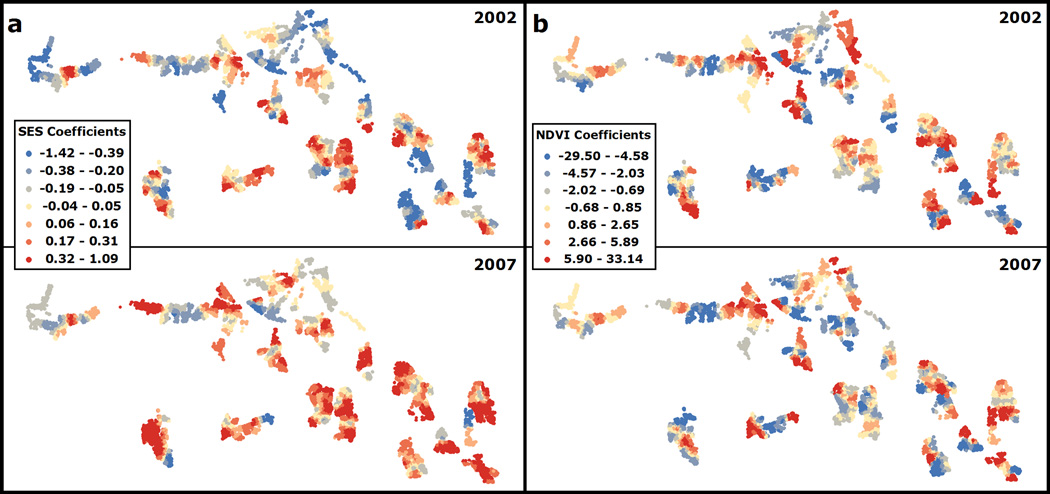
Figure 6.

Figure 6

Open in a new tab

Sub-village scale average model coefficients for the two target associations (a) SES-outmigration and (b) NDVI-outmigration for 2002 and 2007 over 1000 simulations and thus based on 1000 model runs.

Fig. 6 reveals that an increase in natural resource access is associated with greater outmigration propensity for some households while decreasing the propensity for others, even in the same village. This high degree of spatial heterogeneity might be explained by two distinct mechanisms. First, access to natural resources acts as a form of capital which allows a household to free human capital (Aggarwal et al., 2001) and to engage in migration as a form of livelihood diversification (Ellis, 2000). Second, the access to natural capital provides households with employment opportunities, wealth and livelihood security, and thus, might “serve as an amenity, discouraging out-migration” (Gray, 2009, p. 458). Which mechanism is primarily impacting the out-migration decision is a function of a household’s vulnerability and adaptive capacity in times of changing environments (Meze-Hausken, 2000), which is in turn influenced by households’ SES.

At this geographic scale, only a few villages show fairly homogeneous associations within their boundaries for either of the explanatory variables. However, the mean of subvillage coefficient estimates within each village is extremely close to corresponding village scale estimates for both SES and NDVI. For instance, in 2002 the difference between the subvillage mean coefficient estimates and the corresponding village estimate was 0.07 and 0.29 for SES and NDVI, respectively.

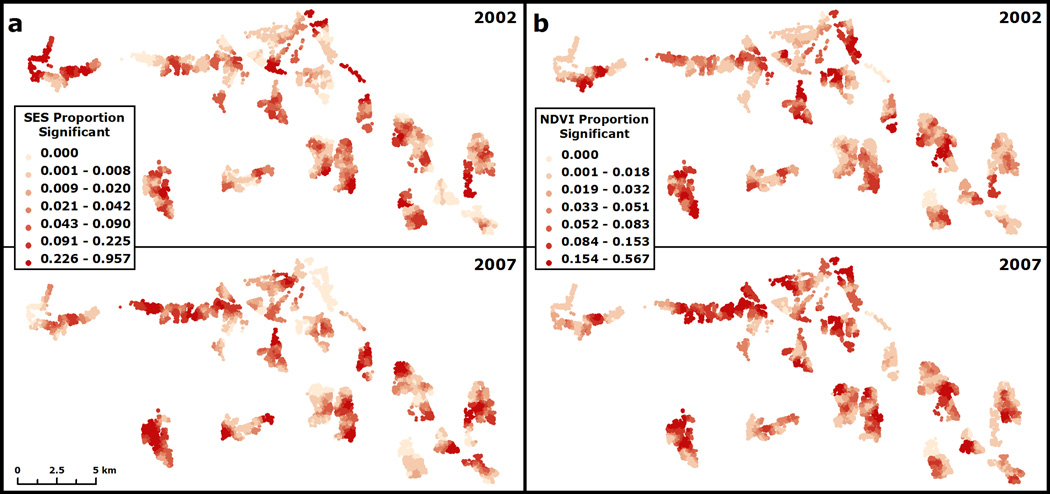
The proportion of significant coefficients (p < 0.05) over the 1000 model simulations (Fig. 7) provide additional information about the average significance of the model associations in explaining household temporary outmigration. The subvillage coefficient estimates show consistent proportions of significant models for both variables in both years. Figure 7 illustrates clustering of significance proportions at the subvillage scale again indicating considerable variation of the observed relationships at this geographic scale.

Figure 7.

Figure 7

Open in a new tab

Sub-village scale proportions of model coefficients tested significant over 1000 simulations and thus based on 1000 model runs for the two target associations (a) outmigration-SES and (b) outmigration-NDVI for 2002 and 2007.

4.4 Multiscale model diagnostics

The simple structure of nested Poisson models allows for the use of robust, well-established diagnostic methods and tests for goodness-of-fit for all three geographic scales. As a visual diagnostic, we plotted the temporary migration counts against the predicted values for each of the three geographic scales. This standard procedure shows a drastic improvement in prediction from the whole-population to subvillage scale (Fig. 8) substantiated by comparing the residuals’ mean squared error at each scale (Table 2).

Figure 8.

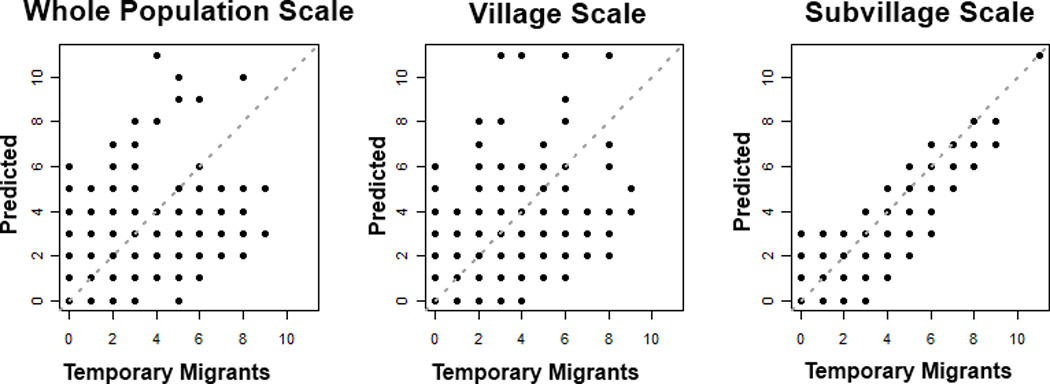
Figure 8

Open in a new tab

Predictive strength of global, village (for all 21 villages) and subvillage (from all 1000 simulations) scale models for 2002. The number of temporary migrants for each household on the x-axis is plotted against the predicted number of temporary migrants on the y-axis. The dotted line indicates the line of exact prediction for reference.

Table 2.

Summary of model diagnostics and clustering of model residuals based on LISA. Village and sub-village scale measures are means across all region-specific regressions. LISA based High-High and Low-Low clusters can be interpreted as spatial grouping of over- and underprediction, respectively.

Whole-population Scale Village Scale Subvillage Scale
Regression
Diagnostics		 LISA Clusters Regression
Diagnostics		 LISA Clusters Regression
Diagnostics		 LISA Clusters
Year MSE AIC High-
High		 Low-
Low		 Mean
MSE		 AIC High-
High		 Low-
Low		 Mean
MSE		 AIC High-
High		 Low-
Low
2002 1.021 163.8 361 302 0.984 158.2 288 336 0.784 150.7 256 228
2007 1.132 181.9 383 261 1.076 176.9 324 294 0.865 168.3 218 173
Open in a new tab

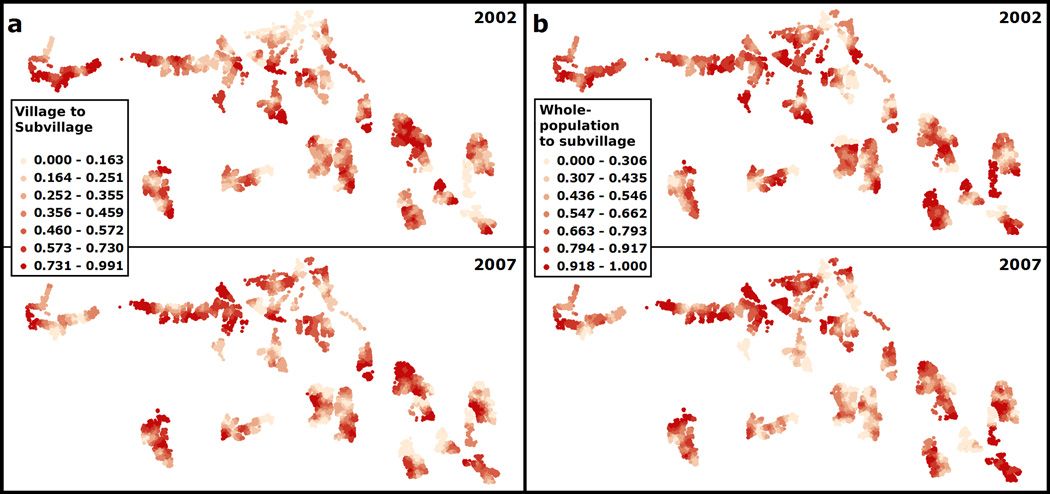
The results of the AIC comparison also show consistent reduction of AIC at finer nested geographic scales for both years (Table 2). When testing for significance using the Vuong’s likelihood ratio test, we found 86 and 62 percent improvements for village scale over the whole-population scale model in 2002 and 2007, respectively. The subvillage scale exhibited 44 and 43 percent mean improvements over the village scale in 2002 and 2007, respectively, and from whole-population scale to subvillage scale, improvement was 64 and 60 percent for 2002 and 2007, respectively. Maps of proportion significant improvements over the village and whole-population scales identify where subvillage scale models better reveal the target associations (Fig. 9).

Figure 9.

Figure 9

Open in a new tab

Proportion of significant improvement of subvillage scale models across the 1000 simulations over (a) the village scale and (b) the global scale models.

Finally, in order to better understand the impacts of increasingly localized, nested geographic scales on the structure of the data and subsequently on model results, two principal concerns must be addressed: (i) induced multicollinearity of the explanatory variables at finer geographic scales, and (ii) spatial autocorrelation of model residuals across geographic scales.

Multicollinearity can confound coefficient estimates and compromise interpretation. The variance-inflation factor (VIF) is a common diagnostic to assess multicollinearity in a dataset (Hill and Adkins, 2007). Most thresholds above which multicollinearity is considered severe vary between 4 and 10 (O’brien, 2007). In the present analyses, most subvillage models led to VIF values below 2; very few were above 4 and none above 7. The whole-population and village scales did not exhibit values above 2 (Fig. 10). Combined, the VIFs suggest multicollinearity is stable and not affecting data structure at finer geographic scales.

Figure 10.

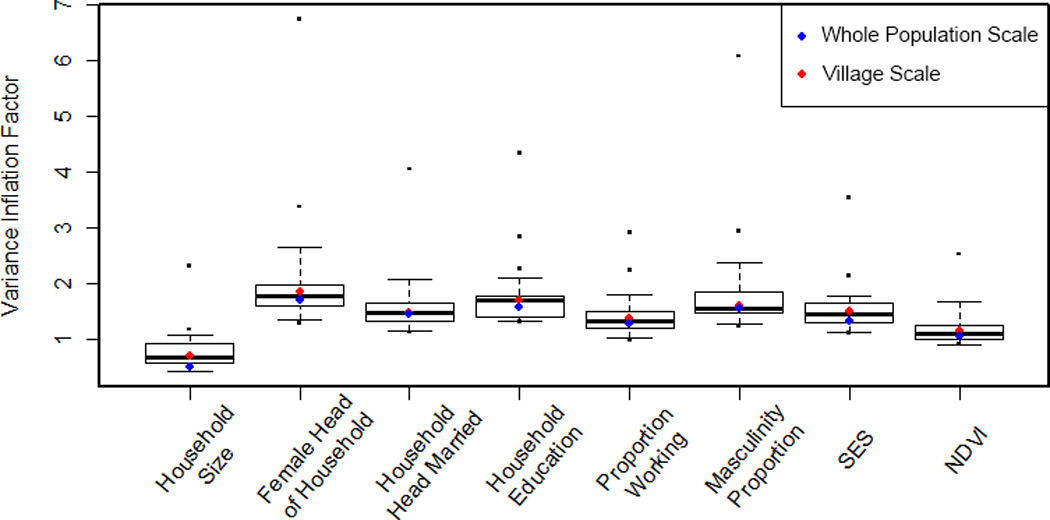
Figure 10

Open in a new tab

Multicollinearity of various explanatory variables. Village scale VIF is displayed as median values across all villages. Subvillage scale values are shown as boxplots across all 1000 simulations.

As for the model residuals, the whole-population scale exhibits significant local spatial autocorrelation of errors (Fig. 4) consisting of a total of 663 and 644 clusters in 2002 and 2007, respectively. At the village scale, this was reduced to 624 and 618 in 2002 and 2007, respectively. The mean model residuals across all 1000 simulations at the subvillage scale exhibited 484 and 391 total clusters in 2002 and 2007, respectively (Table 2). Thus the spatial refinement actually reduces local spatial autocorrelation of the error structure.

5 Concluding Remarks and Outlook

Environmental conditions are increasingly being examined, in concert with socio-economic attributes, as potential factors shaping outmigration especially from rural, natural-resource dependent regions. Yet the effects of geographic scale of input for migration models as well as of spatial dependence and non-stationarity in corresponding associations remain hidden when using global statistical models for the whole population. The framework presented here allows examination of whether refining the geographic scale reduces effects of spatial non-stationarity in migration-environment associations and thus allows for more robust models to be computed. Based on the spatial permutation method, local coefficients can be estimated in a statistically robust way to identify spatial non-stationarity. This approach is built on a Poisson GLM framework (which can readily be applied to other GLM families, i.e. binomial or gamma) for local estimation which includes a suite of well established diagnostic techniques. The strength of this approach is the development of full models with sufficient statistical power even at the sub-village geographic scale thereby allowing for reliable evaluation and interpretation of the results. Comparing model diagnostics such as the AIC and Vuong test across different nested geographic scales revealed that in general a finer scale model for temporary outmigration is indeed more robust and therefore captures the associations between migration and SES and NDVI more reliably. Further, quantification of the variation in our target associations across sub-populations at the same scale (e.g., across all villages) revealed that even within villages there is considerable non-stationarity in such model relationships. This spatial non-stationarity could indicate that community-level dynamics, which exist on the sub-village scale, are very important and influential for migration decisions on the household level. This also raises important questions regarding the degree of variation in migration-related associations that has to be expected within political or administrative units such as villages but is not captured when using traditional model approaches using global statistical models.

In this study we show that the associations between temporary outmigration and explanatory variables, SES and NDVI, produce different but high degrees of spatial variation across the study site, illustrating the inherent complexity in the system and the need for local estimation models. Interestingly, we discovered considerable differences in resulting patterns between the two years of interest suggesting that target associations at even the finest geographic scale change under varying environmental conditions. In other words, there is indication that environmental change impacts model associations, thus suggesting that environmental variables derived at the household level are relevant in explaining temporary outmigration on all geographic scales investigated. Future research will examine interactions between socio-economic factors and environmental measures and will also include refined NDVI-derived measures. Further analysis of data from the AHDSS Surveillance Site for additional points in time will also yield nuance in the substantive interpretation afforded by application of these methodological advancements to population-environmental modeling in the Agincourt study site. In addition, the extensive time series available of NDVI data from satellite imagery will provide a better understanding of the spatio-temporal migration-environment associations in resource-dependent communities.

Highlights.

  • Temporary outmigration in resource-dependent communities in rural South Africa

  • Role of environmental and socioeconomic variables for temporary outmigration

  • Effects of changing geographic scale and non-stationarity on models

  • Subvillage scale community-level dynamics could impact migration decisions

  • Environmental change impacts model associations even at very local scales

Acknowledgements

Supported by NIH 1R03 HD061428, “Environmental Variability, Migration, and Rural Livelihoods.” The work has also benefited from the NICHD-funded University of Colorado Population Center (grant R21 HD51146) for research, administrative, and computing support, and indirect support from the Wellcome Trust (grant 085477/Z/08/Z) through its support of the Agincourt Health and Demographic Surveillance System. The content is solely the responsibility of the authors and does not necessarily represent the official views of the CUPC, NIH, or NICHD.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

1

The AHDSS is operated by the Rural Public Health and Health Transitions Research Unit of the South African Medical Research Council and University of the Witwatersrand.

References

  1. Aggarwal R, Netanyahu S, Romano C. Access to natural resources and the fertility decision of women: the case of South Africa. Environment and Development Economics. 2001;6:209–236. [Google Scholar]
  2. Akaike H. A new look at the statistical model identification. IEEE Trans Automatic Control. 1974;19(6):716–723. [Google Scholar]
  3. Anselin L. Local indicators of spatial association – LISA. Geographical Analysis. 1995;27(2):93–115. [Google Scholar]
  4. Barbieri AF, Carr DL. Gender-specific out-migraiton, deforestation and urbanization in the Ecuadorian Amazon. Global and Planetary Change. 2005;47:99–110. doi: 10.1016/j.gloplacha.2004.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Botha J, Witkowski ETF, Shackleton CM. Market profiles and trade in medicinal plants in the Lowveld, South Africa. Environmental Conservation. 2004;31:38–46. [Google Scholar]
  6. Brunsdon CF, Fotheringham AS, Charlton ME. Geographically weighted regression: A Method for Exploring Spatial Nonstationarity. Geographical Analysis. 1996;28(4):281–298. [Google Scholar]
  7. Cho S-H, Lambert DM, Chen Z. Geographically weighted regression bandwidth selection and spatial autocorrelation: an empirical example using Chinese agriculture data. Applied Economics Letters. 2010;17(8):767–772. [Google Scholar]
  8. Cleveland WS, Grosse E, Shyu WM. Local regression models. In: Chambers JM, Hastie TJ, editors. Statistical Models in S. Wadsworth & Brooks, Pacific Grove; 1991. pp. 309–376. [Google Scholar]
  9. Crookes D. The contribution of livelihood activities in the Limpopo Province: case study evidence from Makua and Manganeng. Development Southern Africa. 2003;20:143–159. [Google Scholar]
  10. Ellis F. The determinants of rural livelihood diversification in developing countries. Journal of Agricultural Economics. 2000;51(2):289–302. [Google Scholar]
  11. Farber S, Páez A. A systematic investigation of cross-validation in GWR model estimation: empirical analysis and Monte Carlo simulations. Journal of Geographical Systems. 2007;9:371–396. [Google Scholar]
  12. Feng SZ, Krueger AB, Oppenheimer M. Linkages among climate change, crop yields and Mexico-US cross-border migration. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:14257–14262. doi: 10.1073/pnas.1002632107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Findley SE. Does drought increase migration - a study of migration from rural Mali during the 1983–1985 drought. International Migration Review. 1994;28:539–553. [PubMed] [Google Scholar]
  14. Fisher JT, Witkowski ETF, Erasmus BFN, Van Aardt JAN, Asner G, Wessels K, Mathieu R. Human-modified landscapes: patterns of fine-scale woody vegetation structure in communal savanna rangelands. Environmental Conservation. 2011;39(1):72–82. [Google Scholar]
  15. Foody GM, Cutler ME, McMorrow J, Pelz D, Tangki H, Boyd DS, Douglas I. Mapping the biomass of Bornean tropical rain forest from remotely sensed data. Global Ecology and Biogeography. 2001;10(4):379–387. [Google Scholar]
  16. Fotheringham AS, Brunsdon C, Charlton M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. New York: Wiley; 2002. 269 pp. [Google Scholar]
  17. Genius M, Strazzera E. A note about model selection and tests for non-nested contingent valuation models. Economics Letters. 2002;74(3):363–370. [Google Scholar]
  18. Giannecchini M, Twine W, Vogel C. Land-cover change and human-environment interactions in a rural cultural landscape in South Africa. The Geographical Journal. 2007;173:26–42. [Google Scholar]
  19. Gray CL. Soil quality and human migration in Kenya and Uganda. Global Environmental Change. 2011;21(2):421–430. doi: 10.1016/j.gloenvcha.2011.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gray CL. Environment, land, and rural out-migration in the southern Ecuadorian Andes. World Development. 2009;37(2):457–468. [Google Scholar]
  21. Griffith D. Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR) Environment and Planning A. 2008;40(11):2751–2769. [Google Scholar]
  22. Gyan C, Shackleton C. Abundance and commercialisation of Phoenix reclinata in the King Williamstown area, South Africa. Journal of Tropical Forest Science. 2005;17:334–45. [Google Scholar]
  23. Hastie T, Tibshirani R. Varying-coefficient models. Journal of the Royal Statistical Society. 1993;Series B 55(4):757–796. [Google Scholar]
  24. Henry S, Schoumaker B, Beauchemin C. The impact of rainfall on the first out-migration: a multi-level event-history analysis in Burkina Faso. Population and Environment. 2004;25(5):423–460. [Google Scholar]
  25. Hill RC, Adkins LC. Collinearity. In: Baltagi BH, editor. A Companion to Theoretical Econometrics. Basil Blackwell, Oxford: 2007. pp. 256–278. [Google Scholar]
  26. Hunter L, Twine W, Johnson A. Adult mortality and natural resource use in rural South Africa: evidence from the Agincourt Health and Demographic Surveillance Site. Society and Natural Resources. 2011;24:256–275. doi: 10.1080/08941920903443327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hunter LM. The Association between environmental risk and internal migration flows. Population and Environment. 1998;19(3):247–277. [Google Scholar]
  28. Hunter LM. The spatial association between U.S. immigrant residential concentration and environmental hazards. International Migration Review. 2000;34:460–488. [Google Scholar]
  29. IPCC. The Physical Science Basis. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL, editors. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom New York, NY: Cambridge University Press; 2007. [Google Scholar]
  30. IPCC. Summary for Policymakers. In: Field CB, Barros V, Stocker TF, Qin D, Dokken DJ, Ebi KL, Mastrandrea MD, Mach KJ, Plattner G-K, Allen SK, Tignor M, Midgley PM, editors. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom New York, NY: Cambridge University Press; 2012. [Google Scholar]
  31. Kok P, O'Donovan M, Bouare O, Van Zyl J. Post Apartheid Patterns of Internal Migration in South Africa. Cape Town, South Africa: Human Sciences Research Council; 2003. [Google Scholar]
  32. Lam NS, Quattrochi DA. On the Issues of Scale, Resolution, and Fractal Analysis in the Mapping Sciences. The Professional Geographer. 1992;44(1):88–98. [Google Scholar]
  33. Lindstrom DP, Ramirez A. Pioneers and followers: migrant selectivity and the development of U.S. migration streams in Latin America. The Annals of the American Academy of Political and Social Sciences. 2010;630:53–77. doi: 10.1177/0002716210368103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Massey DS, Axinn WG, Ghimire DJ. Environmental change and out-migration: evidence from Nepal. Population and Environment. 2010;32(2–3):109–136. doi: 10.1007/s11111-010-0119-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mberu BU. Internal migration and household living conditions in Ethiopia. Demographic Research. 2006;14:509–539. [Google Scholar]
  36. McLeman R, Smit B. Migration as adaptation to climate change. Climatic Change. 2005;76:31–53. [Google Scholar]
  37. McLeman RA, Hunter LM. Migration in the context of vulnerability and adaptation to climate change: insights from analogues. Wiley Interdisciplinary Reviews-Climate Change. 2010;1(3):450–461. doi: 10.1002/wcc.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. McSweeny K. Tropical forests product sale as natural insurance: the effects of household characteristics and the nature of shock in Eastern Honduras. Society and Natural Resources. 2004;17:39–56. [Google Scholar]
  39. Meze-Hausken E. Migration caused by climate change: how vulnerable are people in dryland areas. Migration and Adaptation Strategies for Global Change. 2000;5:379–406. [Google Scholar]
  40. Montello DR. Scale in geography. In: Smelser NJ, Baltes PB, editors. International Encyclopedia of the Social & Behavioral Sciences. Pergamon, Oxford: 2001. pp. 13501–13504. [Google Scholar]
  41. Moran PAP. Notes on continuous stochastic phenomena. Biometrika. 1950;37:17–33. [PubMed] [Google Scholar]
  42. O'Sullivan D, Unwin D. Geographic information analysis. Wiley, Hoboken; 2010. [Google Scholar]
  43. O’brien RM. A caution regarding rules of thumb for variance inflation factors. Quality & Quantity. 2007;41:673–690. [Google Scholar]
  44. Paumgarten F, Shackleton C. The role of non-timber forest products in household coping strategies in South Africa: the influence of household wealth and gender. Population and Environment. 2011;33:108–131. [Google Scholar]
  45. Rodríguez G. [Accessed December 16, 2011];Lecture Notes on Generalized Linear Models. 2007 http://data.princeton.edu/wws509/notes/.
  46. Sayyareh A, Obeidi R, Bar-Hen A. Empiricial comparison between some model selection criteria. Communications in Statistics - Simulation and Computation. 2010;40:72–86. [Google Scholar]
  47. Scheffran J, Battaglini A. Climate and conflicts: the security risks of global warming. Regional Environmental Change. 2011;11:S27–S39. [Google Scholar]
  48. Shackleton S, Campbell B, Lotz-Sisitka H, Shackleton C. Links between the local trade in natural products, livelihoods and poverty alleviation in a semi-arid region of South Africa. World Development. 2008;36(3):505–526. [Google Scholar]
  49. Shackleton S, Shackleton C. Exploring the role of wild natural resources in poverty alleviation with an emphasis on South Africa. In: Hebinck P, Shackleton C, editors. Reforming Land and Resource Use in South Africa: Impact on Livelihoods. Routledge, New York: 2011. pp. 209–234. [Google Scholar]
  50. Vuong QH. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica. 1989;57(2):307–333. [Google Scholar]
  51. Wang J, Rich PM, Price KP, Kettle WD. Relations between NDVI and tree productivity in the central Great Plains. International Journal of Remote Sensing. 2004;25(16):3127–3138. [Google Scholar]
  52. Wheeler DC. Diagnostic tools and a remedial method for collinearity in geographically weighted regression. Environment & Planning A. 2007;39(10):2464–2481. [Google Scholar]
  53. White MJ, Lindstrom DP. Internal migration. In: Poston D, Micklin M, editors. Handbook of Population. Kluwer, New York: 2006. pp. 311–346. [Google Scholar]
  54. Wynberg RP, Laird SA, Shackleton SE, Mander M, Shackleton CM, du Plessis P, den Adel S, Leakey RRB, Botelle A, Lombard C, Sullivan C, Cunningham AB, O’Regan DP. Marula commercialisation for sustainable and equitable livelihoods. Forests Trees and Livelihoods. 2003;13:203–215. [Google Scholar]
  55. Yabiku S, Glick JE, Wentz EA, Haas SA, Zhu L. Migration, health, and environment in the desert southwest. Population and Environment. 2009;30(4–5):131–158. [Google Scholar]

RESOURCES