Summary
Local polynomial regression has received extensive attention for the nonparametric estimation of regression functions when both the response and the covariate are in Euclidean space. However, little has been done when the response is in a Riemannian manifold. We develop an intrinsic local polynomial regression estimate for the analysis of symmetric positive definite (SPD) matrices as responses that lie in a Riemannian manifold with covariate in Euclidean space. The primary motivation and application of the proposed methodology is in computer vision and medical imaging. We examine two commonly used metrics, including the trace metric and the Log-Euclidean metric on the space of SPD matrices. For each metric, we develop a cross-validation bandwidth selection method, derive the asymptotic bias, variance, and normality of the intrinsic local constant and local linear estimators, and compare their asymptotic mean square errors. Simulation studies are further used to compare the estimators under the two metrics and to examine their finite sample performance. We use our method to detect diagnostic differences between diffusion tensors along fiber tracts in a study of human immunodeficiency virus.
1. Introduction
Symmetric positive-definite (SPD) matrix-valued data occur in a wide variety of important applications. For instance, in computational anatomy, a SPD deformation vector (JJT)1/2 is computed to capture the directional information of shape change decoded in the Jacobian matrices J at each location in an image (Grenander and Miller, 2007). In diffusion tensor imaging (Basser et al., 1994), a 3 × 3 SPD diffusion tensor, which tracks the effective diffusion of water molecules, is estimated at each voxel (a 3 dimensional (3D) pixel) of an imaging space. In functional magnetic resonance imaging, a SPD covariance matrix is calculated to delineate functional connectivity between different neural assemblies involved in achieving a complex cognitive task or perceptual process (Fingelkurts et al., 2005). In classical multivariate statistics, a common research focus is to model and estimate SPD covariance matrices for multivariate measurements, longitudinal data, and time series data among many others (Pourahmadi, 2000; Anderson, 2003).
Despite the popularity of SPD matrix-valued data, only a handful of methods have been developed for the statistical analysis of SPD matrices as response variables in a Riemannian manifold. In the medical imaging literature (Fletcher and Joshi, 2007; Batchelor et al., 2005; Pennec et al., 2006), various image processing methods have recently been developed to segment, deform, interpolate, extrapolate and regularize diffusion tensor images (DTIs). Schwartzman (2006) proposed several parametric models for analyzing SPD matrices and derived the distributions of several test statistics for comparing differences between the means of the two (or multiple) groups of SPD matrices. Kim and Richards (2010) developed a nonparametric estimator for the common density function of a random sample of positive definite matrices. Zhu et al. (2009) developed a semi-parametric regression model with SPD matrices as responses in a Riemannian manifold and the covariates in a Euclidean space. Barmpoutis et al. (2007) and Davis et al. (2010) proposed tensor splines and local constant regressions for interpolating DTI tensor fields, but they did not address several important issues of analyzing random SPD matrices including the asymptotic properties of the nonparametric estimate proposed. All these methods for SPD matrices discussed above are based on the trace metric (or affine invariant metric) in the SPD space (Lang, 1999; Terras, 1988). Recently, Arsigny et al. (2007) proposed a Log-Euclidean metric and showed its excellent theoretical and computational properties. Dryden et al. (2009) compared various metrics of the space of SPD matrices and their properties.
To the best of our knowledge, this is the first paper to develop an intrinsic local polynomial regression (ILPR) model for estimating an intrinsic conditional expectation of a SPD matrix response, S, given a covariate vector x from a set of observations (x1, S1), ···, (xn, Sn), where the xi can be either univariate or multivariate. In practice, x can be the arc-length of a specific fiber tract (e.g., right internal capsule tract), the coordinates in the 3D imaging space, or demographic variables such as age. Important applications of ILPR include smoothing diffusion tensors along fiber tracts and smoothing diffusion and deformation tensor fields. Another application is quantifying the change of diffusion and deformation tensors as well as the inter-regional functional connectivity matrix across groups and over time.
Relative to the existing literature on the analysis of SPD matrices, we make several important contributions in this paper.
To account for the curved nature of the SPD space, we propose the ILPR method for estimating the intrinsic conditional expectation of random SPD responses given the covariate. We also derive an approximation of a cross-validation method for bandwidth selection.
Theoretically, we compare the trace metric and the Log-Euclidean metric and establish the asymptotic properties of the ILPR estimators corresponding to each metric.
Theoretically and numerically, we examine the effect that the use of different metrics has on statistical inference in the SPD space.
The rest of the paper is organized as follows. In Section 2, we develop the ILPR method and a cross-validated bandwidth method for nonparametric analysis of random SPD matrix-valued data. In Section 3, we compare the trace metric and the Log-Euclidean metric and derive their ILPR estimators. We investigate the asymptotic properties of the estimators proposed under the Log-Euclidean metric and the estimators under the trace metric in Sections 4.1 and 4.2, respectively. We examine the finite sample performance of the ILPR estimators via simulation studies in Section 5. We analyze a real data set to illustrate a real-world application of the proposed ILPR method in Section 6 before offering some concluding remarks in Section 7.
2. Intrinsic Local Polynomial Regression for SPD Matrices
In this section, we develop a general framework for using intrinsic local polynomial regression in the analysis of SPD matrices and will examine two examples in Section 3. Let Sym+(m) and Sym(m) be, respectively, the set of m × m SPD matrices and the set of m × m symmetric matrices with real entries. The space Sym(m) is a Euclidean space with the Frobenius metric (or Euclidean inner product) given by tr(A1A2) for any A1, A2 ∈ Sym(m), whereas Sym+(m) is a Riemannian manifold, which will be detailed below. There is a one-to-one correspondence between Sym(m) and Sym+(m) through matrix exponential and logarithm. For any matrix A ∈ Sym(m), its matrix exponential is given by . Conversely, for any matrix S ∈ Sym+(m), there is a log(S) = A ∈ Sym(m) such that exp(A) = S.
Standard nonparametric regression models for responses in the Euclidean space estimate E(S|X = x). However, for a random S in a curved space, one cannot directly define the conditional expectation of S given X = x with the usual expectation in Euclidean space. We are interested in answering the following question.
(Q1) How do we define an intrinsic conditional expectation of S at each x, denoted by D(x), in Sym+(m)?
To appropriately define D(x), we review some basic facts about the geometrical structure of Sym+(m) near D(x) (Lang, 1999; Terras, 1988). See Figure 1 for a graphical illustration. We first introduce the tangent vector and tangent space at D(x) in Sym+(m). For a small scalar δ > 0, let C(t) be a differentiable map from (−δ, δ) to Sym+(m) passing through C(0) = D(x). A tangent vector at D(x) is defined as the derivative of the smooth curve C(t) with respect to t evaluated at t = 0. The set of all tangent vectors at D(x) forms the tangent space of Sym+(m) at D(x), denoted as TD(x)Sym+(m), which can be identified with Sym(m). The TD(x)Sym+(m) is equipped with an inner product 〈·, ·〉, called a Riemannian metric, which varies smoothly from point to point. For instance, one may use the Frobenuis metric as a Riemannian metric. Two additional Riemannian metrics for Sym+(m) will be given in Section 3. For a given Riemannian metric, we can calculate 〈U, V 〉 for any U and V on TD(x)Sym+(m) and then we can calculate the length of a smooth curve C(t): [t0, t1] → Sym+(m), which equals , where Ċ(t) is the derivative of C(t) with respect to t. A geodesic is a smooth curve on Sym+(m) whose tangent vector does not change in length or direction as one moves along the curve. For a U ∈ TD(x)Sym+(m), there is a unique geodesic, denoted by γD(x)(t; U), whose domain contains [0, 1], such that γD(x)(0; U) = D(x) and γ̇D(x)(0; U) = U. The Riemannian exponential mapping ExpD(x): TD(x)Sym+(m) → Sym+(m) of the tangent vector U is defined as ExpD(x)(U) = γD(x)(1; U). The inverse of the Riemannian exponential map is called the Riemannian logarithmic map from Sym+(m) to a vector in TD(x)Sym+(m). Finally, the shortest distance between two points D1(x) and D2(x) in Sym+(m) is called the geodesic distance between D1(x) and D2(x), denoted as g(D1(x), D2(x)), which satisfies
Fig. 1.
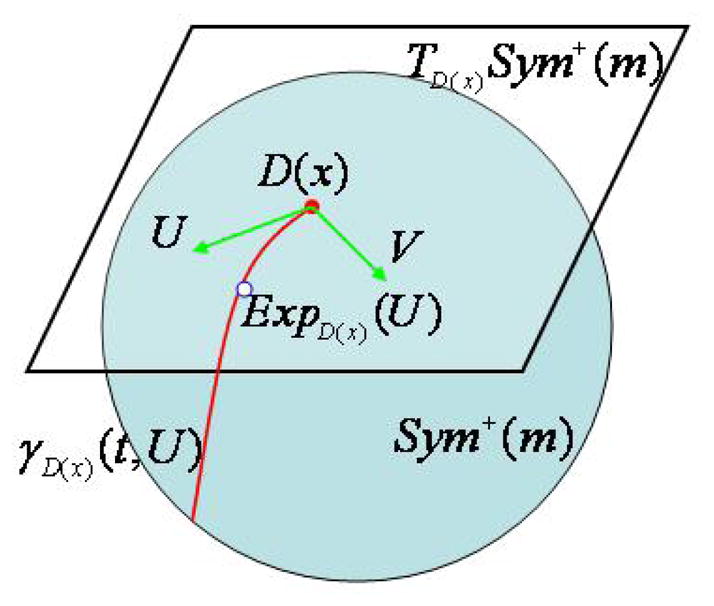
Graphical illustration of the geometrical structure of Sym+(m) near D(x).
| (1) |
We define
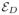 (X) to be LogD(X)(S) in TD(X)Sym+(m). Statistically,
(X) to be LogD(X)(S) in TD(X)Sym+(m). Statistically,
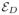 (X) can be regarded as the residual of S relative to D(X). Let vecs(C) = (c11, c21, c22, ···, cm1, ···, cmm)T be an m(m+1)=2×1 vector for any m×m symmetric matrix C = (cij). Thus, the intrinsic conditional expectation of S at X = x is defined as D(x) ∈ Sym+(m) such that
(X) can be regarded as the residual of S relative to D(X). Let vecs(C) = (c11, c21, c22, ···, cm1, ···, cmm)T be an m(m+1)=2×1 vector for any m×m symmetric matrix C = (cij). Thus, the intrinsic conditional expectation of S at X = x is defined as D(x) ∈ Sym+(m) such that
| (2) |
where Om is the m × m matrix with all elements zeros and the expectation is taken componentwise with respect to the multivariate random vector vecs(LogD(x)(S)). In fact, (2) characterizes intrinsic means (Bhattacharya and Patrangenaru, 2005).
Suppose that (xi, Si), i = 1, ···, n is an independent and identically distributed random sample, where Si ∈ Sym+(m). For notational simplicity, we focus on a univariate covariate throughout the paper. We are interested in using the observed data {(xi, Si), i = 1, ···, n} to estimate D(X) defined in (2) at each X = x0. By ignoring the Riemannian metric introduced in TD(X)Sym+(m), we can directly minimize a weighted least square criterion based on the metric related to the regular Frobenius inner product, which is given by
| (3) |
In (3), Kh(u) = K(u/h)h−1, in which h is a positive scalar, and K(·) is a kernel function such as the Epanechnikov kernel (Fan and Gijbels, 1996; Wand and Jones, 1995). However, it is unclear whether the estimate, which minimizes Ln(D(x0)), is truly consistent or not. Therefore, we are interested in solving the second question below.
(Q2) How do we use the observed data to consistently estimate D(X) in (2) at each X = x0?
For a specific Riemannian metric, we consider estimating D(X) at X = x0 by minimizing a weighted intrinsic least square criterion, denoted by Gn(D(x0)) given by
| (4) |
Directly minimizing Gn(D(x0)) with respect to D(x0) leads to a weighted intrinsic mean of S1, ···, Sn ∈ Sym+(m) at x0, denoted by D̂I(x0) (Bhattacharya and Patrangenaru, 2005). It will be shown below that D̂I(x0) is truly a consistent estimate of D(x0).
Local polynomial regression has received extensive attention for the nonparametric estimation of regression functions when both response and covariate are in Euclidean space Fan and Gijbels (1996); Wand and Jones (1995). However, little has been done on developing local polynomial regression when the response is in a Riemannian manifold and the covariates are in Euclidean space. Therefore, we are interested in solving a third question below.
(Q3) How do we define the intrinsic local polynomial regression for estimating D(X) in (2) at each X = x0?
We propose the intrinsic local polynomial regression for estimating D(X) at X = x0 as follows. Since D(x) is in the curved space, we cannot directly expand D(x) at x0 by using a Taylor’s series expansion. Instead, we consider the Riemannian logarithmic map of D(x) at D(x0) in TD(x0)Sym+(m). Let Im be an m × m identity matrix. Since LogD(x0)(D(x)) for different x0 are in different tangent spaces, we may transport them from TD(x0)Sym+(m) to the same tangent space TImSym+(m) through a parallel transport given by
That is, we have
| (5) |
where is the inverse map of φD(x0)(·). Moreover, since Y (x0) = φD(x0)(Om) = Om and Y (x) are in the same space TImSym+(m), we expand Y (x) at x0 by using the Taylor’s series expansion as follows:
| (6) |
where k0 is an integer and Y (k)(x) is the k–th derivative of Y (x) with respect to x divided by k!. Equivalently, D(x) can be approximated by
| (7) |
where α(x0) contains all unknown parameters in {D(x0), Y (1)(x0), ···, Y (k0)(x0)}.
To estimate α(x0), we substitute the approximation of D(x) in (7) into (4) to obtain Gn(α(x0)), which is given by
| (8) |
Subsequently, we calculate an intrinsic weighted least square estimator of α(x0) defined by
| (9) |
Then we can calculate D(x, α̂I(x0; h), k0), denoted by D̂I(x, h), as an intrinsic local polynomial regression estimator (ILPRE) of D(x). When k0 = 0, D(x, α̂I(x0; h), 0) is exactly the intrinsic local constant estimator of D(x0) considered in Davis et al. (2010).
We propose using a leave-one-out cross validation method for bandwidth selection due to its conceptual simplicity. Let be the estimate of D(xi) obtained by minimizing Gn(α(xi)) with (xi, Si) deleted for a given bandwidth h and all i. The cross-validation score is defined as follows:
| (10) |
The optimal h, denoted by ĥ, can be obtained by minimizing CV(h). However, since computing for all i can be computationally prohibitive, we suggest to use the first-order approximation of CV(h), whose details will be given below under each specific metric. Although it is possible to develop other bandwidth selection methods, such as plug-in and bootstrap methods (Rice, 1984; Park and Marron, 1990; Hall et al., 1992; Hardle et al., 1992), we must deal with additional computational and theoretical challenges, which will be left for future research.
3. ILPR under Log-Euclidean Metric and Trace Metric
As discussed in Dryden et al. (2009), various metrics can be defined for tangent vectors on TD(x)Sym+(m). To assess the effect of different metrics on ILPREs, we develop ILPR under two commonly used metrics, including the Log-Euclidean metric and the trace metric.
3.1. Log-Euclidean Metric
In this section, we review some basic facts about the theory of the Log-Euclidean metric, details of which have been given in Arsigny et al. (2007). We introduce the notation ‘L’ into some necessary quantities under the Log-Euclidean metric. We use exp(.) and log(.) to represent the matrix exponential and the matrix logarithm, respectively, whereas we use Exp and Log to represent the Riemannian exponential and logarithm maps, respectively. Let ∂D(x) log.(U) be the differential of the matrix logarithm at D(x) ∈ Sym+(m) acting on an infinitesimal displacement U ∈ TD(x)Sym+(m) (Arsigny et al., 2007). The Log-Euclidean metric on Sym+(m) is defined as
| (11) |
where U and V are in TD(x)Sym+(m). The geodesic γD(x),L(t, U) is given by exp(log(D(x)) + t∂D(x) log.(U)) for any t ∈ R. Let ∂log(D(x)) exp. (A) be the differential of the matrix exponential at log(D(x)) ∈ Sym(m) acting on an infinitesimal displacement A ∈ Tlog(D(x))Sym(m) (Arsigny et al., 2007). The Riemannian exponential and logarithm maps are, respectively, given by
| (12) |
The geodesic distance between D(x) and S is uniquely given by
| (13) |
We consider two SPD matrices D(x) and D(x0). For any UD(x0)∈ TD(x0)Sym+(m), the parallel transport φD(x0),L: TD(x0)Sym+(m) → TImSym+(m) is defined by
| (14) |
Combining (12) and (14) yields
| (15) |
In this case,
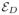 (X) = log(S) − log(D(X)) and E{log(S)|X = x} = log(D(x)).
(X) = log(S) − log(D(X)) and E{log(S)|X = x} = log(D(x)).
Let vec(A) = (a11, …, a1m, a21, …, a2m, ···, am1, ···, amm)T be the vectorization of an m×m matrix A = (aij). Under the Log-Euclidean metric, Gn(D(x0)) in (4) can be written as
| (16) |
To compute the ILPR estimator, we use the Taylor’s series expansion to expand log(D(x)) at x0 as follows:
| (17) |
where αL(x0) contains all unknown parameters in log(D(x0))(k) for k = 0, ···, k0. We compute α̂IL(x0; h) by minimizing Gn(DL(x, αL(x0), k0)). It can be shown that α̂IL(x0; h) has the explicit expression as
| (18) |
where
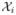 (x) = (1, (xi − x), ···, (xi − x)k0)T. By substituting α̂IL(x0; h) into DL(x, αL(x0), k0), we have D̂IL(x; h, k0) = DL(x, α̂IL(x0; h), k0).
(x) = (1, (xi − x), ···, (xi − x)k0)T. By substituting α̂IL(x0; h) into DL(x, αL(x0), k0), we have D̂IL(x; h, k0) = DL(x, α̂IL(x0; h), k0).
Let ek0+1,i be the (k0 + 1) unit vector having 1 in the i-th entry and 0 elsewhere. Let . The cross-validation score CV(h) can be simplified as follows:
| (19) |
Replacing ai(xi) in (19) by the average of a1(x1), ···, an(xn), we can get the generalized cross-validation (GCV) score as follows:
| (20) |
Without special saying, for the Log-Euclidean metric, we use GCV(h) to select the bandwidth throughout this paper.
3.2. Trace Metric
We review some basic facts about the theory of trace metric (Schwartzman, 2006; Lang, 1999; Terras, 1988; Fletcher et al., 2004; Batchelor et al., 2005; Pennec et al., 2006). We add the notation of ‘T’ into some necessary geometric quantities under the trace metric. Under the trace metric, an inner product of U and V in TD(x)Sym+(m) is defined as
| (21) |
The geodesic γD(x),T (t; U) is given by G(x) exp(tG(x)−1UG(x)−T)G(x)T for any t, where G(x) is any square root of D(x) such that D(x) = G(x)G(x)T. The Riemannian exponential and logarithm maps are, respectively, given by
| (22) |
The geodesic distance between D(x) and S, denoted by gT (D(x), S), is given by
| (23) |
where S1/2 is any square root of S.
We consider two SPD matrices D(x) and D(x0) = G(x0)G(x0)T. For any UD(x0)∈ TD(x0)Sym+(m), the parallel transport φD(x0),T is defined by
| (24) |
Thus, combining (22) and (24) yields
| (25) |
In this case,
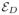 (X) = log(G(X)−1SG(X)−T).
(X) = log(G(X)−1SG(X)−T).
To compute the ILPR estimator, we use the Taylor’s series expansion to expand Y (x) at x0 as follows:
| (26) |
where αT (x0) contains all unknown parameters in G(x0) and Y (k)(x0) for k = 1, ···, k0. Thus, we can compute α̂IT (x0; h) by minimizing Gn(αT (x0)). Under the trace metric, minimizing Gn(αT (x0)) is computationally challenging when k0 > 0, since Gn(αT (x0)) is not convex and may have multiple local minimizers. Thus, standard gradient methods, which strongly depend on the starting value of αT (x0), do not perform well for optimizing Gn(αT (x0)) when k0 > 0. Hence, we develop an annealing evolutionary stochastic approximation Monte Carlo algorithm (see Liang (2010) for good discussion) for computing α̂IT (x0; h). Details can be found in the supplementary document.
To simplify the computation of CVT (h), we suggest the first-order approximation to CVT (h) as follows:
| (27) |
where D̂IT (x; h, k0) = DT (x, α̂IT (x0; h), k0). The CVT (h) is close to Akaike’s information criterion (AIC) (Sakamoto et al., 1999) and pn(h) can be regarded as the number of degrees of freedom. The explicit form of pn(h) is presented in the supplementary document.
4. Asymptotic Properties
We derive the asymptotic properties of ILPREs, such as asymptotic normality, under the Log-Euclidean and trace metrics. Furthermore, we systematically compare the intrinsic local constant and linear estimators under each metric and between the two metrics.
4.1. Log-Euclidean Metric
Under the Log-Euclidean metric, ILPRE is almost equivalent to the LPR estimator for multivariate response in Euclidean space. Thus, we can generalize the existing theory of the local polynomial regression estimator (Fan and Gijbels, 1996; Wand and Jones, 1995). Moreover, we only present the consistency and asymptotic normality of ILPRE for interior points, since the asymptotic properties of ILPRE for boundary points are similar to those for interior points in Euclidean space (Fan and Gijbels, 1996).
To proceed, we need some additional notation. Let a⊗2 = aaT for any vector or matrix a and Iq be an identity matrix of size q = m(m + 1)/2. Let
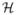 = diag(1, h, ···, hk0) ⊗ Iq. Let u = (u1, ···, uk0)T and v = (v1, ···, vk0)T be k0 × 1 vectors, where uk = ∫xkK(x)dx and vk = ∫xkK(x)2dx for k ≥ 0. Let
= diag(1, h, ···, hk0) ⊗ Iq. Let u = (u1, ···, uk0)T and v = (v1, ···, vk0)T be k0 × 1 vectors, where uk = ∫xkK(x)dx and vk = ∫xkK(x)2dx for k ≥ 0. Let
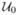 = (ui+j) and
= (ui+j) and
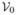 = (vi+j) for 0 ≤ i, j ≤ k0 be two (k0 + 1) × (k0 + 1) matrices for 0 ≤ i, j ≤ k0. Let fX(x) and
be the marginal density function of X and its first-order derivative with respect to x, respectively. We define
= (vi+j) for 0 ≤ i, j ≤ k0 be two (k0 + 1) × (k0 + 1) matrices for 0 ≤ i, j ≤ k0. Let fX(x) and
be the marginal density function of X and its first-order derivative with respect to x, respectively. We define
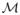 (x0; h) = (
(x0; h) = (
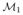 (x0; h)T, ···,
(x0; h)T, ···,
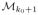 (x0; h)T)T, in which we have
(x0; h)T)T, in which we have
We have the following results, whose proof is similar to that of Theorem 2 in the supplementary document.
Theorem 1
Suppose that x0 is an interior point of fX(.). Under the Log-Euclidean metric and conditions (C1)-(C4) in the appendix, we have the following results.
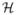 {α̂IL(x0; h) – αL(x0)} converges to 0 in probability as n → ∞.
{α̂IL(x0; h) – αL(x0)} converges to 0 in probability as n → ∞.-
For k0 = 0, under an additional condition (C10) in the appendix and that is continuous in a neighborhood of x0, we have
(28) where with
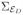 (x) = Cov(vecs[log(S) − log{D(x)}]|X= x) and →L denotes convergence in distribution.
(x) = Cov(vecs[log(S) − log{D(x)}]|X= x) and →L denotes convergence in distribution. -
For k0 > 0, under the conditions of Theorem 1 (ii), we have
(29) where .
Theorem 1 delineates the asymptotic properties of α̂IL(x0; h) for k0 ≥ 0, which covers the asymptotic properties of the intrinsic local constant and linear estimators of D(x0) as k0 = 0, 1. In particular, the asymptotic bias and variance of D̂IL(x0; h, 0) are closely related to those of the Nadaraya-Watson estimator when both response and covariate are in Euclidean space (Fan, 1992). Since vecs(log{D̂IL(x0; h, k0)}) is a subvector of α̂IL(x0; h), we calculate the asymptotic average mean squared error (AMSE) conditional on x = {x1, …, xn} as
Furthermore, for a given weight function w(x), we may consider a constant bandwidth that minimizes the asymptotic average mean integrated squared error (AMISE) as
Finally, we can calculate the asymptotically optimal local bandwidth, denoted by hopt,L(x0; k0), for minimizing AMSE(log{D̂IL(x0; h, k0)}) and the optimal bandwidth, denoted by hopt,L(k0), for minimizing AMISE(log{D̂IL(.; h, k0)}).
By Theorem 1 (iii), AMSE(log{D̂IL(x0; h, 0)}) equals . For the intrinsic local linear estimator, AMSE(log{D̂IL(x0; h, 1)}) is given by . Intrinsic local constant and linear estimators have the same asymptotic covariance and their differences are concerned only with their biases. The local constant estimator has one more term , which depends on the marginal density fX(.). Subsequently, we can get the optimal bandwidths, whose detailed expression can be found in the supplementary document.
4.2. Trace Metric
Under the trace metric, since ILPRE is different from the LPR estimator for multivariate response in Euclidean space, we study the consistency and asymptotic normality of ILPRE for both interior and boundary points.
We need to introduce some notation for discussion. Consider a function
| (30) |
where G is an m×m lower triangle matrix, S ∈ Sym+(m), and Y ∈ Sym(m). Let α = (αG, αY), in which αG = vecs(G) and αY = vecs(Y). Let ∂αψ(S, G, Y) and be the first and second order derivatives of ψ(S, G, Y) with respect to α, respectively. By substituting Y (X) into ∂αψ(S, G, Y) and and using the decomposition of α = (αG, αY), we define
where the expectation is taken with respect to S given X = x. Let 1k0 be a k0 × 1 column vector with all elements ones. Let
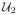 = (ui+j) and
= (ui+j) and
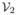 = (vi+j) for 1 ≤ i, j ≤ k0 be two k0 × k0 matrices. We define
= (vi+j) for 1 ≤ i, j ≤ k0 be two k0 × k0 matrices. We define
and w(x0; h) = (w2(x0; h)T, ···, wk0+1(x0; h)T), in which
Finally, let αT (x) = (vecs{G(x)}T, vecs{Y (1)(x)}T, ···, vecs{Y (k0)(x)}T)T.
Theorem 2
Suppose that x0 is an interior point of fX(·). Under the trace metric and conditions (C1)–(C8) in the appendix, we have the following results.
There exist solutions α̂IT (x0; h) to equation ∂Gn(αT (x0))/∂ αT (x0) = 0 such that
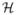 {α̂IT (x0; h) – αT (x0)} converges to 0 in probability as n → ∞.
{α̂IT (x0; h) – αT (x0)} converges to 0 in probability as n → ∞.-
For k0 = 0, if is continuous in a neighborhood of x0, then we have
(31) where .
-
For k0 > 0, if condition (C9) in the appendix is also true, we have
(32) where and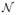 (x) and
(x) and
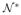 (x) are, respectively, given by
(x) are, respectively, given by
Theorem 2 delineates the asymptotic bias, covariance, and asymptotic normality of α̂IT (x0; h) for k0 ≥ 0. Based on Theorem 2, it is straightforward to derive the asymptotic bias, covariance, and asymptotic normality of D̂IT (x0; h, k0) for k0 ≥ 0. Moreover, to have a direct comparison between the trace and Log-Euclidean metrics, we calculate the asymptotic biases and covariances of log{D̂IT (x0; h, k0)} under these two metrics. Subsequently, we calculate AMSE(log{D̂IT (x0; h, k0)}) and AMISE(log{D̂IT (.; h, k0)}) for a given weight function w(x). Minimizing AMSE(log(D̂IT (x0; h, k0))) and AMISE(log(D̂IT (x0; h, k0))), respectively, leads to the optimal bandwidths, whose detailed expressions can be found in the supplementary document.
We are interested in comparing the asymptotic properties of the intrinsic local constant D̂IT (x0; h, 0) and the local linear estimator D̂IT (x0; h, 1). It follows from the delta method that AMSE(log{D̂IT (x0; h, 0)}) can be approximated as
| (33) |
where GD(x0) = {∂vec(log(G(x0)⊗2))/∂vecs(G(x0))T}T. The asymptotic bias and variance of D̂IT (x0; h, 0) are similar to those of the Nadaraya-Watson estimator when response is in Euclidean space (Fan, 1992). For the intrinsic local linear estimator, .
We consider ILPRE near the edge of the support of fX(x). Without loss of generality, we assume that the design density fX(.) has a bounded support [0, 1] and consider the left-boundary point x0 = dh for some positive constant d. The asymptotic consistency and normality of IL-PRE are valid for the boundary points after slight modifications on the definitions of uk and vk. Denote
and
. Correspondingly, u,
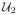 ,
,
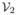 ,
,
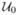 and
and
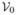 are replaced by ud,
are replaced by ud,
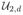 ,
,
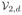 ,
,
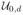 and
and
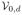 , respectively. Let ck0+2,d = (uk0+2,d, ···, u2k0+1,d)T and
, respectively. Let ck0+2,d = (uk0+2,d, ···, u2k0+1,d)T and
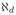 (0+) = (uk0+1,dΨ2(0+), ck0+2,d ⊗ Ψ3(0+))Tvecs(Y
(k0+1)(0+)). For the boundary points, we have the following asymptotic results under the trace metric.
(0+) = (uk0+1,dΨ2(0+), ck0+2,d ⊗ Ψ3(0+))Tvecs(Y
(k0+1)(0+)). For the boundary points, we have the following asymptotic results under the trace metric.
Theorem 3
Suppose that x0 = dh is a left boundary point of fX(.). Under the trace metric and conditions (C1)–(C8) in the appendix, we have the following results.
There exist solutions, denoted by α̂IT (x0; h), to the equation ∂Gn(αT (x0))/∂αT (x0) = 0 such that
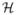 {α̂IT (x0, h) – αT (x0)} converges to 0 in probability as n → ∞.
{α̂IT (x0, h) – αT (x0)} converges to 0 in probability as n → ∞.-
For k0 = 0, conditioning on x = {x1, ···, xn}, we have
(34) where .
-
For k0 > 0, if condition (C9) in the appendix is also true, conditioning on x = {x1, ···, xn}, we have
(35) where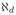 (0+) and
are, respectively, given by
(0+) and
are, respectively, given by
It follows from Theorem 3 (ii) and (iii) that when x0 is at the boundary, the asymptotic average mean squared errors of intrinsic local constant and linear estimators are, respectively, AMSE(log{D̂IT (0+; h, 0)}) = Op(h2 + n−1h−1) and AMSE(log{D̂IT (0+; h, 1)}) = Op(h4 + n−1h−1). The rate of convergence for the intrinsic local constant estimator at boundary points is slower than that at interior points, and thus the intrinsic local constant estimator suffers from the well-known boundary effects. However, the intrinsic local linear estimator adapts automatically at the boundary points and its rate of convergence is not influenced by the location of points. Thus, the intrinsic local linear (or polynomial) estimators share the same property of automatic adaptation to the boundary points as the local polynomial estimators in Euclidean space (Fan and Gijbels, 1996).
5. Simulation
We conducted four sets of Monte Carlo simulations to examine the finite sample performance of ILPREs for SPD matrices under different metrics and noise distributions. It should be emphasized that these simulation studies are intended to have wide applications of SPDs, and thus they are deliberately not limited to DTI.
We set m = 3 and assumed that the true SPD matrix function has the following form:
We considered three noise distributions including a Riemannian log-normal distribution, a log-normal distribution, and the Rician distribution. We used the Rician noise to simulate the ideal noise in diffusion tensor imaging. The three noise models are given as follows:
(a) Riemannian log normal model: Si = G(xi) exp(εi)G(xi)T follows the Riemannian log normal distribution, where D(xi) = G(xi)⊗2 and εi ∈ Sym(3) follows a symmetric matrix variate normal distribution N(0, Σ), in which Σ is a covariance matrix (Schwartzman, 2006).
(b) Log normal model: log(Si) follows a symmetric matrix variate normal distribution N[log{D(xi)}, Σ].
(c) Rician noise model: this noise model is commonly used to simulate ideal noise in diffusion weighted images (Zhu et al., 2007). The diffusion-weighted signal was simulated for 31 gradient directions rk, k = 1, ···, 31 with b-factor bk = 1000s/mm and four baselines with bk = 0s/mm for k = 32, ···, 35. The baseline signal intensity W0 was set at 1500. For a given diffusion tensor D(xi), εR,k and εI,k were independently simulated from a Gaussian random generator with mean zero and standard deviation 60. The diffusion-weighted signal was calculated as for k = 1, ···, 35. Subsequently, the weighted least squares estimate was used to estimate Si (Zhu et al., 2007).
For each simulated data set, we considered three metrics including the trace metric, the Log-Euclidean metric, and the Euclidean metric. For the trace and Log-Euclidean metrics, we calculated the intrinsic local constant and linear estimators developed above for each data set. By following the arguments in Pasternak et al. (2010), we employed the Euclidean metric for estimated diffusion tensors. Under the Euclidean metric, we applied the standard local constant and linear regression methods to estimate the SPD matrix function for each simulated data set, while the bandwidth was selected by using its corresponding generalized cross-validation method. For comparison, we also included a tensor spline method (Barmpoutis et al., 2007) based on the trace metric.
We first generated n = 50 design points xi, i = 1, ···, 50 independently from a N (0, 0. 25) distribution. Then we calculated D(xi) and used it to simulate Si according to one of the three noise distributions (a)–(c). Unless stated otherwise, the covariance matrix 3 for the noise models (a) and (b) was set as follows:
| (36) |
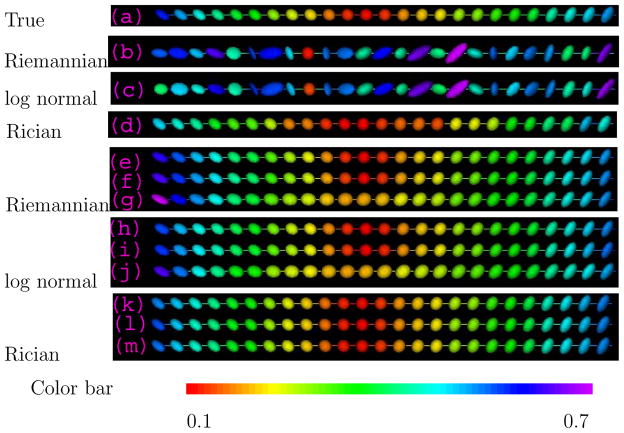
Figure 2(a)–(d) presents the true SPD matrix data and a set of simulated data {(xi, Si): i = 1, ···, 50} under the three noise models. Each SPD matrix Si at the point xi is geometrically represented by an ellipsoid. In this representation, the lengths of the semiaxes of the ellipsoid equal the square root of the eigenvalues of a SPD matrix, while the eigenvectors define the direction of the three axes. In DTI, the ellipsoidal representation is used to represent the local brownian motion of water molecules in the brain. Isotropic diffusion is represented by a sphere, while anisotropic diffusion is represented by an anisotropic ellipsoid. We simulated 100 data sets for each scenario. Note that the Rician noise level is visually less variable than the relatively high levels of the other two.
Fig. 2.
Ellipsoidal representations of (a) the true SPD matrix data along the design points; simulated SPD matrix data along the design points under the three different noise models: (b) Riemannian log normal, (c) log normal and (d) Rician noise models; and estimated SPD matrix data along the design points using three smoothing methods: (e), (h) and (k): ILPR under the trace metric; (f), (i) and (l): ILPR under the Log-Euclidean metric; and (g), (j) and (m): LPR under the Euclidean metric; and under the three different noise models: (e)–(g): Riemannian log normal model; (h)–(j): log normal model; and (k)–(m): Rician noise model, colored with FA values defined in (37).
To compare different smoothing methods for SPD matrices under different scenarios, we calculated two summary statistics including an Average Geodesic Distance (AGD) over all design points and a Local Average Geodesic Distance (LAGD) at each design point. Specifically, AGD is defined as , where x̂i) is an estimated D(xi) based on a specific smoothing method. At each sample point xi, LAGD is given by , where D̂(j)(xi) is the estimated SPD matrix at xi based on the j-th simulated replication. Although we chose all the three metrics for calculating AGD and LAGD, we only present those based on the Euclidean metric for the sake of space. The results of AGD and LAGD for the other two metrics are included in the supplementary document.
5.1. Simulation 1
The first set of simulations compared the finite sample performance of the intrinsic local linear estimators under different metrics and noise distributions. Figure 2(e)–(m) displays a set of the estimated SPD functions using local linear regression estimators under the three metrics for the three different noise models. Inspecting Figure 2(k)–(m) reveals that under the Rician noise model, all three metrics perform well in recovering the true SPD function. This is not surprising given the relatively low noise level shown in Figure 2(d). However, for the other two noise models, our intrinsic local linear regression methods visually outperform the local linear regression based on the Euclidean metric. In particular, a clear swelling effect is observed for the Euclidean metric (Figure 2(g) and (j)). This indicates the importance of appropriate metric selection according to the distribution of a specific SPD data set, which is partially in agreement with the suggestion given in Pasternak et al. (2010). However, our findings also suggest that both the trace and Log-Euclidean metrics are appropriate for the nonparametric analysis of SPD matrices for all three noise distributions. This also agrees with the findings in the medical imaging literature (Fletcher and Joshi, 2007; Batchelor et al., 2005; Pennec et al., 2006) on the interpolation and extrapolation of diffusion tensor fields. It should be noted that the simulation studies in Pasternak et al. (2010) solely focus on the effect of metric on the estimated diffusion tensors and their associated scalar measures, such as the apparent diffusion coefficient. Thus, the recommendation in Pasternak et al. (2010) may not apply to the nonparametric analysis of SPD matrices.
5.2. Simulation 2
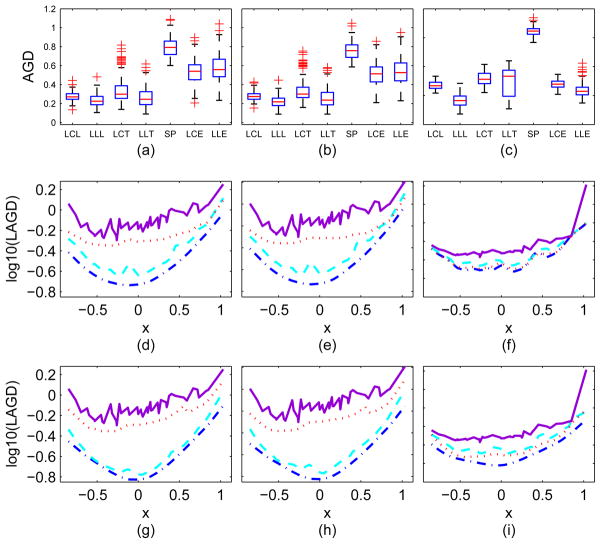
The second set of simulations compared local constant estimators with local linear estimators under the three metrics and the three noise distributions. In addition, we also compared all local regression methods with the tensor spline estimators in Barmpoutis et al. (2007). Inspecting Figures 3 reveals the following findings. As expected, under all metrics, the local linear estimator is superior to the local constant estimator. Also, our ILPREs outperform the corresponding estimators under the Euclidean metric and the tensor spline estimators under the noise models (a) and (b). For the Rician noise model, our ILPREs under the Log-Euclidean metric slightly outperform those under the trace and Euclidean metrics. Moreover, the local constant and linear estimators outperform the tensor spline estimators under all noise distributions. The variations of AGDs for ILPREs under the trace metric are larger than those under the Log-Euclidean metric under all three noise distributions. The U shape of the LAGD curves indicates that interior points have smaller LAGDs than those near the boundaries since there are more design points in the interior than at the boundaries.
Fig. 3.
Comparisons of the local constant and linear estimators under the three metrics and the tensor spline estimators under the three noise models. Panels (a)–(c) the boxplots of 1000×AGDs obtained from seven different estimators, where LCL, LCT, and LCE, respectively, represent the local constant estimators under the Log-Euclidean, trace and Euclidean metrics, where LLL, LLT, and LLE, respectively, represent the corresponding local constant and linear estimators under the metrics, and where SP represents the tensor spline estimator. Panels (d)–(f) of the second row show the log10(LAGD) curves based on LCL (dash-dotted line), LCT (dashed line), LCE (dotted line), and SP (solid line). Panels (g)–(i) of the third row show the log10(LAGD) curves based on LLL (dash-dotted line), LLT (dashed line), LLE (dotted line), and SP (solid line). The columns correspond to the three noise models: column 1: Riemannian log normal; column 2: log normal; and column 3: Rician.
5.3. Simulation 3
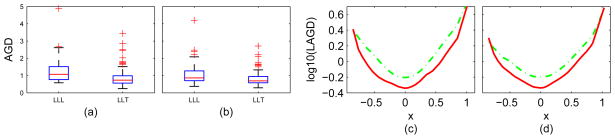
The third set of simulation studies compared the finite sample performance of the intrinsic local linear estimators under the trace, Log-Euclidean and Euclidean metrics and also tensor spline method in Barmpoutis et al. (2007) at a higher noise level. Specifically, we assumed Σ = 4Σ1 for the covariance matrix of N(0, Σ) in the noise models (a) and (b). At high noise levels, most local linear estimators cannot retain the positive definiteness under the Euclidean metric, while the tensor spline method does not converge. Thus, Figure 4 only presents the results under the trace and Log-Euclidean metrics. Inspecting this figure reveals that when the noise level is high, the intrinsic local linear estimators under the trace metric slightly outperform those under the Log-Euclidean metric under the noise models (a) and (b).
Fig. 4.
Comparison of the intrinsic local linear estimators under the Log-Euclidean and trace metrics for the first two noise models at a higher noise level: Panels (a) and (c): Riemannian log normal; Panels (b) and (d): log normal; Panels (a) and (b): the boxplots of AGDs for LLL and LLT; Panels (c) and (d): the log10(LAGD) curves of LLL and LLT. It shows that at a high noise level, the intrinsic local linear estimators under the trace metric slightly outperform those under the Log-Euclidean metric for the first two noise models.
5.4. Simulation 4
The fourth set of simulation studies examined the importance and effect of directly smoothing SPDs on some SPD-derived scalar summary measures under the three noise models. We considered a well-known scalar measure derived from a 3 × 3 SPD matrix, called fractional anisotropy (FA), which describes the variation of the three eigenvalues of a 3 × 3 SPD matrix. FA is a scalar value between zero (all eigenvalues are the same) and one (two eigenvlues equal 0) and given by
| (37) |
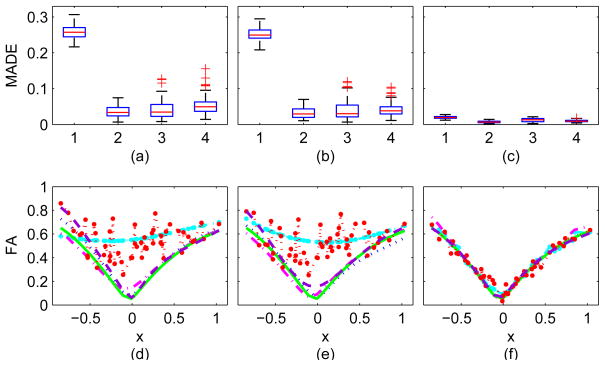
with eigenvalues λ1, λ2, λ3 and their average λ̄. We compared two different methods for smoothing FA’s, here referred to as method A and method B, respectively. The method A first calculates the FA’s from all SPD matrices and then uses the classic local linear regression in Euclidean space to smooth the FA’s. The method B first applies the intrinsic local linear estimator to smooth SPD matrices and then calculates smoothed FA curves based on the smoothed SPD matrices. We further divided method B into three methods according to smoothing methods for SPD matrices under three metrics: trace (method 2), Log-Euclidean (method 3) and Euclidean (method 4) metrics. We assessed each method’s performance via the Mean Absolute Deviation Error (MADE) defined by , where FA(xi) and are, respectively, the true and estimated FA values across all design points.
Figure 5 reveals that method B outperforms method A under the noise models (a) and (b). For the Rician noise model, methods A and B are fairly comparable, but method B based on the Log-Euclidean metric is slightly better. This may indicate the potential improvement gained by directly smoothing DT data over the post smoothing method A. Based on the medians of MADEs (see Figure 5(d)–(f)), method A cannot faithfully reconstruct the trend of the FA curve for the noise models (a) and (b), whereas method B can accurately estimate the FA curve and reveal its critical features such as the valley. It should be noted that the true FA value at the valley does not equal zero.
Fig. 5.
Boxplot of the MADE’s using the four smoothing methods 1–4 representing the first-fourth methods based on 100 replications for three noise models: (a) Riemannian log normal model; (b) log normal model; and (c) Rician model. Smoothed FA curves for the realizations with median MADE for three noise models: (d) Riemannian log normal model; (e) log normal model; and (f) Rician model. In panels (d)–(f), the raw FA curve is the dotted line with circle, true FA curve is the solid line, the estimated FA curve for the first method is the dash-dotted line with circle, the estimated FA curve for the second method is the dotted line, the estimated FA curve for the third method is dash-dotted line and the estimated FA curve for the fourth method is dashed line.
6. HIV Imaging Data
The aim of this analysis is to assess the integrity of white matter in human immunodeficiency virus (HIV) by using DTI and our IPLRE. This clinical study was approved by the Institutional Review Board of the University of North Carolina at Chapel Hill. A sample data set and the code for ILPRE along with its documentation will be accessible from the website http://www.bios.unc.edu/research/bias. We considered 46 subjects with 28 HIV+ subjects (20 males and 8 females whose mean age is 40.0 with SD 5.6 years) and 18 healthy controls (9 males and 9 females whose mean age is 41.2 with SD 7.4 years). Diffusion-weighted images and T1 weighted images were acquired for each subject. The diffusion tensor acquisition scheme includes 18 repeated measures of six non-collinear directions, (1,0,1), (−1,0,1), (0,1,1), (0,1,−1), (1,1,0), and (−1,1,0) at a b-value of 1000 s/mm2 and a b = 0 reference scan. Forty-six contiguous slices with a slice thickness of 2 mm covered a field of view (FOV) of 256 mm2 with an isotropic voxel size of 2 × 2 × 2 mm3. High resolution T1 weighted (T1W) images were acquired using a 3D MP-RAGE sequence. A weighted least square estimation method was used to construct the diffusion tensors (Zhu et al., 2007). Since in the previous DTI findings, the diffusion tensors in the splenium of the corpus callosum were found significantly different between the HIV+ and control groups, we examine the finite sample performance of our method by using this fiber tract. The tensors along the tract were extracted using methodology described in Zhu et al. (2010). Figure 6 displays the splenium of the corpus callosum and the ellipsoidal representation of the full tensors on that tract from one selected subject. This involves three steps: (i) registration and atlas construction, (ii) fiber tracking on the atlas and (iii) collection of tensor data on the atlas fiber tracts.
Fig. 6.
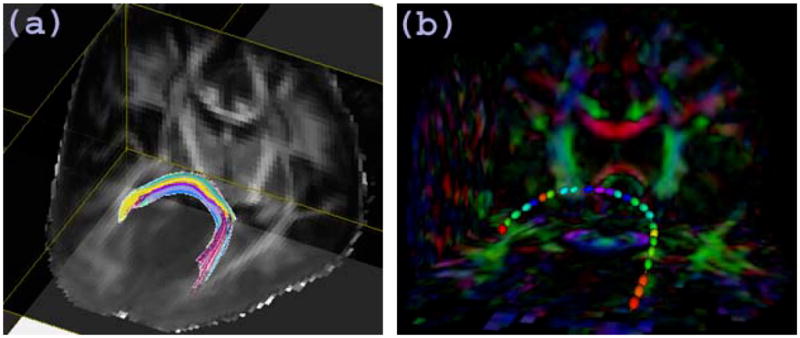
(a)The splenium of the corpus callosum in the analysis of HIV DTI data. (b)The ellipsoidal representation of full tensors colored with FA values on the fiber tract from a selected subject.
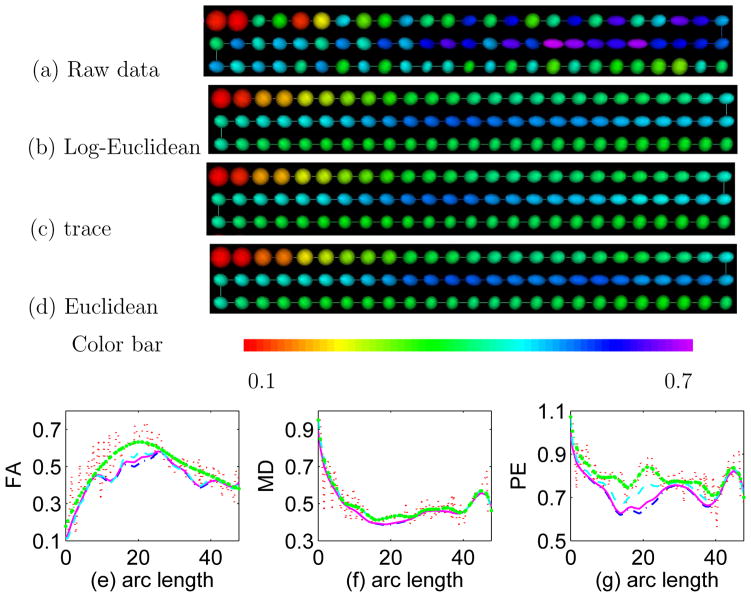
We calculated the intrinsic local linear estimator of the SPD matrices along this selected tract for each subject under the trace and Log-Euclidean metrics and also calculated the local linear estimator under the Euclidean metric. See Figure 7 for the raw and estimated tensors along the fiber tracts from one subject. It is observed from the ellipsoidal representation of diffusion tensor data (Figure 7(a)) that the data are noisy. Figure 7(b)–(e) show that the tensors are more spherical at the beginning with low FA values and more anisotropic in the middle part with high FA values. The methods under the three metrics reveal very similar trend of diffusion tensors changing along the fiber tract, especially in the first row and the last row. This agrees with our simulation results that for diffusion tensor data, all three metrics are comparable. However, some differences appear on the right side of the middle row. The estimated tensors in the middle row are very anisotropic when using the method under the Euclidean metric compared to the other two metrics.
Fig. 7.
(a) The ellipsoidal representations of the diffusion tensor data and estimated tensors using the intrinsic local linear regression under the (b) Log-Euclidean, (c) trace and (d) Euclidean metrics along the splenium of the corpus callosum, colored with FA values. The estimated tensors in the middle right part are more anisotropic using the method under the Euclidean metric. Each set of 3 rows in (a)–(d) represents one tract of tensors and the three rows are read from left to right in the top row, right to left in the middle row and then left to right in the bottom row. (e) FA’s, (f) MD’s and (g) PE’s derived from the raw tensor data (dot line) and estimated tensors using the intrinsic local linear regression under the trace (dash-dot line), Log-Euclidean (solid line) and Euclidean (dashed line) metrics as the function of arc-length along the splenium of the corpus callosum. Estimated FA, MD and PE function along the splenium of the corpus callosum by using the standard local linear regression for scalars (dotted line with circles).
In many applications, it is common to calculate some tensor-derived diffusion measures, including FA, the trace of a diffusion tensor, called MD, and the largest eigenvalue of a diffusion tensor, called PE, based on noisy diffusion tensor data and then apply standard statistical methods to directly carry out statistical inference on these diffusion measures. Since these scalar measures do not capture all information in the full diffusion tensor, they can decrease the sensitivity of detecting subtle changes of the white matter structure. Similar to the simulation of Section 5.4, we applied method A to directly smooth FA, MD and PE values along the selected tract and then we compared them with method B based on the trace, Log-Euclidean, and Euclidean metrics. Figure 7(e)–(g) shows that there is no large difference for methods B under the three metrics. Both methods A and B perform the same for smoothing MD data, whereas they perform differently for smoothing PE and FA curves, especially in the middle part from 10 to 25. This seems to be caused by that fact that FA and PE values are biased due to the well known ‘sorting’ bias in estimating the eigenvalues of DT (Zhu et al., 2007), whereas the estimated MD value is unbiased.
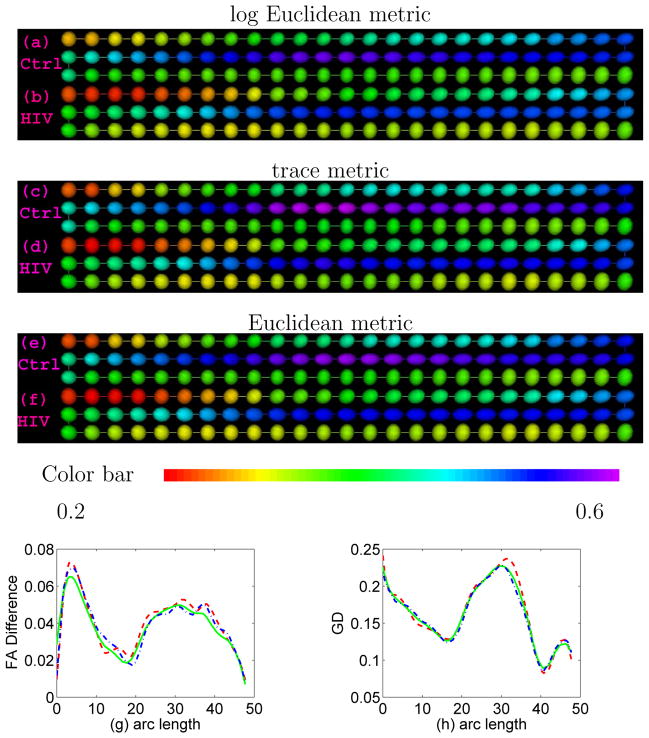
Finally, we estimated the mean diffusion tensor curve for each of the two groups: HIV and control groups. In order to detect meaningful group differences, registration is crucial. The 46 HIV DTI data used in our studies, including the splenium tracts and diffusion tensors on them, were registered in the same atlas space. Figure 8(a)–(f) displays the estimated mean diffusion tensors along the fiber tract for the two groups using the intrinsic local linear regression for SPD matrices under both the Log-Euclidean and trace metrics and also using the local linear regression for SPD matrices under the Euclidean metric. We can observe some obvious changes of diffusion tensors of HIV subjects along the splenium corpus callosum compared with those in the control group. We also calculated the differences of FA values derived from the estimated mean diffusion tensors, which corresponds to the color differences in Figure 8(g), and the geodesic distances between estimated mean tensors at each point along the tract in Figure 8(h). This result agrees with previous DTI findings that the spleninum of the corpus callosum has been detected as abnormal for the HIV group (Filippi et al. (2001) and Chen et al. (2009)).
Fig. 8.
Ellipsoidal representations of estimated mean tensors along the splenium of the corpus callosum for the control and HIV groups using the intrinsic local linear regression under the Log-Euclidean ((a) and (b)), trace ((c) and (d)) and Euclidean ((e) and (f)) metrics colored with FA values. Each set of 3 rows in (a)–(d) represents one tract of tensors and the three rows are read from left to right in the top row, right to left in the middle row and then left to right in the bottom row. (g) FA differences and (h) geodesic distances (GD) between the mean diffusion tensors of HIV and control groups along the splenium of the corpus callosum under the Log-Euclidean (the solid line), trace (the dashed line) and Euclidean (dash-dot line) metrics.
7. Conclusion and Discussion
We have systematically investigated the intrinsic local polynomial regression methods under the trace and Log-Euclidean metrics on the space of SPD matrices. Many issues still merit further research. The proposed cross validation bandwidth selector is straightforward and relatively simple to derive and implement for SPD matrix variate data. However, the relatively high variance of the cross validation bandwidth selector is regarded widely as an impediment to its good performance (Jones et al., 1996; Hardle et al., 1992). It would be great interest to develop variable bandwidth selection methods to capture complicated variations of SPD matrices in the covariate space and better bandwidth selection methods to reduce the variability of cross validation (Fan et al., 1996). From the average diffusion tensor curves for the HIV and control groups in Section 6, we can observe some obvious changes in diffusion tensors of HIV subjects along the spleninium corpus callosum compared with the control group. A topic of future interest should propose tests for comparing the differences across multiple groups of SPD curves by considering varying-coefficient models and additive models among others. The real applicability of the log normal and Riemannian log normal noise models remains unclear. It is of great interest to explore the fit of those noise models to real data in different applications.
Finally, the ILPR method proposed here and theory may be extended to other nonparametric methods (e.g., tensor splines) and manifold-valued data, such as directional data and rotation matrices. For instance, although we have compared our ILPR with Barmpoutis et al. (2007)’s tensor splines, it would be interesting to develop free-knot regression splines for SPD matrices and compare them with our ILPR both theoretically and numerically (Sangalli et al., 2009). Moreover, a smooth spline method based on unrolling and unwrapping procedures in Riemannian manifolds has been developed for fitting smooth curves to spherical data, rotation matrices, and planar landmark data (Jupp and Kent, 1987; Prentice, 1987; Kume et al., 2007). Development of other nonparametric methods, such as ILPR, for the analysis of manifold-valued data and examination of the asymptotic properties of nonparametric estimates under different metrics should be pursued in future research.
Supplementary Material
Acknowledgments
We thank the Editor, an Associate Editor, two referees, and Martha Skup for valuable suggestions, which helped to improve our presentation greatly. We are also thankful to Martin Styner, Pew-Thian Yap, and Zhexing Liu for their help with the visualizations. This work was supported in part by a National Science Foundation grant and National Institute of Health grants.
Appendix. Assumptions
The following assumptions are needed to facilitate development of our methods, although they are not the weakest possible conditions. We need some notation. Recall that ψ(S, G, Y) = gT (S, G exp(Y)GT)2 and α = (αG, αY), where G is an m × m lower triangle matrix, S ∈ Sym+(m), Y ∈ Sym(m), αG = vecs(G), and αY = vecs(Y). We define
-
(C1)
The kernel function K(.) is a continuous symmetric probability density function with bounded support, say [−1, 1].
-
(C2)
The regression function D(x) ∈ Sym+(m) has a continuous (k0 + 1)-th order derivative in a neighborhood of x0.
-
(C3)
The bandwidth h tends to zero and nh → ∞.
-
(C4)
The design density fX(.) is continuous in a neighborhood of x0 and fX(x0) > 0.
-
(C5)
The conditional density f(S|X = x) is continuous in a neighborhood of x0.
-
(C6)
and E[{∂αψS; G; Y (X))}⊗2|X = x] are continuous in a neighborhood of x0.
-
(C7)
The matrix is positive definite in a neighborhood of x0.
-
(C8)
Let ||. || be the L2 norm of a matrix, η0 be a lower triangle matrix, η1 ∈ Sym(m), and Uδ= {(η0, η1): ||η0||2 + ||η1||2 ≤ δ2}. As δ → 0,
are uniformly in x in a neighborhood of x0.
-
(C9)
There exists a b > 0 such that E{||∂αψ(S, G(x0), Y (X))||b+2|X = x} is bounded in a neighborhood of x0.
-
(C10)
The
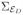 (x) = Cov{
(x) = Cov{
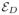 (X)|X = x} is continuous in a neighborhood of x0 and there exists a b > 0 such that E{||
(X)|X = x} is continuous in a neighborhood of x0 and there exists a b > 0 such that E{||
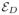 (X)||b+2|X = x} is bounded in a neighborhood of x0.
(X)||b+2|X = x} is bounded in a neighborhood of x0.
Remark
Assumptions (C1)–(C10) are standard conditions for ensuring the asymptotic properties of local polynomial estimators when x0 is an interior point of fX(·) (Fan and Gijbels, 1996; Wand and Jones, 1995). Some conditions can be released with additional technicalities of proofs. For instance, the bounded support restriction on K(·) in (C1) is not essential and can be removed if we put restriction on the tail of K(·). Condition (C2) ensures that Y (x) = log(G(x0) −1D(x)G(x0)−T), G(x), and log(D(x)) have a continuous (k0 + 1)-th order derivative in a neighborhood of x0. Moreover, assume that fX(.) has a bounded support [0, 1]. All assumptions can be easily modified when x0 is a boundary point, say left boundary point x0 = dh or right boundary point x0 = 1 − dh for some d > 0. For instance, we require that conditions (C2)–(C10) hold in the left neighborhood of 0 or the right neighborhood of 1. For condition (C2), we also need to introduce fX(0+) as x0 is the left boundary point and fX(1−) as x0 is the right boundary point. For condition (C7),
 (x) is also needed to make some modifications. For simplicity, we omit these details.
(x) is also needed to make some modifications. For simplicity, we omit these details.
References
- Anderson TW. Wiley Series in Probability and Statistics. 3. 2003. An introduction to multivariate statistical analysis. [Google Scholar]
- Arsigny V, FP, PX, AN Geometric means in a novel vector space structure on symmetric positive definite matrices. SIAM J Matrix Anal Appl. 2007;29:328–347. [Google Scholar]
- Barmpoutis A, Vemuri BC, Shepherd TM, Forder JR. Tensor splines for interpolation and approximation of dt-mri with applications to segmentation of isolated rat hippocampi. IEEE Transations on Medical Imaging. 2007;26:1537–1546. doi: 10.1109/TMI.2007.903195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. Mr diffusion tensor spectroscopy and imaging. Biophysical Journal. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batchelor P, Moakher M, Atkinson D, Calamante F, Connelly A. A rigorous framework for diffusion tensor calculus. Magnetic Resonance in Medicine. 2005;53:221–225. doi: 10.1002/mrm.20334. [DOI] [PubMed] [Google Scholar]
- Bhattacharya R, Patrangenaru V. Large sample theory of intrinsic and extrinsic sample means on manifolds-ii. Annals of Statistics. 2005;33:1225–1259. [Google Scholar]
- Chen YS, An HT, Zhu HY, Stone T, Smith JK, Hall C, Bullitt E, Shen DG, Lin WL. White matter abnormalities revealed by diffusion tensor imaging in non-demented and demented hiv+ patients. NeuroImage. 2009;47:1154–1162. doi: 10.1016/j.neuroimage.2009.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis BC, Bullitt E, Fletcher PT, Joshi S. Population shape regression from random design data. International Journal of Computer Vision. 2010;90:255–266. [Google Scholar]
- Dryden IL, Koloydenko A, Zhou D. Non-euclidean statistics for covariance matrices, with applications to diffusion tensor imaging. Annals of Applied Statistics. 2009;3:1102–1123. [Google Scholar]
- Fan J, Gijbels I. Local polynomical modelling and its applications. Cahpman and Hall; 1996. [Google Scholar]
- Fan J, Gijbels I, Hu T-C, Huang L-S. A study of variable bandwidth selection for local polynomial regression. Statist Sinica. 1996;6(1):113–127. [Google Scholar]
- Filippi C, Ulug A, Ryan E, Ferrando S, van Gorp W. Diffusion tensor imaging of patients with hiv and normal-appearing white matter on mr images of the brain. Ajnr: Am J Neuroradiol. 2001;22:277–283. [PMC free article] [PubMed] [Google Scholar]
- Fingelkurts AA, Fingelkurts AA, Kahkonen S. Functional connectivity in the brain-is it an elusive concepts? Neuroscience and Biobehavioral Reviews. 2005;28:827–836. doi: 10.1016/j.neubiorev.2004.10.009. [DOI] [PubMed] [Google Scholar]
- Fletcher P, Joshi S. Riemannian geometry for the statistical analysis of diffusion tensor data. Signal Processing. 2007;87:250–262. [Google Scholar]
- Fletcher P, Joshi S, Lu C, Pizer S. Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Transactions on Medical Imaging. 2004;23:995–1005. doi: 10.1109/TMI.2004.831793. [DOI] [PubMed] [Google Scholar]
- Grenander U, Miller MI. Pattern Theory From Representation to Inference. Oxford University Press; 2007. [Google Scholar]
- Hall P, Marron JS, Park BU. Smoothed cross-validation. Probability Theory and Related Fields. 1992;92:1–20. [Google Scholar]
- Hardle W, Hall P, Marron JS. Regression smoothing parameters that are not far from their optimum. Journal of American Statistical Association. 1992;87:227–233. [Google Scholar]
- Jones M, Marron J, Sheather S. A brief survey of bandwidth selection for density estimation. Journal of the American Statistical Association. 1996;91:401–407. [Google Scholar]
- Jupp PE, Kent JT. Fitting smooth paths to spherical data. Applied Statistics. 1987;36:34–46. [Google Scholar]
- Kim PT, Richards DS. IMS Lecture Notes Monograph Series. A Festschrift of Tom Hettmansperger. 2010. Deconvolution density estimation on spaces of positive definite symmetric matrices. [Google Scholar]
- Kume A, I, Dryden L, Le H. Shape-space smoothing splines for planar landmark data. Biometrika. 2007;94:513–528. [Google Scholar]
- Lang S. Graduate Texts in Mathematics. Vol. 191. Springer Verlag; New York: 1999. Fundamentals of Differential Geometry. [Google Scholar]
- Liang F. Evolutionary stochastic approximation monte carlo for global optimization. Statistics and Computing. 2010 In press. [Google Scholar]
- Park BU, Marron JS. Comparison of data-driven bandwidth selectors. Journal of American Statistical Association. 1990;85:66–72. [Google Scholar]
- Pasternak O, Sochen N, Basser JP. The effect of metric selection on the analysis of diffusion tensor mri data. Neuroimage. 2010;49:2190–2204. doi: 10.1016/j.neuroimage.2009.10.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennec X, Fillard P, Ayache N. A riemannian framework for tensor computing. International Journal of Computer Vision. 2006;66:41–66. [Google Scholar]
- Pourahmadi M. Maximum likelihood estimation of generalized linear models for multivariate normal covariance matrix. Biometrika. 2000;87:425–435. [Google Scholar]
- Prentice MJ. Fitting smooth paths to rotation data. Journal of the Royal Statistical Society Series C (Applied Statistics) 1987;36:325–331. [Google Scholar]
- Rice J. Bandwidth choice for nonparametric regression. Annals of Statistics. 1984;12:1215–1230. [Google Scholar]
- Sakamoto Y, Ishiguro M, Kitagawa G. Akaike Information Criterion Statistics (Mathematics and its Applications) Springer; 1999. [Google Scholar]
- Sangalli L, Secchi P, Vantini S, Veneziani A. Efficient estimation of three-dimensional curves and their derivatives by free-knot regression splines, applied to the analysis of inner carotid artery centrelines. Journal of the Royal Statistical Society, Ser C. 2009;58:285–306. [Google Scholar]
- Schwartzman A. Ph D thesis. Stanford University; 2006. Random ellipsoids and false discovery rates: Statistics for diffusion tensor imaging data. [Google Scholar]
- Terras A. Harmonic Analysis on Symmetric Spaces and Applications II. Springer-Verlag; Berlin, Heidelberg and New York: 1988. [Google Scholar]
- Wand MP, Jones MC. Kernel Smoothing. London: Chapman and Hall; 1995. [Google Scholar]
- Zhu HT, Chen YS, Ibrahim JG, Li YM, Lin WL. Intrinsic regression models for positive-definite matrices with applications to diffusion tensor imaging. Journal of the American Statistical Association. 2009;104:1203–1212. doi: 10.1198/jasa.2009.tm08096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu HT, Styner M, Tang NS, Liu ZX, Lin WL, Gilmore J. Frats: Functional regression analysis of dti tract statistics. IEEE Transactions on Medical Imaging. 2010;29:1039–1049. doi: 10.1109/TMI.2010.2040625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu HT, Zhang HP, Ibrahim JG, Peterson BG. Statistical analysis of diffusion tensors in diffusion-weighted magnetic resonance image data (with discussion) Journal of the American Statistical Association. 2007;102:1085–1102. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.