Annals of Botany110: 535–553, 2012
Since the publication of this paper, it has become apparent that an error was made in the calculation of the Kendall–Moran estimates presented, with logarithm to the base 10 being used instead of the natural logarithm. As a result of this error, the Kendall–Moran figures were systematically under-estimated in Figs 5 and 6, and the mean-squares in Table 1 were also incorrect. In addition, the error also affected Fig. S1 and Appendix S2 in the Supplementary Data. However, the conclusions of the paper are not affected as the differences amongst the groups compared remain constant whether the calculation uses logarithm to base 10 or the natural logarithm. The authors apologise for this error, and correct versions of Figs 5 and 6 and Table 1 are reproduced below. A corrected version of the Supplementary Data has also been placed online.
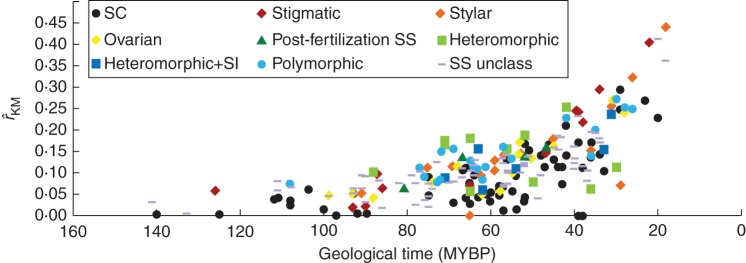
Fig. 5.
Family DR of the Kendall–Moran estimator (r̂KM) for 230 families identified as possessing self-compatibility (SC), possessing heteromorphic, or presenting self sterility unclassified (SS unclass) or one of six SI phenotypes: stigmatic, stylar, ovarian, post-fertilization SS, heteromorphic + SI (Het + SI) or as being polymorphic in the site of SI expression. MYBP = millions of years before present.
Fig. 6.
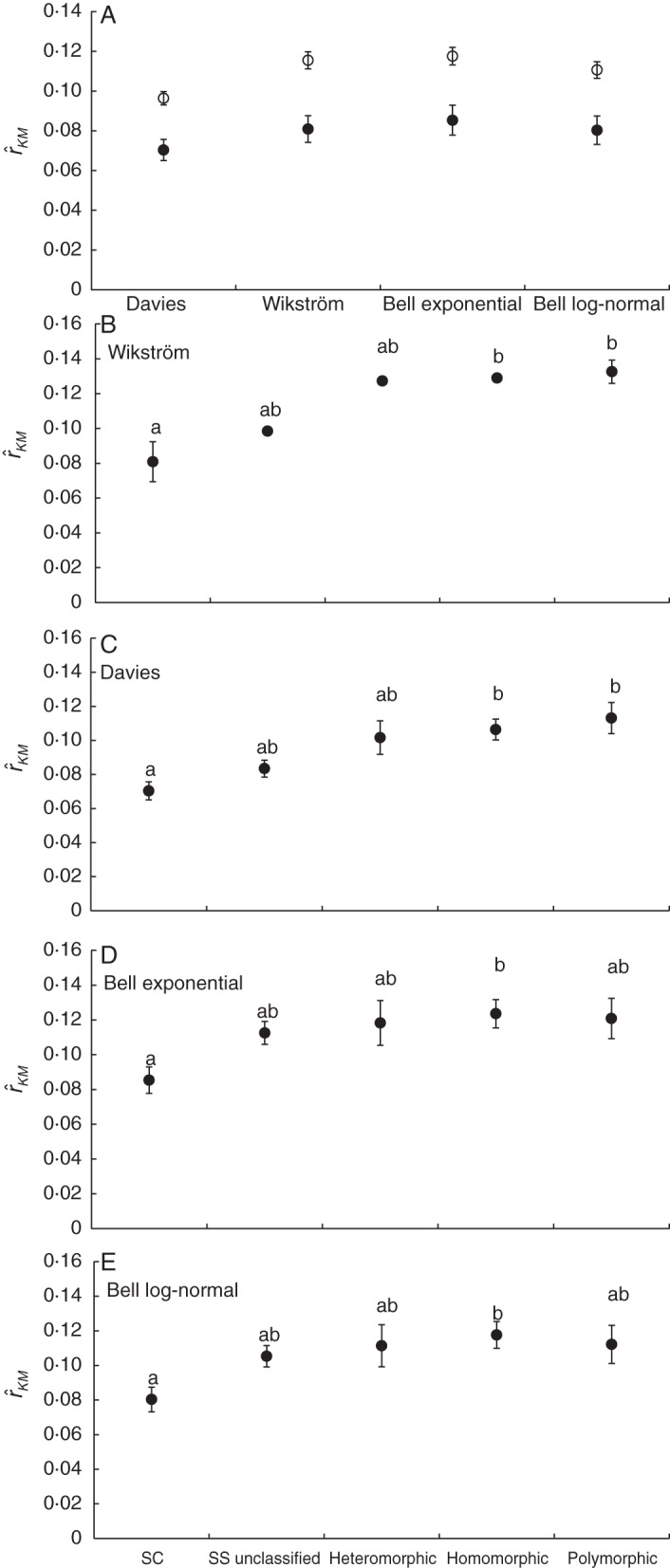
(A) Mean and standard error of the Kendall–Moran estimator of DR (r̂KM) in 164 and 66 families bearing SS/SI and SC, respectively, using the estimates of Wikström et al. (2001), Davies et al. (2004) and exponential and log-normal calibrations of Bell et al. (2010) for the divergence age of the families. Mean and standard error of Kendall–Moran estimator of DR (r̂KM) using the estimates of (B) Wikström et al. (2001), (C) Davies et al. (2004) and (D) exponential and (E) log-normal calibrations of Bell et al. (2010) for the divergence age of the 44 families bearing homomorphic SI, 19 with heteromorphy, 22 with polymorphic basis to SI, 74 families bearing SS unclassified species and for 66 families bearing SC. Means with different letters were found to be significantly different (Tukey HSD test, P < 0·05).
Table 1.
ANOVA results for the fixed-effect model of (A) presence of self-sterility, (B) types of self-sterility and (C) self-sterility/self-incompatibility (SS/SI) phenotype on the Kendall–Moran estimate of family DR using the squared age of divergence of the family as a covariate
| Effect | d.f. | MS effect | MS error | F | P |
|---|---|---|---|---|---|
| (A) Presence of self-sterility | |||||
| Wikström et al. (2001) | |||||
| Presence of self-sterility | 2, 227 | 0·0474 | 0·0030 | 16·00 | <0·0001 |
| Squared age of divergence of the family | 1, 227 | 0·3800 | 0·0030 | 128·14 | <0·0001 |
| Davies et al. (2004) | |||||
| Presence of self-sterility | 2, 227 | 0·0210 | 0·0019 | 11·32 | 0·0009 |
| Squared age of divergence of the family | 1, 227 | 0·2346 | 0·0019 | 126·76 | <0·0001 |
| Exponential Bell et al. (2004) | |||||
| Presence of self-sterility | 2, 203 | 0·0312 | 0·0029 | 10·62 | 0·0013 |
| Squared age of divergence of the family | 1, 203 | 0·2901 | 0·0029 | 98·57 | <0·0001 |
| Log-normal Bell et al. (2004) | |||||
| Presence of self-sterility | 2, 203 | 0·0266 | 0·0026 | 10·06 | 0·0018 |
| Squared age of divergence of the family | 1, 203 | 0·2541 | 0·0026 | 96·05 | <0·0001 |
| (B) Types of self-sterility | |||||
| Wikström et al. (2001) | |||||
| Types of self-sterility | 4, 224 | 0·0166 | 0·0029 | 5·69 | 0·0002 |
| Squared age of divergence of the family | 1, 224 | 0·3594 | 0·0029 | 123·06 | <0·0001 |
| Davies et al. (2004) | |||||
| Types of self-sterility | 4, 224 | 0·0080 | 0·0018 | 4·35 | 0·0021 |
| Squared age of divergence of the family | 1, 224 | 0·2215 | 0·0018 | 121·20 | <0·0001 |
| Exponential Bell et al. (2004) | |||||
| Types of self-sterility | 4, 200 | 0·0086 | 0·0030 | 2·90 | 0·023 |
| Squared age of divergence of the family | 1, 200 | 0·2897 | 0·0030 | 97·52 | <0·0001 |
| Log-normal Bell et al. (2004) | |||||
| Types of self-sterility | 4, 200 | 0·0075 | 0·0027 | 2·81 | 0·0268 |
| Squared age of divergence of the family | 1, 200 | 0·2533 | 0·0027 | 94·90 | <0·0001 |
| (C) Self-sterility/self-incompatibility | |||||
| Wikström et al. (2001) | |||||
| SS/SI phenotype | 8, 220 | 0·0099 | 0·0029 | 3·39 | 0·0011 |
| Squared age of divergence of the family | 1, 220 | 0·3619 | 0·0029 | 124·12 | <0·0001 |
| Davies et al. (2004) | |||||
| SS/SI phenotype | 8, 220 | 0·0052 | 0·0018 | 2·89 | 0·0045 |
| Squared age of divergence of the family | 1, 220 | 0·2222 | 0·0018 | 122·46 | <0·0001 |
| Exponential Bell et al. (2004) | |||||
| SS/SI phenotype | 8, 196 | 0·0057 | 0·0030 | 1·93 | 0·0577 |
| Squared age of divergence of the family | 1, 196 | 0·2889 | 0·0030 | 97·15 | <0·0001 |
| Log-normal Bell et al. (2004) | |||||
| SS/SI phenotype | 8, 196 | 0·0051 | 0·0027 | 2·68 | 0·0082 |
| Squared age of divergence of the family | 1, 196 | 0·2544 | 0·0027 | 171·82 | <0·0001 |
The analyses were performed on the Wikström et al. (2001), Davies et al. (2004) and exponential and log-normal Bell et al. (2010) estimates of the divergence age of families.