Gaussian Mixtures on Tensor Fields for Segmentation: Applications to Medical Imaging

Abstract

In this paper, we introduce a new approach for tensor field segmentation based on the definition of mixtures of Gaussians on tensors as a statistical model. Working over the well-known Geodesic Active Regions segmentation framework, this scheme presents several interesting advantages. First, it yields a more flexible model than the use of a single Gaussian distribution, which enables the method to better adapt to the complexity of the data. Second, it can work directly on tensor-valued images or, through a parallel scheme that processes independently the intensity and the local structure tensor, on scalar textured images.

Two different applications have been considered to show the suitability of the proposed method for medical imaging segmentation. First, we address DT-MRI segmentation on a dataset of 32 volumes, showing a successful segmentation of the corpus callosum and favourable comparisons with related approaches in the literature. Second, the segmentation of bones from hand radiographs is studied, and a complete automatic-semiautomatic approach has been developed that makes use of anatomical prior knowledge to produce accurate segmentation results.

1. Introduction

Tensor features appear in various areas of image processing, with the notable example of DT-MRI (Diffusion Tensor Magnetic Resonance Imaging) (6). Other possible applications are the strain tensor for cardiac motion analysis or elastography (60; 62) or the use of the LST (Local Structure Tensor) (34; 10; 28; 40) for texture analysis.

When dealing with tensor-valued data, traditional approaches for filtering, registration or segmentation have been adapted in order to account for the special properties of this data modality.

In this paper, we introduce mixtures of Gaussians on tensor fields as a new statistical model for the segmentation of tensor valued images. This new model will be later applied to two different medical imaging problems, the segmentation of DT-MRI and the segmentation of bones from hand radiographs.

The segmentation method presented in this paper is based on the flexible and well-known Geodesic Active Regions (GAR) segmentation setting (51). Level set methods are employed for the implementation of curve evolution (24; 47; 50; 49) to complete the segmentation scheme.

In order to validate the proposed segmentation method, two different applications are considered. The first one is the segmentation of the corpus callosum from DT-MRI in a data set of 32 volumes¹. Results show mixtures of Gaussians on tensors to provide higher accuracy and robustness than other related approaches in the literature (71; 44; 45).

The second application of the segmentation method proposed is the segmentation of hand bones from radiographs, an important problem related to the automatic assessment of bone age, for which a golden solution has not been reported yet. Texture is a relevant feature in bone tissue in radiographs, and the introduction of mixtures of Gaussians on tensor fields can also help improve the segmentation of textured images through the use of the LST, widely accepted as a powerful feature extractor for this kind of images. We propose a global scheme that employs both the intensity and the texture information for segmentation, and adaptively adjusts the importance of each of them depending on the image characteristics and the current state of the segmentation process. Our approach benefits from the previous definition of the mixtures of Gaussians on tensor fields and, as it is completely symmetric regarding how the texture and the intensity information are treated, allows for a simple yet e ective technique for balancing the weight of each.

All in all, this paper presents several contributions to the segmentation of tensor fields and its application to different types of medical imaging. As a theoretical core element, we introduce the mixtures of Gaussians on tensor fields and a complete segmentation method based on the GAR model. This method can be directly applied to any tensor-valued image, and it is the case with the extensive DT-MRI dataset that has been employed for the segmentation of the corpus callosum, our second major contribution. With regard to the segmentation of gray level images, the introduction of a parallel segmentation approach that uses both the intensity and the texture (which is represented by means of the LST and is thus a tensor-valued image) is the third main contribution of this work. Finally, a complete segmentation technique for hand bones in radiographs is presented as an application of such scheme.

The paper is organized as follows: first, in Section 2, we review the state of the art in tensor field segmentation, focusing on DT-MRI segmentation and the use of the LST for texture segmentation. Section 3 introduces the mixtures of Gaussians on tensor fields, the key theoretical component in our approach. Later, the complete segmentation scheme proposed will be presented, considering its two possible variants (working directly on tensor-valued images, such as DT-MRI, or on gray-valued textured images, such as hand radiographs). In Section 5, the two medical imaging applications considered in this paper are presented and results are shown and discussed. Finally, we summarize the most important elements of this work in Section 6.

2. State of the art and related work

Much of the early work on analysis and segmentation of tensor data was devoted to DT-MRI, and relied on the obtention of scalar diffusion or anisotropy features from the tensor, such as in (8; 68; 53; 52; 64; 17; 71). Later, Rousson, Brox et al. proposed in (13; 58) to apply the vector-valued version of the GAR model for multivariate Gaussian distributions (59) to the vector consisting of the nonlinearly diffused free components of the LST. This way, the image was treated as though it were multiespectral, being the channels each of the components of the tensor.

The first level set segmentation approach directly working on tensor data was proposed by Feddern et al. (25). In their work, they employ an approach based on the GAC (Geodesic Active Contours) model (15; 39) and adapted to tensor data by using the trace of the LST of the tensor data as an edge detector that stops the evolution of the contour in the presence of edges. Using a completely different approach, a modified k-means algorithm (33) was proposed in (69) to segment the thalamic nuclei from DT-MRI.

Most recent approaches for the segmentation of tensor data make use of variational methods and level sets based on the information given by tensor dissimilarity measures. The Frobenius distance, J-divergence (also known as symmetrized Kullback-Leibler distance) and the Riemannian geodesic distance, among others, were proposed in (66; 35; 65). Different formulations for the statistical modeling of the data were also presented, as the definition of Gaussian distributions directly on the tensor domain (45; 44). When compared to all these approaches, the mixtures of Gaussians for tensor fields presented in this paper constitute a more advanced statistical model, thus enabling the segmentation to adjust to a higher complexity in the data.

In (67), a graph cuts segmentation was proposed using either the Log-Euclidean distance (2) or the J-divergence. This method, however, needs strong user interaction as certain tensors need to be selected belonging to the different regions, thus imposing hard constraints to the segmentation. Ziyan et al., in (72), proposed a spectral segmentation algorithm for the thalamic nuclei from DT-MRI data.

Another recent approach to DT-MRI segmentation was presented by Awate et al. (5; 4), who presented a fuzzy C-means algorithm that, instead of incorporating Gaussian class models, uses nonparametric data-driven statistical models. The motivation underlying this approach lies in the fact that, because of the anatomical characteristics of fiber bundles, they change their orientation significantly. Thus, the tensor statistics do not accurately fit Gaussian models, whereas nonparametric statistical models can efectively adjust to these situations. Using a Log-Euclidean metric, the segmentation of different structures in the white matter is performed.

With respect to the application of tensor field segmentation to the segmentation of textured images through the LST, any segmentation method that makes use of the LST can benefit from all the refinements in tensor field segmentation explained before. However, the LST does not include any intensity information, which can be very valuable in the segmentation process. In (58), this drawback was addressed by adding the intensity to the feature vector otherwise composed of the LST components. Later, in (20), several modified structure tensor architectures were introduced that incorporate the intensity information. However, encoding both the intensity and the LST information either in a vector or a tensor form is not completely appropriate, as the texture information naturally fits a tensor architecture, whereas the intensity information fits a scalar (or vector, in the case of colour images) scheme. In order to overcome this limitation, a combined approach was proposed in (19) where a tensor segmentation scheme is applied to the LST while a scalar approach is used for the intensity, both under the same general framework. This work was able to obtain remarkable results in the segmentation of textured images, showing better results than other well-known texture segmentation methods such as Bouman's approach (11; 12).

The approach described in this paper presents, nevertheless, two main advantages with respect to the method in (19). First, it employs the more appropiate mixtures of Gaussians as a statistical modeling both for the tensor and the intensity information and, second, defines a completely symmetric technique for the estimation of the relative importance of the intensity and texture information. In the former approach, because of the different nature of the respective distances employed for the intensity and the LST (Euclidean and J-divergence or geodesic distance, respectively), the calculation of the relative importance of both elements in the segmentation is not symmetric, and therefore can be biased.

3. Mixtures of Gaussians on tensor fields

In this section, we introduce the main theoretical contribution of this paper, that is, the definition of mixtures of Gaussians on tensor fields. To that end, we first recall Gaussian distributions on tensors, and later present the mixtures of Gaussians. Parameter estimation, a key issue for mixtures of Gaussians, is last addressed.

3.1. Gaussian probability density function of tensors

Let us consider the definition of Gaussian distributions on tensors introduced by Lenglet et al. in (45; 44). Following this definition, the probability density function (PDF) for a certain tensor T_i belonging to the manifold $S^{+}(n,\mathbb{R})$ of the real n × n symmetric positive definite (SPD) matrices is:

$$p({\mathbf{T}}_i\mid \stackrel{‒}{\mathbf{T}},\Lambda )=\frac{1}{\sqrt{{\left(2\pi \right)}^d\mid \Lambda \mid }}\text{exp}\left(-\frac{\phi {\left({\beta }_i\right)}^T{\Lambda }^{-1}\phi \left({\beta }_i\right)}{2}\right)$$ (1)

where T̄ is the empirical mean of the tensor field over a set of N tensors and Λ is the associated covariance matrix, whose size is d × d, with d being the number of free components in a n × n tensor (for 2 × 2 tensors, d = 3, whereas for 3 × 3 tensors, d = 6). The symmetric matrix β_i depends on the chosen metric ${\mathcal{D}}_x$ and is given by ${\beta }_i=-{\nabla }_{{\mathbf{T}}_i}{\mathcal{D}}_x^2({\mathbf{T}}_i,\stackrel{‒}{\mathbf{T}})$. Finally, the map $\phi :S^{+}(n,\mathbb{R})\mapsto {\mathbb{R}}^d$ associates to each matrix β_i its d independent components.

As can be seen, for this Gaussian formulation a metric must be chosen to measure the dissimilarity between tensors. In (45; 44), the Frobenius norm of the difference of tensors, the J-divergence and the geodesic distance were tested, and empirical evidence showed that the geodesic distance outperforms the other two distances, while the J-divergence performs also better than the Frobenius norm.

Once a metric has been chosen, the definition of the PDF is based on the usage of the vector φ( β_i). Grounded on Riemannian geometry, β_i is the initial velocity of the geodesic joining T̄ and T_i (see (45) for details). In Table 1, the definitions of the Frobenius, Kullback-Leibler-based J-divergence and geodesic distances are given, together with their associated values for β_i.

Table 1.

Squared distances and their gradient for T̄ and T_i.

Distance	${\mathcal{D}}^2({\mathbf{T}}_i,\stackrel{‒}{\mathbf{T}})$	${\nabla }_{{\mathbf{T}}_i}{\mathcal{D}}^2({\mathbf{T}}_i,\stackrel{‒}{\mathbf{T}})=-{\beta }_i$
Frobenius norm	trace((T̄ – Ti)(T̄ – Ti)T)	T̄ – Ti
J-divergence	$\frac{1}{4}(\text{trace}({\stackrel{‒}{\mathbf{T}}}^{-1}{\mathbf{T}}_i+{\mathbf{T}}_i^{-1}\stackrel{‒}{\mathbf{T}})-d)$	$\frac{1}{4}({\mathbf{T}}_i^{-1}-{\stackrel{‒}{\mathbf{T}}}^{-1}{\mathbf{T}}_i{\stackrel{‒}{\mathbf{T}}}^{-1})$
Geodesic	$\frac{1}{2}\text{trace}\left({\text{log}}^2\left({\stackrel{‒}{\mathbf{T}}}^{-1∕2}{\mathbf{T}}_i{\stackrel{‒}{\mathbf{T}}}^{-1∕2}\right)\right)$	$\stackrel{‒}{\mathbf{T}}\text{log}\left({\mathbf{T}}_i^{-1}\stackrel{‒}{\mathbf{T}}\right)$

As for the estimation of the parameters of the distributions, the empirical mean tensor T̄ over a set of N random tensors T_i is defined as the minimizer of the expectation of the squared distances between a tensor T and each element:

$$\epsilon \left[{\mathcal{D}}^2(\mathbf{T},{\mathbf{T}}_i)\right]\approx \frac{1}{N}\sum _{i=1}^N{\mathcal{D}}^2(\mathbf{T},{\mathbf{T}}_i)$$ (2)

There are closed-form expressions for the mean tensor using the Frobenius and the J-divergence distances, whereas an iterative algorithm must be employed for the geodesic distance (see (45; 16) for details).

With regard to the empirical covariance matrix Λ, it is estimated by means of

$$\Lambda =\frac{1}{N}\sum _{i=1}^N\phi \left({\beta }_i\right)\phi {\left({\beta }_i\right)}^T$$ (3)

Other efforts have been made in the literature on the statistical characterization of tensor fields. In (27), a method was developed for producing averages and modes of variation in the space of SPD matrices. In (7), the authors use the tensor contraction operation, applied to fourth- and second-order tensors in the exponent of a normal distribution for tensor-valued data. However, only when the fourth-order tensor is isotropic, an explicit analytical expression for the PDF can be obtained.

3.2. Mixtures of Gaussians on tensors

Starting from the definition of Gaussian PDFs over tensor fields seen before, we will define a new PDF consisting of a mixture of Gaussians. For a mixture of K Gaussians, the PDF for a tensor T_i will be:

$$p({\mathbf{T}}_i\mid ϴ)=\sum _{k=1}^K{\alpha }_k\frac{1}{\sqrt{{\left(2\pi \right)}^d\mid {\Lambda }_k\mid }}\text{exp}\left(-\frac{1}{2}{\left(\phi \left({\beta }_i\left({\stackrel{‒}{\mathbf{T}}}_k\right)\right)\right)}^T{\Lambda }_k^{-1}\left(\phi \left({\beta }_i\left({\stackrel{‒}{\mathbf{T}}}_k\right)\right)\right)\right)$$ (4)

where we denote by Θ the set of parameters: α_k, k = 1, . . . , K are the mixing probabilities of the different components of the mixture, and each Gaussian distribution is characterized by its mean tensor T̄_k and its covariance matrix Λ_k.

In order to estimate the parameter vector Θ, a Maximum Likelihood (ML) approach by means of the Expectation-Maximization (EM) algorithm will be followed, as it is customary for mixtures of Gaussians. The EM (23; 55) algorithm is a general method to find the ML estimate of the parameters of an underlying distribution from a dataset when the data are incomplete or, equivalently, there is a many-to-one mapping from an underlying distribution to the distribution governing the observation.

Next, we present the derivation of the EM algorithm for parameter estimation in mixtures of Gaussians on tensors.

3.2.1. EM algorithm for tensor mixtures of Gaussians

Let us consider again the PDF correspoding to a mixture of Gaussians on tensors given in Eq. 4. Hereafter, and in order to simplify the notation, we will express the dependencies of φ(β_i(T̄_k)) simply as φ_i(T̄_k). The log-likelihood we seek to maximize will be given by

$$\text{log}\left(\mathcal{L}\right)=\sum _{i=1}^N\text{log}\left(p({\mathbf{T}}_i\mid ϴ)\right)=\sum _{i=1}^N\text{log}\left(\sum _{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)\right)$$ (5)

where we have denoted by g_k(T_i|Θ_k) the PDF of each of the components of the mixture, with parameters Θ_k = {α_k, T̄_{k, Λk}}. We first derive the log-likelihood with respect to the mean tensor T̄_k:

$$\frac{\partial }{\partial {\stackrel{‒}{\mathbf{T}}}_k}\text{log}\left(\mathcal{L}\right)=\sum _{i=1}^N\frac{1}{{\sum }_{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}\frac{\partial }{\partial {\stackrel{‒}{\mathbf{T}}}_k}\left(\sum _{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)\right)=-\sum _{i=1}^N\frac{1}{{\sum }_{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)\frac{\partial }{\partial {\stackrel{‒}{\mathbf{T}}}_k}\left[-\frac{1}{2}{\left({\phi }_i\left({\stackrel{‒}{\mathbf{T}}}_k\right)\right)}^T{\Lambda }_k^{-1}\left({\phi }_i\left({\stackrel{‒}{\mathbf{T}}}_k\right)\right)\right]$$ (6)

As the relationship between φ(β_i) and T̄ is not simple, and depends on the employed distance, the differentiation we need to perform is not easy to compute. Instead, we will reconsider the Gaussian density function as p(t_i|t̄, Λ), where t_i is a vector consisting of the free components of the tensor T_i and t̄ is the corresponding mean vector. Then, and recalling that we have $\phi \left({\beta }_i\left(\stackrel{‒}{\mathbf{T}}\right)\right):\mathcal{S}\left(n\right)\to \mathcal{S}\left(n\right)\to {\mathbb{R}}^d$, we can directly express the dependence of φ as ${\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right):{\mathbb{R}}^d\to {\mathbb{R}}^d$. Now, we can express $\frac{\partial }{\partial \stackrel{‒}{\mathbf{t}}}\left(\text{log}\mathcal{L}\right)$ as follows:

$$\frac{\partial }{\partial \stackrel{‒}{\mathbf{t}}}\left(\text{log}\mathcal{L}\right)=-\frac{1}{2}\sum _{i=1}^N\frac{\partial }{\partial \stackrel{‒}{\mathbf{t}}}\left[{\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)}^T{\Lambda }^{-1}\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)\right]$$ (7)

For each element i we have

$$\frac{\partial }{\partial \stackrel{‒}{\mathbf{t}}}\left[{\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)}^T{\Lambda }^{-1}\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)\right]=\frac{\partial }{\partial {\phi }_i}\left[{\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)}^T{\Lambda }^{-1}\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)\right]\frac{\partial {\phi }_i}{\partial \stackrel{‒}{\mathbf{t}}}$$ (8)

Indeed, $\frac{\partial }{\partial {\phi }_i}\left[{\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)}^T{\Lambda }^{-1}\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)\right]=2{\left({\phi }_i\left(\stackrel{‒}{\mathbf{t}}\right)\right)}^T{\Lambda }^{-1}$. With respect to $\frac{\partial {\phi }_i}{\partial \stackrel{‒}{\mathbf{t}}}$, it depends on the choice of the tensor distance. Therefore, a closed-form expression for the mean tensor cannot be obtained in general, and a numerical approximation must be made given a tensor size and a chosen metric.

We now can make use of the result in Eq. (8) in order to rewrite Eq. (6):

$$\frac{\partial }{\partial {\mathbf{t}}_{\mathbf{m},\mathbf{k}}}\text{log}\left(\mathcal{L}\right)=\sum _{i=1}^N\frac{1}{{\sum }_{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}\frac{\partial }{\partial {\mathbf{t}}_{\mathbf{m},\mathbf{k}}}\left(\sum _{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)\right)=-\sum _{i=1}^N\frac{{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}{{\sum }_{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}\frac{\partial }{\partial {\mathbf{t}}_{\mathbf{m},\mathbf{k}}}\left[-\frac{1}{2}{\left({\phi }_i\left({\mathbf{t}}_{\mathbf{m},\mathbf{k}}\right)\right)}^T{\Lambda }_k^1\left({\phi }_i\left({\mathbf{t}}_{\mathbf{m},\mathbf{k}}\right)\right)\right]=-\sum _{i=1}^{N}p(k\mid i){\left({\phi }_i\left({\mathbf{t}}_{\mathbf{m},\mathbf{k}}\right)\right)}^T{\Lambda }^{-1}\frac{\partial {\phi }_i}{\partial {\mathbf{t}}_{\mathbf{m},\mathbf{k}}}$$ (9)

where $\frac{\partial {\phi }_i}{\partial {\mathbf{t}}_{\mathbf{m},\mathbf{k}}}$ depends on the choice of the distance measure. Equivalently, the mean tensors T̄_k are obtained as

$${\widehat{\stackrel{‒}{\mathbf{T}}}}_k=\frac{{\sum }_{i=1}^{N}p(k\mid i){\mathbf{T}}_i}{{\sum }_{i=1}^{N}p(k\mid i)}$$ (10)

With regard to the estimation of the parameters Λ_k and α_k, their derivation does not change with respect to the vectorial case:

$${\widehat{\Lambda }}_k=\frac{{\sum }_{i=1}^{N}p(k\mid i)\left({\phi }_i\left({\stackrel{‒}{\mathbf{T}}}_k\right)\right){\left({\phi }_i\left({\stackrel{‒}{\mathbf{T}}}_k\right)\right)}^T}{{\sum }_{i=1}^{N}p(k\mid i)}$$ (11)

$${\widehat{\alpha }}_k=\frac{1}{N}\sum _{i=1}^{N}p(k\mid i)$$ (12)

$$p(k\mid i)=\frac{{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}{{\sum }_{k=1}^K{\alpha }_k{g}_k({\mathbf{T}}_i\mid {ϴ}_k)}$$ (13)

3.2.2. Estimation of the complexity of the mixture

The described estimation procedure of the parameters of a mixture of Gaussians assumes that the number of components K is known in advance. However, this is not usually the case, and therefore the number of components, that is, the complexity of the mixture, has to be estimated as well. The issue of estimating the number of components of the mixture has been addressed before in the literature (26; 1; 56; 29; 41; 9; 57).

For the estimation of the complexity of the mixture of Gaussians on tensor fields, we will follow in this work the approach by Figueiredo et al (26). This method is based on the use of the MML (Minimum Message Length) criterion, implemented by means of a modified EM algorithm that leads to an integrated model selection and estimation procedure. Given a maximum initial number of components of the mixture, K, a modified maximization step is used where the mixture probabilities are updated following a modified expression:

$${\widehat{\alpha }}_k=\frac{\text{max}\left[0,\left(\sum _{i=1}^{N}p(k\mid i)\right)-\frac{N}{2}\right]}{{\sum }_{k=1}^K\text{max}\left[0,\left({\sum }_{i=1}^{N}p(k\mid i)\right)-\frac{N}{2}\right]}$$ (14)

where N is the overall number of parameters that specify each component of the mixture. Using this modified EM algorithm, the estimation of parameters starts using the maximum number of components considered. As the algorithm iterates, the mixture components whose probability is very reduced are annihilated, and so the final parameter estimation is inherently an estimation of the number of components of the mixture.

4. Segmentation method

Once the mixtures of Gaussians on tensors have been introduced together with a ML approach for the estimation of their parameters, we are ready to describe the segmentation approach that will be applied using this model. The segmentation method, which is based on the GAR model, seeks the minimization of the following energy term (see (51) for details):

$$E({\Omega }_1,{\Omega }_2)=-{\int }_{{\Omega }_1}\text{log}p(I\left(\mathbf{x}\right)\mid {\Omega }_1)d\mathbf{x}-{\int }_{{\Omega }_2}\text{log}p(I\left(\mathbf{x}\right)\mid {\Omega }_2)d\mathbf{x}$$ (15)

where $\mathcal{P}\left(\Omega \right)=\{{\Omega }_1,{\Omega }_2\}$ denotes the partition of the image domain Ω. This energy functional is the basis of all the functionals considered in this paper, and has also been employed in a number of other works in the literature (13; 51; 58; 70).

Now, instead of the image I, let us consider the more general field F(x), which can be a scalar or a vector valued image, or alternatively the tensor valued image containing, at each pixel, a diffusion tensor or the LST of the original image. Then, we can rewrite Eq. (15) as

$$E(\mathcal{C},{ϴ}_1,{ϴ}_2)=-{\int }_{{\Omega }_1}\text{log}p(\mathbf{F}\left(\mathbf{x}\right)\mid {ϴ}_1)d\mathbf{x}-{\int }_{{\Omega }_2}\text{log}p(\mathbf{F}\left(\mathbf{x}\right)\mid {ϴ}_2)d\mathbf{x}+\nu \mid \mathcal{C}\mid$$ (16)

where Θ_i, i = {1, 2}, describe the probability distributions over each region, and $\mathcal{C}$ is the contour that divides regions Ω₁ and Ω₂. The last term in the equation is an additional regularizing component that penalizes the length of the segmenting contour.

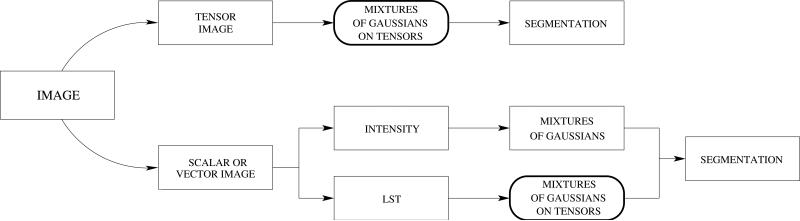
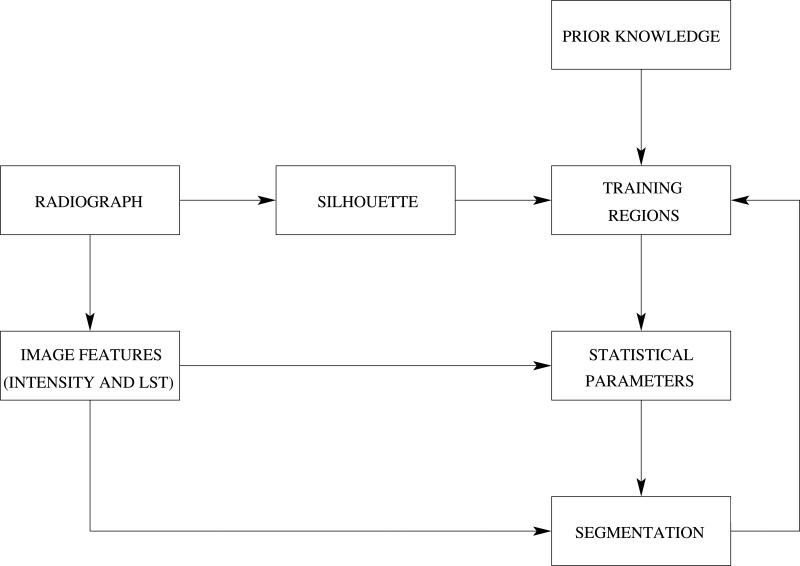
Starting from this model, two different variants of the segmentation method must be considered depending on the type of image under consideration. When dealing with a tensor-valued image, such as the case of DT-MRI, the functional in Eq 16 can be directly applied. However, if the image is scalar or vector-valued, we propose to extract the texture information by means of the LST. Then, the intensity and the LST are processed in parallel, both with a mixtures of Gaussians model. We next present the details of both variants, and depict in Figure 1 an schematic diagram of them.

Figure 1.

Two different variants of the use of mixtures of Gaussians on tensors for segmentation. The first variant, working directly on tensor-valued images, is presented in Section 4.1. The second variant, which works on scalar or vector-valued textured images, is presented in Section 4.2.

4.1. Segmentation of tensor fields: MoGoT

When F(x) is a tensor field, T(x), the energy functional we seek to minimize is

$$E(\mathcal{C},{ϴ}_1,{ϴ}_2)=-{\int }_{{\Omega }_1}\text{log}p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_1)d\mathbf{x}-{\int }_{{\Omega }_2}\text{log}p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_2)d\mathbf{x}+\nu \mid \mathcal{C}\mid$$ (17)

where p(T(x)|Θ_i) follows the mixture of Gaussians model introduced in the preceding section (Eq. (4)).

In order to perform the segmentation, the energy functional must be minimized with respect to the statistical parameters Θ_i and to the segmenting surface, which is represented by means of the level set function ϕ. This is done following the two-step EM technique. For a fixed level set, the statistical parameters are updated with their ML estimators. Next, the segmenting surface is evolved following the level set equation (see (59) for details):

$$\frac{\partial \varphi }{\partial t}\left(\mathbf{x}\right)=\delta \left(\varphi \right)\left(\nu \nabla \cdot \left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)-\frac{p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_1)}{p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_2)}\right)$$ (18)

where δ(ϕ) is the Dirac function. This approach will be referred to as MoGoT (Mixtures of Gaussians on Tensors), and is suitable for the segmentation of tensor-valued images, as it is the case of DT-MRI, and constitutes a refinement of the tensor segmentation scheme successfully employed in (45; 44) on that sort of data.

4.2. Segmentation of textured images: AdMoGIT

We propose a combined approach for the segmentation of textured images, which performs a separate but parallel processing of the intensity information and the texture information, encoded by means of the LST. For the tensor information, the MoGoT segmentation method introduced before can be applied in a straightforward manner. Similarly, scalar mixtures of Gaussians are employed for the intensity information, thus yielding the following combined energy functional:

$$E({\Omega }_1,{\Omega }_2)=\frac{{\beta }_1}{{\beta }_1+{\beta }_2}\left[-{\int }_{{\Omega }_1}\text{log}p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_{t1})d\mathbf{x}-{\int }_{{\Omega }_2}\text{log}p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_{t2})d\mathbf{x}\right]+\frac{{\beta }_2}{{\beta }_1+{\beta }_2}\left[-{\int }_{{\Omega }_1}\text{log}p(\mathbf{I}\left(\mathbf{x}\right)\mid {ϴ}_{c1})d\mathbf{x}-{\int }_{{\Omega }_2}\text{log}p(\mathbf{I}\left(\mathbf{x}\right)\mid {ϴ}_{c2})d\mathbf{x}\right]$$ (19)

where p(T(x)|Θ_ti) and p(I(x)|Θ_ci) are the PDFs corresponding to the mixtures of Gaussians over the LST and over the intensity, respectively, and β₁ and β₂ are weighting factors that balance the relative importance of the LST and the intensity-based term, as further explained in Section 4.2.1.

Once again, the minimization of the energy functional is performed, with respect to the statistical parameters, by means of their ML estimators and, with respect to the segmenting surface, by means of an evolving level set, whose evolution equation is:

$$\frac{\partial \varphi }{\partial t}\left(\mathbf{x}\right)=\delta \left(\varphi \right)\left[\nu \nabla \cdot \left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)-\frac{{\beta }_1}{{\beta }_1+{\beta }_2}\left(\frac{p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_{t1})}{p(\mathbf{T}\left(\mathbf{x}\right)\mid {ϴ}_{t2})}\right)-\frac{{\beta }_2}{{\beta }_1+{\beta }_2}\left(\frac{p(\mathbf{I}\left(\mathbf{x}\right)\mid {ϴ}_{c1})}{p(\mathbf{I}\left(\mathbf{x}\right)\mid {ϴ}_{c2})}\right)\right]$$ (20)

This segmentation scheme will be hereafter referred to as AdMoGIT (Adaptive Mixtures of Gaussians on Intensity and Tensors). In this approach, the choice of the weighting parameters β₁ and β₂ is an important issue, as it balances the influence of the intensity and the texture in the segmentation process. We next introduce an adaptive method to determine this parameters through the segmentation process.

4.2.1. On the use of the KL distance to obtain β₁ and β₂

If β₁ = β₂ in Eq. (20), the LST and the image components are equally weighed and so they have the same importance in the segmentation process. However, it is also possible to adaptively adjust this parameter depending on the relative discriminative power of the LST and the components terms. The estimation of the relative importance of both types of features is related to the problem of the structure-texture decomposition of images, which is an important issue in the literature (31; 3), specially for denoising purposes. Usually, image decomposition is performed via an energy minimization process. This kind of decomposition still needs an initial guess of the splitting parameter between the geometrical and textural components and is beyond of the scope of this paper. Other efforts on measuring the discriminative power of the different channels are those in (14; 61). In the first work, Cardelino et al. considered the PDFs of the different feature channels in both regions Ω₁ and Ω₂ and computed the Kullback-Leibler distance between them. A large value for that distance belonging to a particular channel means that the channel provides good discrimination power. However, in (14) the previous slice of the volume data is employed for this procedure as a correct distinction between both regions is needed, which may not be available in a general case. With regard to the work by Sandberg et al. (61), the variations on the different features between both regions are considered as a criterion to discriminate among the feature channels. Again, this approach needs all channels be commensurate. In (19), a method was proposed for the comparison of the discriminative power of the intensity and tensor information based on the calculation of two distance measures of the separability of the mean tensor or intensity values over the two regions. However, as the tensor and intensity distances employed are not the same, this approach is not symmetric, and thus a bias can appear in the final calculation of the weighting parameters.

In this paper, we propose an approach related to the work by Cardelino et al. Taking into account that the modeling distributions of the chosen features are available, and since the underlying idea for the design of the weighting factors is related to the comparative measurement of the separation of the segmenting classes in terms of the features in the different channels, we will employ the well-known symmetrized Kullback Leibler distance (also named J-divergence) for the calculation of the weighting factors. To that end, these are defined as:

$${\beta }_1=\frac{d_{KL,t}(p(\mathbf{T}\mid {ϴ}_1),p(\mathbf{T}\mid {ϴ}_2))}{d_{KL,t}(p(\mathbf{T}\mid {ϴ}_1),p(\mathbf{T}\mid {ϴ}_2))+d_{KL,c}(p(\mathbf{I}\mid {ϴ}_1),p(\mathbf{I}\mid {ϴ}_2))}$$ (21)

$${\beta }_2=\frac{d_{KL,c}(p(\mathbf{I}\mid {ϴ}_1),p(\mathbf{I}\mid {ϴ}_2))}{d_{KL,t}(p(\mathbf{T}\mid {ϴ}_1),p(\mathbf{T}\mid {ϴ}_2))+d_{KL,c}(p(\mathbf{I}\mid {ϴ}_1),p(\mathbf{I}\mid {ϴ}_2))}$$ (22)

where p(T|Θ_i) is the estimated PDF of the tensor field over region i, and p(I|Θ_i)) is the estimated PDF of the intensity. Symmetrized Kullback-Leibler distances are always employed. As can be seen, we aim to measure the separation between the tensor distributions with relation to the separation between the intensity distributions. Those distributions which are at a larger distance are therefore favoured in the weighting of the energy terms. The described method to obtain β₁ and β₂ presents the advantage of using the complete information about the statistical distributions of the data. Furthermore, the formulation is completely symmetric, as the same measure (i.e. the Kullback-Leibler distance) is employed for the tensor and for the intensity features.

From a practical point of view, there exists a closed form for the J-divergence between two Gaussian distributions with common mean and different covariance matrix. However, for Gaussian distributions on scalars or vectors with different mean values or mixtures of Gaussians, an analytical calculation is, to our knowledge, not available. Even though, numerical integration can be performed easily as, if we recall the definition of the symmetrized Kullback-Leibler distance, we have

$$d_{KL,c}(p(\mathbf{I}\mid {ϴ}_1),p(\mathbf{I}\mid {ϴ}_2))=\frac{1}{2}\int \left[p(\mathbf{I}\mid {ϴ}_1)\text{log}\left(\frac{p(\mathbf{I}\mid {ϴ}_1)}{p(\mathbf{I}\mid {ϴ}_2)}\right)+p(\mathbf{I}\mid {ϴ}_2)\text{log}\left(\frac{p(\mathbf{I}\mid {ϴ}_2)}{p(\mathbf{I}\mid {ϴ}_1)}\right)\right]d\mathbf{I}$$ (23)

The computation of the tensor counterpart of the Kullback-Leibler distance is, however, more problematic, as numerical integration cannot be directly performed. In order to overcome this difficulty, we next propose an alternative procedure to compute the KL distance for the tensor case.

4.2.2. Monte Carlo simulations to approximate the KL distance on tensor distributions

The symmetrized Kullback-Leibler distance between two mixtures of Gaussians on tensor fields p(T|₁) and p(T|₂) is given by

$$d_{KL,t}(p(\mathbf{T}\mid {ϴ}_1),p(\mathbf{T}\mid {ϴ}_2))=\frac{1}{2}{\int }_{\mathcal{S}+\left(n\right)}\left[p(\mathbf{T}\mid {ϴ}_1)\text{log}\left(\frac{p(\mathbf{T}\mid {ϴ}_1)}{p(\mathbf{T}\mid {ϴ}_2)}\right)+p(\mathbf{T}\mid {ϴ}_2)\text{log}\left(\frac{p(\mathbf{T}\mid {ϴ}_2)}{p(\mathbf{T}\mid {ϴ}_1)}\right)+\right]d\mathbf{T}$$ (24)

where ${\mathcal{S}}^{+}\left(n\right)$ is the space of SPD tensors of size n × n where the integration must be performed. Once the explicit analytic integration is discarded, most numerical integration algorithms rely on the approximation of the integrand along intervals of constant size. The problem here, as we are not lying in an Euclidean space, is to define such intervals on ${\mathcal{S}}^{+}\left(n\right)$.

A simple and elegant way to overcome these difficulties is to run a Monte Carlo simulation (48) to perform the numerical integration. In our case, each of the two summands in Eq. (24) can be regarded as

$$\int f_X\left(\mathbf{x}\right)g\left(\mathbf{x}\right)d\mathbf{x}=\mathbb{E}\left\{g\left(\mathbf{x}\right)\right\}$$ (25)

where f_X(x) is a PDF, and therefore ∫ f_X(x)dx = 1. Then, and in order to obtain the expectation of g(x), one can just compute

$$\mathbb{E}\left\{g\left(\mathbf{x}\right)\right\}=\frac{1}{N}\sum _{i=1}^{N}g\left({\mathbf{x}}_i\right)$$ (26)

where the points x_i, i = 1, . . . , N have been generated according to the PDF f_X(x). A procedure for the generation of tensors according to Gaussian distributions is described in (43).

Using the described Monte Carlo technique, the calculation of the symmetrized Kullback-Leibler distance between two distributions on tensors is performed as briefly summarized in Table 2.

Table 2.

Summary of the EM algorithm for mixtures of Gaussians on vectors and tensors.

Numerical calculation of the symmetrized KL distance dK L,t(p(T|Θ1), p(T|Θ2))
Step 1	Generate N tensors T1,i according to p(T|Θ1)
	Generate N tensors T1,i according to p(T|Θ2)
Step 2	$\text{Compute}\frac{1}{N}{\sum }_{i=1}^N{g}_1\left({\mathbf{T}}_{1,i}\right),\text{where}g\left({\mathbf{T}}_{1,i}\right)=\text{log}\left(\frac{p({\mathbf{T}}_{1,i}\mid {ϴ}_1)}{p({\mathbf{T}}_{1,i}\mid {ϴ}_2)}\right)$
	$\text{Compute}\frac{1}{N}{\sum }_{i=1}^N{g}_2\left({\mathbf{T}}_{2,i}\right),\text{where}g\left({\mathbf{T}}_{2,i}\right)=\text{log}\left(\frac{p({\mathbf{T}}_{2,i}\mid {ϴ}_2)}{p({\mathbf{T}}_{2,i}\mid {ϴ}_1)}\right)$
Step 3	$\text{Calculate}{d}_{KL,t}(p(\mathbf{T}\mid {ϴ}_1),p(\mathbf{T}\mid {ϴ}_2))=\frac{1}{2}\left[\frac{1}{N}{\sum }_{i=1}^N{g}_1\left({\mathbf{T}}_{1,i}\right)+\frac{1}{N}{\sum }_{i=1}^N{g}_2\left({\mathbf{T}}_{2,i}\right)\right]$

5. Applications to Medical Image Segmentation

In this section, we describe the application of the segmentation method proposed in this paper to two different modalities of medical images. First, we address the problem of DT-MRI segmentation, for which the mixtures of Gaussians on tensors can work directly as seen in Section 4.1. Afterwards, the segmentation of bones from hand radiographs is studied. For this application, the variant of the proposed segmentation method presented in Section 4.2 needs to be employed, as we are dealing with gray-level textured images.

5.1. DT-MRI Segmentation

As explained in deeper detail in Section 2, the segmentation of tensor fields has evolved in the last few years mostly driven by the appearance of DT-MRI as an emerging medical imaging modality that allows the in vivo measurement of the anisotropy properties of water diffusion in tissues. This new modality opens new possibilities for the analysis of anatomical structures whose visualization is not feasible using conventional MRI.

With regard to the different human anatomical brain structures whose segmentation from DT-MRI has been attempted, the thalamus and its nuclei were segmented in (69; 37). In (71; 36; 38; 42; 46; 44) the corpus callosum was segmented, while the cortico-spinal tract was extracted in (38; 46). Other structures such as the lateral ventricles have been also segmented (42).

We will devote here to the segmentation of the corpus callosum from a set of DT-MRI images. This particular structure has been chosen since it constitutes a valuable benchmark for the evaluation of tensor field segmentation methods, as it has been attempted more commonly than other structures. Besides, the introduction of initial contours for the segmentation can be easily done from slices showing the FA, while the delineation of these initial contours for other structures such as the thalamus nuclei is much more problematic.

5.1.1. Segmentation method

The segmentation will be performed according to the following characteristics:

• The employed dataset consists of DT-MRI volumes of 32 subjects, which were acquired on a 1.5 Tesla scanner. The acquisition parameters were: b value = 1000 sec/mm², TE=1000 msec, TR=89 msec, along six diffusion-sensitizing directions. The images were obtained on 79 planes with 128 × 128 pixels per slice ².

• We will apply the MoGoT segmentation method, based on the definition of mixtures of Gaussians on tensors and intended for tensor-valued images. The maximum number of components for the mixtures of Gaussians over the tensor field will be 5 for each class.

• As for initial contours, the body of the corpus callosum will be roughly delineated for 3 central sagittal slices of the volume, upon the visualization of the FA.

• Following an EM approach, the level set evolution and the update of the parameters of the mixtures of Gaussians are iterated until convergence. In order to reduce the computational expense, the parameters will be updated once every five level set iterations, instead of once every iteration. Also, only a random selection of points uniformly distributed over the image (after the consideration of a mask that delineates the skull) is used for the parameter estimation of the background.

5.1.2. Results

The segmentation method proposed has proved to successfully extract the corpus callosum from DT-MRI images; the following results support this statement.

First, for a sample DT-MRI volume, we show in Figure 2 the segmenting surface at three different stages of the segmentation process. As can be seen, the segmentation evolves from the initial surface, growing appropriately to eventually capture the whole corpus callosum until it reaches a steady state.

Figure 2.

Initial contour and different stages of the evolving level set for a sample DT-MRI volume.

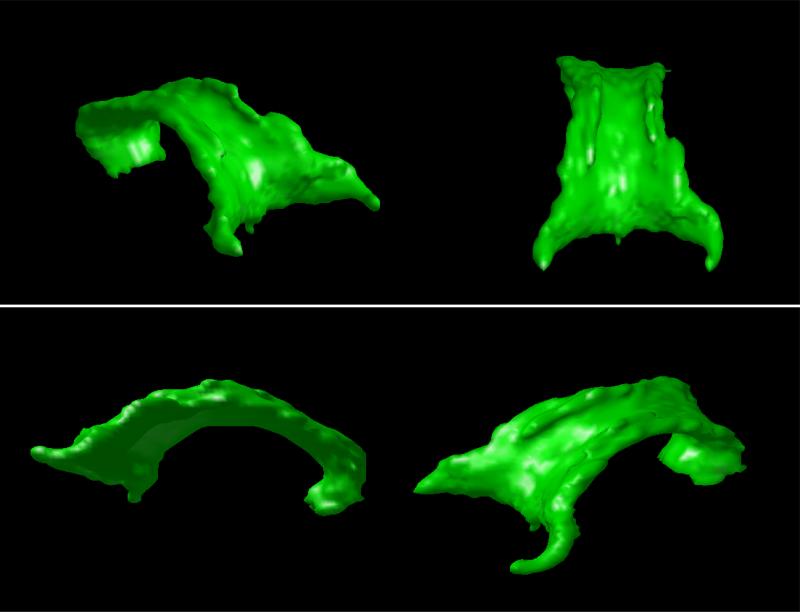
In Figure 3, the segmented corpus callosum for a sample volume is depicted from different viewpoints, in order to better describe the shape of the segmented structure.

Figure 3.

Different perspectives of the segmented corpus callosum.

Results shown so far illustrate the performance of the segmentation method for a single sample volume. In order to show the overall performance for all the volumes in the employed dataset, in Figure 4 we show a selection of the obtained segmentation results.

Figure 4.

Segmentation results for the corpus callosum in a selection of the DT-MRI volumes.

Once the suitability of the proposed method for the segmentation of the corpus callosum has been assessed, we next compare its performance with different variations of the model on a sample DT-MRI volume; specifically:

• In Figure 5(a), we show the obtained segmentation result for the application of our segmentation approach based on the fractional anisotropy data instead of the diffusion tensor (MoGoFA, Mixtures of Gaussians on Fractional Anisotropy). Therefore, scalar mixtures of Gaussians were employed.

• In Figure 5(b), the segmentation result using a strictly supervised version of the MoGoT method is shown (SMoGoT, Supervised Mixtures of Gaussians on Tensors). This implies that the estimation of the parameters of the Gaussian mixtures is performed only once, before the segmentation process starts. This estimation is based on the initial contours delineated by the user on three central sagittal slices, for region 1, and on random points outside this contours, for region 2. These parameters are then employed through all the level set evolution and are not updated as the segmentation evolves. The maximum number of components of the mixtures of Gaussians is, as before, 5.

• In Figure 5(c), the segmentation result for the same sample volume is shown, where the segmentation approach is identical to the one before, except that the maximum number of components of the mixtures of Gaussians has been set to 1.

• Finally, in Figure 5(d), the original segmentation result with the MoGoT segmentation method is shown for comparison (the maximum number of Gaussian components is 5).

Figure 5.

Segmentation results, for a sample volume, using MoGoFA (a); SMoGoT, K_max = 5 (b); SMoGoT, K_max = 1 (c); MoGoT, K_max = 5 (d).

The comparison of the obtained results allows for the discussion of a number of interesting issues. First, it is clear that the use of a scalar descriptor of the tensor as the fractional anisotropy does not suffice for the segmentation of the corpus callosum. Although scalar tensor invariants were employed in (71) for the segmentation of the corpus callosum and other brain structures, our results suggest that a very fine tune of the parameters would be needed for a successful segmentation, thus making it difficult for its general use.

With regard to the use of a supervised version of the proposed segmentation algorithm, results in Figure 5 (b),(c) show that these supervised variants have trouble at successfully segmenting the region of the splenium (posterior part of the corpus callosum). Indeed, the supervised functioning of the segmentation algorithm has a lack of flexibility, as it entirely relies on the parameters estimated in the training stage. Since the initial contours were delineated on three mid-sagittal slices, the estimated parameters are not able to fully capture the variability of the complete corpus callosum. Within a supervised mode, if the number of Gaussian components increases, the flexibility of the estimated model tends to decrease due to an overfitting effect, a fact that explains the smaller extension of segmentation result in Figure 5 (b) with respect to Figure 5(c).

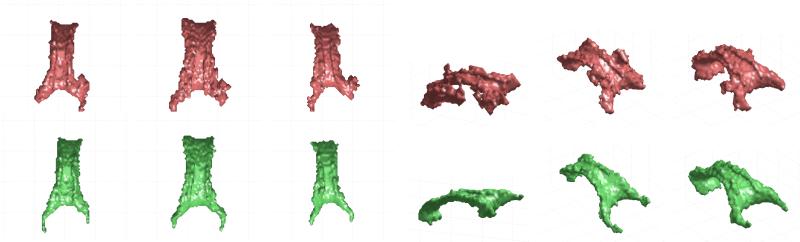
In order to illustrate the effect of using a single Gaussian instead of the mixtures of Gaussians proposed, we show in Figure 6 some segmentation results of our approach compared to those of the segmentation method in (45; 44), based on the use of a single Gaussian for the tensor probability density function (geodesic distance was also employed for this segmentation method, together with the same initial surfaces and identical segmentation parameters). Although this approach was able to obtain good segmentation results on the employed dataset, it encounters some problems in the region of the splenium in some cases when compared to the MoG approach, and it shows lower accuracy and some artifacts for some other subjects.

Figure 6.

Views of the segmentation results for the corpus callosum of different volumes using a single Gaussian model (44; 43) (red) and MoGoT model proposed in this paper (green). Results show a better accuracy of our approach in the region of the splenium (three left cases), and a higher robustness to artifacts (three right cases).

This increased performance showed by the segmentation approach proposed in this paper is related to the ability of the MoG to capture a higher complexity in the data with respect to the single Gaussian model. Even though this point constitutes an advantage of the general MoGoT segmentation method over the single Gaussian approach by Lenglet et al., further investigation must be made on the tradeo between adaptivity and flexibility of the data model in order to advance towards more robust DT-MRI segmentation methods.

Results in Figure 6 visually illustrate some of the advantages of the MoGoT model over a single Gaussian method. In order to provide also quantitative results, an indirect validation using ROI-based tractography was performed. A direct validation would require the manual segmentation of the corpus callosum from the DT-MRI volumes, which was not available for our dataset and is extremely difficult to obtain.

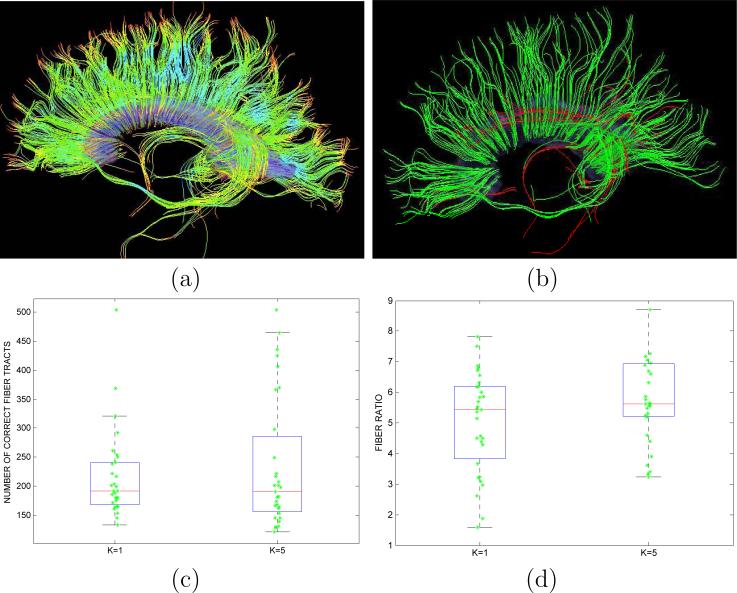
White matter segmentation is commonly employed to define ROIs for subsequent tractography generation and analysis. Then, the performance of a segmentation method is related to its ability to provide ROIs that produce fiber tracts belonging to the desired fiber bundle. Figure 7 (a) shows tractography results using the segmented corpus callosum as ROI for one of the DT-MRI volumes in the dataset. As can be seen, most of the obtained fiber tracts belong to the correct fiber bundle, while some undesired fibers belonging to the cingulum and other adjacent white matter structures are also produced. Considering this scenario and given a tractography method using a fixed set of parameters, the performance of the segmentation method can be measured in terms of the number of correct fibers and the ratio between the correct and incorrect fiber tracts that are generated through the tractography process (see Figure 7 (b)). Figures 7 (c) and (d) provide these results for the proposed segmentation method and the method proposed by Lenglet et al. (45; 44), which is equivalent to using MoGoT with K = 1. Both methods obtain a similar number of correct fiber tracts (there is not a statistically significant difference, p-value=0.4233), while MoGoT, with K = 5, provides a higher ratio of correct/incorrect fibers than Lenglet's method (mean values are 6.2749 and 5.0250, respectively, and there is a statistically significant difference, with p-value=0.0243).

Figure 7.

(a) Tractography results using corpus segmentation as ROI; (b) Correct fiber tracts (green) and incorrect ones (red); (c) Comparison of number of correct fibers using segmentation method by Lenglet et al. (45; 44) (K = 1) and proposed method (K = 5); (d) Comparison of ratio between correct and incorrect fibers using segmentation method by Lenglet et al. (45; 44) (K = 1) and proposed method (K = 5).

In order to provide further evidence about the relevance of the differences between the use of Gaussian mixtures and a single Gaussian model, we show in Table 3 a statistical analysis of the comparison between both approaches. In order to find out whether there are statistically significant differences in the segmentation results using both approaches, a set of shape descriptors was computed for each segmenting surface of the dataset, composed of central moments of different orders. The resulting feature vectors for each approach were afterwards compared using a paired T-test, if Gaussianity was found by means of a Chi-square test, or a Wilcoxon test otherwise. As can be seen from the table, 4 out of 8 shape descriptors are significantly different using both approaches. This indicates that, while the segmentation results are similar (statistically significant differences for all shape descriptors were not expected, as both approaches provide reasonable segmentation results), there are consistent and relevant differences between them.

Table 3.

Results of statistical tests of significance on the difference between the MoGoT model and the single Gaussian approach for DT-MRI segmentation.

Shape moments	T-test (p-value)	Wilcoxon test (p-value)
m 000 ††		0.0001
m 111 †	0.4380
m 112 ††		0.0194
m 121 ††		0.1162
m 211 ††		0.0225
m 221 †	0.0030
m 212 ††		0.1782
m 122 ††		0.1906

Significance is considered for p < 0.05.

^†Paired T-test was performed as Gaussianity could be assumed.

^††Wilcoxon test was applied as Gaussianity could not be assumed.

5.2. Segmentation of Bones from Hand Radiographs

Let us now address the problem of the automatic and semiautomatic segmentation of hand bones from radiographs. The importance of this issue stems from a procedure called bone age assessment, which is frequently employed in pediatric radiology. It is is aimed at determining the state of skeletal evolution of a patient from a radiograph of the non-dominant hand and wrist. Many diseases and syndromes a ecting growth result in a significant discrepancy between bone age and chronological age (54; 30).

Two major methods are used for bone age assessment on children: the Greulich-Pyle method (32) and the Tanner-Whitehouse (TW3) method (63). The former is an atlas-driven method which is based on visually comparing the radiograph with a number of atlas patterns. Bone age is assessed on the basis of the pattern which more accurately resembles the clinical image according to the physician's perception. TW3 method uses a detailed shape analysis of several bones of interest, leading to their individual classification into one of several stages. The subjective nature of the Greulich-Pyle method, and the considerable complexity of TW3 method, make the automation of bone age assessment a highly desirable goal, in order to assist the radiologist in performing a more objective, fast and accurate analysis.

In order to achieve an automatic or semiautomatic expert system for bone age assessment from hand radiographs, the segmentation of the bones of interest is very convenient as a prior step for further analysis based on the segmented shapes or simply as a necessary step for the determination of the regions of interest. To that end, we will employ the AdMoGIT segmentation method described in Section 4.2, i.e. a GAR model over mixtures of Gaussians on the intensity and the LST with an adaptive weighting of both sources of information. Segmentation will be performed in a supervised manner, that is, training regions will be located for the estimation of the statistical parameters of the mixtures of Gaussians prior to the segmentation process. To that end, an automatic procedure has been designed that permits the automatic location of the necessary training regions based on the anatomical prior knowledge.

5.2.1. Segmentation method

The segmentation method proposed is designed to segment all the bones of interest from the viewpoint of the TW3 bone age assessment method. These are the radius and ulna, the five metacarpals and the fourteen phalanges. The segmentation of the carpal bones is more complex, and their use for bone age assessment is limited because it is only relevant within a reduced range of age. Therefore, the segmentation of the carpal bones will not be our priority, although in most of the cases the segmentation of the former will be successfully achieved as well. We show in Figure 8 the workflow of the segmentation process. As can be seen, the statistical parameters from the intensity and the LST are obtained from training regions that are defined using prior anatomical knowledge.

Figure 8.

General workflow of the hand bones segmentation method.

For the estimation of the statistical parameters, training regions must be defined for each class. This task, which is critical for the segmentation to succeed, can be performed in a manual, automatic or semiautomatic fashion. In this work, an elaborated automatic method has been developed that finds the necessary training regions using prior anatomical knowledge about the structure of the hand and its bones. Nevertheless, sometimes it can occur that the segmentation results are not satisfactory due to the fact that the training regions, although correctly placed on the radiograph, do not adequately represent the segmenting classes. In order to solve this, a semi-automatic stage has been included in the segmentation workflow that allows the user to interactively add some training regions in order to refine the obtained segmentation results.

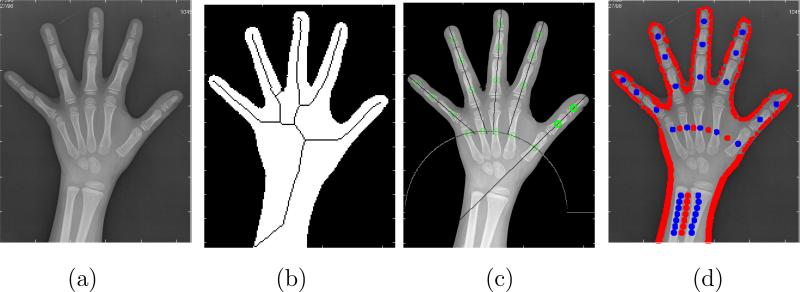
Starting from the hand radiograph, the process to place adequate training regions for each class within each region of influence is primarily based on the location of interior points to the different bones. Circular regions will be then created around these located seeds that will correspond to the training regions of the bone segmentation class. With respect to the soft tissue class, circular regions will be also created around points outside the bones, as well as other points located near the border of the hand silhouette, also known to be outside the bones. The overall method takes advantage of the anatomical prior knowledge about the general shape of the human hand, and also employs signal processing techniques in order to filter 1D profiles extracted from the radiograph along relevant directions, and to locate salient points that correspond to the seeds we seek. The procedure was partly presented in (21; 22) (we refer the reader to these references for further details), and Figure 9 shows several stages of it.

Figure 9.

Automatic method for the location of the training points in the radiograph: (a) Original image; (b) Squeleton of the hand silhouette; (c) Location of the training regions inside the phalanges; (d) Final training regions for bones (blue) and soft tissue (red).

5.2.2. Results

Once the segmentation method has been fully described, we present the experimental results obtained using the described approach.

First, results will be shown and studied in detail for a sample radiograph. The original image is shown in Figure 9 (a). The automatic procedure described before is applied on it in order to obtain the necessary training regions. Points are located in this way for both regions, as shown in Figure 9 (d), where training points belonging to the class bones are coloured in blue and points belonging to class soft tissue are coloured in red.

Once the training regions have been selected, the statistical parameters are estimated, and three sets of parameters are estimated that describe both classes in terms of their intensity and their LST for each region of influence. A maximum number of 5 components was imposed for the mixtures of Gaussians in order to limit the computational burden of the calculations and to avoid an overfitting of the mixtures of Gaussians to the training data.

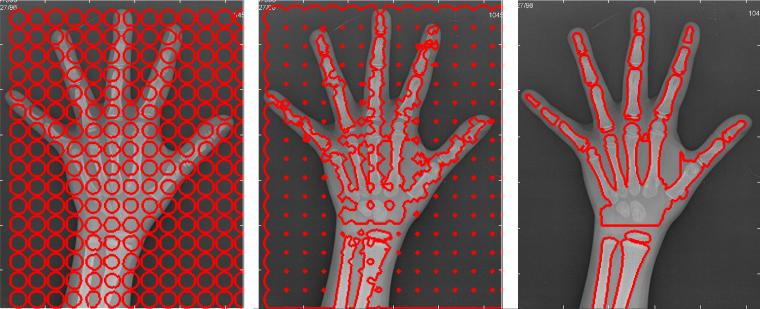
Using the estimated parameters, the iterative segmentation is performed with an evolving level set. Figure 10 shows the evolution of the segmenting contour at an initial, intermediate, and final point.

Figure 10.

Initial, intermediate and final contour for the segmentation of bones on the sample radiograph.

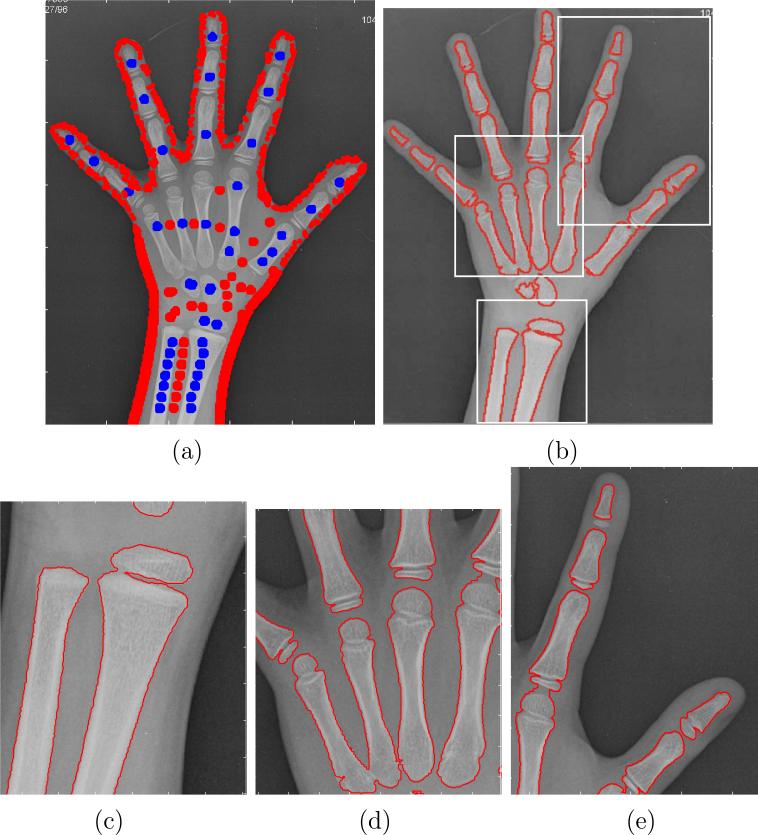
As can be seen, the segmentation results are quite accurate except for the carpal region, where the segmenting contour is not able to detect the two carpal bones that are already present at this stage of skeletal development. As stated before, these bones are not employed in most cases when performing the bone age assessment, because they are only relevant for very early stages of growth. However, a finer refinement of the segmentation results is possible if some manual seeds are placed in order to perform a more accurate estimation of the parameters. In Figure 11 (a), the complete set of training regions considered for a new segmentation is drawn. These training regions include the ones that were automatically placed, and a few more that have been manually included around the carpal bones in order to improve the segmentation results in this specific area. The final segmenting contour is shown in Figure 11 (b), that now accurately fits the bone contours all over the radiograph. Some details of this segmentation result are shown in Figure 11 (c), (d) and (e) that illustrate the accuracy of the segmentation method.

Figure 11.

(a) Training regions including some manually placed points around the carpal bones; (b) Segmentation results using the training regions shown in (a); (c), (d), (e) Segmentation details of the areas indicated as rectangles in (b).

6. Conclusions

In this paper, we have presented a novel approach for image segmentation based on the processing of tensor features using a statistical model consisting of a mixture of Gaussians. Starting from the well-know GAR segmentation framework, this approach can be directly applied to tensor-valued images, yielding a more flexible model than the use of a single Gaussian distribution. When applied to scalar images, our approach can be employed to perform the segmentation taking into account both intensity and texture, with the latter encoded by means of the LST. This way, the flexible mixtures of Gaussians are employed as a statistical model for both types of information. Furthermore, as this combined segmentation approach is completely symmetric, it is possible to evaluate the relative discriminative power of the intensity and the texture so as to balance the relative importance of both terms in the segmentation process.

In order to show the suitability of the proposed methods for the segmentation of medical imaging, we have selected two different applications. The first one is the segmentation of the corpus callosum from DT-MRI, a task that has been attempted in many works devoted to tensor field segmentation in the literature. Results over a large dataset show that our approach is capable of successfully segmenting the corpus callosum, and that using mixtures of Gaussians on tensors as a statistical modeling yields more accurate and robust results when compared to related approaches in the literature.

The second application is the segmentation of bones of interest from hand radiographs, for which and automatic-semiautomatic approach has been designed. The segmentation is performed after training regions have been located making use of anatomical prior knowledge. Then, the results can be further refined by introducing some manual intervention to locate additional training points.