Efficient Designs of Gene-Environment Interaction Studies: Implications of Hardy-Weinberg Equilibrium and Gene-Environment Independence

SUMMARY

It is important to investigate whether genetic susceptible variants exercise the same effects in populations that are differentially exposed to environmental risk factors. Here, we assess the power of four two-phase case-control design strategies for assessing multiplicative gene-environment (G-E) interactions or for assessing genetic or environmental effects in the presence of G-E interactions. With a di-allelic SNP and a binary E, we obtained closed-form maximum likelihood estimates of both main effect and interaction odds ratio parameters under the constraints of G-E independence and Hardy-Weinberg Equilibrium, and used the Wald statistic for all tests. We concluded that i) for testing G-E interactions or genetic effects in the presence of G-E interactions when data for E is fully available, it is preferable to ascertain data for G in a subsample of cases with similar numbers of exposed and unexposed and a random subsample of controls; and ii) for testing G-E interactions or environmental effects in the presence of G-E interactions when data for G is fully available, it is preferable to ascertain data for E in a subsample of cases that has similar numbers for each genotype and a random subsample of controls. In addition, supplementing external control data to an existing casecontrol sample leads to improved power for assessing effects of G or E in the presence of G-E interactions.

1. INTRODUCTION

Many genetic variants have recently been found to be associated with complex human phenotypes in genome-wide association studies (GWAS). Capitalizing on these findings for personalized medicine calls for investigations on the synergy between these genes and environmental risk factors. In the post GWAS era when genotype data for millions of genomic loci has been made available for thousands of people, it is of great interest to consider how to best utilize this existing resource to achieve improved power in G-E interaction studies. Similarly, it is important to consider how to expand case-control studies that did not collect biological samples for cost-effective studies of G-E interactions. In general, the two-phase design, which is a cost-effective option for studying expensive risk factors, has recently been advocated for the study of G-E interactions [1]. In this design, data for either genetic variants or environmental exposures is collected only on a judiciously selected subgroup of subjects. In this work, we consider two-phase case-control study designs for assessing multiplicative G-E interactions. We also evaluate the efficiency of these designs for jointly testing genetic or environmental main and G-E interaction effects, as these joint tests may lead to improved power for detecting genetic variants or environmental risk factors in the presence of G-E interactions [2].

Efficient study designs must be discussed in conjunction with statistical methods for analysis. While the prospective likelihood method for analyzing case-control genetic association studies is frequently applied [3], recent years have seen important advances in the development of statistically efficient methods for assessing G-E interactions. To analyze binary genetic and environmental variables in relation to a rare phenotype, under the constraint of G-E independence, the case-only method, which ignores data from controls and estimates the G-E interaction odds ratio (OR) parameter as the OR for G-E association in cases, is much more precise than the prospective case-control method [4]. This case-only OR estimate is actually the maximum likelihood estimate (MLE) of the same parameter in a log-linear model under the constraint of G-E independence in controls [5]. Chatterjee and Carroll [6] proposed to exploit the G-E independence in the maximum likelihood analysis of case-control data under a logistic regression model. Their method had much improved precision for estimating OR parameters that quantify joint G-E effects. Based on these powerful methods, Mukherjee et al. [7] proposed practical sample size calculation methods for designing case-control G-E interaction studies. In this work, we consider a di-allelic SNP and a binary environmental exposure for a rare phenotype and adopt a retrospective likelihood method for analysis. Our method not only constrains the control population by the G-E independence, but also by the Hardy-Weinberg Equilibrium (HWE) for the genotype variable. The analysis of two-phase designs coupled with this powerful method of analysis yields novel insights into cost-effective designs of G-E interaction studies.

This paper is organized as follows. In Section 2, we provide closed-form formulas for OR parameter estimates that quantify G-E main and interaction effects with standard case-control data. In Section 3, we provide closed-form formulas for the analysis of two-phase case-control data by extending results in Section 2. Using these formulas, we discuss the efficiency of four slightly different two-phase designs, where either G or E is collected only on a subset of cases and controls, or data for G or E from additional controls is supplemented. In Section 4, we perform extensive simulation studies to assess implications of the HWE constraint for testing OR association parameters with the standard case-control data and assess the efficiency of various two-phase design sampling strategies. We discuss practical implications of our findings in Section 5.

2. Maximum Likelihood Estimation with Standard Case-Control Data

Let E denote a binary environmental factor, G denote the count of the minor allele for a di-allelic SNP, and Y denote the case-control status (Y = 1: case; Y = 0: control). Data for (G, E) is collected from n₁ cases and n₀ controls. We describe the association between Y and (G, E) by a logistic regression model

$$\mathrm{logit}p(Y=1\mid G,E)={\beta }_0+{\beta }_{g}f\left(G\right)+{\beta }_{e}E+{\beta }_{1}E\times f\left(G\right)\equiv {\beta }_0+f(G,E;\beta )$$ (1)

where f(G) is a pre-specified function that reflects different numerical codings for G. For example, f(G) can be the count of the minor allele with f(G) = G (log-additive model), can be the presence or absence of the minor allele with f(G) = I_(G>0) (dominant model), or can be an indicator function for the genotype with f(G) = (I_(G=1),I_(G=2)) (co-dominant model). Denote β = (β_g, β_e, β_I). The case-control data for fitting model (1) is summarized in Table 1, for which the standard retrospective likelihood function can be written as ${\prod }_{i=1}^{n_1+n_0}p(G_i,E_i\mid Y_i)$. Following a result in Satten and Kupper [2], this standard likelihood function can also be written as

$$\prod _{i=1}^{n_1+n_0}p(G_i,E_i\mid Y_i=0)\prod _{j=1}^{n_1}\frac{e^{f(G_j,E_j;\beta )}}{\sum _{G,E}{e}^{f(G,E;\beta )p(G,E\mid Y=0)}}.$$ (2)

Table 1.

Case-Control Data for Estimating Odds Ratio Association Parameters.

	Y = 0			Y = 1
	E = 0	E = 1	Total	E = 0	E = 1	Total
G = 0	n 000 a	n 001	n 00+	n 100	n 101	n 10+
G = 1	n 010	n 011	n 01+	n 110	n 111	n 11+
G = 2	n 020	n 021	n 02+	n 120	n 121	n 12+
Total	n 0+0	n 0+1	n 0	n 1+0	n 1+1	n 1

^an_ijk = Σ_i,j,k I(Y = i, G = j, E = k).

Without any constraints, the nuisance probability p(G_j, E_j|Y_j = 0) in the above likelihood can be fully parameterized by 5 parameters. When the phenotype is rare, joint maximization of β and these 5 nuisance parameters leads to an estimate of β that is identical to that obtained from standard prospective likelihood analysis. We assume G-E independence and HWE in the control population, $p(G,E\mid Y=0)=p(G\mid Y=0)p(E\mid Y=0)$ and $p(G,\mid Y=0)2^{I(G=1)}{p}_a^G{(1-p_a)}^{2-G}$, where p_a denotes the minor allele frequency (MAF). Let p_e denote p(E = 1|Y = 0). The retrospective likelihood function can then be written as

$$\begin{array}{cc}\hfill L(\beta ,p_e,p_a)=& \prod _{i=1}^{n_1+n_0}{2}^{I(G_i=1)}{p}_e^{E_i}{(1-p_e)}^{1-E_i}{p}_a^{G_i}{(1-p_a)}^{2-G_i}\hfill \\ \hfill & \prod _{j=1}^{n_1}\frac{e^{f(G_j,E_j;\beta )}}{\sum _{G,E}{2}^{I(G=1)}{e}^{f(G,E;\beta )}{p}_a^G{(1-p_a)}^{2-G}{p}_e^E{(1-p_e)}^{1-E}},\hfill \end{array}$$

which we maximize to obtain the MLE of (β, p_a, p_e). We calculate the estimates in two steps. First, simple algebra leads to solutions ${\widehat{p}}_e=n_{0+1}∕n_0$ and

$$e^{{\widehat{\beta }}_e}=\frac{n_{1+1}{n}_{0+0}}{n_{1+0}{n}_{0+1}}\frac{\sum _G{e}^{{\beta }_{g}f\left(G\right)}p(G\mid Y=0)}{\sum _G{e}^{({\beta }_g+{\beta }_I)f\left(G\right)}p(G\mid Y=0)}.$$ (3)

Then we solve for ${\widehat{p}}_a$ and OR estimates of genetic effects among the exposed and unexposed, e^β_g and e^β*_g = e^β_g+β_I, from the following profile log-likelihood obtained by replacing (p_a, e^β_e) by $({\widehat{p}}_e,e^{{\widehat{\beta }}_e})$ in the likelihood function L(β, p_e, p_a):

$$\begin{array}{cc}\hfill \log L^{\ast }=& \sum _{i=1}^{n_1+n_0}\log p(G_i\mid Y_i=0)+\sum _{j_0=1}^{n_1+0}{\beta }_{g}f\left(G_{j0}\right)-n_{1+0}\log \sum _G{e}^{{\beta }_{g}f\left(G\right)}p(G\mid Y=0)\hfill \\ \hfill & +\sum _{i=1}^{n_1+n_0}({\beta }_g+{\beta }_I)f\left(G_{j1}\right)-n_{1+1}\log \sum _G{e}^{({\beta }_g+{\beta }_I)f\left(G\right)}p(G\mid Y=0).\hfill \end{array}$$

The estimate $e^{{\widehat{\beta }}_I}$ can then be obtained as $e^{{\widehat{\beta }}_g^{\ast }}∕e^{{\widehat{\beta }}_g}$. The estimate of the MAF, ${\widehat{p}}_a=(n_{01}+2n_{02+})∕\left(2n_0\right)$, is the same regardless of the numerical coding adopted for G. Below, we provide explicit formulas for $e^{{\widehat{\beta }}_g}$ and $e^{{\widehat{\beta }}_I}$ corresponding to different numerical codings for G, focusing on results for the most widely used log-additive model for G. We also provide formula for $e^{{\widehat{\beta }}_e}$ under the log additive model for G.

Estimation of OR Parameters under the Log-additive Model for G

Under the log-additive model for G, estimates $(e^{{\widehat{\beta }}_e},e^{{\widehat{\beta }}_g},e^{{\widehat{\beta }}_I})$ can be expressed explicitly as functions of the cell counts in Table 1:

$$e^{{\widehat{\beta }}_e}=\frac{n_{1+0}{n}_{0+0}}{n_{0+1}{n}_{1+1}}\frac{{(n_{111}+2n_{101})}^2}{{(n_{110}+2n_{100})}^2}$$

$$e^{{\widehat{\beta }}_g}=\frac{1-{\widehat{p}}_a}{{\widehat{p}}_a}\frac{n_{110}+2n_{120}}{n_{110}+2n_{100}},$$

$$e^{{\beta }_I}=\frac{(n_{110}+2n_{100})(n_{111}+2n_{121})}{(n_{111}+2n_{101})(n_{110}+2n_{120})}.$$

We found that both G-E independence and HWE constraints are required to obtain these closed-form formulas. That is, the HWE constraint does have an impact on the estimation of parameters that characterize the joint G-E effect. In the above formulas, the MAF estimate ${\widehat{p}}_a$ appeared only in ${\widehat{\beta }}_g$ but not in ${\widehat{\beta }}_I$. Therefore, we may conjecture that the impact will be mainly on the estimation of genetic main effect parameter β_g, but not much on the interaction parameter β_I. In fact,$e^{{\widehat{\beta }}_I}$ is the OR estimate based on a case-only analysis as follows. First, create a contingency table for cases that cross-classifies E and the two alleles, treating each chromosome as a subject and the environmental exposure E as the outcome variable. Then $e^{{\widehat{\beta }}_I}$ is the standard OR estimate from this 2-by-2 table. This result reminds the allelic OR for analyzing standard case-control SNP data, which is valid only under certain conditions [8]. These conditions, when applied to the current context, are as follows: i) the log-additive model is the true model for relating binary E and G in cases and ii) the HWE constraint is valid in the population of unexposed cases. Since the G-E independence and HWE in controls imply the HWE among the unexposed (E = 0), these two conditions are guaranteed as long as the penetrance model (1) is correct.

Interestingly, $e^{{\widehat{\beta }}_g}$ and $e^{{\widehat{\beta }}_g^{\ast }}$ , and thus $e^{{\widehat{\beta }}_I}$, can also be obtained directly via a stratified analysis as follows. That is, $e^{{\widehat{\beta }}_g}$> is the allelic OR based only on the unexposed cases and all n₀ controls regardless of the exposure status, and $e^{{\widehat{\beta }}_g^{\ast }}$ is the allelic OR similarly based only on exposed cases and all n₀ controls. Note that the allelic OR within each stratum is the MLE based on a similar likelihood as (2) where p(G|Y = 0) satisfies the HWE constraint. These observations reveal the impact of G-E independence and HWE constraints: analysis that is stratified on E with the most efficient analysis performed within each stratum results in the most efficient estimates of all association parameters. It is straightforward to obtain the variance-covariance matrix for $({\widehat{\beta }}_e,{\widehat{\beta }}_g,{\widehat{\beta }}_I)$ using results for standard multinomial distributions:

$$\text{var}\left({\widehat{\beta }}_e\right)=\frac{1}{n_{0+0}}+\frac{1}{n_{0+1}}+\frac{1}{n_{1+0}}+\frac{1}{n_{1+1}}+\frac{4n_{110}}{{(n_{110}+2n_{100})}^2}+\frac{4n_{110}}{{(n_{111}+2n_{101})}^2},$$

$$\text{var}\left({\widehat{\beta }}_g\right)=\frac{1}{n_{110}+2n_{120}}+\frac{1}{n_{110}+2n_{100}}+\frac{1}{2n_0{\widehat{p}}_a(1-{\widehat{p}}_a)},$$

$$\text{var}\left({\widehat{\beta }}_I\right)=\frac{1}{n_{110}+2n_{100}}+\frac{1}{n_{111}+2n_{121}}+\frac{1}{n_{111}+2n_{101}}+\frac{1}{n_{110}+2n_{120}},$$

$$\text{cov}\left({\widehat{\beta }}_e,{\widehat{\beta }}_g\right)=\frac{4n_{110}{n}_{1+0}}{{(n_{110}+2n_{100})}^2(n_{110}+2n_{120})},$$

$$\text{cov}\left({\widehat{\beta }}_e,{\widehat{\beta }}_I\right)=\frac{4n_{110}{n}_{1+0}}{{(n_{110}+2n_{100})}^2(n_{110}+2n_{120})}-\frac{4n_{111}{n}_{1+1}}{{(n_{111}+2n_{101})}^2(n_{111}+2n_{121})},$$

$$\text{cov}\left({\widehat{\beta }}_g,{\widehat{\beta }}_I\right)=-\frac{1}{n_{110}+2n_{120}}-\frac{1}{n_{110}+2n_{100}}.$$

Estimation Under the Co-dominant and Dominant Codings for G

We focus on the estimation of β_g and β_I, since $e^{{\widehat{\beta }}_e}$ can not be simplified as that under the log-additive coding. Similar to the log-additive model, closed-form estimates ${\widehat{\beta }}_g$ and ${\widehat{\beta }}_g^{\ast }$ can be obtained via efficient stratified analysis. For the analysis of case-control SNP genotype data under the co-dominant coding, the MLEs for the two OR parameters that exploit the HWE in controls have the same forms as the standard OR estimates based on 2-by-3 contingency tables but with the observed control counts replaced by the expected numbers under the HWE [9]. Let β_g = (β₁, β₂) be the logarithm of the two genetic main effect ORs, and β_I = (β_I1, β_I2) be the two interaction effects log ORs. Then $e^{{\widehat{\beta }}_1}$, $e^{{\widehat{\beta }}_2}$ and $e({\widehat{\beta }}_1+{\widehat{\beta }}_{I1})$, $e({\widehat{\beta }}_2+{\widehat{\beta }}_{I2})$ are obtained by applying results of Chen and Chatterjee [9] directly to unexposed cases and all controls and exposed cases and all controls, respectively. The closed-form formulas are as follows:

$$e^{{\widehat{\beta }}_1}=\frac{1-{\widehat{p}}_a}{2{\widehat{p}}_a}\frac{n_{110}}{n_{100}},e^{{\widehat{\beta }}_2}=\frac{{(1-{\widehat{p}}_a)}^2}{{\widehat{p}}_a^2}\frac{n_{120}}{n_{100}},$$

$$e^{{\widehat{\beta }}_{I1}}=\frac{n_{111}{n}_{100}}{n_{110}{n}_{101}},e^{{\widehat{\beta }}_{I2}}=\frac{n_{121}{n}_{100}}{n_{120}{n}_{101}}.$$

It appears that the HWE constraint indeed has an impact on the estimation of genetic main effects through the estimated MAF ${\widehat{p}}_a$. But the estimated interaction OR parameters $(e^{{\widehat{\beta }}_{I1}},e^{{\widehat{\beta }}_{I2}})$ appeared to be the same as those obtained under only G-E independence constraint, which approach the true parameter values as the sample size increases. Therefore, the estimation of interaction ORs is robust with respect to the HWE constraint under the co-dominant coding for G. Similar to the results under the log-additive coding, $(e^{{\widehat{\beta }}_{I1}},e^{{\widehat{\beta }}_{I2}})$ can be obtained based on the case-only analysis using cases with G = 0 or G = 1 or cases with G = 0 or G = 2, respectively. The estimates of all OR parameters can also be obtained by applying results of Chen and Chatterjee [9] separately to the analysis of all controls together with either exposed or unexposed cases. The variance-covariance matrix for $({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_{I1},{\widehat{\beta }}_{I2})$, following Chen and Chatterjee [9] formula, is as follows:

$$\left[\begin{array}{cccc}\hfill \frac{1}{n_{100}}+\frac{1}{n_{110}}+\frac{1}{2n_0}\frac{1}{{\widehat{p}}_a(1-{\widehat{p}}_a)}\hfill & \hfill \frac{1}{n_{100}}+\frac{1}{n_0{\widehat{p}}_a(1-{\widehat{p}}_a)}\hfill & \hfill -\frac{1}{n_{110}}-\frac{1}{n_{100}}\hfill & \hfill -\frac{1}{n_{100}}\hfill \\ \hfill \hfill & \hfill \frac{1}{n_{100}}+\frac{1}{n_{120}}+\frac{2}{n_0}\frac{1}{{\widehat{p}}_a(1-{\widehat{p}}_a)}\hfill & \hfill -\frac{1}{n_{100}}\hfill & \hfill -\frac{1}{n_{100}}-\frac{1}{n_{100}}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \sum _{i=0,1}\sum _{j=0,1}\frac{1}{n_{1ij}}\hfill & \hfill \frac{1}{n_{100}}+\frac{1}{n_{100}}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \sum _{i=0,2}\sum _{j=0,1}\frac{1}{n_{1ij}}\hfill \end{array}\right]$$

When the dominant coding is adopted for G, the MLE of e^βI, $e^{{\widehat{\beta }}_I}=n_{100}(n_{111}+n_{121})∕\left\{n_{101}(n_{110}+n_{120})\right\}$, is the OR estimate from the case-only analysis with E being the binary outcome variable, which is the same as that obtained under only the G-E independence constraint by Umbach and Weinberg [5]. The estimate of the main effect e^βg under the additional HWE constraint is different from that without the HWE constraint:

$$e^{{\widehat{\beta }}_g}=\frac{{(1-{\widehat{p}}_a)}^2}{{\widehat{p}}_a(2-{\widehat{p}}_a)}\frac{n_{110}+n_{120}}{n_{100}}.$$

The variance-covariance matrix for $(e^{{\widehat{\beta }}_g},e^{{\widehat{\beta }}_I})$ is

$$\left[\begin{array}{cc}\hfill \frac{1}{n_{100}}+\frac{1}{n_{110}+n_{120}}\frac{2{\widehat{p}}_a}{n_{0(1-{\widehat{p}}_a)}{(2-{\widehat{p}}_a^2)}^2}\hfill & \hfill -\frac{1}{n_{100}}-\frac{1}{n_{110}+n_{120}}\hfill \\ \hfill \hfill & \hfill \frac{1}{n_{100}}+\frac{1}{n_{111}+n_{121}}+\frac{1}{n_{101}}+\frac{1}{n_{110}+n_{120}}\hfill \end{array}\right].$$

The Estimation Bias when the G-E Independence or HWE is Violated

All above estimates approach the true parameter values as the sample size increases when the penetrance model (1) and both constraints are correct. It has been well recognized that deviation from the G-E independence constraint can lead to intolerable biases in parameter estimates even when the HWE constraint is not imposed [5,10]. Here, it appears that the consistency of the main effect OR estimates, $(e^{{\widehat{\beta }}_e},e^{{\widehat{\beta }}_g})$, requires that the HWE hold. For the estimation of the interaction OR parameter β_I, under the log-additive model, its consistency requires both G-E independence and HWE constraints. But under other models, only the G-E independence is required. The closed-form formulas we provided facilitate explicit quantification of the magnitude of the bias. We will not further discuss the bias issue since the main interest of the current work is to provide guidelines on optimal study designs. The power for different study designs assuming the above methods for analysis is optimal when the two constraints hold, and the corresponding sample sizes similarly represent the minimum required.

3. Two-Phase Case-Control Designs Under G-E Independence and HWE

In the simplest two-phase case-control design for assessing joint G-E effects, data for either E or G is available for all cases and controls, but that for the other one is available only on a selected subset. Without imposing the G-E independence or HWE constraints, the balanced design [11], which “balances” the numbers of phase II subjects, that is, those for whom both E and G are ascertained, in strata defined by the case-control status and variables completely collected on cases and controls (“phase I variable”), is nearly optimal for estimating the main and interaction effect parameters when analyzed by the maximum likelihood method [12]. Here, we consider four variants of the two-phase design: E is the phase I variable and G is ascertained on a subset of cases and controls (Design I) selected with or without referring to E; G is the phase I variable and E is ascertained on a subset of cases and controls selected with or without referring to G (Design II); Data on E is available on an external set of controls (Supplemented Design I); and data on G is available on an external set of controls (Supplemented Design II). The two supplemented designs are obviously special cases of designs I and II, respectively. Below we focus on the log-additive coding for G, and results under other codings can be obtained in a straightforward manner.

Qualitative Results on Merits of Four Designs

The results above for the standard case-control data immediately suggest efficient two-phase sampling strategies for the estimation and testing of genetic and environmental effects. First consider Design I where E is available for all cases and controls. Above, only the data from cases is used in interaction OR parameter estimates, where cases with E = 1 are used as “cases”, and cases with E = 0 are used as “controls”. To avoid confusion, below we refer to cases with E = 1 as “c-cases” and those with E = 0 as “c-controls”. The accompanying association model is

$$\mathrm{logit}p(E=1\mid G)={\alpha }^0+{\beta }_{I}f\left(G\right),$$ (4)

where f(G) is the same as that in model (1). Now consider that we design such a case-control study. Intuitively, standard principles for designing a retrospective case-control study would apply here: a desirable design would balance the numbers of c-cases and c-controls to achieve an optimal power. For analysis, one can simply ignore the selective sampling and perform standard prospective analysis. The estimate of β_I would be valid, although the intercept parameter estimate is not a consistent estimate of α^o [3]. The most efficient estimate of β_I is obtained by applying the retrospective likelihood method that exploits the HWE [9] to the data from the sampled c-cases and c-controls. Due to the G-E independence in the control sample, stratification on E in controls would not help improve the precision for estimating any association parameters. Therefore, Design I that selects a balanced sub-sample of exposed and unexposed cases and a random sample of controls for ascertaining G is preferable for the estimation and testing of genetic and environmental effects. Similarly, supplementing data for E (Supplemented Design I) is not expected to help the estimation of β_I, although it is expected to lead to improved prediction for estimating p_e and β_e.

For Design II where G is available for all cases and controls, the case-only analysis with model (4) using phase II cases yields valid estimates for both α^o and β_I, although the most efficient analysis would also utilize data for G for cases who are not selected into phase II. Similar as the arguments above, a balanced selection of cases with G = 0, G = 1 and G = 2 is expected to lead to improved efficiency for estimating β_I. In addition, data for G from additional controls (Supplemented Design II) would improve the efficiency for estimating β_g, but not β_I.

Estimation with Design I and Supplemented Design I

Let R be a binary variable taking values 1 or 0 depending on whether a subject is selected into phase II or not. For Design I, we obtained the parameter estimates by maximizing the likelihood function

$$\prod _{h=1}^{n_1}p{(G_h,E_h\mid Y_h=1)}^{R_h}p{(E_h\mid Y_h=1)}^{1-R_h}\prod _{k=1}^{n_0}p{(G_k,E_k\mid Y_k=0)}^{R_k}p{(E_k\mid Y_k=0)}^{1-R_k}.$$

We found that $e^{{\widehat{\beta }}_e}$ has the same form as (3) and ${\widehat{p}}_e=n_{0+1}∕n_0$, the estimates obtained when (E,G) is available for all n₁ cases and n₀ controls. For estimating (p_a, β_g, β_I), we found that the same profile likelihood as that for the standard case-control design above applies, except that only phase II cases and controls who have both G and E measurements are used. Therefore, estimates $(e^{{\widehat{\beta }}_g},e^{{\widehat{\beta }}_I})$ and their variance-covariance matrix are largely the same as those for the standard case-control design above, except that each count in the formula is replaced by the corresponding one in the phase II data. Let m₁ and m₀ denote the respective number of phase II cases and controls, and m_ijk has the same meaning as n_ijk. Under the log-additive coding for G, formulas for $e^{{\widehat{\beta }}_e}$ and var$\left({\widehat{\beta }}_e\right)$ are as follows:

$$e^{{\widehat{\beta }}_e}=\frac{n_{1+1}{n}_{0+0}}{n_{0+1}{n}_{1+0}}\frac{m_{1+0}^2{(m_{111}+2m_{101})}^2}{m_{1+1}^2{(m_{110}+2m_{100})}^2},$$

$$\text{var}\left({\widehat{\beta }}_e\right)=\frac{1}{n_{0+0}}+\frac{1}{n_{0+1}}+\frac{1}{n_{1+0}}+\frac{1}{n_{1+1}}+\frac{4m_{110}}{{(m_{110}+2m_{100})}^2}+\frac{4m_{111}}{{(m_{111}+2m_{101})}^2}.$$

In Supplemented Design I where data on E is available for m additional controls, let $m_1^s$ and $m_0^s$ be the number of supplemented controls with E = 1 and E = 0, respectively. We obtain ${\widehat{p}}_e=\frac{n_{0+1}+m_1^s}{n_0+m_1^s+m_0^s}$. Under the log-additive coding for G, the estimated main environmental effect and its asymptotic variance are as follows:

$$e^{{\widehat{\beta }}_e}=\frac{n_{1+0}(n_{0+0}+m_0^s)}{n_{1+1}(n_{0+1}+m_1^s)}\frac{{(n_{111}+2n_{101})}^2}{{(n_{110}+2n_{100})}^2},$$

$$\text{var}\left({\widehat{\beta }}_e\right)=\frac{1}{n_{0+0}+m_0^s}+\frac{1}{n_{0+1}+m_1^s}+\frac{1}{n_{1+0}}+\frac{1}{n_{1+1}}+\frac{4n_{110}}{{(n_{110}+2n_{100})}^2}+\frac{4n_{111}}{{(n_{111}+2n_{101})}^2}.$$

Estimates of other parameters remain the same as the standard case-control design.

Estimation with Design II and Supplemented Design II

Let R, m, and m_ijk be defined similarly as those for Design I. The likelihood function for Design II, where the selection of cases and controls for collecting E may stratify on G, can be written as

$$\prod _{h=1}^{n_1}p{(G_h,E_h\mid Y_h=1)}^{R_h}p{(G_h\mid Y_h=1)}^{1-R_h}\prod _{k=1}^{n_0}p{(G_k,E_k\mid Y_k=0)}^{R_k}p{(G_k\mid Y_k=0)}^{1-R_k}.$$

Contrary to Design I, one generally can not get closed-form estimates for OR estimates. This result may seem counter-intuitive since E and G appear to be symmetric in their relationship to the phenotype variable. But the difference in the analysis of Design I and Design II is that the distribution of the phase I variable G in Design II is constrained via the HWE, but the phase I variable E in Design I was not constrained. In an important special case where data for both E and G is collected for cases (but E is still available only for a subset of controls), the closed-form solutions exist for all OR parameters. In this case, ${\widehat{p}}_e=m_{0+1}∕m_0$, and

$$e^{{\widehat{\beta }}_e}=\frac{n_{1+0}{m}_{0+0}}{n_{1+1}{m}_{0+1}}\frac{{(n_{111}+2n_{101})}^2}{{(n_{110}+2n_{100})}^2},$$

$$\text{var}\left({\widehat{\beta }}_e\right)=\frac{1}{m_{0+0}}+\frac{1}{m_{0+1}}+\frac{1}{n_{1+0}}+\frac{1}{n_{1+1}}+\frac{4n_{110}}{{(n_{110}+2n_{100})}^2}+\frac{4n_{111}}{{(n_{111}+2n_{101})}^2}.$$

For Supplemented Design II where G is collected from m^s additional controls, the OR estimates and variance-covariance matrix have the same form as those for the standard case-control design, but with ${\widehat{p}}_a=(n_{01+}+2n_{02+}+m_{01}^s+2m_{02}^s)∕\left(2(n_0+m^s)\right)$ where $m_{01}^s$ , $m_{02}^s$ are the respective number of supplemented controls with genotypes 1 and 2.

4. SIMULATION STUDIES

We conducted extensive simulation studies to evaluate the power of different study designs for testing three hypotheses: i) null G-E interaction effect, β_I = 0; ii) null genetic effect, β_g = β_I = 0; and iii) null environmental effect, β_e = β_I = 0. We assumed the log additive model for G and used the Wald statistic for all tests based on the closed-form estimates provided in the above sections. First, we assessed the impact of imposing the HWE constraint on the estimation efficiency and power for testing different sets of association parameters under the standard case-control design. We considered the standard prospective method (“Standard”), the method that imposed the G-E independence constraint but not the HWE constraint (“GE-O”), and the method that imposed both the G-E independence and HWE constraints (“GE-HWE”). The comparison of these methods would shed light on the power improvement incurred by the two constraints. Next, with GE-HWE as the method of analysis, we compared the efficiency of four two-phase sampling strategies for testing the three hypotheses above. We considered a range of penetrance models in the form of (1) by varying the magnitude of OR parameters. For example, G may have an effect only in the presence of E, or E may have an effect only in the presence of G. We first generated data for controls, assuming that E followed a Bernoulli distribution and SNP genotype data G satisfied the HWE. Then we generated (G, E) for cases from the conditional distribution p(G, E|Y = 1) where

$$p(G,E\mid Y=1)=\frac{e^{{\beta }_g\times G+{\beta }_e\times E+{\beta }_I\times G\times E}p(G\mid Y=0)p(E\mid Y=0)}{\sum _{G,E}{e}^{{\beta }_g\times G+{\beta }_e\times E+{\beta }_I\times G\times E}p(G\mid Y=0)p(E\mid Y=0)}.$$

In all tests, we set the nominal level at 0.0001, assuming that 500 tests were performed. In practice, the test of β_g = β_I = 0 may be at a different significance level than that for testing β_e = β_I = 0. Here we used the same level mainly to facilitate power comparison. The test for all three hypotheses had type I error rates that were close to the nominal level, as shown in Table 2. We generated 5,000 replicates for assessing the power of all tests.

Table 2.

Type I Error Rates of GE-HWE at the Nominal Level 0.0001^a.

		Testing βg = βI = 0				Testing βe = βI = 0
MAF	e β e	Standard	GE-O	GE-HWE	e β g	Standard	GE-O	GE-HWE
0.2	1	4.097	4.166	4.000	1	4.398	3.989	4.097
	1.5	4.097	4.342	4.000	1.2	4.398	3.989	4.097
	2	4.398	4.642	4.301	1.5	3.921	4.245	4.155
0.3	1	4.000	4.699	4.222	1	4.523	4.301	4.222
	1.5	3.959	4.523	4.301	1.2	4.097	4.155	4.155
	2	4.097	4.155	3.959	1.5	4.523	4.301	4.222
0.4	1	4.155	4.699	4.097	1	4.046	4.000	4.000
	1.5	4.222	4.301	4.046	1.2	4.097	4.097	4.000
	2	4.222	4.699	4.046	1.5	4.000	4.097	4.155

^aWe generated 100,000 replicates, each with 500 cases and 500 controls for testing β_g = β_I = 0 or 300 cases and 300 controls for testing β_e = β_I = 0.

Displayed in the table is – log₁₀(type I error rate).

Relative Power of GE-HWE for the Standard Case-Control Design

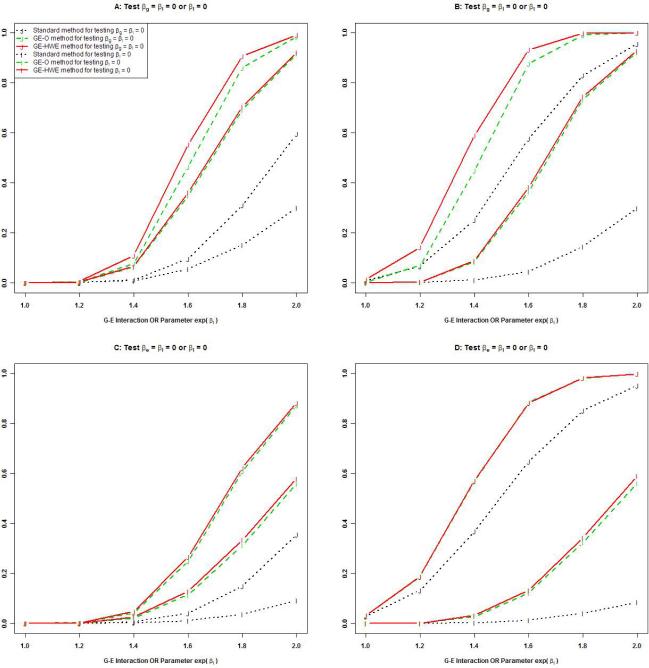
Panels A and B in Figure 1 demonstrate the relative power of the three methods for testing β_I = 0 and β_g = β_I = 0, where β_g = 0 for Panel A and β_g = ln(1.2) for Panel B. For testing β_I = 0, the power of GE-HWE appeared to be similar to that of GE-O, and both are higher than the standard method with the difference rising sharply with the magnitude of β_I. For example, with β_I = ln(1.5), the power difference was around 20%. But with β_I = 1.8, the power difference was around 60%. For testing β_g = β_I = 0, the power of GE-HWE and GE-O was very similar but much higher than the standard method. For example, the power difference was around 60% at β_I = ln(1.8) and β_g = 0 (Panel A) and was around 20% at β_I = ln(1.8) and β_g = ln(1.2). These data indicate that imposing the HWE constraint in addition to the G-E independence had limited influences on testing genetic effects or G-E interactions under the log-additive model for G. Panels C and D display the results for the relative power of the three methods for testing β_I = 0 and β_e = β_I = 0. Regardless of the presence or absence of the main effect of E (Panel C: β_e = 0; Panel D: β_e = log(1.5)), GE-HWE and GE-O have nearly identical power for both tests, and both had higher power than the standard method. This indicates that the HWE constraint hardly has any impact on power for testing β_e = β_I = 0.

Figure 1.

Power of the three methods under the standard case-control design. Panels A and B display the power for testing β_I = 0 or β_g = β_I = 0 in the absence (panel A) or presence (panel B) of the genetic main effect (e^βg = 1.2). Other parameters included p_e = 0.3, p_a = 0.3, and e^βI = 1.5. Each of the 1,000 replicates included 500 cases and 500 controls. Panels C and D display the power for testing β_I = 0 or β_e = β_I = 0 in the absence (panel C) or presence (panel D) of the environmental main effect (e^βe = 1.5). Other parameters included p_e = 0.3, p_a = 0.3, and e^βg = 1.2. Each of the 1,000 replicates included 300 cases and 300 controls. The size of the test was set at 0.0001.

We quantified the relationship between all parameter values and the ratio of power for GE-HWE to that for the standard method using simulation studies. We first obtained the relative power for a wide range of parameter setups. Then we performed linear regression analysis, using the log relative power as the outcome variable and the true parameter values as explanatory variables. The estimated mean log relative power for testing β_I = 0, β_g = β_I = 0, and β_e = β_I = 0 is 3.5−1.1p_a −0.33p_e +0.43β_g +0.17 β_e −2.88β_I, 1.51−0.44p_a −0.35p_e −0.57β_g −0.15β_I, and 1.6 − 0.5p_a − 0.56p_e + 0.02β_g + 0.44β_e − 0.30β_I, respectively. Therefore, the magnitude of β_I plays a dominant role in the relative power for testing G-E interactions, but the magnitude of β_g and β_e plays a greater role in testing genetic and environmental effects, respectively.

Table 3 presents the mean estimates, averaged estimated asymptotic variances, and empirical variances of the three methods, where the data was generated using the same parameter setup as that for panels A and B in Figure 1. The mean estimates with GE-HWE appeared to be close to the true parameter values. The averaged estimated asymptotic variances for all parameter estimates appeared to be close to their empirical counterparts. The empirical variances of main effect parameters estimated with GE-HWE were generally close to those of GE-O but smaller than that those under the standard method, and that for the interaction parameter β_I could be smaller by more than 60%.

Table 3.

Performance of GE-HWE for Estimation under G-E Independence and HWE

		Standard Method		GE-O		GE-HWE
Panela	Parameters	$\overline{\widehat{\beta }}$ b	$\text{var}\left(\widehat{\beta }\right)$ d	$\overline{\widehat{\beta }}$ b	$\overline{\mathrm{v}\widehat{a}\mathrm{r}\widehat{\beta }}$c/$\text{var}\left(\widehat{\beta }\right)$d	$\overline{\widehat{\beta }}$ b	$\overline{\mathrm{v}\widehat{a}\mathrm{r}\widehat{\beta }}$c/$\text{var}\left(\widehat{\beta }\right)$d
A	βg = 0.182	0.181	0.016	0.181	0.015/0.013	0.181	0.013/0.013
	βe = 0.405	0.401	0.037	0.403	0.028/0.028	0.403	0.028/0.028
	βI = 0.405	0.413	0.042	0.408	0.017/0.018	0.407	0.017/0.018
B	βg = 0	0.000	0.017	−0.001	0.016/0.015	−0.001	0.014/0.015
	βe = 0.405	0.406	0.037	0.405	0.028/0.028	0.407	0.027/0.028
	βI = 0.588	0.593	0.042	0.591	0.018/0.019	0.589	0.018/0.018

^aParameters used were the same as the corresponding panel in Figure 1.

^bThe averaged estimate based on 1,000 replicates.

^cThe averaged estimated asymptotic variance based on 1,000 replicates..

^dThe empirical variance based on 1,000 replicates..

Power of Design I and Design II for Testing β_g = β_I = 0 and β_e = β_I = 0

We investigated efficient two-phase design strategies for testing the genetic effect β_g = β_I = 0 and environmental effect β_e = β_I = 0 using GE-HWE for analysis. In each replicate, we first generated (Y, G, E) for 1,000 cases and 1,000 controls. Then we created a two-phase sample by selecting an equal proportion of cases and controls into phase II, and either data for G (Design I) or E (Design II) were deleted for those unselected. For cases, we selected the phase II subset either randomly or following a “balanced design” strategy by stratifying on E in Design I or G in Design II. The balanced design included all cases with E = 1 for a rare exposure in Design I, and it included as equal as possible numbers of cases with G = 0, G = 1, or G = 2 in Design II, respectively. With a small MAF, all cases with G = 2 are selected. To further evaluate the impact of control selection on the efficiency of the design, we considered two-phase designs with 300 phase II cases but a varying proportion of phase II controls ranging from 30% to 100%.

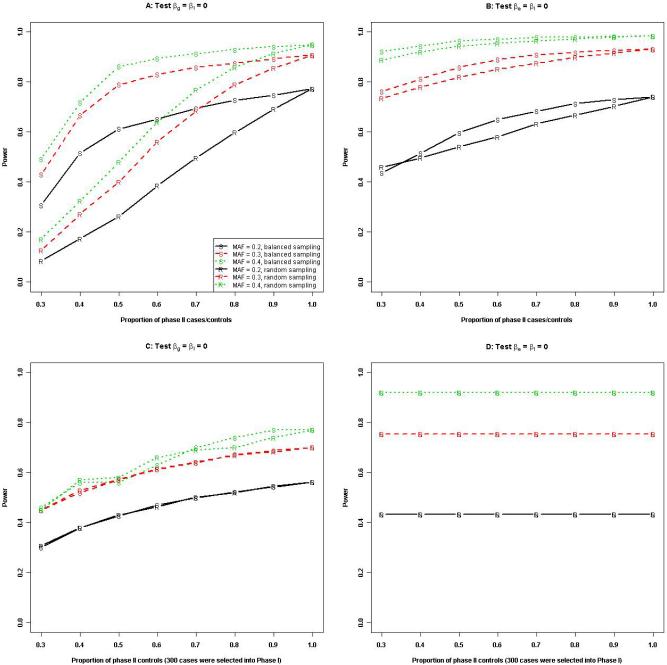
Figures 2 displays the power of Design I for testing β_g = β_I = 0 and β_e = β_I = 0 as a function of the proportion of phase II cases and/or controls. In general, the power under balanced sampling for testing β_g = β_I = 0 was much higher than that under random sampling, with the power difference becoming greater at smaller phase II case/control proportions and larger MAF (Panel A). But the difference between the two sampling strategies was small for testing β_e = β_I = 0 (Panel B). With a fixed subset of phase II cases, the power for testing genetic and environmental effect is nearly identical under both stratified and random sampling of controls (Panels C and D), and it increased with the proportion of selected controls for testing β_g = β_I = 0 (Panel C) but remained constant for testing β_e = β_I = 0 (Panel D). These results suggest that sampling stratified on E in cases is generally preferred for testing genetic effects or G-E interactions when data on E is available on all subjects. Parameter estimates corresponding to Panel C are presented in Table 4.

Figure 2.

Power of GE-HWE under Design I when phase II subjects were selected randomly or by stratifying on E. Phase I included 1,000 cases and 1,000 controls, and the significance level was set at 0.0001. Panels A and B present the power when an equal number of cases and controls were selected into phase II. Panels C and D present the power when 300 cases were selected into phase II by stratifying on E and varying numbers of controls were selected either randomly or also by stratifying on E. Other parameters included p_e = 0.15, e^βg = 1.2, e^βe = 1.2, and e^βI = 1.5.

Table 4.

Estimation with GE-HWE under Design I. The Parameters were the Same as Those Used in Figure 3C, Where 1,000 Cases and 1,000 Controls had data on E, and 300 Cases were Selected into Phase II Stratified on E.

		Stratified Sampling				Random Sampling
		300a		800		300		800
MAF	OR	$\overline{\widehat{X}}$ a	$\overline{\mathrm{v}\widehat{a}\mathrm{r}\widehat{X}}$b/$\text{var}\left(\widehat{X}\right)$c	$\overline{\widehat{X}}$ a	$\overline{\mathrm{v}\widehat{a}\mathrm{r}\widehat{X}}$b/$\text{var}\left(\widehat{X}\right)$c	$\overline{\widehat{X}}$ a	$\overline{\mathrm{v}\widehat{a}\mathrm{r}\widehat{X}}$b/$\text{var}\left(\widehat{X}\right)$c	$\overline{\widehat{X}}$ a	$\overline{\mathrm{v}\widehat{a}\mathrm{r}\widehat{X}}$b/$\text{var}\left(\widehat{X}\right)$c
0.2	βe = 0.182	0.185	0.024/0.024	0.185	0.024/0.024	0.185	0.024/0.024	0.185	0.024/0.024
	βg = 0.182	0.183	0.029/0.029	0.181	0.023/0.023	0.182	0.029/0.029	0.181	0.023/0.023
	βI = 0.405	0.405	0.035/0.035	0.405	0.035/0.035	0.405	0.035/0.035	0.405	0.035/0.035
0.3	βe = 0.182	0.178	0.031/0.031	0.178	0.031/0.031	0.178	0.031/0.031	0.178	0.031/0.031
	βg = 0.182	0.181	0.023/0.022	0.180	0.018/0.018	0.180	0.023/0.022	0.179	0.018/0.017
	βI = 0.405	0.411	0.029/0.028	0.411	0.029/0.028	0.411	0.029/0.028	0.411	0.029/0.028
0.4	βe = 0.182	0.184	0.041/0.038	0.184	0.041/0.038	0.184	0.041/0.038	0.184	0.041/0.038
	βg = 0.182	0.194	0.020/0.022	0.201	0.016/0.016	0.191	0.020/0.022	0.202	0.016/0.015
	βI = 0.405	0.394	0.027/0.024	0.394	0.027/0.024	0.394	0.027/0.024	0.394	0.027/0.024

^aThe averaged estimate based on 1,000 replicates.

^bThe averaged estimated asymptotic variance based on 1,000 replicates.

^cThe empirical variance based on 1,000 replicates.

Figure 3 displays the power of Design II for testing β_g = β_I = 0 and β_e = β_I = 0 as a function of the proportion of phase II cases and controls. In general, for testing β_g = β_I = 0, the difference between the two sampling strategies appeared to be small (Panel A), and the power remained constant with a varying proportion of phase II controls (Panel C) when the subset of phase II cases is fixed. On the other hand, the power under balanced sampling for testing β_e = β_I = 0 was much higher than that under random sampling, with the power difference getting greater at smaller phase II case/control proportions and larger prevalence of E (Panel B). The power under both balanced and random sampling of controls when the subset of phase II cases was fixed slightly increased with the proportion of selected controls (Panel D). These results suggest that sampling stratified on G in cases for ascertaining data for E is generally preferred for assessing environmental effects.

Figure 3.

Power of GE-HWE under Design II when phase II subjects were selected randomly or by stratifying on G. Phase I included 1,000 cases and 1,000 controls, and the significance level was set at 0.0001. Panels A and B present the power when an equal number of cases and controls were selected into phase II. Panels C and D present the power when 300 cases were selected into phase II by stratifying on G and varying numbers of controls were selected either randomly or also by stratifying on G. Other parameters included e^βg = 1.2, e^βe = 1.2, e^βI = 1.5, and p_a = 0.2.

Power of Supplemented Designs I and II

Figure 4 displays the power of Supplemented Design I for testing β_e = β_I = 0 as a function of the number of supplemented controls m at different values of p_e. The magnitude of power increase due to the supplement of additional control data for E increased with β_e, β_I, and p_e, particularly when m was less than 500. For example, with p_a = 0.2, p_e = 0.15, β_g = log(1.2), β_e = β_I = log(1.5) (Panel A), supplementing E from 500 and 2, 000 additional controls to data from 500 cases and 500 controls led to around 20% and 40% increase in power, respectively. But with β_e reduced to log(1.2), the respective increase was only around 5% and 10%. The power of Supplemented Design I for testing β_I = 0 and β_g = β_I = 0 remained constant regardless of the number of supplemented controls (data not shown).

Figure 4.

Power of GE-HWE for testing β_e = β_I = 0 under Supplemented Design I, where data for (G, E) for 300 cases and 300 controls was supplemented by data for E from varying numbers of controls. The significance level was set at 0.0001. The OR for the genetic main effect was e^βg = 1.2, and the MAF was p_a = 0.2.

Figure 5 displays the power of Supplemented Design II for testing β_g = β_I = 0 as a function of m, the number of additional controls with data on G. Similar as Supplemented Design I, the power increase at a given m appeared to be larger with increasing β_g. For example, with p_a = 0.2, p_e = 0.15, β_g = log(1.2), and β_I = log(1.5) (Panel A), supplementing G from 500 and 2000 controls to 300 cases and 300 controls led to 10% and 24% increase in power, respectively. But with p_a = 0.2, p_e = 0.15, β_g = log(1.2), and β_I = log(1.3), the respective increase was only 7% and 16%. In the absence of genetic main effect (β_g = 0), the respective increase became negligible. The increase also became sharper with a greater p_a. Not surprisingly, the power of Supplemented Design II for testing β_I = 0 and β_e = β_I = 0 remains nearly constant regardless of the number of supplemented controls (data not shown).

Figure 5.

Power of GE-HWE for testing β_g = β_I = 0 under Supplemented Design II where data for (G, E) for 500 cases and 500 controls was supplemented by data for G from varying numbers of controls. The significance level was set at 0.0001. The OR for the environmental main effect was e^βe = 1.5, and the MAF was p_e = 0.15.

DISCUSSION

We assessed the efficiency of two-phase case-control designs for assessing genetic and environmental effects when the control population is constrained by the G-E independence and HWE. A balanced selection of the exposed and unexposed cases appears to be a nearly optimal strategy for testing G-E interactions when data for cases can not be completely ascertained. Random sampling of controls suffices in the sense that stratified sampling in controls does not lead to improved power for association analysis. Supplementing data for G or E from additional controls generally does not help improve the power for testing G-E interactions. For testing genetic effects in the presence of G-E interactions, supplementing data for G from additional controls is helpful, particularly when the genetic effect is moderate or large. Similarly, supplementing data for E from additional controls is helpful for assessing environmental effects in the presence of G-E interactions, and the power increase becomes higher with increased environmental effects. Although we considered a binary environmental variable in this work, we expect that our conclusions hold when the environmental variable is continuous.

We obtained closed-form formulas for odds ratio association parameter estimates assuming a di-allelic SNP and a binary environmental variable. Regardless of the numerical coding adopted for the SNP genotype, we found that the estimation of the G-E interaction odds ratio parameter requires only the data of cases. In particular, the allelic odds ratio estimate in the case-only G-E interaction analysis is the MLE under the log-additive coding for the SNP genotype. Thus, our results generalized the case-only analysis with a binary genotype variable to a broader range of numerical coding schemes. For testing genetic effects or environmental effects in the presence of G-E interactions, incorporating the HWE constraint leads to improved power, although the HWE constraint hardly has any effect on the power for testing G-E interaction effects beyond that it is required to obtain closed-form estimates under the log-additive coding.

In this work, we assumed that the same numerical coding for the genotype variable was adopted in the main and multiplicative interaction effects. If the specification of the main effects is incorrect, the test for interaction would be invalid. In practice, one may base a test for interaction on a model where the co-dominant coding is adopted for the main effect of G. Then a valid test is guaranteed under the null hypothesis of no interaction. We did not consider this approach in this paper, mainly because we did not find closed-form estimates for OR parameters and because our conclusions for two-phase designs appeared to hold under this model.