Abstract
Metabolic pathway analysis, one of the most important fields in biochemistry, is pivotal to understanding the maintenance and modulation of the functions of an organism. Good comprehension of metabolic pathways is critical to understanding the mechanisms of some fundamental biological processes. Given a small molecule or an enzyme, how may one identify the metabolic pathways in which it may participate? Answering such a question is a first important step in understanding a metabolic pathway system. By utilizing the information provided by chemical-chemical interactions, chemical-protein interactions, and protein-protein interactions, a novel method was proposed by which to allocate small molecules and enzymes to 11 major classes of metabolic pathways. A benchmark dataset consisting of 3,348 small molecules and 654 enzymes of yeast was constructed to test the method. It was observed that the first order prediction accuracy evaluated by the jackknife test was 79.56% in identifying the small molecules and enzymes in a benchmark dataset. Our method may become a useful vehicle in predicting the metabolic pathways of small molecules and enzymes, providing a basis for some further analysis of the pathway systems.
Introduction
Metabolism defines a series of chemical reactions that occur in a cell, maintaining the lives of living organisms by supplying the necessary molecules and energy [1]. Metabolism is composed of metabolic pathways in which chemical reactions are organized in such a way that one molecule is transformed into another through a cascade of reactions recruiting small molecules and enzymes. Thus, small molecules and enzymes are part of the basic components of metabolic pathways. Determining the functioning of the small molecules and enzymes of each metabolic pathway is key to understanding the metabolic pathway and its biological functions.
During the past decade, large amounts of information concerning different organisms have been gathered on both the genetic and metabolic levels. Some databases pertaining to chemicals and proteins, such as KEGG (Kyoto Encyclopedia of Genes and Genomes) [2], [3], ENZYME [4], STITCH (Search Tool for Interactions of Chemicals) [5] and STRING (Search Tool for the Retrieval of Interacting Genes/Proteins) [6], have been established, from which descriptions of the properties of small molecules and enzymes can be readily acquired. Such information also provides an opportunity to study the metabolic pathways in greater detail computationally. A computational approach is another avenue by which to gain insight into metabolic pathways, apart from biochemical experiments. In recent years, some efforts [1], [7], [8] have been made to tackle the problem by mapping small molecules to the corresponding metabolic pathways. However, besides small molecules, enzymes are also important basic components of metabolic pathways. As far as we know, this study is the first to map small molecules and enzymes to the metabolic pathways simultaneously, thus providing some additional information for use in studying metabolic pathways.
A large body of data concerning protein-protein interactions and chemical-chemical interactions has been applied extensively to predicting the attributes of proteins and compounds [8], [9], [10], [11], [12], [13], [14]. This work led to the conclusion that interactive proteins or interactive compounds were more likely to share common biological functions than non-interactive ones. Most of these approaches studied chemical-chemical interactions or protein-protein interactions separately to construct classification models. In this study, we proposed a novel method, integrating interactions among chemicals and proteins including chemical-chemical interactions, protein-protein interactions, and chemical-protein interactions, to predict metabolic pathways in which small molecules and enzymes of yeast participate. Since some small molecules and enzymes participate in more than one metabolic pathway, our method sorts the probabilities of metabolic pathways to which a small molecule or enzyme may belong rather than predicting only the most probable metabolic pathway.
Materials and Methods
Benchmark Dataset
The dataset of small molecules to be studied was downloaded from the FTP site of the public database KEGG [2], [3] at ftp://ftp.genome.jp/pub/kegg (June, 2011), from which we extracted 17,641 small molecules. After excluding small molecules that do not participate in any metabolic pathway, 4,487 small molecules were retained. The dataset of enzymes of yeast were also acquired from the FTP site of the public database KEGG [2], [3] at ftp://ftp.genome.jp/pub/kegg (November, 2010). Likewise, those enzymes that do not participate in any metabolic pathway were excluded. Thus, we retained 655 enzymes of yeast, whose data on participation in metabolic pathways is available.
As described above, 4,487 small molecules and 655 enzymes of yeast have recoverable information concerning their participation in metabolic pathways. These samples were used to comprise a dataset S ce. However, not all samples can be used in our method due to the lack of interaction information. Those not having any interactions with other compounds or proteins in S ce were excluded. Finally, we obtained 4,002 samples including 3,348 small molecules and 654 enzymes, formulated by S = S c∪S e, where S denotes the benchmark dataset consisting of 4,002 samples, S c the dataset consisting of 3,348 small molecules, and S e the dataset set consisting of 654 enzymes.
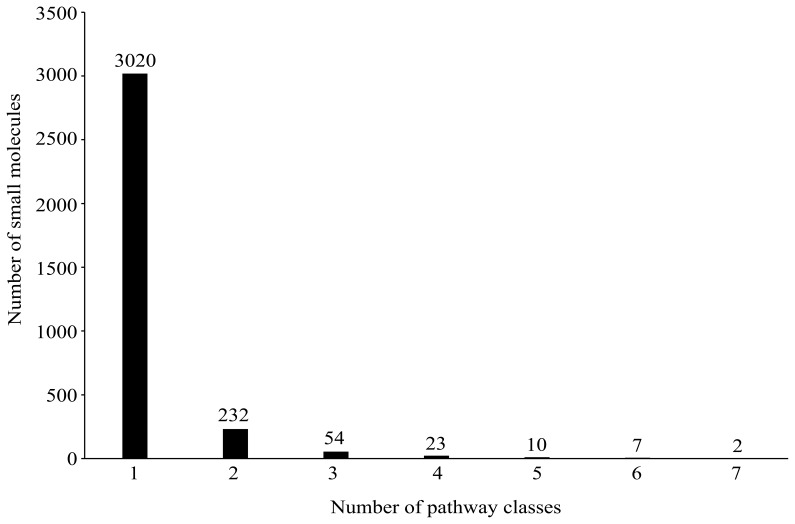
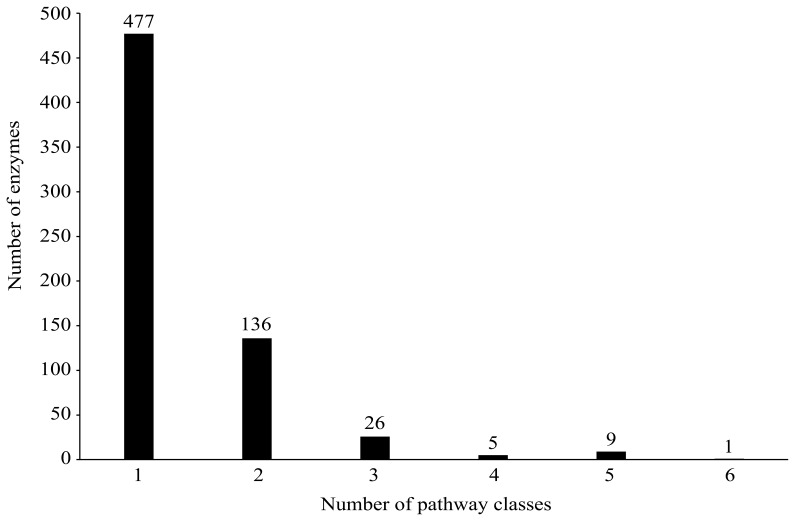
According to KEGG (http://www.genome.jp/kegg/pathway.html), there exist more than 150 metabolic pathways, classified into 11 major metabolic pathway classes (see column 2 of Table 1 ). Subsequently, 3,348 small molecules and 654 enzymes were mapped into the 11 major metabolic pathway classes. The distribution of these small molecules and enzymes is shown in Table 1 . The coding of small molecules and enzymes in each of the 11 major metabolic pathway classes can be found in Online Supporting Information S1. From column 3 of Table 1 , the sum of small molecules in all pathways is greater than the total number of small molecules in the dataset, indicating that some small molecules belong to more than one pathway class. In detail, 3,020 small molecules belong to only one pathway class, while others belong to more than one pathway class - see Figure 1 for the number of small molecules versus the number of pathway classes. Likewise, as given in column 4 of Table 1 , some enzymes also appear in more than one pathway class. In detail, 477 enzymes appear in only one pathway class, while others appear in at least two pathway classes (see Figure 2 for detail). In view of this, it appears to be a multi-label problem to predict the pathway classes of small molecules and enzymes. Similar to the cases in predicting some other attributes of proteins and compounds [11], [12], [15], [16], [17], the proposed method needs to provide a series of candidate pathway classes for a query small molecule or enzyme.
Table 1. Distribution of 3,348 small molecules and 654 enzymes of yeast in the 11 metabolic pathway classes.
| Tag | Metabolic pathway class | Number of small molecules | Number of enzymes | Total |
| M 1 | Carbohydrate Metabolism | 394 | 198 | 592 |
| M 2 | Energy Metabolism | 151 | 146 | 297 |
| M 3 | Lipid Metabolism | 399 | 84 | 483 |
| M 4 | Nucleotide Metabolism | 133 | 107 | 240 |
| M 5 | Amino Acid Metabolism | 489 | 158 | 647 |
| M 6 | Metabolism of Other Amino Acids | 156 | 44 | 200 |
| M 7 | Glycan Biosynthesis and Metabolism | 47 | 18 | 65 |
| M 8 | Metabolism of Cofactors and Vitamins | 350 | 87 | 437 |
| M 9 | Metabolism of Terpenoids and Polyketides | 507 | 18 | 525 |
| M 10 | Biosynthesis of Other Secondary Metabolites | 509 | 17 | 526 |
| M 11 | Xenobiotics Biodegradation and Metabolism | 709 | 21 | 730 |
| Total | – | 3,844 | 898 | 4,742 |
Figure 1. The number of small molecules against the number of pathway classes.
Figure 2. The number of enzymes against the number of pathway classes.
Construction of Hybrid Network
It is known that interactive proteins and compounds are more likely to share common biological functions [8], [9], [12], [13], [14], [18] than would non-interactive ones; given a compound, its biological functions may share the same functions with its interactive proteins. Conversely, the biological functions of a protein may also be similar to the functions of its interactive compounds. In this case, if a compound and a protein are interactive with one another, it would be more likely that they appear in the same metabolic pathway. In view of this, a hybrid interaction network was constructed as follows.
The constructed network takes small molecules and enzymes as its nodes, and an edge is drawn between two nodes if and only if the corresponding small molecule and enzyme can interact with one another. Different combinations of the participants lead to three kinds of interactions: chemical-chemical interactions, chemical-protein interactions, and protein-protein interactions. The data concerning chemical-chemical interactions and chemical-protein interactions was acquired from STITCH (http://stitch.embl.de/) [5], a well-known database containing known and predicted interactions of chemicals and proteins derived from experiments, literature and other databases. To more accurately represent the interaction network, each edge in the network was labeled with a score given as the edge weight to quantify the interaction confidence, i.e., the likelihood that an interaction may occur. For any two small molecules c 1 and c 2, their interaction confidence score, i.e., the weight of the edge with c 1 and c 2 as endpoints, was denoted by Qcc(c 1, c 2). Specifically, if the interaction between c 1 and c 2 does not exist in STITCH, their interaction confidence score was set to 0, i.e., Qcc(c 1, c 2) = 0. Likewise, the weight of the edge with one small molecule c and one enzyme e as endpoints was denoted by Qcp(c, e). In particular, the confidence score was set to be 0 if the interaction between c and p does not exist in STITCH. The data concerning protein-protein interactions was retrieved from STRING (http://string.embl.de/) [6], a large database containing known and predicted protein interactions including direct (physical) and indirect (functional) interactions that were derived from several sources such as experimental repositories and computational prediction methods. Like the previous case of chemical-chemical interactions and chemical-protein interactions, each edge with two proteins p 1 and p 2 as endpoints was labeled with a score, denoted by Qpp(p 1, p 2), to quantify the interaction confidence, i.e., the likelihood that an interaction may occur. In particular, if p 1 and p 2 are non-interactive proteins according to the data in STRING, their interaction confidence score was set to 0, i.e., Qpp(p 1, p 2) = 0.
Prediction Method
To describe the method more clearly, it is necessary to introduce some notations - let M 1, M 2, …, M 11 denote 11 metabolic pathway classes, where M 1 denotes “Carbohydrate Metabolism”, M 2 the “Energy Metabolism”, and so forth (see column 1 and 2 of Table 1 ). In addition, if one supposes that there are n samples in the training set, say s 1, s 2, …, sn. The pathway class of a sample si can be formulated as.
| (1) |
where
| (2) |
Toward a query sample (small molecule or enzyme) s, its pathway class was predicted by not only its neighbors in the network but also the weights of edges between the query one and its neighbors. Let N(s) denote a node set consisting of the neighbors of s. The likelihood that s belongs to Mj was calculated by.
| (3) |
where
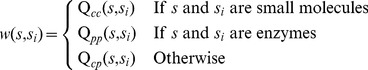 |
(4) |
Obviously, the larger the value of 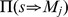 is, the more likely s belongs to Mj. If
is, the more likely s belongs to Mj. If 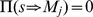 for some j, it implies that there are no interactive compounds or proteins of the query sample s in the training set that belong to pathway class Mj. In this case, it is thought that the probability of s belonging to Mj is zero. For a query sample s, if the results obtained from Eq. 3 are
for some j, it implies that there are no interactive compounds or proteins of the query sample s in the training set that belong to pathway class Mj. In this case, it is thought that the probability of s belonging to Mj is zero. For a query sample s, if the results obtained from Eq. 3 are
| (5) |
which suggests that it is most likely that s belongs to is M 3, followed by M 6, and so forth. Also, M 3 is called the 1-st order predicted pathway class of s, and M 6 the 2-nd order predicted pathway class of s, and so forth.
Jackknife Test
In statistical prediction, the jackknife test [19], one of the cross-validation methods, is often used to evaluate various predictors for their effectiveness. Compared with other cross-validation methods (independent dataset test and subsampling test), the jackknife test is deemed to be more objective [20], [21], [22]. For a given benchmark dataset, each sample can always be assigned to a unique predicted result through the jackknife test. Therefore, many investigators adopt this method to evaluate the accuracies of their predictors [19], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31]. It was also adopted here to evaluate the generalization of predicting the metabolic pathways.
Accuracy Measurement
For any query sample (small molecule or enzyme), the prediction method described in Section “Prediction method” will provide a series of candidate pathway classes. For the j-th order predicted pathway class, its prediction accuracy 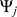 can be calculated by
can be calculated by
| (6) |
where CMj denotes the number of samples that are predicted correctly according its j-th order predicted pathway class, and N denotes the total number of samples in the dataset. For these 11 prediction accuracies, high 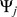 with small j and low
with small j and low 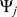 with large j indicate that the method arranges the candidate pathway classes well. The first order prediction accuracy is more important than others, because it has the smallest index of j.
with large j indicate that the method arranges the candidate pathway classes well. The first order prediction accuracy is more important than others, because it has the smallest index of j.
Since the 11 prediction accuracies calculated by Eq. 6 cannot evaluate the prediction method on the whole, another measurement is needed to calculate the probability of all pathway classes that are correctly predicted according to the first m predicted candidate pathways classes as follows [11], [15].
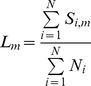 |
(7) |
where Si,m denotes the number of the correctly predicted pathway classes of the i-th sample among its first m predicted candidate pathway classes, and Ni denotes the number of pathway classes that the i-th sample belongs to. Usually, we calculate Eq. 7 by taking m as the smallest integer equal to or greater than the average number of samples’ pathway classes in the dataset, which is calculated by
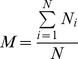 |
(8) |
Obviously, a large Lm always implies a good performance for mapping small molecules or enzymes into correct metabolic pathway class.
Results and Discussion
Performance of the Prediction Method for Small Molecules
In the training dataset, 3,348 small molecules comprised the dataset S c. The pathway classes of these molecules were predicted by the prediction method described in Section “Prediction method” by the jackknife test based on all samples in benchmark dataset. Here, an example is given to demonstrate how we made the prediction. “C07277”, belonging to M 9, is a sample in S c. Its interactive compounds and proteins were shown from row 1 to 6 in Table 2 . Using Eq. 3, the likelihood that “C07277” belongs to each of 11 pathway classes was calculated and shown in Table 3 . As a result, “C07277” belongs to M 1 with the highest likelihood, followed by M 9, M 10 and M 4. The 1-st order predicted pathway class was not its true pathway class, while its 2-nd order predicted pathway class was its true pathway class. After the pathway classes of each sample in S c were predicted, 11 ordered prediction accuracies were obtained by Eq. 6 and listed in column 2 of Table 4 , from which we can see that the first order prediction accuracy was 77.12%. It is also observed form column 2 of Table 4 that the prediction accuracy generally followed a descending trend when increasing the order number, which indicates that our method sorted the predicted pathway classes well. The average number of pathway classes for small molecules was 1.15 (3,844/3,348) according to Eq. 8, i.e., M = 1.15. Thus we consider the first 2 predicted pathway classes for each small molecule. After collecting these pathway classes calculated according to Eq. 7, it was observed that the probability that all true pathway classes were covered by them was 83.81%. Our results are comparable to that in [8], where the results were obtained by only chemical-chemical interactions.
Table 2. The interactive compounds and proteins of C07277 and YLL058W.
| Row index | Compound/Enzyme | Compound/Enzyme | Interaction confidence score | Tag of metabolic pathway class a |
| 1 | C07277 | C00103 | 409 | M 1, M 9, M 10 |
| 2 | C07277 | C00363 | 441 | M 4 |
| 3 | C07277 | C00507 | 416 | M 1 |
| 4 | C07277 | C03319 | 446 | M 9, M 10 |
| 5 | C07277 | C11912 | 63 | M 9 |
| 6 | C07277 | YDL055C | 298 | M 1 |
| 7 | YLL058W | C00087 | 317 | M 2 |
| 8 | YLL058W | C00109 | 900 | M 1, M 5 |
| 9 | YLL058W | C00155 | 900 | M 2, M 5 |
| 10 | YLL058W | C00283 | 317 | M 2, M 5 |
| 11 | YLL058W | C00542 | 904 | M 2 |
| 12 | YLL058W | C01077 | 900 | M 2, M 5 |
| 13 | YLL058W | C02291 | 900 | M 5 |
| 14 | YLL058W | C05688 | 900 | M 6 |
| 15 | YLL058W | C05699 | 900 | M 6 |
| 16 | YLL058W | YAL012W | 463 | M 2, M 5 |
| 17 | YLL058W | YGL184C | 241 | M 2, M 5 |
The information in this column represents the metabolic pathway classes of the compound or enzyme in column 3.
Table 3. The likelihood of C07277 and YLL058W belonging to each pathway class.
| Test sample | Likelihood for each pathway class | Remark a |
| C07277 | M 1: 1,123 | Sum of confidence scores in row 1,3,6 of Table 2 |
| M 2: 0 | – | |
| M 3: 0 | – | |
| M 4: 441 | Sum of confidence scores in row 2 of Table 2 | |
| M 5: 0 | – | |
| M 6: 0 | – | |
| M 7: 0 | – | |
| M 8: 0 | – | |
| M 9: 918 | Sum of confidence scores in row 1,4,5 of Table 2 | |
| M 10: 855 | Sum of confidence scores in row 1,4 of Table 2 | |
| M 11: 0 | – | |
| YLL058W | M 1: 900 | Sum of confidence scores in row 8 of Table 2 |
| M 2: 4,042 | Sum of confidence scores in row 7,9,10,11,12,16,17 of Table 2 | |
| M 3: 0 | – | |
| M 4: 0 | – | |
| M 5: 4,621 | Sum of confidence scores in row 8,9,10,12,13,16,17 of Table 2 | |
| M 6: 1,800 | Sum of confidence scores in row 14,15 of Table 2 | |
| M 7: 0 | – | |
| M 8: 0 | – | |
| M 9: 0 | – | |
| M 10: 0 | – | |
| M 11: 0 | – |
The information in this column shows the means by which the likelihood in column 2 was calculated by using the data in Table 2.
Table 4. The prediction accuracies obtained by our method for small molecules, enzymes, and all samples.
| Prediction order | Prediction accuracy forsmall molecules (Sc) | Prediction accuracy forenzymes (Se) | Prediction accuracy fortotal samples S = Sc∪Se |
| 1 | 77.12% | 92.05% | 79.56% |
| 2 | 19.12% | 22.48% | 19.67% |
| 3 | 7.38% | 10.55% | 7.90% |
| 4 | 3.61% | 4.13% | 3.70% |
| 5 | 2.75% | 4.13% | 2.97% |
| 6 | 1.40% | 1.83% | 1.47% |
| 7 | 0.96% | 0.76% | 0.92% |
| 8 | 0.51% | 0.76% | 0.55% |
| 9 | 0.45% | 0.61% | 0.47% |
| 10 | 0.30% | 0.00% | 0.25% |
| 11 | 0.15% | 0.00% | 0.12% |
Performance of the Prediction Method for Enzymes
In addition to the small molecules, there were 654 enzymes in the training dataset, which comprised dataset S e. Our prediction method was also applied to predict their metabolic pathway classes, evaluated by the jackknife test. Likewise, “YLL058W”, a sample in S e, was selected to demonstrate how its predicted pathway classes were obtained. “YLL058W” belongs to two pathway classes: M 2 and M 5. Its interactive compounds and proteins were shown from row 7 to 17 in Table 2 and the likelihood of “YLL058W” belonging to each of 11 pathway classes was shown in Table 3 , from which we can see that “YLL058W” belonging to M 5 is most likely, followed by M 2, M 6 and M 1. The first two predicted pathway classes were its true pathway classes. After processing by Eq. 6, 11 ordered prediction accuracies were obtained. These accuracies were listed in column 3 of Table 4 , from which we can see that the first order prediction accuracy was 92.05%. The average number of pathway classes for enzymes was 1.37 (898/654) according to Eq. 8, i.e., M = 1.37, meaning that the average success rate by a random guess would be 12.46% (1.37/11), which is much lower than that by our method. Like the 11 ordered prediction accuracies for small molecules, those for enzymes also generally followed a descending trend when increasing the order number (cf. Table 4 ), which suggests that the predicted pathway classes were sorted quite well. As described above, the average number of pathway classes for enzymes was 1.37. Eq. 7 was calculated by taking m = 2, yielding a probability of 83.41% that all true pathway classes were covered by the first 2 predicted classes.
Performance of the Prediction Method for All Samples
The predicted results for all samples in the benchmark dataset S combined the results of small molecules in dataset S c and enzymes in dataset S e. Listed in column 4 of Table 4 were 11 ordered prediction accuracies, from which the first ordered prediction accuracy was 79.56%. The average number of pathway classes for the samples in S was 1.18 (4,742/4,002) according to Eq. 8, i.e., M = 1.18, meaning that the average success rate by a random guess would be 10.73% (1.18/11), much lower than that obtained by our method. Meanwhile, it is observed from column 4 of Table 4 that the 11 prediction accuracies followed a descending trend when increasing the order number, suggesting that the predicted pathway classes, for both small molecules and enzymes, were sorted quite well by our method. Since the average number of pathway classes for all samples in S was 1.18, the first two predicted pathway classes for each sample were considered. After collecting these pathway classes calculated by Eq. 7 by taking m = 2, 83.74% true pathway classes were covered by the first 2 predicted pathway classes.
Confidence Scores of Small Molecules or Enzymes
As illustrated by the above sections, our method is very effective in predicting the metabolic pathway classes of small molecules and enzymes, indicating that interactive small molecules or enzymes are very likely to appear in a common metabolic pathway. In this section, we analyze the confidence score and illustrate the value in utilizing such scores.
The network constructed contains 4,002 samples and 100,754 interactions, including 66,942 chemical-chemical interactions, 19,695 chemical-protein interactions, and 14,117 protein-protein interactions. As described in Section “Construction of hybrid network”, each interaction was labeled with a confidence score ranging from 1 to 999, quantifying the likelihood that an interaction occurs. For each integer k in the interval [1, 999], the following rate was calculated for each kind of interaction.
| (9) |
where Ik is the number of interactions with confidence score to be at least k, and IMk is the number of interactions with their confidence score to be at least k and their corresponding small molecules or enzymes belonging to at least one common pathway class. The superscript of Eq. 9 was to differentiate three different kinds of interactions – 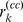 is for chemical-chemical interaction,
is for chemical-chemical interaction, 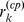 for chemical-protein interaction, and
for chemical-protein interaction, and 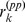 for protein-protein interaction. It is clear that the value of Eq. 9 quantifies the contribution of the interactions with confidence score at least k for predicting the pathway classes of small molecules and enzymes in our method. For each kind of interaction, we can plot a curve with
for protein-protein interaction. It is clear that the value of Eq. 9 quantifies the contribution of the interactions with confidence score at least k for predicting the pathway classes of small molecules and enzymes in our method. For each kind of interaction, we can plot a curve with 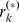 as its Y-axis and the subscript k as its X-axis. For clarity, the curve for chemical-chemical interactions is named the chemical-chemical curve, the curve for chemical-protein interactions is the chemical-protein curve, and that for protein-protein interactions is the protein-protein curve. Shown in
Figure 3
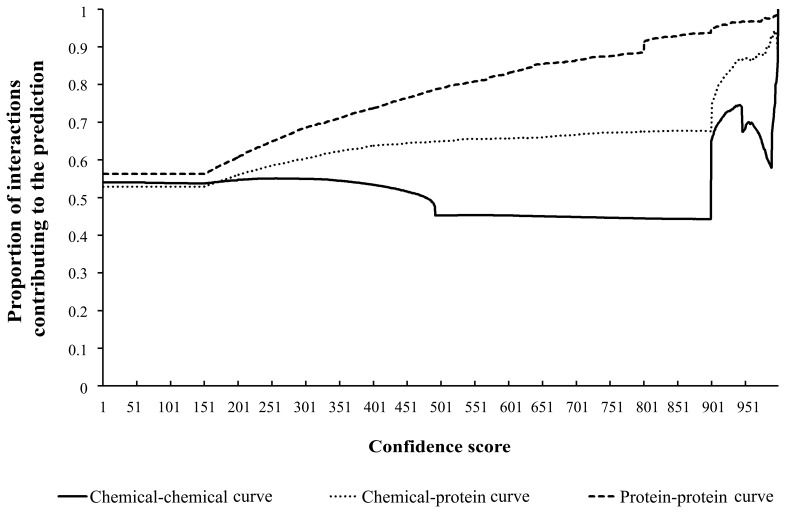
are three curves, from which we can see that the chemical-protein curve and protein-protein curve generally follow an increasing trend when increasing the confidence score; while the chemical-chemical curve does not look good in terms of its overall trend – the rate remains at a low level (between 40%−60%) when k < ∼900, and when k > ∼900, the rate starts to increase quickly. These data indicate that the proportions of the interactions contributing to the prediction in the method become higher and higher with the increasing of confidence score, meaning that the confidence scores of interactions are related to the prediction of enzymes and compounds in a metabolic pathway. It is, therefore, foreseeable that as the interactions become more evidenced in STRING and STITCH, predictions requiring confidence scores will also be improved accordingly. Finally, it is important to note that when taking all interactive enzymes or compounds into consideration, more than half of the interactions would provide contributions to the prediction, indicating that using interaction information of proteins and chemicals to predict their metabolic pathways is reasonable. It is also the basis upon which our method performs well.
as its Y-axis and the subscript k as its X-axis. For clarity, the curve for chemical-chemical interactions is named the chemical-chemical curve, the curve for chemical-protein interactions is the chemical-protein curve, and that for protein-protein interactions is the protein-protein curve. Shown in
Figure 3
are three curves, from which we can see that the chemical-protein curve and protein-protein curve generally follow an increasing trend when increasing the confidence score; while the chemical-chemical curve does not look good in terms of its overall trend – the rate remains at a low level (between 40%−60%) when k < ∼900, and when k > ∼900, the rate starts to increase quickly. These data indicate that the proportions of the interactions contributing to the prediction in the method become higher and higher with the increasing of confidence score, meaning that the confidence scores of interactions are related to the prediction of enzymes and compounds in a metabolic pathway. It is, therefore, foreseeable that as the interactions become more evidenced in STRING and STITCH, predictions requiring confidence scores will also be improved accordingly. Finally, it is important to note that when taking all interactive enzymes or compounds into consideration, more than half of the interactions would provide contributions to the prediction, indicating that using interaction information of proteins and chemicals to predict their metabolic pathways is reasonable. It is also the basis upon which our method performs well.
Figure 3. Three curves showing the changes of proportions of interactions contributing to the prediction when increasing the confidence score, where the chemical-chemical curve addresses chemical-chemical interactions, chemical-protein curve chemical-protein interactions, protein-protein curve protein-protein interactions.
The X-axis is the confidence score. The Y-axis is the proportion of interactions contributing to the prediction. Generally, chemical-protein curve and protein-protein curve are ascending with the increase of confidence score, while chemical-chemical curve remains at a low level for low confidence scores and starts to increase quickly for high confidence scores.
Analysis of Samples with Incorrect 1-st Order Predictions
Although our method performs well, where the 1-st order prediction accuracy for all samples achieved 79.56%, 818 samples (818/4002, 20.44%) achieved incorrect 1-st order predictions. The distribution of these misclassified samples in the 11 pathway classes is shown in Table 5 . We investigate these samples in depth and explain why these samples were misclassified as follows. Based on the principle of the method, the likelihood that a misclassified sample belongs to its 1-st order predicted pathway class was greater than those of true pathway classes, while the likelihood of a sample belonging to one class is calculated by summing the confidence scores between the sample and its neighbors belonging to that class. Thus, it would be interesting to investigate sum terms of the likelihood that a misclassified sample belongs to a 1-st order predicted pathway class and true pathway classes. The misclassified sample “C00439” belongs to pathway class M 5, while its 1-st order predicted pathway class was M 8. Shown in Table 6 are the interactive compounds and enzymes of “C00439” in M 5 and M 8, and the last row of Table 6 shows the likelihood of “C00439” belonging to M 5 and M 8. Two difficult situations were observed from Table 6 as follows: (1) sum terms for 1-st order predicted pathway class were greater than those of true pathway classes; (2) sum terms with values greater than 700, which is deemed the threshold of interactions with high confidence [32], [33], for 1-st order predicted pathway class were greater than those of true pathway classes. Due to the method of calculating the likelihood (cf. Eq. 3), it is highly possible that a query sample satisfying one of the above situations would be predicted incorrectly. Among 818 misclassified samples, 556 (556/818, 67.97%) samples fit the first situation; while 604 (604/818, 73.84%) samples fit the second situation. Furthermore, 762 (762/818, 93.15%) samples fit at least one of the two situations. As a result, these samples were all misclassified. On the other hand, the incompleteness of the interaction information may be another important reason. When interactions, especially those with high confidence scores, for the true class are missing in the calculation, the prediction is likely to be incorrect.
Table 5. The distribution of samples with incorrect 1-st order predicted pathway class in 11 pathway classes.
| Metabolic pathway class | Number of misclassified samples |
| Carbohydrate Metabolism | 105 |
| Energy Metabolism | 32 |
| Lipid Metabolism | 79 |
| Nucleotide Metabolism | 26 |
| Amino Acid Metabolism | 146 |
| Metabolism of Other Amino Acids | 79 |
| Glycan Biosynthesis and Metabolism | 21 |
| Metabolism of Cofactors and Vitamins | 107 |
| Metabolism of Terpenoids and Polyketides | 107 |
| Biosynthesis of Other Secondary Metabolites | 95 |
| Xenobiotics Biodegradation and Metabolism | 113 |
| Total | 910 a |
The value in this cell is larger than the total number of samples with incorrect 1-st order prediction because some samples belong to more than one pathway class.
Table 6. Interactive compounds and enzymes of C00439 in pathway classes M 5 and M 8.
| Index | Interactive compounds and enzymes in M 5 | Interactive compounds and enzymes in M 8 | ||
| Compound/Enzyme | Confidence score | Compound/Enzyme | Confidence score | |
| 1 | C01045 | 940 | C00101 | 934 |
| 2 | C00785 | 938 | C00445 | 927 |
| 3 | C00101 | 934 | C00025 | 923 |
| 4 | C00025 | 923 | C00001 | 899 |
| 5 | C00014 | 901 | C00018 | 899 |
| 6 | C03680 | 899 | C00664 | 899 |
| 7 | C01817 | 511 | C03479 | 899 |
| 8 | C05568 | 388 | C14818 | 899 |
| 9 | C00135 | 302 | C14819 | 899 |
| 10 | C00073 | 283 | C00504 | 739 |
| 11 | C02170 | 191 | C00234 | 438 |
| 12 | – | – | C00992 | 378 |
| 13 | – | – | C00440 | 205 |
| 14 | – | – | YGL125W | 177 |
| Likelihood | – | 7,210 | – | 10,115 |
Conclusions
By integrating the data for chemical-chemical interactions, chemical-protein interactions, and protein-protein interactions, a multi-label prediction model was developed to identify the metabolic pathway classes of small molecules and enzymes. Since interactive chemicals and proteins are more likely to involve a common pathway, the first order prediction accuracy achieved by our method was 79.56%, much higher than the average success rate by a random guess. Our analysis shows that interactive chemicals or proteins with higher confidence scores would be more likely to participate in the same metabolic pathway. We hope that this method may facilitate the understanding of metabolic pathway systems. It is also anticipated that prediction accuracy will increase as more and more interaction information concerning chemicals and proteins becomes available.
Supporting Information
List of the 4,002 samples, including 3,348 small molecules and 654 enzymes of yeast, classified into 11 metabolic pathway classes.
(PDF)
Funding Statement
National Basic Research Program of China (2011CB510102, 2011CB510101), Innovation Program of Shanghai Municipal Education Commission (No.12YZ120, No. 12ZZ087). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Lu J, Niu B, Liu L, Lu WC, Cai YD (2009) Prediction of Small Molecules Metabolic Pathways Based on Functional Group Composition. Protein and Peptide Letters 16: 969–976. [DOI] [PubMed] [Google Scholar]
- 2. Kanehisa M, Goto S (2000) KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Research 28: 27–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kanehisa M, Goto S, Hattori M, Aoki-Kinoshita K, Itoh M, et al. (2006) From genomics to chemical genomics: new developments in KEGG. Nucleic Acids Research 34: D354–D357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Bairoch A (1994) The ENZYME data bank. Nucleic Acids Research 22: 3626–3627. [PMC free article] [PubMed] [Google Scholar]
- 5. Kuhn M, von Mering C, Campillos M, Jensen LJ, Bork P (2008) STITCH: interaction networks of chemicals and proteins. Nucleic Acids Res 36: D684–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Jensen LJ, Kuhn M, Stark M, Chaffron S, Creevey C, et al. (2009) STRING 8-a global view on proteins and their functional interactions in 630 organisms. Nucleic acids research 37: D412–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Cai YD, Qian Z, Lu L, Feng KY, Meng X, et al. (2008) Prediction of compounds’ biological function (metabolic pathways) based on functional group composition. Molecular Diversity 12: 131–137. [DOI] [PubMed] [Google Scholar]
- 8. Hu LL, Chen C, Huang T, Cai YD, Chou KC (2011) Predicting Biological Functions of Compounds Based on Chemical-Chemical Interactions. PLoS ONE 6: e29491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Sharan R, Ulitsky I, Shamir R (2007) Network-based prediction of protein function. Molecular systems biology 3: 88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Huang T, Shi XH, Wang P, He Z, Feng KY, et al. (2010) Analysis and prediction of the metabolic stability of proteins based on their sequential features, subcellular locations and interaction networks. PLoS ONE 5: e10972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Hu LL, Huang T, Shi X, Lu WC, Cai YD, et al. (2011) Predicting functions of proteins in mouse based on weighted protein-protein interaction network and protein hybrid properties. PLoS ONE 6: e14556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Chen L, Zeng WM, Cai YD, Feng KY, Chou KC (2012) Predicting Anatomical Therapeutic Chemical (ATC) Classification of Drugs by Integrating Chemical-Chemical Interactions and Similarities. PLoS ONE 7: e35254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Bogdanov P, Singh AK (2010) Molecular Function Prediction Using Neighborhood Features. Ieee-Acm Transactions on Computational Biology and Bioinformatics 7: 208–217. [DOI] [PubMed] [Google Scholar]
- 14. Kourmpetis YAI, van Dijk ADJ, Bink MCAM, van Ham RCHJ, ter Braak CJF (2010) Bayesian Markov Random Field Analysis for Protein Function Prediction Based on Network Data. PLoS ONE 5: e9293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hu LL, Huang T, Cai YD, Chou KC (2011) Prediction of Body Fluids where Proteins are Secreted into Based on Protein Interaction Network. PLoS ONE 6: e22989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Chou KC, Cai YD (2005) Predicting protein localization in budding yeast. Bioinformatics 21: 944. [DOI] [PubMed] [Google Scholar]
- 17. Chou K, Shen H (2010) A new method for predicting the subcellular localization of eukaryotic proteins with both single and multiple sites: Euk-mPLoc 2.0. PLoS ONE 5: e9931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ng KL, Ciou JS, Huang CH (2010) Prediction of protein functions based on function-function correlation relations. Computers in Biology and Medicine 40: 300–305. [DOI] [PubMed] [Google Scholar]
- 19. Chou KC, Zhang CT (1995) Prediction of protein structural classes. Critical reviews in biochemistry and molecular biology 30: 275–349. [DOI] [PubMed] [Google Scholar]
- 20. Chou KC, Shen HB (2007) Recent progress in protein subcellular location prediction. Analytical Biochemistry 370: 1–16. [DOI] [PubMed] [Google Scholar]
- 21. Chou KC (2011) Some remarks on protein attribute prediction and pseudo amino acid composition. Journal of theoretical biology 273: 236–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Chou KC, Shen HB (2010) Cell-PLoc 2.0: an improved package of web-servers for predicting subcellular localization of proteins in various organisms. Natural Science 2: 1090–1103. [DOI] [PubMed] [Google Scholar]
- 23. Shao X, Tian Y, Wu L, Wang Y, Jing L, et al. (2009) Predicting DNA-and RNA-binding proteins from sequences with kernel methods. Journal of Theoretical Biology 258: 289–293. [DOI] [PubMed] [Google Scholar]
- 24. Zeng Y, Guo Y, Xiao R, Yang L, Yu L, et al. (2009) Using the augmented Chou's pseudo amino acid composition for predicting protein submitochondria locations based on auto covariance approach. Journal of Theoretical Biology 259: 366–372. [DOI] [PubMed] [Google Scholar]
- 25. Li FM, Li QZ (2008) Predicting Protein Subcellular Location Using Chou's Pseudo Amino Acid Composition and Improved Hybrid Approach. Protein and Peptide Letters 15: 612–615. [DOI] [PubMed] [Google Scholar]
- 26. Lin H, Wang H, Ding H, Chen YL, Li QZ (2009) Prediction of Subcellular Localization of Apoptosis Protein Using Chou’s Pseudo Amino Acid Composition. Acta Biotheoretica 57: 321–330. [DOI] [PubMed] [Google Scholar]
- 27. Chen L, He ZS, Huang T, Cai YD (2010) Using compound similarity and functional domain composition for prediction of drug-target interaction networks. Medicinal Chemistry 6: 388–395. [DOI] [PubMed] [Google Scholar]
- 28. Sun XD, Huang RB (2006) Prediction of protein structural classes using support vector machines. Amino Acids 30: 469–475. [DOI] [PubMed] [Google Scholar]
- 29. Huang Y, Li YD (2004) Prediction of protein subcellular locations using fuzzy k-NN method. Bioinformatics 20: 21–28. [DOI] [PubMed] [Google Scholar]
- 30. Matsuda S, Vert JP, Saigo H, Ueda N, Toh H, et al. (2005) A novel representation of protein sequences for prediction of subcellular location using support vector machines. Protein Science 14: 2804–2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Mondal S, Bhavna R, Mohan Babu R, Ramakumar S (2006) Pseudo amino acid composition and multi-class support vector machines approach for conotoxin superfamily classification. Journal of theoretical biology 243: 252–260. [DOI] [PubMed] [Google Scholar]
- 32. Von Mering C, Jensen LJ, Snel B, Hooper SD, Krupp M, et al. (2005) STRING: known and predicted protein–protein associations, integrated and transferred across organisms. Nucleic acids research 33: D433–D437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kuhn M, Szklarczyk D, Franceschini A, Campillos M, Von Mering C, et al. (2010) STITCH 2: an interaction network database for small molecules and proteins. Nucleic acids research 38: D552–D556. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
List of the 4,002 samples, including 3,348 small molecules and 654 enzymes of yeast, classified into 11 metabolic pathway classes.
(PDF)