Hydrogen Donor-Acceptor Fluctuations from Kinetic Isotope Effects: A Phenomenological Model

Abstract

Kinetic isotope effects (KIEs) and their temperature dependence can probe the structural and dynamic nature of enzyme-catalyzed proton or hydride transfers. The molecular interpretation of their temperature dependence requires expensive and specialized QM/MM calculations to provide a quantitative molecular understanding. Currently available phenomenological models use a non-adiabatic assumption that is not appropriate for most hydride and proton-transfer reactions, while others require more parameters than the experimental data justify. Here we propose a phenomenological interpretation of KIEs based on a simple method to quantitatively link the size and temperature dependence of KIEs to a conformational distribution of the catalyzed reaction. The present model assumes adiabatic hydrogen tunneling, and by fitting experimental KIE data, the model yields a population distribution for fluctuations of the distance between donor and acceptor atoms. Fits to data from a variety of proton and hydride transfers catalyzed by enzymes and their mutants, as well as non-enzymatic reactions, reveal that steeply temperature-dependent KIEs indicate the presence of at least two distinct conformational populations, each with different kinetic behaviors. We present the results of these calculations for several published cases and discuss how the predictions of the calculations might be experimentally tested. The current analysis does not replace molecular quantum mechanics/molecular mechanics (QM/MM) investigations, but it provides a fast and accessible way to quantitatively interpret KIEs in the context of a Marcus-like model.

The detailed mechanisms of enzyme-catalyzed H-transfer reactions have tantalized researchers for many years, owing to the important intellectual questions and medicinal applications associated with enzymes. It is now well accepted that both enzyme-catalyzed and non-enzymatic hydrogen transfers involve quantum mechanical tunneling, the phenomenon where a particle passes through an energy barrier due to its wave-like properties. Since tunneling is highly mass dependent, kinetic isotope effects (KIEs) are excellent probes of these reactions. In recent years, the temperature dependence of KIEs has emerged as an important indication of the nature of tunneling and has suggested that fluctuations of the donor-acceptor distance (DAD) may be mechanistically important.^1–9 Here the DAD is defined as the distance between the two heavy atoms transferring the hydrogen.

Conventional transition state theory (TST) models chemical kinetics under a set of assumptions where the width of the barrier is unimportant; all that affects the rate is the height of the barrier. Some attempts to account for the effects of tunneling on KIEs rely on corrections to TST of the form

$$KIE=\frac{k_L}{k_H}=\frac{Q_L\cdot k_L^{TST}}{Q_H\cdot k_H^{TST}}$$ [1]

where k^TST is the TST rate for the light (L) or heavy (H) isotope, and Q is the correction for tunneling effects for each isotope. The tunneling correction is generally based on a parabolic barrier with some more sophisticated treatments available, but the barrier is assumed to be static.¹⁰ Tunneling corrections can reproduce both temperature-dependent and temperature-independent KIEs, but such simple corrections to TST cannot reproduce small and temperature-independent KIEs where the rate is temperature dependent (E_a>0). Certain enzymatic, as well as non-enzymatic, reactions, however, exhibit just that: large activation energies, but temperature-independent KIEs that are not inflated.^11–19 To account for this behavior, many researchers have adapted Marcus theory of electron tunneling²⁰ to the situation of hydrogen tunneling (Figure 1). The Marcus-like models^6,8,21 (also known as full-tunneling models,²² environmentally-coupled tunneling,¹ and vibrationally-enhanced tunneling⁵) suggest that heavy-atom motions bring the system to a tunneling-ready state (TRS), where the vibrational energy levels for the hydrogen in the reactant and product states are degenerate and tunneling can occur.^{1,2,8,9,23–28} This type of model gives a rate constant (k) with the functional form

$$k=\frac{\mid V{\mid }^2}{\hslash }\sqrt{\frac{\pi }{\lambda k_{B}T}}{e}^{-\frac{{(\Delta G°+\lambda )}^2}{4k_{B}T\lambda }}{\int }_0^{\infty }F(m,DAD)e^{E\left(DAD\right){∕}_{k_{B}T}}dDAD$$ [2]

In this equation the factors in front of the integral include the electronic coupling between the reactants and products (V) and the thermally averaged equilibrium probability of heavy-atom “reorganization” to reach the TRS, which depends on the reaction driving force (ΔG°), the reorganization energy (λ), and the absolute temperature (T); k_B is Boltzmann's constant. These factors are nearly completely insensitive to the mass of the transferred particle, so only the integral contributes to the isotope effects. The integral computes the probability of tunneling to form products once the system reaches the TRS. The first factor inside the integral gives the probability of tunneling as a function of the mass (m) of the transferred particle (H, D, or T) and the DAD. The second factor in the integral is a Boltzmann factor giving the probability of being at any given DAD. Thus, since the thermal reorganization to reach the TRS is isotopically insensitive, but tunneling at the TRS is isotopically sensitive, the model accounts for either temperature-dependent or temperature-independent rates with temperature-dependent or temperature-independent KIEs. Previous studies have reported all four possibilities for both enzymatic and non-enzymatic systems, requiring a flexible model that can accommodate all of these outcomes. We note that this kind of model assumes that all the motions of the system are in thermal equilibrium with the environment, in accordance established theories.^3,9,23,29,30

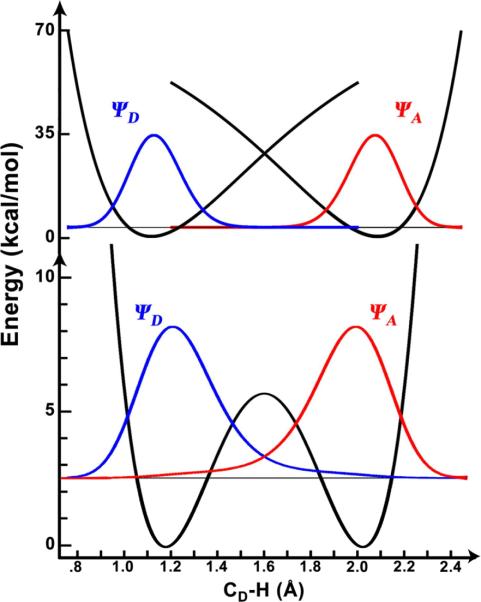
Figure 1.

Marcus-like model of hydrogen tunneling. The heavy atoms reorganize to bring the reactant (blue) and product (red) potential surfaces to a point of transient degeneracy (‡, the TRS) where the hydrogenic wavefunction (green) can pass from the donor well to the acceptor well, referred to as tunneling. The TRS actually represents a seam in multi-dimensional space, including all conformations where the reactant and product surfaces are degenerate. Figure 2 highlights how the fluctuation of the DAD along this seam dictates the probability of tunneling at the TRS.

Interestingly, several enzymes that exhibit temperature-independent KIEs have mutants where KIEs are temperature dependent. Qualitative arguments have rationalized that differences in thermal fluctuations of the DAD (the Boltzmann factor in the integral of eq. 2) can account for both behaviors (Figure 2).^1,8 In the case of temperature-dependent KIEs, thermal excitations that populate conformations with shorter DADs, where the heavy isotope can tunnel, will lower the KIE as temperature increases. In contrast, if the enzyme stabilizes a TRS with a very short DAD, where tunneling is efficient for both isotopes, then thermal activation will not alter the magnitude of the KIE.³¹ Although this model appears to account for the wide range of experimental observations, few attempts have tried to quantitatively link the size and temperature dependence of KIEs to the population distribution along the DAD coordinate,^14,24,32 and in most cases, detailed QM/MM simulations have been necessary to achieve a molecular understanding of the reaction.^26,33–35

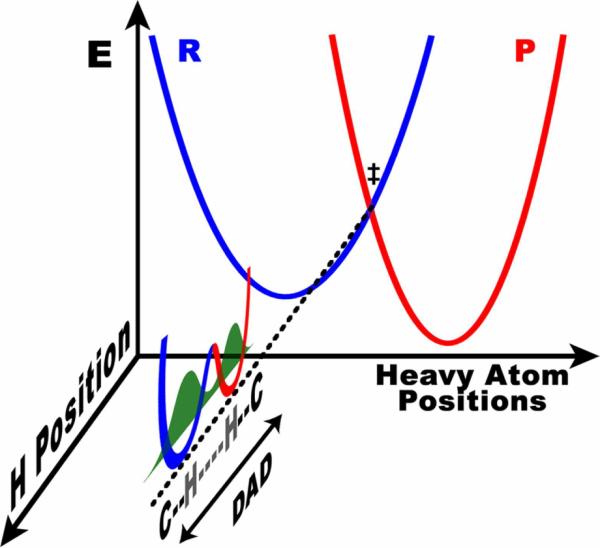
Figure 2.

PES of the DAD coordinate along the seam where the reactant and product surfaces are degenerate (the TRS). Slices along the orthogonal tunneling coordinate are shown at three different DADs, demonstrating the change in overlap between reactant (blue) and product (red) wavefunctions. The wavefunction overlap at each distance is proportional to the tunneling probability at that distance and is isotopically sensitive. The present model uses the temperature dependence of KIEs to determine the population distribution of DADs, which is dictated by this PES.

To assist experimentalists in quantitative analysis of data, we expand on previous efforts to connect the temperature dependence of KIEs to a simple physical model. The value of such a phenomenological model, like that of most statistical models, is that it captures the essential physics of the problem for initial assessment of the system under study without all of the molecular detail of an explicit simulations. Although cases where a detailed molecular interpretation is required to understand the chemistry motivate high level simulations, e.g., QM/MM, they are not necessary in many situations where an analysis using a modified TST or Marcus-like models provides sufficient physical insight into the reaction dynamics (including assessment of whether molecular simulation is needed). We apply the proposed model to several different enzymes and their mutants, including dihydrofolate reductase (DHFR),^12,36–39 morphinone reductase (MR),¹⁴ thymidylate synthase (TSase),^13,40 alcohol dehydrogenase (ADH),^11,41 formate dehydrogenase (FDH),⁴² and pentaerythritol tetranitrate reductase (PETNR),¹⁵ as well as two non-enzymatic sigmatropic rearrangements.^17,43 In contrast to some previous fitting models we maintain that the experimental data correspond to a single exponential relationship, and thus, any fitting model must be limited to two adjustable parameters. The question for the experimentalist trying to interpret data is what physical quantities those parameters represent. Fits to the Arrhenius equation and the parameters of that equation have limited physical meaning (i.e., ΔE_a and A_H/A_D) for these kinds of reactions. The method described here allows experimental enzymologists and organic chemists to obtain a quantitative interpretation of their results in terms of a distribution of DADs, but without requiring the expertise, time, and resources necessary to conduct costly QM/MM simulations.^{3–5,26,33–35,44–48} Furthermore, the present calculations result in a number of intriguing predictions that could be examined experimentally.

Methods

We conducted all geometry optimizations and potential-energy surface (PES) scans at the B3LYP/6–31+G* level with Gaussian 03.⁴⁹ We did all other calculations with Mathematica 7.⁵⁰

The overall framework used here follows the model developed by Kuznetsov and Ulstrup (ref. 23, eq. 2), but with significant modifications relative to other attempts to implement this type of model.^14,24,32,51 Since the factors outside the integral of eq. 2 are essentially isotopically insensitive (i.e., affected by motions of many heavy atoms with little or no contribution of the isotopically labeled atom), the following ratio of integrals contains the experimental 1° KIEs:

$$KIE=\frac{k_L}{k_H}=\frac{{\int }_{r1}^{r2}F(m_L,DAD)e^{E\left(DAD\right)}{∕}_{kTDAD}}{{\int }_{r1}^{r2}F(m_H,DAD)e^{E\left(DAD\right)}{∕}_{kTDAD}}$$ [3]

As mentioned above, the first factor in each integral represents the probability of tunneling as a function of the DAD and the mass of the transferred particle and the second factor is a Boltzmann factor, giving the probability of being at any given DAD. The integral is formally over all DADs, but in reality it is negligible outside of a small region within which the DAD is short enough to give a non-zero tunneling probability (DAD < r2) but long enough that van der Waals repulsions between the donor and acceptor are small (DAD > r1). Since when calculating KIEs many of the assumptions and expressions that are not isotopically sensitive drop from the equation, and because many experiments directly measure KIEs, without measuring individual rates,²¹ this equation should have greater utility than individual rate equations.

The Tunneling Probability

Previous calculations of this type have based the tunneling probability on non-adiabatic models using harmonic^24,51 or Morse^14,32 potentials to describe the donor and acceptor wells. For many reactions, though, adiabatic coupling is very important.⁵² Thus, we allow for strong coupling between the donor and acceptor wells, which is more relevant to hydride and proton transfers and gives markedly different results (see below). As with previous models, we assume that the probability of tunneling as a function of DAD does not differ among similar reactions. For computational simplicity, therefore, we base our calculations on the hypothetical symmetric transfer of H⁻ from reduced to oxidized nicotinamide moieties, in a manner similar to a model for symmetric H-transfer in solution.⁵³ The donor and acceptor moieties are analogous to the ubiquitous nicotinamide biological cofactor NAD(P)⁺. A hydrogen truncates the nicotinamide rings where they normally link to the ribosyl moiety of NAD(P)⁺, so the system contains a total of 33 atoms (Figure 3) and an overall charge of +1. Heavy-atom geometries of the two nicotinamide moieties are optimized at a range of DADs from 2.6 Å to 3.5 Å with the C-H-C angle constrained at 180° and the hydrogen at the midpoint between the donor and acceptor C4 atoms. We previously found this approach sufficient for assessment of the structure of the TRS in yeast ADH.⁵⁴ At each DAD, we scanned the PES for linear hydrogen transfer with all other atoms frozen and fit these scans (least-squares) to symmetric quartic potentials (Figure 4). When the system reaches the TRS, the hydrogen is localized in the donor well. Before the degeneracy of the TRS is broken, the donor wavefunction evolves so that some probability density ends up in the acceptor well (Figure 3). To calculate the time evolution of the probability density, we construct donor and acceptor wavefunctions for each isotope from linear combinations of the ground (φ₀ and first excited (φ₁) eigenstates of the potentials in figure 4.

$${\psi }_{Donor}=\frac{1}{\sqrt{2}}{\phi }_0+\frac{1}{\sqrt{2}}{\phi }_1$$ [4]

$${\psi }_{Acceptor}=\frac{1}{\sqrt{2}}{\phi }_0-\frac{1}{\sqrt{2}}{\phi }_1$$ [5]

When the system reaches the TRS, the non-stationary donor wavefunction evolves in time by coherent oscillations between the donor and acceptor state with a period (τ) dependent on the tunneling splitting (ΔE_t),⁵⁵ where

$$\tau (m,DAD)=\frac{\hslash }{\Delta {\mathrm{E}}_{\mathrm{t}}}$$ [6]

and ΔE_t is the difference in energy between φ₀ and φ₁:

$$\Delta {\mathrm{E}}_{\mathrm{t}}=E\left({\phi }_1\right)-E\left({\phi }_0\right)$$ [7]

We calculate ΔE_t for each DAD for H, D, and T by numerical solution of the Schrödinger equation as described previously.⁵⁴ To get an expression for ΔE_t as a function of DAD, we fit (least-log-squares) the calculated values to a sum of two exponentials, which correspond to the behaviors above and below the barrier, respectively (Figure 5). When the zero-point energy (ZPE) of the hydrogen is above the barrier, the process is not formally tunneling, but an advantage of this methodology is that the calculations smoothly transition between the region of tunneling²⁷ and the region of over-the-barrier events.⁵⁶

Figure 3.

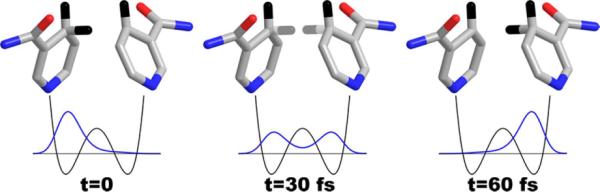
The time evolution of the ¹H-wavefunction tunneling between two NAD⁺ moieties frozen with a DAD of 3.2 Å. All the heavy atoms used in the calculations are shown, along with hydrogens of particular interest. When the system reaches the TRS (t=0) the hydrogen is effectively localized in the donor well, but its probability density evolves over time, as shown. The coherent oscillation of this wave packet dephases due to environmental perturbations yielding some finite probability of decaying to the acceptor state, resulting in net transfer. An exponential decay with time constant of 10 fs models the dephasing, which is consistent with more sophisticated calculations.^57–59

Figure 4.

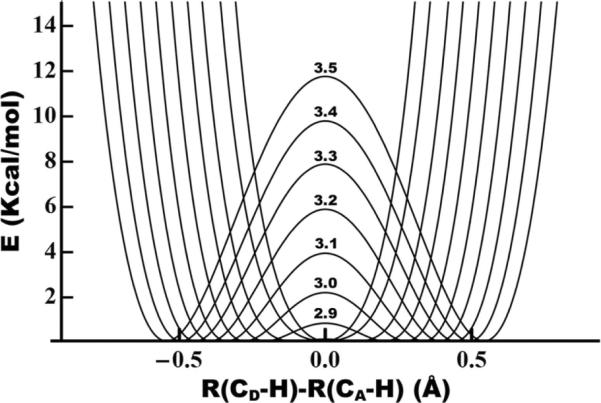
PESs for linear C-H→C transfer between two NAD⁺ moieties with the heavy atoms frozen at a range of DADs (defined as the distance from C4 of donor to C4 of acceptor). Each surface is a symmetric quartic fit (least squares) to a scan of 15–25 points (depending on the DAD) calculated at the B3LYP/6–31+G* level. The DAD in Å is labeled above the barrier for each surface. From this figure it is clear that below 2.8 Å there is no barrier to H-transfer and calculations of ZPE indicate that the hydrogen is above the barrier at even longer distances, depending on the isotope (cf. Fig. 5).

Figure 5.

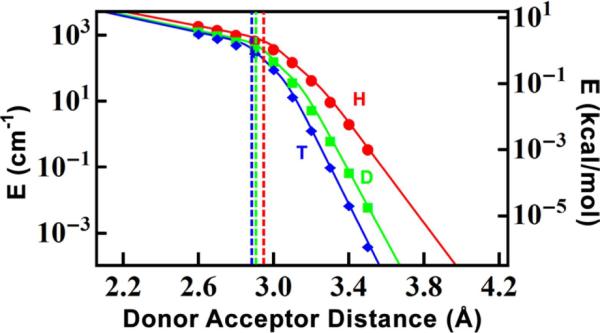
Tunnel splitting (△E_t) of the three isotopes of hydrogen as a function of DAD (eq. 7), calculated as the difference in energy of the first two eigenstates of the potentials in Fig 4. The vertical lines indicate the DAD at which each isotope's ZPE is greater than the height of the reaction barrier.

The oscillations of the hydrogen wavefunction result in a probability density in the acceptor well (corresponding to net transfer) as a function of time (t) after reaching the TRS given by the expression

$$P(t,m,DAD)=-\frac{1}{2}\left(1+\cos \left(\frac{2\pi }{\tau (m,Dad)}t\right)\right)$$ [8]

After reaching the TRS, however, environmental perturbations lead to dephasing of the coherent wavefunction, such that the oscillations effectively cease after a short dephasing time. Calculating the rate of dephasing is not within the scope of the present model, but we can approximate the rate as an exponential decay with time constant of θ=10 fs.⁵⁷ This approximation is consistent with other treatments that calculated the decay of the probability flux correlation function based on the spectral density of the environment,^58,59 a method first described for solution reactions⁶⁰ that has found much subsequent use in solution and enzymes.^25,61 Furthermore, the general behavior of the model is not sensitive to the value of θ within the range of 1fs<θ<100fs. Using this exponential dephasing, the overall probability of tunneling as a function of DAD (Figure 6) is

$$F(m,DAD)=\frac{{\int }_0^{\infty }{e}^{\left(t{∕}_{\theta }\right)}\ast P(t,m,DAD)dt}{{\int }_0^{\infty }{e}^{\left(t{∕}_{\theta }\right)}dt}$$ [9]

We expect this term to be nearly invariant among different hydride transfers between carbon atoms, and at least to yield reasonable trends for other types of hydride and proton transfers. The utility of this function for several different reactions is explored below.

Figure 6.

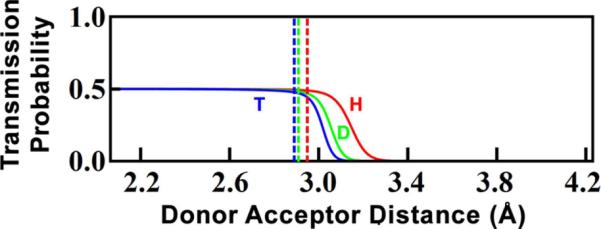
Transmission probability for each of the three isotopes of hydrogen as a function of DAD (eq. 9). The vertical lines indicate the DAD at which each isotope's ZPE is greater than the height of the reaction barrier.

The DAD Population Distribution

In equation 3, the Boltzmann factor within the integral represents the population distribution along the DAD coordinate. This term dictates the size and temperature dependence of the KIEs. We analyze experimental data that range from reactions with completely temperature-independent KIEs (within experimental error) to reactions with steeply temperature-dependent KIEs. Most surprisingly, we find that a model with a single population could not fit the steeply temperature-dependent KIEs. Thus, we present two models below: a single-population model for KIEs with little or no temperature dependence and a model with two populations that accounts for KIEs with all levels of temperature dependence. We use these two forms of the Boltzmann factor in eq. 3 to fit the KIEs. Importantly, we use only two parameters to fit the data with either model. Since experiments measure the temperature dependence of KIEs across a narrow temperature range, and this dependence follows a single exponential relationship, at most two fitting parameters are justified.

Temperature Independent KIEs: One Population

Previous methods used a harmonic potential to approximate the PES that describes the DAD coordinate,^{14,24,32,33,51} and where possible, we follow this standard. This gives a Gaussian population distribution of the form

$$e^{E\left(DAD\right)∕k_{B}T}=e^{f{(DAD-DA{D}_0)}^{2∕k_{B}T}}$$ [10]

where the average DAD (DAD₀) and the force constant (f) of the corresponding harmonic potential are adjustable fitting parameters when this factor is substituted into eq. 3. Formally speaking, this distribution is normalized, but since the probability distribution of DADs is not mass-sensitive, the normalization constants for the two isotopes are equal and thus cancel one another. This type of distribution can fit KIEs with little to no temperature dependence, but even allowing for physically unreasonable parameters, this distribution cannot lead to the small, steeply temperature-dependent KIEs observed in some reactions (Figure S1).

Temperature Dependent KIEs: Two Populations

It is not surprising that simple distributions like Eq. 10 fail in some cases. For reactions where the donor and acceptor are not well constrained in reactive orientations, they are unlikely to have the same steep potential-energy gradient at long separations (when held by “soft” protein or solvent forces) as when closely approaching each other (under van der Waals radii), as implied by a harmonic potential. Our efforts to fit the temperature-dependent KIEs with more sophisticated functions lead to the conclusion that at least two distinct populations are required to fit these experimental data in the context of a Marcus-like model.

After exploring a number of ways to describe the population distribution in systems with steeply temperature-dependent KIEs, we find that the simplest model that can fit the data is as follows: One population is centered at a short enough DAD (DAD_short) that all isotopes cross the dividing surface between reactant and product with similar probabilities (i.e. the KIE is unity for this population). We choose this population as the zero of free energy (G=0) for computational simplicity. A second, lower-energy population is centered at a longer DAD (DAD_long), where the overall tunneling probability is lower but the isotope effect is larger. In the present model, the precise DAD of the shorter population does not significantly affect the fit to the data, so long as the DAD is short enough that the ZPEs of all three isotopes are above the reaction barrier (cf. vertical lines in Figure 6). This population effectively corresponds to a semiclassical transition state.^34,62,63 We assume that the two conformational populations are in thermal equilibrium with one another and that the temperature-dependent change in the relative populations gives rise to the temperature dependence of the KIEs. Thus, the population distribution (the Boltzmann factor in Eq. 3) has the form

$$e^{-E\left(DAD\right)∕k_{B}T}=\delta (DAD-DA{D}_{short})+e^{-\Delta G∕k_{B}T}\delta (DAD-DA{D}_{long})$$ [11]

where the two fitting parameters are DAD_long (the DAD of the population at longer distance) and ΔG (the difference in free energy between the two populations). Including a distribution about the average DADs of the two populations requires more parameters and does not yield a better fit, so we leave the populations as delta functions. As with Eq. 10, this distribution function need not be normalized to calculate KIEs.

Fitting the KIEs

We fit (least-squares) experimental KIEs as a function of temperature to eq. 3, using both the single Gaussian distribution (eq. 10) and the two-population distribution (eq. 11). Except in cases where one attempts to fit steeply temperature-dependent KIEs to a single population, the fits converge to 16-digit precision within a few seconds, using a Sony laptop with an Intel Core2Duo P8700 processor (2.53 GHz) and 8 GB of RAM. The Mathematica program for conducting this type of fitting is available free of charge on the web at http://chemmath.chem.uiowa.edu/webMathematica/kohen/marcuslikemodel.html.

Results and Discussion

We propose a simple phenomenological model that enables quantitative fitting of experimental KIEs and their temperature dependence, yielding up to two physically meaningful parameters that describe the distribution(s) of DADs. To do so, we have modeled the tunneling probability, assuming adiabatic coupling between the donor and acceptor wells. This approach expands the space of possible reactions that can be modeled beyond those where strictly non-adiabatic tunneling is appropriate.^24,32 Several studies have provided in-depth analyses of the differences between adiabatic and non-adiabatic approaches in this type of vibronic model.^52,64 Here, we find that the coupling of the donor and acceptor increases the length of the C-H bond and substantially decreases the height of the barrier, yielding large regions of wavefunction overlap at DADs where non-adiabatic models predict negligible probabilities of tunneling (Figure 7). As a result, our adiabatic model demonstrates that tunneling occurs from DADs relatively close to the van der Waals distance of the two heavy atoms (3.4 Å for carbon). While several high level simulations suggest tunneling from DADs between 2.6–2.8 Å,^34,63 we have shown that there is no barrier to H-transfer at that distance (Figure 4) and that distance actually corresponds to the semi-classical transition state. Tunneling from longer DADs, however, is consistent with a model of the TRS of yeast ADH based on 2° KIEs⁵⁴ as well as high level QM/MM simulations of DHFR.²⁶ A further advantage of the present method is that we need not assume that every reactive trajectory occurs by tunneling. The transferred hydrogen in the current model behaves as a quantum particle, regardless of the electrostatic environment applied by the heavy atoms of the system. Whether above the barrier or below the barrier, the hydrogen is wave-like.⁵⁶ Thus, as shown in Figure 6, the transmission probability smoothly transitions between DADs where the ZPE is below the barrier to those where it exceeds the barrier height. Even for these over-the-barrier trajectories, though, the heavy-atom reorganization remains the primary motion leading to H-transfer^65,66 (i.e., “the reaction coordinate is the solvent coordinate”⁵⁶). In this type of mechanism, all isotopes cross the dividing surface to products with similar probability once they are above the barrier. As discussed below, this result turns out to be of vital importance in describing steeply temperature-dependent KIEs.

Figure 7.

Comparison of the wavefunction overlap between donor (blue) and acceptor (red) states of ¹H for the nonadiabatic limit, using Morse potentials (top), and the adiabatic limit used in the present calculations (bottom). In both examples the DAD is set at 3.2 Å. The Morse wavefunctions are the ground eigenstates of the Hamiltonian and the wavefunctions for the double-well potential were constructed as linear combinations of the ground and first excited eigenstates of the Hamiltonian.

Our approach also expands the range of temperature dependencies of KIEs that can be quantitatively interpreted by a full-tunneling model. The previous phenomenological methods, which used only single harmonic potentials to describe the DAD coordinate, cannot reproduce the steep temperature dependence of KIEs that has been observed in a number of systems (See SI). By allowing for two populations along the DAD coordinate, the present model fits a variety of KIEs that have been reported for biological hydride and proton transfers, as well as non-enzymatic H-transfers (see examples below). As discussed under methods, the nature of the experimental data (KIEs over a narrow temperature range, which conform to a single exponential) allows for at most two meaningful fitting parameters.

Fitting the KIEs

The present method gives good fits to experimental KIEs exhibiting a wide range of temperature dependences (ΔE_a), resulting in physically meaningful population distributions along the DAD coordinate in a variety of reactions. The fitted parameters for each reaction are presented in Table 1. The experimental data are from measurements by a number of independent researchers who used an assortment of techniques, and all cases represent intrinsic KIEs that are not masked by kinetic complexity. To give a sense of the quality of the fits, we present the results for the enzyme DHFR and two series of mutants in Figure 8.^38,39,67 The model achieves similar accuracy for the other systems we examine (see details and figures in the SI): the nicotinamide-dependent C-H→C transfers in thermophilic ADH from B. stearothermophilus, bsADH,^11,41 and FDH⁴², the C-H→N transfer between flavin and nicotinamide in two flavoenzymes, MR¹⁴ and PETNR,¹⁵ the hydride (C-H→C) and proton (C-H→O) transfers that are part of the kinetic cascade in TSase,^13,40 and two non-enzymatic [1,5]sigmatropic rearrangements.^17,43 Given the method of parameterizing the tunneling probability (Eq. 9), the details of the current model are most applicable to C-H→C transfers involving nicotinamide cofactors (DHFR, bsADH, and FDH). One should interpret the precise results for the other three enzymes (MR, PETNR, and TSase) and the non-enzymatic reactions with caution, but we believe the overall trends among those reactions are fairly robust. In order to obtain more accurate results for those reactions, one could re-parameterize the tunneling probability (Eq. 9) to focus on H-transfers more relevant to those systems.

Table 1.

Experimental ΔE_a and resulting fitting parameters for the systems studied here.

Enzyme/Reaction	Mutation/conditions/reactants	ΔEaa	Fitting Parameters
			1 Population		2 Populations		Reference
			DAD0b	f c	DADlongb	ΔGd
DHFR active site mutants	WT	−0.1±0.2	3.058	>250	3.057	>2.5	12
	I14V	0.30±0.07	3.082	200	3.064	2.3	67
	I14A	0.38±0.03	3.093	190	3.072	2.4	39
	I14G	3.31±0.07	NA	NA	3.307	3.8	67
DHFR distal mutants	WT	−0.1±0.2	3.058	>250	3.057	>2.5	12
	G121V	0.25±0.02	3.084	390	3.072	2.8	36
	M42W	0.55±0.03	3.119	80	3.072	1.9	37
	G121V-M42W	3.7±0.2	NA	NA	3.342	4.4	38
bsADH f	WT > 30 °	0.1±0.2	3.094	>100	3.086	>2.0	11
	WT < 30 °	0.7±0.2	NA	NA	3.158	1.1	11
	L176V > 30 °	1.7±0.9	NA	NA	3.232	2.3	41
	L176V< 30 °	2.3±0.5	NA	NA	3.282	3.1	41
	L176A > 30 °	1.6±0.5	NA	NA	3.231	2.3	41
	L176A < 30 °	0.8±0.6	NA	NA	3.158	1.3	41
	L176G > 30 °	1.4±0.5	NA	NA	3.212	1.9	41
	L176G < 30 °	1.0±0.7	NA	NA	3.177	1.4	41
	L176Δ > 30 °	1.8±0.3	NA	NA	3.244	2.5	41
	L176Δ < 30 ° g	−0.4±0.3	3.095	>1000	3.094	>4.0	41
	V260A > 40 °	1.8±0.7	NA	NA	3.239	2.4	41
	V260A < 40 °	0.0±0.4	3.094	>100	3.091	>2.0	41
MR f	W106A	0.0±0.4	3.110	>150	3.110	>2.5	14
	WT	2.0±0.4	NA	NA	3.211	2.3	14
	V108L	2.1±0.4	NA	NA	3.235	2.6	14
PETNR f	NADH	0.1±0.2	3.120	>400	3.117	>3	15
	NADPH	1.4±0.1	NA	NA	3.175	1.9	15
TSase	H−-transfer	0.0±0.6	3.062	>100	3.061	>2	13
	H+-transfer	8.3±0.3	NA	NA	3.612	9.5	40
FDH	WT	−0.03±0.04	3.057	>1000	3.056	>3	42
[1,5]-sigmatropic rearrangement f	Pentadiene h	1.4	3.553	16	3.145	2.3	43
	Quinolizine	−0.01±0.02	3.101	>2000	3.100	>5	17

^aH/T KIEs except where noted. All energies are in kcal/mol. In some cases raw data were not published so we used approximations of the actual data points and errors based on visual inspection of published figures (on log scales) in the fittings. Thus, the ΔE_a shown here may differ from previously published values, but corresponds to the data points used in the modeling.

^bIn Å errors are <5% of reported value; not applicable (NA) for systems with ΔE_a>1 kcal/mol at 298 K.

^cIn kcal·mol⁻¹·Å⁻²; only a lower bound is given for systems within error of ΔE_a=0; the lower bound is the value such that the calculated ΔE_a (in the middle of the observed temperature range, using the best fit value for DAD₀) is equal to the upper error of the observed ΔE_a (ΔE_a + σ); errors for other systems are <15% of reported value.

^dOnly a lower bound is given for systems within error of ΔE_a=0; errors for other systems are <15% of reported value.

^eNot applicable (NA) for systems with ΔE_a>1 kcal/mol at 298 K;

^fH/D KIEs.

^gThis model is not designed to fit inverse temperature dependence (ΔE_a<0).

^hErrors unavailable because individual data points were not published; measurements were done at T>450 K, so the one population model was successful despite ΔE_a>1 kcal/mol.

Figure 8.

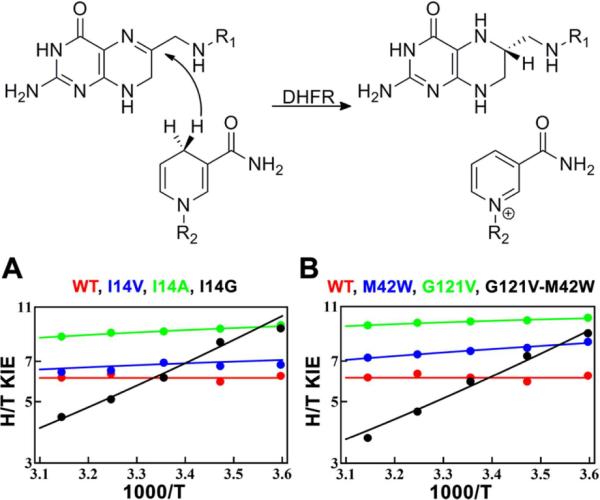
The reaction catalyzed by DHFR and the fits to KIEs from a series of active-site mutants (A), and a series of distal mutants (B). All fits correspond to the two-population model. Experimental data are from refs. 38, 39, and 67.

We display the KIEs of Figure 8 (and those in the SI) as Arrhenius plots (1/T vs. KIE on log scale), following the tradition of phenomenological analysis of KIEs by the Arrhenius or Eyring equations^1,8

$$KIE=\frac{k_L}{k_H}=\frac{A_L}{A_H}{e}^{\Delta E_a∕kT}$$ [12]

where A_i is the Arrhenius pre-exponential factor for isotope i, and ΔE_a is the difference in activation energy between the two isotopes. By this analysis, temperature-independent KIEs give a ΔE_a close to 0, often associated with $\frac{A_L}{A_H}$ greater than the semi-classical limits (i.e., greater than unity). Some temperature-dependent KIEs, however, show a very large ΔE_a that cannot be accounted for by mere isotopic differences in ZPE and, furthermore, show $\frac{A_L}{A_H}$ much lower than the semiclassical limit. For other reactions, $\frac{A_L}{A_H}$ is close to unity and ΔE_a also falls within the semiclassical limits. Despite this large variation in the behavior of KIEs, the method described here provides excellent fits to the entire range of results, using either a single population (where possible) or two distinct populations. Among the systems examined here, we find a cutoff at around ΔE_a=1.5 kcal/mol (at 298 K) for H/T KIEs, above which a single conformational population cannot fit the KIEs (See SI). Thus, as seen in Table 1, all of the systems where the H/T KIE exhibits ΔE_a>1 kcal/mol at 298 K can only be fit with the model that uses two populations. Thus, in those systems, the parameters in the single population model are listed as not applicable (NA). Since the experimental data conform to a single exponential function, two parameters are necessary and sufficient to describe the data. In the cases where ΔE_a=0 (within experimental error), the information content of the experimental data reduces to a single parameter $\left(\frac{A_L}{A_H}\right)$, so only a lower bound is given for the second fitting parameter in each model in Table 1. Truly temperature independent KIEs imply no DAD sampling (f=∞ or ΔG=∞), so the lower bound indicates the certainty (based on experimental errors) that the KIEs are truly temperature independent; a larger lower bound means more certainty. It is important to note that different values of this lower bound report on the quality of the data analyzed rather than the nature of the system under study. One of the mutant enzymes in ref. 14 (V108A) apparently exhibited inverse temperature dependence (ΔE_a<0), but the data and statistics are far from the quality of other data in the same work. Given the quality of these data and the fact that negative ΔE_a could not be appropriately modeled by either one population or two populations, and since much higher levels of theory have examined only a few such cases,⁶⁸ we do not address these data here.

In general, the distributions we obtain using a single population for DHFR and its remote mutants agree qualitatively with QM/MM simulations that calculated the DAD PES for these enzymes,²⁶ suggesting that this kind of model truly captures the essential physics involved in H-transfer. Furthermore, in most cases our fits agree with the trends found using nonadiabatic-tunneling models.^24,32 The fits to KIEs with little temperature dependence (ΔE_a<1 kcal/mol) show a correlation between ΔE_a and both the average DAD and the force constant of the corresponding harmonic potential (Table 1): a steep force constant and a short DAD gives a small ΔE_a, while a longer DAD and a smaller force constant gives a larger ΔE_a. Thus, in accordance with another recent analysis,³⁰ small force constants give smaller KIEs at higher temperatures because barrier compressions decrease rather than increase nuclear quantum effects. Barrier compression decreases the width and height of the barrier (Figure 4), allowing the isotopes to behave more similarly to one another. This behavior is consistent with the qualitative arguments that have emerged during recent years to describe these experimental results.^1,8

The observation that changes, such as mutations, alternate substrates, and non-physiological temperature ranges, can change temperature-independent KIEs into temperature-dependent KIEs motivates the hypothesis that the conformational distribution along the DAD coordinate is important for enzyme-catalyzed reactions.^14,24,26,38 In the context of small ΔE_a, the DAD potential has a lower force constant and longer average DAD.^14,24,32,51 We cannot, however, model the steeply temperature-dependent KIEs (ΔE_a > 1 kcal/mol at 298 K) with a single population and require at least two populations at the TRS. As with the one-population model, some clear trends emerge in how the interplay between the two populations affects the temperature dependence of the KIEs with ΔE_a > 1 kcal/mol (Table 1). If the DAD of the long population is especially long and much lower in energy, the system exhibits larger ΔE_a.

The molecular interpretation of the two conformational substates for reactions with large ΔE_a warrants further discussion. Perhaps the simplest interpretation of the models presented here comes in the context of the series of active-site mutants for E. coli DHFR (Figure 8A). This set of experiments examined the effects of a hydrophobic residue in the active site (I14) that appears to hold the nicotinamide ring of the H-donor in place through steric effects.^39,67 As the size of the residue decreases from I to V to A to G, ΔE_a gets larger and larger. The wild type has ΔE_a≈0, and thus, both fitting models converge to a single, narrowly defined conformation with a DAD of 3.06 Å. At the other end of the series, the I14G mutant has a ΔE_a of 3.31 kcal/mol, and only the model with two populations can fit the data. One can interpret this as an indication that the missing side chain leaves so much space in the active site that the substrates can adopt different conformations, as also suggested by molecular dynamics (MD) studies.⁶⁷ The I14V and I14A mutants (ΔE_a of 0.30 kcal/mol and 0.38 kcal/mol, respectively) can be modeled by either a single population or two populations. The results of a single population suggest that they have a smaller force constant and longer average DAD than the wild type; under the two-population model they have a smaller ΔG and shorter DAD_long than I14G. Since both models give adequate fits to these systems, the present methods cannot indicate a preference for one interpretation over the other, and higher-level simulations will be necessary to make a judgment.

A closer examination of the differences between wild-type DHFR and its I14G mutant reveals how two distinct populations may lead to the steep temperature dependence of KIEs exhibited by the mutant (Table 1 and Figure 8A). In the mutant, the vast majority of the TRS population has a DAD long enough (3.33 Å) that the probability of H-tunneling is much larger than the probability for T (or D). A small portion of the population (≈0.1 % at 298 K), however, is at a short enough DAD that all isotopes can cross the dividing surface between reactant and product equally well. At low temperatures, far greater overall population resides at the long DAD, where ¹H has a large advantage in tunneling, leading to a large KIE. Increasing temperature populates the short DAD (from which heavy isotopes can also be transferred), so the relative advantage of ¹H tunneling from the longer DAD decreases, resulting in strongly temperature-dependent KIEs. For the wtDHFR, on the other hand, a change in temperature will have the same effect on both isotopes: it will not cause a population shift, and the KIE change with temperature will be minimal.

The idea of a “steric hole” opening in the active site in the DHFR I14G mutant is a reasonable and intuitively satisfying explanation, but a similar interpretation of the conformational distributions of the G121V-M42W double mutant (residues distant from the active site, Figure 8B), for example, seems less obvious. A limitation of the present model is that it merely finds a 1-D distribution of DADs, without regard to other conformational fluctuations that may be important.⁴⁴ Thus, the distributions obtained represent ensembles of conformations, i.e., different states of “pre-organization”.^1,8

bsADH

In all cases, the analysis of temperature independent KIEs leads to a single population of DADs with a narrow distribution. This is true whether data are analyzed by one or two populations, as the large ΔG for the two population model simply indicates one meaningful population. The finding of distinct populations along the DAD coordinate is reminiscent of a recent suggestion that anomalously large Arrhenius pre-exponential factors in bsADH (and its mutants) result from the sampling of distinct conformations, each of which has different kinetic properties.⁶⁹ Additionally, pre-steady-state experiments on a mutant of MR also suggested multiple kinetically distinct, reactive conformations and indicated that steady-state rate measurements cannot probe the nature of such conformations.⁷⁰ Here we have shown that analysis of the temperature dependence of KIEs can uncover such reactive conformations, regardless of how the intrinsic KIEs were measured. Another recently published model of KIEs also suggested distinct reactive conformations.⁷¹ Like the two-conformation model presented here, the model by Mulholland and coworkers⁷¹ proposed one reactive conformation that proceeds by tunneling and one that surmounts the barrier. Like that model, our two states model for temperature dependent KIEs does not depend on DAD fluctuations (only ΔG° between the states). This being said, nothing in the functional form of the model excludes the possibility of DAD fluctuations as we use for temperature independent KIEs. A difficulty with that model, however, is that it requires 9 parameters to describe data that fit to a single exponential (or two exponentials if the individual rates of the isotopes are considered). The model presented here, though, uniquely fits the temperature dependence of KIEs using just two fitting parameters.

Conclusions

We present a simple and user-friendly adiabatic model of H-tunneling in hydride and proton-transfer reactions that can be used to generate a population distribution along the DAD coordinate by fitting to experimental KIEs and their temperature dependence. Practically, this new fit converts the isotope effect on entropy and enthalpy one gets from fitting to the Arrhenius or Eyring equations into two parameters indicative of the distribution of DADs. We suggest these two parameters provide a more molecular interpretation of the experimental data than ΔEa and A_H/A_D. We demonstrate the utility of this fit for several enzymatic and non-enzymatic systems, including a number of different types of C-H→C and other H-transfers. This simple, quantitative fitting of the experimental data, which is readily accessible to all experimentalists, gives a physically meaningful picture of how the temperature dependence of KIEs reflects the arrangement of H-donor and H-acceptor. In the case of enzymatic reactions, this model provides parameters that correlate with the effects of mutations, alternative substrates, or changes in conditions that alter the ensemble of reactive conformations. For the non-enzymatic reactions, the parameters correlate with the rigidity of the reacting system, e.g. an intramolecular reaction in a fused ring system versus reactants with more conformational flexibility (see SI). Importantly, the results imply that reactions with steeply temperature-dependent KIEs must occur from at least two distinct conformational substates: one that involves inefficient tunneling from a long DAD and one where heavy-atom rearrangement (isotopically insensitive enzyme or solvent motion) brings the system to a short DAD where the ZPE of the transferred particle is above the barrier. In contrast to earlier phenomenological models, the current procedure also reproduces small, steeply temperature-dependent KIEs (see SI). Like previous phenomenological methods, the model presented here does not assume non-statistical dynamic effects and uses the equilibrium distribution of DADs to calculate the tunneling probability. Since the model here that allows for multiple conformations can explain the full range of experimental data, while a single-population model cannot, this two-population model is more generally applicable. Of course, all the reactions studied here may occur from many different substates, and our model projects the full ensemble of substates onto two populations because the most one can extract from the given experimental data (KIEs and their temperature dependence) is two states, defined by two parameters. Additional experiments, as well as high-level calculations and simulations, will be necessary to determine more details of conformations that contribute to H-transfers for each specific system. This new tool is not meant to replace proper molecular calculations by QM/MM methods, but those techniques are expensive and highly specialized, whereas this program is very simple to use and is available, free of charge at http://chemmath.chem.uiowa.edu/webMathematica/kohen/marcuslikemodel.html

Abbreviations

KIE

kinetic isotope effect

DAD

donor acceptor distance

TST

transition state theory

TRS

tunneling ready state

DHFR

dihydrofolate reductase

ADH

alcohol dehydrogenase

MR

morphinone reductase

PETNR

pentaerythritol tetranitrate

TSase

thymidilate synthase

PES

potential energy surface

ZPE

zero point energy

MD

molecular dynamics

QM/MM

quantum mechanics/molecular mechanics