Super-resolution reconstruction to increase the spatial resolution of diffusion weighted images from orthogonal anisotropic acquisitions

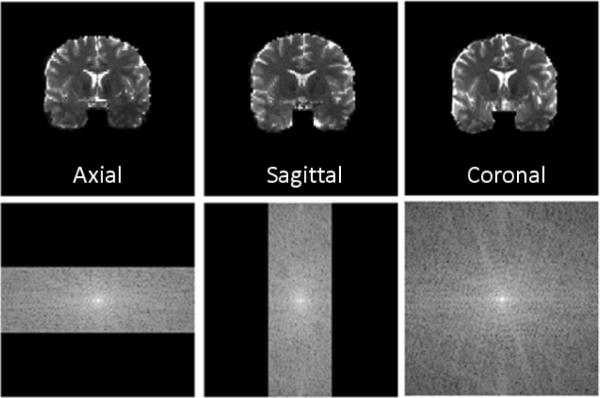
Abstract

Diffusion-weighted imaging (DWI) enables non-invasive investigation and characterization of the white matter but suffers from a relatively poor spatial resolution. Increasing the spatial resolution in DWI is challenging with a single-shot EPI acquisition due to the decreased signal-to-noise ratio and T2* relaxation effect amplified with increased echo time. In this work we propose a super-resolution reconstruction (SRR) technique based on the acquisition of multiple anisotropic orthogonal DWI scans. DWI scans acquired in different planes are not typically closely aligned due to the geometric distortion introduced by magnetic susceptibility differences in each phase-encoding direction. We compensate each scan for geometric distortion by acquisition of a dual echo gradient echo field map, providing an estimate of the field inhomogeneity. We address the problem of patient motion by aligning the volumes in both space and q-space. The SRR is formulated as a maximum a posteriori problem. It relies on a volume acquisition model which describes how the acquired scans are observations of an unknown high-resolution image which we aim to recover. Our model enables the introduction of image priors that exploit spatial homogeneity and enables regularized solutions. We detail our SRR optimization procedure and report experiments including numerical simulations, synthetic SRR and real world SRR. In particular, we demonstrate that combining distortion compensation and SRR provides better results than acquisition of a single isotropic scan for the same acquisition duration time. Importantly, SRR enables DWI with resolution beyond the scanner hardware limitations. This work provides the first evidence that SRR, which employs conventional single shot EPI techniques, enables resolution enhancement in DWI, and may dramatically impact the role of DWI in both neuroscience and clinical applications.

1. Introduction

Diffusion-weighted imaging (DWI) is a key imaging technique for the investigation and the characterization of the brain white matter architecture and microstructure. It relies on the acquisition of multiple 3-dimensional diffusion-weighted images, probing the capability of the water to diffuse in various diffusion directions and scales. DWI requires a fast acquisition technique to ensure a moderate scan duration time, and to ensure measurement of the DW-signal before it nulls out. Single-Shot Echo-Planar Imaging (SS-EPI) is the most commonly employed sequence in DWI. It acquires a whole slice after a single excitation, generally covering the whole brain in less than ten seconds for each 3-dimensional DWI. However, spatial resolution is strongly limited with SS-EPI. While individual axon diameter is on the order of 1–30μm (Mori and van Zijl, 2002), typically achievable DWI resolution is on the order of 2×2×2mm³. Consequently, due to strong partial volume effect, DWI has been limited to the investigation of the major fiber “highways” in the brain. Increasing the resolution of DWI acquisitions holds out the potential (1) to allow investigation of smaller white matter fascicles not visible at conventional resolution, and (2) to reduce partial volume averaging of white matter fascicles, enabling a more accurate white matter and brain connectivity assessment.

Resolution enhancement is challenging

Resolving finer structures, i.e. increasing the spatial resolution, requires sampling of higher frequencies in k-space². This is highly challenging with an SS-EPI acquisition. First, increasing the resolution makes the acquisition highly demanding on the scanner gradient coils, which have to switch as quickly and as linearly as possible when achieving the spatial encoding. Second, the time to encode a larger k-space in a single shot is not negligible and leads to larger echo time (TE). This is fundamental in DWI because the DW-signal exponentially decreases with increasing TE (Qin et al., 2009), as described by the Stejskal-Tanner equation (Stejskal and Tanner, 1965) :

$$S_i=S_{0,i}{e}^{-\text{TE}∕\text{T2}}{e}^{-b{D}_i},$$

where S_i is the diffusion signal in a voxel i, S_0,i is the non-attenuated signal, TE is the echo time, T2 the T2 relaxation time in the tissue, b is the b-value or b-factor (Le Bihan, 1991) and D_i is the Apparent Diffusion Coefficient (ADC) in the voxel i. Consequently, encoding a larger k-space leads to an increased TE, which in turn leads to a drop in SNR for all of the diffusion measurements, regardless of the applied b-value b.

SS-EPI is very sensitive to magnetic field inhomogeneities caused by susceptibility changes at tissue interface, such as air and tissue. Particularly, areas in the temporal lobes near the petrous bone and areas in the frontal lobe near the frontal sinuses are commonly affected. The field inhomogeneity gives rise to phase perturbation in k-space which accumulates during the acquisition of each slice (Jezzard and Balaban, 1995). This results in severe distortion in the form of voxel shifts in the image space, of largest magnitude in the phase-encoding direction (Jezzard and Balaban, 1995). Consequently, the increased TE due to the larger k-space encoding leads to increased accumulation of errors during the spatial encoding. This leads to severely increased geometric and intensity distortion in the phase encoding direction.

Ultimately, reducing the voxel size is challenging in MRI because the SNR is directly proportional to the voxel size, and proportional to the square root of the number of averages. Decreasing the voxel size by a factor α (e.g. α = 8 to reduce the voxel size from 2×2×2mm³ to 1×1×1mm³) requires α² (e.g. 64) averages to ensure a similar SNR. A 5 minute acquisition would become a 5 hour scan, which is not realistic.

Solutions to achieve higher resolution in DWI include improvements to the MRI scanner hardware itself. Among them, employing higher magnetic fields (7 Tesla, 11 Tesla) enables MR imaging with higher SNR. Using stronger and faster gradients enables imaging with lower echo time, reducing the distortion and limiting the drop in SNR caused by the larger spatial encoding. Using gradient coils dedicated to the diffusion encoding, known as Gradient Insert (Kimmlingen and et al, 2004), has also been proposed to reduce the TE. These solutions are effective but require a hardware upgrade of the scanner.

Recent works in ultra-high field DWI (7 Tesla or more) have investigated segmented EPI techniques, in which each slice is acquired in multiple shots, reducing the TE for each shot. These techniques, originally designed to attenuate the severe distortion at high field, can also be employed for encoding a larger k-space for resolution enhancement in DWI, at the expense of multiplying the scan duration time by the number of shots. However, phase inconsistencies resulting from even minimal physiological motion during the application of the sensitizing gradients are still challenging to correct in DWI.

Increasing the resolution via algorithmic contributions

Another solution to increasing the resolution is to consider algorithmic contributions. In tract density imaging (TDI), Calamante et al. (2010) have explored the application of interpolation of fiber tracts inside voxels of size smaller than the resolution of the DW-acquisition. This model-based interpolation technique provides an elegant manner to visualize dense tractography streamlines in a 3-D volume. However, TDI does not provide any resolution enhancement of the imaging data. The obtained image contains exactly the same information as the tractography, and higher frequencies in k-space are not sampled. In contrast, we propose in the next section to increase the spatial resolution by both algorithmic contributions and modification of the acquisition strategy.

Increasing the resolution via super-resolution reconstruction

In this work, we propose to increase the resolution by acquisition of orthogonal anisotropic DW acquisitions and by recovering the underlying high resolution images with an approach inspired by super-resolution reconstruction techniques. Super-resolution reconstruction (SRR) approaches were originally developed for the reconstruction of high-resolution (HR) images from a set of low-resolution (LR) images in video sequences (Irani and Peleg, 1993). To our knowledge, only Peled and Yeshurun (2001) have investigated SRR in DWI. They proposed to employ the Irani-Peleg SRR technique (Irani and Peleg, 1993) from a set of spatially subpixel-shifted scans in the in-plane dimension. However, MRI being a Fourier acquisition technique, in-plane shifting has been shown to be equivalent to a global phase shift in k-space (Greenspan, 2002). Such a technique does not enable any resolution enhancement in MRI but is equivalent to interpolation by zero-padding of the raw data in the temporal domain. Recently, Greenspan (2009) has shown that employing subpixel-shifted scans in the slice-select dimension does provide resolution enhancement in anatomical MRI. However, this has never been employed for DWI. Gholipour et al. (2010) have employed multiple orthogonal fast slice scans and have developed a model-based super-resolution reconstruction technique to acquire high-resolution anatomical images of moving subjects in fetal imaging. Finally, Jiang et al. (2009) have investigated DWI of moving subjects by (1) registering each slice to a common reference, (2) correcting the diffusion gradient orientation for each slice and (3) by estimating a diffusion tensor at each voxel by using scattered data interpolation. This model is based on a tensor, which is not appropriate for modeling more complex diffusion phenomena.

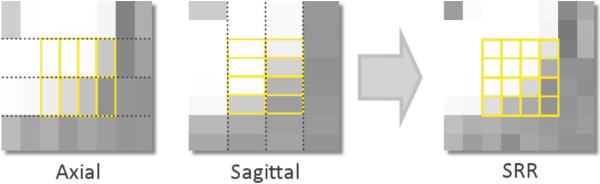
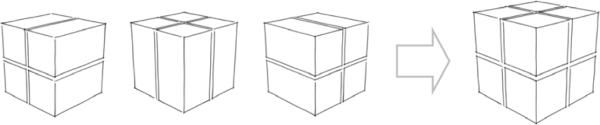
Building upon our preliminary work (Scherrer et al., 2011), we propose to perform the super-resolution reconstruction of DW images from thick slice orthogonal acquisitions (see Fig.1). Employing thick slice orthogonal acquisitions amounts to sampling higher frequencies in k-space along only two axes, in different orthogonal directions. Each acquisition contains higher frequencies in k-space in two of the three axes, and this enables the enhancement of resolution in 3-D. However, reconstruction from orthogonal acquisitions is challenging in DWI. Indeed, orthogonal acquisitions require phase-encoding direction changes, leading to very different geometric and intensity distortion. This makes the precise alignment of the images impossible. Locally, overlapping voxels across acquisitions may represent a different brain location, which strongly perturbs the reconstruction.

Figure 1.

Scheme illustrating the super-resolution reconstruction from the acquisition of two orthogonal thick slices.

Here we propose for the first time to achieve super-resolution reconstruction (SRR) from distortion compensated anisotropic orthogonal DW acquisitions. First, DW images are corrected for distortion by acquisition of a field map (Jezzard and Balaban, 1995; Cusack et al., 2003). This provides us with an estimate of the field inhomogeneity, which can in turn be employed to correct for the voxel shift in the image space. Second, we propose a technique to align each volume both in space and in q-space to account for possible patient motion. Third, we formulate the super-resolution reconstruction from multiple scans as a maximum a posteriori (MAP) estimation problem. Our approach is formulated in the image space and relies on an image acquisition model. The forward model links the generation of the acquired volumes with the unknown HR volume we aim to recover. The super-resolution reconstruction is the inverse problem, which involves estimating the original HR volume that generates the acquired anisotropic volumes. Our MAP formulation enables introduction of image priors that exploit spatial homogeneity and provide regularized solutions.

The paper is organized as follows: we detail the field-map based EPI distortion correction in Section 2.1, and the alignment in space and q-space in Section 2.2. In Section 2.3, we describe the actual super-resolution reconstruction from distortion compensated anisotropic acquisitions, and provide the pseudo-code of the complete DWI-SRR optimization procedure. Section 2.4 describes the various experiments performed to evaluate our approach, which includes numerical simulations, synthetic SRR and real world SRR. We report the experimental results in Section 3. Particularly, we show that SRR outperforms the acquisition of a single isotropic scan for the same acquisition duration time. It provides more detailed structures and better tractography results. This work provides the first evidence that SRR enables resolution enhancement in DWI.

2. Material and Methods

2.1. Correction for EPI distortion by field-map unwarping

Orthogonal DW-images experience very different distortion because they cannot be acquired with the same phase-encoding direction. Since super-resolution imaging relies on the fusion of spatial information from these multiple acquisitions, this distortion must be compensated for to ensure that overlapping voxels among the acquisitions represent the same brain location.

We correct for geometric and intensity distortion by field-map unwarping, utilizing the phase field inhomogeneity map provided by the dual echo acquisition. We consider that the pixel mis-location due to magnetic susceptibility differences occurs only in the phase encoding direction and is negligible in the read-out direction (Jezzard and Balaban, 1995). The voxel shift Δy_r (in mm) at a location r is corrected from the phase value ϕ_r (in radians) of the phase field map via the following expression (Jezzard and Balaban, 1995):

$$\Delta y_r={(2\pi .\Delta T_E.B_{pe})}^{-1}{\varphi }_r.\Delta q_y,$$

where ΔT_E is the difference in echo times of the dual echo gradient acquisition (in seconds), B_pe is the bandwidth per pixel (in Hz/pixel), and Δq_y is the voxel spacing (in mm/pixel) of the EPI image along the phase encoding direction. The image intensity values were corrected using the Jacobian of the unwarping model to account for the effect of signal stretching or shrinking.

2.2. Correction for possible motion by alignment in space and q-space

We consider K orthogonal distortion compensated low-resolution (LR) diffusion-weighted acquisitions containing G sensitizing-gradients each. The KG volumes should all be in precise alignment to enable the super-resolution reconstruction. First we perform an alignment in space: we register each volume to a reference volume, chosen as the B = 0 s/mm² volume of the first DWI LR acquisition. Each gradient orientation is compensated for the rotation component of the transformation, providing a gradient set ${\mathrm{g}}^k=(g_1^k,\dots ,g_G^k)$ for each acquisition k.

In the presence of motion, the DW-images may represent different gradient-sensitization directions in the patient coordinate system among the K acquisitions (see Fig.2). However, it is essential that the images combined by the SRR technique correspond to the exact same “scene”, namely that they correspond to the same gradient direction with respect to the anatomy, and show identical diffusion-attenuation patterns. Consequently, we propose to perform an alignment of the volumes in q-space (see Fig.3). We consider that the DW-signal varies smoothly in q-space and propose to resample the gradient images. We consider the gradients of the first DWI LR acquisition as the reference gradients g̃ = g¹. We align in q-space all other k ≥ 2 DWI acquisitions so that their gradients exactly match g̃. This is done by using interpolation in q-space. At each voxel, we consider the G intensity values corresponding to the gradients g̃^k (red arrows in Fig.3). We then compute the new intensity values corresponding to the gradients g̃ (blue arrows in Fig.3). The interpolation is performed via Kriging (Matheron, 1963), a general and efficient statistical interpolation framework originally introduced for geology and mining applications. This enables us to easily perform scattered data interpolation. It determines the weights of the contribution of each observed data via the resolution of a simple linear system. In the absence of motion (i.e. a gradient g_j exactly matches a gradient g̃_j′), the interpolated intensity exactly matches the observed intensity. As a result, the K LR acquisitions are all aligned in space and represent the same diffusion sensitizing-gradient set g̃.

Figure 2.

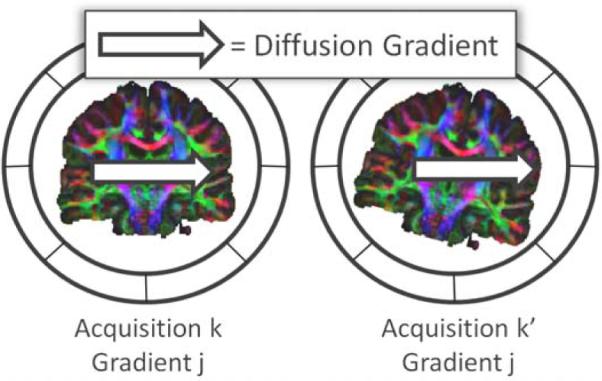
In presence of motion, the DW-images for the same applied diffusion-sensitization gradient may represent different gradient directions in the patient coordinate system among the acquisitions.

Figure 3.

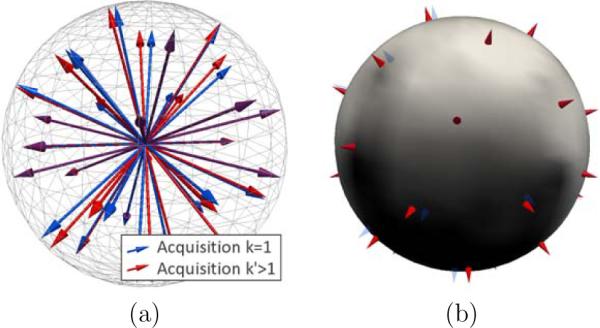
Alignment in q-space. We consider the first acquisition (k = 1, in blue) as the reference (a), providing the reference gradient directions g̃ (in blue). The gradient images of an acquisition k > 1 are resampled so that its gradient directions g^k (in red) correspond to the reference gradients g̃. At each voxel, we compute the novel intensities corresponding to the gradients g̃ by interpolation in q-space from the observed intensities corresponding to g^k (b).

2.3. Super-resolution model-based reconstruction

In this section we consider that all of the LR volumes are aligned in space and in q-space. The super-resolution reconstruction technique we now address is performed for each gradient direction separately. For each gradient g̃_j, we aim to recover the HR image x_j underlying the K LR images y_j = (y_1,j, .…, y_K,j). By omitting the gradient dependency to simplify the notations, we consider the K LR volumes y = (y₁, .…, y_K) to be the observable degraded versions of the same unknown HR volume x we aim to recover. x is estimated according to the maximum a posteriori principle, by maximizing:

$$\begin{array}{cc}\hfill {\widehat{\mathbf{x}}}_{\text{MAP}}& =\text{arg}\underset{\mathbf{x}}{\text{max}}p(\mathbf{x}\mid \mathbf{y})=\text{arg}\underset{\mathbf{x}}{\text{max}}p(\mathbf{y}\mid \mathbf{x})p\left(\mathbf{x}\right)\hfill \\ \hfill & =\text{arg}\underset{\mathbf{x}}{\text{max}}[\text{ln}p(\mathbf{y}\mid \mathbf{x})+\text{ln}p\left(\mathbf{x}\right)],\hfill \end{array}$$ (1)

which decomposes into a likelihood term and a prior term.

Likelihood term p(y|x): we consider a model that describes how the LR volumes are obtained from the unknown HR volume. We propose the following acquisition model:

$${\mathbf{y}}_k={\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{M}}_k\mathbf{x}+{∊}_k,$$ (2)

where the volumes y_k and x are expressed as column vectors by a lexicographical reordering of the pixels, D_k is a down-sampling matrix, M_k is the warping matrix that maps the HR volume x to the LR volume y_k and ∊_k is the residual noise vector. B_k is the blur, or point spread function (PSF) of the MRI signal acquisition process. It is constructed from the imaging parameters. The PSF can be separated into three components corresponding to the slice-selection direction and the phase- and frequency-encoding directions. We currently consider a PSF in the slice-selection direction only, which describes the slice selection profile (Noll et al., 1997; Greenspan, 2002; Jiang et al., 2007). We consider a Gaussian slice selection profile of variance ${\sigma }_{\text{PSF}}^2$. Consequently, on the basis of Eq.2, the unknown HR volume x goes through geometric and signal modifying operations, including motion, signal averaging, and resampling, to generate the acquired LR volume y_k. Assuming a Gaussian noise with zero-mean and variance σ_k for ∊_k, the likelihood of the LR volume y_k under the model described by Eq.2 can be written as:

$$p({\mathbf{y}}_k\mid \mathbf{x},{\sigma }_k)=\frac{1}{{\sigma }_k\sqrt{2\pi }}\text{exp}\left(-\frac{{\Vert {\mathbf{y}}_k-{\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{M}}_k\mathbf{x}\Vert }^2}{{\sigma }_k^2}\right).$$ (3)

Assuming statistical independence of the noise between the acquisitions, we have $p(\mathrm{y}\mid \mathrm{x},\sigma )={\Pi }_{k=1}^{K}p({\mathrm{y}}_k\mid \mathrm{x},{\sigma }_k)$ with σ = (σ₁, …, σ_K).

Prior term p(x): the term p(x) in Eq.1 enables us to incorporate a prior knowledge on x. In this work we consider a regularization prior that exploits spatial homogeneity. More precisely, we favour smoothness of x by setting p(x|λ) = exp(−λ∥Qx∥²) where the matrix Q is symmetric positive definite and represents a linear high-pass operation. The parameter λ controls the regularization strength. In this work, Q is chosen as the 3-D discrete Laplacian corresponding to the following approximation of the partial derivative for a 3-D image I indexed by u ∈ IN³, and for a direction u_m ∈ IN³ (m ∈ {1, 2, 3}):

$${\partial }_m\mathbf{I}\left(\mathbf{u}\right)\approx \left(\mathbf{I}(\mathbf{u}+{\mathbf{u}}_m)-2I\left(u\right)+\mathbf{I}(\mathbf{u}-{\mathbf{u}}_m)\right)∕\left(2\Vert {\mathbf{u}}_m\Vert \right).$$ (4)

Ultimately, by considering the same σ_k across acquisitions, maximization of the posterior distribution in Eq.1 leads to the following minimization:

$$\widehat{\mathbf{x}}=\text{arg}\underset{\mathbf{x}}{\text{min}}\sum _{k=1}^K{\Vert {\mathbf{y}}_k-{\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{M}}_k\mathbf{x}\Vert }^2+\lambda {\Vert \mathbf{Qx}\Vert }^2.$$ (5)

DWI-SRR optimization procedure

The matrix D_kB_kM_k is especially large, and the classical solution through the computation of the pseudo-inverse prohibitive. Instead we use a steepest descent iterative minimization approach. Differentiation of Eq.5 leads to the following update at each step:

$${\widehat{\mathbf{x}}}^{n+1}={\widehat{\mathbf{x}}}^n-\alpha \left[\sum _{k=1}^K{\mathbf{M}}_k^T{\mathbf{B}}_k^T{\mathbf{D}}_k^T({\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{M}}_k{\widehat{\mathbf{x}}}^n-{\mathbf{y}}_k)+\lambda Q^{T}Q{\widehat{\mathbf{x}}}^n\right],$$ (6)

where α is the step size and ${\mathrm{M}}_k^T$ denotes the transpose of M_k. The iterative algorithm is initialized by setting ${\widehat{\mathrm{X}}}^0$ equal to the mean of the aligned LR volumes. The iterative minimization is stopped when ${\Vert {\widehat{\mathrm{X}}}^{n+1}-{\widehat{\mathrm{X}}}^n\Vert }_1\langle {\mathcal{T}}_{\text{STOP}}$.

The complete DWI-SRR optimization procedure including distortion compensation, space and q-space alignment and the actual reconstruction is synthesized by the following pseudo-code:

FOR each LR study k

FOR each gradient image of k

Correct for distortion with the field-map

${\mathrm{M}}_k^T\leftarrow$ Register to the reference volume

Apply the transform to the gradient

ENDFOR

ENDFOR

FOR each output gradient g_g

FOR each LR study k

y_k ← Compute the gradient image for g_g

(q-space interpolation)

ENDFOR

Compute ${\widehat{\mathrm{X}}}^0\leftarrow$ Mean of the ${\mathrm{M}}_k^T{\mathrm{D}}_k^T{\mathrm{y}}_k$

WHILE ${\Vert {\widehat{\mathrm{X}}}^n-{\widehat{\mathrm{X}}}^{n-1}\Vert }_1\ge {\mathcal{T}}_{\text{STOP}}$

${\widehat{\mathrm{X}}}^{n+1}\leftarrow$ Update with Eq. 6

ENDWHILE

ENDFOR

2.4. Methods

Implementation

The complete DWI-SRR optimization procedure was C++. The super-resolution reconstruction implementation was optimized with various techniques to reduce the processing burden. The ${\mathrm{M}}_k^T{\mathrm{B}}_k^T{\mathrm{D}}_k^T{\mathrm{D}}_k{\mathrm{B}}_k{\mathrm{M}}_k$ and ${\mathrm{M}}_k^T{\mathrm{B}}_k^T{\mathrm{D}}_k^T{\mathrm{y}}_k$ matrices were precomputed, and the derivative of the Laplacian corresponding to the finite difference scheme in Eq.4 was computed analytically. To accelerate the convergence, the steepest descent algorithm was implemented with a variable per-voxel step-size α which incorporated inertia: the step-size was multiplied by 1.1 when the sign of two consecutive computed gradients did not change, and divided by two otherwise. α is initialized to 0.01 and constrained to lie in [0.1, 10⁻⁶]. The FWHM for the Gaussian slice model was set to half the slice thickness, by setting ${\sigma }_{\text{PSF}}=\left(\text{slice thickness}\right)∕\left(4\sqrt{2\text{ln}2}\right)$. Other parameters were set to λ = 0.001 and ${\mathcal{T}}_{\text{STOP}}={10}^{-5}$.

Numerical simulations

First, we evaluated our approach with numerical simulations. Since in this case the images did not experience motion or EPI distortion, these two steps were ignored. The DW-signal for tensors was simulated with a b-value of 1000s/mm² for 15 directions, and the DW-images corrupted by Rician noise (SNR of 30dB for the b=0s/mm² image). Linear down-sampling with a factor of 4 was applied to each gradient image in each of the three directions, providing three simulated LR acquisitions. Then, the super-reconstruction from the three LR acquisitions was performed, and compared to the original image. Various tensor estimations were performed, and the corresponding fractional anisotropy (FA) maps were qualitatively compared.

Synthetic SRR scenario

Second, we simulated a SRR scenario by down-sampling a real DWI acquisition in each of the three orthogonal directions. The real DWI acquisition was performed on a Siemens Trio 3T scanner with a 32 channel head coil and the following parameters: FOV=220mm, matrix=128×128, 68 slices, resolution=1.7×1.7×2mm³, 30 directions at B = 1000s/mm², 5 B = 0s/mm². The B = 0s/mm² images were averaged together. Down-sampling factors of 2 and 4 were considered to simulate the orthogonal axial, coronal and sagittal thick slice acquisitions. The super-resolution reconstruction at the original resolution was estimated and qualitatively compared to the original image. The SRR estimation time was approximately 2 hours on a 3Ghz Intel Xeon (3 to 4 minutes per gradient image). The SRR was quantitatively compared to the original acquisition by assessing the Peak Signal to Noise Ratio (PSNR). The PSNR is a commonly employed measure when assessing the quality of an image reconstruction algorithm. It is defined by $20{\log }_{10}(\text{MAX}∕\sqrt{\text{MSE}})$ with MAX being the maximum image intensity and MSE the mean square error. Higher values indicate better reconstructions.

SRR from DWI acquisitions

Finally, we investigated the super-resolution reconstruction from real DWI acquisitions. We acquired K = 3 anisotropic DWI scans (axial, coronal, and sagittal) on a Siemens Trio 3T scanner with a 32 channel head coil and the following parameters: FOV=220mm, matrix=176×176, in-plane resolution=1.25×1.25mm², slice-thickness=2.5mm, 5 b=0s/mm², 30 directions at b=1000s/mm². The number of slices was chosen to cover the whole brain, varying from 58 to 71 depending on the acquisition orientation. The total acquisition duration time for the three scans was 17min00sec.

For comparison, we acquired an isotropic DWI scan with parameters chosen to match the acquisition time of the three previous scans : matrix=146×146, resolution=1.5×1.5×1.5mm³, 100 slices, same sensitizing gradient orientations, two averages, 16min32sec.

Finally, a dual echo gradient echo field map image was acquired with TE_1/2 = 5.19/7.65ms and resolution=2×2×2.5mm³. The unwrapped phase field map required for the distortion compensation was generated by the scanner. The phase field map image was processed with median filtering with one voxel radius, and Gaussian smoothing with full width at half maximum (FWHM) of 2.

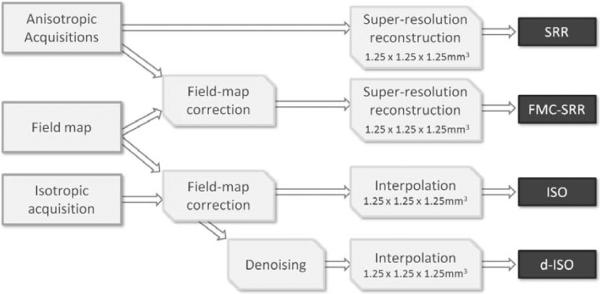
Both the anisotropic and the isotropic acquisitions were corrected for distortion by utilizing the field-map unwarping technique described in Section 2.1. The unwarping processing time was approximately twenty seconds per image. The SRR of each corrected DW-image was achieved to create an isotropic volume of 1.25×1.25×1.25mm³ (FMC-SRR, see Fig.4). To investigate the effect of the distortion compensation, we also achieved the SRR without any field-map correction (SRR) at the same isotropic resolution. We compared the SRR technique to the isotropic acquisition by resampling the 1.5×1.5×1.5mm³ DW-images to 1.25×1.25×1.25mm³ as well (ISO). Finally, we investigated the effectiveness of applying a post-processing noise correction technique to the isotropic acquisition (d-ISO). We employed the Joint Linear Minimum Mean Squared Error (LMMSE) noise filter proposed by Tristán-Vega and Aja-Fernández (2010).

Figure 4.

Schematic describing the experimental setup to evaluate the SRR reconstruction from real acquisitions.

Color fractional anisotropy (color-FA) maps were computed by considering the normalized primary eigenvector of each tensor as a vector in the RGB space, modulated by the tensor FA (Douek et al., 1991). We qualitatively compared the color-FA maps of ISO, d-ISO, SRR and FMC-SRR.

We quantitatively compared the four experiments via residual bootstrapping (Chung et al., 2006). The residual bootstrap is a model-based resampling technique. From an estimated tensor-field, it generates a set of virtual new DWI acquisitions by randomly sampling the model residuals, simulating new acquisitions with a different but realistic noise. A new tensor-field was estimated from each virtual acquisition, and the corresponding variance of the FA assessed. The obtained FA variance is related to the estimation uncertainty. A lower value indicates a lower uncertainty, indicating a better quality of the data. The average FA variance for the four experiments ISO, d-ISO, SRR and FMC-SRR was compared in a common 3-D region of interest.

Finally, tractography experiments were achieved. We considered tractography of the corpus callosum, of the pyramidal tracts and of the medial cerebellar peduncle. The same seeding region and the same tractography parameters were employed when generating tract streamlines from ISO, d-ISO, SRR and FMC-SRR. The streamlines were color-coded with color-FA map and compared.

3. Results

Numerical simulations

Fig.5 reports the results of the numerical simulations, showing the tensors and corresponding FA maps for the original simulated acquisition (Fig.5a and e), for one of the LR acquisitions (Fig.5b and f), for the mean of the three LR acquisitions (Fig.5c and g) and for the SRR (Fig.5d and h). As expected, the estimation from a low-resolution acquisition (Fig.5b and f) is very poor. Fig.5c shows that the tensor directions are well estimated from the mean of the LR acquisitions. However, as seen on the FA map in Fig.5h, the SRR provides a more accurate reconstruction of the complete tensor, providing a sharper FA map.

Figure 5.

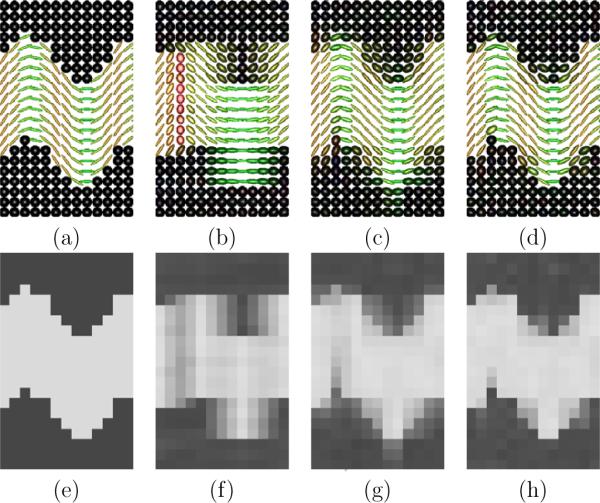
Numerical simulations. Fig.a. Original tensors used to simulate the DW signal. Fig.b–d: Tensors estimated resp. from a single LR acquisition, from the mean of the LR acquisitions and from the SRR. Fig.e–h: Corresponding tensor fractional anisotropy. It shows the tensor directions to be well estimated from the mean (Fig.c). However, the SRR provides a much more accurate reconstruction of the complete tensor (see the better FA uniformity in Fig.h).

Synthetic SRR scenario

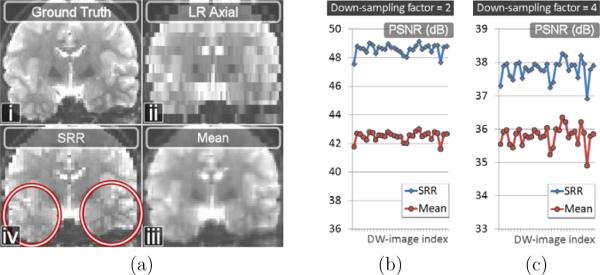
Fig.6a shows the b = 0s/mm² image of an original acquisition (Fig.6a.i), the artificially down-sampled image corresponding to a simulated axial acquisition (Fig.6a.ii), the mean of the three thick-slice acquisitions (Fig.6a.iii) and the SRR (Fig.6a.iv). It shows the SRR to be qualitatively better contrasted and less blurry than the mean of the LR images. Quantitatively, we report in Fig.6b–c the reconstruction accuracy for each of the thirty gradient images. It shows an increase of PSNR on the order of 6dB and 2dB with SRR for our two synthetic down-sampling scenarios. In Fig.7 we compare the 3-dimensional angular reconstructions of the diffusion signal at four voxels, for the mean of the LR images (first line) and the super-resolution reconstruction (second line). For each voxel 1 to 4, the angular reconstruction shapes were generated in spherical coordinates by modifying the radial coordinate of a 3-d sphere. For each gradient direction, the radial coordinate was set to the reconstructed DW-image intensity. The angular reconstructions were color-coded according to the error in image intensity between the reconstructed DW-image and the ground-truth. Consistent with Fig.5 and Fig.6, we show that the super-resolution approach provides a much better reconstruction of the complete diffusion attenuation profile compared to the mean of the LR acquisitions.

Figure 6.

Fig.a: Synthetic SRR scenario from a real acquisition. a.i: b = 0 image. a.ii: Axial down-sampled b = 0 image with a factor of 4. a.iii: Mean of the b = 0 images of the LR acquisitions. a.iv: SRR of the b = 0 image. The SRR is better contrasted and is less blurry than the mean. Fig.b and Fig.c: Quantitative evaluation of the reconstruction accuracy in term of PSNR for the two- and four- down-sampling factors, for each of the thirty gradient directions (x axis).

Figure 7.

3-Dimensional angular reconstructions of the diffusion signal at four voxels whose position is shown on the b = 0s/mm² image (left image). The voxels were chosen to have a high FA (FA > 0.9). The obtained 3-D shapes are proportional to the apparent diffusion coefficient (ADC). We compared the 3-D reconstruction performed from the mean image (first line) and from the SRR estimate (second line). The stick indicates the major fiber direction estimated by a single-tensor model. The color indicates difference between the reconstructed and ground truth intensities (difference in image intensity). It shows the SRR estimate provides a much better reconstruction for each gradient image.

SRR from DWI acquisitions

We now report the results of the SRR from real anisotropic orthogonal acquisitions. Fig.8 illustrates the field-map distortion compensation that was applied to each DW-image. It depicts how orthogonal EPI acquisitions are subject to different geometric distortion depending on the phase-encoding direction (Fig.8b,d). Fig.8c,e shows that the field-map unwarping substantially reduces the distortion.

Figure 8.

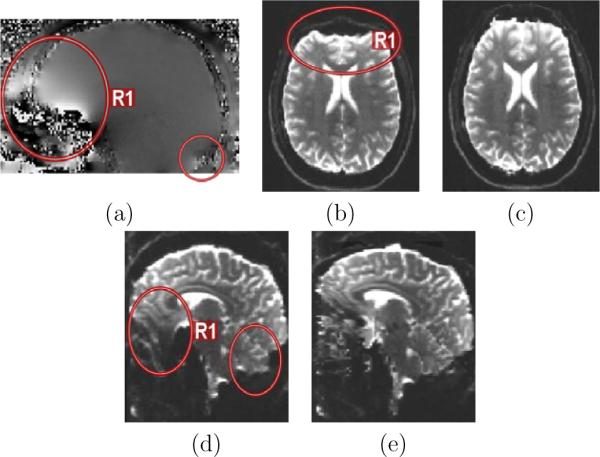
Field-map based distortion correction. (a): Phase field-map generated from the dual-echo gradient echo sequence. The frontal lobe close to the sinuses is typically affected (region R1). (b): Axial acquisition with EPI distortion (b=0s/mm², phase-encoding direction: anterior to posterior). (c): Corrected image. (d): Coronal acquisition with distortion (sagittal view, phase-encoding direction: head to foot). (e): Corrected image. The red circles highlight regions of high distortion.

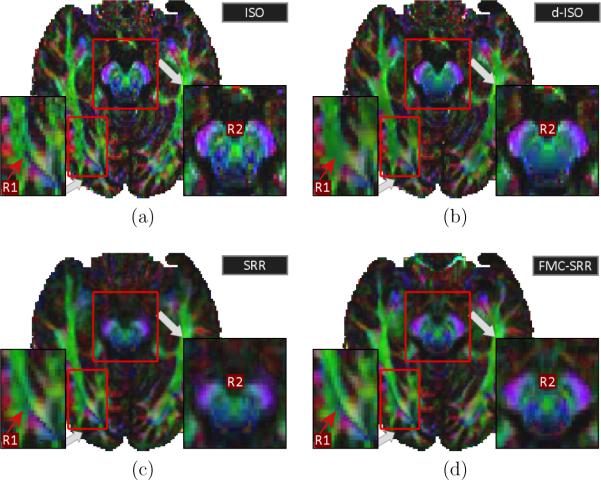
Fig.9 illustrates the color-FA maps for ISO, d-ISO, SRR and FMC-SRR Particularly, the color-FA of ISO (Fig.9a) is noisier, is corrected when denoising in post-processing (d-ISO, Fig.9b). However, fine structures are smoothed and lost when applying the noise correction (region R1).

Figure 9.

Color-FA maps for (a):ISO, (b):d-ISO, (c):SRR and (d): FMC-SRR (axial view). R1 points out that fine structures are well conserved with FMC-SRR, despite the large slice thickness employed for each anisotropic acquisition. R2 highlights a region in which SRR (without distortion compensation) provides blurred results. Importantly, the structures in the region R2 are more detailed with FMC-SRR than with d-ISO.

Fig.9c shows that non-compensation of the distortion (SRR) leads to a less detailed color-FA map (region R2). Fig.9d shows that fine structures far smaller than the slice thickness (2.5mm) of the anisotropic acquisitions are well conserved with FMC-SRR (region R1). Importantly, structures in the region R2 appear to be more detailed with FMC-SRR than with d-ISO or SRR.

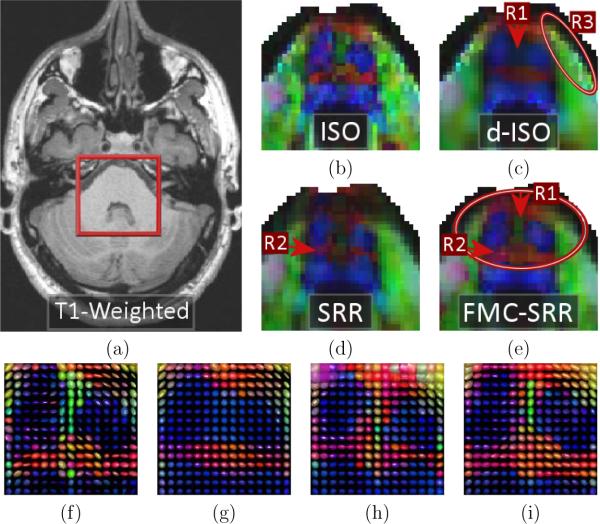
Fig.10 shows a zoom of the color FA maps in a region of the brain stem. Consistent with Fig.9a, it shows that ISO provides a highly noisy color-FA (Fig.10b) and more generally a noisy tensor estimation (Fig.10f). d-ISO provides smoother results (Fig.10c) but with interpolation artifacts (region R3) and more blurred structures than FMC-SRR (region R1, and Fig.10g). Fig.10d (SRR) shows that misalignment of the uncorrected acquisitions leads to a missing structure (R2) in the color-FA because the whole tensors are poorly estimated (Fig.10h). FMC-SRR provides the more detailed structures (Fig.10e/i).

Figure 10.

Zoom on the color-FA maps in a region of the brain stem. (a): T1-weighted image showing the zoom location (axial view). Color-FA maps and estimated tensors for (b/f): ISO, (c/g): d-ISO, (d/h): SRR and (e/i): FMC-SRR. The color-FA for ISO is highly noisy, while the noise reduction technique employed in d-ISO makes the structures fuzzy (region R1) and produces artifacts (R3). In SRR some structures are missing due to the non-correction of distortion (R2). FMC-SRR provides the most detailed structures (R1).

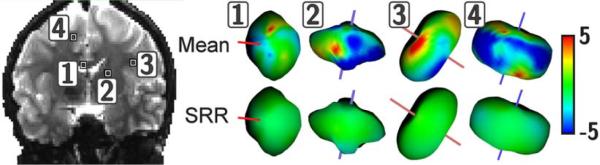
Fig.11 illustrates the bootstrap results. It shows that the estimation uncertainty is much higher with ISO. The uncertainty with the other techniques is comparable.

Figure 11.

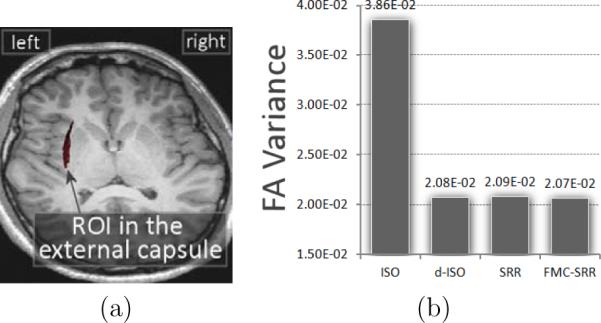
Assessment of the estimation uncertainty by averaging the FA variance from the residual bootstrap in a 3-D region of interest. (a): region of interest considered, in the left external capsule. (b): average of the FA variance in the ROI.

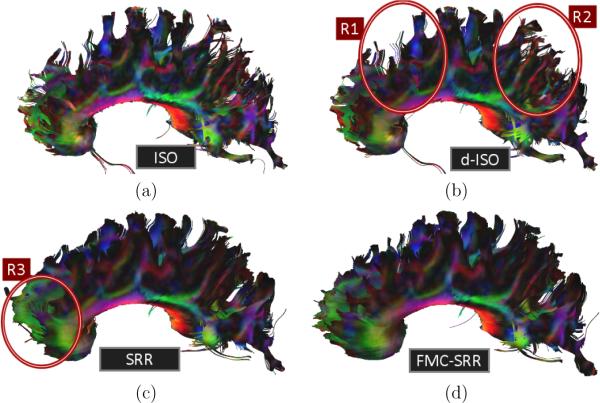
Fig.12 reports the tractography results for the corpus callosum. ISO (Fig.12a) provides poor results due to the high noise corruption. The noise filtering in d-ISO (Fig.12b) enables a better connectivity assessment. However, a number of streamlines remain disorganized (regions R1 and R2). FMC-SRR (Fig.12d) outperforms the other approaches. Particularly, streamlines in the frontal part (region R3) better represent the anatomy. Without distortion correction (SRR, Fig.12b), the anisotropic scans were poorly aligned in the frontal region (see Fig.8a,b) and the tracts prematurely stopped.

Figure 12.

Tractography results for the corpus callosum from (a): ISO, (b): d-ISO, (c): SRR and (d): FMC-SRR.

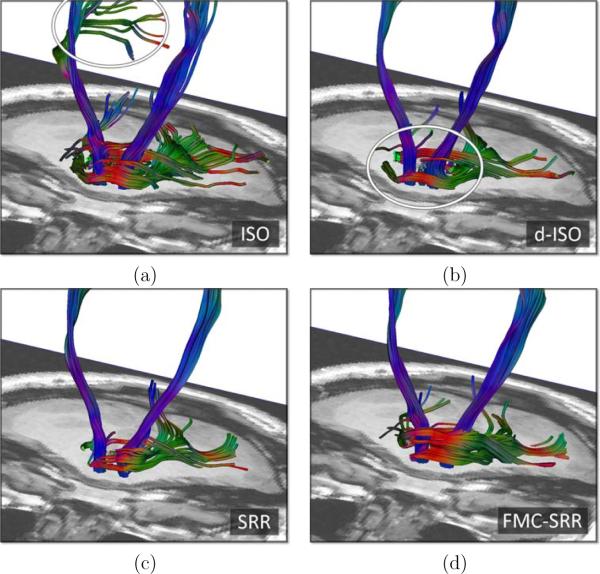
Finally, Fig.13 reports the tractography results for the pyramidal tracts and for the medial cerebellar peduncle. The streamlines generated from ISO are strongly impacted by the noise (Fig.13.a), while with d-ISO or SRR the medial cerebellar peduncle is poorly recovered (Fig.13.b and c). FMC-SRR (Fig.13.d) provides the best results for the tractography of both the pyramidal tracts and the medial cerebellar peduncle.

Figure 13.

Tractography results for the pyramidal tracts (vertical streamlines) and the medial cerebellar peduncle, corresponding to a region close to the region in Fig.10, from (a): ISO, (b): d-ISO, (c): SRR and (d): FMC-SRR.

4. Discussion

Increasing the spatial resolution requires sampling of higher frequencies in k-space which is very challenging in DWI. Sampling of a larger k space along each axis is difficult because of (1) the dramatically lower SNR associated with a smaller voxel size, (2) the increased spatial encoding limitations for the gradient coils, and (3) the increased TE, which in turn leads to higher distortion and a lower SNR. Instead, we have proposed to employ anisotropic orthogonal DWI acquisitions, which amounts to densely oversampling k-space along only two axes (see Fig.14). First, this achieves a better SNR due to the larger voxel size. Second, this reduces the spatial encoding burden for each scan. The underlying isotropic high-resolution DW-images are then recovered in the image space with a super-resolution technique.

Figure 14.

Employing anisotropic orthogonal acquisitions amounts to densely oversampling k-space along only two axes.

Because orthogonal DWI scans have different phase-encoding directions, they experience different distortion patterns. We have proposed to compensate each acquisition for distortion prior to the reconstruction. This is achieved by acquisition of a field-map (Jezzard and Balaban, 1995), providing an estimate of the field inhomogeneity caused by susceptibility changes at tissue interface, which is used to correct for the voxel mislocation. We have shown that distortion compensation is essential when achieving the super-resolution reconstruction. Without correction, overlapping voxels across acquisitions do not represent the exact same brain location, which severely perturbs the reconstruction. It leads to blurred (Fig.9c-R2) and missing (Fig.10d-R2) structures, even in regions not known to be strongly affected by the susceptibility artifact. Ultimately, it leads to prematurely stopped tractography streamlines (Fig.12c).

Our approach requires three DWI acquisitions that image the same gradient directions. However, in case of patient motion during the scans, each triplet of DW-image may represent different gradient directions in the patient coordinate system. We have taken into account possible patient motion by aligning the volumes not only in space, but also in q-space. Our super-resolution reconstruction technique is performed in the image space via a MAP formulation. It relies on a realistic image generation model that models the anisotropic DW images we acquire as observations of an underlying isotropic high-resolution acquisition. Our MAP formulation enables introduction of image priors to ensure regularized solutions, and allows the estimation of the high-resolution DW images.

Based on numerical simulations and synthetic SRR scenarios, we have shown that the SRR estimate outperforms the mean of the anisotropic acquisitions. The SRR led to high contrast and less blurry gradient images (Fig.6a). We quantitatively showed an increase of PSNR on the order of 6dB and 2dB for our two synthetic down-sampling scenarios (Fig.6b–c). This led to a better reconstruction of the whole diffusion attenuation profile (Fig.7) and ultimately to a better reconstruction of the whole diffusion tensor (Fig.5).

Based on real distortion compensated acquisitions, we have shown that the SRR outperforms the acquisition of a single isotropic scan for the same scan duration time. Acquisition of a single isotropic acquisition led to a much lower SNR impacting the color FA (Fig.9a, 10b), the FA (Fig.11), the estimation certainty (Fig.11) and the tractography (Fig.12a). Denoising the isotropic acquisition (d-ISO) successfully corrected for noise (Fig.9a) and provided a higher estimation certainty (Fig.11). However, it led to blurred structures (Fig.9b-R2, Fig.10c/g), due to both the noise filtering and the interpolation necessary to resample the 1.5×1.5×1.5mm³ images to the resolution obtained by SRR (1.25×1.25×1.25mm³). Additionally, we observed artifacts caused by the interpolation with d-ISO (Fig.10c-R3). In contrast, FMC-SRR provided more detailed structures (Fig.9d-R2, Fig.10e/i). The two columns in the brain stem (Fig.10e) were better separated because SRR enables sampling of higher frequencies in k-space and consequently enables a better representation of fine edges. The estimation uncertainty was low with FMC-SRR (Fig.11). Ultimately, FMC-SRR provided the best tractography results (Fig.12d and 13d).

In this work, we acquired anisotropic acquisitions with high-resolution sampling along two axes (r_HR × r_HR = 1.25 × 1.25mm²) and low resolution sampling along the last axis (r_LR = 2r_HR = 2.5mm). The underlying high-resolution volumes were reconstructed at the isotropic resolution r_HR × r_HR × r_HR. We can observe that, with these settings, the super-resolution reconstruction problem is overdetermined. As illustrated in Fig.15, this amounts to estimating each group of eight voxels of the HR volume from twelve measurements: there are more observations than data to estimate. Interestingly, the maximum achievable isotropic resolution r_iso × r_iso × r_iso when acquiring three orthogonal acquisitions with same field of view and resolution r_HR × r_HR × r_LR can be theoretically determined. It is defined by $r_{\mathrm{iso}}={\left(\frac{r_{\mathrm{LR}}.r_{\mathrm{HR}}^2}{3}\right)}^{1∕3}$. This corresponds to the case for which the number of voxels to estimate matches exactly the number of observations.

Figure 15.

When using anisotropic acquisitions with the slice-thickness dimension twice the size of the in-plane resolution, the SRR problem is over-determined. It amounts to estimating each group of eight voxels of the high-resolution volume (right) from twelve measurements (left).

There is a natural link between our approach and the compressive sensing (CS) techniques (Lustig et al., 2007) which have emerged in the last decade. Compressive sensing and sparse reconstruction in MRI are based on a random oversampling of k-space. In this work, we have instead densely oversampled k-space by imaging with anisotropic acquisitions. This has the advantage of imaging with a conventional SS-EPI acquisition, without requiring modification of the scanner sequence, making the SRR approach widely accessible. However, SRR and CS fundamentally differ in the way they reconstruct the images. In sparse reconstruction methods, the images are recovered in k-space, making a number of operations such as interpolation typically challenging. In our approach, we instead achieve the reconstruction in the image space, based on an image generation model.

Future work will investigate the comparison of other EPI distortion correction techniques. Perfect compensation of the distortion is indeed essential to ensure that overlapping voxels in each acquisition represent the exact same brain location. This is well illustrated by Fig.10, in which the distortion compensation provides a clear improvement, even for a region not particularly known to be affected by the susceptibility artifact. The field-map unwarping is effective for moderate distortion, but is known to be limited in highly distorted region in which it is difficult to compute smooth phase maps. Particularly, we will investigate a hybrid approach combining deformable registration and field-map unwarping, which has been reported to provide even better distortion compensation (Gholipour et al., 2011; Irfanoglu et al., 2011).

We will investigate multiple enhancement to our SRR model. Particularly, introduction of novel priors such as the brain anatomy description provided by a high-resolution T2 weighted scan may enable improved SRR in DWI. More realistic noise models such as the non-central χ-distribution may better represent the noise properties, particularly when using parallel imaging (Dietrich et al., 2008) as widely employed in DWI. Finally, alternative numerical optimization algorithms may speed up the convergence and offer a faster reconstruction.

Using orthogonal anisotropic acquisitions enables sampling of higher frequencies in k-space. However, the corners of the 3-D k-space are not sampled with this technique. These regions of k-space could be sampled by acquiring more images, each appropriately rotated.

5. Conclusion

This work is the first report that acquisition of anisotropic orthogonal acquisitions and reconstruction of the underlying isotropic high-resolution acquisition with a super-resolution technique enables resolution enhancement in DWI. Particularly, the SRR outperforms the results provided by a single isotropic acquisition for the same scan duration time. DWI with SRR reveals more detailed fine structures because it samples higher frequencies in k-space. Ultimately, SRR provides a better connectivity assessment. Importantly, such a technique may enable DW imaging with unprecedented resolution. Indeed, the maximum isotropic spatial resolution is intrinsically limited by the scanner hardware, depending on the magnetic field strength and the strength and speed of the encoding gradients. By relaxing the spatial encoding burden for each acquisition, SRR may enable DW imaging with resolution beyond the limits dictated by the scanner hardware. SRR, which employs conventional SS-EPI techniques, allows us to achieve DW imaging with higher spatial resolution to provide new insight in neuroscience and clinical applications.

Highlights

• Reconstruction from distortion compensated anisotropic orthogonal DWI acquisitions

• Employs conventional single-shot EPI acquisitions, but samples higher frequencies in k-space

• Enables resolution enhancement in DWI.

• Better results than acquisition of a single isotropic scan for the same scan duration time.

• Enables DW imaging with unprecedented resolution, beyond the scanner limitations