A METHOD FOR IN-SITU CHARACTERIZATION OF RF HEATING IN PARALLEL TRANSMIT MRI

Abstract

In ultra high field magnetic resonance imaging, parallel radio-frequency (RF) transmission presents both opportunities and challenges for specific absorption rate (SAR) management. On one hand, parallel transmission provides flexibility in tailoring electric fields in the body while facilitating magnetization profile control. On the other hand, it increases the complexity of energy deposition as well as possibly exacerbating local SAR by improper design or delivery of RF pulses. This study shows that the information needed to characterize RF heating in parallel transmission is contained within a local power correlation matrix. Building upon a calibration scheme involving a finite number of magnetic resonance thermometry measurements, the present work establishes a way of estimating the local power correlation matrix. Determination of this matrix allows prediction of temperature change for an arbitrary parallel transmit RF pulse. In the case of a three transmit coil MR experiment in a phantom, determination and validation of the power correlation matrix was conducted in less than 200 minutes with induced temperature changes of <4 degrees C. Further optimization and adaptation are possible, and simulations evaluating potential feasibility for in vivo use are presented. The method allows general characteristics indicative of RF coil/pulse safety determined in situ.

INTRODUCTION

High magnetic field strength has many well-known advantages for magnetic resonance (MR) imaging and spectroscopy. These advantages include high signal-to-noise (SNR) and high spatial and spectral resolution, and yet, despite the substantial clinical and research promise of high field MR, several challenges still continue to complicate its use. At high field strength, and correspondingly high operating frequency, the operating wavelength for proton imaging becomes smaller compared to the dimensions of the human body resulting in larger and more significant interactions between the electromagnetic fields and dielectric tissues (1). These interactions can result in substantial distortions of radiofrequency (RF) magnetic field distribution, causing unwanted spatial variations in tissue contrast. Meanwhile, the concomitant electric (E) field also becomes increasingly complex, resulting in possible E field hot spots and elevated subject-dependent specific absorption rate (SAR). Mitigating the interactions between RF fields and the body is among the most difficult challenges associated with in-vivo high-field MRI. Control of these interactions was in fact one motivation for the invention of parallel RF transmission.

The advent of parallel RF transmission brought about a new paradigm wherein RF pulses simultaneously drive distributed elements of a multi-port transmit antenna to effect both spatial and temporal variations in the RF magnetic (B1) and electric (E) fields (2,3). The resulting increase in degrees of freedom as compared with traditional RF transmission was shown to enable the tailoring of E fields and the containment of global SAR while improving flip angle profile control (2). For a given coil-subject setup, flip angle profile and global SAR controls are realized through design of the individual RF and gradient pulses. The practical control of flip angle profile in vivo is enabled by subject-specific B1 calibration, which captures the complex effects of coil-subject geometry, composition and interaction on the B1 maps, while information required for global SAR control may be obtained through calibration of a power correlation matrix (4–6). Both the information provided from the B1 maps and E field interference related information can be exploited together to improve flip angle profile while simultaneously reducing SAR (2,7,8).

Global and local SAR are measures of the rate at which energy is absorbed by the body when exposed to an RF field and are measures of safety with regard to RF heating. Several schemes were recently proposed for tracking of global power deposition in an imaged body in the scanner (4–6,9). However, experimental quantification of local SAR has continued to pose a fundamental challenge, both for routine scanning and for rigorous evaluation of the safety and suitability of transmit array coils. As a result, excessively restrictive power limits are commonly used, preventing the flexible usage of parallel transmit technology. Efforts to evaluate local SAR have often relied upon electromagnetic field calculations in numerical simulations or experimental findings in "average" subjects (10). Commonly used techniques such as the finite difference time domain (FDTD) method or the finite element method (FEM) have been used as a development platform for evaluating the safety and performance of array coils and/or RF pulse designs. However, it remains unclear to what extent simulation results, even guided to some (9) extent by current experimental measures may be extrapolated to match the true conditions in an individual body in the scanner.

This work builds upon a SAR prediction model (2,9), which relates global or local power deposition to RF pulse waveforms or RF shimming coefficients via a quadratic function. The model indicates that local power deposition due to parallel transmission can be characterized by a single mathematical structure called the local power correlation matrix. This matrix provides information about the correlation of local E fields among transmit coils at various locations within the imaged body. In this work, it is demonstrated that measurements of temperature change in response to a set of predesigned RF heating pulses, via a finite number of MR thermometry acquisitions, enable practical calibration of the local power correlation matrix. Once the power correlation matrix is determined for a particular voxel, the local RF heating effect for an arbitrary RF pulse may be predicted for that location. Close agreement between predicted and measured temperature distributions are shown for a variety of RF pulses under experimental and simulated conditions.

THEORY AND METHODS

RF energy dissipation and tissue heating

Pennes’ bio-heat equation describes the thermal energy balance for perfused tissue (11):

$$\rho C\frac{\partial T}{\partial t}=\nabla .(k\nabla T)+h_b+h_q+h_e$$ [1]

where ρ, C and k refer to tissue density, specific heat capacity and thermal conductivity, respectively, h_b is the blood-to-tissue heat transfer rate and h_q energy transfer due to matabolism. The RF energy deposition rate is expressed by h_e, which is a driving force for temperature rise as result of Joule heating and is proportional to the square of the local E field strength $h_e=\frac{1}{2}\sigma |\mathrm{E}{|}^2$, where σ is the tissue conductivity. Temporal and volume averages of h_e, when further scaled by appropriate density or mass, constitute SAR as defined in FDA and IEC guidelines (12,13).

Linearity allows decomposition of the net E field as a weighted superposition of E fields corresponding to N individual sources effecting weights $w_p^{(1)}\cdots w_p^{(\mathrm{N})}$, where p represents the time interval that a certain pulse weighting is applied. In phasor notation: ${\mathbf{E}}_p(\mathbf{r})={\displaystyle {\sum }_{n=1}^{\mathrm{N}}}{w}_p^{(n)}{\mathbf{e}}^{(n)}(\mathbf{r})$ where e⁽ⁿ⁾ is the E field resulting from a unit weight in the n^th source and zero weights for all other sources. This leads to the following expression for local RF energy deposition rate (4,14):

$$h_e=\frac{\sigma (\mathbf{r})}{2}{|{\mathbf{E}}_p(\mathbf{r})|}^2=\frac{\sigma (\mathbf{r})}{2}{\mathbf{E}}_p{(\mathbf{r})}^{*}·{\mathbf{E}}_p(\mathbf{r})=\frac{\sigma (\mathbf{r})}{2}{\left({\displaystyle \sum _{m=1}^N}{w}_p^{(m)}{\mathbf{e}}^{(m)}(\mathbf{r})\right)}^{*}·\left({\displaystyle \sum _{n=1}^N}{w}_p^{(n)}{\mathbf{e}}^{(n)}(\mathbf{r})\right)={{\mathbf{w}}_p}^{\mathit{H}}\mathbf{\Lambda }(\mathbf{r}){\mathbf{w}}_p$$ [2]

where ^* denotes complex conjugate and ^H denotes conjugate transpose. Equation [2] shows that the local RF energy deposition can be expressed as a quadratic function of ${\mathbf{w}}_p=[w_p^{(1)}\cdots w_p^{(\mathrm{N})}]$. The matrix Λ(r) is referred to as the local power correlation matrix at spatial location r and it captures the effects of E field interference and tissue conductivity on local RF energy deposition. The total local energy deposition by a given parallel transmission pulse can be expressed as:

$${\xi }_{\mathit{\text{local }}}(\mathbf{r})={\displaystyle {\sum }_{p=1}^{\mathrm{P}}}\delta t*h_{e,p}(\mathbf{r})={\mathbf{w}}_{\mathit{\text{full}}}^{\mathit{H}}{\left(\begin{array}{ccc}\hfill \mathbf{\Lambda }(\mathbf{r})\delta t\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \ddots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{\Lambda }(\mathbf{r})\delta t\hfill \end{array}\right)}_{\text{NP}\times \text{NP}}{\mathbf{w}}_{\mathit{\text{full}}}$$ [3]

where w_full is a vector collecting all P sets of the RF pulse weights over the heating duration and δt is the RF pulse waveform sampling interval. Equation [3] indicates that there is a compact structure to local energy deposition. With proper calibration of the Λ matrix, local energy deposition at any spatial location can be calculated in a deterministic fashion for any RF pulse waveform w_full.

To spatially resolve RF energy deposition in vivo is a challenging problem. The present method uses MR thermometry to noninvasively map temperature and to further provide inputs for determining Λ(r). This can be explained using the Pennes’ bio-heat equation (Eq.1), which suggests that if an RF transmit experiment is conducted at a time scale short enough compared to that of heat diffusion and at a magnitude overpowering other energy transfer processes, the local RF energy deposition rate is proportional to local temperature rise, ΔT(r) (15):

$$\mathrm{\Delta }T(\mathbf{r})=\frac{{\xi }_{\mathit{\text{local }}}(\mathbf{r})}{\rho (\mathbf{r})C(\mathbf{r})}=\frac{\mathit{\text{SAR}}(\mathbf{r})}{C(\mathbf{r})}$$ [4]

where SAR(r) is the local specific absorption rate produced by the parallel RF transmission pulse. Combining equations [3] and [4] yields:

$$\frac{{\mathbf{w}}_{\mathit{\text{full}}}^H{\left(\begin{array}{ccc}\hfill \mathbf{\Lambda }(\mathbf{r})\delta t\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \mathbf{\Lambda }(\mathbf{r})\delta t\hfill \end{array}\right)}_{\text{NP}\times \text{NP}}{\mathbf{w}}_{\mathit{\text{full}}}}{\rho (\mathbf{r})C(\mathbf{r})}=\mathrm{\Delta }T(\mathbf{r})$$ [5]

Equation [5] shows that local temperature change is proportional to local RF energy deposition, where local specific heat capacity and tissue density are the scaling factors between the two. With temperature change from MR thermometry as sensor data, the quadratic model can be determined with a calibration scheme same as that given by Zhu et al. (8). Even though it is difficult to quantify local power deposition without knowing local specific heat capacity or tissue density, calibration of Λ(r)/(ρ(r)C(r)) and the resulting capability of predicting temperature changes are highly relevant. This is because temperature change is directly correlated with tissue damage (16,17) and is therefore a direct measure of RF safety. For the sake of simplicity the scaling terms ρ(r) and C(r) are incorporated inside Λ(r) in further discussions of the local power correlation matrix. In the present work MR thermometry employs proton resonance frequency shift (PRF) method (18), which exploits a chemical shift that is linearly proportional to the change in local temperature.

Experiments

Experiments were performed on a 7T Siemens whole-body MR scanner (Siemens Medical Solutions, Erlangen, Germany) equipped with an 8-channel parallel transmit system (1kW peak power per transmit channel). RF transmission and detection were provided by three 7cm × 7cm transmit/receive coils and one receive-only coil with the same dimensions. An additional receive coil was introduced to improve the receive sensitivity inside the phantom. The coils were placed around a cylindrical former with an 18cm diameter. Two of the transmit coils (TC1 and TC3 in Figure 1B) were partially overlapped to reduce mutual inductance, while the remaining transmit coil (TC2) and the receive-only coil (RC4) were separated from TC1 and TC3 by ~90 degree arc lengths, allowing independent tuning and matching of all coils. During RF transmission, all transmit coils were connected to independent RF amplifiers. Imaging was conducted on a cylindrical agar phantom of 20cm diameter and 25cm length with the following ingredients: 2300g water, 100g agar, 1600g sugar, 40g NaCl and 1g benzoic acid. The resulting mixture was heated to approximately 85 degrees Celsius and allowed to cool to room temperature to form a stable gel with conductivity and relative permittivity of approximately 0.77 Siemens/meter and 58, respectively, measured using a dielectric probe (Agilent 85070E Dielectric Probe Kit, Agilent Technologies, Germany). These values approximate the dielectric properties of muscle at 297.2MHz (19). Two low-conductivity oil phantoms were placed adjacent to the coils to control for any non-temperature-related phase drift between scans. The T₂^* of the phantom was measured to be 9.3ms, using a multi-echo gradient echo (GRE) sequence. For an initial validation of the MR thermometry measurements and characterization of the heating of the phantom, four fluoroptic MR-compatible temperature probes (Luxtron) were inserted into the phantom and a high duty cycle RF pulse was played out on all coils. Then at intervals of 5 minutes MR thermometry was performed to confirm that the temperature measured using MR thermometry coincided with the temperature measured using the probes. Additionally, it was confirmed that over a range of 15 degrees Celsius heating increased in a linear fashion with respect to time and was not saturated.

Figure 1.

A. Schematic of the experimental calibration and validation procedure. B. Photograph of the transmit-receive coils and agar gel phantom used in the experiments. Transmit-receive elements TC1–3 are shown in the photograph. The receive-only coil (not seen) is opposite to TC2 on the other side of the phantom.

The Λ matrix was calibrated using the first nine experimental steps, with the transmit coil weights given in Table 1. In addition to the calibration steps, 3 more experimental steps with randomly chosen RF coil weightings (Table 1) were performed to check if the measured temperature change maps matched the maps predicted using the model. Each of the nine calibration steps and three validation steps consisted of four procedures, as illustrated in Figure 1A: 1) A phase map was acquired prior to RF heating using a spoiled 2D GRE sequence. 2) RF was applied with weights w in the absence of encoding gradients, to generate heat in the phantom. 3) A post-heating spoiled GRE phase map was acquired with the same sequence as in procedure 1. 4) No RF or gradient pulses were played out for a 10-minute cool down period. The phase difference between the two GRE sequences was used to calculate the temperature change map. The parameters for the 2D spoiled GRE were as follows: TE=7ms (approximately equal to the T₂* of the gel phantom), TR=100ms, transmit voltage=13.4volts, matrix size = 128×128, number of slices=3, voxel size=2.5 × 2.5 × 5mm³, acquisition time = 66s and number of averages=5. RF heating corresponding to a unit pulse amplitude was generated by play out, in procedure 2, of a rectangular 4ms pulse with 25% duty cycle, transmit voltage=125V and duration=300s. The parameters for the RF heating pulse were chosen empirically given the coil size, phantom properties, and RF amplifier peak power and duty cycle limitations. Gradients were disabled during the RF heating sequence to eliminate gradient heating. Total time it took to conduct the entire experiment (steps 1–12) was just under 200 minutes. The measured and the predicted temperature change maps were then analyzed and compared.

Table 1.

Experimental coil weightings used to characterize Λ. Steps 1–9 were used to calibrate the model and steps 10–12 were used to validate the accuracy of the model-based temperature change predictions.

Step	Coil 1		Coil 2		Coil 3
	Amp	Phase	Amp	Phase	Amp	Phase
	1	1	0	0	0	0	0
2	0	0	1	0	0	0
3	0	0	0	0	1	0
4	1	0	1	0	0	0
5	1	0	1	90	0	0
6	0	0	1	0	1	0
7	0	0	1	0	1	90
8	1	0	0	0	1	0
9	1	0	0	0	1	90
10	0.68	45.97	0.71	49.33	0.64	5.76
11	0.71	15.84	0.26	59.65	0.98	83.83
12	0.95	34.35	0.88	42.97	1.00	78.10

Simulations

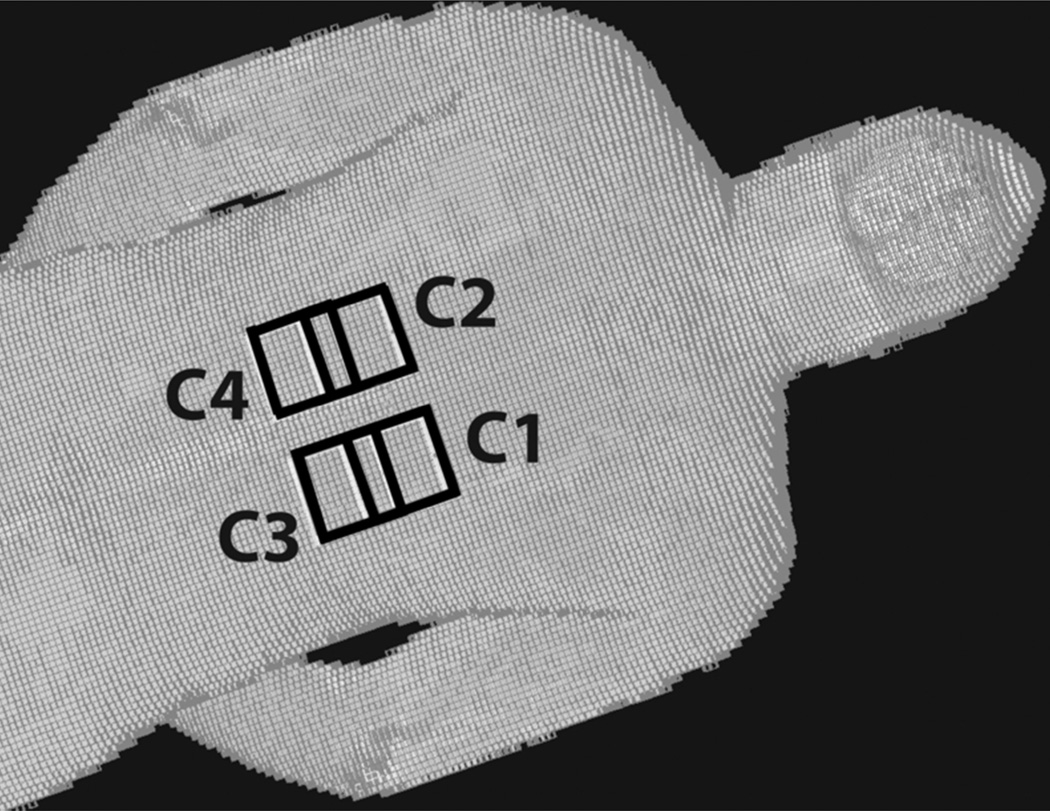
Numerical simulations were performed to assess the validity of the calibration and prediction method, while accounting for the perfusion, diffusion and metabolic energy terms in the bio-heat equation (Eq 1). Commercially available Finite Difference Time Domain (FDTD) software (xFDTD, Remcom, PA, USA) was first used to quantify local RF power deposition. Four surface coils measuring 7cm × 7cm were placed on the torso of a Hugo human body mesh model (Figure 2). The coils were overlapped by 2.5cm in the head-foot direction and gapped by 3cm in the left-right direction. One sinusoidal current port was defined for each coil to simulate a 4-channel parallel transmit experiment. Simulation parameters include: driving frequency 297Mhz, convergence setting −60dB, resolution 5mm³ isotropic and grid size 155×110×416.

Figure 2.

FDTD model of a human body mesh (Hugo) with four transmit coils (C1–4) shown in black placed on top of the body mesh.

A total of 24 different FDTD simulations were performed with port weights shown in Table 2. The calculated SAR maps from the FDTD simulations were then transferred to a finite difference temperature simulator as specified by Collins et al. (20) to quantify heating effects with the bio-heat equation (Eq. 1). All SAR maps had a 10g average local SAR for 6 minutes of less than 10 W/kg for the torso area and 2W/kg for the whole body, as limited by the IEC (12). The temperature simulation was first initialized with no exposure to RF, allowing the temperature of the body model to reach a physiologically realistic temperature steady state (~37 degrees C) with the environment of the scanner room at 23 degrees C. Then each calculated SAR map obtained with different port weights as shown in Table 2 was used to calculate the temperature change resulting from RF heating. The RF duration for the simulations was set to 60 seconds. Between any two successive heating periods, a 5 minute cool-down period with no exposure to RF was applied to allow the temperature of the human body model to cool down or return to steady state. This 5 minute cool-down period was chosen empirically. Over the entire course of the 24 steps the maximum local temperature rise in the emulated human body was kept below 1 degree C, as specified by the FDA and IEC safety limits (12,13). Temperature difference maps due to the RF heating in each step were then used for the calibration and validation of the power correlation matrix-based local heating prediction model. In particular, the first sixteen temperature difference maps were used to calibrate the model, and the last 8 temperature difference maps were used to test if the calibrated model was able to predict parallel RF transmission induced temperature change accurately. To examine the effects of the diffusion, perfusion and metabolic energy occurring in the emulated human body on the accuracy of the heating prediction model, a second series of simulations were performed with an identical setup as that of the first except that the RF heating duration was set to 300 seconds and injected RF power was reduced by 80%. Between the two series, accuracy of the predicted temperature change maps were compared.

Table 2.

Simulated coil weightings used to characterize Λ. Steps 1–16 were used to calibrate the model and steps 17–24 were used to validate the accuracy of local heating predictions based on the model.

Step	Coil 1		Coil 2		Coil 3		Coil 4
	Amp	Phase	Amp	Phase	Amp	Phase	Amp	Phase
1	2.828	0	0	0	0	0	0	0
2	0	0	2.828	0	0	0	0	0
3	0	0	0	0	2.828	0	0	0
4	0	0	0	0	0	0	2.828	0
5	2	0	2	0	0	0	0	0
6	2	0	2	90	0	0	0	0
7	0	0	2	0	2	0	0	0
8	0	0	2	0	2	90	0	0
9	0	0	0	0	2	0	2	0
10	0	0	0	0	2	0	2	90
11	2	0	0	0	2	0	0	0
12	2	0	0	0	2	90	0	0
13	0	0	2	0	0	0	2	0
14	0	0	2	0	0	0	2	90
15	2	0	0	0	0	0	2	0
16	2	0	0	0	0	0	2	90
17	2.4	−63	7.2	−2	2.2	−84	1.8	−58
18	4	−24	5.6	−5	3.8	37	2.2	20
19	7.4	53	2.8	−13	3.4	−32	1.6	−17
20	3.4	59	6.2	6	2.8	3	2.4	−75
21	1	46	2.2	−50	2.8	−61	2.2	−75
22	3	30	0.2	25	3.2	43	1.6	−2
23	2.8	−72	1.4	−13	1.4	−1	2	32
24	3.4	−79	1.4	−72	4.4	43	3.2	−44

RESULTS

Experiments

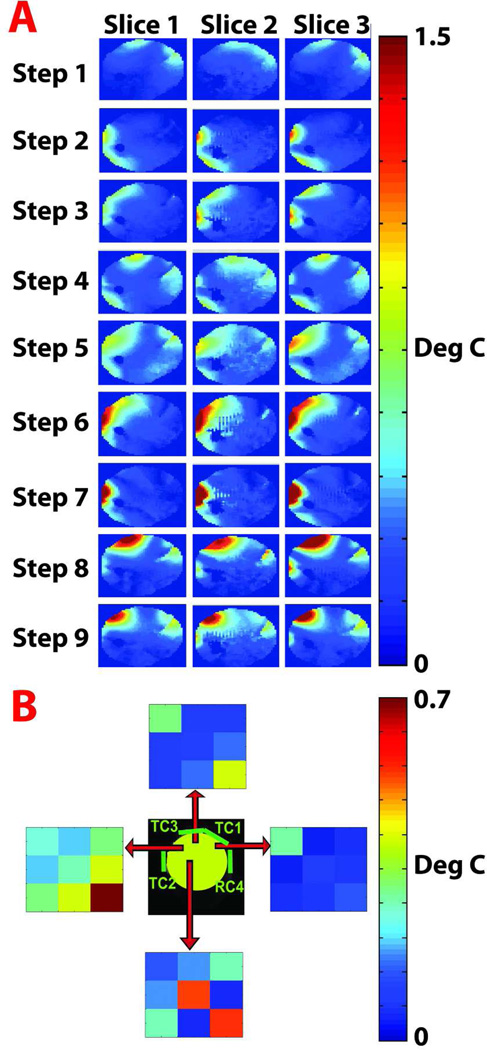
Results of the experimental calibration procedure are summarized in Figure 3. Figure 3A shows temperature change maps measured in three axial slices in each step of the calibration process. Distinct spatial variations in the temperature change distribution can be observed between the steps and, to a lesser extent, between nearby slices. The maximal temperature change for the calibration and prediction steps was < 4 degrees C. Each calibration step (each row in Figure 3A) corresponds to a set of complex RF weightings applied to the array coil according to Table 1. Figure 3B shows the absolute value of the Λ matrix at different spatial locations across one axial slice. The origin of the red arrow represent the voxel represented by the corresponding Λ matrix. The top Λ matrix is dominated by heating contributions from coils 1 and 3, with little E field correlation among the coils. In the left Λ matrix, power correlation can be observed among all coils, with the strongest contribution from coil 3. The bottom Λ matrix indicates strong contributions from coils 2 and 3 with some E field correlation between coils 1 and 3. Finally, the right Λ matrix is dominated by coil 1 alone with minor contributions from the other coils.

Figure 3.

Results of the experimental calibration procedure. A. Temperature difference maps measured for three slices in each step of the calibration process. Each step (each row of temperature change maps) corresponds to a different set of RF amplitude and phase weightings applied to each coil, as specified in Table 1. B. Absolute value of Λ matrix elements for four different voxel positions indicated by the origin of each red arrow.

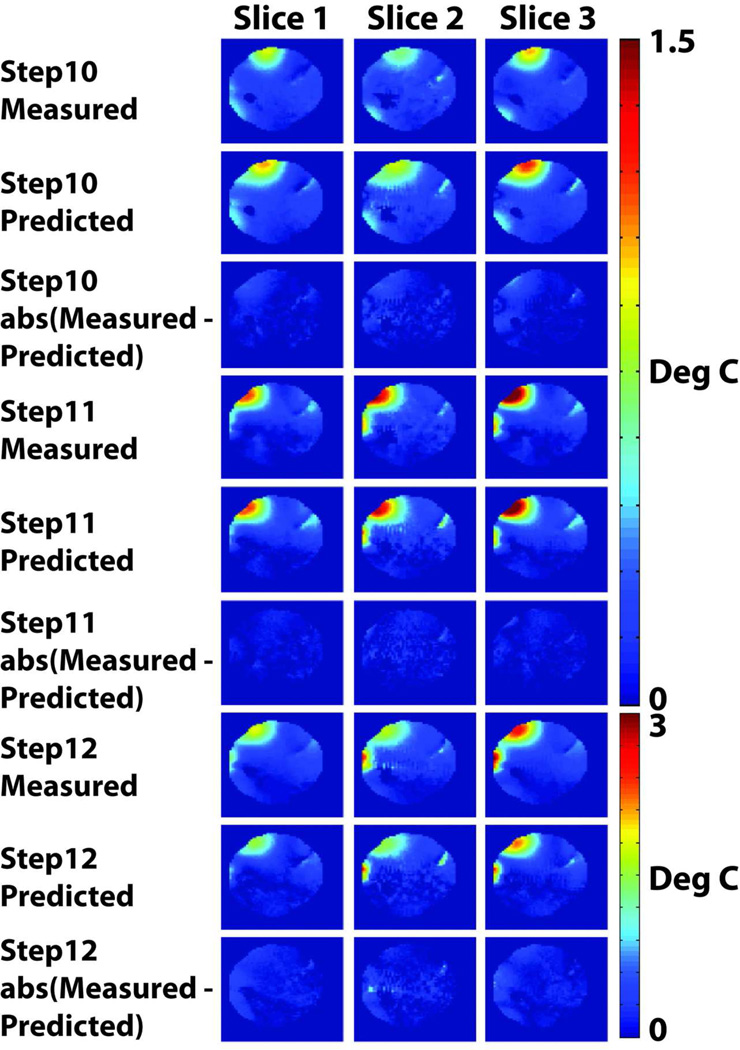
Figure 4 illustrates the predictive capability of the power correlation matrix-based local heating prediction model. Temperature change maps measured for each randomly selected set of coil weighting in steps 10–12 of Table 1 are juxtaposed with predicted temperature change maps derived by using the same set of weighting as input to the local heating prediction model. The predicted and measured maps show a maximal temperature change of less than 4 degrees C. The root mean squared error between the measured and predicted temperature change maps for the three slices of interest are presented in Table 3.

Figure 4.

Results of the experimental prediction and validation procedure, demonstrating the predictive capability of the local SAR model. For each set of the randomly selected coil weightings indicated in steps 10–12 of Table 1, and in each of three axial slices, a temperature change map measured using MR thermometry is compared with the predicted temperature change map derived by using the known coil weights as inputs for the local heating prediction model. Good agreement between measurements and predictions is observed, as indicated also by the difference maps beneath each measured/predicted pair.

Table 3.

The root mean squared error between the measured and predicted temperature change maps for the three slices of interest.

	Slice 1	Slice 2	Slice 3
Random Step 10	0.094	0.173	0.094
Random Step 11	0.070	0.209	0.070
Random Step 12	0.223	0.399	0.223

Simulations

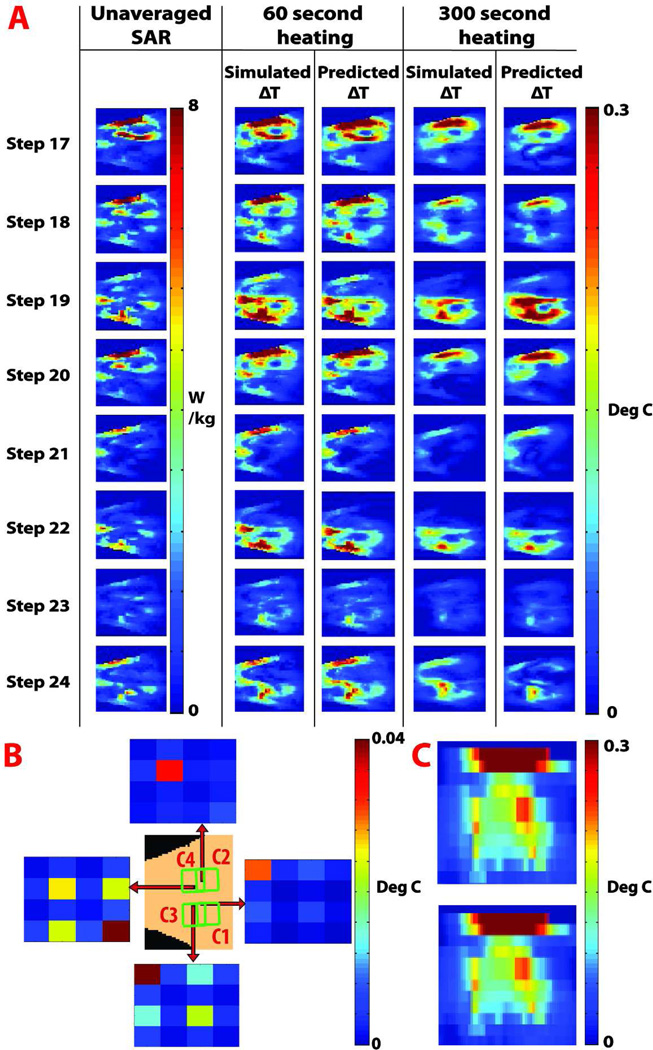
For the simulation study Figure 5A shows agreement between eight predicted temperature change maps and corresponding maps calculated directly from simulation software. For a coronal slice of interest, the maximum temperature change and root mean square error between simulated and predicted values for the 60 second heating case was 0.735 and 0.018 degrees, respectively. For the 300 second case the maximum temperature change and root mean square error between simulated and predicted values was 0.47 and 0.04 degrees, respectively. The results from the individual steps showing the root mean squared errors and maximal temperature changes are summarized in Table 4. In Figure 5B, the absolute values of Λ matrix entries are plotted for different voxel locations, illustrating the spatial dependency of the Λ matrix. The origin of the red arrow indicates the voxel location of the corresponding Λ matrix. The power correlation matrices reflect the complex interaction of electric fields associated with the coil elements and the body. The top Λ matrix is dominated by E fields contributions from coil 2. The left Λ matrix represents a voxel whose local SAR is dominated by the E field from coils 2 and 4, with a strong cross-correlation between the coils. In the bottom Λ matrix, E fields from coils 1 and 3 predominate, and a correlation between these fields is observed. In the right Λ matrix, the E field for coil 1 predominates. Figure 5C, compares the simulated (bottom) and predicted (top) temperature change in an axial slice of interest in the human body model, showing heating entering inside the body.

Figure 5.

RF heating in an emulated human body. A. Results of the prediction and validation procedure. Unaveraged SAR maps and directly simulated coronal temperature change maps are juxtaposed next to temperature change maps predicted using the calibrated heating prediction model, for each of the validation experiments 17–24 from Table 1. Results shown are for the 60 and 300 second heating cases at a coronal slice of interest. B. Results of the calibration procedure, illustrating the spatial dependency of the power correlation matrix Λ for a coronal slice of interest. 4 × 4 color plots represent the absolute value of Λ matrix entries, and each plot shows Λ at a different voxel position, indicated by the origin of the corresponding red arrows. C. Predicted (top) and directly quantified (bottom) temperature change map for an axial slice of interest, showing the prediction capability of the model in a deeper region inside the human body model, while accounting for perfusion and diffusion effects.

Table 4.

Maximal temperature change and the root mean squared error between the simulated and predicted temperature change maps for the 60 and 300 second heating cases.

Step	RMSE, 60 seconds heating	Max temp change, 60 seconds heating	RMSE, 300 seconds heating	Max temp change, 300 seconds heating
17	0.011	0.735	0.019	0.472
18	0.010	0.565	0.016	0.298
19	0.016	0.533	0.040	0.336
20	0.012	0.588	0.026	0.357
21	0.010	0.290	0.020	0.125
22	0.003	0.448	0.008	0.290
23	0.003	0.191	0.008	0.098
24	0.018	0.348	0.026	0.260
Max	0.018	0.735	0.040	0.472

DISCUSSION

RF heating in parallel transmit MR can be characterized with a mathematical structure identified here as the local power correlation matrix. Once calibrated, the local power correlation matrix determines energy deposition for any arbitrary parallel transmit RF pulse. The structure of the matrix reflects, in terms of E field or local RF power deposition, the coil- and subject-specific interaction amongst the coil elements of the array coil and the subject being imaged. Using a finite number of MR thermometry acquisitions, measuring temperature change in response to a set of predesigned calibration pulses, the present method calibrates the power correlation matrix and further predicts the local RF heating effect of an arbitrary RF pulse for any location of interest in the subject. The method has a potential advantage in that it offers a way of in situ SAR evaluation by characterizing and predicting the RF heating effect for the actual imaging setting, in contrast to SAR evaluation by quantifying EM fields in numerical simulations. With numerical simulations there is no assurance that the EM fields quantified with approximate coil and subject models in simulations match that actually generated in the MR experiments (21) as tissue electrical properties and their distributions are typically unknown and the coil structural details can be differ between experiment and simulation. Both of these factors may affect the local power deposition in the body (21). In addition, since temperature change rather than RF power deposition is directly correlated with tissue damage and safety (22), utilization of temperature change to calibrate and, in turn, to further predict temperature change for an arbitrary RF pulse is another potential advantage of the present method.,

It is worth noting that the off-diagonal entries of the power correlation matrix, and the underpinning phase relationships between E fields from different coil elements, can have a significant impact on RF heating. Consider the left Λ matrix in Figure 3B, for which the off-diagonal Λ_2,3 or Λ_3,2 entries are larger than the diagonal Λ_2,2 entry. For the sake of physical insight, one may construct a similar situation with a simplified illustration in which coil element 2 has an E field vector [e_x e_y e_z]=[1 1 1] and coil element 3 has an E field vector [e_x e_y e_z]=[2 2 2], leading to a Λ matrix with significant off-diagonal entries: ${\mathrm{\Lambda }}_{2,2}=3\frac{\sigma (r)}{2},{\mathrm{\Lambda }}_{3,3}=12\frac{\sigma (r)}{2}\text{ and }{\mathrm{\Lambda }}_{2,3}=6\frac{\sigma (r)}{2}$. The resulting temperature change from a unit pulse driving coil element 2 alone plus the temperature change from a unit pulse driving coil element 3 alone will then be substantially smaller than the temperature change if unit pulse driving is applied to coil elements 2 and 3 simultaneously. The ability to capture the effects of constructive and destructive interference between coil fields is a unique feature of the power correlation matrix model.

Characterizing the full interaction effects by calibrating the off-diagonal entries in the power correlation matrix however, causes the total number of calibration steps to scale quadratically with the number of parallel transmit channels driving the array coil, necessitating management of time cost per step in cases involving in vivo use of a large channel-count array coil. Accordingly, one advantage of using simulation software compared to this method is that simulations can be conducted faster, especially for large coil arrays, making simulations software more suited for rapid off-line evaluation of novel coil array designs.

Effect of heat transfer and diffusion on calibration accuracy is another factor impacting the timing of calibration steps in practice. The RF heating sequence used in the MR experiment of the present work was arranged to deliver a significant amount of RF energy in a relatively short period of time. Each channel injected an average of ~44 watts of forward power into the sample using a 25% duty cycle in order to facilitate detection of RF heating with MR thermometry. During this time thermal diffusion smoothed the temperature difference over a distance of $\sqrt{2\mathrm{\beta }\mathrm{\Delta }\mathrm{t}}$, where Δt is the duration of the heating period and β is heat diffusivity. The value of β in our phantom gel is 0.0014 cm²/s, and over a heating period of 300 seconds the characteristic temperature diffusion length was 0.9 cm (15). Utilization of RF amplifiers with higher duty cycles and higher peak power capabilities could allow shortening of the RF heating period further and, as a result reduce the characteristic temperature diffusion length to a sub-voxel size allowing tracking of RF heating effects more closely.

With simulations that employ a realistic human body model and solve both Maxwell and bio-heat equations, feasibility of using the present method for in vivo calibration and prediction was assessed. The results were promising -- within the SAR limits per the IEC regulatory restrictions (12), there are various calibration protocols that allow the present method to accurately model local heating. In the presence of perfusion, diffusion and metabolic energy terms in the bio-heat equations (Eq. 1), a protocol working with shorter calibration/heating steps tends to give more accurate results. For instance, in the 300 second heating case, the diffusion, perfusion and metabolic energy terms in the bio-heat equation introduced larger errors into the calibrated model than in the 60 second heating case (Table 4). Clearly, further optimization of calibration protocols, including the timing of the heating and waiting periods, are necessary for in vivo application of the present method. In terms of accuracy of the method, it relies on sufficient E field magnitude inducing a temperature change, which is detectable by MR thermometry. As result, it is highly desirable to have a robust and sensitive MR thermometry tool that detects small temperature changes while overcoming motion, SNR, phase drift and other challenges in vivo MR presents.

Since the SNR of temperature-related phase difference maps is directly proportional to the signal amplitude (23), the transmit $(B_1^{+})$ and receive $(B_1^{-})$ sensitivities affect the quality of the MR thermometry measurement and nulls in either can limit accurate detection of temperature changes. One has the option of setting up the transmit or receive coil for MR thermometry entirely independent of the parallel transmit coil array to be calibrated, which facilitates MR thermometry. For instance, during MR thermometry $B_1^{+}$ can be shimmed to avoid low $B_1^{+}$ regions with a volume transmit coil and good $B_1^{-}$ coverage can be achieved with a phased array coil, while during the playout of the calibration pulses, the volume transmit coil and the phased array coil remain deactivated. In the experimental setup employed in this work three transmit-receive coils and one receive-only coil were placed around a phantom to yield an SNR of 331 at the center of the phantom. In this work, a basic MR thermometry sequence was used to sample 3 slices of the phantom volume with 5 averages. In vivo MR thermometry is challenging, yet active research continues to bring about technical advances (23,24). Improved MR thermometry sequences may be leveraged directly by the present method to allow reduction of the RF heating duration/intensity and the wait time between steps, as well as to enable large volume coverage, supporting application of the present method in vivo.