Békésy’s contributions to our present understanding of sound conduction to the inner ear

Abstract

In our daily life we hear airborne sounds that travel primarily through the external and the middle ear to the cochlear sensory epithelium. We also hear sounds that travel to the cochlea via a second sound conduction route, bone conduction. This second pathway is excited by vibrations of the head and body that result from substrate vibrations, direct application of vibrational stimuli to the head or body, or vibrations induced by airborne sound. The sensation of bone-conducted sound is affected by the presence of the external and middle ear but not completely dependent on their function. Measurements of the differential sensitivity of patients to airborne sound and direct vibration of the head are part of the routine battery of clinical tests used to separate conductive and sensorineural hearing losses. George von Békésy designed a careful set of experiments and pioneered many measurement techniques on human cadaver temporal bones, in physical models, and in human subjects to elucidate the basic mechanisms or air and bone conducted sound. Looking back one marvels at the sheer number of experiments he performed on sound conduction, mostly by himself without the aid of students or research associates. Békésy’s work had a profound impact on the field of middle ear mechanics and bone conduction fifty years ago when he received his Nobel Prize. Today many of Békésy’s ideas continue to be investigated and extended, some have been supported by new evidence, some have been refuted, while others remain to be tested.

A. Introduction

Although Békésy received recognition from the Nobel committee in 1961 for his work on the cochlea, his interest in the biomechanics of hearing started with the middle ear (Békésy, 1974). After his PhD he discovered that the best laboratory in Hungary was the telephone, telegraph and radio station laboratory. Being centrally located in Europe, Hungary spent resources to keep its transmission lines in good shape and build newer high quality lines. In doing so the question was whether improvements in the quality to telephone communication were best attained by improvements in the telephones or the cables. In order to begin such an analysis the young Békésy wished to know “which improvements the ear would appreciate.” Thus his first experiments investigated the mechanical properties of the eardrum in order to match the properties of the telephone earphone such that sound transmission was optimized (Békésy, 1974). In effect Békésy was working on what is often referred to as the “last inch problem” in telecommunications.

During the period of 1932 to 1949 Georg von Békésy published seven papers (Békésy 1932, 1936, 1939, 1941, 1947, 1948, 1949) that at the time of his Nobel prize award had a profound influence on our understanding of how airborne sound and direct vibrations of the skull stimulated the inner ear¹. The publications included measurements of the motion of the tympanic membrane (TM) and ossicles, acoustic measurements of the sound pressure at the cochlear windows, estimates of the sound pressure transfer from the ear canal to the inner ear, the effect of significant conductive pathologies on air-conducted sound, and the vibration of the head and body caused by sound. In the last of the above set of papers, Békésy considered the question of how the middle ear anatomy and its location in the skull evolved for sound conduction while at the same time minimizing perception caused by sound and vibrations through bone conduction from of one’s own vocal apparatus (Békésy, 1949). In the years since then, some of his work has been supported by more modern techniques, some has been repudiated by newer measurements, and some has been almost forgotten. This paper is organized into discussions of separate sound-conductive processes that Békésy investigated.

We impose two large divisions in this review: Békésy’s work on: A) the conduction of airborne sound to the inner ear, and B) bone-conducted sound. We also impose a spatial organization dealing with peripheral processes first. Such an organization does not fit a simple temporal review of his papers, nor does it fit a simple organization by the contents of each publication. Those were simpler times, and each of Békésy’s publications in this area reported on multiple measurements that addressed multiple subtopics associated with sound conduction.

One issue in all of Békésy’s work is his near exclusive use of unfixed cadaveric material. While this choice has a large impact on studies of inner ear mechanics, in which the gain of the cochlear amplifier has been lost, its impact on studies of the middle ear and other sound conduction paths is much smaller: The passive mechanical properties of tissues are not much altered by death, as long as the tissues are kept fresh and moist. Comparisons of multiple middle-ear mechanical measurements in collections of live-human and cadaveric ears show great similarities (Rosowski et al. 1990; Goode et al. 1996; Chen et al. 2009), and where they exist, there are generally significant similarities between modern results and Békésy’s.

B. Conduction of airborne sound to the inner ear

1. Measurements and theories of eardrum motion

One of the more influential studies performed by Békésy was his direct measurement of the sound-induced motion of human cavaderic TMs with a capacitive probe (1941). The early maps of TM displacement that he produced suggested a simple mechanism: the TM acted as a loudspeaker cone, at least at frequencies less than 2 kHz. The TM cone was elastically supported at its rim, and the circularly asymmetric mounting of the manubrium of the malleus on the TM introduced asymmetric motions along the surface of the cone. The largest low-frequency motions that Békésy reported occurred in the inferior half of the TM, opposite the regions of reduced motion that resulted from the load of the manubrium on the superior half of the TM (Figure 1A). This picture is consistent with the ossicles and TM rotating about an anatomical axis defined by the ligamentous attachments of the malleus head and incus body, with larger displacements of the TM and manubrium occurring at larger distances from the axis. The reduced displacements observed at the rim of the TM were also consistent with the idea that only a fraction of the TM area (the ‘effective area’ e.g., Wever and Lawrence 1954; or the ‘coupled’ area. e.g., Zwislocki 1962) contributed to the motion of the ossicular chain.

Figure 1.

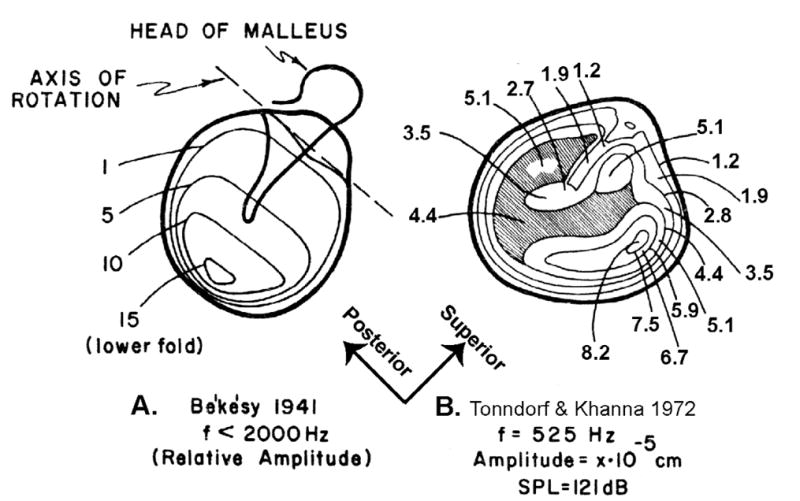
A comparison of Békésy’s (1941) map of the magnitudes of sound-induced displacements of the TM and a map of Tonndorf and Khanna (1972). Stimulus conditions are noted below each map. (Modified from Tonndorf and Khanna 1972).

While other measurements made at non-physiological stimulus pressures (e.g., Kirikae 1961) contradicted Békésy’s measurements of TM motion, it wasn’t until the application of laser holography in the late 1960’s and early 1970’s that new data using more physiological stimulus levels became available (Tonndorf and Khanna 1970, 1972; Khanna and Tonndorf 1972). These newer data had some features in common with the Békésy results, but also showed substantial differences (Figure 1B). The main commonalities were the apparent in-phase motion of the entire TM at low frequencies, with the largest motions at regions other than those bounded by the manubrium. The largest differences were that the regions of maximal motion were in the anterior and posterior halves of the membrane, on either side of the manubrium, not in the quadrant inferior to the manubrium as described by Békésy. Laser holography, with its much greater spatial resolution, also demonstrated that the patterns of TM motion became much more complicated as the stimulus frequency was increased above 2 kHz. The data of Tonndorf and Khanna have been confirmed and expanded by recent measurements using advanced holographic techniques (Rosowski et al. 2008; Cheng et al. 2010; Rosowski et al. 2011) and scanning laser-Doppler vibrometry (Decraemer 1999; Fay et al. 2005; de La Rochefoucauld and Olson 2010). These data suggest a much more complicated motion of the TM, with multiple modes of motion including standing-wave-like modes and traveling wave-like motions. How these different motions are coupled to the ossicular chain is a point of continuing study.

2. Measurements of ossicular motion and sound conduction

In his 1941 paper Békésy also described capacitive probe measurements of the sound-induced motion of the stapes in a human cadaveric preparation with the inner ear drained of fluid. These measurements show an amplitude of motion that is similar to that seen in more modern measurements with the inner ear intact (Puria 2003; Nakajima et al. 2005), but with a frequency dependence that is not generally observed today: Most modern measurements suggest the stapes is stiffness bound at low frequencies and has a displacement amplitude that is relatively constant at frequencies below 1000 Hz, whereas Békésy’s measurements indicate that the stapes displacement for uniform sound-pressure stimulation decreases significantly between 0.1 and 0.5 kHz. It is unlikely that this difference is attributable to draining the cochlear fluid.

In that same 1941 paper Békésy used a pressure balancing technique to estimate the ‘open-circuit’ sound pressure produced by the middle ear. In this technique, the motion of the stapes produced by an ear-canal tonal stimulus of frequency f and known ear canal sound pressure was balanced to zero by a sound pressure of controlled amplitude and phase produced in the inner ear. The magnitude of the ‘open-circuit’ pressure transform ratio was the ratio of the sound pressure magnitude generated within the inner ear and the ear canal stimulus pressure. The magnitude of this pressure ratio was relatively flat at frequencies between 0.1 and 2 kHz with a magnitude of 20 to 25 dB and seemed to fall off rapidly above 2 kHz. In the succeeding years, techniques were developed to directly measure the sound pressure within the intact inner ear that results from ossicular motion (Nedzelnitsky 1980; Dancer and Franke 1980; Puria et al., 1997; Olson 1998; Aibara et al. 2001; Nakajima et al. 2009). Measurements in cadaveric preparations of the ratio of this pressure to the ear canal stimulus pressure look very similar across different laboratories. A direct comparison of more modern measurements to Békésy’s by Puria et al (1997) demonstrates that the modern measurements of middle-ear sound pressure transfer in cadaveric ears with the inner ear intact suggest a lower overall amplitude of middle ear gain at frequencies below 2 kHz and an increased gain above 2 kHz. The differences at low frequencies are generally explainable by the differences in the state of the preparation. The difference at higher frequencies may reflect an increased ability to accurately measure sound pressures in the vestibule of live animals and cadaveric humans at higher frequencies.

Békésy addressed the sound-induced motion of the ossicles in a less-quantitative manner in his 1933 paper (“On the physics of the middle ear …”). In that paper he reported a measurement of the impulse response of a human cadaveric middle ear, which is consistent with a lowest resonant frequency of the middle ear near 1 kHz. He also described his estimates of three-dimensional ossicular motion in response to sound. Using a single low-frequency sound stimulus, he described a coupled rotation of the malleus and incus around a line through the posterior-incudal ligament, and a combination of a piston-like and rotary motion of the stapes; the stapes footplate rotated about its short axis, such that the posterior footplate tended to move out-of-phase with the anterior footplate. At higher stimulus pressures, Békésy also described a rotation of the footplate about its short axis. More modern measurements of 3-D ossicular motion support the existence of many of the modes of ossicular motion suggested by Békésy, but generally suggest that the rotary components occur in tandem with a significant piston-like in-out motion of the stapes (e.g., Hato et al. 2003; Decraemer and Khanna 2004; Sim et al. 2010). These more modern measurements also suggest significant motion modes not observed by Békésy including motion of the axis of malleo-incudal rotation (Decraemer and Khanna 2004) as well as flexing of the ossicular joints (Willi et al. 2002).

While better descriptions of three-dimensional motion of the ossicles, especially the stapes, are in hand today, we still do not understand the consequence of these complex motions. Decraemer et al. (2007) compared significant complexities in the 3-D motion of the stapes in live gerbils with measurements of the sound pressure in the vestibule, and concluded that the measured sound pressure in the inner ear is nearly proportional to the simple piston-like motions. Huber et al. (2008) demonstrated that non-piston-like motions of the guinea-pig cochlea can produce measurable evoked neural activity that is within an order of magnitude of the activity produced by controlled-piston-like motions, but again the significance of these responses is unknown.

3. Effect of total and partial eardrum perforations

As part of his 1936 paper Békésy investigated the effect of perforations of the eardrum on middle-ear function. Two separate perforation conditions were investigated using quite different techniques.

The effect of total perforation was quantified by measuring behavioral hearing thresholds in a population of patients with one normal ear and one ear with a unilateral loss of the TM, malleus and incus. Békésy hypothesized that the hearing loss in the ears without TM and ossicles should be related to the decreased sound pressure difference between the oval and round window. He further hypothesized that this loss should be larger at lower frequencies where the wavelength of sounds were longer and the differences in pressure between the two windows smaller. Comparison of the thresholds measured in the two ears show the expected 40–60 dB conductive loss in the abnormal ear at frequencies above 100 Hz. However, at lower frequencies, the measured differences in hearing threshold were smaller than expected. To explain this contradictory finding, Békésy introduced the concept of what others (Ranke et al. 1952; Tonndorf and Tabor 1962) have named the normal cochlear ‘third-window’, which would allow the sound-induced flow of cochlear lymphs from the inner ear. However, Békésy also expressed some concerns about the possibility of experimental artifacts and noted that the low-frequency noise in the measurement environment was not well controlled. Other potential artifacts are the earphones used in the stimulus methods that could have introduced significant low- frequency cross-talk between the ears, or introduced a significant vibratory stimulus, both of which could act to reduce the thresholds when the pathological ear was tested and could explain the difference between the low-frequency results and Békésy’s window-pressure difference theory. To our knowledge, the results of a well-controlled repetition of these measurements have not been reported.

Békésy (1936) also reported optical measurements of the effects of a small, ~1 mm, perforation on the motion of the manubrium of the malleus in a temporal bone preparation with intact middle-ear cavities. The perforation-induced loss in manubrial motion was only apparent at frequencies below 400 Hz and the loss was greatest at the lowest frequencies measured. Békésy also notes that the magnitude and frequency dependence of the loss depended on the size of the hole, the compliance of the TM and the volume of the middle- ear cavity without showing any supporting data. The relationship between these different parameters was not quantified till over 60 years later when Voss and colleagues (1998, 2001a, b) explicitly demonstrated the interaction of these three variables in determining the magnitude of and frequency dependence of perforation induced hearing losses and developed a simple model that explained the perforation-induced hearing losses in both cadaveric and live human ears (Voss et al. 2001c; Mehta et al. 2006).

4. Measurements of the sound pressure at the two cochlear windows

In his 1947 paper (‘The sound pressure difference between the round and the oval windows…’) Békésy revisited the issue of how the sound pressures outside of the two cochlear windows contributed to the hearing response. The primary experiment he described was the measurement of sound pressures at the two windows that resulted from a stimulus in the ear canal with the TM and ossicles removed. Békésy placed two calibrated microphones within a drained cadaveric inner ear, where one microphone was sealed within the oval window, and the other the round window. He then described the magnitude and phase of the window pressure difference relative to the sound pressure stimulus. As he intuited, the magnitude difference was smallest (about −33 dB) at the lowest frequency he measured (0.25 kHz) and largest (about −20 dB) at the highest measured frequency (3 kHz). Similar window-pressure differences have been observed using more modern techniques in ears with intact inner ears (Voss et al. 2008).

From these measurements made without a TM and ossicles, Békésy calculated that the hearing loss produced by the total loss of the TM and ossicles should vary between 45 and 60 dB. He thought this calculated hearing loss was too large compared to clinical observations and invoked the presence of normal cochlear ‘third-windows’ (Békésy 1936) to explain the difference between his observations at frequencies less than 0.2 kHz and what he considered the larger hearing losses predicted from the pressure difference measurements. Others (Peake et al. 1992; Voss et al. 2008) have pointed out that the window-pressure-difference theory does fit Békésy’s (1936) and other clinical measurements of hearing loss in cases of loss of TM and ossicular chain at frequencies above 0.2 kHz (Figure 2). Indeed, the window pressure-difference theory has been successfully used to explain the results of TM and ossicular pathology as well as the effects of middle-ear reconstruction (Wüllstein 1960; Peake et al. 1992; Merchant et al. 1995, 1997; Voss et al. 2008).

Figure 2.

Data from Voss et al. 2007. Calculations of the hearing loss induced by TM perforations of various sizes. The maximal hearing loss predicted from the window pressure difference with total TM perforation compares well with the audiometric measurements described in Békésy’s 1936 paper.

5. Continuing studies

Some less-developed ideas of Bekesy’s are relevant to continued research today.

a. Middle ear delay

In his 1941 paper Békésy noted that sinusoidal motion of the manubrium lagged behind the sound pressure stimulus at frequencies above 1 kHz. More recently, the lag between middle-ear motions and the sound pressure in the ear canal over much of the frequency range of hearing has been characterized by a delay that seems to vary between different animal species (Puria and Allen 1998; Olson, 1998; Overstreet and Ruggero 2002; O’Connor & Puria 2008; Ravicz et al. 2008). The processes that contribute to this delay appear to be distributed throughout the middle ear and are presently the point of much experimentation (de La Rochefoucauld et al. 2008).

b. Mechanical properties of the TM

Békésy made some comments about indentation studies of the TM to determine its mechanical properties. The issue of the TM mechanical properties, including its anisotropy and inhomogeneity has been a point of continued research (e.g. Fay et al. 2005; Decraemer and Funnell 2008; Luo et al 2009). Of particular interest is a determination of the damping within the TM, where this property can greatly influence the spatial patterns of TM motion in response to sound (Funnell, Decraemer and Khanna 1987).

C. Bone-conduction pathways to the inner ear

Bone-conduction (BC) hearing is the perception of sound transmitted through the bones of the skull to the sensory epithelium of the cochlea. The scientific exploration of BC hearing began with the invention of the tuning fork in the 18^th century, and by the 19^th century the existence of bone conduction was generally accepted. The idea of BC hearing gained prominence as clinicians started to exploit it as a means of differentially diagnosing conductive vs. sensorineural hearing loss, and it appeared in a significant number of publications. At the time of these early publications, there was significant excitement around the investigation of BC hearing, since it was thought that it might involve an entirely different mode of hearing compared to hearing through the air-conduction (AC) pathway.

Békésy pioneered a more scientific and systematic approach to the understanding of BC hearing. He stated that “hearing by bone conduction takes place any time the head is brought into contact with a vibrating body,” and recognized that vibrations of the skull propagate to the cochlea via a multitude of pathways.

1. Common cochlear mechanisms for air-conduction and bone-conduction hearing

Békésy (1932) postulated that, if a BC tone could be compensated for by an AC tone such that no sound is heard at all, then one could be assured that the basilar membrane moves in precisely the same manner due to BC or AC. He surmised that, for both AC and BC methods of stimulation, the vibrations of the basilar membrane (BM) would be produced by movements of the perilymph near the stapes, and further that there would be no other way of stimulating the sensory epithelium. In his paper ‘Nature of bone conduction’ (1932), Békésy reported successful demonstrations of AC and BC tone cancellation using a 400 Hz tone at 57 dB above the threshold of hearing. The experiment was made more complicated by the fact that the forehead-mounted bone vibrator he was using stimulated both ears at the same time, such that cancellation needed to be achieved simultaneously for both ears.

AC/BC cancellation experiments have since been verified by others, in many different animals, and with extended ranges of frequency and level (Lowy, 1942; Wever and Lawrence, 1954; Tonndorf, 1966; Khanna et al., 1976; Clavier et al., 2010). These experiments were all conducted with direct vibration of the skull and possibly with an occluded ear canal, which is known to alter BC hearing. Stenfelt (2006) performed cancellations at different levels and using other sounds at the same time to investigate the robustness of cancellation. More recently, McKinley (2009) demonstrated AC/BC cancellation with the BC stimulation arising from a sound field rather than from direct vibration of the skull.

Purcell et al. (1999) and Clavier et al. (2010) measured the distortion-product otoacoustic emission (DPOAE) input/output (I/O) functions generated first using two AC tones (AC/AC), and then with one of the frequencies generated using a bone vibrator (AC/BC). This allowed calibration of the bone transducer by adjusting the level of the BC signal such that the resulting AC/BC and AC/AC I/O functions match one another. Since the production of DPOAEs arises from the nonlinear active behavior of the outer hair cells within the organ of Corti, this experiment further demonstrates the equivalence of AC and BC stimuli as far as the inner workings of the cochlea are concerned. The one caveat here is the potential for the AC transducer to occlude the ear canal and alter BC hearing.

Once Békésy established that AC and BC both stimulated the cochlea via a common mechanism, he proceeded to hypothesize about the different pathways through which BC stimuli could reach the cochlea.

2. Békésy’s three conceptual mechanisms of hearing by bone conduction

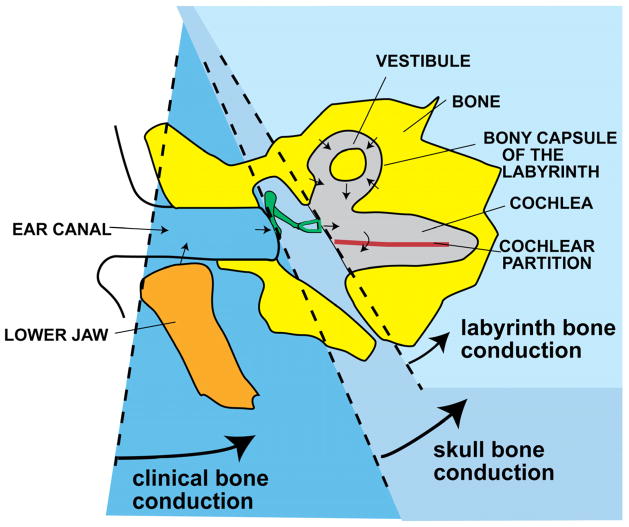
After conducting a significant number of experiments, Békésy (1954) came up with a hypothetical conceptual framework for understanding bone conduction that consists of three basic mechanisms for BC hearing (Figure 3). He referred to these as 1) “labyrinth bone conduction,” which he attributed solely to the compression of the bone surrounding the cochlea; 2) “skull bone conduction,” which he defined as the contributions of the vibrating skull bone to the motion of the middle-ear ossicles as well as to the mechanism of labyrinth bone conduction; and 3) “clinical bone conduction,” which he defined as the contributions of lower jaw and ear-canal wall vibrations to the mechanisms of skull-bone and labyrinth-bone conduction. These hypothetical mechanisms are described below, along with modern interpretations.

Figure 3.

Békésy’s scheme for conceptualizing the pathways contributing to hearing by bone conduction. The lightest blue area represents hearing sensation due to compression of the cochlear labyrinth; the medium-blue area represents the drive to ossiclular motion due to skull bone vibration, which also contributes to the first pathway; and the darker blue, clinical bone conduction, represents the contribution of lower-jaw movement to the first two pathways (reproduced from Békésy, 1954).

c. Labyrinth bone conduction

The compression and expansion of the skull bone, either due to a vibrator or a sound field, can result in the compression and expansion of the bony capsule surrounding the cochlea. These distortions to the fluid-filled space of the inner ear are thought to force the incompressible fluid of the inner ear to be displaced through the relatively compliant oval and round windows, leading to motion of the BM and the sensation of hearing in the process. Békésy termed this mode of hearing “labyrinth bone conduction.” Because the round-window membrane is more compliant than the stapes and annular ligament of the oval window, it is thought that more fluid is displaced through the round window than the oval window. In addition, given the larger volume of the scala vestibuli, it is thought that more fluid would flow from the scala vestibuli to the scala tympani. These ideas predate Békésy’s publication (1932) and were originally formulated by Herzog (1926) and Krainz (1926). Békésy’s contributions were that he added the volume of the semicircular canals to the volume of the scala tympani and he attempted to test the hypothesis. In interpreting his AC/BC cancellation experiments, he argued that the fluid displaced at the stapes due to cochlear compression was compensated for by the stapes being pushed back due to AC stimulation (see Bárány, 1938). However, the existence of this mode of hearing has never been experimentally verified. It has been argued that one requirement for the compressional stimulation of the inner ear is the existence of wave motion in the temporal bone, and as such it is likely that it may only become important at frequencies above 4 kHz (Stenfelt and Goode, 2005). However, others have argued against the necessity for wave motion and point out that uniform compression of the cochlear walls can lead to motion of the fluid within the inner ear through the cochlear windows (Songer and Rosowski 2010).

Beyond Békésy’s sole focus on the compressional vibration of the cochlear walls as a source of direct BC stimulation to the cochlea, inertial forces acting on the inner-ear fluids in response to skull-bone vibrations have since been shown to produce a hearing sensation. It has been estimated that, for a BC stimulation of 80 to 100 dB HL, the fluid displacement required is less than one-millionth of the total fluid volume in the cochlea (Stenfelt and Goode, 2005). Stenfelt and Goode (2005) suggest that the fluid-inertia component is more prominent at lower frequencies when the skull bone motion is approximately that of a rigid body.

d. Skull bone conduction

Békésy defined a second component called “skull bone conduction” consisting of 1) any effects resulting from inertial forces imparted to the middle-ear ossicles due to the vibrating skull, and 2) the contributions of the skull vibration to the compressional component and fluid-inertial component discussed above. Békésy considered two ways that BC hearing can originate in the middle ear, due to the relatively loose attachment of the three middle-ear ossicles to the middle-ear cavity walls by the eardrum, suspensory ligaments, tensor tympani, and stapedius muscle. First, he posited that when a person’s head moves, the inertia of the ossicles will produce a relative motion between the ossicles and the cochlea (1949, 1953). (It is generally accepted that it was Bárány (1938) that first proposed this idea (Stenfelt and Goode, 2005)). Second, Békésy (1949) posited that a motion transmitted to the skull would deform it such that there is relative movement between the ossicles and the cochlea (Stenfelt et al, 2002; Homma et al, 2009).

Békésy (1949) also argued that the middle ear is located in a relatively stress-less zone of the skull, such that it is largely isolated from skull deformations. According to Békésy’s hypothesis, since humans have thick skulls, their middle ears could achieve this vibrational isolation by being buried deep within the bony temporal bone along a “stress- less zone” (sometimes called the neutral axis in mechanics) for deformation. On the other hand, for smaller animals whose thin skulls couldn’t offer much in the way of vibrational isolation by themselves, he argues instead that the middle ear should be strategically located inside of a tympanic cavity forming a stress-less zone. When skull vibrations deform such a cavity, the relative movement between the middle ear and the cochlea would be minimized because the forces that reach a stress-less zone are by definition at a minimum. These concepts were also thought by Békésy to be important for minimizing the hearing of one’s own voice via the BC pathway discussed in a following section. However, it has been difficult to experimentally test these ideas. If Békésy were alive today, he might be inclined to investigate them using computational models.

e. Clinical bone conduction

The third BC pathway that Békésy considered was movement of the lower jaw relative to the skull. The medial half of the ear canal consists of a bony duct lined with cartilage and soft tissue that lies in close proximity to the temporal-mandibular joint between the temporal bone and the mandible. Given this arrangement, Békésy expected the relative motions of the mandible to produce skull vibrations that result in the generation of sound pressure in the ear canal, in addition to possibly contributing to the other two BC pathways described above. This BC-generated pressure in the ear canal would then propagate through the normal AC pathway to complete what Békésy and later Tonndorf (1966) considered to be an important pathway for BC hearing. This mode of BC hearing has since been confirmed to exist, but has been shown to be not as significant as other mechanisms of BC hearing (Howell and Williams 1989; Stenfelt et al, 2003).

3. Hearing one’s own voice

In keeping with his belief that scientists might benefit by following the tradition of using anecdotes and using the Arabian story telling style for publications (Békésy 1974), Békésy began one of his more interesting papers (1949) by recalling a time spent aboard a ship during which he was struck by the fact that the ship’s foghorns could be heard from many miles away out in the open sea, yet they remained barely audible from within the ship’s cabin. He understood that this feat was achieved by (i) mounting two out-of-phase sound generators to a single vertical pole, such that their vibrations would cancel through the pole instead of being transmitted to the cabin, and (ii) the selection of horns with radiation patterns that distributed sound energy widely in the horizontal (azimuthal) plane, but restricted sound radiation to within just a few degrees in the vertical plane. He then proposed, in a reciprocal manner, that the middle ear might be designed to increase the sensitivity of the ear to sounds originating from the external environment, while at the same time decreasing its sensitivity to self-generated sounds originating from within the organism.

Békésy appreciated the need for such designs in non-mammals. Both the frog and rooster, for example, generate relatively loud vocalizations that can be heard from far away, so how do these animals keep from damaging their own delicate hearing organs from their own vocalizations? In the frog, Békésy observed that there is a wide Eustachian tube opening that acoustically connects the eardrum to the vocal apparatus. This allows the pressure difference between the inside and outside of the eardrum to be reduced, and reduces the stimulus to the ear. In the case of the rooster, he pointed out that it features a mechanical method of narrowing or closing off the cartilaginous ear canal by lifting its head up when crowing. This attenuates the AC pathway and thus reduces the stimulus to the ear during vocalization. Békésy recognized that the situation is far more complicated in mammals while performing a series of studies to shed light on the design of the middle ear for BC hearing.

Békésy was one of the first to determine the relative contribution to hearing of AC sound vs. BC sound during vocalization. He did this by measuring the decrease in the loudness of one’s own voice after using a special apparatus to remove the AC pathway without significantly affecting the BC pathway. The observed attenuation due to eliminating AC was about 6 dB, demonstrating that hearing one’s own voice by BC is about as loud as hearing it by AC. Recent measurements show that the relative contributions of the two pathways to the perception of self-vocalized sound varies with frequency and the specific phoneme that is produced. The BC signals are generally larger at frequencies below 2 kHz, and the largest bone-conducted signals result from the production of nasals and vowels, which induce significant vibrations of the head and neck. Above 2 kHz the AC component dominates the perception of one’s own voice regardless of the phoneme produced (Reinfeldt et al., 2010).

Robert Bárány (1909, 1910), another Nobel Prize winner in inner-ear physiology (awarded in 1914 and received in 1916), reported that when a normal eardrum is loaded by putting Vaseline or mercury on its surface, hearing by BC improved while hearing by AC remained intact or was only slightly modified. Later, his son Ernst Bárány (1938) proposed an explanation for this observation, stating that “the balance of the chain of ossicles had been disturbed by the load.” He further pondered over the three “peculiarly formed bones” in the middle ear and why they might be useful for air conduction. It is now generally accepted that the ossicles in the middle ear function to reduce mass inertia by allowing rotation through the anterior-posterior axis to produce a hinging-type motion (Bekesy 1941). But for larger mammals, the shape of the ossicles might also be useful to further reduce mass inertia at high frequencies by allowing an alternate twisting-type motion through a superior-inferior axis (Puria and Steels, 2010). Bárány (1938) had postulated that the shape of the middle-ear bones evolved to not only maximize hearing by AC, but also to minimize the hearing of one’s own voice and other internally generated sounds by the BC pathway.

Békésy agreed with Barany’s ideas and further suggested that the ossicles might lie along an axis that minimizes their vibrations resulting from phonation. Békésy claimed that the vocal cords produce maximal vibrations along the vertical direction, but that their vibrations in the direction of the ear canal axes were smaller. He postulated and observed in many mammals that the long axis of the stapes footplate should be at right angles to the vertical axis of the neck. By way of analogy to the out-of-phase drivers found in the foghorn, he argued that the symmetrically opposed motions in the vibration of the vocal cords might serve to minimize the conduction of sound to the cochlea.

Most of the studies performed by Békésy with regard to the minimization of hearing one’s own voice and internally generated sounds were focused on the frequency region below 4–5 kHz. It is known that when the energy in human speech is calculated for auditory filter bands, the amount of energy in bands above 4–5 kHz is within 10 dB of the lower frequency bands (Moore et al., 2008), so it may also be important to extend to higher frequencies Békésy’s analyses of hearing one’s own voice by the BC route.

Since Békésy and Bárány’s time, the idea that the middle-ear anatomy and physiology might have evolved to minimize hearing by the BC pathway seems to have been largely forgotten. Thus it remains for future researchers to quantitatively determine whether or not middle-ear anatomy and positioning do indeed reduce sensitivity to the hearing of one’s own voice.

4. The emergence of a more quantitative understanding of bone conduction

Prior to the 1960s, the majority of BC studies were either devoid of quantitative support or based only upon indirect evidence. This all changed in the early 1960s, however, with the development of techniques on laboratory animals, mostly cats, by Prof. Juergen Tonndorf. This was a departure from relying mostly on human subjects as was done by Békésy and his contemporaries. Much of our modern quantitative understanding of BC can be traced back to a series of seven papers in which Tonndorf presented the results of his experiments (Tonndorf, 1966).

Tonndorf described a number of different BC components, many of which are listed in Figure 4, that contribute in varying degrees to the total response. The definitions of these BC components were influenced by the work of Békésy, Bárány, Wever and Lawrence (1954), and others. Tonndorf indicated that some of the BC components could be further subdivided into additional components, and provided evidence to support this. This emphasis on diverse BC pathways was a departure from previous thinking that attempted to explain the entirety of BC phenomena in terms of a single unifying mechanism such as compressional BC or inertial BC, at the exclusion of others.

Figure 4.

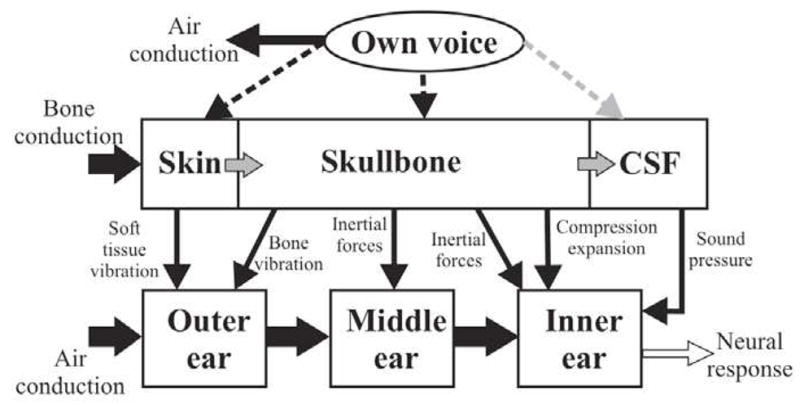
Overview of the different sound pathways thought to be important for hearing by bone conduction (reproduced with permission from Stenfelt and Puria, 2010 and Stenfelt 2011).

For nearly three decades following Tonndorf’s papers on the subject, there appear to have been very few additional studies published on BC. The reason for this is not clear, but one possibility is that Tonndorf had seemingly settled many of the questions and theories posed by Békésy and his contemporaries.

a. Back to human cadaver measurements

Because Tonndorf investigated the theoretical questions of BC using mostly laboratory animals, a detailed quantitative analysis of BC as it relates to human hearing still remained unavailable by the end of the 20^th century. Starting in the 21^st century, Stefan Stenfelt began a series of extensive BC experiments on human cadavers. He started with five of the mechanisms described by Tonndorf, divided mostly along the anatomical lines shown in Figure 4, and attempted to quantify the role of each of the anatomical components. One emerging consensus is that fluid inertia is likely the most significant mechanism of BC, at least for the speech frequency region, with the other contributors likely to lie within 10 dB. The reader is directed to reviews summarizing his work (Stenfelt and Goode, 2005; Stenfelt and Puria 2010; Stenfelt, 2011).

Both Tonndorf’s work and Stenfelt’s earlier work involved identifying and quantifying the basic mechanisms of BC. However, quantitatively testing for the existence of mechanisms by which the BC transmission of one’s own voice might be minimized has apparently not been attempted since Békésy.

b. Computational models

Another approach to understanding BC hearing is the use of finite element computational models. While these had previously been used for understanding structure-function relationships for the AC pathway, Bohnke and Arnold (2006) were the first to apply finite element methods to the study of BC. More recently, Homma et al. (2009) used a finite element model, validated against measurements from cadaver ears, to suggest that a peak in threshold near 2 kHz in BC hearing is caused by an incus “pivoting mode” that is excited much more by the BC pathway than by the AC pathway. In another study, Homma et al. (2010) used finite element modeling methods to confirm Békésy (1932; 1941), Bárány (1938), Huizig (1960) and other investigators’ findings that ear-canal static pressure can reduce sensitivity to BC hearing, and that such pressures produce an increase in the elastic modulus of the eardrum. The Homma et al. modeling study further indicated that the elastic modulus of suspensory attachments of the middle-ear ossicles to the skull walls also increase with static pressure.

One unanswered question pertains to the sensitivity of the fluid-inertial mechanism to the directional orientation of BC vibrations of the cochlea and middle ear. To address this, it was shown using an uncoiled 3D tapered box model of the cochlea that the BM response does depend on the direction of the input displacement (Kim et al., 2011). To further understand this, the input volume velocities of the oval and round windows were decomposed into anti-symmetric (slow wave) and symmetric (fast wave) volume velocities (Peterson and Bogert, 1950). When normalized by the anti-symmetric volume velocity component, the BM response was found to no longer depend on the direction of displacement. Furthermore the BM response, in the 0.1–10 kHz range, was the same regardless of AC stimulation or BC stimulation, when normalized by the anti-symmetric component of the oval and round window volume velocities. This finding may serve to extend Békésy’s (1955) concept of “paradoxical movements,” in which he observed waves on the BM traveling along the base-to-apex direction regardless of the location and type (AC or BC) of cochlear stimulation, in that the finding suggests that the characteristic wave behavior persists even when the input direction of BC stimulation is changed (Kim et al. 2011).

5. Developments in bone-conduction technology

Much of the recent renewed effort to build upon the foundational BC research of Békésy and others stems from the desire to develop new or improved technologies, such as BC transducers that can extend the frequency range of BC testing, a new class of BC hearing aids, and the development of hearing protection systems suitable for extremely high noise environments.

a. Transducers that extend bone-conduction testing above 6 kHz

The diagnosis of conductive, sensorineural, and mixed hearing loss relies on clinical measurements of AC and BC thresholds. While AC threshold measurements can be made in the 0.125 to 20 kHz frequency range, BC threshold measurements typically only extend to 6 kHz due to transducer shortcomings, thus eliminating diagnostic information at high frequencies for both sensorineural and conductive mechanisms. To extend this frequency range, Popelka et al. (2010) introduced the use of a new magnetostrictive transducer capable of measuring BC thresholds for frequencies up to 16 kHz and levels up to 85 dB HL. These new BC transducers, when combined with standard AC transducers, can be used to characterize sensorineural and conductive sensitivity for higher frequencies than is possible with present clinical diagnostic BC technology.

b. Bone-conduction hearing aids

Sensorineural hearing impairment is normally treated with an acoustic hearing aid (HA), some component of which must be inserted into the ear canal. However, some subjects have a condition called congenital ear canal atresia, in which the canal is blocked and thus it is not possible to insert an HA into it. In these cases a BC hearing device (BCHD) is used instead, which features a vibrator that transmits a signal through the skull to the cochlea, bypassing the ear canal and the middle ear in the process. A headband is used to apply a static pressure against the skull to keep the vibrator in place, but this can be uncomfortable and tends to result in poor speech perception, thus limiting its usefulness (Snik et al., 1995). To mitigate these deficiencies, a bone-anchored hearing aid (BAHA) has been developed as an alternative (Hakansson et al., 1990; Tjellstrom and Granstrom, 1994; Wazen et al., 1998). In this design, a skin-penetrating titanium implant is embedded into the skull by a surgeon and the BAHA is attached to this, which avoids the static pressure problems and provides better coupling to the skull, but has the additional shortcomings of requiring surgery and carrying an ongoing risk of infection. It remains to be seen what future BC technologies might emerge to further improve upon this class of hearing device.

c. Bone-conduction hearing in high noise environments

Pilots and aircraft mechanics are exposed to aircraft noise reaching levels as high as 150 dB SPL, which places them at significant risk of permanent hearing loss. While conventional protective headphones can provide some degree of protection against the damaging effects of sound transmitted through the AC pathway, they become inadequate at these extreme noise levels as the unmitigated sound reaching the cochlea through the BC pathway approaches dangerous levels itself. Because of this limitation due to the BC pathway, the total amount of hearing protection possible with conventional headphones tops out at around 40–45 dB at 2 kHz (Berger et al., 2003). Finding new methods to mitigate sound conduction to the inner ear will require researchers and engineers to further explore and make effective use of the basic mechanisms of BC hearing (McKinnley et al., 2005; McKinley, 2009).

D. Summary

While Békésy started out striving to improve upon the newly founded field of telephone communications, he became a pioneer himself in the field of auditory biomechanics. When he entered the field, many of the mechanisms for air and bone conducted sound transmission to the sensory epithelium were poorly described. Békésy established the scientific and analytic methodologies to test both previous theories and new theories, which he posited. Forty years after Békésy’s death, his discoveries in the sound conduction pathways to the inner ear continue to have profound impacts on the modern cell phone, hearing aids for the hearing impaired, and sound protection for people exposed to high level sound pressures.

HIGHLIGHTS.

• We review Békésy’s work on how sound is conducted to the inner ear.

• We discuss that work’s influence on present day thinking and research.

• Prominent remaining questions are summarized.