On the Inherent Precision of mcDESPOT

Abstract

A statistical analysis of the mcDESPOT protocol for characterizing two exchanging water proton pools—a seven-dimensional problem that fits to multiple flip angle measurements of both spoiled and refocused gradient echoes—is presented. Theoretical calculations of the Cramér-Rao lower bounds of the variance of fitted model parameters were made using a variety of model system parameters, meant to mimic those expected in human white matter. The results, validated by Monte Carlo simulations, indicated that mcDESPOT signals acquired at feasibly attainable signal to noise ratios cannot provide parameter estimates with useful levels of precision. Precision can be greatly improved by constraining solutions with a priori model information, although this will generally lead to biased parameter estimates with less specificity. These results indicate that previous, apparently successful applications of mcDESPOT to human white matter may have used data fitting methods that implicitly constrained parameter solutions, or that the two-pool model of white matter may not be sufficient to describe the observed water proton signal in mcDESPOT acquisitions. In either case, mcDESPOT-derived estimates of two-pool model parameters cannot yet be unambiguously related to specific tissue characteristics.

INTRODUCTION

Myelin is a cellular dielectric material in the central and peripheral nervous systems of vertebrates, which acts to increase the conduction velocity of electrical signals along neuronal axons. Structurally, myelin is composed of a lipid bilayer membrane wrapped many times around the neuronal axon, with thin layers of water molecules between layers of membrane. This myelin water can be distinguished, at least to some significant degree, in magnetic resonance imaging (MRI) due to its short and relatively unique transverse relaxation time constant (T₂) (1–4).

The standard approach for measuring the myelin water fraction (MWF, i.e., the relative water proton content from myelin within a voxel) utilizes a single-slice multiple spin-echo pulse sequence with robust RF refocusing and appropriate gradient spoiling of signal from non-spin-echo coherence pathways (5). The resulting multi-exponential decay signal is then fitted with a spectrum of T₂ time constants, from which the MWF is defined as the fraction of signal within a range of relatively short T₂ time (typically 10–50 ms at 1.5T) (6, 7). While variations and optimizations of this approach have been reported (8–12), it remains relatively slow, sensitive to noise, and generally limited to single slice coverage. A few alternative approaches have been proposed to provide multi-slice or 3D mapping of myelin content (13–15), but none has established widespread use as yet.

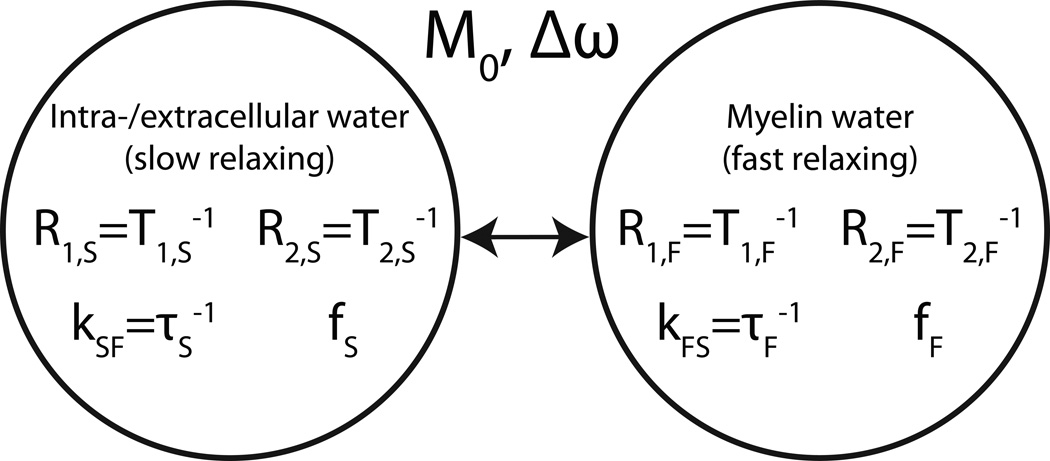
One such method, the multi-component driven equilibrium single pulse observation of T₁ and T₂ (mcDESPOT) (15), is particularly attractive because it uses a combination of clinically-standard gradient echo pulse sequences—spoiled gradient echo (SPGR) and balanced steady state free precession (bSSFP)—which are readily amenable to multislice or 3D implementation. Each sequence is repeated with a range of excitation flip-angles and the ensemble of data is fitted to a two-pool model of longitudinal and transverse relaxation that includes intercompartmental water exchange (see Fig 1). The inclusion of intercompartmental water exchange rate as a model parameter makes mcDESPOT unique and especially compelling given the potential for the mean residence time of water in myelin to be a measure of myelin thickness (16, 17). Recent studies using mcDESPOT report low-variance estimates of model parameters in human spinal cord (18) and human infant brain (19), but to date, no rigorous statistical analysis of this method has been reported to provide a guideline for the utility of mcDESPOT.

Figure 1. Two-compartment relaxation model.

Relevant model parameters include longitudinal relaxation times T₁, transverse relaxation times T₂, signal fractions f, exchange rate k, main field off-resonance factor Δω, and total signal amplitude M₀.

This study attempts to quantify the precision of model parameter estimates resulting from mcDESPOT, such as the fast-decaying signal fraction (f_F) which has been interpreted similarly to the MWF, by calculating the Cramér-Rao lower bounds (CRLB) of their variances. The CRLB is a statistic which, via analytical proof based on the probability space of an underlying model, sets a lower limit on parameter uncertainty due to the propagation of error induced by measurement noise. In accordance with the principle that bias can be traded-off for precision of estimated parameters, the CRLB of fitted parameters resulting from an example constrained fitting strategy is also investigated.

THEORY

Two-Compartment Model

Consider a two-pool model of water protons, comprised of a faster-relaxing pool (F) and a more slowly-relaxing pool (S). The total equilibrium magnetization is M₀, and each pool is characterized by a fractional proton density (f), longitudinal and transverse relaxation rate (R₁ and R₂), and first order exchange constant (k). At equilibrium, detailed balance dictates that f_Fk_FS = f_Sk_SF and f_S = 1−f_F, resulting in seven independent model parameters: M₀, k_FS, f_F, R_1F, R_2F, R_1S, and R_2S. Alternatively, the relaxation rates can be equivalently expressed as time constants (T₁ = 1/R₁ and T₂ = 1/R₂) and the exchange rate can be expressed as a mean residence time, τ_F = 1/k_FS.

Under the condition that each pool is well mixed at all time, the evolution of magnetization in this model is described by the 6 coupled Bloch-McConnell equations (20)

$$\frac{\mathrm{d}\mathbf{M}}{\text{dt}}=\mathbf{\text{AM}}+\mathbf{C}$$ [1]

In response to periodic instantaneous radiofrequency (RF) excitation pulses aligned with the x-axis, the steady-state solution to these equations is of the form

$${\mathbf{M}}_{\text{SS}}={\left[\mathbf{I}-{\mathrm{e}}^{\mathbf{A}·\mathit{\text{TR}}}\mathbf{R}(\alpha )\right]}^{-1}\left({\mathrm{e}}^{\mathbf{A}·\mathit{\text{TR}}}-\mathbf{I}\right){\mathbf{A}}^{-1}\mathbf{C},$$ [2]

where TR is the period of repetition, A and C are the 6×6 coefficient and 6x1 constant matrices, respectively, from the Bloch-McConnell differential equations, R(α) is a 6×6 rotation matrix describing RF excitation with nutation angle α, and I is the 6×6 identity matrix. Expansions of these matrices can be found in Appendix I. This work utilizes the magnitude of the steady-state transverse magnetization (|M_x,F + M_x,S +iM_x,F + iM_x,S) calculated via Eq [2] as the forward model and signal equation for the bSSFP sequence.

Under the condition that all transverse magnetization is reduced to zero prior to each RF pulse (i.e., spoiled gradient echo), R_SPGR(α) reduces to the 2×2 identity matrix scaled by cos(α), the A and C terms in Eq [1] become

$${\mathbf{A}}_{\text{SPGR}}=\left[\begin{array}{c}\hfill -R_{1\mathrm{F}}-k_{\text{FS}}\hfill \\ \hfill k_{\text{FS}}\hfill \end{array}\begin{array}{c}\hfill k_{\text{SF}}\hfill \\ \hfill -R_{1\mathrm{S}}-k_{\text{SF}}\hfill \end{array}\right]\text{ and}$$ [3]

$${\mathbf{C}}_{\text{SPGR}}=M_0\left[\begin{array}{c}\hfill R_{1\mathrm{F}}{f}_{\mathrm{F}}\hfill \\ \hfill R_{1\mathrm{S}}{f}_{\mathrm{S}}\hfill \end{array}\right],$$ [4]

and using the equilibrium condition, f_Fk_FS = f_Sk_SF, Eqs [3] and [4] combine to

$${\mathbf{C}}_{\text{SPGR}}=-M_0{\mathbf{A}}_{\text{SPGR}}\left[\begin{array}{c}\hfill f_{\mathrm{F}}\hfill \\ \hfill f_{\mathrm{S}}\hfill \end{array}\right].$$ [5]

Thus, Eq [2] reduces to

$${\mathbf{M}}_{\text{SS}}=M_0\text{ sin }(\alpha ){\left[\mathbf{I}-{\mathrm{e}}^{{\mathbf{A}}_{\text{SPGR}}·\mathit{\text{TR}}}\text{ cos}(\alpha )\right]}^{-1}\left(\mathbf{I}-{\mathrm{e}}^{{\mathbf{A}}_{\text{SPGR}}·\mathit{\text{TR}}}\right)\left[\begin{array}{c}\hfill f_{\mathrm{F}}\hfill \\ \hfill f_{\mathrm{S}}\hfill \end{array}\right].$$ [6]

where the sin(α) term reflects sampling of the steady state longitudinal magnetization with the final RF pulse. Equation [6] is used herein as the forward model and the signal equation for the spoiled gradient echo sequence. Although noise in MR magnitude images has been shown to follow the Rice distribution (21), it is assumed by this work that the signal magnitude in each sequence is measured with additive Gaussian noise. This approximation is nearly correct as long as the signal remains above approximately twice the noise floor (22), a very loose constraint for quantitative MR using simple gradient-echo sequences.

The Cramér-Rao Lower Bound

Consider a model g(x,θ), where x ∈ ℝ^N is an independent parameter vector (e.g., RF pulse flip angles) and θ ∈ ℝ^M is a vector of model parameters (e.g., two-pool parameters in Fig 1). Assume we have a random estimate θ̂ of model parameters based on noisy observations, y ∈ ℝ^N. This estimate of model parameters abides by a probability distribution described by a covariance matrix, Σ_θ̂, bounded by the Cramér-Rao lower bound (CRLB) (23):

$${\mathbf{\Sigma }}_{\hat{\mathbf{\theta }}}\ge \frac{\partial \mathrm{E}[\hat{\mathbf{\theta }}]}{\partial \mathbf{\theta }}{\mathbf{ℱ}}^{-1}\frac{\partial \mathrm{E}{[\hat{\mathbf{\theta }}]}^T}{\partial \mathbf{\theta }},$$ [7]

where ℱ is the Fisher information matrix (FIM), E[·] is the expectation operator, 𝒜 ≥ ℬ implies that (𝒜 − ℬ) is a nonnegative-definite matrix, and the derivative of one vector with respect to another follows the convention (∂a/∂b)_ij ≡ ∂a_i/∂b_j. The positive square roots of the diagonal elements of this covariance matrix are then lower bounds of the standard deviation of the estimated model parameters

$${\sigma }_{{\theta }_j}\ge \sqrt{{\left(\frac{\partial \mathrm{E}[\hat{\mathbf{\theta }}]}{\partial \mathbf{\theta }}{\mathbf{ℱ}}^{-1}{\frac{\partial \mathrm{E}[\hat{\mathbf{\theta }}]}{\partial \mathbf{\theta }}}^T\right)}_{\mathit{\text{jj}}},}$$ [8]

which can inform on the practical identifiability of model parameters under specific experimental conditions. It should be noted that maximum likelihood estimators such as least-square estimators in the presence of normally distributed noise, including the genetic algorithm proposed for mcDESPOT fitting by Deoni (15), have been proven (24) to achieve the CRLB if such a bound is attainable. Nonlinearity in the signal within a statistically relevant range of the true intrinsic parameters θ, however, can increase the actual estimate variance substantially over the CRLB. Nevertheless, in the experimental portion of the following work, the statistic is presented as a definite variance rather than a lower bound.

The central element of Eq [7], the FIM, is a matrix populated by expected curvature values of the parameter vector θ’s M-dimensional log-likelihood hypersurface. The fact that an estimate’s maximal precision is defined by the shape of its probability manifold may be somewhat intuitive: if the estimate’s “probability peaks” are sharp, the probability maximum will be better defined and thus less susceptible to noise. Calculation of the FIM is straightforward: when observed data y_i, i = 1 to N, are normally distributed about g(x_i, θ) with variance ${\sigma }_i^2$ , the FIM can be calculated as

$${ℱ}_{\mathit{\text{jk}}}={\displaystyle \sum }_{i=1}^N\left(\frac{1}{{\sigma }_i^2}\frac{\partial g_i}{\partial {\theta }_j}\frac{\partial g_i}{\partial {\theta }_k}\right),$$ [9]

or, in matrix form as

$$\mathbf{ℱ}={\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}$$ [10]

where J_ij = ∂g_i/∂θ_j (the Jacobian matrix) and Σ is the diagonal covariance matrix of the added noise.

The CRLB also includes the estimator gradient matrix, ∂E[θ̂]/∂θ, which incorporates the gradient of the estimator bias. For unbiased estimators, E[θ̂] = θ, so ∂E[θ̂]/∂θ = I, the identity matrix, and does not contribute to the CRLB. For biased estimators, however, this term does not reduce to identity and can be computed numerically by repeated parameter estimation with varied model parameter values. A more comprehensive explanation of the CRLB and its components can be found in Appendix II.

METHODS

Unconstrained mcDESPOT Cramér-Rao bounds

For five model tissues with various slow-decaying T₁/T₂ ratios and intercompartmental exchange rates (Table 1, parameter sets 1–5), the CRLB of fitted parameters were calculated using Eq [8] and for two previously published mcDESPOT protocols. The first mcDESPOT protocol (15) was comprised of 7 SPGR acquisitions with varied RF flip angle (α_SPGR = 2°, 4°, … , 14°; TR_SPGR = 6.5 ms; BW_SPGR = 20 kHz) and 9 bSSFP acquisitions with varied RF flip angle (α_SSFP = 6°, 14°, … , 70°; TR_SSFP = 5 ms; BW_SSFP = 60 kHz). The second, more recently reported mcDESPOT protocol (25) included the same SPGR acquisitions but 18 SSFP acquisitions using the same 9 flip angles each repeated with and without a 180° RF phase increment per TR period (Δø= 180° or 0°). This second protocol allows fitting of an off-resonance term, Δω, as an 8^th independent model parameter, although the present work used the on-resonance condition for all cases. In order to compare these two methods assuming equal total acquisition time, the original protocol was calculated using 18 SSFP acquisitions by simply repeating each SSFP measurement one time. All simulations assumed no errors in RF flip angle and no off-resonance effects.

Table 1. Tissue parameter sets.

Parameter sets 1–4 were chosen based on parameter values in previous mcDESPOT studies (15, 18, 19) and with varying slow-decaying T₁/T₂ ratios and exchange rates in order to display different SSFP signal characteristics. Set 5 represents a scenario in which the T₁/T₂ ratios of each compartment are equal. Sets 6–8 were used with a range of f_F values and varying one other parameter within the range provided. Note that set 8 with k_FS = 0 represents two pools in slow exchange. Sets 9–11 demonstrate by example different tissue models that result in effectively identical mcDESPOT signals.

Parameter Set	T1,S (ms)	T1,F (ms)	T2,S (ms)	T2,F (ms)	fF (%)	kFS (s−1)
1	800	450	100	20	20	10
2	800	450	100	20	20	2.5
3	1500	450	100	20	20	10
4	1500	450	100	20	20	2.5
5	2250	450	100	20	20	10
6	800	450	75 – 150	20	5 – 45	10
7	800	450	100	15 – 30	5 –45	10
8	800	450	100	20	5 –45	0 – 50
9	970	415	80.0	12	15	11.1
10	965	527	83.7	16.6	23	6.7
11	965	579	86.9	19.3	28	5

As noted above, the estimator gradient matrix terms in Eq [8] were ignored for the unconstrained fitting analysis. The FIM was computed using Eq [10], which includes the Jacobian and noise covariance matrices. The Jacobian matrix was calculated as defined above, J_ij = ∂g_i/∂θ_j, where the derivative of the signal equation, Eq [6] for SPGR and Eq [2] for SSFP, was evaluated at the 25 different RF flip angles (x_i; 7 for SPGR and 18 for SSFP) and with respect to 7 (or 8) different model parameters (θ_j). Each derivative was estimated from a forward-difference calculation of the signal with respect to a step size in the model parameter by a factor of 1 × 10⁻⁴. The noise covariance matrix was computed assuming Gaussian noise with standard deviations σ_SPGR = 1 × 10⁻³ M₀, with M₀ = 1 (a.u.), and ${\sigma }_{\text{SSFP}}=\sqrt{3}{\sigma }_{\mathit{\text{SPGR}}}$ due to the greater receiver BW for the SSFP acquisitions. The noise was defined as uncorrelated between acquisitions, so the covariance matrix was diagonal. At these values of noise variance, the maximum image signal-to-noise ratio (SNR) was on the order of 100 for all tissue models. However, as there is no elegant way to define a consistent noise level in terms of SNR when tissue and scan parameters are repeatedly changed, referential values of SNR in the following are given as roughly one-tenth the ratio M₀/σ_SPGR.

As an informative measure, the condition number of each Jacobian matrix was calculated as the ratio of its highest singular value to its lowest. This value was a rough estimate of the ratio of relative error in estimated parameters to the relative error in signal (26). Specifically, an infinite condition number corresponds to a rank-deficient Jacobian and unsolvable estimation problem, while a large condition number can indicate that certain parameters may be unidentifiable at feasible SNRs.

Constrained mcDESPOT Cramér-Rao bounds

The CRLB of fitted parameters were also calculated while constraining both transverse relaxation rates (R_2,S, R_2,F) and the water exchange rate (k_FS). For the best case scenario, when R_2,S, R_2,F and k_FS were constrained to their correct model values, the estimator gradient matrix remained an identity matrix, and the Jacobian was reduced by removing the columns associated with the three constrained parameters (see Appendix II). Fisher information matrices and CRLB were then calculated as usual using Eq [10] and [8] and assuming parameter set 1 in Table 1. For the more general, biased, scenario, when a priori constraints were not correct, the estimator gradient matrix was determined numerically as follows. Noiseless mcDESPOT signals were generated using various tissue models (Table 1, parameter sets 6–8) and these signals were fitted with the signal equations (Eq. [2] and [6]) using a minimum χ² criteria (27) and while constraining R_2,S, R_2,F and k_FS to one of three sets of values (A–C, Table 2). Each fit was repeated with varied initial conditions in order to ensure that the global minimum χ² value was found, which thus provided the expected value of fitted parameters, E[θ̂]. This process was repeated while individually perturbing each model parameter by a factor 1 × 10⁻⁴ and then the estimator gradient matrix, ∂E[θ̂]/∂θ, was formed from the series of forward-difference derivative approximations. The noise covariance matrix was generated as above and, finally, the CRLB was calculated using Eq [8].

Table 2.

Time constant constraints. Constraint set A was applied to parameter sets 6–8 in Table 1 (see Figure 5, panels b–d), and sets A, B, and C were all applied to parameter set 1 in Table 1 (Figure 5, panel a). Constraint set D was used alongside parameter set 1 in Table 1 in a Monte Carlo simulation to validate CRLB calculations (Figure 2).

Constraint Set	T2,S (ms)	T2,F (ms)	kFS (s−1)
A	150	20	10
B	100	30	10
C	100	20	15
D	125	35	5

Validation of the Cramér-Rao bound

Monte Carlo simulations were used to validate both the unbiased and biased CRLB calculations using model tissue 1 (Table 1) and constraint set D (Table 2). Equations [2] and [6] were used to generate mock mcDESPOT data to which random Gaussian noise was added. For the unconstrained case, with 7 or 8 free model parameters and relatively large CRLB, a very high SNR was used to allow robust and efficient fitting; σ_SPGR = 1 × 10⁻⁷ M₀ and ${\sigma }_{\mathit{\text{SSFP}}}=\sqrt{3}{\sigma }_{\mathit{\text{SPGR}}}$. For the constrained case, with only 4 or 5 free model parameters, the CRLB were much smaller so a correspondingly lower SNR was used to ensure that variance in parameter estimates was dominated by propagated noise and not inaccuracies in the fitting algorithm; σ_SPGR = 1 × 10⁻³ M₀ and ${\sigma }_{\mathit{\text{SSFP}}}=\sqrt{3}{\sigma }_{\mathit{\text{SPGR}}}$. For both cases then, the noisy data were fitted with Eq [2] and [6] to a minimum χ² criterion using standard non-linear regression tools (lsqnonlin function in MATLAB) and varied initial conditions. Each signal was fitted 100 times using initial guesses that were randomly distributed about the known solution with standard deviation equal to 10 times the predicted CRLB. If the best 20 of these 100 fits converged to solutions with less than 0.01% parameter variability, then the solution was considered the global minimum. This threshold was chosen to be significantly less than the variability in parameter solutions predicted by the CRLB. If this stop criterion was not achieved, the algorithm was repeated with 100 new seed vectors. After satisfactorily fitting 10000 signals with independently generated additive noise, the variances of all fitted parameters were calculated and compared to the CRLB.

RESULTS

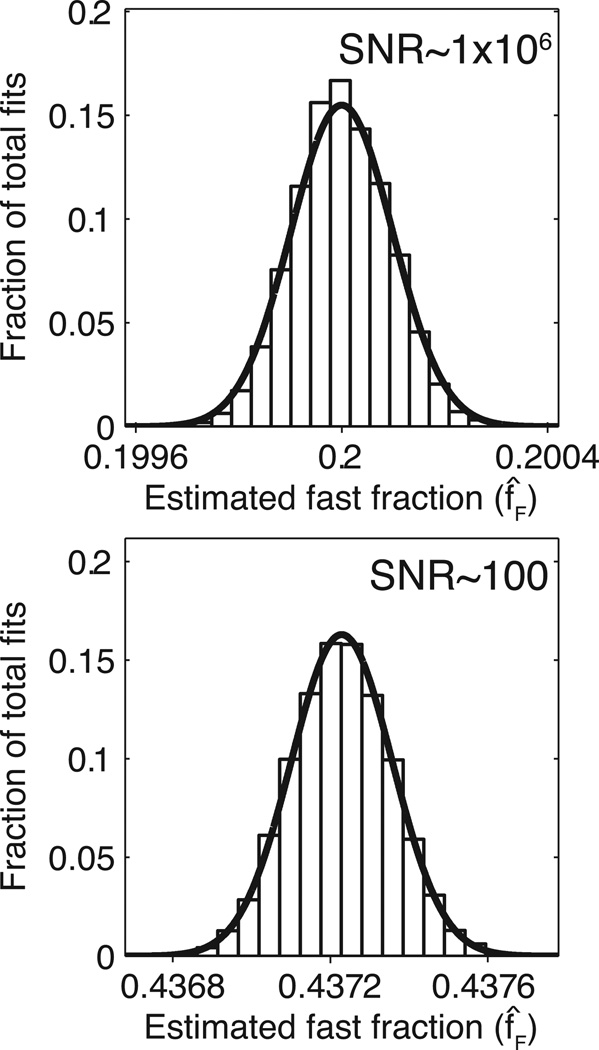
The Monte Carlo simulations provided parameter variances that agreed well with the calculated Cramér-Rao lower bounds. The panels in Fig 2 consist of histograms displaying the results of both unbiased and biased fast-signal fraction estimates from the Monte Carlo simulations, while the superimposed curves represent predicted distributions based on the calculated CRLB. Similar results were found for all model parameters—CRLB and Monte Carlo derived variances differed by no more than 8% for any parameter.

Figure 2. Monte Carlo simulation results and their theoretical Cramér-Rao bounds.

The histograms represent bins created from 10,000 trials, while the overlaid curves follow a Gaussian distribution with mean equal to E[f̂_F] and variance equal to the CRLB. Top: unbiased 7-parameter fitting using parameter set 1 in Table 1 and SNR ~10⁶; bottom: biased 4-parameter fitting using intrinsic parameters from set 1 in Table 1, constraint set D in Table 2, and SNR ~100.

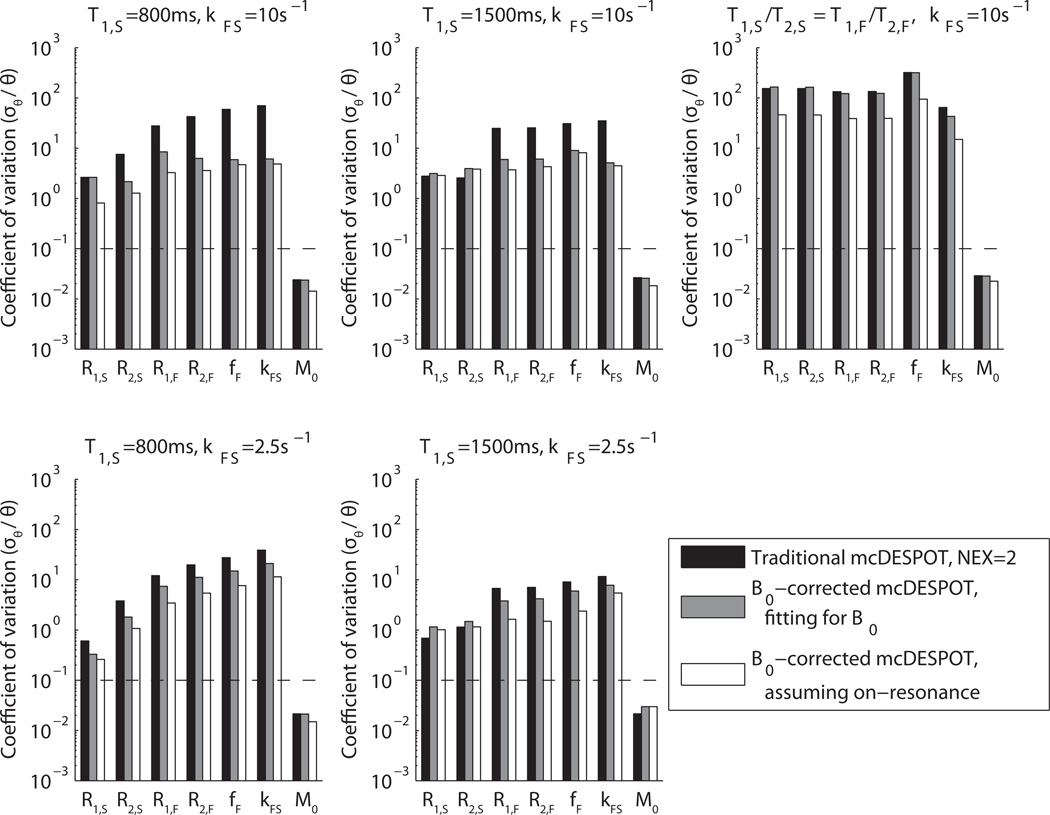
When examining unconstrained estimators of all model parameters, the Cramér-Rao bounds were very high at feasible signal-to-noise ratios. Figure 3 shows the results of the unbiased CRLB calculations presented as coefficients of variation (c_θ = σ_θ/θ) at σ_SPGR= 1 × 10⁻³ M₀. The CRLB vary significantly between model tissues, but in all cases c_θ >> 10% for all parameters except total proton density, M₀. (In many cases, a practical estimation precision is.c_θ ≤10%.) These large CRLB for mcDESPOT agree with the condition number ~10⁵ found for the model’s Jacobian matrix for a variety of typical tissue parameters, indicating a very large propagation of error from image signal intensities to estimated model parameters. Interestingly, evaluating the forward model using both alternating and non-alternating RF phase cycling schemes improved estimate precision by up to an order of magnitude. While this was not a sufficient improvement to guarantee identifiable estimates at practical SNR, it is worth noting that even with the addition of an 8^th free parameter, Δω, the precision of other parameter estimates improved. Neglecting this parameter while still acquiring at both phase cycling schemes gives an additional, sometimes significant improvement to estimate precision, but forfeits the inhomogeneity-correcting accuracy gains detailed by Deoni (25).

Figure 3. Unconstrained Cramér-Rao bounds as coefficients of variation.

Three methods are presented using five sets of intrinsic parameter values (1–5 in Table 1). This study was performed at σ_SPGR = 1×10⁻³ M₀, which corresponds to a clinically-feasible SNR for gradient echo sequences, and it should be noted that coefficients of variation scale with image SNR. The dotted lines on each plot are a reference goal for quantitative precision. In all cases, estimates of all parameters except M₀ have impractically high variance. There is a surprising improvement in precision when multiple phase cycling patterns are utilized in SSFP acquisitions, despite the addition of an eighth free parameter.

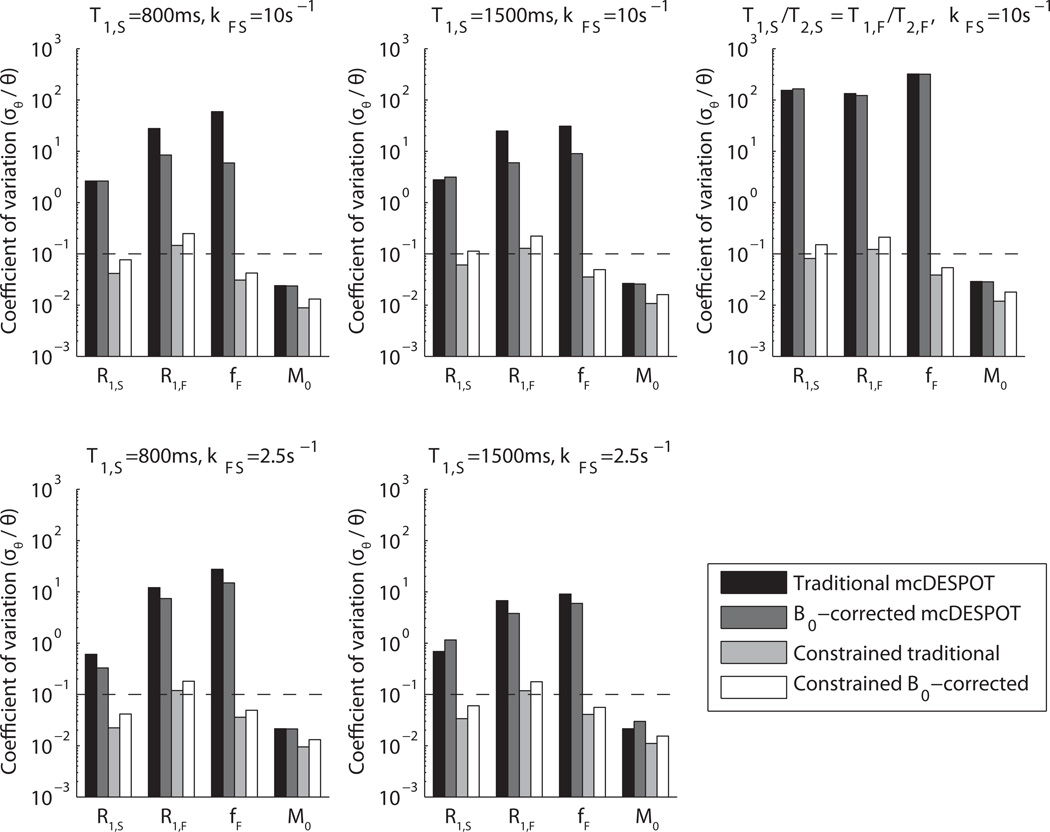
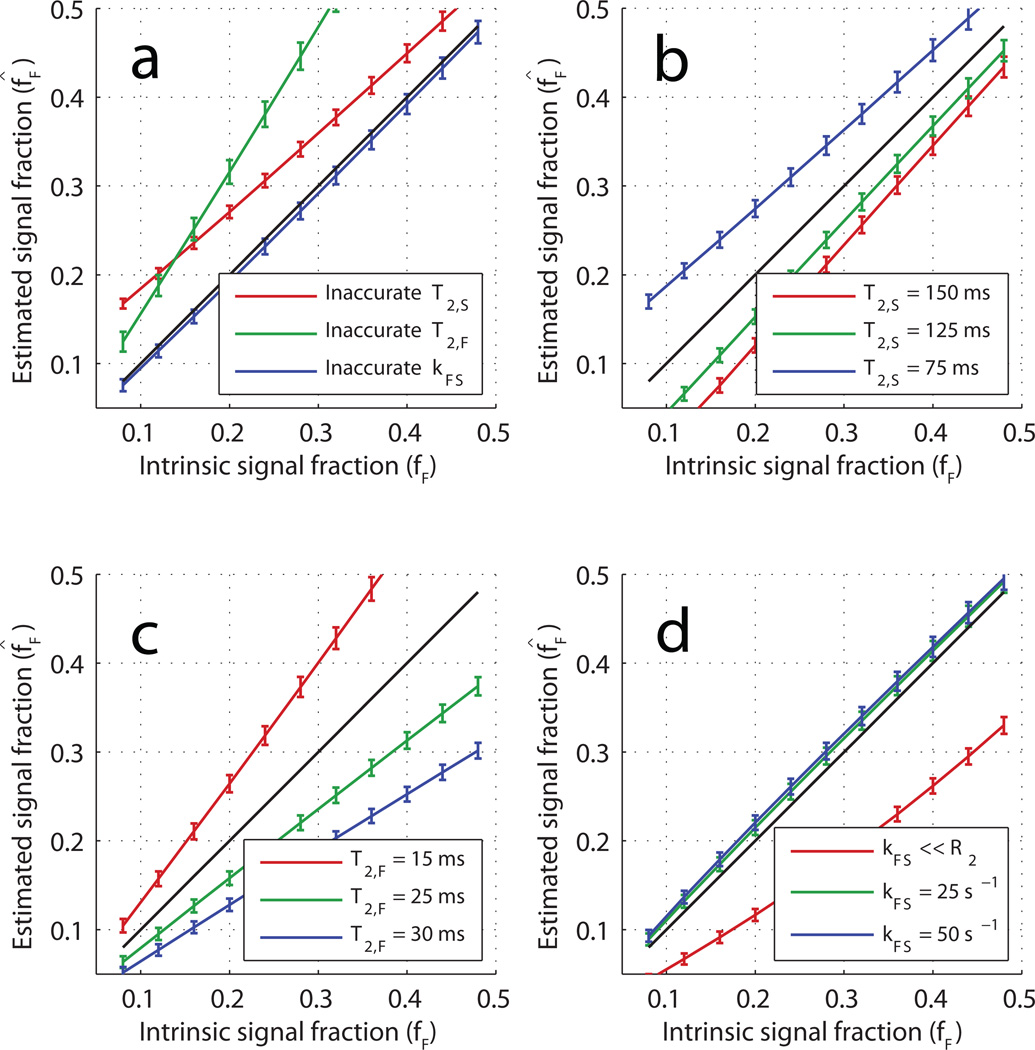
The scenario in which exchange and transverse relaxation rates are constrained provided much improved precision; Fig 4 shows an improvement in up to three orders of magnitude, regardless of bSSFP acquisition scheme. Again, this coincides well with an observed reduction in the condition number of the Jacobian to ~100 when columns with the signal derivative with respect to R_2,S, R_2,F and k_FS were removed. The price paid for the improved estimate precision is an increased estimate bias. Figure 5 demonstrates the relationship between short-lived signal fraction estimates (f̂_F) and corresponding true model values (f_F) for two different tissue models and a variety of a priori R_2,S, R_2,F and k_FS constraints. The error bars represent estimate standard deviations based on the CRLB at σ_SPGR = 1 × 10⁻³ M₀. In general, although the estimates showed a substantial bias (more than 100% of the intrinsic value in some cases), there is a monotonic, nearly linear relationship between the estimates and the true model values.

Figure 4. Constrained Cramér-Rao bounds as coefficients of variation.

Parameter values are listed as sets 1–5 in Table 1, and accurate constraints on T_2,S,T_2,F, andk_FS are assumed. This study was performed at σ_SPGR = 1 × 10⁻³ M₀, which corresponds to a clinically-feasible SNR for gradient echo sequences, and it should be noted that coefficients of variation scale with image SNR. The dotted lines on each plot are a reference goal for quantitative precision. There is a drastic improvement in free-parameter precision when the T₂s and exchange rate are constrained. Acquiring using multiple phase cycling patterns in the SSFP images does not benefit precision as it does when parameters are left unconstrained, but still removes a source of bias; i.e., the implicit assumption of B₀ homogeneity described previously (25).

Figure 5. Biased estimates of fast-decaying signal fraction.

All panels show estimated fast fraction (f̂_F) vs the model value (f_F) when the model values of T_2,S, T_2,F, and k_FS are constrained to specific values. In all cases, the relationship between f̂_F and f_F is monotonic and close to linear. The error bars are the CRLB calculated using σ_SPGR = 1 × 10⁻³ M₀. By panel: a) the results when using model parameter set 1 (Table 1) and constraint sets A–C (Table 2)—in each case, one of the three constrained parameters was constrained to an incorrect value; b) the results of incorrectly constraining T_2,S over a range of model values (model parameter set 6 and constraint set A); c) the results of incorrectly constraining T_2,F over a range of model values (model parameter set 7 and constraint set A); d) the results of incorrectly constraining k_FS over a range of model values (model parameter set 8 and constraint set A).

DISCUSSION

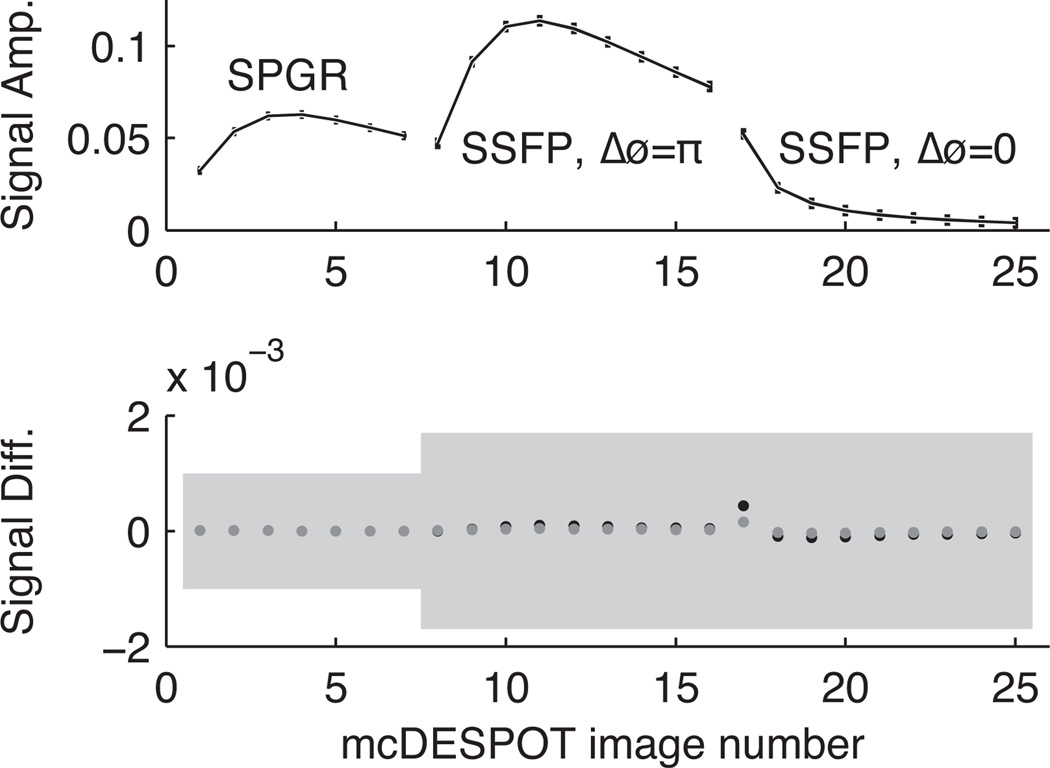
Numerical computations demonstrate that mcDESPOT, as previously described, cannot provide parameter estimates of a two-pool system with usable precision. A less rigorous but perhaps more intuitive demonstration of this can be seen in Fig 6, which shows mcDESPOT signals from 3 different model tissues (Table 1, parameter sets 9–11) and the differences between these signals compared with added noise at the σ_SPGR = 1 × 10⁻³ M₀ level. In this example, f_F varied between 15% and 28% across the three tissues, but their resulting mcDESPOT signal differences are approximately 3 orders of magnitude smaller than the standard deviation of the added noise. Clearly, with this level of noise, any of these three signals could be equally-well fitted with any of the three parameters sets.

Figure 6. mcDESPOT signal differences relative to appropriate noise levels.

Top: a reference mcDESPOT signal containing two bSSFP curves (using both alternating and non-alternating RF excitation phase every repetition) and one SPGR curve. Bottom: differences between the reference signal above and signals with very distinct parameter values. For example, f_F values vary between 15% and 28%. Nevertheless, the uncertainty due to noise is still very large compared to the signal differences, so one would expect difficulty in differentiating the signals.

These findings of impractically high parameter variance from mcDESPOT, however, are incongruent with previous in vivo studies, which show maps of mcDESPOT-derived MWF (i.e., f_F in a white matter model) that exhibit relatively low variance (18, 19). It thus appears that the model presented here does not accurately reflect the in vivo scenario. Two possible sources for this difference are: 1) the estimator used for the in vivo studies, and/or 2) the model used to characterize the tissue. In the first case, while Deoni et al proposed sophisticated genetic and region-contraction algorithms (15, 25), these in-turn may have inadvertently constrainted the solution vector, θ̂, to a value different from the global χ² minimum. This would be a result of inappropriate shrinkage of parameter space between iterations in the problem solving algorithm, an effect which is difficult to combat in highly correlated, large-dimensional spaces such as mcDESPOT’s 7 or 8 free parameters. In this case, the estimator gradient matrix would not be an identity matrix and its norm would be less than one, resulting in a decrease in the CRLB in accordance with Eq [8].

The second case is that the two-pool model, upon which mcDESPOT and the CRLB calculations herein are based, does not satisfactorily describe the complex microstructure of white matter. This would not be surprising, given the spectrum of axonal diameters and glia found in any given volume of white matter. To be more specific, the sensitivity in vivo of the signal to an apparent signal fraction or T₂ value may be greater than the sensitivity would be for a perfect two-pool system. For example, magnetization transfer effects, which are not presently incorporated into the mcDESPOT model, are known to affect both bSSFP (28, 29) and SPGR (30) signals. The relatively large macromolecular pool that is thought to exchange magnetization with myelin water (31–34) will reduce the apparent T₂s in a DESPOT2 (bSSFP) measurement (35) and may result in significantly reduced variance in the estimates of the apparent fast-relaxing signal in a two-pool model. This effect would suggest that the mcDESPOT measure of MWF is to some degree a measure of macromolecular proton fraction, much like a qMT measurement provides. Such a scenario would explain observations of mcDESPOT-estimates of f_F in gray matter that exceed expected myelin water fractions (18). At this point, neither the estimator nor the model (nor some combination) can be definitively identified as the source of differences between in vivo studies and the CRLB.

Beyond the unconstrained mcDESPOT methods used to date, the results in Fig 4 show that constraining some model parameters—for example, both R₂s and k_FS—to a priori values allows for much improved precision of the remaining parameter estimates. It may be reasonable to expect R_2,F to be relatively invariant across tissues and subjects, at least in the absence of a condition of myelin edema; however, there is good reason to believe that water exchange rate, k_FS, will depend on myelin thickness and axon diameter (16, 17), and the intra-/extra-axonal water relaxation rate, R_2,S, will vary greatly with inflammation. Thus, it may generally be difficult to know R_2,F, R_2,S, and k_FS a priori.

Figure 5 reports some effects of incorrect parameter constraints on the estimated fast signal fraction, f̂_F. Panel a) indicates that, when comparing otherwise similar tissues, this constrained mcDESPOT will report on changes or differences in f_F, despite erroneous constraints. More specifically, these results suggest that constrained mcDESPOT, measured with peak image SNR ≈ 100, can identify a difference of as little as 5% intrinsic signal fraction within 95% confidence. Conversely, the other panels of Fig 5 show how differences in k_FS and R₂s will alter the estimated fast signal fraction. While somewhat intuitive, it is worth noting that the bias incurred due to an incorrect relaxation rate constraint (panels b, c) increases as the respective compartment’s signal fraction increases. A less expected result of the simulations is that the constrained mcDESPOT protocol predicts f_F quite poorly when the intrinsic exchange rate is slow compared to the constraint (panel d). Thus, even assuming sources of signal inaccuracy (e.g., hardware limitations, B₁ field inhomogeneity) can be perfectly corrected, the utility of constrained mcDESPOT will depend very much on the application, and one should be cautious interpreting changes or differences in f̂_F as reflecting changes or differences in MWF.

We note that particular constraint scenario is presented here is an example and is not necessarily the best strategy. However, although not shown, a variety of other strategies were investigated and no combination of constraints was found that provided simultaneous low variance estimates of both k_FS and f_F. Thus, in the context of white matter imaging, we conclude that there is no viable mcDESPOT strategy to estimate MWF independently from the effects of inter-compartmental water exchange, or vice versa. Of course, the same is true for a conventional multiple spin echo measurement of transverse relaxation.

Finally, the observation that the parameter estimate precision can be improved substantially by repeating the bSSFP scan with and without 180° RF phase alteration (although the improvement did not occur under the constrained mcDESPOT scenario) reveals a novel mechanism for further optimizing mcDESPOT or other quantitative studies using bSSFP. Investigation of the parameter covariance matrix (Eq [7]) shows that 180° changes in the RF phase increment alter the sign of some parameter covariances (off-diagonal terms in Σ_θ̂), which results in a net reduction in covariance between parameters when signals acquired with both 0° and 180° increments are fitted concurrently. It is conceivable that other RF phase increments offer the effect of further diagonalizing Σ_θ̂, and, in turn, improving parameter estimate precision.

CONCLUSIONS

The work detailed here has demonstrated, through propagation-of-error analysis, the inability of mcDESPOT signals to precisely estimate parameters of a two-pool model with exchange. The results of this analysis were validated by both Monte Carlo simulations and the calculation of a condition number representing the seven- or eight-dimensional inverse problem inherent to mcDESPOT. Previous demonstrations of low variance parameter estimates from in vivo studies of white matter may be due to effective constraints being imparted on the parameter estimates in previously described mcDESPOT analysis, or may be due to an insufficiency of the two-pool model to describe white matter for these measurements. Regardless of the source of discrepancy, further study is required before mcDESPOT data can be unambiguously interpreted.

APPENDIX I

The full, general description of matrices M, A, R, and C in Eqs [1] and [2] are:

$${\mathbf{M}}_{\text{SS}}={\left[\begin{array}{c}\hfill M_{x,\mathrm{F}}\hfill \\ \hfill M_{x,\mathrm{S}}\hfill \\ \hfill M_{y,\mathrm{F}}\hfill \\ \hfill M_{y,\mathrm{S}}\hfill \\ \hfill M_{z,\mathrm{F}}\hfill \\ \hfill M_{z,\mathrm{S}}\hfill \end{array}\right]}_{\text{SS}}$$ [A1]

$$\mathbf{A}=\left[\begin{array}{cccccc}\hfill -R_{2,\mathrm{F}}-k_{\text{FS}}\hfill & \hfill k_{\text{SF}}\hfill & \hfill \mathrm{\Delta }\omega \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill k_{\text{FS}}\hfill & -R_{2,\mathrm{S}}-k_{\text{SF}}& \hfill 0\hfill & \hfill \mathrm{\Delta }\omega \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\mathrm{\Delta }\omega \hfill & \hfill 0\hfill & \hfill -R_{2,\mathrm{F}}-k_{\text{FS}}\hfill & \hfill k_{\text{SF}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\mathrm{\Delta }\omega \hfill & \hfill k_{\text{FS}}\hfill & \hfill -R_{2,\mathrm{S}}-k_{\text{SF}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -R_{1,\mathrm{F}}-k_{\text{FS}}\hfill & \hfill k_{\text{SF}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill k_{\text{FS}}\hfill & \hfill -R_{1,\mathrm{S}}-k_{\text{SF}}\hfill \end{array}\right]$$ [A2]

$$\mathbf{R}(\alpha )=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \text{cos}(\alpha )\hfill & \hfill 0\hfill & \hfill \text{sin}(\alpha )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \text{cos}(\alpha )\hfill & \hfill 0\hfill & \hfill \text{sin}(\alpha )\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\text{sin}(\alpha )\hfill & \hfill 0\hfill & \hfill \text{cos}(\alpha )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\text{sin}(\alpha )\hfill & \hfill 0\hfill & \hfill \text{cos}(\alpha )\hfill \end{array}\right]$$ [A3]

$$\mathbf{C}=M_0\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill R_{1,\mathrm{F}}{f}_{\mathrm{F}}\hfill \\ \hfill R_{1,\mathrm{S}}{f}_{\mathrm{S}}\hfill \end{array}\right]$$ [A4]

and I is the 6×6 identity matrix.

APPENDIX II

Following notation in the Theory section, the so-called score vector, v, which is the relative rate of change of the signal likelihood function, f, with respect to model parameters is

$$v_j\equiv \frac{1}{f(\mathbf{y},\mathbf{\theta })}\frac{\partial f\left(\mathbf{y},\mathbf{\theta }\right)}{\partial {\theta }_j}=\frac{\partial }{\partial {\theta }_j}\text{log }f(\mathbf{y},\mathbf{\theta }).$$ [A5]

When f is multivariate Gaussian, v can be reduced to

$$v_j={\displaystyle \sum }_{i=1}^N\frac{\left({\mathrm{y}}_i-{\mathrm{g}}_i(\mathbf{\theta })\right)}{{\sigma }_i^2}\frac{\partial {\mathrm{g}}_i\left(\mathbf{\theta }\right)}{\partial {\theta }_j}$$ [A6]

or, in matrix form as a column vector,

$$\mathbf{v}={\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{r}$$ [A7]

where J is the Jacobian matrix as traditionally defined for the true signal g(θ), Σ is the diagonal covariance matrix of the added noise, and r is a column vector of noise values. Note that since the expectation of additive noise is zero, the expectation of the score vector is a zero vector. The covariance matrix of the score vector v, also known as Fisher information, is then calculated as follows:

$$\text{cov}\left(\mathbf{v}\right)=\mathrm{E}\left[{\mathbf{\text{vv}}}^T\right]-\mathrm{E}\left[\mathbf{v}\right]\mathrm{E}\left[{\mathbf{v}}^T\right]=\mathrm{E}\left[{\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}{\mathbf{\text{rr}}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}\right]-\mathbf{0}={\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathrm{E}\left[{\mathbf{\text{rr}}}^T\right]{\mathbf{\Sigma }}^{-1}\mathbf{J}={\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{\Sigma }{\mathbf{\Sigma }}^{-1}\mathbf{J}={\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}$$ [A8]

where the symbol E[·] represents the expectation operation over the likelihood function f with respect to y. Furthermore, the covariance of v with the estimate vector θ̂ can be calculated as:

$$\text{cov}\left(\hat{\mathbf{\theta }},\mathbf{v}\right)=\mathrm{E}\left[\hat{\mathbf{\theta }},{\mathbf{v}}^T\right]-\mathrm{E}\left[\hat{\mathbf{\theta }}\right]\mathrm{E}\left[{\mathbf{v}}^T\right]=\mathrm{E}[\hat{\mathbf{\theta }}\left(\frac{1}{f(\mathbf{y},\mathbf{\theta })}\frac{\partial }{\partial \mathbf{\theta }}f(\mathbf{y},\mathbf{\theta })\right)]={\displaystyle \int }\hat{\mathbf{\theta }}\left(\frac{\partial }{\partial \mathbf{\theta }}f(\mathbf{y},\mathbf{\theta })\right)\mathrm{d}\mathbf{y}.$$ [A9]

Because the estimate θ̂ is not directly dependent on underlying parameters θ, the order of differentiation and integration can be reversed, leaving

$$\text{cov}\left(\hat{\mathbf{\theta }},\mathbf{v}\right)=\frac{\partial }{\partial \mathbf{\theta }}{\displaystyle \int }\hat{\mathbf{\theta }}f(\mathbf{y},\mathbf{\theta })\mathrm{d}\mathbf{y}=\frac{\partial \mathrm{E}[\hat{\mathbf{\theta }}]}{\partial \mathbf{\theta }}.$$ [A10]

Substituting [A10] into the multivariate Cauchy-Schwarz inequality results in a formal statement of the Cramér-Rao bound:

$$\text{cov}\left(\hat{\mathbf{\theta }}\right)\ge \text{cov}\left(\hat{\mathbf{\theta }},\mathbf{v}\right)\text{cov}{\left(\mathbf{v}\right)}^{-1}\text{cov}{\left(\hat{\mathbf{\theta }},\mathbf{v}\right)}^T\ge \frac{\partial \mathrm{E}[\hat{\mathbf{\theta }}]}{\partial \mathbf{\theta }}{\left[{\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}\right]}^{-1}\frac{\partial \mathrm{E}{[\hat{\mathbf{\theta }}]}^T}{\partial \mathbf{\theta }}.$$ [A11]

Note that [A11] states that the distribution of an estimate is inversely proportional to the model’s squared sensitivity to the estimated parameter, which is a generalization of the well-known propagation of error theorem to a possibly biased set of estimates given multiple random points of data. In a further, potentially more significant parallel to the propagation of error theorem, the uncertainty in parameter estimates defined by the CRLB scales inversely with SNR.

Due to the fact that the FIM is purely a function of the true signal and noise variance, information content is unaffected by the choice of estimator. Thus, information is conserved even when the contrast of the estimate is enhanced; the multiplication by ∂E[θ̂]/∂θ causes biased estimates which enjoy greater contrast than their unbiased counterparts to receive a proportional penalty to random deviation. Only by constraining covarying parameters to a priori values and eliminating their respective elements from the FIM before inverting—or by decreasing the problem dimensionality in any similar manner—can estimate precision truly be improved. Stated mathematically, the conditional covariance matrix of the parameters remaining unconstrained is the Schur complement of the covariance matrix block pertaining to the constrained parameters (36):

$$\text{cov}\left({\hat{\mathbf{\theta }}}_{\text{free}}\right)\ge \frac{\partial \mathrm{E}[{\hat{\mathbf{\theta }}}_{\text{free}}]}{\partial {\mathbf{\theta }}_{\text{free}}}\left[{\mathbf{\Sigma }}_{\text{free}}-{\mathbf{\Sigma }}_{\mathrm{f},\mathrm{c}}\left({\mathbf{\Sigma }}_{\text{cons}}^{-1}\right){\mathbf{\Sigma }}_{\mathrm{c},\mathrm{f}}\right]\frac{\partial \mathrm{E}{[{\hat{\mathbf{\theta }}}_{\text{free}}]}^T}{\partial {\mathbf{\theta }}_{\text{free}}}$$ [A12]

where

$$\text{cov}\left(\hat{\mathbf{\theta }}\right)\ge {\left[{\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}\right]}^{-1}=\left[\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{\text{cons}}\hfill & \hfill {\mathbf{\Sigma }}_{\mathrm{c},\mathrm{f}}\hfill \\ \hfill {\mathbf{\Sigma }}_{\mathrm{f},\mathrm{c}}\hfill & \hfill {\mathbf{\Sigma }}_{\text{free}}\hfill \end{array}\right]$$ [A13]

and

$$\hat{\mathbf{\theta }}=\left[\begin{array}{c}\hfill {\hat{\mathbf{\theta }}}_{\text{cons}}\hfill \\ \hfill {\hat{\mathbf{\theta }}}_{\text{free}}\hfill \end{array}\right],$$

where subscripts “free” and “cons” refer to the freely fitted and constrained parameters. These equations imply that the uncertainty in free parameter estimates is reduced according to the free parameters’ squared covariance with constrained parameters (Σ_f,c).