Integrating Prior Knowledge in Multiple Testing under Dependence with Applications to Detecting Differential DNA Methylation

Summary

DNA methylation has emerged as an important hallmark of epigenetics. Numerous platforms including tiling arrays and next generation sequencing, and experimental protocols are available for profiling DNA methylation. Similar to other tiling array data, DNA methylation data shares the characteristics of inherent correlation structure among nearby probes. However, unlike gene expression or protein DNA binding data, the varying CpG density which gives rise to CpG island, shore and shelf definition provides exogenous information in detecting differential methylation. This paper aims to introduce a robust testing and probe ranking procedure based on a non-homogeneous hidden Markov model that incorporates the above-mentioned features for detecting differential methylation. We revisit the seminal work of Sun and Cai (2009, J. R. Stat. Soc. B. 71, 393-424) and propose modeling the non-null using a non-parametric symmetric distribution in two-sided hypothesis testing. We show that this model improves probe ranking and is robust to model misspecification based on extensive simulation studies. We further illustrate that our proposed framework achieves good operating characteristics as compared to commonly used methods in real DNA methylation data that aims to detect differential methylation sites.

1. Introduction

The field of epigenetics is an emerging area of research and has reshaped a new genetics paradigm. One of the best known epigenetic marks is DNA methylation which plays a critical role in regulating gene expression in various cellular processes, including embryonic development, genomic imprinting, X-chromosome inactivation, and chromosome stability (Esteller, 2008; Robertson, 2005). DNA methylation occurs at the cytosine bases and involves the addition of a methyl group by DNA methyltransferase (DNMT) enzymes. The modified cytosine bases are usually immediately adjacent to a guanine base (i.e. the CpG dinucleotides) and results in the inaccessibility of transcription factors to these regions. An increasing number of diseases has been shown to be associated with aberrant DNA methylation (Robertson, 2005). The CpG island hypermethylation of tumor suppressor genes has been established as a common mechanism of gene inactivation in cancer. In contrast, global hypomethylation which leads to genomic instability has also been recognized as an important contributor to tumorigenesis (Esteller, 2008).

In the last few years, there is a great interest in genome-wide DNA methylation profiling. Several platforms are available for DNA methylation profiling, including the high-throughput arrays and more recently, the next generation sequencing instruments. Prior to hybridization or sequencing, a variety of experimental techniques are available for treating methylated DNA. The three main categories are bisulfite conversion-based methods, restriction enzyme-based methods and immunoprecipitation-based methods (see Laird (2010) for complete review). As the technology improves, a common characteristic shared by these platforms is the high resolution genome-wide coverage of the CpG loci. For example, the new Illumina Infinium HumanMethylation450 BeadChip for typing the bisulfite converted DNA interrogates more than 450,000 CpG loci which encompasses > 96% of RefSeq genes (Sandoval et al., 2011). On the other hand, the CHARM array (Irizarry et al., 2008) based on restriction enzyme digestion covers approximately 2.1 M probes genome-wide.

DNA methylation analysis is usually carried out to identify differential methylated probes or regions. As thousands to millions of probes are involved, this falls within the context of large-scale multiple testing. In this article, we introduce an inference framework that incorporates exogenous information including array design and genomic annotation for improving detection of differential methylation sites. Our work can be viewed as a more flexible version of the seminal work by Sun and Cai (2009). We extend the modeling framework of Sun and Cai (2009) to allow for exogenous information to be incorporated systematically and address several practical issues such as the choice of non-null distribution. We begin by describing several distinct features of DNA methylation data which motivates the choice of our modeling framework in Section 2. Section 3 describes our proposed framework. We show that the proposed framework improves the detection and outperforms other existing methods in extensive simulations (Section 4) and case studies (Section 5) which include two different platforms (the CHARM array (Irizarry et al., 2008) based on restriction enzyme digestion and Infinium HumanMethylation450 Array based on bisulfite conversion). Although our model is developed using DNA methylation as our motivating dataset, the proposed framework is general and readily applicable to other datasets involving large-scale testing under dependence. We conclude with a discussion in Section 6.

2. Motivation

The study of DNA methylation has previously been focused and restricted to CpG islands, i.e, genomic regions that contain high frequency of CG dinucleotides. However, recent work has demonstrated that most tissue and cancer specific methylation alterations occur in sequences up to 2 kb distant from CpG islands known as the CpG island shores (Irizarry et al., 2009; Doi et al., 2009). Several array platforms have been designed to provide unbiased whole genome coverage of DNA methylation profiles. For instance, both the CHARM array (Irizarry et al., 2008) and Infinium HumanMethylation450 BeadChip interrogate not only CpG islands but also CpG island shores (within 2 kb from CpG islands), shelves (>2 kb from CpG islands) and flanking regions, thus offering a comprehensive view of methylation on all designable RefSeq genes. An additional feature of the Infinium HumanMethylation450 BeadChip is the utilization of two different assay chemistry technology, namely Infinium I and Infinium II primer extension assays (Sandoval et al., 2011). A major difference between these two assays is in the number of bead types used to probe each CpG locus. In Infinium I assays, two separate bead types are used to measure methylated and unmethylated states whereas Infinium II assays rely on one bead type and distinguish methylated from unmethylated states based on single base extension. Infinium I assays cover one third of the total number of CpG loci and is designed for regions with more CG dinucleotides. More than 70 % of Infinium I probes lie in CpG islands. On the other hand, approximately 35 %, 45% and 20 % of Infinium II probes belong to CpG islands, shores and shelves, respectively. This suggests inherent difference in the quality of DNA methylation measured by these two assays.

A common goal of DNA methylation profiling is in identifying differential methylated sites (Irizarry et al., 2009; Doi et al., 2009). Without loss of generality, suppose that we are in the setting of testing for differential methylation between conditions 1 and 2. Similar to gene expression analysis, popular test statistics for summarizing the methylation difference between the two conditions at each CpG locus/probe include the t-statistic or the non-parametric Mann-Whitney U statistic. The most commonly used method usually proceeds to identify significantly differential methylated loci by controlling for the Benjamini Hochberg False Discovery Rate (BH-FDR) (Benjamini and Hochberg, 1995) under the assumption that the CpG loci are independent. However, in array based methylation platforms, the location of the CpG loci along the genome induce a natural dependence structure. The spacing between two consecutive CpG loci in Infinium HumanMethylation450 BeadChip varies with median distance of approximately 300 bps. As a comparison, the CHARM array (Irizarry et al., 2008) covers 2.1 M probes genome-wide with median distance of 37 bps between two probes. Figure 1 show the autocorrelation plot of the probe-wise t-statistic on Chromosome 1 for both the CHARM and Infinium platform, which demonstrate the presence of substantial spatial correlations among nearby CpG loci. In addition, the correlation is stronger in the CHARM array consistent with the smaller probe spacing in this platform. It is therefore imperative to incorporate the observed correlation structure in the hypothesis testing framework for declaring significantly differential methylated CpG loci. In the next section, we described our proposed framework that accounts for probe dependence.

Figure 1.

Autocorrelation plot on CHARM array and Infinium HumanMethylation450 BeadChip in Chromosome 1. The t-statistics for the CHARM array correspond to the comparison between normal brain versus liver, normal liver versus spleen and colon tumor versus normal, respectively. The plot for normal brain versus spleen exhibits similar patterns and is not shown. The t-statistics for the Infinium array correspond to the comparison between mutant versus wildtype tumors.

3. A non-homogeneous HMM based FDR control

We briefly review some definitions in multiple testing framework. We follow the notations of Genovese and Wasserman (2002). Suppose that we have m tests (here each test corresponds to a CpG locus), where m₀ of them are are null (not differential methylated) and m₁ are non-null (differential methylated). The possible outcomes of a multiple-testing framework is summarized in Web Table 1. The FDR is defined as E(N_1|0/R|R > 0)P (R > 0), whereas the false non-discovery rate FNR is defined as E(N_0|1/S|S > 0)P (S > 0) (Genovese and Wasserman, 2002; Sun and Cai, 2009), where R (S) is the number of rejected (not rejected) tests and N_1|0 (N_0|1) is the number of false rejection (non-rejection). A multiple hypothesis procedure is said to be valid if it controls the FDR at the pre-specified nominal α level, and optimal if it has the smallest FNR among all FDR procedures at level α. Although BH-FDR procedure controls the FDR at the nominal level under various dependence structure, it has been shown to be suboptimal and inefficient (Sun and Cai, 2009). Recently, Sun and Cai (2009) introduced a Hidden Markov Model (HMM) based approach that incorporates the dependence structure in the multiple testing framework. They showed that the HMM based method is optimal when the HMM parameters are known. In the case where the parameters are unknown, this procedure is asymptotically optimal by plugging in the consistent estimates. We extend the work of Sun and Cai (2009) to allow for a more flexible model structure and introduce an inference procedure for DNA methylation data based on a non-homogeneous HMM (NHMM) framework, which utilizes informative features observed in the methylation array platforms.

3.1 Incorporating informative features in transition probabilities

Without loss of generality, we consider a z-score transformation to the differential methylation test statistics. Let Z_j = Φ⁻¹(F_fdj(t_j)),, where F_dfj is the cumulative distribution function (cdf) of a standard t variable with df_j degrees of freedom, and Φ is the standard Gaussian cdf. Following the notation of Sun and Cai (2009), let θ_j be the unobserved state of CpG locus j, where θ_j = 1 if CpG locus j is non-null, i.e., differential methylation between conditions 1 and 2 and θ_j = 0 otherwise. The testing framework of Sun and Cai (2009) was based on a homogeneous HMM with stationary transition probabilities. However, in DNA methylation arrays, there are several factors that could potentially give rise to non-stationary transition probabilities. For example, given the varying spacing between two adjacent loci, we expect the dependence to decrease with larger distances. In addition, as mentioned in Section 2, Infinium HumanMethylation450 BeadChip utilizes two different primer extension assays (Infinium I and II) for probing methylation levels. The inherent difference in the chemistry of Infinium I and II assays and the genomic regions covered by these assays, i.e., Infinium I mostly in CpG islands, could play a role in the hidden state transition. Irizarry et al. (2009) showed that stronger pattern of methylation perturbation in colon cancer occur in CpG island shores compared to CpG islands. Taken together, all these observations implies that we might benefit from considering possible factors arising from array design and genomic annotations that affect the transition probabilities to improve the multiple testing framework.

To address the potential non-stationary transition probabilities, we model the hidden state transition via a logistic regression:

$$\begin{array}{l}{\pi }_s(\mathit{x})=P({\theta }_1=s\mid {\mathit{X}}_1=\mathit{x})=\frac{exp({\lambda }_s+{\mathit{\rho }}_s^t\mathit{x})}{{\sum }_{s=0}^{1}exp({\lambda }_s+{\mathit{\rho }}_s^t\mathit{x})},\\ a_{rs}(\mathit{x})=P({\theta }_j=s\mid {\theta }_{j-1}=r,{\mathit{X}}_j=\mathit{x})=\frac{exp({\sigma }_{rs}+{\mathit{\rho }}_s^t\mathit{x})}{{\sum }_{s=0}^{1}exp({\sigma }_{rs}+{\mathit{\rho }}_s^t\mathit{x})},\text{for}j\ge 2,\end{array}$$

where λ_s, σ_rs ∈ ℝ and ρ_s ∈ ℝ^D. Here X_j denotes a matrix of D columns with candidate covariates including probe spacing, assay type and genomic annotations. When X_j includes probe spacing, certain restriction is imposed on the coefficient ρ_s to ensure that probabilities of self transition decrease with probe spacing. Details are given in Web Appendix A.2.

We assume that Z_j’s are conditionally independent given θ_j, where Z_j|θ_j = s ~ f_s(Z_j). Since Z_j’s are z-score transformed test statistics, f₀(Z_j) ~ N (0, 1). We defer the discussion on the choice of non-null distribution f₁ to Section 3.2. This gives rise to a non-homogeneous HMM (NHMM). NHMM with the logistic regression transition has been shown to be a useful framework in climate research (Robertson et al., 2004).

Inference for significantly differential methylated CpG loci is based on the local index of significance, LIS introduced in Sun and Cai (2009),

$${\text{LIS}}_j=P({\theta }_j=0\mid \mathit{Z},\mathit{X})$$

where Z is the vector of Z_j’s. Let LIS₍₁₎, …, LIS_(J) be the ranked LIS values and H₍₁₎, …, H_(J) be the corresponding hypotheses. We reject all H_(i), i = 1, …, k, where $k=max\left\{i:1/i{\sum }_{j=1}^i{\text{LIS}}_{(j)}(z)\le \alpha \right\}$. Sun and Cai (2009) showed that the testing procedure based on LIS produces more efficient rankings of the hypotheses than the traditional p-values and results in optimal testing procedure.

For computational efficiency, the model is trained on individual chromosomes in estimating the unknown parameters and computing the LIS statistics. One possible approach to combine the analyses from different chromosomes is to apply LIS procedure to each chromosome at a pre-specified FDR level, followed by aggregating the list of significant LIS from each chromosome. This is also known as the separate analysis proposed by Efron (2008). However, Wei et al. (2009) showed that the separate analysis is sub-optimal, i.e., this procedure does not yield the smallest FNR. Instead of first declaring significant tests at chromosomal level, they suggested pooling the LIS statistics across all chromosomes and apply the FDR control to these pooled LIS statistics. Therefore, in our proposed NHMM-FDR approach, we aggregate the LIS statistics from all chromosomes and rank them genome-wide in declaring statistically significant CpG loci. The estimation of the unknown parameters in the NHMM-FDR procedure is given in Web Appendix A.1.

3.2 Choice of non-null model f₁

The HMM framework of Sun and Cai (2009) and our proposed NHMM model require the specification of the non-null distribution f₁. Sun and Cai (2009) modeled f₁ using Gaussian mixtures, i.e., $f_1={\sum }_{l=1}^L{c}_{l}N({\mu }_l,{\sigma }_l^2)$. Although Gaussian mixtures is fiexible for various functions approximation, the number of mixture components L is unknown. Sun and Cai (2009) suggested choosing appropriate L based on Bayesian Information Criterion (BIC). This requires one to run the HMM for each possible L which can be computationally intensive. We propose approximating the non-null f₁ using non-parametric Gaussian kernel density estimation, i.e., $f_1=1/n{\sum }_{j=1}^n{K}_h(Z-Z_j)$ where K_h(.) is the kernel and h is the bandwidth. One could argue that kernel density estimation also requires the tuning of the bandwidth h, analog to L in Gaussian mixtures. However, as we illustrate in simulation studies in Section 4, the rule-of-thumb method of Silverman (1986) for setting the bandwidth as h = 0.9 min(σ, IQR/1.34)n^−1/5 is generally sufficient and works well in practice. Here n is the total number of loci, σ is the sample standard deviation and IQR is the interquartile range.

A subtle issue that we would like to raise here is in the context of two-sided hypothesis testing. For instance, suppose that H₀: μ = 0 and H₁: μ ≠ 0, and our test statistics is the z-score Z_j. Common methods based on p-values ranking such as BH-FDR control provide equal statistical significance to both Z_j = z and Z_j = −z. However, in the HMM framework of Sun and Cai (2009), the LIS values P(θ_j = 0|Z = z, X) is not necessary equal to P(θ_j = 0|Z = −z, X) depending on f₁. In the ideal scenario where the underlying data is generated from a Markov model, approximating f₁ as Gaussian mixtures or Gaussian kernel density estimates performs well. However, when the correlation structure among the tests is non-Markovian, we show that restricting the non-null f₁ to be a symmetric distribution is more robust and improves the probe ranking in both simulations and case studies. In some extreme cases where we have skewed non-null f₁ with fewer negative valued test statistics, the unrestricted estimated non-null f₁ from Gaussian mixtures may only be capturing positive mean values. In such cases, probes with large negative test statistics could be ranked lower among the list of probes. Therefore, using a symmetric non-null may be preferred as it yields a more straightforward interpretation by allowing for positive or negative deviation from H₀ to carry comparable statistical significance.

In the next section, we first evaluate the performance of our proposed NHMM-FDR control as compared to HMM and other commonly procedures in a simulation study. We then assess the performance of HMM based methods for the different choices of non-null f₁ under both the Markov data generator as well as under model misspecification. Subsequently, we revisit these issues and implement our proposed method in real DNA methylation data in Section 5.

4. Simulation studies

4.1 HMM with non-stationary transition probabilities

In this section, we carry out simulation studies to investigate the numerical performance of our proposed NHMM-FDR procedure in DNA methylation data. In Infinium Human-Methylation450 BeadChip, the median number of probes per chromosome is approximately 21,000. To mimic the real data, we use CpG annotation (Island, Shore, Shelf, None) and inter-probe distance information from 20,000 consecutive probes in our simulation. We vary the parameters λ_s, σ_rs ∈ ℝ and ρ_s ∈ ℝ^D in the non-homogeneous transition probabilities to obtain overall non-null proportions of 0.05, 0.10 and 0.2. The observations Z_j’s are generated from Gaussian distribution, i.e., Z_j|θ_j ~ (1 − θ_j)N (0, 1) + θ_jN (μ_k, 1). Similar to Sun and Cai (2009); Wei et al. (2009), we vary μ_k from 1 to 4 in increments of 0.5. We compare the performance of Benjamini Hochberg FDR (BH) (Benjamini and Hochberg, 1995) and Efron’s local FDR (locfdr) (Efron, 2004) to our proposed NHMM-FDR. “locfdr” is a special case of LIS when all the tests are independent. However, “locfdr” estimates the mixture emission distribution using either a natural spline or a polynomial and the proportion of null is then estimated from the central histogram counts of the empirical mixture density under the assumption that the central peak of the empirical density consists mainly of null cases. Therefore, we also include the results where the parameters in the emission distribution are estimated from the EM algorithm as a comparison to the spline/polynomial version of “locfdr”. We denote this procedure as “Indep”. To assess the extent of non-stationarity in the transition probabilities in affecting the multiple testing procedure, we also compare the performance of the original LIS procedure of Sun and Cai (2009). We denote this procedure as “HMM”. Each simulation scenario is repeated 100 times and we consider nominal FDR level of 0.10.

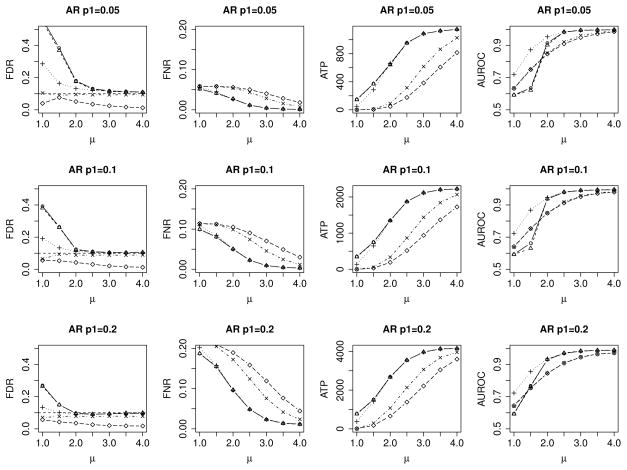
Figure 2 compare the average empirical FDR, FNR and average number of true positives ATP for the different methods at nominal FDR of 0.10, respectively. The “BH”, “Indep” and “locfdr” procedures are controlled at the nominal FDR (top row of Figure 2). Our proposed method “NHMM” attains the nominal FDR except for the case where μ_k = 1 and the non-null proportion p₁ is 0.05, i.e., low signal to noise ratio. In this particular case, we see inflated empirical FDR because in some iterations, “NHMM” only declared 1 CpG to be significant which happens to be false positive and resulting in empirical FDR of 1.00. On the other hand, “HMM” procedure generally yield inflated empirical FDR in most scenarios because the non-stationarity results in inaccurate estimation of the transition probabilities.

Figure 2.

Average empirical FDR, FNR, ATP and AUROC for various signal levels μ_k at nominal FDR of 0.10. Column 1 compares the empirical FDR versus μ_k. Column 2 compares the empirical FNR versus μ_k. Column 3 compares the ATP versus μ_k. Column 4 compares the AUROC versus μ_k. Rows 1, 2 and 3 correspond to non-null proportion of 0.05, 0.1 and 0.2, respectively. NHMM (○), HMM (△), Indep (+), BH (×) and locfdr (◇).

Column 2 of Figure 2 also shows that “NHMM” procedure results smallest FNR among all methods. In addition, “NHMM” also yields the largest ATP compared to other methods as given in Column 3 of Figure 2. Finally, we also compare the sensitivity and specificity of the different procedures. In Column 4 of Figure 2, we compare the average area under Receiver Operating Characteristics curves (AUROC). As evident from this figure, “NHMM” outperforms all other methods especially in cases when the signals μ_k is small with more efficient probe ranking.

4.2 Gaussian mixtures versus kernel density estimates

4.2.1 HMM with Gaussian mixture f₁

Sun and Cai (2009) showed that if LIS procedure is robust against misspecified number of mixture components. In this simulation, we follow the simulation setting in Section 4.3.1 of Sun and Cai (2009) for 20,000 probes to evaluate the performance of approximating f₁ with a kernel density estimate (with rule-of-thumb bandwidth described in Section 3.2) which is computationally more efficient than fitting f₁ with a Gaussian mixtures that requires one to run the algorithm multiple times with varying L.

Following Sun and Cai (2009), we simulate from a two-state HMM with null N(0, 1) and non-null from a three-component normal mixture 0.4N(μ, 1) + 0.3N(1, 1) + 0.3N(3, 1) but misspecify f₁ with a two-component model. The transition probability matrix is taken to be a₀₀ = 0.95 and a₁₁, where we vary a₁₁ between 0.2 and 0.8. In addition, we also vary μ_k from −4 to −1 in increments of 0.5. We also fit a HMM model with f₁ approximated using Gaussian kernel density estimate described above. In top (middle) row of Web Figure 2, we choose μ = −2 (a₁₁ = 0.8) and compare the empirical FDR, FNR, ATP and AUROC as a function of a₁₁ (μ). We report the average run time in Web Table 2, which demonstrates the computational savings of using kernel density estimate. The performance of HMM using either misspecified Gaussian mixtures or kernel density estimate with rule-of-thumb bandwidth is comparable and outperforms “BH” and “locfdr”.

4.2.2 HMM with non-parametric empirical f₁

Next, we consider simulating the data using a non-parametric f₁ estimated from the CHARM colon tumor versus normal of Irizarry et al. (2009). Specifically, we utilize the locfdr package of Efron (2004) to obtain the estimated f₁ as shown in Web Figure 3. Similar to above, we compare the empirical FDR, FNR, ATP and AUROC as a function of a₁₁ in the bottom row of Web Figure 2 at nominal FDR of 0.10. For the HMM method where we assume f₁ is a Gaussian mixture, we vary L from 1 to 5 and use BIC to select the best L. The empirical FDR levels for all methods are still acceptable, although they appear to be more variable. It is interesting to note that at small a₁₁ values, the HMM method with f₁ estimated from kernel density estimate outperforms the HMM method with Gaussian mixture f₁ in terms of AUROC, i.e., more efficient probe ranking in this particular simulation setup.

4.2.3 Autoregressive model

In this section, we consider an autoregressive (AR) model instead of a HMM to induce dependence among the probes. We first simulate an AR process of order 3, Z_j = 0.3Z_j−1 −0.1Z_j−2 +0.1Z_j−3 +ε_j. Since nearby or consecutive probes generally exhibit similar differential methylation patterns, we mimic this observation by randomly choosing segments of probes with size generated from Poisson(5)+1 to be non-null. For each segment of non-null (differential methylated probes), we consider a loaded coin toss with probability 0.6 of getting a head. If the toss shows a head (tail), we add μ (−μ) to all the Z_j’s within this segment. We vary the proportion of non-null p₁ from 0.05 to 0.2, and μ_k from 1 to 4. We evaluate the performance of HMM method under this misspecified correlation structure. In addition, we also fit HMM with symmetric kernel density f₁ to the simulated data. Similar to Section 4.2.2, we vary L from 1 to 5 for the HMM method where we assume f₁ is a Gaussian mixture and select the best L using BIC. We compare the empirical FDR, FNR, ATP and AUROC as a function of μ_k in Figure 3.

Figure 3.

Average empirical FDR, FNR, ATP and AUROC for various signal levels μ_k at nominal FDR of 0.10. Column 1 compares the empirical FDR versus μ_k. Column 2 compares the empirical FNR versus μ_k. Column 3 compares the ATP versus μ_k. Column 4 compares the AUROC versus μ_k. Rows 1, 2 and 3 correspond to non-null proportion of 0.05, 0.1 and 0.2, respectively. HMM-kernel density estimate (○), HMM-Gaussian mixtures (△), HMM-symmetric kernel density estimate (+), BH (×) and locfdr (◇).

For small μ_k values, i.e., low signal, the FDR control for the HMM methods is inflated under the underlying true AR model. However, the degree of inflation is reduced when we model the non-null f₁ using a symmetric kernel density estimate, despite simulating from an asymmetric true non-null as described above. It is also interesting to note that for this simulation setup, the HMM model with symmetric kernel density estimate results in the most efficient probe ranking as given by the highest AUROC across the range of μ_k and p₁. This illustrates that in cases where the underlying dependence structure is non-Markovian, the FDR control using HMM models can be inaccurate when the signal is weak. However, the HMM models still result in more efficient probe ranking compared to the model under independence assumption, as the Markovian structure attempts to account for the observed correlation among the probes.

5. Case studies

We apply our proposed NHMM based FDR procedure to two DNA methylation datasets. The first dataset is the methylation data of Irizarry et al. (2009) performed on the CHARM array (Irizarry et al., 2008) which is publicly available from the Gene Expression Omnibus under accession number GSE23841. This dataset consists of quantile normalized normal brain, liver and spleen tissues, as well as colon tumor and normal tissues in 5 replicates. Following Irizarry et al. (2009), we consider these pairwise comparisons to detect differential methylated CpG loci, i.e., colon tumor versus normal, brain versus liver, brain versus spleen and liver versus spleen. For expository purposes, we analyze the subset of colon tumor versus normal. The second dataset is the methylation dataset (unpublished) generated by the Chiang Lab at University of North Carolina-Chapel Hill which encompasses 10 mutant and 20 wildtype tumor samples performed on Infinium HumanMethylation450 BeadChip. The objective is to identify differential methylated CpG loci between mutant and wildtype samples. For both datasets, we compute probe specific t-statistics on logit transformed percent methylation values, followed by z-score transformation.

We consider both the Gaussian mixtures and non-parametric kernel density estimates for the non-null. Since the hypothesis of interest is two-sided in these case studies, i.e., detecting both hyper- and hypo-methylated sites, we also consider fitting a symmetric kernel density non-null as described in Section 3.2. For Gaussian mixtures non-null, we choose appropriate L based on BIC. We consider L = 1, 2 and 3. For computational efficiency, we estimate the model parameters for “HMM” and “NHMM” by chromosomes, and allow for L to vary within each chromosome. We then combine the estimated LIS and apply FDR thresholding to the pooled LIS to obtain optimal genome-wide FDR control. Similar to Section 4, we compare the performance of NHMM, HMM, Indep, BH and locfdr.

5.1 Tissue differential methylation in CHARM array

We annotate each probe according to the CpG islands track information downloaded from UCSC (Gardenia-Garden and Frommer, 1987). We define “Shore” as regions within 2 kb of CpG islands and “Shelf” as flanking regions within 2kb of “Shore” (i.e, between 2 to 4 bp of CpG islands). In addition, we also compute the percentage of CpG dinucleotides and GC content within a window of 200 bps at each probe. For the NHMM model, we model the transition probabilities using inter-probe distance (Dist), CpG annotation (Annot), GC content (GC) and CpG content (CpG) as covariates and compare the goodness of fit for each model using BIC. The inter-probe distance is log transformed for numerical stability (Web Appendix A.2). Since our aim is to assess if the inclusion of additional covariates in the NHMM transition probabilities improves the model fit, and there is no straightforward way to define the effective number of parameters in kernel density estimation, we only penalize for the number of parameters in the transition probabilities in BIC calculation.

Table 1(A) compares the model fit via BIC scores for the different non-null for the comparison between colon tumor and normal samples. “NHMM: X” and “NHMM: X+Y” refer to NHMM models with X_j = (X_j) and X_j = (X_j, Y_j) in the transition probabilities, respectively, where X, Y=(Annot, Dist, CpG, GC). Since Annot, CpG and GC are correlated, we do not include these covariates simultaneously in the model to avoid multicollinearity. Within each non-null type, both HMM and NHMM improve the model fit compared to the model by assuming probe independence. In addition, there is also gain in the model for “NHMM: GC” compared to regular HMM, suggesting that GC content is informative in parametrizing the transition probabilities. However, inter-probe distance does not appear to provide much improvement to the model fit, since the vast majority of the probes (> 90%) have almost constant spacing, i.e., between 30 and 40 bps.

Table 1.

Model comparisons based on BIC and AUROC for differential methylation between (A) colon tumor and normal, (B) mutant and wildtype.

	(A) CHARM array: Tumor vs Normal
Model	Gaussian Mix		Kernel		Symmetric Kernel
	BIC	ROC	BIC	ROC	BIC	ROC
Indep	6255209	0.736	6253765	0.762	6267078	0.798
HMM	6034529	0.589	6032994	0.609	6115280	0.935
NHMM: Annot	6033897	0.572	6038521	0.620	6114225	0.935
NHMM: Dist	6030418	0.585	6036719	0.620	6116526	0.923
NHMM: CpG	6033151	0.591	6031488	0.610	6113411	0.936
NHMM: GC	6031330	0.571	6027941	0.612	6111181	0.936
NHMM: Dist+Annot	6036219	0.593	6059388	0.626	6154113	0.867
NHMM: Dist+CpG	6029085	0.585	6077415	0.669	6128384	0.902
NHMM: Dist+GC	6027936	0.571	6037543	0.622	6115147	0.922
BH		0.823
locfdr		0.763

(B) Infinium 450K array: Mutant vs Wildtype
Model	Gaussian Mix	Kernel	Symmetric Kernel
	BIC	BIC	BIC
Indep	1711200	1709446	1837982
HMM	1633735	1632363	1778867
NHMM: Annot	1632220	1630790	1775630
NHMM: Assay	1633350	1631917	1776883
NHMM: Dist	1625176	1623628	1764338
NHMM: CpG	1632316	1630918	1774458
NHMM: GC	1633613	1632222	1777564
NHMM: Dist+Annot	1623574	1622009	1762342
NHMM: Dist+CpG	1624100	1622709	1774413
NHMM: Dist+GC	1625293	1623703	1764196

Irizarry et al. (2009) reported a list of significantly differential methylated regions at FDR of 0.05 as follows. First, they computed the z-scores as ΔM/s.e.m(ΔM) and the corresponding p-values, where ΔM is the difference of averaged methylation values and s.e.m. is the probe specific standard errors for ΔM. Next, contiguous regions of probes with p-values <0.001 were grouped into regions. Significance tests were performed on areas of each region (Bullmore et al., 1999) and statistically significant areas were identified via permutation test and empirical Bayes approach (Efron et al., 2001). Their strategy in identifying differential methylated regions is another way to account for the correlation structure among nearby probes. Using this list of differential methylated regions as gold standard, we compare the sensitivities and specificities of the competing methods, i.e., NHMM, HMM, Indep, BH and locfdr, and summarize the results in terms of AUROC in Table 1(A). The models with Gaussian mixtures and kernel density non-null result in poor AUROC. On the other hand, when we restrict the non-null f₁ to be a symmetric kernel density, the AUROC increases drastically for HMM and NHMM methods, and outperforms Indep, BH and locfdr. The possible explanation for this observation is that the underlying correlation structure may not be Markovian based from our simulation in Section 4.2.3. However, using the LIS obtained from HMM or NHMM framework improves the probe rankings compared to the usual p-values ranking given by the BH method which ignores the correlation structure.

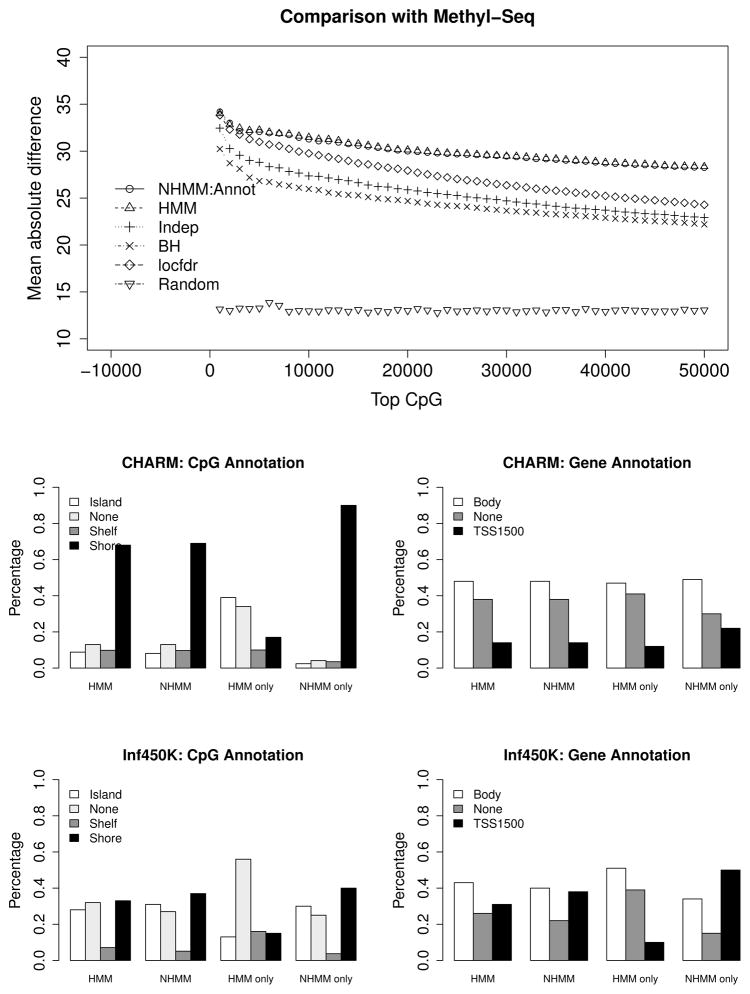
To further validate the results obtained from the different methods, we download an independent whole genome bisulfite Methyl-Seq data from the Gene Expression Omnibus under accession number GSE32399 which consists of a Stage 3, CIMP-H colon tumor and an adjacent normal colonic mucosa. We compute the average Methyl-Seq differential methylation between tumor and normal for the subset of CpG’s that maps to each probe in the CHARM array. For each of the NHMM (we use NHMM: Annot for expository purposes), HMM, Indep, BH and locfdr method under symmetric kernel density above, we obtain the top X CHARM probes ranked by each method and compute the mean absolute Methyl-Seq difference, where X varies from 1000 to 50000. A more reliable method will yield larger mean absolute Methyl-Seq difference, i.e., larger difference in magnitude between colon tumor and normal. Top panel of Figure 4 plots the mean absolute Methyl-Seq difference for the top X probes ranked ordered within each method. Both the NHMM and HMM method result in more superior probe ranking as the mean absolute difference between colon tumor and normal on this independent Methyl-Seq data is uniformly larger than the other methods, followed by locfdr, Indep and BH. We also provide the mean absolute difference for a randomly chosen subset of X probes (given by the inverted triangles), which is much lower than all the methods. This indicates that the Methyl-Seq data is comparable to the CHARM array data (which supports its usage as a validation data) and all the methods are identifying meaningful set of differential methylated probes in the CHARM array.

Figure 4.

Top panel compares the mean absolute differential methylation between tumor and normal in an independent Methyl-Seq data. Probes are ranked ordered within each method. Middle left (right) panel compares the CpG annotation (gene annotation) of the top 5% probes ranked by “HMM” and “NHMM: Annot” on the CHARM array. “HMM only” and “NHMM only” refer to the probes unique to “HMM” and “NHMM: Annot”, respectively. Bottom panels are similar to middle panels, which compares the results of the top 5% probes ranked by “HMM” and “NHMM: Dist+Annot” on the Infinium HumanMethylation450 BeadChip.

Based on the validation results above, both the HMM and NHMM methods result in more efficient probe ranking compared to the models under independence assumption. To elucidate the subtle difference between NHMM and HMM, we compare the annotation of the top 5% probes ranked by each method. Middle left panel of Figure 4 displays the distribution of probes in CpG annotation (Island, Shelf, Shore, None) identified by HMM and NHMM, as well as the subset of probes unique to each method (labeled “HMM only” and “NHMM only”). Most of the probes unique to NHMM map to CpG Shore. Middle right panel of Figure 4 compares the distribution of the gene annotation of these probes, where “TSS1500” and “Body” refer to upstream 1.5 kb of transcription start site and transcription start to end, respectively. A higher proportion of the probes unique to NHMM map to TSS1500 compared to HMM.

5.2 Mutant vs wildtype in Infinium HumanMethylation450 BeadChip

We described and motivated the idea of modeling the transition probabilities using potential informative features such as CpG annotation, inter-probe distance, assay type, GC and CpG content in Section 3.1. Similar to Section 5.1, we evaluate the model fit of incorporating these features in our Infinium HumanMethylation450 BeadChip dataset from an experiment comparing 10 mutant and 20 wildtype tumor samples. In Table 1(B), we report the BIC scores for Indep, HMM and NHMM (with different combination of covariates in transition probabilities).

Within each non-null distribution, the first observation is that accounting for the dependence structure in HMM and NHMM improves the model fit significantly compared to treating each CpG as independent cases. Second, the NHMM fit is improved when probe spacing (Dist) is included in the model. In addition, incorporating CpG annotation, GC content or CpG content improves the model fit over HMM. The NHMM fit by incorporating the probe spacing and CpG annotation (“NHMM: Dist+Annot”) yield smaller BIC scores overall. Although assay type, CpG content, GC content and CpG annotation are associated, CpG annotation appears to be more informative in this data set. We further compare the annotation of the top 5% probes ranked by “HMM” and “NHMM: Dist+Annot”. Similar to Section 5.1, a higher proportion of probes unique to “NHMM” map to CpG Shore and TSS1500 regions.

6. Discussion

This paper presents a flexible framework for large-scale multiple testing under dependence. We extend the HMM framework of Sun and Cai (2009) to allow for incorporation of exogenous information which can improve the model fit based on a non-homogeneous hidden state transition. Although we use DNA methylation as our motivating dataset, our proposed framework is directly applicable to other types of genomic datasets including tiling array gene expression and SNP data. In the DNA methylation data, we study the inclusion of inter-probe distance, assay type and CpG information in the transition probabilities as a proof of principle to demonstrate the flexibility of a NHMM framework. We choose to model the hidden state transition using a logistic regression because it allows for other factors that could give rise to non-stationary transition probabilities to be included easily in the model. Our case studies suggest that CpG annotation and inter-probe distance are informative in modeling the transition probabilities.

In both the HMM and NHMM framework, we proposed modeling the non-null f₁ using a non-parametric kernel density estimate with rule-of-thumb bandwidth which is at least as flexible as Gaussian mixtures of Sun and Cai (2009) as shown in our simulation and case studies. Using a kernel density estimate with pre-specified bandwidth is computationally more efficient compared to Gaussian mixtures which requires one to run the algorithm multiple times with different candidate number of mixture components. We also discuss several reasons why we may want to restrict the non-null to be a symmetric distribution in two-sided hypothesis tests. Although HMM and NHMM are versatile framework for capturing correlation structure, the Markovian structure may not be valid in practice. We demonstrate that our proposed data driven NHMM procedure controls FDR and is superior when the underlying data generating mechanism is Markovian with non-stationary transition probabilities. However, when the underlying dependence structure is non-Markovian (e.g., an AR process), we show that using a Markov model with symmetric non-null is still robust and yields more efficient probe ranking in both the simulations and case studies. We acknowledge that the FDR control may be inaccurate if the underlying correlation structure deviates significantly from a Markov model. Other models that control for FDR under dependence (Leek and Storey, 2008; Friguet et al., 2009; Efron, 2010) could be explored and extended to incorporate exogenous information identified in this paper to improve detection of differential methylation.

In DNA methylation data and other types of genomic data, interesting events such as differential methylation usually involve contiguous probes which define a region. Our proposed NHMM model arise as a natural framework for capturing this regional effect. By integrating the genomic structure and array design in the model, this could lead to a better understanding of the DNA methylation patterns. Software implementing our proposed framework is available as an R package NHMMfdr at http://www.unc.edu/~pfkuan/softwares.htm