GPU-Accelerated Voxelwise Hepatic Perfusion Quantification

Abstract

Voxelwise quantification of hepatic perfusion parameters from dynamic contrast enhanced (DCE) imaging greatly contributes to assessment of liver function in response to radiation therapy. However, the efficiency of the estimation of hepatic perfusion parameters voxel-by-voxel in the whole liver using a dual-input single-compartment model requires substantial improvement for routine clinical applications. In this paper, we utilize the parallel computation power of a graphics processing unit (GPU) to accelerate the computation, while maintaining the same accuracy as the conventional method. Using CUDA-GPU, the hepatic perfusion computations over multiple voxels are run across the GPU blocks concurrently but independently. At each voxel, non-linear least squares fitting the time series of the liver DCE data to the compartmental model is distributed to multiple threads in a block, and the computations of different time points are performed simultaneously and synchronically. An efficient fast Fourier transform in a block is also developed for the convolution computation in the model. The GPU computations of the voxel-by-voxel hepatic perfusion images are compared with ones by the CPU using the simulated DCE data and the experimental DCE MR images from patients. The computation speed is improved by 30 times using a NVIDIA Tesla C2050 GPU compared to a 2.67 GHz Intel Xeon CPU processor. To obtain liver perfusion maps with 626400 voxels in a patient’s liver, it takes 0.9 min with the GPU-accelerated voxelwise computation, compared to 110 min with the CPU, while both methods result in perfusion parameters differences less than 10⁻⁶. The method will be useful for generating liver perfusion images in clinical settings.

1. Introduction

The liver has a dual-blood supply; one is from the hepatic artery and another from the portal vein. In the normal liver parenchyma, portal venous perfusion contributes to 70–80% of the total perfusion, and hepatic arterial perfusion about 20–30% (Chiandussi et al 1968). Diseases and tumors in the liver can alter both portal venous and hepatic arterial perfusion in the tissue (Hashimoto et al 2006, Leggett et al 1997, Van Beers et al 2001). Quantitative arterial and portal venous perfusion derived from dynamic contrast enhanced (DCE) imaging by fitting a pharmacokinetic model has shown clinical values for detection of hepatic cancers, diagnosis of liver cirrhosis and its severity, and assessment of therapy effectiveness(Thng et al 2010, Materne et al 2002, Goetti et al 2011). Recently, Cao et al. (Cao et al 2012, Cao et al 2007) show volumetric hepatic perfusion images derived from DCE-CT or DCE-MRI have the potential to assess global and spatial liver function change in response to radiation therapy. To quantify both arterial and hepatic venous perfusion, a dual-input single-compartment model is commonly used to fit the DCE data by minimizing a multivariable nonlinear least-squares (NLS) cost function (Dawson 2007, Materne et al 2002, Thng et al 2010). As MRI and CT technologies are advancing, it is possible to acquire volumetric liver DCE images with both high spatial and temporal resolutions. However, fitting the volumetric liver DCE images to the kinetic model voxel-by-voxel is very time consuming, which hinders utilization of the volumetric hepatic perfusion measurements in clinical applications.

Several studies have proposed computationally efficient methods to fit the liver DCE data to the pharmacokinetic model (Cao et al 2007, Hagiwara et al 2008, Materne et al 2002, Pandharipande et al 2005). The methods linearize the kinetic model by directly using either the derivative of the liver DCE time-concentration curve or the integrals of the two blood input functions, and then estimate the perfusion parameters by a linear least squares (LLS) fitting. Although the LLS methods speed up the perfusion estimation by up to 10 times compared with the conventional NLS method (Murase et al 2007), a LLS fitting can generate biased results even though the data noise is white (Feng et al 1996). Also, time delays of the contrast agent (CA) bolus arrival from the artery and portal vein to the liver parenchyma, which can have a great impact on the perfusion estimation (Miyazaki et al 2008), have been either ignored or only partially considered in the LLS models (Murase et al 2007, Cao et al 2006).

A graphics processing unit (GPU), originally designed for graphic rendering, possesses a great arithmetic capability, and is well suited for computationally-intensive, highly-parallelizable applications (Owens et al 2008). Recent advances in the GPU programming architecture have enabled GPU for a variety of computations in science and medicine (Jia et al 2011, Pratx and Xing 2011). Therefore, an alternative to accelerating voxelwise hepatic perfusion quantification is to utilize the GPU. In this paper, we implemented CUDA-based parallel computation to fit DCE MR images with the liver dual-input single-compartment model in order to estimate volumetric hepatic perfusion maps. Our parallel computation strategy can be generalized, and several components of our programs can be directly adopted for fitting DCE images to other pharmacokinetic models.

2. Methods and Materials

2.1. Pharmacokinetic Model of Hepatic Perfusion

Liver parenchyma receives a dual blood supply from the hepatic artery and the portal vein, and then it drains blood into the central vein. A dual-input single compartment model that is commonly used to describe the pharmacokinetics and fit DCE data is expressed as follows (Cao et al 2006, Materne et al 2002):

$$\frac{{d\overline{C}}_l(t)}{dt}=k_a{C}_a(t-{\tau }_a)+k_p{C}_p(t-{\tau }_p)-k_l{\overline{C}}_l(t)$$ (1)

where C_a and C_p are CA concentrations of respective artery and portal vein; C̄_l is the modeled CA concentration at liver parenchyma where the acquired CA concentration is denoted as C_l; k_a, k_p and k_l are arterial inflow, portal venous inflow and central venous outflow rate constants, respectively; and τ_a and τ_p are time delays of the CA bolus arrival from the artery and portal vein, respectively, to the parenchyma. The differential equation (1) is solved as:

$${\overline{C}}_l(t)=\underset{0}{\overset{t}{\int }}(k_a{C}_a(\tau -{\tau }_a)+k_p{C}_p(\tau -{\tau }_p))e^{-k_l(t-\tau )}d\tau =f(t)\otimes h(t)$$ (2)

where we denote f (t) = K_a C_a (t − τ_a) + k_p C_p (t − τ_p) and h(t) = e^−k_lt, and ⊗ is a convolution operator.

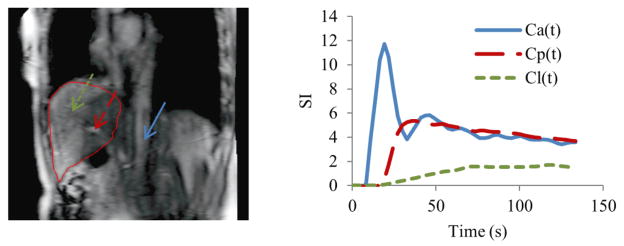
To estimate perfusion parameters k_a, k_p, k_l, τ_a and τ_p, time-concentration curves C_l, C_a and C_p are derived from DCE images (figure 1) and fitted to the kinetic model in equation (2) by minimizing a NLS cost function E between the acquired C_l and modeled C̄_l,

Figure 1.

Left: a sagittal MRI slice that covers VOIs to determine arterial input (C_a), portal venous input (C_p) and time-course signals of liver tissue (C_l). Right: time-concentration curves of C_a, C_p and C_l. Blue Arrow: aorta; red arrow: portal vein; green arrow: liver tissue.

$$E=\sum _{i=0}^{N_t-1}{(C_l(iT)-f(iT)\otimes h(iT))}^2$$ (3)

where T is a sampling time interval of DCE imaging, and N_t is a total number of time points acquired during dynamic imaging. The NLS minimization with respect to the five parameters (k_a, k_p, k_l, τ_a, τ_p) is commonly solved by the Nelder-Mead “Simplex” optimization algorithm (Lagarias et al 1998, Nelder and Mead 1965). The Simplex algorithm is an iterative optimization procedure that heuristically updates the solution according to the cost function values at the previous iterations. Given that in our study the number of voxels in the liver MR images of the patients with intrahepatic cancers is as large as 10⁶, it is very time consuming to estimate hepatic perfusion voxel-by-voxel throughout the whole liver.

2.2. GPU-Accelerated Perfusion Quantification

We aimed to accelerate volumetric hepatic perfusion quantification without compromising accuracy by using a GPU. To maximally utilize the GPU, computation should be structured to expose as much parallelization as possible (Owens et al 2008). Two types of computations in the volumetric DCE quantification can be parallelized: one is to simultaneously estimate perfusion among the N_v voxels, and another is to concurrently compute the cost function values from the N_t-time point curves in one voxel. Synchronization of the N_t -time point parallel computation is required in order to obtain a cost function value per voxel (equation (3)). On the other hand, parallel computations for multiple voxels should be asynchronous to allow individual convergence behaviors in the Simplex minimization of the voxels since the voxels are independent of each other. In the following subsections, we describe the implementations of these two parallelization strategies on the GPU using the compute unified device architecture (CUDA) from NVIDIA (Nvidia 2010).

2.2.1. Introduction of GPU and CUDA

A GPU device is comprised of a number of multiprocessors (MPs), each of which consists of multiple streaming processors, or processor cores, for massive parallel computation. CUDA abstracts the complexity in programming the graphic hardware, and provides a general-purpose parallel computing platform (Nvidia 2010). In CUDA, multiple copies of a C/C++ function, called a kernel, are executed as parallel threads on the GPU, multiple threads are scaled as a block, and all the blocks that are designed for a specific task compose a grid. The threads can access a large amount of, but slow, off-chip device memory, a limited amount of, but fast, on-chip shared memory, a constant cache, and a texture cache. Therefore, developing a CUDA GPU-accelerated application involves both the partition of computation units into parallel executions in a hierarchical grid-block-thread configuration for maximal parallelization, and the explicit management of memory access for optimal performance.

2.2.2. Parallelization of Multivoxel Perfusion Computation

In CUDA, the threads in a block can share data through the shared memory and synchronize their kernel executions, but there is no explicit support for the synchronization of threads across different blocks. Therefore, we configure N_v blocks for parallel computations for N_v voxels, and one block exclusively performs computation for one voxel. The computations across the blocks are concurrent but independent. The following subsections describe how the NLS fitting for one voxel is performed on the threads of a block.

2.2.3. Parallelization of the NLS Cost Function Calculation

The perfusion quantification at each voxel is to minimize the NLS cost function of equation (3) by the Simplex algorithm. The cost function (equation (3)) calculations include (1) a convolution of two time curves (f(iT) and h(iT)) with N_t time points of each; (2) a square of the difference between the measured and modeled values at each time point; and (3) a sum of the square differences over N_t time points. The most expensive computation is the convolution if it is straightforwardly computed, which requires every time point of f(iT) to be multiplied by every point of h(iT). Alternatively, the time-domain convolution can be computed in the Fourier domain, in which the convolution becomes a complex-number multiplication at each frequency component. Therefore, Fourier transform (FT) and its inverse transform have to be implemented on a GPU block in order to be called upon to calculate the cost function value at each of the Simplex iterations on the block. Although CUDA provides a parallel Fast Fourier Transform library (CUFFT), the CUFFT can only be called by the host CPU to perform transforms of multiple-batch data on the whole GPU but not on a block. Therefore, we developed a Block-FFT to perform the FT in order to execute the Fourier domain convolution on a block.

Block-FFT

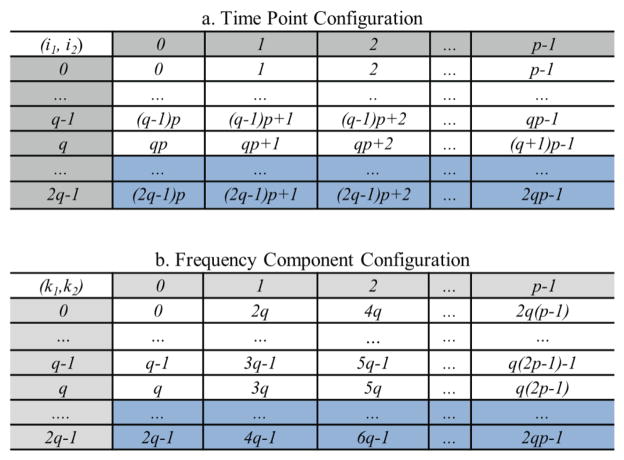
First, a time curve with N_t time points is zero-padded to have N_t=qp (i.e., q×p) points, where p is a power of 2, q is a small integer greater than 1, and N_t is as close to the number of the original time points as possible. To avoid the circular convolution problem due to the Fourier domain multiplication (Oppenheim et al 1999), the curve is further zero-padded to 2N_t points. Next, we organize 2N_t points of the curve into a 2q×p table (row×column) and order them along the row first (figure 2a), where the temporal index i of the curve is rewritten by two dimensional (2D) indices as i= pi₁+i₂ (0 ≤ i₁≤2q−1, 0 ≤ i₂ ≤ p−1). According to the general Cooley-Tukey algorithm (Duhamel and Vetterli 1990), FT of a curve (f) with 2N_t points can be written as:

$$F_k=F_{2{qk}_2+k_1}=\sum _{i_2=0}^{p-1}\{W_{2N_t}^{i_2{k}_1}(\sum _{i_1=0}^{2q-1}{f}_{{pi}_1+i_2}{W}_{2q}^{i_1{k}_1})\}{W}_p^{i_2{k}_2}$$ (4)

where $W_P^Q=exp(-j2\pi Q/P)$ for integers P and Q, called a twiddle factor in FT, and k (0 ≤ k ≤ 2N_t-1) is a frequency index and also expressed by 2D indices as k =2qk₂+k₁ (0 ≤ k₁ ≤2q−1, 0 ≤ k₂ ≤p−1). Using the configuration of the 2q×p table in figure 2a, FT of curve f in equation (4) can be done by performing a 2q-point FT along each column (inner parenthesis), and finally performing a p-point FT along each row (outer parenthesis). As a result, the frequency components during the FT can be stored in a 2q×p complex-number table as in figure 2b, in which the frequency components are ordered along the column first.

Figure 2.

Configurations of time points (top) and frequency components (bottom) designed for the Block-FFT. Both tables contain 2q rows and p columns. i₁ and k₁ are row indices and i₂ and k₂ are column indices for the time and frequency component table, respectively. Time points in rows q+1 to 2q−1 (shaded) are zero due to zero padding. The frequency components in shaded rows q+1 to 2q−1 can be determined by complex conjugation of real signal FT.

To further speed up computation and reduce memory usage, the complex conjugation of FT of the real data is used. By organizing the frequency components into the 2q×p frequency table as in figure 2b, $F_{2{qk}_2+k_1}=F_{2q(p-1-k_2)+(2q-k_1)}^{\ast }$, and thus, computation and data storage for the frequency components from row q+1 to 2q−1 can be omitted. In addition, the time points of the curve from row q to 2q−1 in the time table figure 2a are zeros (due to zero padding) and do not have to be stored. As a result, (q+1)×p memory are allocated on the shared memory of a block for the (q+1)×p complex frequency components (rows 0 to q of figure 2b). Rows 0 to q−1 of the real part of the allocated memory are also used to load the N_t time points of a time curve before its FT. In our CUDA codes, a block is configured to have (q+1)×p threads as a 2D matrix (figure 3), each of which executes the computation for one frequency component in the table memory figure 2b.

Figure 3.

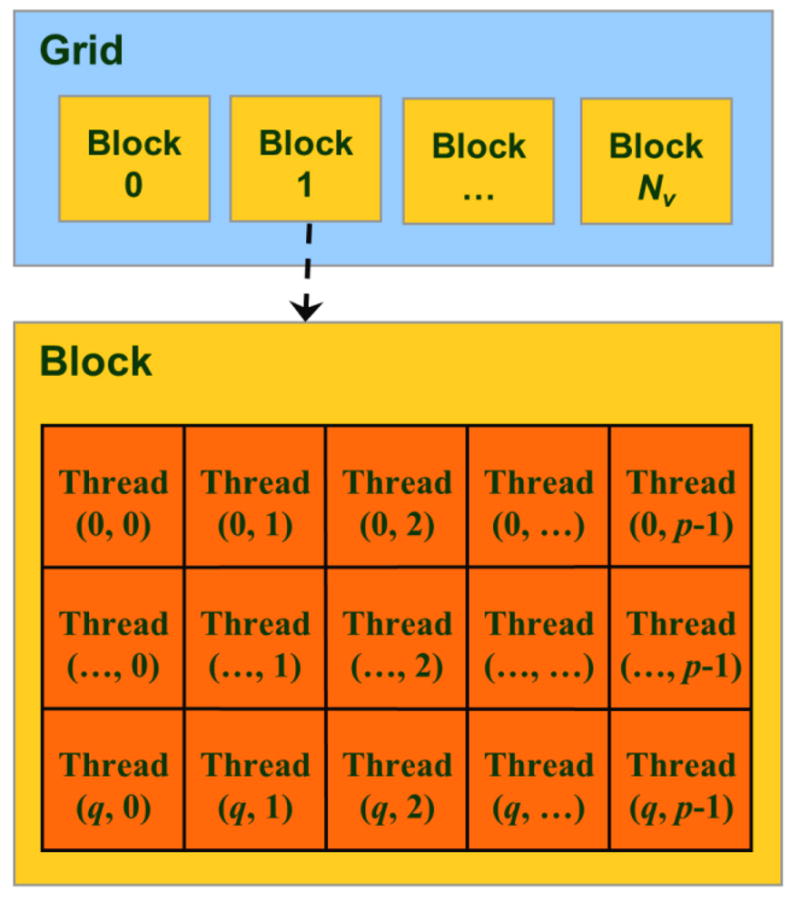
CUDA thread-block-grid hierarchy for the Block-FFT. The threads in a block are indexed with (k₁, k₂) used in figure 2b, and so one-to-one corresponds to the frequency component computation.

With one-to-one correspondences of the table memory cells and threads, the Block-FFT performs calculations on each thread as follows: (1) compute ${\displaystyle \sum _{i_1=0}^{q-1}}{f}_{{pi}_1+i_2}{W}_{2q}^{i_1{k}_1}$ along the column with a total of q points; (2) multiple $W_{2N_t}^{i_2{k}_1}$ to the column-FT results in each cell (k₁, k₂) of the table; and (3) perform FFT along the row with a total of p points. In the third step, the recursive radix-2 FFT algorithm (Moreland and Angel 2003) is utilized since p (the number of components in a row) is a power of 2. As a total, each thread performs q+1+log₂(p) complex-number multiplications and q+log₂(p) complex-number additions to perform the FT of a 2qp-point curve. Of note, q is designed to be a small integer; thus the q-point FT would not slow down the Block-FFT, but q is greater than 1 in order to utilize the complex conjugation relationship of the frequency components between the rows in the frequency table. Using the same principle, the inverse Block-FFT is implemented by inversing the three-step process and replacing the twitter factor with its complex conjugate, and then dividing the real components of the results by the number of points.

NLS cost function calculation

The NLS cost function calculation at each trial solution of (k_l, k_a, k_p, τ_a, τ_p) during the Simplex searching process involves three time-concentration curves. The curves C_a and C_p, used by all the voxels, are loaded into the texture memory and accessed by all the blocks. Each of the liver dynamic curves C_l after zero padding to N_t is stored as a contiguous segment in the device memory to allow the threads in a block to efficiently access the coalescent data.

To compute the convolution f (iT) ⊗ h(iT) in the cost function, C_a(iT) and C_p(iT) are read from the texture memory, linearly interpolated according to the given time delays (τ_a, τ_p), summed into f(iT), and maintained in the frequency component table in the share memory. Its Fourier transform F(k) is obtained by performing the Block-FFT as described in the previous subsection. Then, the analytical form of FT of h(iT) after zero-padding to 2N_t points, $H(k)=\frac{1-{(-1)}^k{e}^{-k_l{N}_{t}T}}{1-e^{-k_{l}T}{W}_{2N_t}}$, is multiplied by F(k) in each cell of the frequency component table according to their frequency correspondences. Finally, the convolution result C̄_l (iT) is obtained by the inverse Block-FFT. Table 1 shows the operation counts per thread for the convolution on the GPU, as well as the operation numbers of a CPU for the time-domain and frequency-domain convolutions.

Table 1.

Operation counts for convolutions in time-domain, and frequency-domain^a on the CPU and GPU.

Operations	Time-domain convolution	Frequency-domain convolution on CPUb	Frequency-domain convolution on GPUc
Complex Multiplications		p(q+1)(2log2p+2q+3)	2log2p+2q+3
Complex Additions		p(q+1)(2log2p+2q)	2log2p+2q
Real Multiplications	pq(pq+1)/2	4p(q+1) (2log2p+2q+3)	4(2log2p+2q+3)
Real Additions	pq(pq−1)/2	2p(q+1)(4log2p+4q+3)	2(4log2p+4q+3)

^aFrequency-domain convolution includes FFT, frequency component multiplication and inverse FFT.

^bThe FFT on CPU is based upon the Cooley-Tukey algorithm.

^cThe Block-FFT is utilized for convolution on the GPU. The counts are operations on each thread.

After each thread calculates the squared distance between C̄_l (iT) and C_l(iT) at a time point i, the cost function value is a summation of the squared distances over all the time points in the table memory cells using a naïve parallel scan algorithm executed on the block (Daniel 2005).

2.2.4. Implementation of the Simplex Algorithm on GPU

The Nelder-Mead Simplex method is a direct search method to minimize a scalar-valued nonlinear function of n real variables using function values only. In the Simplex method, a vector of the n variables of a possible solution is defined as a vertex. The search begins with a simplex with n+1 vertices and the associated function values, and then one new vertex is calculated and tested. The search is continued until reaching stopping criteria. In our NLS cost function, there are five unknown parameters (k_l, k_a, k_p, τ_a, τ_p). Thus, a six-vertex simplex plus an extra vertex as the new solution are maintained and updated based on their cost function values by following the Simplex searching scheme. For fast access, the memories for the 7 vertices and their cost function values are allocated in the shared memory. The Simplex search scheme in the NLS fitting is implemented on a block and exactly as the one reported by Lagarias et al (Lagarias et al 1998). Branching to a new vertex in the Simplex searching is only based on the cost function values of the vertices, and all the threads in a block follow the same branching path. Figure 4 shows the flowchart of the GPU-accelerated voxelwise perfusion quantification.

Figure 4.

Flowchart of the GPU-accelerated voxelwise hepatic perfusion estimation.

2.3. GPU and CPU Implementations

The GPU computation was implemented by GNU C with a CUDA 4.0 toolkit on an NVidia Tesla C2500 GPU card. The card has 14 MPs and each MP has 32 cores. The host computer has a 6-core 2.67GHz Intel Xeon CPU X5650. The NLS fitting of the DCE images requires a high-precision cost function calculation. Therefore, double-precision computation and memory allocation were used on the GPU. For the purpose of comparison, the conventional hepatic perfusion computation was implemented on the host CPU by using GNU C programming and named as C-CPU. The C-CPU method performed voxel-by-voxel perfusion computation which minimized equation (3) without parallelization. The Simplex algorithm in the CPU method used the same search scheme as Lagarias et al (Lagarias et al 1998), adopted from Numeric Recipes 3.0 (Press et al 2007). Convolution in the cost function was also calculated in the Fourier domain by using the FFT in the GNU Scientific Library (GSL) (Galassi et al 2009). Both the CPU and GPU computations started with the same initial solution and were terminated when a difference between the maximal and minimal function values of the vertices in the simplex was less than 10⁻⁸ or the iteration number was greater than 600.

In order to evaluate the efficiency of GPU computation, computation time per voxel was calculated by averaging the total computation time over the same number of voxels for the GPU and C-CPU methods. The total time for the GPU computation included the time to load the DCE data into the GPU device memory from the host CPU memory, estimating perfusion parameters over a given number of voxels on the GPU, and exporting the resultant perfusion parameters to the CPU memory. In the C-CPU computation, only the voxel-by-voxel perfusion estimation time was included.

2.4. Evaluation Experiments

2.4.1. Simulation Studies

Simulated data with known perfusion parameters were used to evaluate the accuracy and efficiency of liver perfusion quantification on the GPU. We obtained an arterial input C_a and a portal venous input C_p from our previous IRB-approved DCE-CT study (Cao et al 2006, Cao et al 2007), in which the DCE data was acquired at a temporal resolution of 1sec for 2 min. The curves C_a and C_p were interpolated to obtain curves with the following numbers of time points: 32, 64, 128, 256, 320 and 448. A time-concentration curve C_l was simulated from C_a and C_p using equation (2), where k_a, k_p and k_l were set to be 20, 100 and 400 ml/100g/min, respectively, and t_a and t_p were 1s and 2 s, respectively. These parameters are typical for normal hepatic perfusion (Cao et al 2006). The C_l curve was replicated up to 10000 voxels. The perfusion parameters of these voxels were estimated in parallel on the GPU, and in serial on the host CPU. Both computations were initialized with 10 ml/100g/min, 80 ml/100g/min, 200 ml/100g/min, 2 s and 3 s for k_a, k_p, k_l, τ_a and τ_p, respectively. The computation time per voxel with respect to the number of voxels (N_v) and the number of time points (N_t) were measured for both the GPU and C-CPU computations.

To evaluate the accuracy of the GPU perfusion computation, Gaussian noise was added to the simulation data. The noise is quantified by the contrast-to-noise ratio (CNR) that was defined as the ratio of the signal peak to the standard deviation of the curve at the baseline. We used the typical CNR of 150 and 100 for C_a and C_p, respectively, and varied the CNRs of C_l from 10 to 100 by steps of 10. For each tested CNR, the noisy signals with 128 time points were generated 1000 times. The perfusion parameters were estimated by both the GPU and C-CPU methods, as well as the method implemented in Matlab on the CPU, named as Matlab-CPU, using the Matlab optimization function “fminsearch”. The function “fminsearch” used the Simplex search algorithm in exactly the same way as our GPU and C-CPU computations. The means and standard deviations of k_a, k_p and k_l estimated by the three methods were compared with respect to the noise levels.

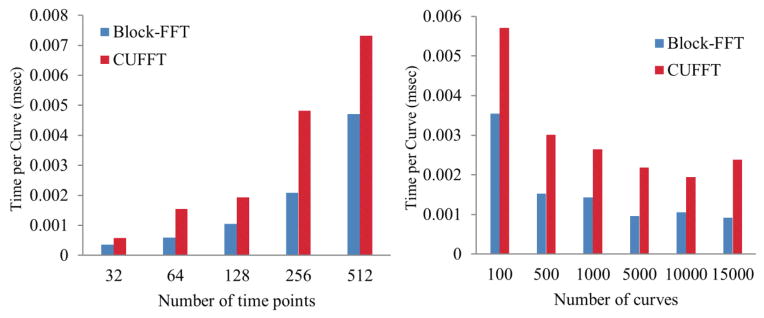
We also evaluated the speed of the Block-FFT by comparing it with the CUFFT of multiple liver curves on the GPU. First, the curves were zero padded to double the number of points in order to perform convolution computation in Fourier domain. Then, the zero-padded curves C_l of Nv voxels were Fourier transformed and then inverse Fourier transformed on the GPU using the Block-FFT and the CUFFT. Both computations were invoked in the same way by the CPU for parallel FT of the N_v voxels. The CUFFT performed the transformation by its real-to-complex Fourier transform and complex-to-real inverse Fourier transform. We compared the time per curve transform between the two implementations with respect to the number of curves (N_v) and the number of time points in the curve (N_t). To evaluate the accuracy of the Block-FFT, a root mean squared error (RMSE) of a curve transformed by forward FT and followed by inverse FFT to the original curve was calculated.

2.4.2. Patients Hepatic Perfusion Studies

DCE-MRI scans of three patients with intra-hepatic cancers were obtained in a prospective IRB-approved protocol. The DCE data were acquired during a bolus injection of 15mL Gd-DTPA at a rate of 2 mL/sec on a clinical 3T MR scanner (Philips Achieva 3.0T; Philips Healthcare, Netherlands). A 3D DCE MRI covering the whole liver was obtained every 2.37 sec for a total of 2 min with a gradient echo pulse sequence (TR/TE/FA: 4.48/2.15/20°; Matrix: 320×320×66; FOV: 33×33×19.8 cm; SENSE factor: 2 in 2 different directions). The 3D data was acquired in sagittal/coronal orientation to avoid the inflow effect.

An arterial input (C_a) and a portal venous input (C_p) were obtained from VOIs of the aorta and portal vein, respectively, on the MR images. The voxel numbers of the aorta and portal vein VOIs were approximately 800 and 400, respectively. The MR time-intensity signals were converted to the CA time-concentration curves by assuming a linear relationship between the CA concentration and the relaxivity (R1) enhancement after the CA administration. As the original DCE data had 42–48 temporal phases, we attached zero-intensity phases to the ends of the time series to have 48 phases (i.e. N_t=48). The GPU and C-CPU methods were applied to estimate volumetric perfusion maps from the DCE data. In the GPU computation, N_t of 48 was decomposed to be 3×16 (q×p) so that a GPU block was configured to have 4×16 ((q+1)×p) threads. According to availability of the device memory, the liver dynamic curves from the first 60000 voxels were loaded into the device memory, and the GPU was configured into 60000 blocks for parallel perfusion quantification over the 60000 voxels. After completing the first 60000-voxel computations, the liver data of the next 60000 voxels were loaded into the GPU for perfusion estimation. The process was stopped when computations for all the voxels in the liver volume were done. The absolute differences of perfusion parameters between GPU and C-CPU computations were calculated at each voxel to evaluate the accuracy of the GPU computation.

3. Results

3.1. Simulation Studies

The comparison of the computation speeds of the Block-FFT and the CUFFT of the curves with 32–512 (N_t) time points over 100–15000 (N_v) voxels is shown in figure 5. As expected, the computation time per curve increased with the number of time points, but deceased with the number of curves that can be computed in parallel for both methods. However, the Block-FFT was 40–60% faster than the CUFFT, due to the fact that the Block-FFT ignores the computation of the zero-padded points in the curves and applies the complex conjugates in frequency components of a real signal FT. The RMSE of a curve transformed by FT and followed by inverse FT was 2.33E-14 by the Block-FFT, compared to 2.46E-16 and 1.11E-16 by the CUFFT and CPU GSL FFT, respectively. The small non-significant discrepancy of the RMSEs between the Block-FFT and CUFFT might be due to the numerical implementation of π in the Fourier transformation.

Figure 5.

Performances of the Block-FFT and CUFFT of time curves with N_t time points and over N_v voxels. Left: computation time per curve transform vs the number of time points over N_v=10000 voxels. Right: computation time per curve transform vs the number of voxels for a curve with 128 time points.

To compute liver perfusion over a large number of voxels, multiple blocks run estimations simultaneously for multiple voxels on the GPU. Table 2 shows the performance of the GPU computation on the simulated DCE data. The computation time per voxel by GPU substantially decreased with the number of voxels due to parallel computation, and was much faster than by the C-CPU method except for only one voxel computed on the GPU (N_v=1). For the DCE data with 32, 64, 128, 256, 320 or 448 time points and 10,000 voxels, the computation speeds by the GPU were 34, 32, 30, 28, 29 and 31 times faster than by the C-CPU method, respectively. Table 2 also provides q×p decompositions of 32, 64, 128, 256, 320 and 448 time points, in which N_t (=qp) were selected as close to the number of DCE imaging time points as possible and q was as small as possible but greater than 1. For the DCE data with the number of time points different from the examples in table 2, the dynamic data can be zero-padded to have a curve length the same as one of these cases.

Table 2.

Computation times of liver perfusion by GPU and C-CPU

Number of time points		GPU time per voxel (msec)							CPU time per voxel (msec)
Nt	q×p	1a	10	50	100	1000	5000	10000
32	2×16	25.49	2.59	0.57	0.39	0.32	0.31	0.30	10.36
64	2×32	27.60	2.84	1.16	1.03	0.65	0.61	0.61	19.76
128	2×64	32.06	3.22	2.17	1.97	1.40	1.32	1.31	39.11
256	4×64	41.85	4.19	3.31	3.30	2.96	2.95	2.94	82.48
320	5×64	47.78	4.82	3.80	3.81	3.41	3.38	3.39	99.98
448	7×64	60.92	6.10	4.84	4.83	4.34	4.31	4.31	136.71

^aThe row is the number of voxels computed in parallel by the GPU method.

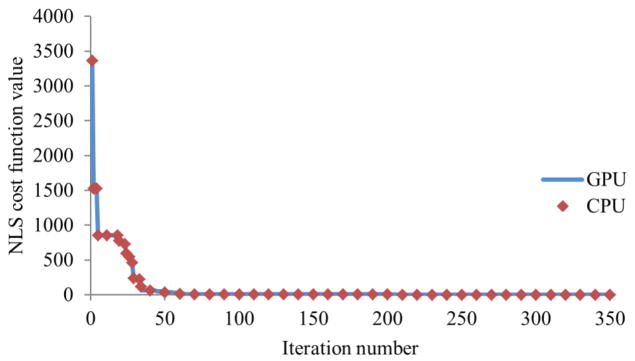
The convergent behavior of the Simplex minimization for liver perfusion computation implemented on GPU was evaluated and compared to C-CPU and Matlab-CPU computations. Figure 6 shows the GPU method, CPU computations implemented with C and Matlab followed the exact same convergence course and were terminated after the same number of iterations for the given termination criteria when initiated by the same simplex.

Figure 6.

Convergence behaviors of the Simplex minimization implemented in the GPU and C-CPU methods. Both methods have the exactly same convergence behavior, which is also the same as the one obtained from the Matlab-CPU method.

The accuracy and stability of the GPU-based liver perfusion quantification under the influence of noise were evaluated. Table 3 shows the means and standard deviations of the parameters estimated from the 1000 simulated data by the GPU, C-CPU and matlab-CPU methods. For the simulated DCE data with CNRs of 10 to 100, there were no differences in the means and standard deviations of the perfusion estimates among the three methods.

Table 3.

Means and standard deviations of perfusion parameters estimated by the GPU, C-CPU and Matlab-CPU methods.

CNR	GPU computation (ml/100g/min)			C-CPU estimation (ml/100g/min)			Matlab-CPU estimation (ml/100g/min)
	kl	ka	kp	kl	ka	kp	kl	ka	kp
∞a	400.0	20.0	100.0	400.0	20.0	100.0	400.0	20.0	100.0
100	400.1 ± 7.1	19.6 ± 1.3	100.4 ± 1.6	400.1 ± 7.1	19.6 ± 1.3	100.4 ± 1.6	400.1 ± 7.1	19.6 ± 1.3	100.4 ± 1.6
90	399.7 ± 13.2	19.5 ± 1.8	99.2 ± 3.0	399.7 ± 13.2	19.5 ± 1.8	99.2 ± 3.0	399.7 ± 13.2	19.5 ± 1.8	99.2 ± 3.0
80	398.3 ± 19.1	19.5 ± 2.5	100.0 ± 4.6	398.3 ± 19.1	19.5 ± 2.5	100.0 ± 4.6	398.3 ± 19.1	19.5 ± 2.5	100.0 ± 4.6
70	398.2 ± 25.7	19.1 ± 2.9	100.4 ± 6.5	398.2 ± 25.7	19.1 ± 2.9	100.4 ± 6.5	398.2 ± 25.7	19.1 ± 2.9	100.4 ± 6.5
60	399.1 ± 29.4	19.4 ± 3.5	100.3 ± 7.5	399.1 ± 29.4	19.4 ± 3.5	100.3 ± 7.5	399.1 ± 29.4	19.4 ± 3.5	100.3 ± 7.5
50	398.9 ± 32.6	19.2 ± 3.9	99.1 ± 8.3	398.9 ± 32.6	19.2 ± 3.9	99.1 ± 8.3	398.9 ± 32.6	19.2 ± 3.9	99.1 ± 8.3
40	398.9 ± 40.7	19.3 ± 4.3	99.9 ± 10.6	398.9 ± 40.7	19.3 ± 4.3	99.9 ± 10.6	398.9 ± 40.7	19.3 ± 4.3	99.9 ± 10.6
30	400.0 ± 49.2	19.2 ± 5.0	101.0 ± 12.3	400.0 ± 49.2	19.2 ± 5.0	101.0 ± 12.3	400.0 ± 49.2	19.2 ± 5.0	101.0 ± 12.3
20	401.9 ± 54.4	19.3 ± 5.2	101.3 ± 13.7	401.9 ± 54.4	19.3 ± 5.2	101.3 ± 13.7	401.9 ± 54.4	19.3 ± 5.2	101.3 ± 13.7
10	398.4 ± 59.3	19.4 ± 5.5	99.7 ± 15.6	398.4 ± 59.3	19.4 ± 5.5	99.7 ± 15.6	398.4 ± 59.3	19.4 ± 5.5	99.7 ± 15.6

^a∞ is the data without noise

3.2. Experimental Patient Study

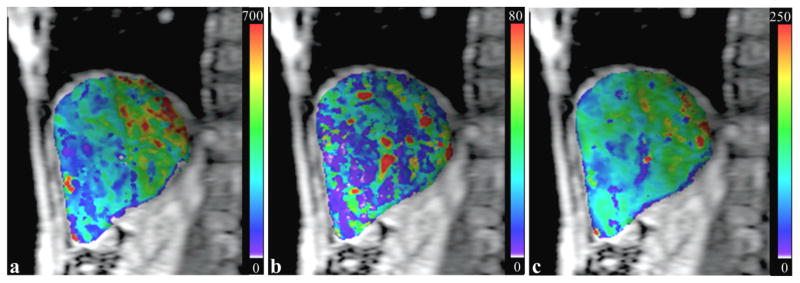
The volumetric hepatic perfusion parameters maps of the patients were estimated from DCE MRI by using the GPU and C-CPU computations. Figure 7 shows examples of slices of the liver perfusion parameters, estimated by the GPU method, in a patient. The means of the absolute differences of perfusion parameters over all the voxels in the liver between the GPU and C-CPU computations were in the order of magnitude from 10⁻⁴ to 10⁻⁵ in all three patients (Table 4).

Figure 7.

Hepatic perfusion maps of a liver slice estimated by the GPU computation. (a): estimated k_l map; (b): estimated k_a map; (c): estimated k_p map. The perfusion parameters are in a unit of ml/100g/min.

Table 4.

The absolute differences of perfusion parameters between the GPU and C-CPU computations of all liver voxels.

	Patient 1	Patient 2	Patient 3
kl	2.4E-7 ± 3.4E-6	1.5E-7 ± 2.6E-6	1.2E-7 ± 2.3E-6
ka	1.7E-7 ± 2.3E-5	1.0E-7 ± 8.3E-6	6.1E-8 ± 2.1E-6
kp	2.4E-7 ± 2.2E-5	1.3E-7 ± 5.8E-6	7.7E-8 ± 1.8E-6

As well as showing that the GPU and C-CPU produced similar accuracy in liver perfusion quantification, the computation times per voxel by GPU and C-CPU were 0.25 msec and 10.74 msec, respectively. Table 5 shows the total times of the GPU and CPU perfusion quantifications in the whole livers of the three patients. For a liver with approximately 600000 voxels, the voxelwise perfusion computation lasted approximately 2 hours by C-CPU, 2.5 min by single GPU, and less than 1 min by 3 GPUs.

Table 5.

Total computation times for the voxelwise hepatic perfusion quantifications in three patients using the GPU and C-CPU computations.

	Voxel number	1 GPU (min)	2 GPUs (min)	3 GPUs (min)	CPU(min)
Patient 1	576556	2.31	1.27	0.83	103.01
Patient 2	663980	2.63	1.44	0.95	117.08
Patient 3	638728	2.73	1.50	0.98	116.35

4. Discussion and Conclusions

In this report, we developed a CUDA parallel computation method on an NVIDIA Tesla C2050 GPU to improve the speed of voxelwise hepatic perfusion quantification from DCE images. The parallel computations are not only executed over multiple voxels, but also over multiple time points in the cost function calculation. In addition, an efficient block-based FFT algorithm was implemented to convolve two time curves in the Fourier domain. Overall, we were able to achieve an approximately 30-fold improvement in the computation speed using a single GPU card, compared with using a CPU without compromise of the accuracy of the estimated parameters. The computation can be further accelerated if multiple GPUs are utilized. The parallel programming techniques reported here quell the longstanding concern about the computation time for voxelwise quantification of the hepatic perfusion over the whole liver in a clinical setting. Also, the framework as well as the components of the CUDA programming implementations, e.g., block-based FFT and parallel computation for the cost function over time points, can be generalized for other pharmacokinetic modeling of DCE data to substantially accelerate perfusion estimation in other organs.

GPU is a dedicated device for parallel computation. To achieve the best performance of the GPU computation, the first objective of the CUDA programming is to maximally parallelize the computation. Using the block-thread hierarchy in CUDA, perfusion parameters of multiple voxels are computed independently across multiple blocks, and Simplex minimization of one voxel is executed on a block with a parallel calculation of cost function values over multiple time points. Furthermore, individual convergence behavior of the Simplex optimization (figure 6) is allowed on each block to accommodate the different perfusion characteristics at a voxel.

We implement a Block-FFT for the Fourier domain convolution of two time curves. The Block-FFT is designed to run on a block for an arbitrary length of the time curve. By arranging a curve into a q×p table with q>1, the memory allocations for frequency components from row q+1 to 2q−1 in the frequency table can be omitted (figure 2). This reduction of the memory usage in the Block-FFT makes it possible to store the data on the limited shared memory for fast access. However, if the shared memory in an MP is not enough for any dataset, the frequency component table can be allocated on the device memory but with a tradeoff for slow device memory access. In CUDA program, a block is configured to (q+1)×p threads to match the dimensions of the time or frequency table. Note that this configuration is also limited by the maximal number of threads within a block. Our implementation allows perfusion quantification from DCE data with 448 time points or less on the Tesla C2050 GPU. The maximal number of threads in one block for the GPU card is 1024, which is quite generous for DCE data acquired in a clinical setting.

We report a method to accelerate voxel-by-voxel liver perfusion computation from volumetric DCE imaging by using the dual-input single-compartment model. The hepatic perfusion consists of two phases, i.e., the arterial and portal venous perfusion. Although a single vascular input model is popularly used for characterizing the vascular behavior of a highly arterialized tumor, the dual-input single-compartmental model is more reasonable in representing the underlying physiology of hepatic perfusion, particularly in situations where the clinical and scientific interests are not limited to the tumor, e.g., cirrhosis, and drug and radiation effects on the liver parenchyma (Hashimoto et al 2006, Leggett et al 1997, Van Beers et al 2001). The latter studies (Cao et al 2012, Cao et al 2007) show it is not only that portal venous perfusion needs to be considered but also it is necessary to map the whole liver perfusion voxel-by-voxel. Finally, although our method is designed to accelerate the perfusion quantification using the conventional hepatic dual-input single compartment model, the GPU-based parallel computation framework can be applied to other pharmacokinetic models to speed up the computation (Tofts 1997, Koh et al 2008) since the convolution and optimization of a least squares cost function are the common computations in these models.

In conclusion, the GPU method greatly speeds up the computation of voxelwise hepatic perfusion from DCE data. The method may make volumetric perfusion evaluation practical in clinical applications. The quantitative liver perfusion imaging may improve detection of liver disease and assessment of tissue therapeutic response beyond region-based quantifications.