Abstract
Rats are widely used in experimental neurobiological research, and rat brain atlases are important resources for identifying brain regions in context of experimental microsurgery, tissue sampling, and neuroimaging, as well as comparison of findings across experiments. Currently, most available rat brain atlases are constructed from histological material derived from single specimens, and provide two-dimensional or three-dimensional (3-D) outlines of diverse brain regions and fiber tracts. Important limitations of such atlases are that they represent individual specimens, and that finer details of tissue architecture are lacking. Access to more detailed 3-D brain atlases representative for a population of animals is needed. Diffusion tensor imaging (DTI) is a unique neuroimaging modality that provides sensitive information about orientation structure in tissues, and is widely applied in basic and clinical neuroscience investigations. To facilitate analysis and assignment of location in rat brain neuroimaging investigations, we have developed a population-averaged three-dimensional DTI atlas of the normal adult Sprague Dawley rat brain. The atlas is constructed from high resolution ex vivo DTI images, which were nonlinearly warped into a population-averaged in vivo brain template. The atlas currently comprises a selection of manually delineated brain regions, the caudate putamen complex, globus pallidus, entopeduncular nucleus, substantia nigra, external capsule, corpus callosum, internal capsule, cerebral peduncle, fimbria of the hippocampus, fornix, anterior commisure, optic tract, and stria terminalis. The atlas is freely distributed and potentially useful for several purposes, including automated and manual delineation of rat brain structural and functional imaging data.
Keywords: DTI, white matter, delineation
1. Introduction
Because of the rat’s ability to accurately predict the human response, the rat has become the most widely studied experimental animal model for biomedical research, which might involve microsurgical techniques, serial sampling of the cerebrospinal fluid (CSF), and repetitive in vivo neuroimaging (Cenci et al., 2002; Cozzi et al., 2008). The rat exhibits physiological characteristics similar to those of humans and therefore, several strains, substrains, and genetically modified rats are employed to mimic various neurological disorders such as Huntington Disease (von Hörsten et al., 2003), Amyotrophic lateral sclerosis (Vermeiren et al., 2006), and Alzheimer disease (Liu et al., 2008).
Several atlases of the rat brain have been developed and provide invaluable resources for a wide range of applications in various types of neuroscience studies, including visualization, identification, and precise localization of specific brain areas, stereotaxic surgery, delineation of brain regions of interest (ROI), and registration of information such as gene expression locations. To date, the most widely used rat brain atlases are the stereological, histology-derived atlases of the Wistar and Sprague Dawley (SD) rat brain by Paxinos and Watson (1986, 2007) and Swanson (1992, 1998, 2004), respectively. These atlases describe the brain in a series of two-dimensional diagrams, indicating the names and boundaries of areas and nuclei. Despite their widely use, the histology-based atlases have several limitations. First, histology-based atlases are inherently two-dimensional and restricted to standard section planes. Second, the procedures of specimen fixation, sectioning, and staining involved in histological processing can deform the brain shape, which might be a source of significant inaccurate localization of brain areas. During the last decade, several average in vivo templates of the rat brain and atlases of its major structures have been developed with magnetic resonance imaging (MRI), a non-invasive, three-dimensional, and in vivo imaging technique, which enables accurate identification of a large number of anatomical structures (Schweinhardt et al., 2003; Schwarz et al., 2006; Hess et al., 2005). However, all proposed atlases lack orientational information about the white matter anatomy, which constitutes a complex network of axons connecting different brain regions. This is conclusively due to the homogeneous appearance of the white matter structures in conventional MRI and in histology preparations. The lack of clear anatomical boundaries hampers identification and delineation of specific white matter fiber bundles.
Magnetic resonance diffusion tensor imaging (DTI) is a widely explored, and exceptional modality for quantifying the random walks of water molecules in biological tissue (Basser et al., 1994). Unlike other MR techniques, it offers the possibility of characterizing and visualizing the structural connectivity of distinct anatomical networks within the brain in vivo and non-invasively (Jones, 2008). With DTI, the estimated displacement profile of the diffusingmolecules can be interpreted as an ellipsoidal iso-probability surface - described by a diffusion tensor (DT). In the white matter, the first eigenvector of the DT, thus the preferred local displacement direction of the water molecules, coincides with the orientation of major fiber tracts, as a result of which DTI provides rich anatomical contrast highly suitable for accurate delineation of white matter regions and subregions (Lin et al., 2001; Kaufman et al., 2005; Dauguet et al., 2007).
To provide a resource for efficient three-dimensional parcellation and analysis of rat brain neuroimaging data, we here present an accurate three-dimensional atlas of the normal adult SD rat brain constructed from precise, manually delineated anatomical labels. Selected grey and white matter structures were manually delineated in a high-resolution, diffusion weighted and anatomical MRI scan obtained ex vivo with the brain in situ within the skull. To minimize bias due to sample-specific features in the ex vivo sample, we nonlinearly mapped the ex vivo atlas onto a population-averaged in vivo rat brain template. The construction of that population-averaged template allowed studying the anatomical variation within the sample population (Aggarwal et al., 2009). The proposed atlas offers an average anatomical template for accurate identification of the white and grey matter structures which could, for example, be used for ROI delineation of the rat brain imaging data.
2. Materials and Methods
2.1. Animal samples and preparation
Animal procedures were approved by the local institutional animal welfare committee at the Universities of Oslo and Antwerp, and were in compliance with National Institutes of Health and European Community guidelines for the use and care of laboratory animals. For the construction of the in vivo population-averaged template, nine inbred male SD aged ~12 months were used, while for the ex vivo atlas, one inbred male SD rat aged ~18 months was used. The animals were bred at the Franz-Penzoldt-Center, Experimental Therapy, Friedrich-Alexander-University of Erlangen-Nürnberg, Germany.
Before ex vivo MR imaging, the specimen was prepared for active staining according toJohnson et al. (2002), with a contrast agent mixed with a fixative to enhance the MRI signal. Following a brief inhalation induction with 4% isoflurane (Abbott Laboratories, Illinois, USA), the animal was deeply anesthetized by intraperitoneal injection of sodium pentobarbital (50 mg/kg) and transcardially perfused with 120 ml of a mixture of 0.9% saline, ProHance® (10:1 v:v; gadoteridol, Bracco Diagnostics, Inc, Princeton, NJ), and Heparin (5000 IE units / ml; Leo Pharma A/S, Ballerup, Denmark), followed by 120 ml of freshly prepared 4% paraformaldehyde with ProHance (10:1, v:v). The animal head was isolated and stored in 0.9% saline with ProHance (10:1 v:v). During all procedures the brain was left in situ within the cranium to limit physical distortions.
2.2. In vivo MR imaging
Diffusion weighted images (DWIs) were acquired at the Bio-Imaging Lab on a 9.4T Bruker Biospec scanner (Ettlingen, Germany) using a fast spin echo sequence with an encoding scheme of 6 diffusion weighting gradient directions using b = 800 s/mm2, TR/TE= 2200/34 ms, δ = 5ms/Δ = 18ms, acquisition matrix = 256×128 (zerofilled to 256 × 256), FOV= 35 × 35mm2, slice thickness= 0.43mm. Additionally, one image without diffusion weighting (b0) was acquired. For each animal, diffusion weighted datasets were acquired for 7 repetitions (two averages each), which resulted in a total scan time of ~ 4h.
2.3. Ex vivo imaging
DWIs were acquired at the Duke Center for In Vivo Microscopy using a 7T Magnex 7.0 T/210 mm bore magnet controlled by GE EXCITE consoles. Specimens were imaged in a solenoid rf coil fabricated from a continuous sheet of high frequency microwave substrate (Roger Corp, Rogers, Ct). A diffusion-weighted spin-echo pulse sequence with extended dynamic range (Johnson et al., 2007) was used to acquire 3D volume images (FOV = 45×22.5×22.5mm3, TR/TE= 100/15.6ms, NEX=2). Diffusion encoding was performed using a pair of half-sine gradient pulses (δ = 3.2ms/Δ = 8.3ms), using b = 800 s/mm2. A reduced encoding DTI methodology (Jiang et al., 2004) was employed, such that each dataset consisted of a fully encoded 512 × 256 × 256 (readout × phase × slice) matrix-size b0 (i.e., b ≈ 0) and 12 reduced encoded (512 × 128 × 128) diffusion-weighted images sensitized in each of an optimized set of 12 directions (Papadakis et al., 1999). Each reduced encoded diffusion-weighted image was reconstructed to 512 × 256 × 256 matrix size by a corrected keyhole algorithm (Jiang and Hsu, 2005) with the b0 image as the constraining reference, resulting in 88 µm isotropic resolution. The acquisition time for the complete DTI dataset was approximately 18h. An rf refocused spin echo image with the same FOV and resolution was acquired with TR = 50ms, TE = 5ms, and NEX=1. Active staining with Prohance reduces the T1 of all the tissues to < 100ms so this sequence produces anatomical images similar to those one would obtain with proton density weighting in unstained tissues.
2.4. DTI data analysis
The DTI model is given by:
| (1) |
In Eq. (1), gi is the ith component of diffusion weighted gradient direction g and b probes the diffusion weighting strength. S (b) and S0 are the diffusion weighted and non diffusion weighted signal intensities, respectively. Dij is the ijth element of the fully symmetric apparent diffusion tensor D. The DTI model is parameterized by θ, which includes 7 parameters: S0 and 6 independent elements of D, [Dxx, Dyy, Dzz, Dxy, Dxz, Dyz].
The parameter vector θ was estimated voxelwise by fitting Eq. (1) to the natural logarithmof the diffusion weighted data - corrected for motion and eddy currents using the FSL toolbox (Jenkinson et al., 2002)- such that the sum of the weighted squared differences was minimized (Koay et al., 2006; Chung et al., 2006). Several diffusion parameters, such as the fractional anisotropy (FA), mean (MD), radial (D⊥) and axial (D‖) diffusivity, were calculated voxelwise by means of the eigenvalue decomposition of the related diffusion tensors (Le Bihan et al., 2001).
2.5. Population-averaged brain template
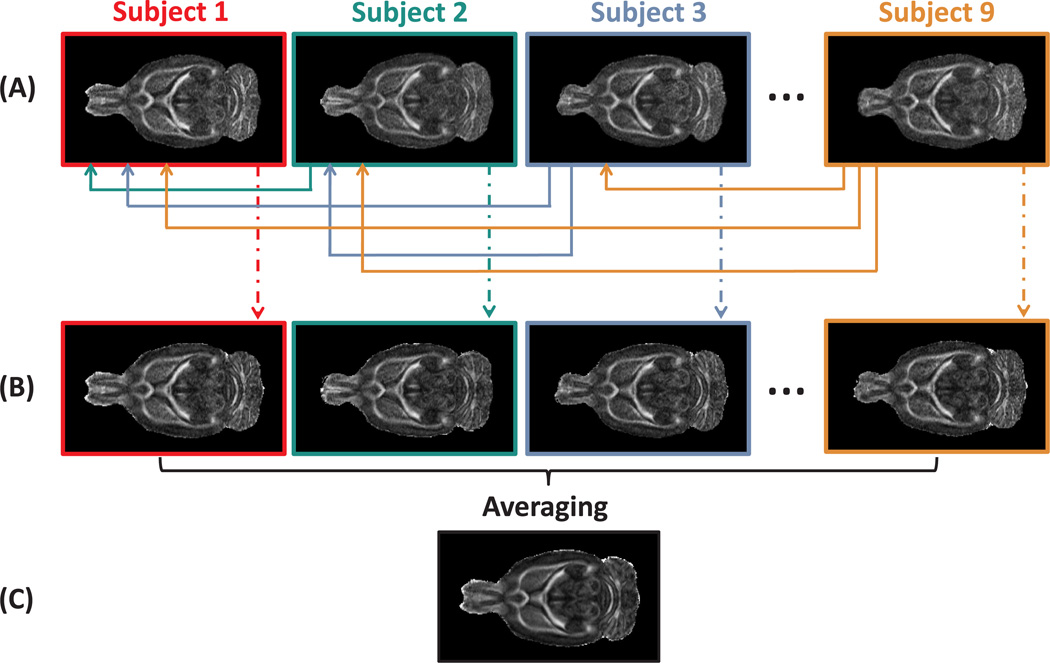
All nine in vivo diffusion weighted datasets were used to create a population-averaged DTI template that robustly preserves the orientational DT information and contains a minimal bias towards any specific individual dataset. First, all images were affinely aligned to a randomly chosen subject in order to correct for global misalignments. The affine registration was performed with in-house ITK software based on maximizing the mutual information between FA maps as they provide high white/grey matter contrast (Maes et al., 1997). Next, for each dataset, a mean shape template, defined as a minimal deformation target (MDT) byKochunov et al. (2001), was constructed by nonrigidly transforming a single image in a way that the deformed image requires the least amount of deformation to all other images in the group. An identical MDT brain should be obtained regardless of the image from which it was constructed. Although, in practice, all MDTs were very similar, some unresolved residual variations, explained by the topology preserving property of the coregistration algorithm, were noticeable. Those variations were reduced by a voxel-wise averaging over all MDTs, resulting in a template that is called the population-averaged DTI template (see Fig. 1; Wang et al., 2005; Van Hecke et al., 2008).
Figure 1.
An overview of the in vivo population-averaged template construction. In (A), the FA maps of the subjects, affinely aligned to an arbitrarily chosen subject, are shown. The deformation field which maps subject j onto subject i is calculated and denoted as Tij, with i < j, and j = 1 ⋯ 9. The calculation of the deformation fields was done with a nonrigid registration algorithm based on a viscous fluid model. Next, for subject i, an average mean deformation field is computed as the average deformation to all other subjects: , with Tji the inverse of Tij. The average deformation fields, Ti, are applied to the corresponding DTI datasets (B). The average of the deformed DTI datasets resulted in the population based atlas (C). In (B) and (C), the DTI datasets are represented by the FA maps.
This used nonrigid coregistration algorithm computes a fluid-model based deformation field via voxel-by-voxel diffeomorphic mapping from a multichannel floating image to a multichannel reference image (D’Agostino et al., 2003). Mutual information was used as a cost function. The calculation of the deformation field was steered by all unique diffusion tensor elements in order to take full advantage of the relevant information that was encoded 5 in DTI data, particularly the tensor orientation, and thus to reduce local misalignments in the white matter tracts (Van Hecke et al., 2007). Since all images acquired in this study included orientational information, tensor reorientation (PPD) and recalculation of the DWIs was performed after the deformation in order the preserve the alignment of the diffusion tensors and the underlying structures (Alexander et al., 2001).
2.6. Manual delineation of brain structures on ex vivo MR data
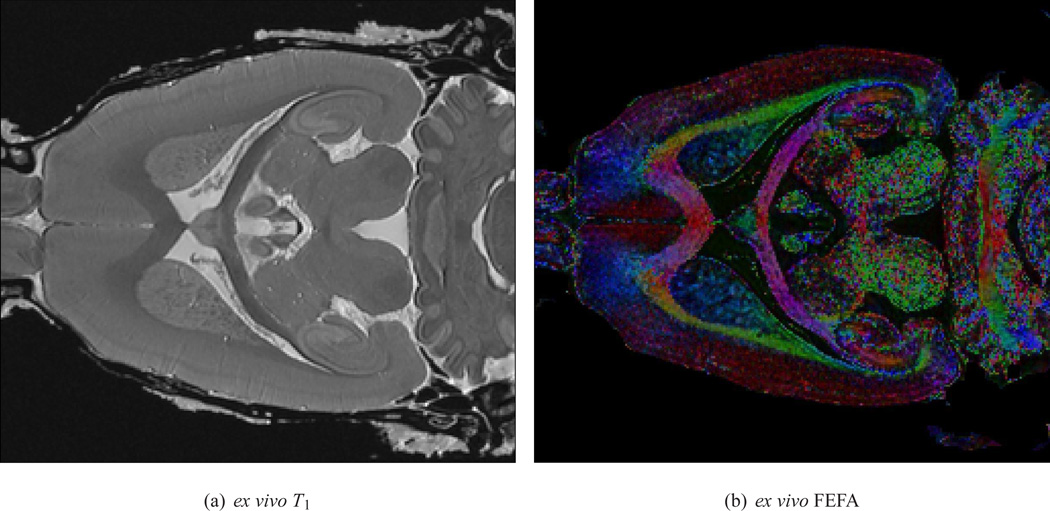
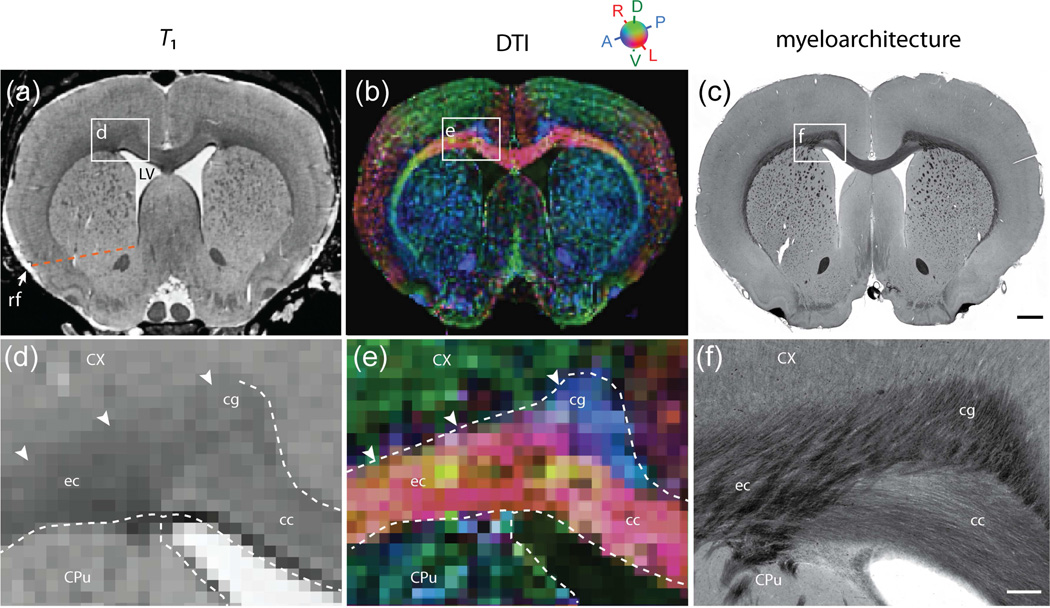
In the ex vivo DTI volume, a selection of white matter and grey matter regions were manually segmented on basis of T1-weighted (Fig. 2(a)) and DTI contrast (FA and principal eigenvector orientation; Fig. 2(b)), following a stepwise procedure to utilize complementary information in the structural and diffusion data. Image processing and anatomical delineations were performed using the ITK-SNAP (version 1.6;Yushkevich et al. (2006); www.itksnap.org) and Amira® (Visage imaging, Inc., San Diego, CA) software packages. First, structures were delineated on basis of T1 white/grey matter contrast observed in coronal, sagittal, and horizontal image slices (Fig. 3(a,d)). Secondly, in regions where anatomical boundaries were ambiguous or invisible in T1-weighted images, DTI maps were used to adjust boundaries (Fig. 3(b,e)). To this end, the orientation of the principal eigenvector was co-displayed with the T1-images, in separate channels for anterioposterior (blue), mediolateral (red), and dorsoventral (green) orientations. The observed diffusion orientations were evaluated against anatomical landmarks visible in series of coronally and sagittally oriented histological sections (Fig. 3(c,f); T.B. Leergaard, A.M. Dale, and J.G. Bjaalie, unpublished work, see alsoLeergaard et al. (2010)) stained for myelin following a standard procedure modified from Woelche (1942). Two standard rat brain atlases were used as reference (Swanson, 2004; Paxinos and Watson, 2007), and additional predefined anatomical criteria (see below) were employed to close anatomical boundaries when these were not unequivocally visible in T1 or DTI images. This particularly concerned locations where myelinated fibers pass between white matter fiber bundles and GM, the transition from hyperintensive to hypointensive T1 contrast is gradual and boundaries ambiguous. The lateral ventricles and the associated ependymal layer were segmented from T1 images (Swanson, 2004).
Figure 2.
(a) A single horizontal slice of the ex vivo T1 image, and (b) the direction encoded (DEC) FA map, with RGB-colors representing the orientation of the first eigenvector of the DTs and intensity values in proportion to the FA value, of a single ex vivo sample are shown. The red, green and blue color correspond to the mediolateral, dorsoventral, and anterioposterior orientations, respectively. These maps were used for the manual delineation of the anatomical structures.
Figure 3.
Coronal ex vivo T1-weighted (a,d) and DTI (b,e) slices, shown together with corresponding images (c,f) of a coronal, myelin stained section from a different animal. White frames in (a–c) indicate the position of the enlarged images in (d–f). Images were manually segmented on basis of T1, supplemented by DTI contrast in regions where T1 contrast was insufficient. The detailed interpretation of DTI images was aided by inspection of myelin fiber orientations in corresponding histological section images. It not possible to distinguish the cingulum (cg) and corpus callosum (cc) in the T1 images, but the anterioposteriorly oriented fibers of the cg (e, f) are stand out in DT images (blue color in (b,e)). The dorsal boundary of the external capsule (ec) is ambiguous in T1-weighted images (arrowheads in (d)), but readily identified mediolaterally oriented diffusion orientations in DTI (red color in (b,e)). The dotted line in (a) indicates the imaginary boundary between the dorsal caudate putamen (CPu) and the nucleus accumbens, drawn as a line between the rhinal fissure and ventral tip of the lateral ventricle. Scalebars, 1mm and 250 µm.
2.6.1. White matter
The corpus callosum (cc) consists of mediolaterally oriented commisural fibers that continue in the external capsule (ec) underlying the cerebral cortex (Cx) (e.g. Heimer et al., 1967; Sargon et al., 2003). The cc and ec were here segmented as one structure. The boundary of the ec and the overlying Cx is ambiguous due to the high number of myelinated fibers passing between both structures (Fig. 3(a,d)). Here, DTI maps provided excellent contrast between coherent fibers oriented along the ec, and radial fiber orientations in the Cx (Fig. 3(b,e)). The cingulum (cg) bundle lies dorsomedial to the ec, and contains anterioposteriorly oriented limbic fibers (e.g. White, 1959; Swanson and Cowan, 1979). The boundary between the cg and ec is indistinguishabl in T1 contrast (Fig. 3(a)), but readily segmented in DTI images showing anterioposterior and mediolateral orientations associated to the cg and cc/ec, respectively (Fig. 3(b,e)). Subcortically projecting corticofugal axons pass through the striatum (giving rise to its characteristic striated texture) and converge into the internal capsule (ic), which is continuous with the cerebral peduncle (cp) and pyramidal tract (py) (e.g. Coleman et al., 1997). We here delineated the ic and cp as one structure. The ic was defined as a coherent region of white matter (i.e. a continuous cluster of voxels with hyperintensive T1 contrast) located in between the globus pallidus (GP) and the thalamus, thus excluding the dispersed and apparently solitary fiber bundles within the striatum. Obviously, these discontinuities relate to the thickness of fiber bundles relative to the employed voxel size. The further trajectory of the ic/cp was readily delineated in T1-weighted images to the level of the pons, where DTI images were used to differentiate the cp from the ascending medial lemniscus (ml). The anterior commissure (ac), which decussates anterior of the fornix (f) columns, has an anterior part (aca) extending anteriorly into the olfactory bulb (OB), and a posterior part (acp) extending laterally into the striatum. Both the aca and acp were readily identified in both T1 and DTI images. The optic tract (opt) contains fibers from the optic nerves and runs along the ventrolateral surface of the diencephalon from the optic chiasm (och) to the lateral geniculate nucleus of the thalamus. It is difficult to distinguish from neighboring fiber tracts in T1 images, but detectable in DTI maps showing mediolateral and dorsoventrally oriented diffusion. The fimbria (fi) and fornix (f) of the hippocampus contain the main output fiber bundles of the hippocampus, and were mainly delineated from DTI images, aided by histological material showing the corresponding orientations of myelinated fibers. The fi forms a band of white matter along the lateral and rostral aspects of the hippocampus, and the f a distinct flat bundle close to the midline below the cc (Amaral and Lavenex, 2007). The boundary of the fi towards the lateral ventricle (LV) and its ependymal lining was delineated in T1 images.
2.6.2. Subcortical grey matter
Most parts of the basal ganglia (the striatum, the globus pallidus (GP), entopeduncular nucleus (EP), and the substantia nigra (SN)) were segmented on basis of the T1-weighted images. The striatum includes the caudate-putamen (CPu) complex and the core of the nucleus accumbens (Acb) (Gerfen, 2004), and was dorsally delinated along the ec, and ventrally along the relatively hyperintensive contrast of the olfactory tubercle. Since the posterior limit of the striatum is ambiguous, it was arbitrarily set at the most anterior level where the distinct CA3 field of the hippocampus is visible in coronal slices. The striatum is usually divided into a dorsal (CPu) and ventral (Acb) region on basis of hodology and neurochemistry (Voorn et al., 2004). As the boundary between the CPu and Acb is unclear in histological and tomographical material, it is usually defined by an imaginary line between the inferior tip of the LV and the rhinal fissure (rf) (Ingham et al., 1998; Van de Berg et al., 2000; Voorn et al., 2004). In our material, the following subdivisions of the dorsal and ventral striatum were employed: Anterior of the decussation of the ac, a line was drawn between the rf to the inferior tip of the LV. In further anterior regions where the LV could not be distinguished in T1 images, the ventromedial tip of the cc was used as a substitute landmark. Posterior of the decussation of the ac a line was drawn between the left and right rf.
2.7. Correction of ex vivo atlas
Because the ex vivo atlas is based on a single rat brain, it might be biased towards subject-specific anatomical features. To minimize these effects, we mapped the high-resolution, ex vivo images and parcellation map nonrigidly, i.e. using the viscous fluid model, into the in vivo population-averaged space.
3. Results
3.1. Population-averaged DTI template
3.1.1. Registration quality
The construction of the population-averaged was initialized by the affine alignment of each in vivo dataset to a single, arbitrarily chosen, reference in vivo dataset. After affine registration, however, there was still a considerable amount of misregistration noticeable as shown in Fig. 4(a). In the figure, the intersubject FA variance, voxelwise calculated across all affinely aligned subjects, is visualized on top of the corresponding average FA map. As shown in Fig. 4(b), the amount of misregistration has been significantly reduced by applying the second step of the construction of the population-averaged DTI brain template, which involved nonrigid deformation of the datasets. Fig. 4(b) shows the FA variance, calculated after warping each subject onto the population-averaged DTI template, on top of the population-averaged FA map. One may in particular appreciate the clearly decreased FA variance in all boundaries of the white matter structure, corresponding to a sharper white/grey matter contrast.
Figure 4.
(a) The average in vivo FA template (in grey colour scale) of a single horizontal slice after affine alignment of all subjects to a single, arbitrarily chosen, subject, overlaid with the intersubject FA variance map (shown in spectral colour scale). Blue regions indicate low variability, while red indicate high variability. (b) Compared to (a), the FA variance and average was calculated after warping each subject onto the population-averaged DTI template.
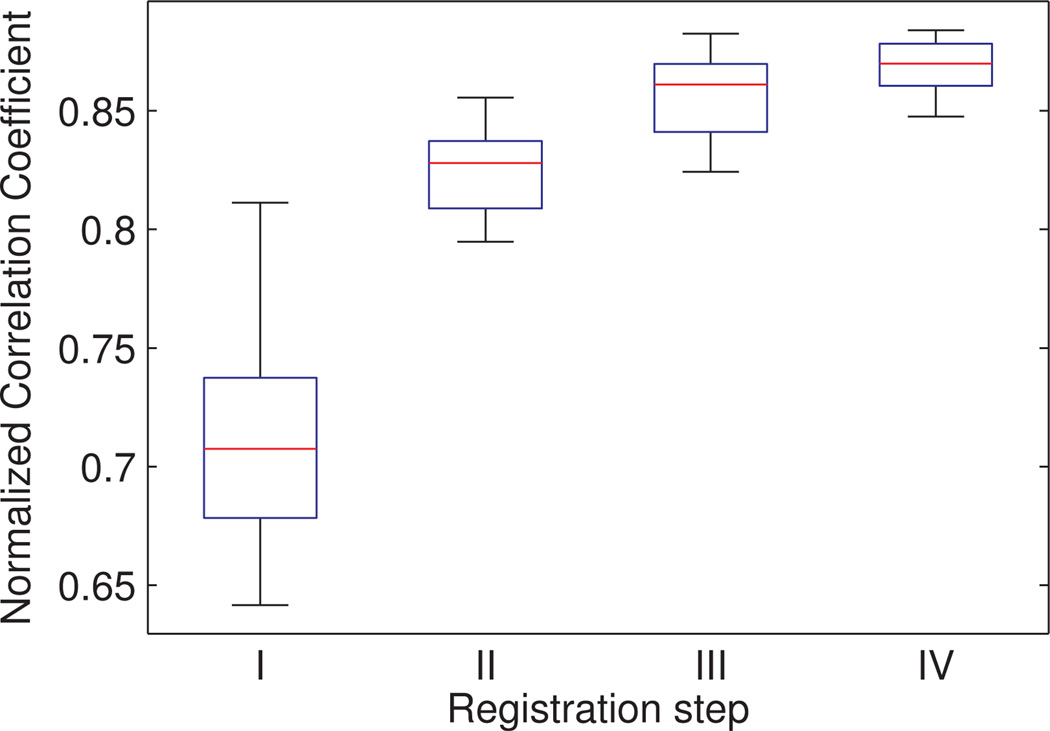
To further quantify and compare the quality of the different registration steps, we evaluated similarity between aligned DTI datasets - represented by their FA maps - using the normalized correlation coefficient. We calculated the similarity between pairs of DTI datasets, which were (I) not aligned (original data), (II) affinely aligned, (III) nonrigidly aligned to a single subject, and (IV) nonrigidly aligned to the population-averaged DTI brain template. Note that (I), (II), and (IV) were steps included in the construction of the population-averaged DTI brain template, while (III) was only evaluated for comparison purposes. For each registration step, an FA map was generated for all nine individual subjects. Each set of FA maps resulted in 36 pairwise calculated normalized correlation coefficients, which could be used to compare the image alignment across the different registration steps (see Fig. 5). Adding a nonrigid coregistration step during atlas construction resulted in a significantly increase of pairwise normalized correlation coefficients. Furthermore, the construction of a population-averaged template (IV) yielded significantly higher correlation coefficients compared to the subject-based atlas construction approach (III). Statistical difference between the consecutive steps was demonstrated with a paired student t-test, with significance level set to 0.05.
Figure 5.
Similarity between pairs of DTI datasets (represented by the FA map), which were (I) not aligned (original data), (II) affinely aligned, (III) nonrigidly aligned to a single subject, and (IV) nonrigidly aligned to the population-averaged DTI brain template, was evaluated with the normalized correlation coefficient. Each set of FA maps resulted in 36 pairwise calculated normalized correlation coefficients, of which the median value is indicated by the red lines. The lower and upper edges of the boxes correspond to the 25th and 75th percentiles, respectively.
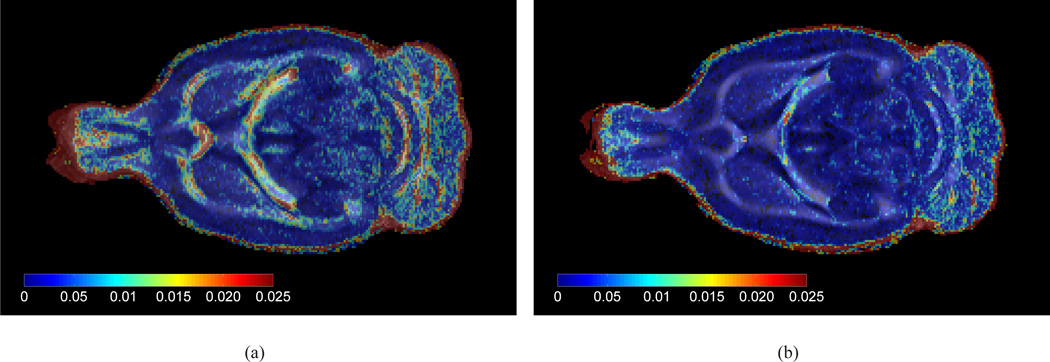
3.1.2. Anatomical variability
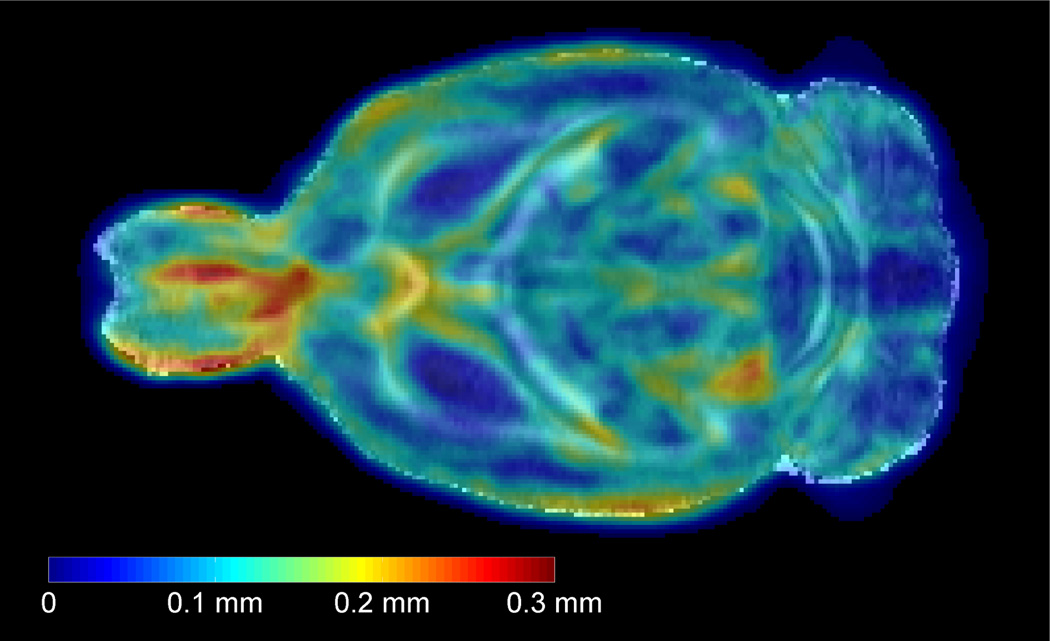
To evaluate the degree of anatomical variability within the sample population, a deformation field was computed for each single subject by warping the population-averaged brain template to each subject using the nonrigid coregistration algorithm. The deformation fields, i.e. the length of the deformation vectors, quantify the anatomical differences among the individual brains and the average anatomy, represented by the population-averaged template in each voxel. By voxelwise averaging the length of the deformation vectors over all studied rats, an anatomical variability magnitude (AVM) map is obtained (Aggarwal et al., 2009). The intensity levels in the map denote distances in millimeters, and represent the average anatomical variability in the adult rat brain across the sample population (see Fig. 6). The average spatial variability in the whole brain was calculated to be 0.075 ± 0.050mm. The highest degree of variability across subjects, up to as 0.3mm, was seen in the olfactory bulb. Tissues around the LV and central part of the cc also tended to have large variability (up to 0.2mm).
Figure 6.
A single horizontal slice of the in vivo population-averaged FA template (in grey colour scale) overlaid with the anatomical variability magnitude (AVM) map (shown in spectral colour scale). The intensity levels in the AVM map denote distances in millimeters, and represent the average anatomical variability in the adult rat brain across the sample population. Blue regions indicate low anatomical variability, while red indicate high anatomical variability.
3.2. Manual delineation of ex vivo data
A selection of white matter and grey matter regions were manually segmented on basis of T1-weighted (Fig. 2(a)) and a direction encoded (DEC) FA map that more effectively visualizes the directional information embedded in the primary eigenvector, i.e., the local fiber orientation (Fig. 2(b)). The boundaries of several structures that are difficult to distinguish in anatomical images are well differentiated in the colored DEC map. Two examples are visualized in Fig. 3. First, it is not possible to distinguish the cg and cc in the T1 images, the DEC map however reveals that the fiber orientation of the cg, as running anterioposteriorly (blue), is almost perpendicular to the main direction of corpus callosum, which runs mediolateral (red). Second, the dorsal boundary of the ec is ambiguous in T1-weighted images (arrowheads in (3(d)), but readily identified mediolaterally oriented diffusion orientations in DTI.
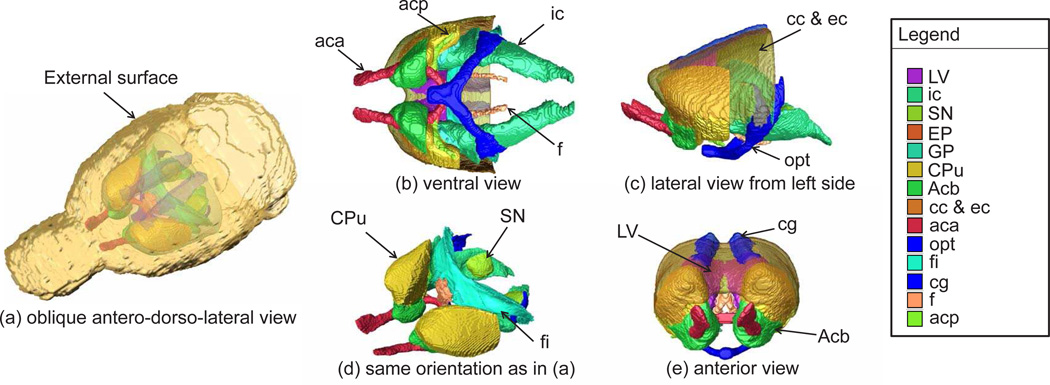
In Fig. 7, 3D rendering images of the delineated brain structures - Acb, CPu, GP, EP, S N, cc/ec, ic, fi, f, acp, aca, opt, cg, and LV - were visualized using AMIRA software®.
Figure 7.
3D rendering images of the delineated brain structures: the nucleus accumbus (Acb), caudate putamen complex (CPu), globus pallidus (GP), entopeduncular nucleus (EP), substantia nigra (SN), external capsule (ec), corpus callosum (cc), internal capsule (ic), fimbria of the hippocampus (fi), fornix (f), posterior (acp) and anterior part (aca) of anterior commisure, optic tract (opt), cingulum (cg), and lateral ventricle (LV) were manually segmented with ITK-SNAP and visualized using AMIRA software®.
3.3. Correction of ex vivo data
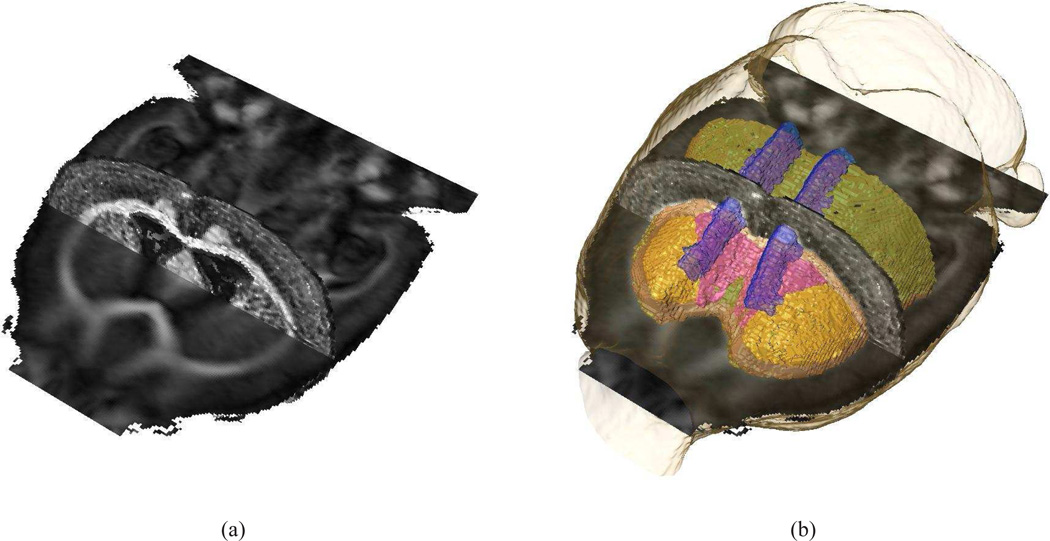
A nonrigid coregistration algorithm was used to minimize the morphological differences between in vivo and ex vivo samples. In Fig. 8(a), a horizontal and coronal section of the FA maps of the in vivo population based atlas and the ex vivo subject, respectively, are shown to indicate the accurate alignment of both datasets. In Fig. 8(b), a 3D rendering of cc/ec, cg, and LV are superimposed onto Fig. 8(a). The proper alignment of the anatomical labels, the in vivo, and ex vivo data is evident from Fig. 8. The corrected ex vivo atlas, i.e. the deformed ex vivo DTI and T1 data and the corresponding parcellation map, can be obtained by contacting the corresponding author. Data are provided in Amira® and NifTi format.
Figure 8.
A horizontal and coronal section of the FA maps of the in vivo population based atlas and the ex vivo subject, respectively, are shown (a) to indicate the accurate alignment of both datasets after applying a nonrigid coregistration algorithm to minimize morphological differences between both samples. In (b), a 3D rendering of cc/ec, cg, and LV are superimposed onto (a); Coloring in accordance to Fig. 7.
4. Discussion
In this study, we have proposed an anatomically labeled DTI atlas of the average brain of the adult SD rat, the most widely used rat strain in laboratory animal research. Furthermore, the SD rat is so far the preferred strain to produce transgenic rat models of human neurodegenerative pathologies (e.g. Bugos et al., 2009; von Hörsten et al., 2003; Vermeiren et al., 2006; Liu et al., 2008).
The construction of brain atlases has been a topic of intense research for the last decades. Standard rat brain atlases consist of drawings based on histological studies of a Wistar and SD rat brain by Paxinos and Watson (1986, 2007) and Swanson (1992, 1998, 2004), respectively. The atlases describe the brain as a series of 2D sections with boundaries of areas and nuclei indicated, and names assigned to the delineated structures. Nevertheless, the use of such atlases for neuroimaging studies are hampered by the 2D format, resulting in discontinuous 3D structures after coarse alignment of the individual slices, as well as a lack of an analytical power for comparison of atlas and image data. While the diagrams presented in the atlases of Paxinos and Watson (1986, 2007) and Swanson (1992, 2004) are developed from study of several animals, they do not systematically incorporate anatomical variation across subjects within the given strain. Next, the lack of CSF pressure, and skull encasement constraints inherent to histological processing affect the brain, as a result of which morphological differences occur between the histology-derived atlases and in vivo data acquired with, e.g., MRI (Schwarz et al., 2006).
It has long been appreciated that MRI can advance the construction of brain atlases since it is a non-invasive, 3D and in vivo imaging technique, which enables accurate identification of a large number of anatomical structures. Therefore, recently, some MRI templates of the rat brain and digital atlases of its major brain structures have been developed. Firstly,Schweinhardt et al. (2003) constructed an MRI template that could be used to normalize subjects to the stereotaxic space defined by Paxinos and Watson (2007). They created an MRI template based on high resolution T2-weighted images of five female SD rats. A large set of anatomical landmarks were manually identified in each set of images and in the atlas. For each animal, an affine transformation that maps the set of landmarks of the corresponding image volume onto the atlas landmarks was estimated. These transformation matrices were used to resample the individual volumes into the stereotaxic space.Schwarz et al. (2006) constructed a stereotaxic T2 template using 97 adult male SD rats. In addition, tissue classes were developed to guide delineation of the brain parenchyma from CSF. The MRI template was spatially normalized to the stereotaxic space of the Paxinos atlas by affine registration of the MRI brain tissue class map to the outline contour atlas images, corresponding to Paxinos’ figures 4 – 78 (Paxinos and Watson, 2007). Furthermore,Hess et al. (2005) aimed an automatic identification and structure assignment of activated voxel groups from functional MRI by using a labeled standard atlas. Therefore, they constructed a T2 atlas from 54 SD rats using an affine coregistration technique to transform the individual subjects to the common reference template.
Our work distinguishes fromthe preceding studies concerning rat atlas construction since (I) a population-averaged brain atlas was constructed to obtain a template that represents the unbiased average anatomy. (II) During the construction, a nonrigid coregistration technique was used to avoid local misalignment inaccuracies, and partial volume averaging of anatomically distinct structures, due to intersubject morphological differences as shown in Fig. 4. (III) Accurate manual delineation of brain white matter structures was conducted on high resolution ex vivo diffusion weighted scans.
A high-resolution population-averaged MRI based atlas has a wide range of potential use, for example, as a reference space for coregistration of brain image data and for assigning anatomical labels to such data (Hjornevik et al., 2007). Our DTI atlas is particularly useful tool for quantitative DTI group analyses, often based on a exploratory approach with voxel based statistical comparison or a hypothesis-driven manual ROI analysis. For voxels based comparisons our atlas provides an excellent spatial reference template for coregistration, while during ROI analyses, our atlas can be used to guide the manual delineation of anatomical structures. We have successfully conducted such analyses in studies on diffusion MRI changes in rats transgenic for Huntington disease (Antonsen et al., 2010).
To allow even more consistent and reproducible ROI delineations, one could use the DTI atlas to enable automated atlas-based delineation. For such purposes, the atlas is warped to the studied images by a spatial transformation, such that labels defined in the atlas are accurately projected onto the anatomically corresponding structures in the images under study. For ROI based comparisons of disease models, it is of importance that disease related changes are not averaged out by warping the data to an atlas. Therefore, we advise to apply the DTI atlas for standardized and automated ROI delineation by first warping brain volumes to the atlas, and subsequently use the inverse deformation field to map the atlas labels to the original data volume. An important source of inaccurate atlas-based delineation of ROIs includes registration errors. Therefore, it is important to note that affine registrations often lead to insufficient correlation between manual and automated ROI approaches due to nonlinear intersubject anatomical or age dependent differences. Therefore, we advise to use the atlas in combination with a nonlinear coregistration algorithm. Although in-house coregistration software based on the viscous fluid model was used in the study, many other algorithm - often freely distributed - might be useful. Commonly used software packages are SPM and FSL in which the nonrigid deformations are defined by a linear combination of three dimensional discrete cosine transform (DCT), respectively, cubic B-spline basis functions (Ashburner and Friston, 1999; Smith et al., 2004). A more thorough overview and evaluation of the broad range of nonrigid coregistration algorithms was given byKlein et al. (2009).
We would like to emphasize that the diffusion parameters that can be derived from the atlas are not ground truth values that can be used as a reference in future DTI studies. Although the diffusion of water molecules is a physical property of the tissue being measured, the estimated diffusion coefficients depend on scanner settings such as the b-value and, thus, the comparison between various DTI studies get hampered (e.g. Horsfield, 2001).Veraart et al. (2011) demonstrated that amore accurate and b-value independent estimation of the diffusion parameters can be obtained with diffusion kurtosis imaging (DKI), a recently proposed higher order diffusion model (Jensen et al., 2005). However, given a fixed acquisition time, an equally precise parameter estimation with DKI requires a decreased resolution, which might cause a lack of anatomical detail. Note that we preferred to put emphasis on the anatomical detail instead of the quantification accuracy in this study.
Future developments might include delineations of more anatomical structures and establishment of a spatial reference coordinate system based on internal anatomical landmarks, in line with the criteria used for defining the Waxholm space in the adult, male C57BL/6 mouse brain (Hawrylycz et al., 2009, 2011; Johnson et al., 2010). This will further increase the application value of the atlas for integration and comparison of different data modalities.
Acknowledgement
This work was partly supported by the Institute for the Promotion of Innovation through Science and Technology in Flanders (IWT-Vlaanderen) and partially by SBO grant 060819 ”Quantiviam” of IWT and by IAP-grant P6/38 of the Belgian Science Policy. The project was as well partly funded by grants from The Research Council of Norway (TBL). Ex vivo MR imaging was performed at the Duke Center for In Vivo Microscopy, an NIH/NCRR national Biomedical Technology Research Center (P41 RR005959) and Small Animal Imaging Resource Program (U24 CA092656). In vivo data were acquired at the bio-imaging lab (University of Antwerp). We are grateful to Stephan von Hörsten for providing animals, Boma Fubara and Yvette van Dongen for helpful advice and assistance with specimen preparation, Laurence Hedlund for logistical assitance, Gary Cofer for assistance with MR acquisition, Hong Qu for assistance with image processing, and Jan G. Bjaalie for valuable discussions.
References
- Aggarwal M, Zhang J, Miller M, Sidman R, Mori S. Magnetic resonance imaging and micro-computed tomography combined atlas of developing and adult mouse brains for stereotaxic surgery. Neuroscience. 2009;162(4):1339–1350. doi: 10.1016/j.neuroscience.2009.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander DC, Pierpaoli C, Basser PJ, Gee JC. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imaging. 2001;20(11):1131–1139. doi: 10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- Amaral D, Lavenex P. Hippocampal neuroanatomy. In: Andersen P, Morris R, Amaral D, Bliss T, O’Keefe J, editors. The Hippocampus. New York: Oxford University Press; 2007. Ch. 3. [Google Scholar]
- Antonsen BT, Jiang Y, Veraart J, Van Dongen Y, Qu H, Urbach Y, Raber K, Nguyen HP, Sijbers J, von Hörsten S, Johnson GA, Leergaard TB. Altered ex vivo diffusion mri in basal ganglia of transgenic huntington’s disease rats. 7th Forum of European Neuroscience Abstracts 0.46.2. 2010 Jul [Google Scholar]
- Ashburner J, Friston K. Nonlinear spatial normalization using basis functions. Human Brain Mapping. 1999;7:254–266. doi: 10.1002/(SICI)1097-0193(1999)7:4<254::AID-HBM4>3.0.CO;2-G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, Le Bihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994 Jan;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bugos O, Bhide M, Zilka N. Beyond the rat models of human neurodegenerative disorders. Cell Mol Neurobiol. 2009;29(6–7):859–869. doi: 10.1007/s10571-009-9367-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cenci MA, Whishaw I, Schallert T. Animal models of neurological deficits: how relevant is the rat? Nat Rev Neurosci. 2002;3(7):574–579. doi: 10.1038/nrn877. [DOI] [PubMed] [Google Scholar]
- Chung S, Lu Y, Henry RG. Comparison of bootstrap approaches for estimation of uncertainties of DTI parameters. NeuroImage. 2006 Nov;33(2):531–541. doi: 10.1016/j.neuroimage.2006.07.001. [DOI] [PubMed] [Google Scholar]
- Coleman KA, Baker GE, Mitrofanis J. Topography of fibre organisation in the corticofugal pathways of rats. J Comp Neurol. 1997;381(2):143–157. doi: 10.1002/(sici)1096-9861(19970505)381:2<143::aid-cne3>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Cozzi J, Fraichard A, Thiam K. Use of genetically modified rat models for translational medicine. Drug Discov Today. 2008;13(11–12):488–494. doi: 10.1016/j.drudis.2008.03.021. [DOI] [PubMed] [Google Scholar]
- D’Agostino E, Maes F, Vandermeulen D, Suetens P. A viscous fluid model for multimodal non-rigid image registration using mutual information. Medical Image Analysis. 2003;7(4):565–575. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
- Dauguet J, Peled S, Berezovskii V, Delzescaux T, Warfield S, Born R, Westin C. Comparison of fiber tracts derived from in-vivo DTI tractography with 3D histological neural tract tracer reconstruction on a macaque brain. NeuroImage. 2007;37(2):530–538. doi: 10.1016/j.neuroimage.2007.04.067. [DOI] [PubMed] [Google Scholar]
- Gerfen CR. Basal ganglia. In: Paxinos G, editor. The rat nervous system. third edition. San Diego: Elsevier Academic Press; 2004. [Google Scholar]
- Hawrylycz M, Baldock RA, Burger A, Hashikawa T, Johnson GA, Martone M, Ng L, Lau C, Larsen SD, Nissanov J, Puelles L, Ruffins S, Verbeek F, Zaslavsky I, Boline J. Digital atlasing and standardization in the mouse brain. PLoS Comput Biol. 2011;7(2):e1001065. doi: 10.1371/journal.pcbi.1001065. 02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawrylycz M, Boline J, Burger A, Hashikawa T, Johnson G, Martone M, Ng L, Nissanov J, Puelles L, Ruffins S, et al. The INCF Digital Atlasing Program: Report on Digital Atlasing Standards in the Rodent Brain. 2009 [Google Scholar]
- Heimer L, Ebner FF, Nauta WJ. A note on the termination of commissural fibers in the neocortex. Brain Res. 1967;5(2):171–177. doi: 10.1016/0006-8993(67)90085-6. [DOI] [PubMed] [Google Scholar]
- Hess A, Kreitz S, Brune K. Functional atlas of the rat brain. Berlin Heidelberg: Springer; 2005. pp. 73–77. [Google Scholar]
- Hjornevik T, Leergaard TB, Darine D, Moldestad O, Dale AM, Willoch F, Bjaalie JG. Three-dimensional atlas system for mouse and rat brain imaging data. Frontiers in Neuroinformatics. 2007 doi: 10.3389/neuro.11.004.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horsfield MA. Using diffusion-weighted MRI in multicenter clinical trials for multiple sclerosis. J Neurol Sci. 2001;186(Supplement 1):S51–S54. doi: 10.1016/s0022-510x(01)00492-0. [DOI] [PubMed] [Google Scholar]
- Ingham CA, Hood SH, Taggart P, Arbuthnott GW. Plasticity of synapses in the rat neostriatum after unilateral lesion of the nigrostriatal dopaminergic pathway. J Neurosc. 1998;18(12):4732–4743. doi: 10.1523/JNEUROSCI.18-12-04732.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17(2):825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432–1440. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Hsu E. Accelerating MR diffusion tensor imaging via filtered reduced-encoding projection-reconstruction. Magn Reson Med. 2005;53(1):93–102. doi: 10.1002/mrm.20311. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Pandya K, Smithies O. Three-dimensional diffusion tensor microscopy of fixed mouse hearts. Magn Reson Med. 2004;52(3):453–460. doi: 10.1002/mrm.20191. [DOI] [PubMed] [Google Scholar]
- Johnson G, Badea A, Brandenburg J, Cofer G, Fubara B, Liu S, Nissanov J. Waxholm Space: An image-based reference for coordinating mouse brain research. NeuroImage. 2010;53(2):365–372. doi: 10.1016/j.neuroimage.2010.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson GA, Ali-Sharief A, Badea A, Brandenburg J, Cofer G, Fubara B, Gewalt S, Hedlund LW, Upchurch L. High-throughput morphologic phenotyping of the mouse brain with magnetic resonance histology. NeuroImage. 2007;37(1):82–89. doi: 10.1016/j.neuroimage.2007.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson GA, Cofer GP, Gewalt SL, Hedlund LW. Morphologic Phenotyping with MR Microscopy: The Visible Mouse. Radiology. 2002;222(3):789. doi: 10.1148/radiol.2223010531. [DOI] [PubMed] [Google Scholar]
- Jones D. Studying connections in the living human brain with diffusion MRI. Cortex. 2008;44(8):936–952. doi: 10.1016/j.cortex.2008.05.002. [DOI] [PubMed] [Google Scholar]
- Kaufman J, Ahrens E, Laidlaw D, Zhang S, Allman J. Anatomical analysis of an aye-aye brain (Daubentonia madagascariensis, Primates: Prosimii) combining histology, structural magnetic resonance imaging, and diffusion-tensor imaging. The Anatomical Record Part A: Discoveries in Molecular, Cellular, and Evolutionary Biology. 2005;287(1):1026–1037. doi: 10.1002/ar.a.20264. [DOI] [PubMed] [Google Scholar]
- Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang M-C, Christensen GE, Collins DL, Gee J, Hellier P, Song JH, Jenkinson M, Lepage C, Rueckert D, Thompson P, Vercauteren T, Woods RP, Mann JJ, Parsey RV. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009;46(3):786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay C, Chang L, Carew J, Pierpaoli C, Basser P. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. Journal of Magnetic Resonance. 2006;182(1):115–125. doi: 10.1016/j.jmr.2006.06.020. [DOI] [PubMed] [Google Scholar]
- Kochunov P, Lancaster JL, Thompson P, Woods R, Mazziotta J, Hardies J, Fox P. Regional spatial normalization: toward an optimal target. J Comput Assist Tomogr. 2001;25(5):805–816. doi: 10.1097/00004728-200109000-00023. [DOI] [PubMed] [Google Scholar]
- Le Bihan D, Mangin J-F, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H. Diffusion tensor imaging: Concepts and applications. J Magn Reson Imaging. 2001;13(4):534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- Leergaard TB, White NS, De Crespigny A, Bolstad I, D’Arceuil H, Bjaalie JG, Dale AM. Quantitative Histological Validation of Diffusion MRI Fiber Orientation Distributions in the Rat Brain. PLoS ONE. 2010;5(1):e8595. doi: 10.1371/journal.pone.0008595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin CP, Tseng W, Cheng H, Chen J. Validation of diffusion tensor magnetic resonance axonal fiber imaging with registered manganeseenhanced optic tracts. NeuroImage. 2001;14(5):1035–1047. doi: 10.1006/nimg.2001.0882. [DOI] [PubMed] [Google Scholar]
- Liu L, Orozco IJ, Planel E, Wen Y, Bretteville A, Krishnamurthy P, Wang L, Herman M, Figueroa H, Yu WH, Arancio O, Duff K. A transgenic rat that develops alzheimer’s disease-like amyloid pathology, deficits in synaptic plasticity and cognitive impairment. Neurobiol Dis. 2008;31(1):46–57. doi: 10.1016/j.nbd.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;16(2):187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- Papadakis NG, Xing D, Huang CLH. A comparative study of acquisition schemes for diffusion tensor imaging using MRI. J Magn Reson. 1999;137(1):67–82. doi: 10.1006/jmre.1998.1673. [DOI] [PubMed] [Google Scholar]
- Paxinos G, Watson C. The Rat Brainin Stereotaxic Coordinates. Sydney: Academic Press; 1986. [Google Scholar]
- Paxinos G, Watson C. The rat brain in stereotaxic coordinates. Academic press; 2007. [DOI] [PubMed] [Google Scholar]
- Sargon MF, Mas N, Senan S, Ozdemir B, Celik HH, Cumhur M. Quantitative analysis of myelinated axons of commissural fibers in the rat brain. Anat Histol Embryol. 2003;32(3):141–144. doi: 10.1046/j.1439-0264.2003.00446.x. [DOI] [PubMed] [Google Scholar]
- Schwarz AJ, Danckaert A, Reese T, Gozzi A, Paxinos G, W Watson C, Merlo-Pich EV, Bifone A. A stereotaxic MRI template set for the rat brain with tissue class distribution maps and co-registered anatomical atlas: Application to pharmacological MRI. NeuroImage. 2006 Aug;32(2):538–550. doi: 10.1016/j.neuroimage.2006.04.214. [DOI] [PubMed] [Google Scholar]
- Schweinhardt P, Fransson P, Olson L, Spenger C, Andersson JL. A template for spatial normalisation of MR images of the rat brain. J Neurosci Methods. 2003 Oct;129(2):105–113. doi: 10.1016/s0165-0270(03)00192-4. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, Luca MD, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, Stefano ND, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(Supplement 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Swanson L. Brain maps: structure of the rat brain. Amsterdam: Elsevier; 1992. [Google Scholar]
- Swanson L. Brain maps: structure of the rat brain: a laboratory guide with printed and electronic templates for data, models and schematics. 2nd Edition. Amsterdam: Elsevier; 1998. [Google Scholar]
- Swanson LW. A Laboratory Guide with Printed and Electronic Templates for Data, Models and Schematics. 3rd Edition. Amsterdam: Elsevier; 2004. Brain Maps: Structure of the Rat Brain. [Google Scholar]
- Swanson LW, Cowan WM. The connections of the septal region in the rat. J Comp Neurol. 1979;186(4):621–655. doi: 10.1002/cne.901860408. [DOI] [PubMed] [Google Scholar]
- Van de Berg WD, Blokland A, Cuello AC, Schmitz C, Vreuls W, Steinbusch HW, Blanco CE. Perinatal asphyxia results in changes in presynaptic bouton number in striatum and cerebral cortex-a stereological and behavioral analysis. J Chem Neuroanat. 2000;20(1):71–82. doi: 10.1016/s0891-0618(00)00078-8. [DOI] [PubMed] [Google Scholar]
- Van Hecke W, Leemans A, D’Agostino E, De Backer S, Vandervliet E, Parizel PM, Sijbers J. Nonrigid coregistration of diffusion tensor images using a viscous fluid model and mutual information. IEEE Trans Med Imaging. 2007;26(11):1598–1612. doi: 10.1109/TMI.2007.906786. [DOI] [PubMed] [Google Scholar]
- Van Hecke W, Sijbers J, D’Agostino E, Maes F, De Backer S, Vandervliet E, Parizel P, Leemans A. On the construction of an inter-subject diffusion tensor magnetic resonance atlas of the healthy human brain. NeuroImage. 2008;43(1):69–80. doi: 10.1016/j.neuroimage.2008.07.006. [DOI] [PubMed] [Google Scholar]
- Veraart J, Poot DHJ, Van Hecke W, Blockx I, Van der Linden A, Verhoye M, Sijbers J. More accurate estimation of diffusion tensor parameters using diffusion kurtosis imaging. Magn Res Med. 2011;65(1):138–145. doi: 10.1002/mrm.22603. [DOI] [PubMed] [Google Scholar]
- Vermeiren C, Hemptinne I, Vanhoutte N, Tilleux S, Maloteaux J-M, Hermans E. Loss of metabotropic glutamate receptor-mediated regulation of glutamate transport in chemically activated astrocytes in a rat model of amyotrophic lateral sclerosis. J Neurochem. 2006;96(3):719–731. doi: 10.1111/j.1471-4159.2005.03577.x. [DOI] [PubMed] [Google Scholar]
- von Hörsten S, Schmitt I, Nguyen HP, Holzmann C, Schmidt T, Walther T, Bader M, Pabst R, Kobbe P, Krotova J, Stiller D, Kask A, Vaarmann A, Rathke-Hartlieb S, Schulz JB, Grasshoff U, Bauer I, Vieira-Saecker AMM, Paul M, Jones L, Lindenberg KS, Landwehrmeyer B, Bauer A, Li X-J, Riess O. Transgenic rat model of Huntington’s disease. Hum Mol Genet. 2003;12(6):617–624. doi: 10.1093/hmg/ddg075. [DOI] [PubMed] [Google Scholar]
- Voorn P, Vanderschuren LJ, Groenewegen HJ, Robbins TW, Pennartz CM. Putting a spin on the dorsal-ventral divide of the striatum. Trends Neurosci. 2004;27(8):468–474. doi: 10.1016/j.tins.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Wang Q, Seghers D, DAgostino E, Maes F, Vandermeulen D, Suetens P, Hammers A. Construction and validation of mean shape atlas templates for atlas-based brain image segmentation. LNCS. 2005;3565:689–700. doi: 10.1007/11505730_57. [DOI] [PubMed] [Google Scholar]
- White LEJ. Ipsilateral afferents to the hippocampal formation in the albino rat. J Comp Neurol. 1959;113:1–14. doi: 10.1002/cne.901130102. [DOI] [PubMed] [Google Scholar]
- Woelche M. Eine neue methode der markscheidenfarbung. J Psychol Neurol. 1942;51:199–202. [Google Scholar]
- Yushkevich P, Piven J, Hazlett H, Smith R, Ho S, Gee J, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. NeuroImage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]