Abstract
A new method to generate a bifurcating distributive system is presented. The method utilizes random points inside a given area and is sensitive to the global and local concentrations of the points. The algorithm is highly efficient compared to the current area-halving algorithms.
INTRODUCTION
All higher biological organisms require internal distributive systems to supply nutrients and to remove heat and waste. Some well-known examples include the veins on leaves, the lung airways, and the arterial (or venous) system for blood. A theoretical model is needed to study the function and dynamics of such distributive systems since in many cases experiments may be either impossible for some parameter ranges or too costly in terms of equipments and specimens. Due to the complexity of the numerous and somewhat chaotic branchings of the actual system, modelling has been extremely difficult.
One important conceptual criterion for any theoretical distributive system is as follows: Any location in a given region should be reachable by a path through the system. In other words, the system should “cover” a given region. Since the topological dimension of the branching system is one, we need its Hausdorff-Besicovitch dimension to be increased to be the same as the dimension of the region. In this sense the branching system is a fractal.
Mandelbrot [1] proposed a few area-filling fractal branching systems which resemble river drainage basins. The final boundary shapes, however, are highly irregular. He also generated fractal bifurcating trees, one of which is an area-filling model of the lung airways. The Mandelbrot lung has a specific rectangular shape of dimensions by 1.
In order to take into account the final shape of the region to be covered, an area splitting algorithm was first suggested by Nelson and Manchester [2]. Their method is as follows. A ray which contains the first branch divides a given area by half. The length of the branch is one half the length of the ray within the available region. Starting from the tip of the first branch the sub-areas are halved again and higher generation branches are similarly determined. This algorithm would generate the Mandelbrot lung if the region is a rectangle with aspect ratio : 1. A similar algorithm with varying branch length ratios was proposed by Wang and Bassingthwaighte [3]. It was shown that, if the angles between branches are not constrained, the distributive system would cover the region, i.e., the fractal dimension equals two and every point in the region can be reached.
The area-halving algorithms are extremely tedious due to the fact that for N generations of branching there are 2N – 1 computations of areas of various irregular shapes. In this paper we shall introduce a much more efficient method in the construction of distributive systems in given region by using a Monte Carlo method. One of the advantages is that area integrations are no longer required.
MONTE CARLO METHOD
The Monte Carlo method makes use of random numbers to simulate specific problems [4,5]. Although the method was known in the eighteenth century, its importance has not been realized until the past 30 years, when the advent of the computer makes the necessary calculations more feasible. For example, the area of a flat surface with complicated boundary may be estimated as follows. Let the surface be placed inside a rectangle and generate a large number random points inside the rectangle. The area of the surface is then proportional to the number of points within the boundary of the surface. Usually about 1000 random points are required for 2 digit accuracy in area.
Now we can certainly use Monte Carlo method to directly supplant the area computations in the area-halving algorithms. There is, however, another approach which dispenses the area concept altogether. The method is described in the next section.
BRANCHING SYSTEMS SERVICING A COLLECTION OF POINTS
Consider a collection of points on a plane. The points may or may not be randomly distributed. The following algorithm would construct a bifurcating branching system which serves these points
The center of mass of the points is found by averaging the individual coordinate positions.
From a given starting point, a dividing line connecting the center of mass is constructed. A branch from the starting point lies on this line and has a length a certain fraction of the distance to the center of mass.
The dividing line thus separates two sub-collection of points with new starting points at the tip of the branch just found.
The process is repeated until the sub-collection contains only one point. Then the branch ends at that point.
Figure 1 shows 50 random points in square. A branching system is generated to serve all 50 points. Since the branches are attracted towards the centers of mass, we find more branchings in regions where the points are more concentrated. Figure 2 shows the same distribution of points, but with a different starting point. Connectivity between points are also different.
Figure 1.
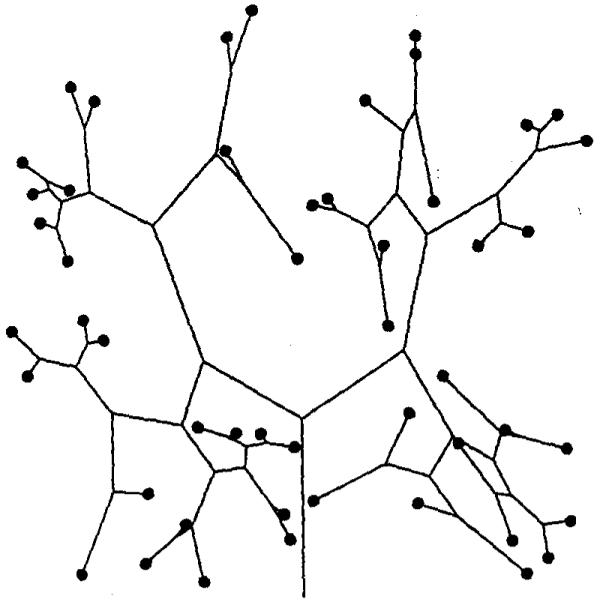
Figure 2.
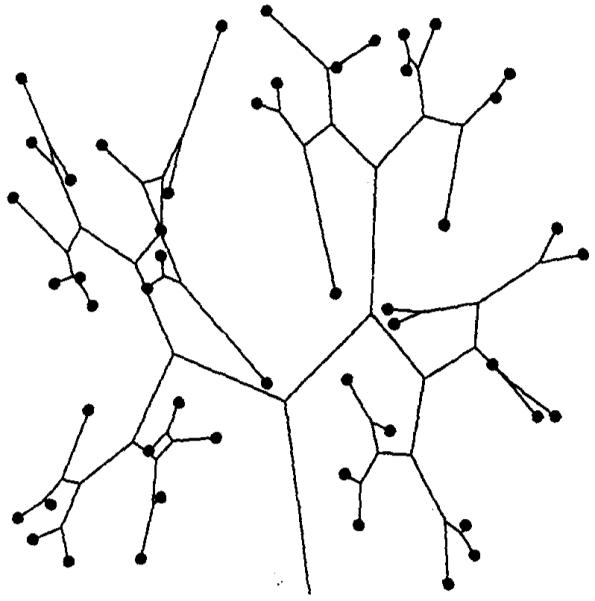
The above algorithm would be equivalent to the area-halving algorithm in [2,3] if the points are numerous and evenly spaced. There is no doubt every point can be reached by the distributive branching system. If there are infinite number of points covering an entire area, then the system would cover the area. The fractal dimension of the branch tips would be two.
REPRESENTING A GIVEN AREA BY A COLLECTION OF POINTS
In order to construct a branching system covering a given area by the present method, the area must be represented by large number of random points. We shall discuss the methods to generate random points for different geometries. Let R[ ] be a pseudo-random number in [0,1] supplied by the computer. If the area is a square of size 1 × 1, then the coordinates of random point are{R[ ], R[ ]}. For rectangles, let the range of one coordinate be from a to b, then the random coordinate is given by a + (b – a)R[ ]. It is also possible to bend some boundaries. For example, the algorithm x = [ ], y = 1/2 sin2(πx) + 1/5 R[ ] gives the band depicted in Figure 3.
Figure 3.

If random points are to be evenly distributed in a circle of unit radius, the algorithm is θ = 2πR[ ], r = (R[ ])1/2 in polar coordinates. For example the algorithm x = r cos θ, y = 0.5r sin θ gives the 2:1 elliptic area of Figure 4.
Figure 4.

For general irregular areas one can choose a simpler circumscribing boundary where random points can be distributed. Then the points outside the irregular area are discarded.
DENSITY VARIATIONS
Suppose in Cartesian coordinates the density of the points is dependent on x.
| (1) |
Since R[ ] is statistically even, the elemental distance dR is also even. We find
| (2) |
or
| (3) |
where c1, c2 are constants. Then solve for x to get the distribution algorithm
| (4) |
For example, if the density is proportional to x in [0,1], Equation (3) yields
| (5) |
Since R is in [0,1] and x is in [0,1], we find c1 = ½ and c2 = 0. Solving for x,0 the random coordinate is x = (R[ ])1/2. Figure 5 shows a linear density distribution given by the algorithm. In general, if the density is proportional to xα, we find the coordinate is
| (6) |
If the density is proportional to eαx, the coordinate is
| (7) |
where c1, c2 are adjusted for the range of x.
Figure 5.

Similarly, if density is proportional to h(r) in polar coordinates, the random coordinate r is generated by the inverse of
| (8) |
Here the extra r is due to the Jacobian determinant. For h(r) = rα, the relation is
| (9) |
For statistically constant density, α = 0 and we obtain the previous algorithm for an evenly filled circle. Of interest is the normal distribution, where h(r) = exp(−αr2). The radial coordinate is given by
| (10) |
A normal distribution of random points (c1 = −1, c2 = 1, α = 5) is shown in Figure 6.
Figure 6.

EXAMPLES OF BRANCHING NETWORKS USING MONTE CARLO POINTS
In biological systems, there are so many cells to be nourished that it is impossible to devise a distributive system to service every individual cell. Instead, the Monte Carlo points do not represent cells, but serve as a vehicle for the construction of the branching network. Thus direct connections to the points are not necessary, or even desired.
Figure 7 shows a system which starts from the center and spreads more or less evenly inside a circle. The network is similar to that depicted in Figure 8a of Reference [3] which is deterministic. Due to the natural randomness of the Monte Carlo points, the system of Figure 7 also reflects some stochastic variations. Figure 8 shows a system for the annulus. Such an area shape is very difficult to apply the area-halving algorithm, but poses no problems for the random points algorithm. Figure 9 shows the distributive network for a strip, starting from an exterior point. Notice the branch tips are most attracted towards heavier concentrations of the points. Figure 10 shows the case when random points are spread on a circular arc. The branching system corresponding to a normal distribution of points is shown in Figure 11.
Figure 7.
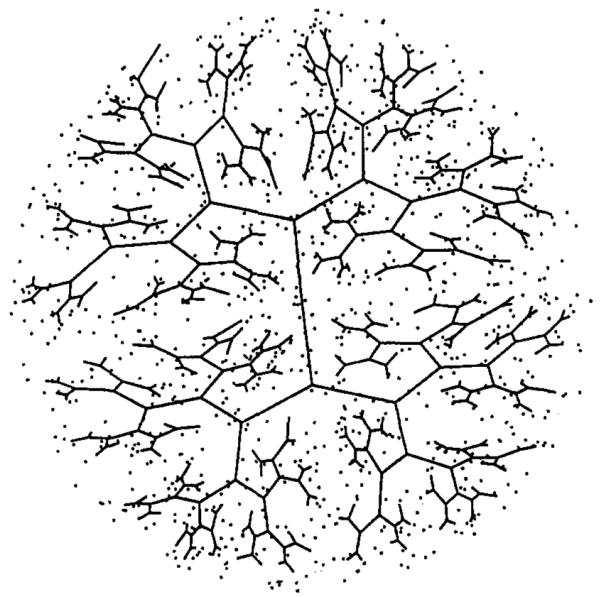
Figure 8.
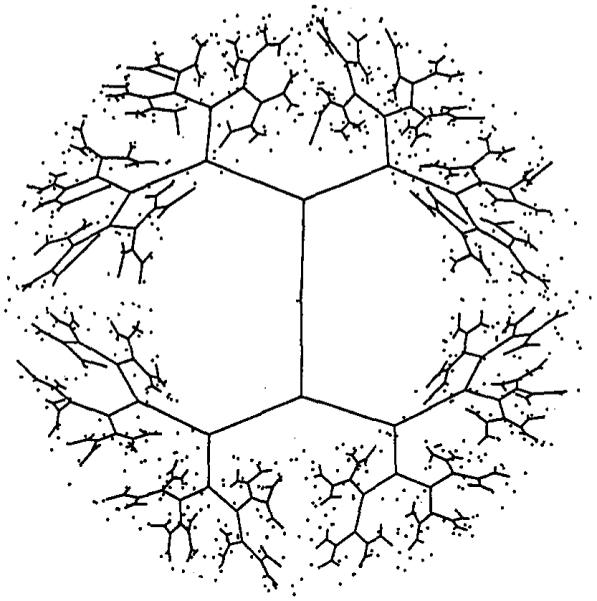
Figure 9.
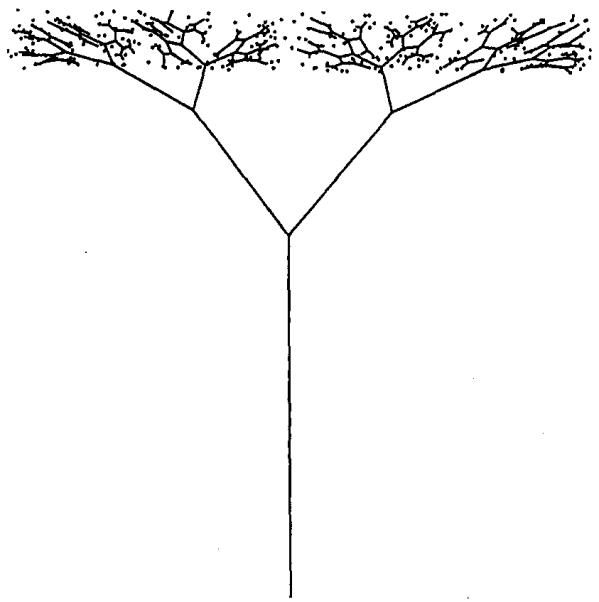
Figure 10.
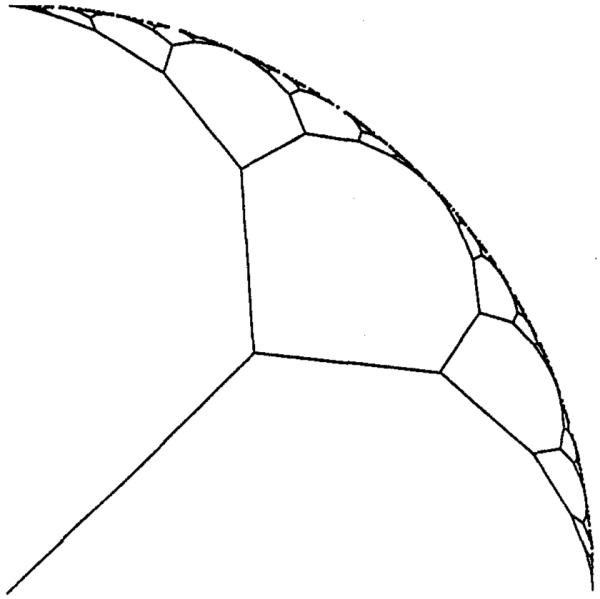
Figure 11.

DISCUSSION
Theoretically, an infinite sequence of truly random points would not repeat itself and would cover the entire range. Since our branching algorithm eventually connects each point, the tips would be area-filling with fractal dimension two. In reality, there is always a smallest functional scale, for example, a cell. Thus we really don’t need to extend to infinite generations.
In our algorithm, one free parameter is the ratio of the distance of starting point to branch tip and the distance of starting point to center of mass. This fraction, taken as 0.65 in our examples, could vary for each branch without altering the area-filling property. The system could be optimized according to some criteria by adjusting the fractions. The criterion could be the minimization of some costs in terms of length, volume, resistance or energy (see e.g., [6-9]). By adjusting this fractional length for each bifurcation, some specific optimization criteria could be included in our area-filling algorithm. This has not been done for several reasons. First, our aim is to introduce a new distributive system through the Monte Carlo method and the inclusion of a lengthy optimization feature distracts from our purpose. Second, real systems need not strictly follow optimality. Experimental data show branching angles for arterial systems which may deviate from the optimum as much as 100%. Nevertheless, the calculated “cost” for such deviations is less than 2% [10]. Such a low penalty may easily be assumed by other factors. In this respect, our choice of a uniform branching length fraction of 0.65 is quite reasonable, since the bifurcations in our examples (Figures 7-11) are, in general, close to theoretical optimum.
The present algorithm using random points has the following advantages over other area-filling algorithms.
The present algorithms are highly efficient, since area integrations are not needed. The starting point can also be outside the given area.
Global density variations can be taken into account. In numerous cases in biology, the level of nutrient or oxygen needs are stratified.
Local density differences are due to the random points. For a given area, the systems generated each time would be different but has the same statistical properties. This natural randomness occurs also in real biological systems.
In conclusion, the algorithm presented here has very high potential in simulating the distributive systems in biology.
REFERENCES
- 1.Mandelbrot BB. Fractal Geometry of Nature. Freeman; New York: 1983. [Google Scholar]
- 2.Nelson TR, Manchester DK. Modelling of lung morphogenesis using fractal geometries. IEEE Trans. Med. Imag. 1988;7(4):321–327. doi: 10.1109/42.14515. [DOI] [PubMed] [Google Scholar]
- 3.Wang CY, Bassingthwaighte JB. Area-filling distributive network model. Math. Comput. Modelling. 1990;13(10):27–33. [Google Scholar]
- 4.Hammersley JM, Handscomb DC. Monte Carlo Methods. Methuen Co.; London: 1965. [Google Scholar]
- 5.Kalos MH, Whitlock PA. Monte Carlo Methods. I. Basics, Wiley; New York: 1986. [Google Scholar]
- 6.Murray CD. The physiological principle of minimum work I, the vascular system and the cost of blood volume. Proc. Nat. Acad. Sci. 1926;12:207–214. doi: 10.1073/pnas.12.3.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Murray CD. The physiological principle of minimum work applied to the angle of branching of arteries. J. Gen. Physiol. 1926;9:835–841. doi: 10.1085/jgp.9.6.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zamir M. Optimality principles in arterial branching. J. Theor. Biol. 1976;62(l):227–251. doi: 10.1016/0022-5193(76)90058-8. [DOI] [PubMed] [Google Scholar]
- 9.Zamir M. Nonsymmetrical bifurcations in arterial branching. J. Gen. Physiol. 1978;72(6):837–845. doi: 10.1085/jgp.72.6.837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zamir M, Bigelow DC. Cost of departure from optimality in arterial branching. J. Theor. Biol. 1984;109(3):401–409. doi: 10.1016/s0022-5193(84)80089-2. [DOI] [PubMed] [Google Scholar]


