Maximizing the Reliability of Genomic Selection by Optimizing the Calibration Set of Reference Individuals: Comparison of Methods in Two Diverse Groups of Maize Inbreds (Zea mays L.)

Abstract

Genomic selection refers to the use of genotypic information for predicting breeding values of selection candidates. A prediction formula is calibrated with the genotypes and phenotypes of reference individuals constituting the calibration set. The size and the composition of this set are essential parameters affecting the prediction reliabilities. The objective of this study was to maximize reliabilities by optimizing the calibration set. Different criteria based on the diversity or on the prediction error variance (PEV) derived from the realized additive relationship matrix–best linear unbiased predictions model (RA–BLUP) were used to select the reference individuals. For the latter, we considered the mean of the PEV of the contrasts between each selection candidate and the mean of the population (PEVmean) and the mean of the expected reliabilities of the same contrasts (CDmean). These criteria were tested with phenotypic data collected on two diversity panels of maize (Zea mays L.) genotyped with a 50k SNPs array. In the two panels, samples chosen based on CDmean gave higher reliabilities than random samples for various calibration set sizes. CDmean also appeared superior to PEVmean, which can be explained by the fact that it takes into account the reduction of variance due to the relatedness between individuals. Selected samples were close to optimality for a wide range of trait heritabilities, which suggests that the strategy presented here can efficiently sample subsets in panels of inbred lines. A script to optimize reference samples based on CDmean is available on request.

AMONG the different methods that use molecular markers for selection, genomic selection (GS) has received considerable attention in the last decade. The objective of this approach is to predict the breeding values of candidates based on their molecular marker genotypes. A prediction formula is developed using the genotypes and phenotypes of reference individuals forming a calibration set (Meuwissen et al. 2001). The GS formula potentially includes all the marker effects, without preselection based on a significance threshold. If the marker density is sufficient, this permits the model to capture an important part of the genetic variance (Yang et al. 2010). Compared to traditional marker-assisted selection (MAS), the efficiency of which is limited by the power of marker-trait association tests, GS is expected to be more efficient, especially for highly polygenic traits (Bernardo and Yu 2007). GS was first used in animal breeding, particularly dairy cattle, and its use clearly improved the selection efficiency (Hayes et al. 2009a). It is now also widely studied by plant breeders, and interesting results were obtained (Jannink et al. 2010; Crossa et al. 2010; Albrecht et al. 2011).

Powerful statistical tools and relevant data sets (genotypes and phenotypes to train the prediction model) are key factors for the predictive efficiency. There are two ways to use the genotypic data in genomic selection. The first way is to estimate the marker effects in the calibration set and then to predict the breeding values of the selection candidates by multiplying their genotypes by the marker effects. This approach is used, for example, in the mixed model called random regression–best linear unbiased predictions (RR–BLUP; Whittaker et al. 2000; Meuwissen et al. 2001). The second approach is to use the marker genotypes to estimate a relationship matrix between phenotyped individuals of the reference population and nonphenotyped individuals, candidates to selection. This relationship matrix can then be used to estimate a variance/covariance matrix between the genetic values in a mixed model called RA–BLUP (RA for realized additive relationship matrix; Zhong et al. 2009), or G–BLUP. It has been proven that RR and RA–BLUP are statistically equivalent under conditions presented by Habier et al. (2007), Goddard (2009), and Hayes et al. (2009b).

The implementation of genomic selection is facilitated by recent advances in genotyping. We now have access to genotyping arrays, which provide genotypes of very good quality at low cost. The costs of sequencing are also decreasing and it is, or will soon become, possible to genotype the genetic material by sequencing (Huang et al. 2009; Metzker 2009; Elshire et al. 2011). In plant breeding, large collections of individuals are usually available to the breeder, corresponding to germplasm released by public institutes, private germplasm released at the end of their protection by patent (PVP), and individuals that have been used as parents of the current breeding program. All this material can be easily genotyped and potentially used to create the calibration set. Conversely, although there have been very important advances in the automatization of phenotyping, it is still very expensive to obtain relevant phenotypes with a high heritability for a large set of individuals. In addition, multi-environment trials are needed to test individuals under different conditions and estimate the genotype x environment interactions (GEI). As a result, it is now clearly admitted that the collection of phenotypic data relevant in terms of traits and environmental conditions with respect to the breeding objectives is the most limiting factor for running genomic selection and that it is also a key factor that needs to be optimized, with the constraint of a limited budget. Beyond plant breeding, this issue extends to a large extent to animal selection for traits that are either destructive or costly to measure, such as traits related to disease resistance or fertility (Boichard and Brochard 2012).

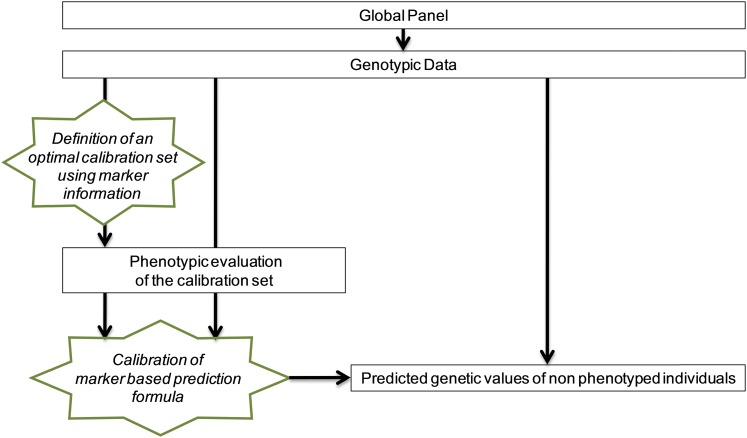
The question is then how to choose the reference individuals (calibration set) to phenotype, to maximize the reliability of the prediction of nonphenotyped individuals that are candidates to selection. Indeed, it has been shown that the accuracy of genomic predictions (that is the correlation between predicted and true breeding values) is highly influenced by the population used to calibrate the model (Albrecht et al. 2011; Pszczola et al. 2012). In a situation in which a large collection of individuals is available, one objective is to define which ones must be included in the calibration set to discriminate as accurately as possible which individuals from the selection population are the best ones (Figure 1). A first way to perform sampling could be to choose the individuals that capture most of the diversity present in the population. Another criterion could be to select the calibration set that minimizes the prediction error variance (PEV) of the genetic values. This criterion is valid at the individual level but does not take into account the genetic variance of the contrasts between individuals and may result in the sampling of close relatives. One classical way of evaluating the efficiency of a given selection method is to compute its accuracy, defined as the correlation between predicted and true values, which is an important factor of the expected genetic gain. This criterion is directly available in simulation studies in which true genetic values are known or can be indirectly measured by using cross-validation approaches in experimental data.

Figure 1.

Optimization of calibration set to implement genomic selection in a diversity panel. This procedure was tested on two independent maize diversity panels.

A few studies have used the expected accuracy, estimated as $\sqrt{1-\text{PEV}/{\sigma }_{\text{g}}^2\hspace{0.17em}}$ (where ${\sigma }_{\text{g}}^2$ is the additive genetic variance, and PEV represents the part of ${\sigma }_{\text{g}}^2$ that is not accounted for by the predictions) to compare experimental designs and statistical models for dairy cattle (VanRaden 2008; Hayes et al. 2009c; Pszczola et al. 2012). In these articles, individuals were assumed to be unrelated. As a consequence this criterion has the same disadvantage as PEV: it doesn’t consider the decrease of genetic variance when close relatives are sampled.

To account for this possible decrease in genetic variance, it is possible to directly maximize the expected reliabilities of the contrasts between each selection candidate and the population mean. It can be implemented with the generalized coefficient of determination (Laloë 1993), which expresses the precision of any contrast between individuals. This criterion is the squared correlation between the true and the predicted contrast of genetic values. It is a function of the PEV and of the genetic variance. The generalized coefficient of determination (CD) is used by animal geneticists to optimize experimental designs. In particular it can be used to track disconnectedness, i.e., individuals that cannot be compared because they (or their relatives) were not phenotyped at least once in the same environment. The generalized CD was used, for example, to compare the efficiency of testing designs in beef cattle (Laloë and Phocas 2003) and sheep (Kuehn et al. 2007).

In plant breeding, the generalized CD was used by Maenhout et al. (2010) to get the most accurate BLUPs from phenotypic data available from a breeding company. The phenotypic data of breeding companies are very unbalanced, some phenotypes being disconnected from the others. Maenhout et al. (2010) assumed that the genotyping budget was limited, and they wanted to use the phenotypes already available for predicting the value of untested hybrids. Their challenge was, then, how to choose the individuals to genotype in order to optimize the use of available phenotypes. With this exception, to our knowledge, this criterion was paid little attention in plant breeding so far and it could be used for different applications such as the optimization of the sampling of the calibration set in genomic selection.

Since phenotyping is now the limiting factor in genome-wide analysis, we consider the case in which all the individuals are genotyped but only a proportion is going to be phenotyped (calibration set). In this article, we propose a method based on the generalized CD to optimize the sampling of the calibration set for predicting as accurately as possible the nonphenotyped individuals (Figure 1). To validate our optimization algorithm, we used phenotypic data for flowering time, plant biomass, and dry matter content, collected on two maize inbred panels for which genotypic information is available and compared several strategies for selecting the calibration set.

Materials and Methods

Genetic material

Our optimization procedure was evaluated on two maize diversity panels developed for the European program “CornFed.” These are composed respectively of 300 Flint lines and 300 Dent lines. This material includes 242 lines from the panel presented by Camus-Kulandaivelu et al. (2006) and lines derived from recent breeding schemes: 58 Dent lines from PVP (Mikel 2006; Nelson et al. 2008), 128 from the University of Hohenheim (Riedelsheimer et al. 2012), 81 from the Misión Biológica de Galicia and the Estación Experimental de Aula Dei, Spain (CSIC), 35 from the Centro Investigacións Agrarias de Mabegondo, Spain (CIAM), 23 from the Eidgenössische Technische Hochschule Zürich (ETHZ), and 33 from the Institut National de la Recherche Agronomique (INRA). This collection was created with the objective of covering European and American diversity of interest for temperate climatic conditions, as available from public institutes. Choice was guided by pedigree to avoid as far as possible overrepresentation of some parental materials.

Field data

The Flint and Dent lines were respectively crossed to a Dent and a Flint tester. The two panels were evaluated separately for flowering time and biomass production in two adjacent trials at five locations in 2010: Mons (France), Pontevedra and Mabegondo (Spain), and Roggenstein and Einbeck (Germany). The hybrids within each panel were divided into two groups according to their expected precocity. These two groups were evaluated as two blocks. A small number of randomly chosen entries was replicated within blocks (18 entries) and across blocks (18 entries) to estimate experimental error and an eventual block effect. Male flowering time (Tass_GDD6), plant dry matter yield (DM_Yield), and dry matter content (DMC) were registered for each plot. DMC and DM_Yield were observed at only four of the five locations for the Flint panel. Male flowering time was registered when 50% of the plants were shedding pollen and then converted into growing degree days (GDD) in base 6°, using the mean daily air temperature measured at each location. These traits were used here as examples, to test the optimized sampling algorithm. Plants with obviously extreme phenotypes were excluded from the study (between 2.2 and 2.8% of the data were removed for each trait).

Least-squares means were calculated with the GLM procedure (SAS Institute, 2008) by adjusting for block and trial effects (the phenotypes are compiled in File S1 and File S2). Trait heritability at the level of the experimental design was estimated with a mixed model (Trial as fixed effect, genotypes and genotypes × trial as random effects) after removing the block effects. Heritability was calculated as

$$h^2=\frac{{\sigma }_{\text{g}}^2}{{\sigma }_{\text{g}}^2+{\sigma }_{\text{g}\times \text{E}}^2/\text{nTrial}+{\sigma }_{\text{E}}^2/\text{nRep}},$$

where ${\sigma }_{\text{g}}^2$ is the additive genetic variance, ${\sigma }_{\text{E}}^2$ is the environmental variance, ${\sigma }_{\text{g}\times \text{E}}^2$ is the interaction variance, nTrial is the number of trials, and nRep is the mean number of replicates over the whole experimental design.

Genotyping, diversity, and relationship matrix

The two diversity panels were genotyped with the 50k SNPs array described by Ganal et al. (2011). This Illumina array includes 49,585 SNPs. Individuals, which had marker missing rate and average heterozygosity >0.1 and 0.05, respectively, were eliminated. Markers, which had missing rate and average heterozygosity >0.2 and 0.15, respectively, were eliminated. In total, 261 Flint lines and 261 Dent lines passed the genotyping and phenotyping filter criteria. To avoid the bias noted by Ganal et al. (2011) in the diversity analysis, we used only the markers that were developed by comparing the sequences of nested association mapping founder lines (PANZEA SNPs; Gore et al. 2009) to estimate Nei’s index of diversity (Nei 1978) and relationship coefficients (30,027 and 29,094 markers passed the filter criteria for the Dent and the Flint lines, respectively, see File S1 and File S2). Nei’s index of diversity of each Panzea SNP was calculated and averaged over the genome to estimate diversity in the two panels.

One easy way to estimate the relationship between individuals with molecular markers is to calculate for each pair of individuals the proportion of shared alleles, also called identity-by-state (IBS). With biallelic markers it can be calculated as

$$\mathbf{A}\mathbf{\_}\mathbf{IBS}=\frac{\mathbf{G}{\mathbf{G}}^{\mathbf{\prime }}+{\mathbf{G}}_{\mathbf{2}}{\mathbf{G}}_{\mathbf{2}}^{\mathbf{\prime }}}{K},$$

where G is the matrix of genotypes (with dimension number of individuals × number of markers) coded as 0, 0.5, and 1 for the homozygote, the heterozygote, and the other homozygote, respectively, K is the total number of markers, and ${\mathbf{G}}_2=1-\mathbf{G}$, where 1 is a matrix of ones.

In this formula, a same weight is given to all markers. Another formula was proposed by Leutenegger et al. (2003), Amin et al. (2007), and Astle and Balding (2009) in which a particular weight, depending on the allele frequency, is given to each marker,

$$\mathbf{A}\_\mathbf{f}\mathbf{r}\mathbf{e}{\mathbf{q}}_{i,j}=\frac{1}{K}{\displaystyle {\sum }_{k=1}^K\frac{\left(G_{i,k}-p_k\right)\left(G_{j,k}-p_k\right)}{p_k\left(1-p_k\right)}},$$

where i and j indicate individuals, G_i,k is the genotype of individual i at marker k, and p_k is the frequency of the allele coded 1 of marker k in the panel. This estimator attributes a higher weight to similarity for rare alleles and to markers with low diversity. The allele frequencies p_k are estimated in a reference population (here each panel). We consider here the diversity panel as the base population; as a result the mean of the values of genomic relationship matrix A_freq is equal to zero. This formula can give negative estimates of relationship coefficient. Negative coefficients have no sense in terms of probability, but can be interpreted as negative correlations. These two genomic relationship matrices are positive semidefinite (Astle and Balding 2009) and invertible when the number of markers is sufficient and identical individuals are removed. Genomic relationship matrices, as described above, were estimated independently in both panels.

Statistical model

The genomic predictions were based on the RA–BLUP model, which allows a more direct derivation of PEV and CD for the breeding values (see below), using the following mixed model

$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+\mathbf{Z}\mathbf{u}+\mathbf{e},$$

where y is a vector of phenotypes, β is a vector of fixed effects (in our case only the intercept), u is a vector of random genetic values, and e is the vector of residuals. X and Z are design matrices.

The variance of the random effects u is $\text{var}\left(u\right)=A{\sigma }_{\text{g}}^2$, where A is the genomic relationship matrix and ${\sigma }_{\text{g}}^2$ is the additive genetic variance in the panel. The variance of the residuals e is $\text{var}\left(e\right)=I{\sigma }_{\text{e}}^2$, where I is the identity matrix. The prediction of u is obtained by solving Henderson’s (1984) equations

$$\left[\begin{array}{cc}{\mathbf{X}}^{\mathbf{\prime }}\mathbf{X}& \mathbf{X}\mathbf{\prime }\mathbf{Z}\\ \mathbf{Z}\mathbf{\prime }\mathbf{X}& \mathbf{Z}\mathbf{\prime }\mathbf{Z}+\mathbf{\lambda }{\mathbf{A}}^{\mathbf{-}\mathbf{1}}\end{array}\right]\left[\begin{array}{c}\widehat{\mathbf{\beta }}\\ \widehat{\mathbf{u}}\end{array}\right]=\left[\begin{array}{c}\mathbf{X}\mathbf{\prime }\mathbf{y}\\ \mathbf{Z}\mathbf{\prime }\mathbf{y}\end{array}\right],$$

where $\lambda ={\sigma }_{\text{e}}^2/{\sigma }_{\text{g}}^2$ is the ratio between the residual and the additive variances in a simplified situation; in our case

$$\lambda =\frac{{\sigma }_{\text{E}}^2/\mathrm{nRep}+{\sigma }_{g\times \text{E}}^2/\text{nTrial}}{{\sigma }_g^2}$$.

A is the genomic relationship matrix. Note that in this model we consider that a trait is determined by a large number of genes, each having small and independent effects. Genetic effects are assumed to follow a Gaussian distribution according to the central limit theorem (Fisher 1918).

Optimization criteria and CD

The final objective is to identify the individuals from the population that are best suited to build the calibration panel. One strategy for reaching this objective is to maximize the precision of the prediction of the difference between the value of each nonphenotyped individual and the mean of the total population of candidate individuals, which includes the phenotyped and the nonphenotyped individuals. This difference can be viewed as a specific contrast between genetic values of individuals.

A classical approach for this is to compute the expected PEV of each individual, which can be obtained from

$${\left[\begin{array}{cc}{\mathbf{X}}^{\mathbf{\prime }}\mathbf{X}& \mathbf{X}\mathbf{\prime }\mathbf{Z}\\ \mathbf{Z}\mathbf{\prime }\mathbf{X}& \mathbf{Z}\mathbf{\prime }\mathbf{Z}+\mathbf{\lambda }{\mathbf{A}}^{-\mathbf{1}}\end{array}\right]}^{-\mathbf{1}}=\left[\begin{array}{cc}{\mathbf{C}}_{\mathbf{1}\mathbf{1}}& {\mathbf{C}}_{\mathbf{1}\mathbf{2}}\\ {\mathbf{C}}_{\mathbf{2}\mathbf{1}}& {\mathbf{C}}_{\mathbf{2}\mathbf{2}}\end{array}\right],$$

where $\mathbf{P}\mathbf{E}\mathbf{V}\left(\widehat{\mathbf{u}}\right)=\text{Var}\left(\widehat{\mathbf{u}}-\mathbf{u}\right)=\text{diag}({\mathbf{C}}_{22})\times {\sigma }_{\text{e}}^2$.

More generally, the PEV of any contrast c of the predicted performances can be calculated as

$$\text{diag}\left[\frac{{\mathbf{c}}^{\mathbf{\prime }}{\left({\mathbf{Z}}^{\mathbf{\prime }}\mathbf{M}\mathbf{Z}+\mathbf{\lambda }{\mathbf{A}}^{-\mathbf{1}}\right)}^{-\mathbf{1}}\mathbf{c}}{\mathbf{c}\mathbf{\prime }\mathbf{c}}\right]\times {\sigma }_{\text{e}}^2,$$

where c is a contrast, i.e., $1^{\mathit{\text{'}}}c=0$. M is an orthogonal projector on the subspace spanned by the columns of X: $\mathbf{M}=\mathbf{I}-\mathbf{X}{\left(\mathbf{X}\mathbf{\prime }\mathbf{X}\right)}^{-}\mathbf{X}\mathit{\prime }$ and ${\left({\mathbf{X}}^{\mathbf{\prime }}\mathbf{X}\right)}^{-}$ is a generalized inverse of X′X (Laloë 1993).

A complementary approach to optimizing the choice of individuals to be phenotyped is to estimate the expected reliability of the prediction of contrasts. Laloë (1993) expressed the precision of any contrast with the generalized CD, defined as the squared correlation between the true and the predicted contrast of genetic values. This CD is equivalent to the expected reliability of the contrast

$$\mathbf{C}\mathbf{D}\left(\mathbf{c}\right)=\text{diag}\left[\frac{\mathbf{c}\prime \left(\mathbf{A}-\mathbf{\lambda }{\left(\mathbf{Z}\mathbf{\prime }\mathbf{M}\mathbf{Z}+\mathbf{\lambda }{\mathbf{A}}^{-\mathbf{1}}\right)}^{-\mathbf{1}}\right)\mathbf{c}}{\mathbf{c}\mathbf{\prime }\mathbf{A}\mathbf{c}}\right]$$

The CD takes values between 0 and 1, a CD close to 0 meaning that the prediction of the contrast is not reliable, whereas CD close to 1 means that the prediction is highly reliable. The CD is a balance between PEV and the genetic variance (of the contrast), which takes into account relationship (Laloë et al. 1996).

Note that compared to the approach of Hayes et al. (2009c) who considered $\sqrt{1-\text{PEV}/{\sigma }_{\text{g}}^2}$ an estimation of accuracy, the term c′Ac in the CD takes into account covariances between the candidate individuals. The use of generalized CD instead of PEV as optimization criterion is expected to prevent the selection of very closely related individuals.

The set of individuals to phenotype within each panel (Dent or Flint) was optimized by minimizing the mean of the PEVs of the contrast between each nonphenotyped individual and the mean of the panel: PEVmean = mean[diag(PEV(C))], where C is a matrix of contrasts: each column is a contrast between an unphenotyped individual and the mean of the population. Dimensions of C are total number of individuals × number of nonphenotyped individuals.

We also optimized the sampling by maximizing the mean of the CDs of the contrast between each nonphenotyped individual and the mean of the panel: CDmean = mean[diag(CD(C))]. In this case, the individuals that we decide not to phenotype are those that are the most reliably predicted with those that are phenotyped. In other words, we optimize the choice of individuals to phenotype, so that their phenotypes are as useful as possible to predict the unphenotyped individuals (Figure 1). We expect this strategy to sample key individuals that cover the panel variability as well as possible.

These approaches based on PEVmean or CDmean were used with the two relationship matrices described above: the IBS matrix A_IBS and the genomic relationship matrix A_freq.

These criteria, PEVmean and CDmean, were compared to other criteria expected to improve the calibration set sampling: we also considered as selection criteria the mean and the maximum of the genomic relationship matrix A_freq between the individuals in the calibration set (respectively denoted by Amean and Amax). These two criteria Amean and Amax were minimized to maximize the variability in the calibration set.

Optimization algorithm

Several exchange algorithms and simulated annealing (Kirkpatrick et al. 1983; Černý 1985) classically used to optimize experimental designs (Atkinson et al. 2007) were implemented in R 2.14.0 to optimize the different criteria. A simple exchange algorithm, further referred to as Algo1, was retained. At each step the random exchange of one individual between the calibration set and the set of nonphenotyped individuals is accepted if the criterion were improved and was rejected otherwise. More complex algorithms did not give significantly better results and needed more iterations to converge. They were therefore not retained for further investigations.

For each panel, we used Algo1 50 times to select a certain number of individuals (10, 30, 50, 70, 100, 150, or 200) for phenotyping, each time with a different random initial sample. Preliminary tests showed that 50 repetitions were sufficient to obtain stable results. We then used the true phenotypes of these individuals (calibration set) to predict the remaining individuals (validation set). We compared results obtained for optimized calibration sets with those obtained for randomly determined calibration sets (50 random sets for each calibration set size). This procedure was applied to each trait in each panel.

Observed prediction reliability and robustness of the optimization to variation of heritability

To compare the ability of the phenotyped individuals to predict the unphenotyped individuals (the validation set of individuals), we calculated the observed reliability of the predictions. The genomic selection reliability is defined by the square correlation between the genomic estimated breeding values (GEBV) and the true breeding values (TBV): ${\text{corr}}^{\text{2}}(\mathbf{GEBV,TBV})$, which is the square of the genomic selection accuracy (Dekkers 2007). We do not have access to the TBV of the candidate plants. Considering that $\text{corr}\left(\mathbf{GEBV,Y}\right)=\text{corr}\left(\mathbf{GEBV,TBV}\right)\times \text{corr}\left(\mathbf{Y,TBV}\right)$, where Y stands for the observed phenotypic performance, we estimated the genomic selection reliability as ${\text{corr}}^{\text{2}}\mathbf{(GEBV,Y)}/h^2$, since $h^2={\text{corr}}^{\text{2}}\mathbf{(Y,TBV)}$. For each panel and each calibration set size we compared the observed prediction reliabilities using the optimized or the random set.

In the CD calculation, the only parameter that is related to the trait is the variance ratio λ. This parameter is related to the heritability of the trait: $\lambda =\left(1-h^2\right)/h^2$ . We need to set a specific value for λ to use the sampling algorithm. But in practice, the calibration set will probably be phenotyped for traits of different heritabilities. It is thus important to know, for a set optimized with a specific value of λ, for which range of heritabilities it is optimum. To answer this question, we compared the CDmean of selection candidates obtained after sampling the calibration set with different values of lambda. If the CDmean obtained with different lambda values are correlated, one can assume that close subsets of individuals would be selected by the sampling approach.

For this, random sets of individuals were successively selected, and each time the CDmean was calculated (with the genomic relationship matrix) using three different values for λ: 4, 1, and 0.25 corresponding to heritabilities of 0.2, 0.5, and 0.8. The correlations between the three series of CDmean were then calculated.

Link between the PEV and the observed prediction error

For the Flint and the Dent panels independently, 50 sets of 150 individuals were sampled randomly or with the optimization algorithm (CDmean). These calibration sets were used to predict the genetic values of the unphenotyped individuals from the same panel. We calculated the PEVs of the contrasts between each predicted individual and the mean of the population (using a λ corresponding to the estimated heritability) and compared it to the observed prediction error (defined as the difference between the observation and the prediction). This comparison is interesting to check if our statistical model gives good estimates of the PEV and then indirectly if the estimated variance/covariance matrix fits the true variance/covariance matrix.

Genetic properties of optimized calibration sets

To visualize the genetic properties of the calibration sets optimized with CDmean, two kinds of tools were used: a principal coordinates analysis (PCoA) on the distance matrices (Gower 1966), and a network representation of the genomic relationship matrix.

A PCoA was performed on the distance matrix of each panel (we considered the distance between two individuals by one minus their relationship coefficient A_freq_ij). The individuals were then plotted using their coordinates on the two axes of the PCoA explaining most of the total variance. This representation gives an idea of the variability present in each panel. Using these graphs, we visualized the individuals selected by the sampling algorithm based on CDmean. It gives a rough idea of the variability of the panel captured by the calibration set.

To further understand how the individuals selected to be part of the calibration set relate to the other individuals of the population we used a visualization of the genomic relationship matrix. We represented the individuals in a network, in which two individuals are linked when their relationship coefficient (A_freq_ij) is >0.2, unlinked otherwise (Rozenfeld et al. 2008; Thomas et al. 2012). For this, the genomic relationship matrix was transformed in a matrix of Boolean indicating if the coefficients were >0.2 or not. The networks of the two panels were drawn with a Fruchterman and Reingold’s force-directed placement algorithm (Fruchterman and Reingold 1991) with the package “network” in R.

Results

Trait variation

Tass_GDD6, DMC, and DM_Yield have an important variability in the two panels (Table 1). The average of these traits are only slightly different between the two panels because the Dent lines (usually late lines) were crossed to a Flint tester (early lines) and the Flint lines to a Dent tester. The genotype × environment interaction and the residual variances were low compared to the genetic variances for Tass_GDD6. The residual and interaction variances are relatively more important for DMC but remain below genetic variance. The residual variance was greater than the genetic variance for DM_Yield and the interaction variance was equal to the genetic variance in the Dent panel. The heritability of these traits is between 0.65 (DM_Yield in the Dent panel) and 0.95 (Tass_GDD6 in both panels).

Table 1 . Statistics on Flowering time (Tass_GDD6, growing degree days), dry matter yield (DM_Yield, t × ha^-1), and dry matter content (DMC, %) in the two panels of hybrids.

	Dent			Flint
	Tass_GDD6	DM_Yield	DMC	Tass_GDD6	DM_Yield	DMC
Mean	864.5	17.0	33.4	872.4	15.9	32.4
Genotypic variance	1354.5 ***	1.9 ***	13.0 ***	1692.1 ***	2.1 ***	8.6 ***
Trial × genotype variance	77.5 ***	1.9 ***	4.1 ***	95.8 ***	0.7 *	6.1 ***
Residual variance	292.2 ***	3.6 ***	6.5 ***	355.2 ***	3.9 ***	8.1 ***
Heritability	0.95	0.65	0.87	0.95	0.67	0.72

The variances were estimated in a mixed model with Genotype, Trial × genotype and Residual as random effects, *P < 0.05, ***P < 0.001. The observations were previously corrected by block effects. The heritability corresponds to the broad-sense entry-mean heritability.

Description of the diversity and of the genomic relationship matrix

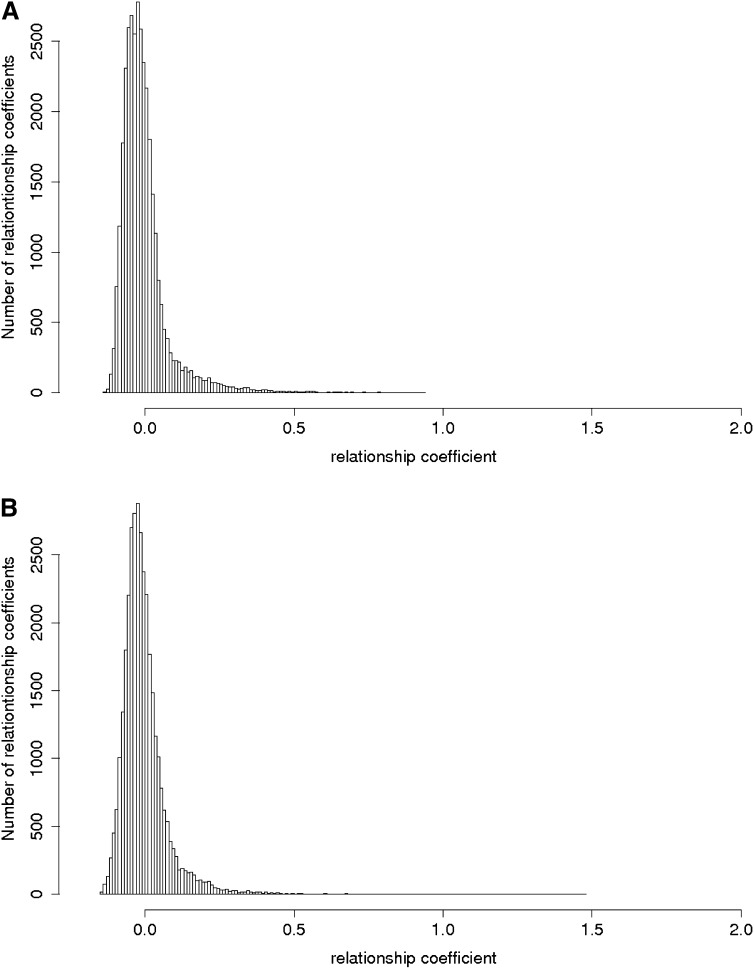
The index of diversity (Nei 1978) in the Dent and the Flint panels was 0.34 and 0.32, respectively, leading to a mean A_IBS of 0.66 and 0.68, respectively. Histograms of the genomic relationship coefficients A_freq_ij in the Flint and the Dent panels show that most of the coefficients are <0.1, but some pairs of individuals are closely related in particular in the Flint panel (Figure 2). For these individuals the identity-by-state can be up to 0.99. The coefficient A_freq_ij of these pairs of individuals can almost reach 2 if the two individuals share many rare alleles. Three Dent and five Flint pairs were almost identical despite all the care that was used to create these diversity panels.

Figure 2.

Histograms of the relationship coefficients between pairs of individuals. (A) Dent and (B) Flint. The relationship coefficients were extracted from A_freq. The two panels are considered as the reference populations; as a consequence the mean of the relationship coefficients is equal to zero in each panel.

Observed prediction reliability and robustness of the optimization to variation of heritability

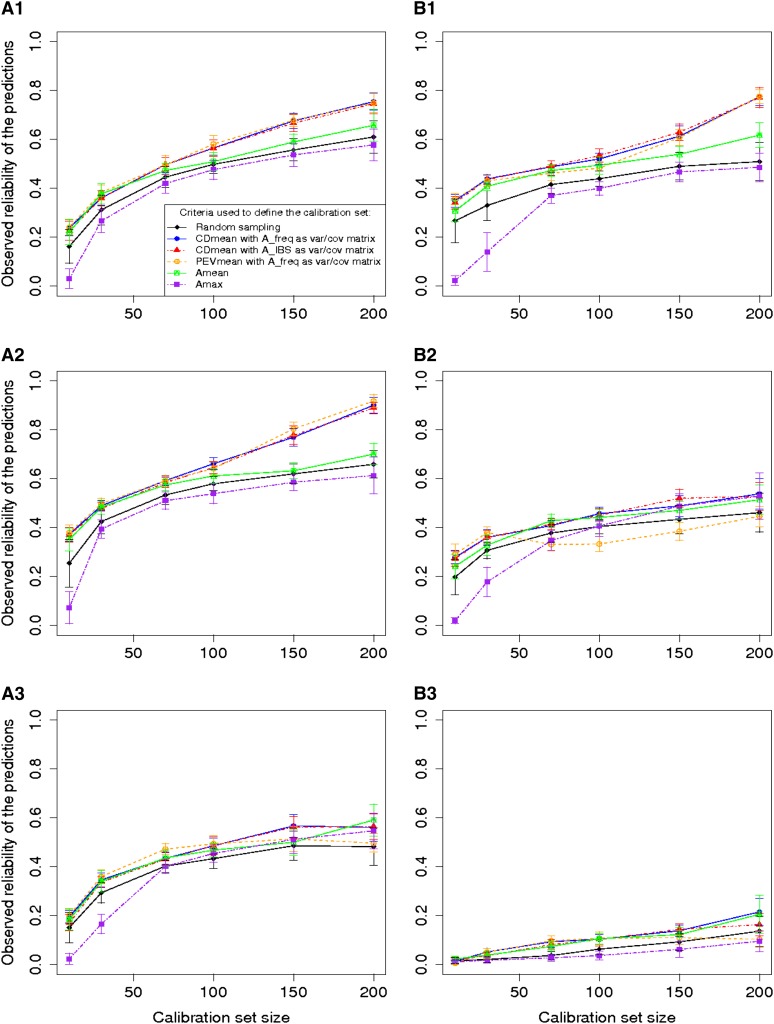
The reliabilities were lower in the Flint than in the Dent panel for the three traits and particularly for DM_Yield. For DM_Yield in the Flint panel the reliabilities are <0.3 even with a calibration set of size 200 (Figure 3). As expected the observed reliability increased with the size of the calibration set. For the random samples, an increase of the calibration set size generates an increase of the reliability following the law of diminishing returns (Figure 3). For the set optimized with PEVmean and CDmean, this trend is less clear. Within calibration set sizes, there were clear differences between the reliabilities obtained with the different approaches. All the approaches except the minimization of Amax gave better reliabilities than the reliabilities obtained after random sampling. The approach based on PEVmean was better than random sampling most of the time, but it was equivalent or worse than random sampling in few situations (particularly for DMC in the Flint panel). The reliabilities obtained by minimizing Amax in the calibration set were always lower or equivalent to those obtained by random sampling, whereas the minimization of Amean always gave higher reliabilities than random sampling (Figure 3).

Figure 3.

Reliability of the predictions of Tass_GDD6 (A1 and B1), DMC (A2 and B2) and DM_Yield (A3 and B3) using different sampling algorithms on the Dent panel (A1, A2, and A3), and the Flint panel (B1, B2 and B3). The calibration sets were randomly sampled or defined by maximizing CDmean with a relationship matrix based on the IBS or weighted by the allelic frequencies; minimizing PEVmean with a relationship matrix weighted by the allelic frequencies; minimizing the mean (Amean) or the maximum (Amax) of the relationship coefficient between the reference individuals. The individuals that are not in the calibration set are in the validation set. As a consequence, for each calibration set size the reliability is calculated with a different number of individuals. For each point, the vertical line indicates an interval of 2σ_R (σ_R being the standard deviation of observed reliabilities over the 50 runs). Optimization of PEVmean and CDmean was made with h² corresponding to the heritability measured for each trait in each panel.

The approach based on CDmean always gave higher reliabilities than random sampling. The use of A_IBS as variance/covariance matrix gave lower reliabilities. Considering the results obtained in the two panels with the different calibration set sizes, CDmean with A_freq was the best method.

The correlations between the CDmeans computed for the three levels of heritability were >0.90 most of the time (Table 2) and always >0.70. The CDmeans calculated with the intermediate value of h² (h² = 0.5) had minimum correlations of 0.86 and 0.91 with the CDmeans calculated with the two extreme heritabilities (0.2 and 0.8), for the Flint and Dent panels, respectively.

Table 2 . Correlation between the CDmeans calculated with different values of λ.

Calibration set	Dent			Flint
Size	λ=4 ; λ=1	λ=4 ; λ=0.25	λ=1 ; λ=0.25	λ=4 ; λ=1	λ=4 ; λ=0.25	λ=1 ; λ=0.25
10	0.99	0.98	1.00	0.99	0.97	0.99
50	0.93	0.82	0.97	0.91	0.81	0.98
70	0.86	0.71	0.97	0.95	0.89	0.99
100	0.93	0.86	0.98	0.97	0.94	0.99
200	0.99	0.96	0.99	0.97	0.93	0.99

For each calibration set size, the CDmeans of 200 random samples were calculated with three different values of λ. Each value of the table indicates the correlation between CDmeans calculated with two values of λ. The values in italics are the correlations <0.9. The three values of λ (4, 1, 0.25) are, respectively, equivalent to heritabilities of 0.2, 0.5, and 0.8.

Link between the PEV and the observed prediction error

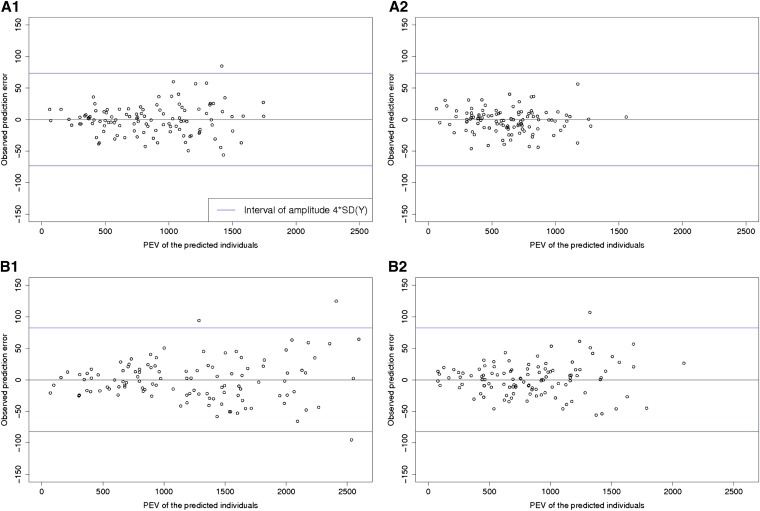
Another way of checking the reliability of our statistical models was to compare the expected PEVs and the observed prediction errors (Table 3 and Figure 4). Figure 4 illustrates the results obtained after 1 of the 50 repetitions of the algorithm on Tass_GDD6. This showed that the larger observed prediction errors mostly corresponded to high PEV, particularly for Flints.

Table 3 . Means of the expected and observed error variances in the Dent and Flint panels for Tass_GDD6.

	Dent		Flint
	Mean PEVmean	Observed prediction error variance	Mean PEVmean	Observed prediction error variance
Random set	865.6	654.7	1204.1	973.8
Optimized set	610.8	367.9	857.9	699.8

The calibration set was composed of 150 individuals randomly sampled, or sampled with the algorithm based on CDmean. The procedure was repeated 50 times.

Figure 4.

PEV and observed prediction errors for Tass_GDD6 (calibration set size, 150 individuals). (A1 and A2) Dent panel (261 hybrids), calibration set randomly sampled (A1) or optimized with CDmean (A2). (B1 and B2) Flint panel (261 hybrids), calibration set randomly sampled (B1) or optimized with CDmean (B2). The blue lines indicate an interval of 4SD(Y) [SD(Y) being the standard deviation of the adjusted means]. The PEVs were calculated with a λ value corresponding to the estimated heritability of each panel.

The PEVs obtained with the approach based on CDmean were lower than the PEVs obtained with a random calibration set. This expectation was validated by the observed prediction errors, which were lower with CDmean than with random sampling.

Genetic properties of optimized calibration sets

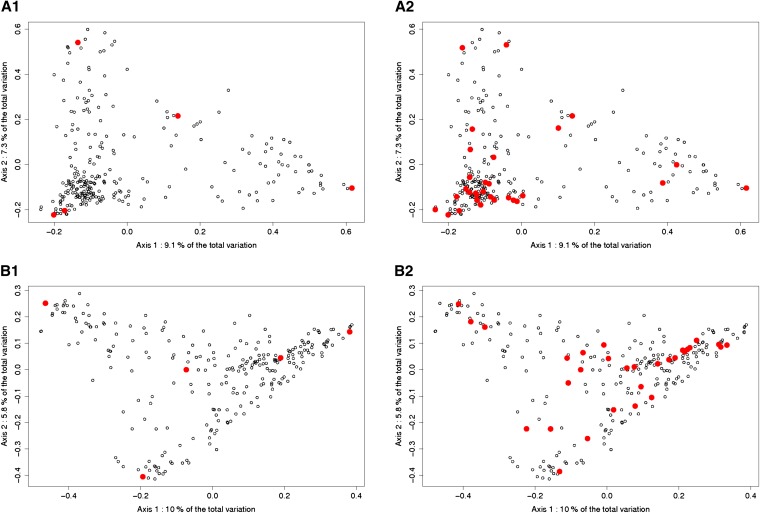
The two first PCoA axes represented, respectively, 16.4 and 15.8% of the total variability in the Dent and the Flint panels (Figure 5). When the calibration set was small, the algorithm tended to select individuals on the extremities of the graph. When the calibration set was larger, the algorithm selected representative individuals. For example, in A2 many individuals were selected from the lower left cluster, where most individuals were placed. These patterns were stable across runs.

Figure 5.

Principal coordinates analysis on the Dent and the Flint panel. Axis1 and Axis2 are the two first components of a PCoA on the distance matrix of the corresponding panel. The individuals selected by the algorithm based on CDmean are represented by red dots, other by circles. A1 and A2: PCoA on the Dent panel, calibration set composed of 5 individuals (A1) and 30 individuals (A2). B1 and B2: PCoA on the Flint panel, calibration set composed of 5 individuals (B1) and 30 individuals (B2).

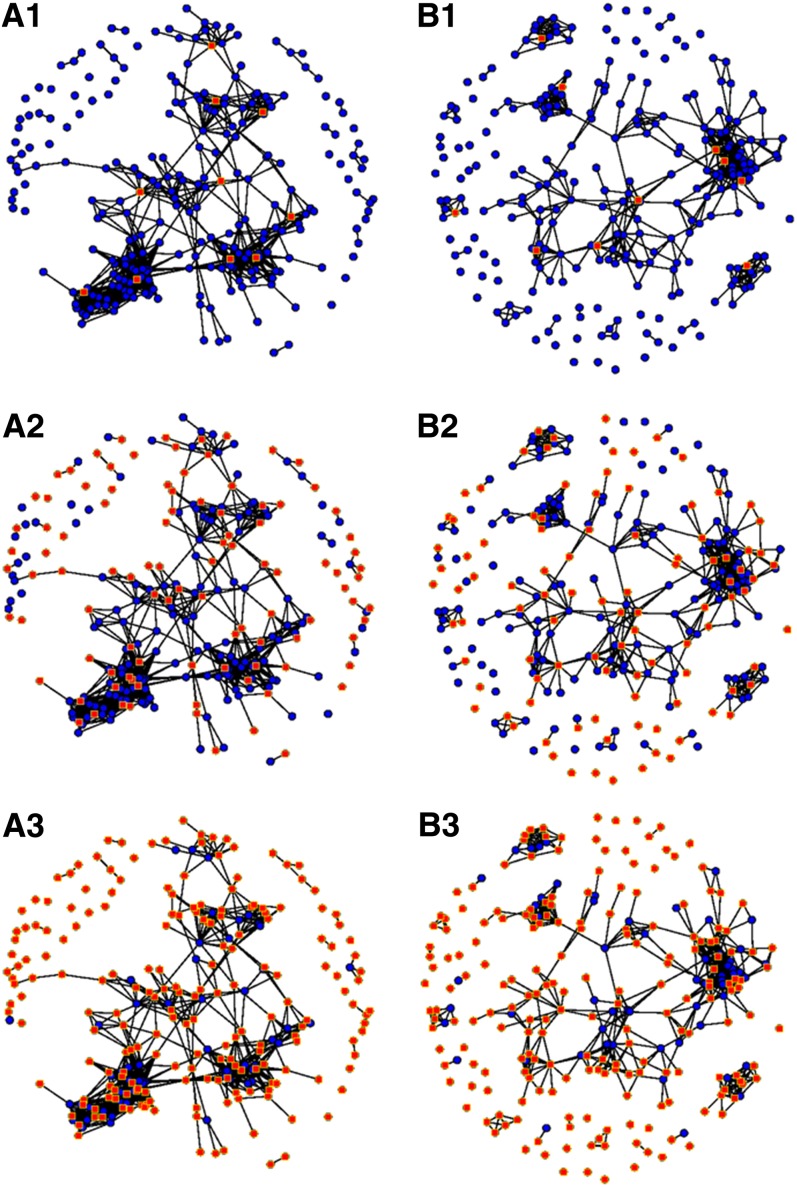
Figure 6 presents pairs of individual with a genomic relationship coefficient >0.2 (A_freq_ij) as linked by an edge. This visual representation gives a global idea of the relationships in the panels: individuals related to others are clustered into groups, while more originals lines are isolated on the graph. When few lines were phenotyped, the algorithm selected individuals representing the biggest clusters. But when the calibration set size was bigger, it was composed of few individuals in the clusters and many isolated individuals. At a given calibration set size, the algorithm selected all the “isolated” lines and few lines in the kinship clusters. When increasing even further the calibration set size, the few individuals that were not in the calibration set were located at the center of the kinship clusters.

Figure 6.

Network representation of the genomic relationship coefficients. (A1, A2, and A3) Dent panel, 3 calibration set sizes: 10 (A1), 100 (A2), and 200 (A3). (B1, B2 and B3) Flint panel, 3 calibration set sizes: 10 (B1), 100 (B2), and 200 (B3). These networks are drawn with a Fruchterman and Reingold’s force-directed placement algorithm. Each node represents an individual; the pairs of individuals with a relationship coefficient >0.2 are linked by an edge. The individuals selected by the CDmean algorithm are represented by red squares and others by blue points.

Discussion

The objective of this study was to maximize the reliability of genomic predictions by optimizing the composition of the calibration set of individuals based on genotypic data only (Figure 1). To do so, we used different criteria that were expected to be related to the reliability of the genomic prediction. These criteria can be used before collecting phenotypic data to optimize the calibration set. The algorithms based on these criteria were tested on two independent panels that included inbred lines of different origins and on three traits with heritabilities ranging from 0.65 to 0.95. There were clear differences of observed reliabilities between the two panels and between the three traits (Figure 3). The limited number of degrees of freedom available for estimating error variance may affect the estimation of heritabilities, which may affect the scale of observed reliabilities for a given panel–trait combination (through the division by h²). The low reliabilities obtained for the Flint panel for DM_Yield may be explained by a combination of (i) low precision of data used for prediction (similar, however, to that of Dent panel for the same trait), (ii) looser pedigree structure than in the Dent panel, and (iii) larger nonadditive effects possibly related to more important plant lodging, which deserve further investigations.

Whatever the differences in reliability range among panel–trait combinations, all the optimization criteria except Amax (the maximum of the relationship coefficients between the reference individuals) increased the observed reliability compared to random sampling.

The only exception to this was PEVmean for intermediate calibration set sizes for DMC in Flint panel. In particular, the approaches based on CDmean and Amean always gave higher reliabilities than random sampling whatever calibration set sizes. For Amean this is in accordance with Pszczola et al. (2012), who showed that the relatedness between the reference individuals and between the candidates and the reference individuals has a strong effect on the accuracy. For calibration sets of reduced size, Amean and CDmean yielded similar reliabilities because they both sampled the less-related individuals. For larger calibration sets, the approach based on CDmean gave better results, which can be explained by the consideration of the whole network of kinship, whereas Amean considers only the mean. CDmean explicitly takes into account the information brought by the experiment.

The optimization based on PEV was one of the most efficient approaches. However, the approach uniquely based on PEV (PEVmean) has two important drawbacks, which can explain why it can sometimes be worse than random sampling (Figure 3): (i) it doesn’t take into account the decrease of genetic variance due to kinship, (ii) and it is highly dependent on the trait heritability. The first point can be neglected if all the individuals are independent. In this case the approaches based on PEVmean and on CDmean are equivalent. But most of the time the individuals considered by breeders are to some extent related, even in diversity panels like those considered in the present study. Not considering these relationship coefficients can lead to biased estimation of accuracy. This can partly explain why the formulas used in animal genetics, which consider the individuals as unrelated, overestimate accuracy compared to what is found by using cross-validation (VanRaden 2008; Hayes et al. 2009c; Pszczola et al. 2012). In the CD calculation, the covariance between the candidate individuals is taken into account by c′Acσ_g², and as a result the reliability is better estimated.

The second point, sensitivity to heritability, is very important because the calibration set is often phenotyped for many traits of interest with different heritability levels. The calibration set has thus to be optimal for a wide range of heritability levels. Both PEV and CD depend on λ, which is directly related to the trait heritability. To test the effect of λ on the different methods, we used the algorithm on Tass_GDD6 with a λ of 1 corresponding to a heritability of 0.5. The reliabilities obtained with CDmean with the two λ values are very close, whereas PEVmean can be less accurate than random sampling if the λ value used for the optimization is different from the true λ (Supporting Information, Figure S1). The robustness of CDmean to variation of heritability is confirmed in Table 2, which shows that if an intermediate value of λ is chosen, the calibration set is close to optimality for a wide range of heritabilities. In fact this second point is related to the first one: the reduction of variance due to relationship is not taken into account in the PEV calculation, which makes it highly dependent on the trait heritability. For example, if the set is optimized by minimizing the PEV with a very low heritability, the calibration set is composed only of highly related individuals (results not shown), whereas if the heritability is high, the calibration set would explore the whole variability of the panel. In the CD calculation the term c′Ac prevents selection of individuals too closely related.

The absence of a clear plateau for CDmean method according to calibration size in Figure 3 leads us to check whether improvement in reliability observed with CDmean-based optimization may be partly explained by the selection of validation sets (the complement to calibration set in our main approach) presenting a broad variation. To address this issue, we performed a different cross-validation procedure on Tass_GDD6. We considered here validation sets determined a priori. In a first step 30 individuals were randomly sampled to define the validation set. In a second step calibration sets were sampled from the remaining individuals at random or using different approaches to optimize the prediction reliability for the validation set. Although a diminishing return according to calibration population size increase was observed, the ranking in methods (Figure S2) was consistent with what was found before (Figure 3). This shows that an increase in reliability for CDmean cannot be attributed mostly to the extraction of an “easy to predict” validation set. We also performed the optimization on the adjusted means of DMC and DM_Yield of each single trial and found consistent results: the different approaches were ranked in the same order except for one trial for which the reliabilities were very low whatever the calibration set size and the method (results not shown).

Previous elements show that CDmean is preferable to PEVmean and is a criterion of choice to predict reliability and to optimize the calibration set. Under our conditions, using the optimized sampling algorithm based on CDmean and using A_freq as variance/covariance matrix, an optimized set of approximately 100 lines can reach the same reliability as random samples of approximately 200 lines. Cost of heavy phenotypic evaluations could therefore be substantially reduced by using an optimized calibration set.

This approach can also be used to estimate the precision of a particular prediction after collecting phenotypic data (Figure 4). This information is important because it would help the breeders to select the best individuals considering not only the best predicted values but also associated reliabilities. This information would also be useful to identify situations in which a complementary sampling of the calibration data set is needed to increase the reliability of the predictions of original individuals that were poorly predicted with the initial calibration set.

When the calibration set is small, it appears that the algorithm based on CDmean samples individuals that are “extreme” on the PCoA representation (Figure 5). As a consequence, the variability explained by the main axes is well captured by the calibration set. When the calibration set is larger, the selected individuals are spread across the whole graph, and they are always separated by a minimum distance. When two individuals are highly related, the algorithm never selects both of them as clearly illustrated by network visualizations (Figure 6). The number of clusters depends on the threshold used to determine if two individuals appear related or not. We used a threshold on A_freq_ij of 0.2 because the clusters of related lines were then clearly visible. When the calibration set is small, the individuals selected are in the biggest clusters. This choice permits reliable prediction of more individuals than if isolated lines were selected. If the calibration set becomes larger, both isolated and linked individuals are selected. It can be explained by the fact that when the clusters are represented by a sufficient number of phenotyped individuals, it brings more information to phenotype an isolated individual than an additional one in the clusters. At a certain calibration set size, the only lines that are not in the calibration set are in the center of the clusters. These lines are among the most typical of each group; they are also the most easily predicted when many genetically close lines are phenotyped.

In addition to these general trends, we showed that the selection of the reference individuals by the approaches based on CDmean or PEVmean depends on the method used to estimate the variance/covariance matrix. This relationship matrix should reflect the variance/covariance between individuals at the QTL positions. It is thus possible that the best formula with which to estimate A is not the same for different traits, according to the weight that is given to the markers. The use of A_freq instead of A_IBS slightly increased the observed reliability of the predictions. It shows that A_freq gave better estimates of the relationship coefficient between individuals than A_IBS, at least with our data. In the case of highly polygenic traits, we consider that the QTL are spread on the whole genome, and so we use markers covering the whole genome to estimate the variance/covariance matrix. We need a number of markers high enough to have at least one marker in high linkage disequilibrium (LD) with each QTL. Goddard et al. (2011) showed that an incomplete coverage of the genome by markers can be a cause of overestimation of the accuracy. CDmean and PEVmean could be subject to this bias because we used a variance/covariance matrix estimated with markers to calculate these criteria. Goddard et al. (2011) proposed calculating a variance/covariance matrix based on the genomic relationship matrix and on the pedigree to predict accuracy without bias. In our case the pedigree was not available and so we could not use their correction. However, our marker density compared to LD was such that a risk of having an important bias was limited.

The approaches we proposed were tested on two independent diversity panels and three traits and globally consistent results were obtained. It would be interesting to test these approaches on other types of populations, in particular in the presence of strong population structure. We have considered here two heterotic groups separately. It may be interesting to test the approach to optimizing samples including lines of different heterotic groups, with the objective of obtaining accurate predictions across and within heterotic groups. It would then be required to have an important coverage of the genome to capture ancestral LD, otherwise the reliability would be overestimated as discussed before. Breeders are also interested in applying genomic selection in multifamilial populations (Albrecht et al. 2011; Zhao et al. 2012). Albrecht et al. (2011) showed that in such situations the prediction reliabilities are highly dependent on the composition of the calibration set. In particular, if few families are not represented in the calibration set, the observed reliabilities are lower than if few individuals are sampled in each family. Optimizing the calibration set therefore deserves specific attention in this case. CDmean could be used to optimize the sampling if the proper contrasts are considered: between each individual and its family mean, between each individual and the mean of the population, and between each family. These questions deserve consideration in future studies. Our study was based on diversity panels, and we could not evaluate how the reliability would evolve across the next generations derived from these materials. This aspect also has to be studied, because the gain of time due to selection on predicted values instead of phenotypic observations is the main interest of genomic selection. It would therefore be important to evaluate how often the prediction formula must be recalibrated.

Finally, although displaying contrasted heritabilities and possibly different contribution of nonadditive effects (see above), the three traits considered here are known to be highly polygenic (see Chardon et al. 2004 and Buckler et al. 2009 for Tass_GDD6), which justified the choice of the RA–BLUP model. For traits depending on major genes, this model might be inappropriate or nonoptimal and it may be preferable to use Bayesian or neural network models (Jannink et al. 2010). Our optimization criterion is based on the BLUP theory and so would be inappropriate if major genes are involved. It is, however, possible that CDmean would also be to some extent useful in increasing the reliability of Bayesian methods. It would be interesting to derive a similar criterion from the Bayesian theory to predict reliability before collecting phenotypes.